A Cross-Estimation Method for Spaceborne Synthetic Aperture Radar Range Antenna Pattern Using Pseudo-Invariant Natural Scenes
Abstract
:1. Introduction
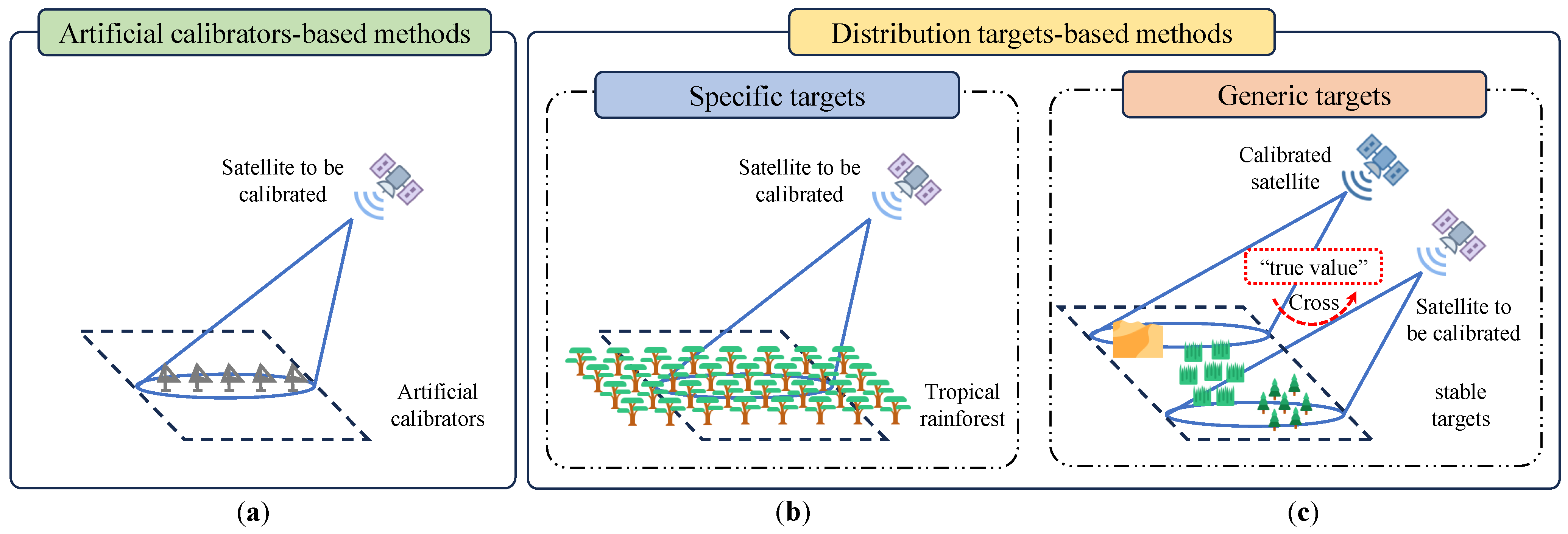
- Selection of Stable Reference Targets: To ensure that the backscattering values derived from calibrated SAR images can be used as reference values for the uncalibrated SAR images, the reference targets need to satisfy two criteria. The first is temporal stability, which ensures the consistency of the overpass times of the two SAR satellites. The second is spatial stability, which aims to minimize the influence of registration errors following image alignment [6]. This study proposes a method for selecting reference targets for relative radiometric cross-calibration, assessing spatial uniformity and stability using standard deviations, and evaluating temporal stability through amplitude correlation between the two SAR images. Targets that meet both criteria are selected as reference targets.
- Registration of Heterogeneous SAR Images: Uncalibrated satellite images exhibit amplitude imbalances in the range direction compared to calibrated images [7,8]. Classic image registration methods cannot achieve accurate alignment in this context. This study proposes a refined registration method based on iterative estimation, which uses the coarse estimated antenna pattern to minimize the impact of amplitude imbalance in uncalibrated images on registration. The uncalibrated antenna pattern gain is obtained by calculating the average power of each range direction in the overlapping area of the two satellite images, and a coarse estimate of the antenna pattern is fitted. The maximum correlation coefficient method is then used to achieve pixel-level registration between the calibrated satellite image and the uncalibrated satellite image, which has been compensated using the coarse estimated antenna pattern. A more accurate estimation of the range-direction antenna pattern is achieved using precisely registered images.
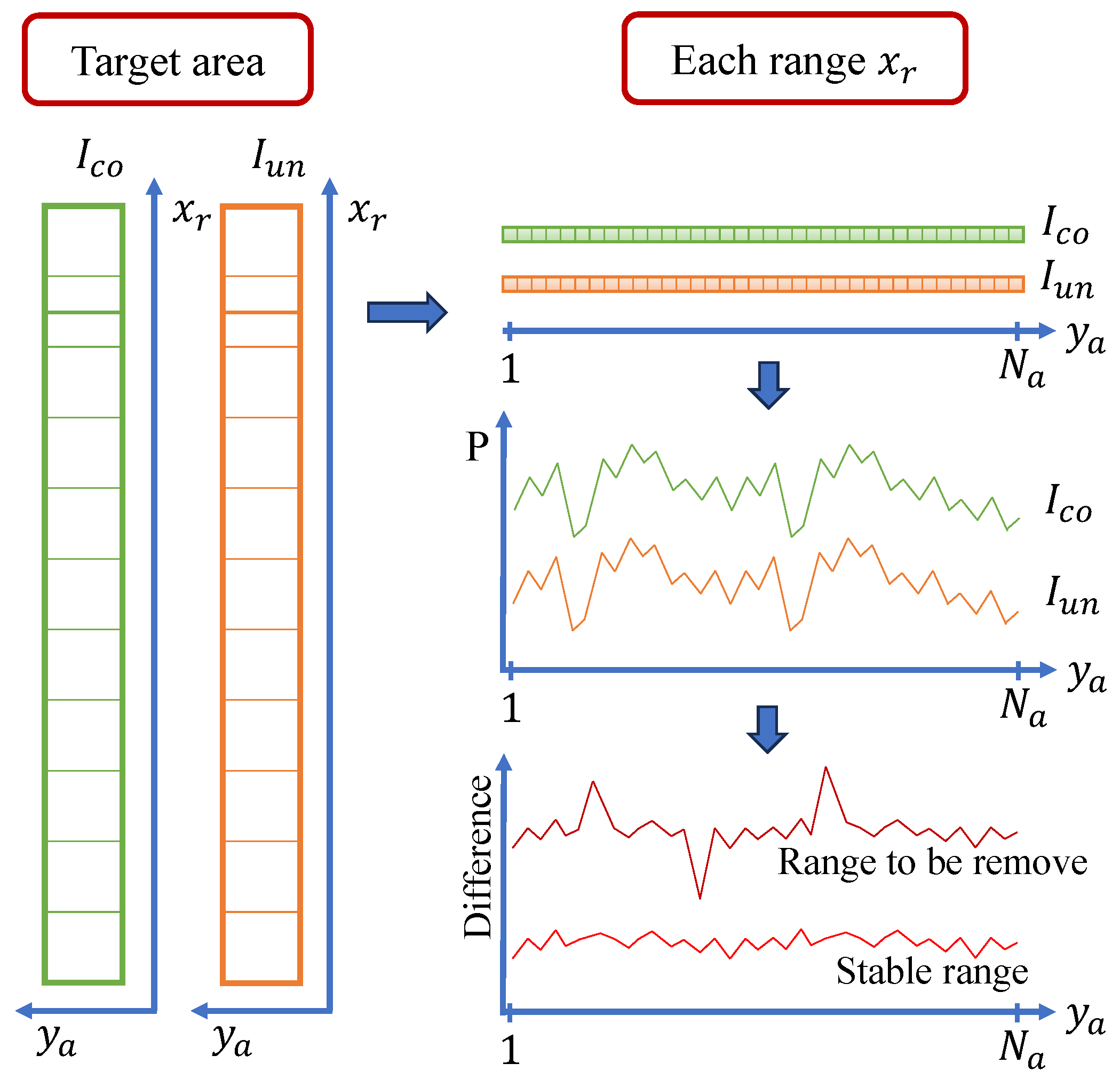
- Extraction of Range-Direction Stable Power: SAR relative radiometric calibration requires calibrating the non-uniform gain variations caused by the antenna pattern. Sufficient sampling across the entire range direction is needed for accurate estimation while avoiding interference from strong noise and other outliers. Current SAR absolute radiometric cross-calibration methods use artificial stable targets [9] or stable points from homogeneous natural surfaces [10], but these stable points only provide limited range sampling. This study proposes a method for extracting stable power to support cross-estimating range antenna patterns. The standard deviation of power differences for corresponding pixels in the two images is calculated for each range, and the images are segmented into multiple subsets along the range direction. Range power values with relatively low standard deviations are selected within each subset, and the mean power of these values is taken as the stable power.
- A method for selecting target regions for cross-estimating antenna patterns is proposed, identifying temporally and spatially stable targets as calibration scenes for SAR range antenna pattern cross-estimation. This method addresses the issue of the current lack of reference target selection methods for antenna pattern estimation.
- A method for fine registration of heterogeneous SAR images based on iterative estimation is proposed, enabling pixel-level alignment of the reference SAR image and the uncalibrated SAR image in the cross-estimation of range antenna patterns. This approach addresses the significant amplitude differences between two SAR satellites caused by radiometric imbalance in the uncalibrated satellite, thereby facilitating precise image registration.
- A method for extracting stable power in the range direction based on difference screening is presented, significantly reducing the impact of outliers in SAR images while ensuring sufficient sampling across the entire range. This approach achieves accurate extraction of stable power values, improving the accuracy of antenna pattern fitting.
2. Related Work
3. Methodology
3.1. Cross-Estimation Model
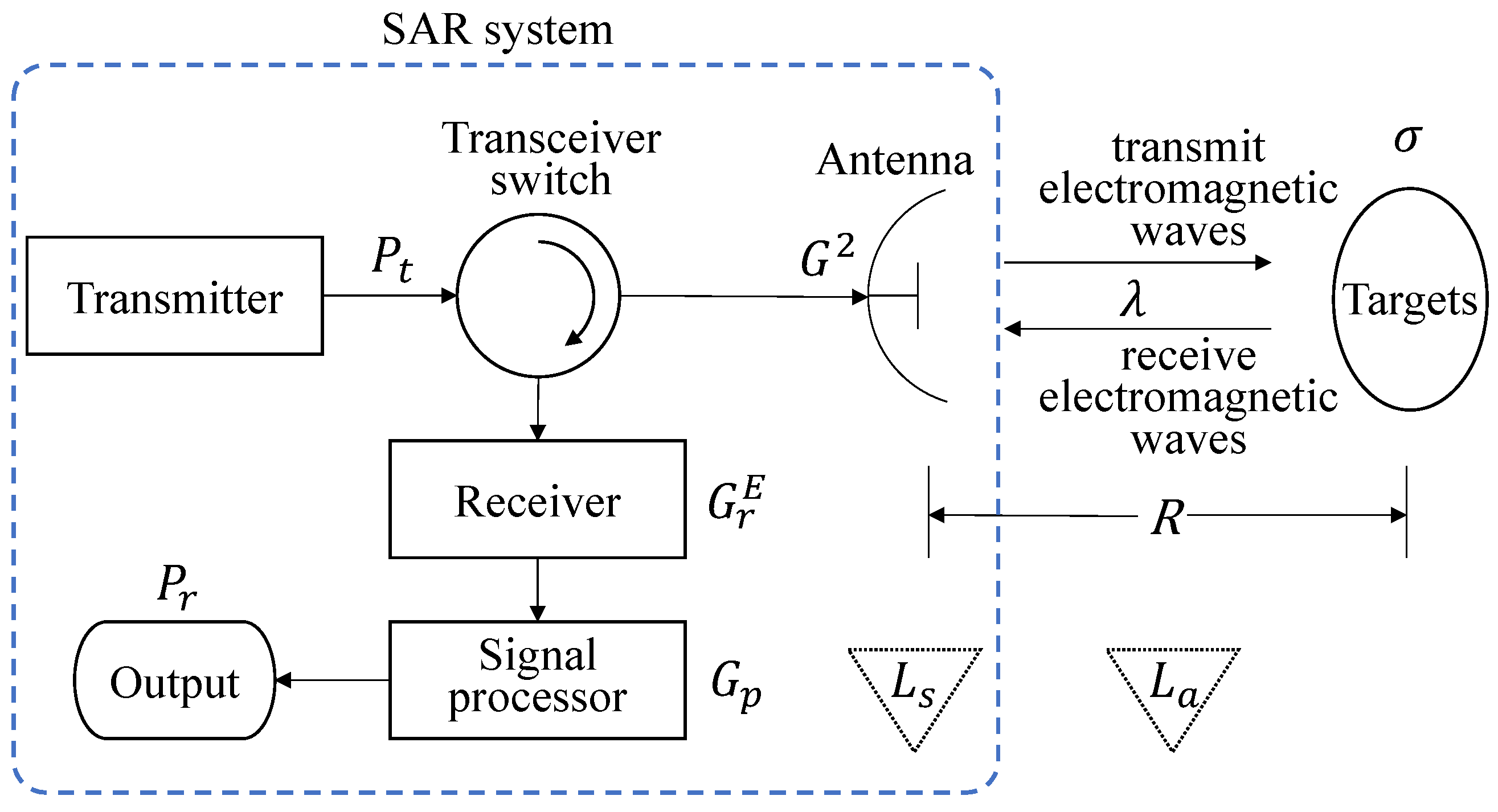
3.1.1. The Received Power of the Uncalibrated SAR Satellite Without Antenna Pattern Correction Derived from the Radar Equation
3.1.2. The Received Power of the Calibrated SAR with Antenna Pattern Correction Derived from the Radar Equation
3.1.3. A Constant Coefficient Independent of the Elevation Angle
3.2. Methodological Process
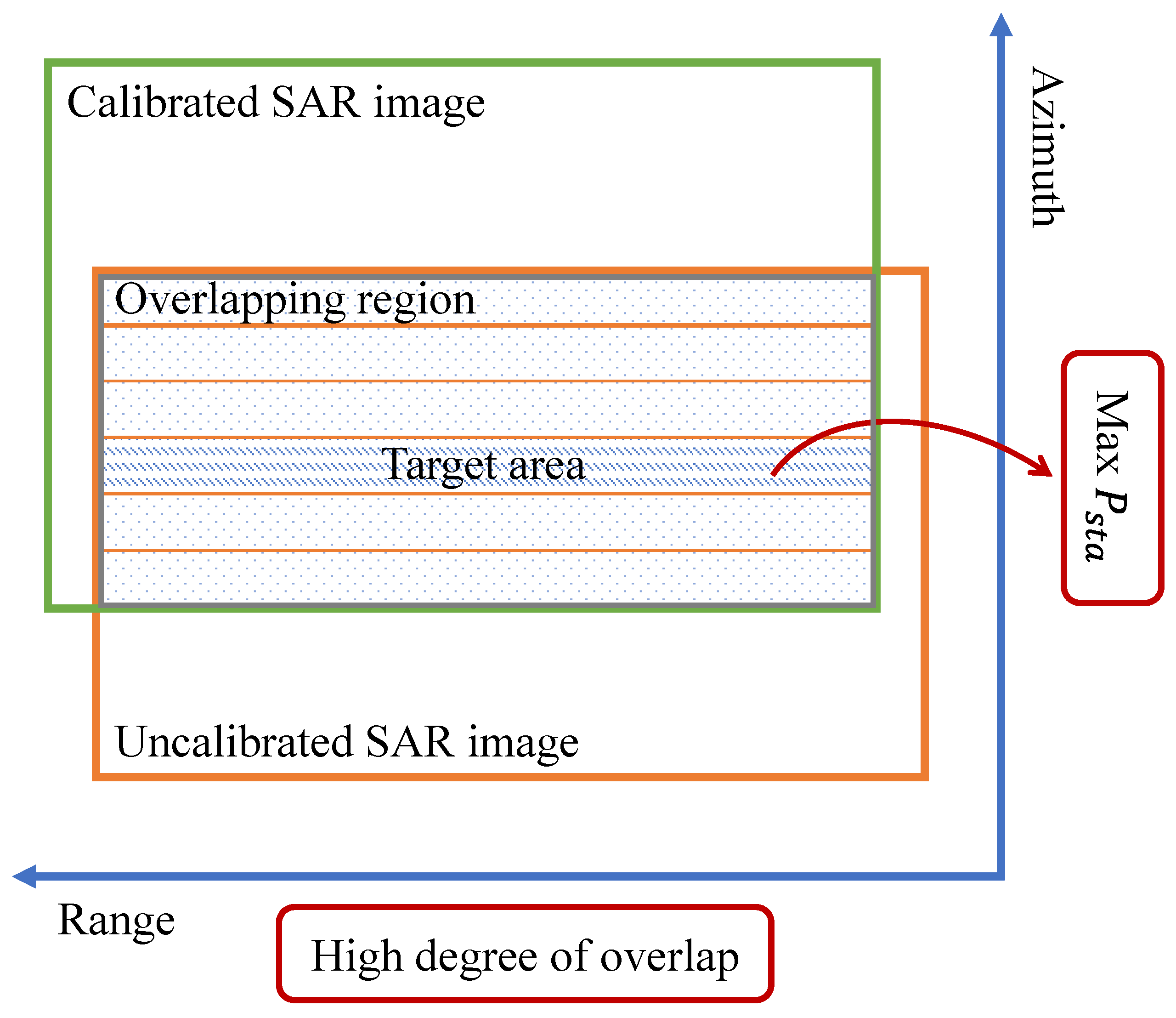
3.2.1. Selection of Cross-Estimation Target Areas
3.2.2. Registration of Target Region Images
3.2.3. Stable Power Value Extraction and Total Gain Calculation
3.2.4. Antenna Pattern Fitting
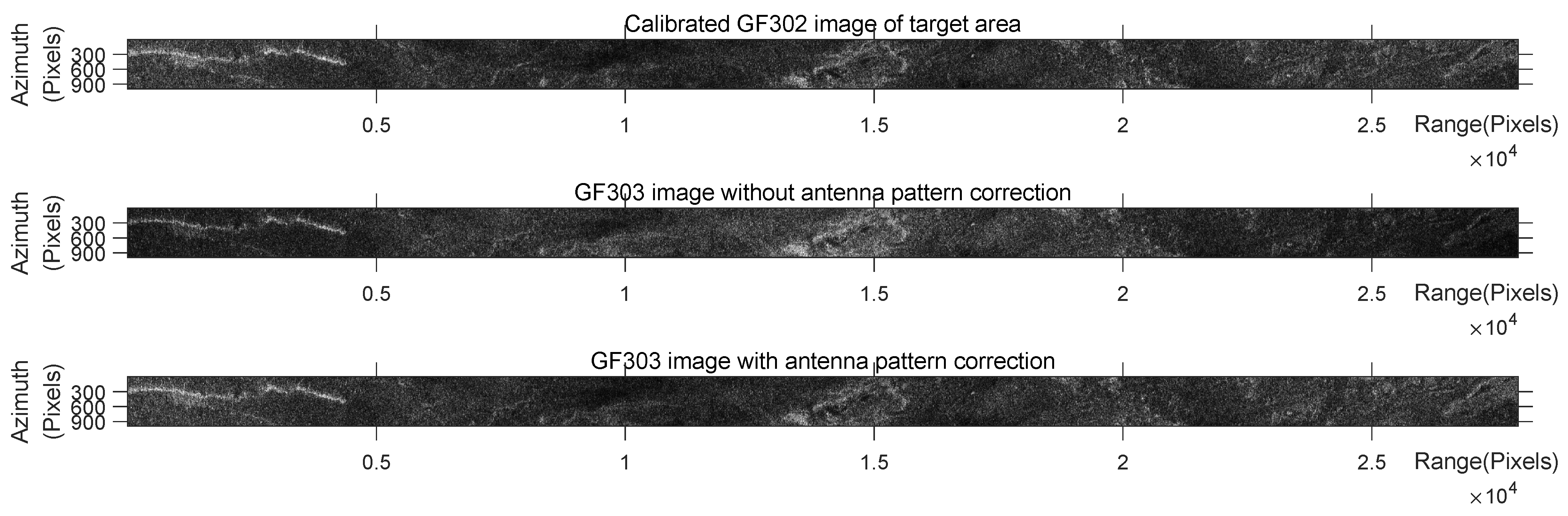
3.2.5. Antenna Pattern Correction
4. Experiment and Discussion
4.1. Experimental Data
4.2. Experimental Results
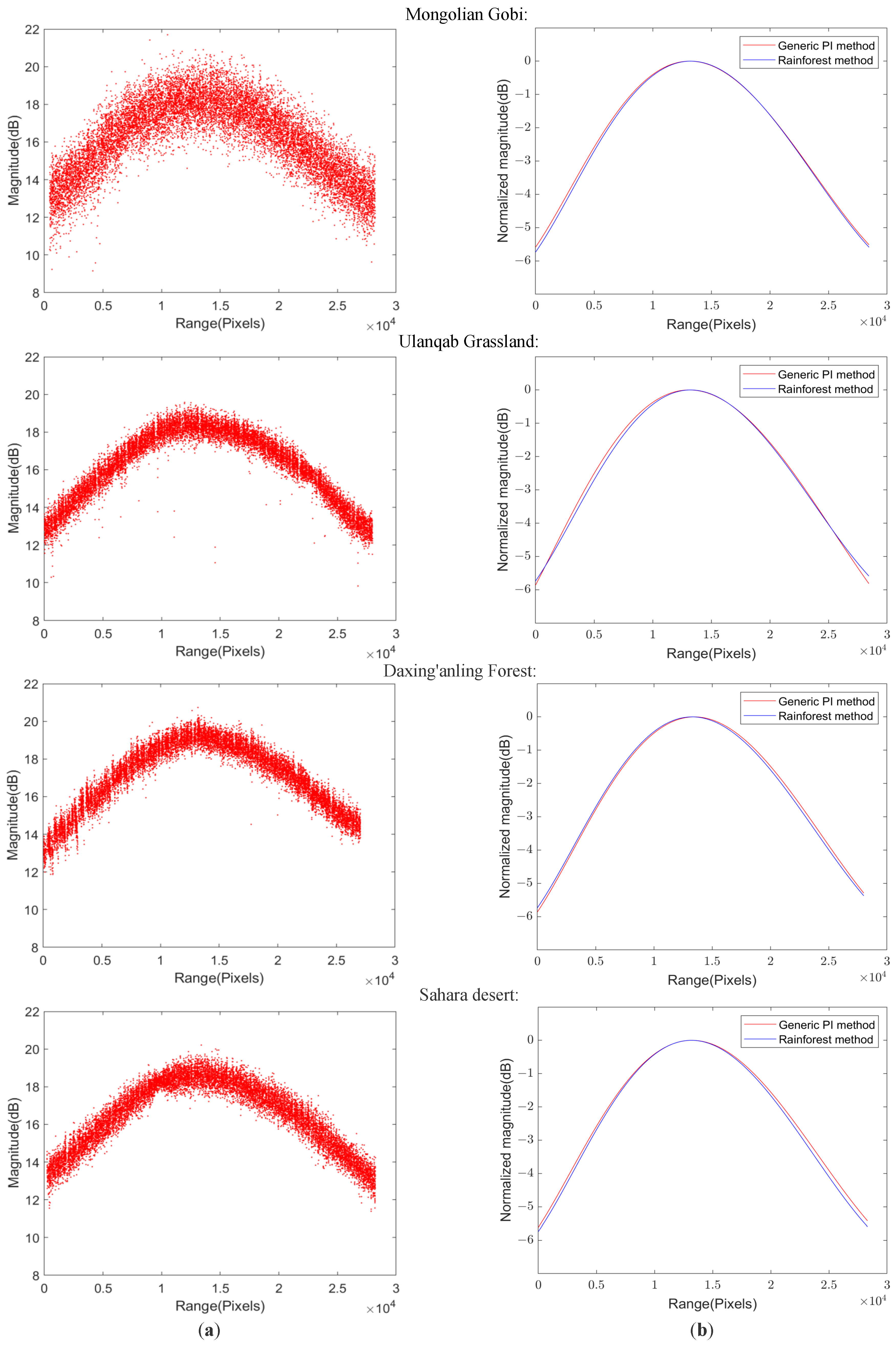
4.2.1. Analysis of Applicability Across Different Scenes
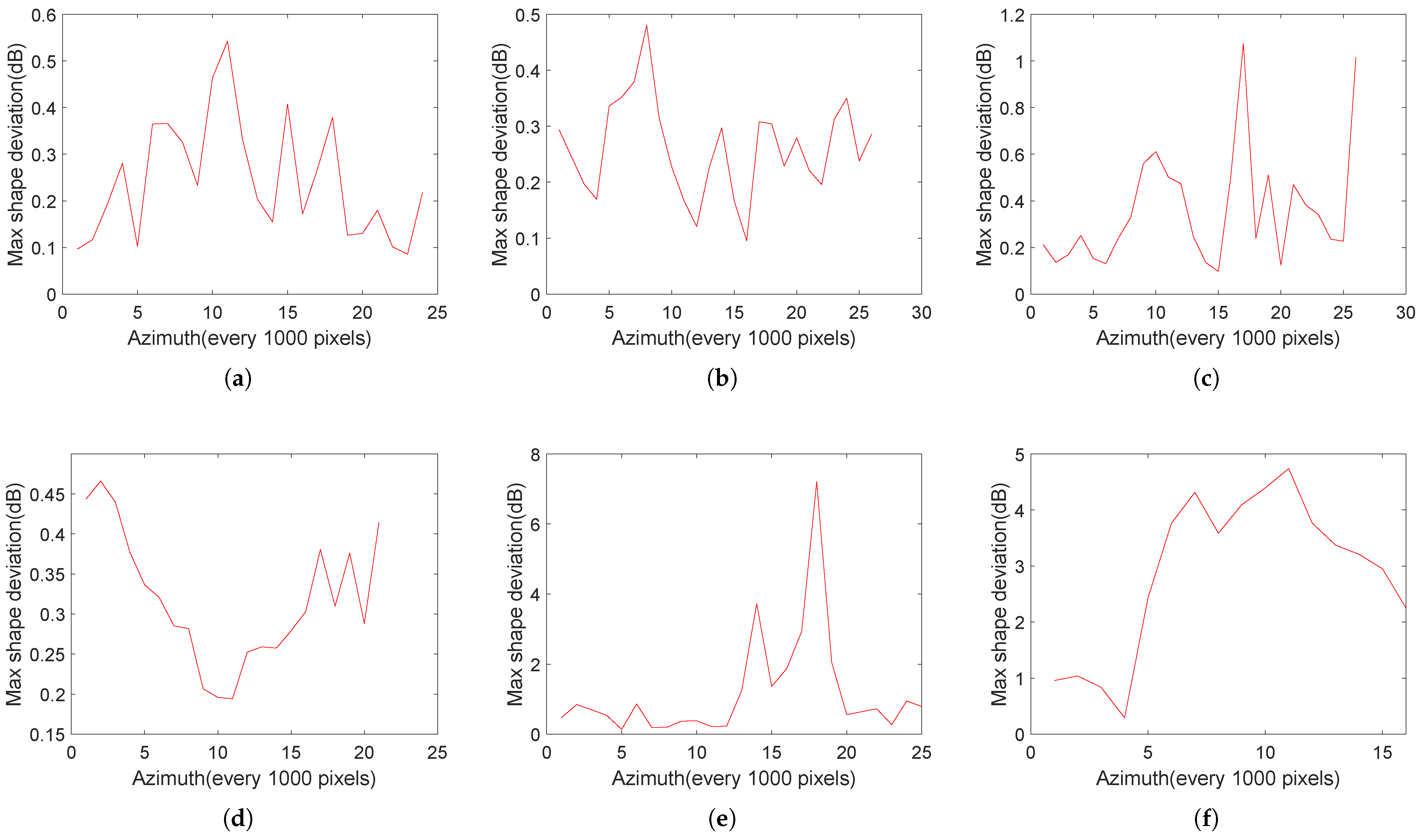
4.2.2. Impact of Fine Registration on Estimation Accuracy
4.2.3. Impact of Stable Range Power Extraction on Estimation Accuracy
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Curlander, J.C.; McDonough, R.N. Synthetic Aperture Radar: Systems and Signal Processing; Wiley: New York, NY, USA, 1991; Volume 11. [Google Scholar]
- Ossowska, A.; Kim, J.H.; Wiesbeck, W. Influence of mechanical antenna distortions on the performance of the HRWS SAR system. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 2152–2155. [Google Scholar] [CrossRef]
- Su, X.; Li, D.; Ye, S.; Ma, Y.; Cui, Z.; Ouyang, S. Structure design and thermal deformation simulation of spaceborne SAR antenna. In Proceedings of the 2021 2nd China International SAR Symposium (CISS), Shanghai, China, 3–5 November 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Ji, L.; Wang, H. Analysis of On-orbit Thermal Deformation of Flexible SAR Antenna. In Proceedings of the 2021 2nd China International SAR Symposium (CISS), Shanghai, China, 3–5 November 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Seifert, P.; Blötscher, H. Preparatory investigations concerning the calibration of spaceborne SAR-systems. In Proceedings of the IGARSS 1991: Proceedings of the 11th Annual International Geoscience and Remote Sensing Symposium, Espoo, Finland, 3–6 June 1991; Volume 3, pp. 1381–1384. [Google Scholar] [CrossRef]
- Eriksson, L.E.; Demchev, D.; Hildeman, A.; Dierking, W. Alignment of L-and C-band SAR images for enhanced observations of sea ice. In Proceedings of the IGARSS 2022–2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 3798–3801. [Google Scholar] [CrossRef]
- Bachmann, M.; Schwerdt, M.; Bräutigam, B. Accurate Antenna Pattern Modeling for Phased Array Antennas in SAR Applications—Demonstration on TerraSAR-X. Int. J. Antennas Propag. 2009, 2009, 492505. [Google Scholar] [CrossRef]
- Li, H.; Zhang, H.; Chen, Q.; Gao, Y.; Shi, X.; Zhang, L. Accuracy analysis of radiometric calibration in-orbit for SuperView Neo-2 SAR satellite. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2024, 17, 2234–2244. [Google Scholar] [CrossRef]
- Zakharov, A.; Zherdev, P.; Sokolov, A. Intercalibration of ERS AMI and ENVISAT ASAR with ground-based parabolic antennas. In Proceedings of the Envisat & ERS Symposium, Salzburg, Austria, 6–10 September 2004; pp. 6–10. [Google Scholar]
- Zhou, Y.; Zhuang, L.; Duan, J.; Zhang, F.; Hong, W. Synthetic aperture radar radiometric cross calibration based on distributed targets. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2022, 15, 9599–9612. [Google Scholar] [CrossRef]
- Dobson, M.C.; Ulaby, F.T.; Brunfeldt, D.R.; Held, D.N. External calibration of SIR-B imagery with area-extended and point targets. IEEE Trans. Geosci. Remote. Sens. 1986, GE-24, 453–461. [Google Scholar] [CrossRef]
- Shen, Y.; Klein, J.; Freeman, A. Tone generators in SAR applications. In Proceedings of the 10th Annual International Symposium on Geoscience and Remote Sensing, College Park, MD, USA, 20–24 May 1990; p. 1121. [Google Scholar]
- Seifert, P.; Lentz, H.; Zink, M.; Heel, F. Ground-based measurements of inflight antenna patterns for imaging radar systems. IEEE Trans. Geosci. Remote. Sens. 1992, 30, 1131–1136. [Google Scholar] [CrossRef]
- Thompson, A.A.; Racine, D.; Luscombe, A.P. RADARSAT2 antenna calibration using Ground Receivers/Transmitters. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; Volume 3, pp. 1465–1467. [Google Scholar]
- Moore, R.K.; Hemmat, M. Determination of the vertical pattern of the SIR-B antenna. Int. J. Remote. Sens. 1988, 9, 839–847. [Google Scholar] [CrossRef]
- Hawkins, R.K. Determination of antenna elevation pattern for airborne SAR using the rough target approach. IEEE Trans. Geosci. Remote. Sens. 1990, 28, 896–905. [Google Scholar] [CrossRef]
- Freeman, A.; Alves, M.; Chapman, B.; Cruz, J.; Kim, Y.; Shaffer, S.; Sun, J.; Turner, E.; Sarabandi, K. SIR-C data quality and calibration results. IEEE Trans. Geosci. Remote. Sens. 1995, 33, 848–857. [Google Scholar] [CrossRef]
- Shimada, M.; Freeman, A. A technique for measurement of spaceborne SAR antenna patterns using distributed targets. IEEE Trans. Geosci. Remote. Sens. 1995, 33, 100–114. [Google Scholar] [CrossRef]
- Fang, Y.; Moore, R.K. Inflight vertical antenna patterns for SIR-C from Amazon rain-forest observations. Remote. Sens. Environ. 1997, 59, 407–414. [Google Scholar] [CrossRef]
- Lukowski, T.; Hawkins, R.; Cloutier, C.; Wolfe, J.; Teany, L.; Srivastava, S.; Banik, B.; Jha, R.; Adamovic, M. RADARSAT elevation antenna pattern determination. In Proceedings of the IGARSS’97. 1997 IEEE International Geoscience and Remote Sensing Symposium Proceedings. Remote Sensing—A Scientific Vision for Sustainable Development, Singapore, 3–8 August 1997; Volume 3, pp. 1382–1384. [Google Scholar] [CrossRef]
- Moore, R.K.; Rediawan, H. Further analysis of SIR-C antenna patterns for radiometric corrections: Use of new calibration areas. In Proceedings of the IGARSS’99. IEEE 1999 International Geoscience and Remote Sensing Symposium, Hamburg, Germany, 28 June–2 July 1999; Volume 1, pp. 437–439. [Google Scholar] [CrossRef]
- Zink, M.; Rosich, B. Antenna elevation pattern estimation from rain forest acquisitions. In Proceedings of the SAR Workshop on Calibration/Validation, London, UK, 24–26 September 2003; Volume 526, p. 11. [Google Scholar]
- Yun, R.; Guo, W.; Wei, M. Algorithm for radiometric calibration of satellite-borne SAR in the Amazon rainforest. Radar Sci. Technol. 2007, 5, 139–143. [Google Scholar]
- Jiang, S.; Qiu, X.; Han, B.; Hu, W. A quality assessment method based on common distributed targets for GF-3 polarimetric SAR data. Sensors 2018, 18, 807. [Google Scholar] [CrossRef]
- Shi, L.; Li, P.; Yang, J.; Zhang, L.; Ding, X.; Zhao, L. Polarimetric SAR calibration and residual error estimation when corner reflectors are unavailable. IEEE Trans. Geosci. Remote. Sens. 2020, 58, 4454–4471. [Google Scholar] [CrossRef]
- Semunegus, H.; Berg, W.; Bates, J.J.; Knapp, K.R.; Kummerow, C. An extended and improved Special Sensor Microwave Imager (SSM/I) period of record. J. Appl. Meteorol. Climatol. 2010, 49, 424–436. [Google Scholar] [CrossRef]
- Kamei, A.; Nakamura, K.; Yamamoto, H.; Nakamura, R.; Tsuchida, S.; Yamamoto, N.; Sekiguchi, S.; Kato, S.; Liu, C.C.; Hsu, K.H.; et al. Cross Calibration of Formosat-2 Remote Sensing Instrument (RSI) Using Terra Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER). IEEE Trans. Geosci. Remote. Sens. 2012, 50, 4821–4831. [Google Scholar] [CrossRef]
- Angal, A.; Xiong, X.; Shrestha, A. Cross-calibration of MODIS reflective solar bands with Sentinel 2A/2B MSI instruments. IEEE Trans. Geosci. Remote. Sens. 2020, 58, 5000–5007. [Google Scholar] [CrossRef]
- Gross, G.; Helder, D.; Leigh, L. Extended Cross-Calibration Analysis Using Data from the Landsat 8 and 9 Underfly Event. Remote. Sens. 2023, 15, 1788. [Google Scholar] [CrossRef]
- Xie, Y.; Feng, D.; Shao, W.; Han, J.; Chen, Y. Radiometric Cross-Calibration of HY-1C/COCTS Based on Sentinel-3/OLCI. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2024, 17, 10422–10431. [Google Scholar] [CrossRef]
- Chander, G.; Hewison, T.J.; Fox, N.; Wu, X.; Xiong, X.; Blackwell, W.J. Overview of intercalibration of satellite instruments. IEEE Trans. Geosci. Remote. Sens. 2013, 51, 1056–1080. [Google Scholar] [CrossRef]
- Cao, C.; Xiong, X.; Wu, A.; Wu, X. Assessing the consistency of AVHRR and MODIS L1B reflectance for generating fundamental climate data records. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Miesch, C.; Cabot, F.; Briottet, X.; Henry, P.J. Assimilation of satellite data over the Sahara desert for intercalibration of optical satellite sensors. In Proceedings of the Sensors, Systems, and Next-Generation Satellites V. SPIE, Toulouse, France, 17–21 September 2001; Volume 4540, pp. 469–475. [Google Scholar]
- Angal, A.; Xiong, X.; Thome, K.; Wenny, B.N. Cross-calibration of Terra and Aqua MODIS using RadCalNet. IEEE Geosci. Remote. Sens. Lett. 2020, 18, 188–192. [Google Scholar] [CrossRef]
- Zink, M.; Olivier, P.; Freeman, A. Cross-calibration between airborne SAR sensors. IEEE Trans. Geosci. Remote. Sens. 1993, 31, 237–245. [Google Scholar] [CrossRef]
- Chen, X.; Zhou, Y.; Ma, F.; Yin, Q.; Zhang, F. Optimized selection of pseudo-invariant calibration sites for radiometric cross-calibration of spaceborne SAR sensors. In Proceedings of the 2023 SAR in Big Data Era (BIGSARDATA), Beijing, China, 20–22 September 2023; pp. 1–4. [Google Scholar]
- Zhou, Y.; Yang, B.; Yin, Q.; Ma, F.; Zhang, F. Improved SAR Radiometric Cross-Calibration Method Based on Scene-Driven Incidence Angle Difference Correction and Weighted Regression. IEEE Trans. Geosci. Remote. Sens. 2024, 62, 1–16. [Google Scholar] [CrossRef]
- Mahafza, B.R. Radar Systems Analysis and Design Using MATLAB; Chapman and Hall/CRC: New York, Ny, USA, 2005. [Google Scholar] [CrossRef]
- Mladenova, I.E.; Jackson, T.J.; Bindlish, R.; Hensley, S. Incidence Angle Normalization of Radar Backscatter Data. IEEE Trans. Geosci. Remote. Sens. 2013, 51, 1791–1804. [Google Scholar] [CrossRef]
- Torres, R.; Navas-Traver, I.; Bibby, D.; Lokas, S.; Snoeij, P.; Rommen, B.; Osborne, S.; Ceba-Vega, F.; Potin, P.; Geudtner, D. Sentinel-1 SAR system and mission. In Proceedings of the 2017 IEEE Radar Conference (RadarConf), Seattle, WA, USA, 8–12 May 2017; pp. 1582–1585. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, F.; Tian, B.; Liang, D.; Yang, A. High-Frequency Glacial Lake Mapping Using Time Series of Sentinel-1A/1B SAR Imagery: An Assessment for the Southeastern Tibetan Plateau. Int. J. Environ. Res. Public Health 2020, 17, 1072. [Google Scholar] [CrossRef]
- Oh, Y.; Sarabandi, K.; Ulaby, F.T. An empirical model and an inversion technique for radar scattering from bare soil surfaces. IEEE Trans. Geosci. Remote. Sens. 1992, 30, 370–381. [Google Scholar] [CrossRef]
- Oh, Y.; Kweon, S.K.; Hwang, J.H. Soil moisture retrieval from single-polarized measurements of well-calibrated radars for bare soil surfaces. In Proceedings of the Conference Proceedings of 2013 Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Tsukuba, Japan, 23–27 September 2013; pp. 45–48. [Google Scholar]
- Feng, Y.; Lei, Z.; Tong, X.; Xi, M.; Li, P. An improved geometric calibration model for spaceborne SAR systems with a case study of large-scale Gaofen-3 images. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2022, 15, 6928–6942. [Google Scholar] [CrossRef]
- Mu, M.; Li, Z.; Xu, B.; He, X.; Han, K.; Du, X.; Han, Q.; Wang, A. LT-1A/B Satellite SAR Geometric Calibration and Absolute Location Error Analysis. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2024, 17, 16497–16510. [Google Scholar] [CrossRef]
- Kim, J.; Fessler, J.A. Intensity-based image registration using robust correlation coefficients. IEEE Trans. Med. Imaging 2004, 23, 1430–1444. [Google Scholar] [CrossRef]
- Evangelidis, G.D.; Psarakis, E.Z. Parametric image alignment using enhanced correlation coefficient maximization. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 1858–1865. [Google Scholar] [CrossRef]
- Luo, D.; Wu, Y.; Chen, Y.; Yuan, Z.; Liu, Y. An improved ORB image matching algorithm based on phase correlation method. Electron. Qual. 2023, 8, 22–26. [Google Scholar] [CrossRef]
- Huang, J.; Chen, J.; Guo, Y.; Wang, P. Analysis and Correction of Antenna Pattern Effects in AMAO Spaceborne SAR Images. Remote. Sens. 2022, 14, 2141. [Google Scholar] [CrossRef]


| Method | Reference Target | Operating Complexity | Cost | Imaging Swath | Accuracy | Frequency |
|---|---|---|---|---|---|---|
| Artificial calibrator method | Artificial calibrators | Complex | High | Narrow | High | Low |
| Tropical rainforest method | Stable tropical rainforests | Simple | Low | Wide | Medium | Low |
| The proposed method | Generic pseudo-invariant scene | Medium | Low | Wide | Medium | High |
| Groups | Scene | Satellite | Acquisition Time | Latitude and Longitude |
|---|---|---|---|---|
| a | Mongolian Gobi | GF302 | 3 June 2023 | 43.5445°N, 108.1588°E |
| GF303 | 2 June 2023 | 43.4320°N, 108.1407°E | ||
| b | Ulanqab Grassland | GF302 | 16 October 2023 | 42.7768°N, 112.1318°E |
| GF303 | 15 October 2023 | 42.7666°N, 112.1479°E | ||
| c | Daxing’anling Forest | GF302 | 22 May 2024 | 52.4663°N, 114.9489°E |
| GF303 | 21 May 2024 | 52.5037°N, 114.9751°E | ||
| d | Sahara desert | GF302 | 22 December 2023 | 24.0124°N, 0.7805°W |
| GF303 | 21 December 2023 | 23.7720°N, 0.7393°W | ||
| e | Nam Lake | GF302 | 30 December 2023 | 30.9049°N, 90.7801°E |
| GF303 | 29 December 2023 | 30.8587°N, 90.8072°E | ||
| f | Yellow Sea | GF302 | 19 May 2024 | 32.8141°N, 123.9271°E |
| GF303 | 18 May 2024 | 32.3250°N, 124.0477°E | ||
| g | Amazon rainforest | GF303 | 29 June 2023 | 1.4180°S, 72.1038°W |
| Scene | Gobi | Grassland | Forest | Desert |
|---|---|---|---|---|
| Max shape deviation | <0.12 dB | <0.11 dB | <0.14 dB | <0.17 dB |
| Scene | Max Shape Deviation (Not Fine Registration) | Max Shape Deviation (Fine Registration) |
|---|---|---|
| Gobi | 0.2378 dB | 0.1166 dB |
| Grassland | 0.2113 dB | 0.1099 dB |
| Forest | 0.2860 dB | 0.1317 dB |
| Desert | 0.2879 dB | 0.1694 dB |
| On average | 0.2558 dB | 0.1319 dB |
| Scene | Max Shape Deviation (No Stable Power Extraction) | Max Shape Deviation (Stable Power Extraction) |
|---|---|---|
| Gobi | 0.1581 dB | 0.1350 dB |
| Grassland | 0.1352 dB | 0.1207 dB |
| Forest | 0.1949 dB | 0.1655 dB |
| Desert | 0.2205 dB | 0.1859 dB |
| On average | 0.1772 dB | 0.1518 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, C.; Duan, J.; Zhou, Y.; Teng, F.; Zhang, F.; Hong, W. A Cross-Estimation Method for Spaceborne Synthetic Aperture Radar Range Antenna Pattern Using Pseudo-Invariant Natural Scenes. Remote Sens. 2025, 17, 1459. https://doi.org/10.3390/rs17081459
Xu C, Duan J, Zhou Y, Teng F, Zhang F, Hong W. A Cross-Estimation Method for Spaceborne Synthetic Aperture Radar Range Antenna Pattern Using Pseudo-Invariant Natural Scenes. Remote Sensing. 2025; 17(8):1459. https://doi.org/10.3390/rs17081459
Chicago/Turabian StyleXu, Chuanzeng, Jitong Duan, Yongsheng Zhou, Fei Teng, Fan Zhang, and Wen Hong. 2025. "A Cross-Estimation Method for Spaceborne Synthetic Aperture Radar Range Antenna Pattern Using Pseudo-Invariant Natural Scenes" Remote Sensing 17, no. 8: 1459. https://doi.org/10.3390/rs17081459
APA StyleXu, C., Duan, J., Zhou, Y., Teng, F., Zhang, F., & Hong, W. (2025). A Cross-Estimation Method for Spaceborne Synthetic Aperture Radar Range Antenna Pattern Using Pseudo-Invariant Natural Scenes. Remote Sensing, 17(8), 1459. https://doi.org/10.3390/rs17081459









