Spatial and Temporal Characteristics of Mesoscale Eddies in the North Atlantic Ocean Based on SWOT Mission
Abstract
1. Introduction
2. Study Area
3. Data and Methods
3.1. Data Sources
3.2. Identification Method of Mesoscale Eddies
- (1)
- The shape test allows a maximum shape error of 55 percent, where the shape error is defined as the ratio of the deviation area between the eddy and the fitted circle to the area of the fitted circle. The center of the fitted circle is considered the recognized center of the eddy, and the area is equivalent to the region enclosed by the outermost closed contour of the eddy;
- (2)
- The influence range of a mesoscale eddy includes at least 4 pixels and at most 1000 pixels, where each pixel in this study corresponds to a size of 1/8° × 1/8°;
- (3)
- Starting from the maximum (for AE) or minimum (for CE) ADT value, the ADT contours are identified outward in 0.2 cm increments to determine whether they are closed, continuing until the edge of the mesoscale eddy is found;
- (4)
- Each AE or CE is required to have a single maximum (for AE) or minimum (for CE) ADT, i.e., only one center is allowed per eddy;
- (5)
- The amplitude (A) of the eddy must satisfy cm, where amplitude is defined as the difference in ADT between the eddy center and the outermost closed contour.
3.3. Tracking Method of Mesoscale Eddies
3.4. Relevant Parameters and Calculation Methods
3.5. Filtering Method
4. Experimental Result
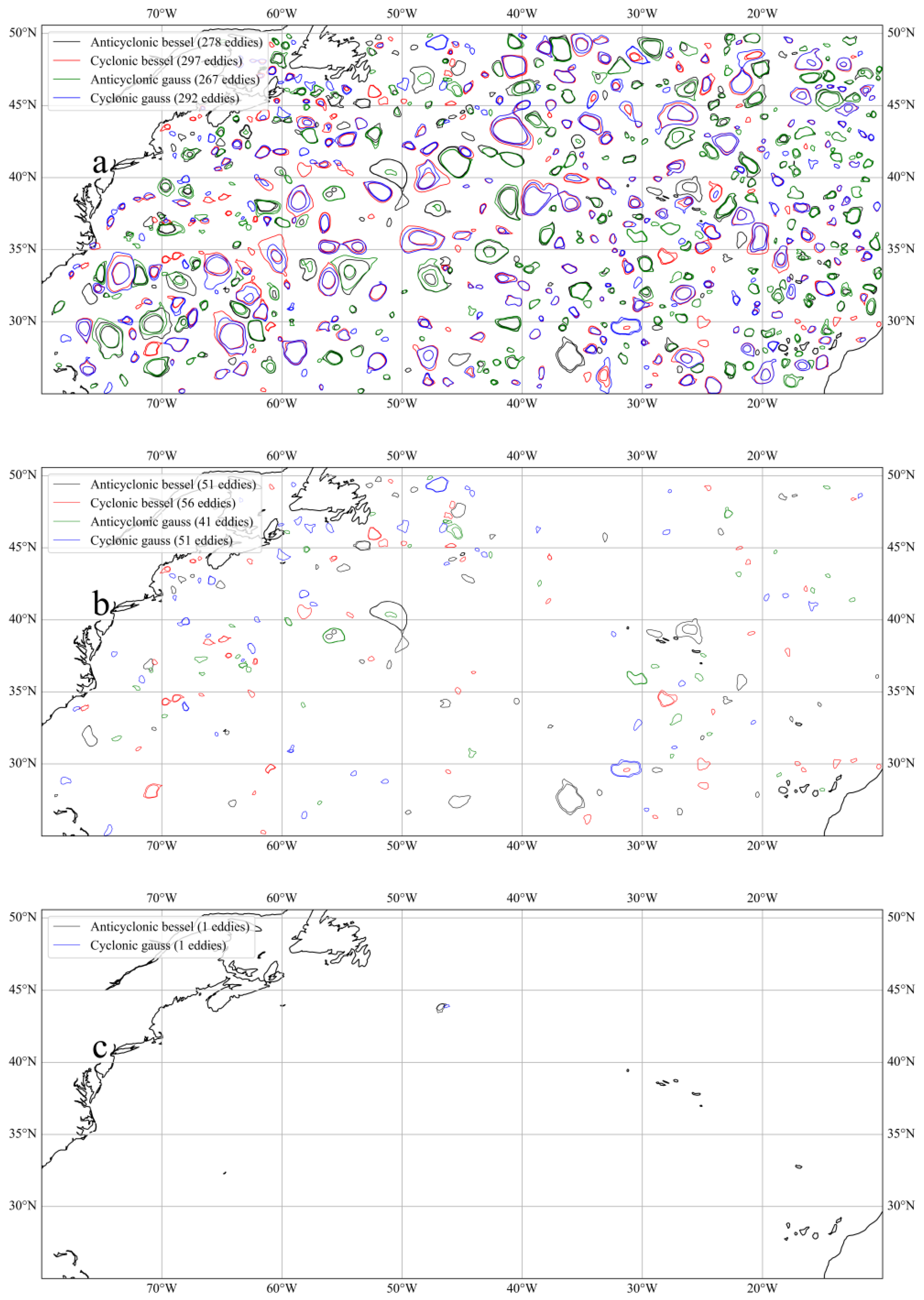
4.1. Single-Day Eddy Characteristics Identified at Different Filter Wavelengths
4.2. Characteristics of Long-Term Dynamic Parameters at Different Filter Wavelengths
4.3. Eddy Trajectory Analysis
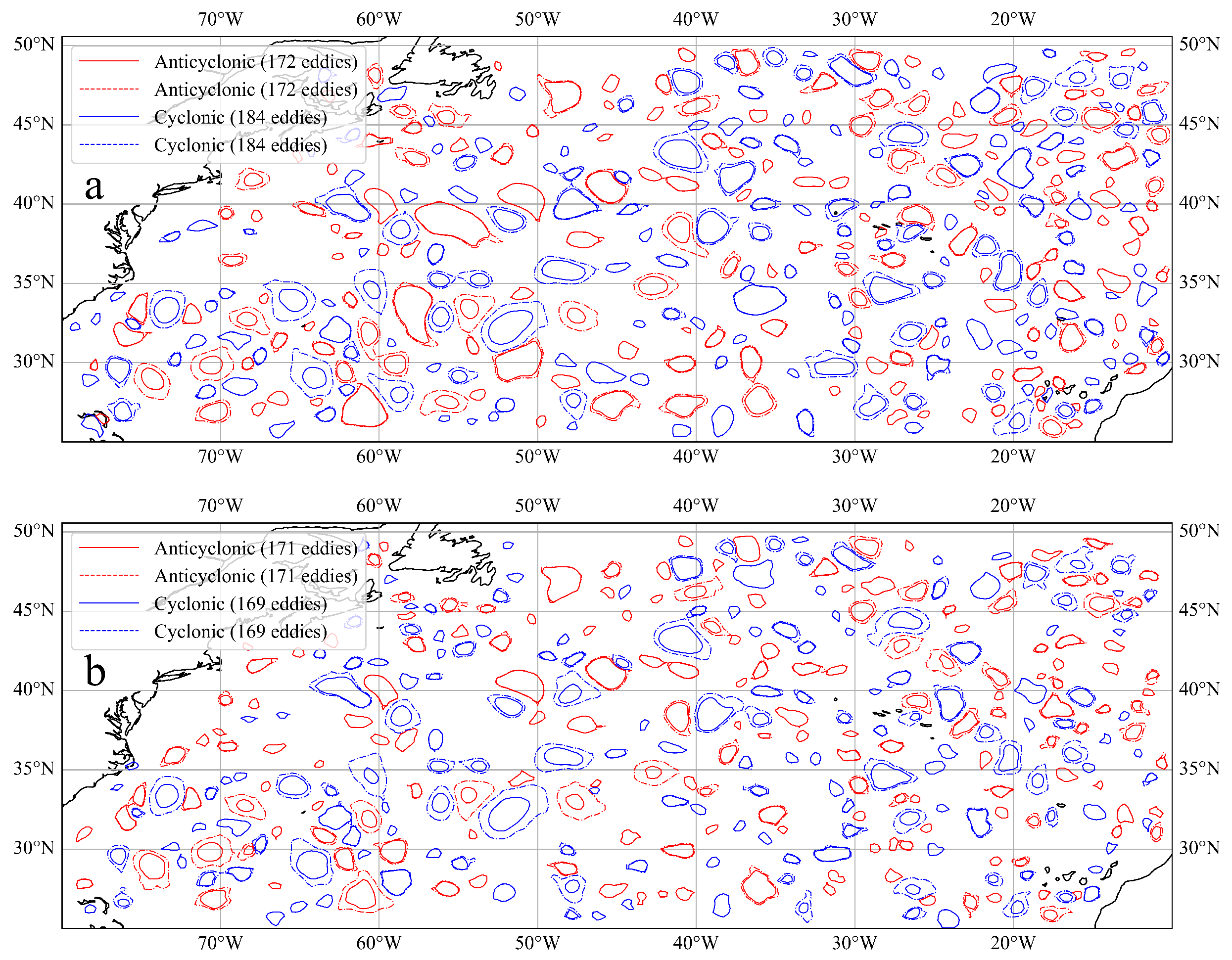
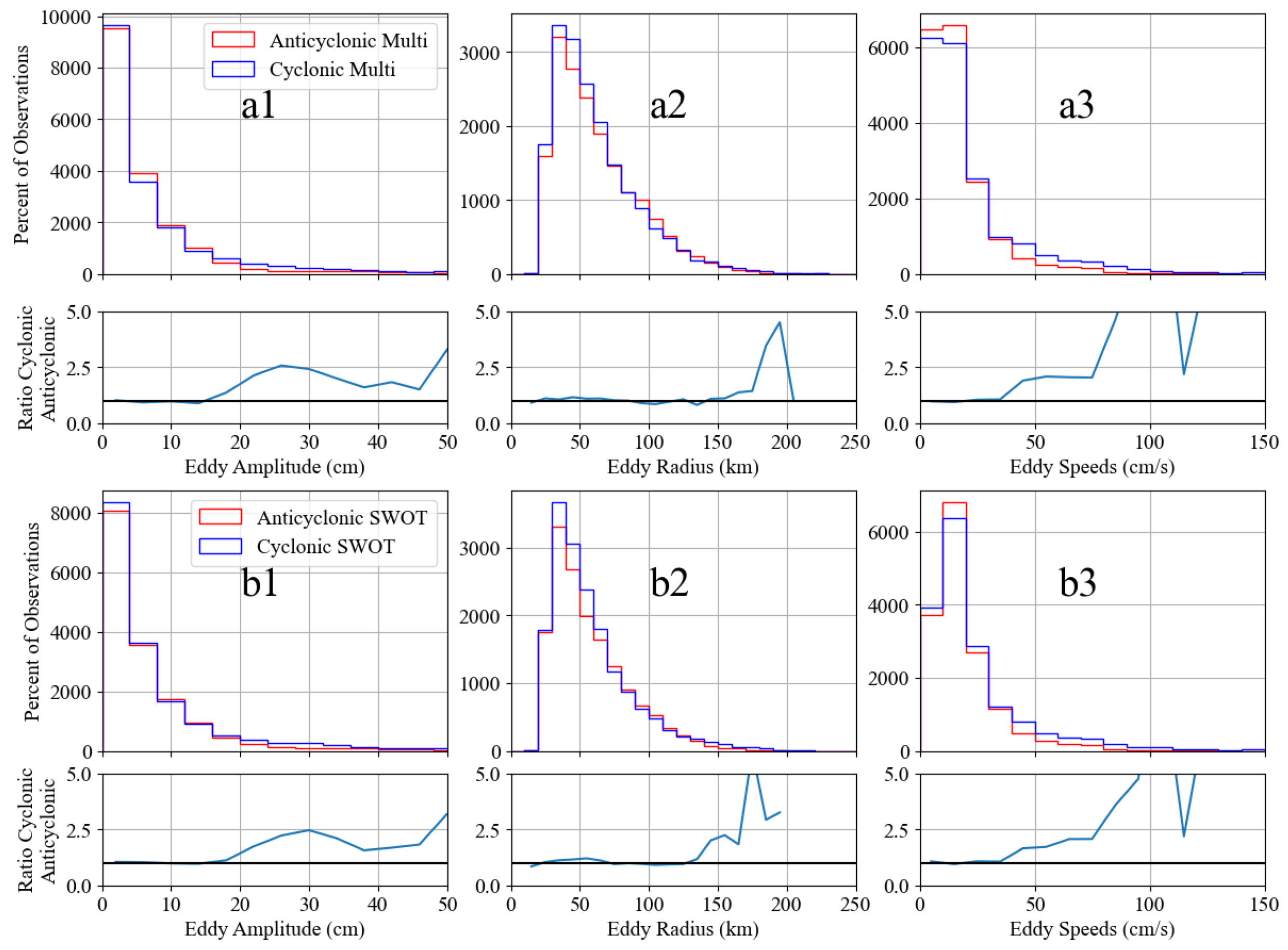
5. Comparison of Eddy Detection from Different Data Sources
6. Discussions
6.1. Influence of Different Filters on Eddy Identification
6.2. The Influence of Submarine Topography on Eddy Identification
6.3. Limitations and Future Directions
7. Conclusions
- (1)
- The energy of mesoscale eddies primarily originates from the instabilities of strong boundary currents. As the filter wavelength decreases, the number of identified CE and AE eddies increases; however, the ratio between them consistently remains close to 1.1:1. At different filter wavelengths, the distribution characteristics of the dynamic parameters for cyclonic and anticyclonic eddies are generally similar, predominantly concentrated in the ranges of small amplitude, small radius, and low rotation velocity. With a decrease in filter wavelength, the range of eddy dynamic parameters becomes narrower, and the number of CEs with large amplitude, large radius, and high rotation velocity becomes more prominent. At the same filter wavelength, the dynamic parameters of eddies identified using different filters are broadly consistent, although minor differences in aspects such as position and size can be observed.
- (2)
- Based on the eddy identification results over a period of 117 days, the majority of mesoscale eddies have lifetimes ranging from 7 to 21 days, with those exhibiting larger amplitudes and effective radii tending to have longer lifetimes. In contrast, smaller eddies generally have shorter lifetimes. Strong mesoscale eddies with lifetimes exceeding 45 days are more likely to form extended trajectories. These long-lived eddies are primarily concentrated in regions of strong circulation and high EKE in the North Atlantic. In comparison, eddies located farther from strong current regions exhibit lower EKE, slower propagation speeds, and shorter trajectories.
- (3)
- This study confirms the exceptional capability of SWOT data in accurately capturing small- and medium-scale eddies. As SWOT satellite observational data continue to accumulate, its role in elucidating multi-scale ocean dynamic processes will be further enhanced, providing critical support for an in-depth understanding of ocean dynamic mechanisms.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| TAO | the tropical Atlantic Ocean |
| NA | the North Atlantic |
| GS | the Gulf Stream |
| SSH | Sea surface high |
| SWOT | Surface Water and Ocean Topography |
| PET | py-eddy-tracker |
| EKE | Eddy kinetic energy |
| CE | Cyclonic eddies |
| AE | Anticyclonic eddies |
| T/P | Topex/Poseidon |
| POP | Parallel Ocean Program |
| SST | Sea surface temperature |
| SSH | Sea surface height |
| KaRIn | Ka-band Radar Interferometer |
| ADT | Absolute dynamic topography |
| OW | Okubo–Weiss |
| WA | Winding angle |
References
- Feng, S.; Li, F.; Li, S. Introduction to Marine Science; Higher Education Press: Beijing, China, 1999. (In Chinese) [Google Scholar]
- Beckmann, A.; Böning, C.W.; Brügge, B.; Stammer, D. On the generation and role of eddy variability in the central North Atlantic Ocean. J. Geophys. Res. Ocean. 1994, 99, 20381–20391. [Google Scholar] [CrossRef]
- Sasaki, H.; Klein, P.; Qiu, B.; Sasai, Y. Impact of oceanic-scale interactions on the seasonal modulation of ocean dynamics by the atmosphere. Nat. Commun. 2014, 5, 5636. [Google Scholar] [CrossRef]
- Klein, P.; Lapeyre, G.; Siegelman, L.; Qiu, B.; Fu, L.L.; Torres, H.; Su, Z.; Menemenlis, D.; Le Gentil, S. Ocean-scale interactions from space. Earth Space Sci. 2019, 6, 795–817. [Google Scholar] [CrossRef]
- McGillicuddy, D.J., Jr.; Anderson, L.A.; Bates, N.R.; Bibby, T.; Buesseler, K.O.; Carlson, C.A.; Davis, C.S.; Ewart, C.; Falkowski, P.G.; Goldthwait, S.A.; et al. Eddy/wind interactions stimulate extraordinary mid-ocean plankton blooms. Science 2007, 316, 1021–1026. [Google Scholar] [CrossRef]
- Chelton, D.B.; Gaube, P.; Schlax, M.G.; Early, J.J.; Samelson, R.M. The Influence of Nonlinear Mesoscale Eddies on Near-Surface Oceanic Chlorophyll. Science 2011, 334, 328–332. [Google Scholar] [CrossRef]
- Dong, C.; McWilliams, J.C.; Liu, Y.; Chen, D. Global heat and salt transports by eddy movement. Nat. Commun. 2014, 5, 3294. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, W.; Qiu, B. Oceanic mass transport by mesoscale eddies. Science 2014, 345, 322–324. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Tian, J.; Qiu, B.; Zhao, W.; Chang, P.; Wu, D.; Wan, X. Observed 3D structure, generation, and dissipation of oceanic mesoscale eddies in the South China Sea. Sci. Rep. 2016, 6, 24349. [Google Scholar] [CrossRef]
- Fu, L.L.; Alsdorf, D.; Morrow, R.; Rodriguez, E.; Mognard, N. SWOT: The Surface Water and Ocean Topography Mission. Wide-Swath Altimetric Elevation on Earth; Technical Report; NASA Jet Propulsion Laboratory: Pasadena, CA, USA, 2012.
- Stammer, D. Global characteristics of ocean variability estimated from regional TOPEX/POSEIDON altimeter measurements. J. Phys. Oceanogr. 1997, 27, 1743–1769. [Google Scholar] [CrossRef]
- Brokaw, R.J.; Subrahmanyam, B.; Trott, C.B.; Chaigneau, A. Eddy surface characteristics and vertical structure in the Gulf of Mexico from satellite observations and model simulations. J. Geophys. Res. Ocean. 2020, 125, e2019JC015538. [Google Scholar] [CrossRef]
- Zhu, Y.; Liang, X. Characteristics of Eulerian mesoscale eddies in the Gulf of Mexico. Front. Mar. Sci. 2022, 9, 1087060. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, C.; McGillicuddy, D.J., Jr.; Liu, Y.; Barnes, B.B.; Kourafalou, V.H. Mesoscale eddies in the Gulf of Mexico: A three-dimensional characterization based on global HYCOM. Deep. Sea Res. Part II Top. Stud. Oceanogr. 2024, 215, 105380. [Google Scholar] [CrossRef]
- Aguedjou, H.; Dadou, I.; Chaigneau, A.; Morel, Y.; Alory, G. Eddies in the Tropical Atlantic Ocean and their seasonal variability. Geophys. Res. Lett. 2019, 46, 12156–12164. [Google Scholar] [CrossRef]
- Ioannou, A.; Speich, S.; Laxenaire, R. Characterizing mesoscale eddies of eastern upwelling origins in the Atlantic Ocean and their role in offshore transport. Front. Mar. Sci. 2022, 9, 835260. [Google Scholar] [CrossRef]
- Kang, D.; Curchitser, E.N. Gulf Stream eddy characteristics in a high-resolution ocean model. J. Geophys. Res. Ocean. 2013, 118, 4474–4487. [Google Scholar] [CrossRef]
- Waseda, T.; Mitsudera, H.; Taguchi, B.; Yoshikawa, Y. On the eddy-Kuroshio interaction: Evolution of the mesoscale eddy. J. Geophys. Res. Ocean. 2002, 107, 3-1–3-9. [Google Scholar] [CrossRef]
- Abdalla, S.; Kolahchi, A.A.; Ablain, M.; Adusumilli, S.; Bhowmick, S.A.; Alou-Font, E.; Amarouche, L.; Andersen, O.B.; Antich, H.; Aouf, L.; et al. Altimetry for the future: Building on 25 years of progress. Adv. Space Res. 2021, 68, 319–363. [Google Scholar] [CrossRef]
- Woodworth, P.L.; Menéndez, M. Changes in the mesoscale variability and in extreme sea levels over two decades as observed by satellite altimetry. J. Geophys. Res. Ocean. 2015, 120, 64–77. [Google Scholar] [CrossRef]
- Yu, Y.; Sandwell, D.; Gille, S. Seasonality of the sub-mesoscale to mesoscale Sea Surface variability from multi-year satellite altimetry. J. Geophys. Res. Ocean. 2023, 128, e2022JC019486. [Google Scholar] [CrossRef]
- Stammer, D.; Böning, C.W. Generation and distribution of mesoscale eddies in the North Atlantic Ocean. In The Warm Watersphere of the North Atlantic Ocean; Bornträger: Berlin, Germany, 1996. [Google Scholar]
- Stammer, D.; Wunsch, C. Temporal changes in eddy energy of the oceans. Deep. Sea Res. Part II Top. Stud. Oceanogr. 1999, 46, 77–108. [Google Scholar] [CrossRef]
- Brachet, S.; Le Traon, P.Y.; Le Provost, C. Mesoscale variability from a high-resolution model and from altimeter data in the North Atlantic Ocean. J. Geophys. Res. Ocean. 2004, 109. [Google Scholar] [CrossRef]
- Qiu, B.; Nakano, T.; Chen, S.; Klein, P. Bi-directional energy cascades in the Pacific Ocean from equator to subarctic gyre. Geophys. Res. Lett. 2022, 49, e2022GL097713. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Y.; Qiu, B.; Luo, Y.; Cai, W.; Yuan, Q.; Liu, Y.; Zhang, H.; Liu, H.; Miao, M.; et al. Submesoscale inverse energy cascade enhances Southern Ocean eddy heat transport. Nat. Commun. 2023, 14, 1335. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Miao, M.; Qiu, B.; Tian, J.; Jing, Z.; Chen, G.; Chen, Z.; Zhao, W. Submesoscale eddies detected by SWOT and moored observations in the Northwestern Pacific. Geophys. Res. Lett. 2024, 51, e2024GL110000. [Google Scholar] [CrossRef]
- Fu, L.L.; Ubelmann, C. On the transition from profile altimeter to swath altimeter for observing global ocean surface topography. J. Atmos. Ocean. Technol. 2014, 31, 560–568. [Google Scholar] [CrossRef]
- Tchonang, B.C.; Benkiran, M.; Le Traon, P.Y.; Jan van Gennip, S.; Lellouche, J.M.; Ruggiero, G. Assessing the impact of the assimilation of swot observations in a global high-resolution analysis and forecasting system–part 2: Results. Front. Mar. Sci. 2021, 8, 687414. [Google Scholar] [CrossRef]
- Fu, L.L.; Pavelsky, T.; Cretaux, J.F.; Morrow, R.; Farrar, J.T.; Vaze, P.; Sengenes, P.; Vinogradova-Shiffer, N.; Sylvestre-Baron, A.; Picot, N.; et al. The surface water and ocean topography mission: A breakthrough in radar remote sensing of the ocean and land surface water. Geophys. Res. Lett. 2024, 51, e2023GL107652. [Google Scholar] [CrossRef]
- Chester, D.; Malanotte-Rizzoli, P.; Lynch, J.; Wunsch, C. The eddy radiation field of the Gulf Stream as measured by ocean acoustic tomography. Geophys. Res. Lett. 1994, 21, 181–184. [Google Scholar] [CrossRef]
- Stommel, H. The Gulf Stream: A Physical and Dynamical Description; University of California Press: Berkeley, CA, USA, 2023. [Google Scholar]
- Fofonoff, N. The Gulf Stream. In Evolution of Physical Oceanography: Scientific Surveys in Honor of Henry Stommel; MIT Press: Cambridge, MA, USA, 1981; pp. 112–139. [Google Scholar]
- Rossby, T. The North Atlantic Current and surrounding waters: At the crossroads. Rev. Geophys. 1996, 34, 463–481. [Google Scholar] [CrossRef]
- Mason, E.; Pascual, A.; McWilliams, J.C. A new sea surface height–based code for oceanic mesoscale eddy tracking. J. Atmos. Ocean. Technol. 2014, 31, 1181–1188. [Google Scholar] [CrossRef]
- Yongchui, Z.; Ning, W.; Lin, Z.; Kefeng, L.; Haodi, W. The surface and three-dimensional characteristics of mesoscale eddies: A review. Adv. Earth Sci. 2020, 35, 568. [Google Scholar]
- Chaigneau, A.; Gizolme, A.; Grados, C. Mesoscale eddies off Peru in altimeter records: Identification algorithms and eddy spatio-temporal patterns. Prog. Oceanogr. 2008, 79, 106–119. [Google Scholar] [CrossRef]
- Chaigneau, A.; Eldin, G.; Dewitte, B. Eddy activity in the four major upwelling systems from satellite altimetry (1992–2007). Prog. Oceanogr. 2009, 83, 117–123. [Google Scholar] [CrossRef]
- Meng, W.; Yanwei, Z.; Zhifei, L.; Jiawang, W. Temporal and spatial characteristics of mesoscale eddies in the northern South China Sea: Statistics analysis based on altimeter data. Adv. Earth Sci. 2019, 34, 1069. [Google Scholar]
- Sorrentino, R. Electronic Filter Simulation & Design; McGraw-Hill Professional: New York, NY, USA, 2007. [Google Scholar]
- Robinson, A.R. Eddies in Marine Science; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Le Traon, P.Y.; Rouquet, M.C.; Boissier, C. Spatial scales of mesoscale variability in the North Atlantic as deduced from Geosat data. J. Geophys. Res. Ocean. 1990, 95, 20267–20285. [Google Scholar] [CrossRef]
- Jacobs, G.; Barron, C.; Rhodes, R. Mesoscale characteristics. J. Geophys. Res. Ocean. 2001, 106, 19581–19595. [Google Scholar] [CrossRef]
- Faghmous, J.H.; Frenger, I.; Yao, Y.; Warmka, R.; Lindell, A.; Kumar, V. A daily global mesoscale ocean eddy dataset from satellite altimetry. Sci. Data 2015, 2, 1–16. [Google Scholar] [CrossRef]
- Dong, C.; Liu, L.; Nencioli, F.; Bethel, B.J.; Liu, Y.; Xu, G.; Ma, J.; Ji, J.; Sun, W.; Shan, H.; et al. The near-global ocean mesoscale eddy atmospheric-oceanic-biological interaction observational dataset. Sci. Data 2022, 9, 436. [Google Scholar] [CrossRef]
- Roden, G.I. Effect of seamounts and seamount chains on ocean circulation and thermohaline structure. Seamounts, Isl. Atolls 1987, 43, 335–354. [Google Scholar]
- Lavelle, J.W.; Mohn, C. Motion, commotion, and biophysical connections at deep ocean seamounts. Oceanography 2010, 23, 90–103. [Google Scholar] [CrossRef]
- White, M.; Bashmachnikov, I.; Aristegui, J.; Martins, A.; Pitcher, T.; Morato, T.; Hart, P.; Clark, M.; Haggan, N.; Santos, R. Physical processes and seamount productivity In Seamounts: Ecology, Fisheries and Conservation; Wiley: Hoboken, NJ, USA, 2007; pp. 65–84. [Google Scholar]
- Hillier, J.; Watts, A. Global distribution of seamounts from ship-track bathymetry data. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Wessel, P.; Sandwell, D.T.; Kim, S.S. The global seamount census. Oceanography 2010, 23, 24–33. [Google Scholar] [CrossRef]
- Yesson, C.; Clark, M.R.; Taylor, M.L.; Rogers, A.D. The global distribution of seamounts based on 30 arc seconds bathymetry data. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2011, 58, 442–453. [Google Scholar] [CrossRef]
- Watts, A. Science, seamounts and society. Geoscientist 2019, 290, 10–16. [Google Scholar]
- Martin, S.; Manucharyan, G.E.; Klein, P. New Estimation of Global Mesoscale Surface Currents with Enhanced Resolution Through a Deep Learning Synthesis of Satellite Observations. In Proceedings of the 2024 Ocean Sciences Meeting, AGU, New Orleans, LA, USA, 18–23 February 2024. [Google Scholar]
- Martin, S.A.; Manucharyan, G.E.; Klein, P. Deep learning improves global satellite observations of ocean eddy dynamics. Geophys. Res. Lett. 2024, 51, e2024GL110059. [Google Scholar] [CrossRef]

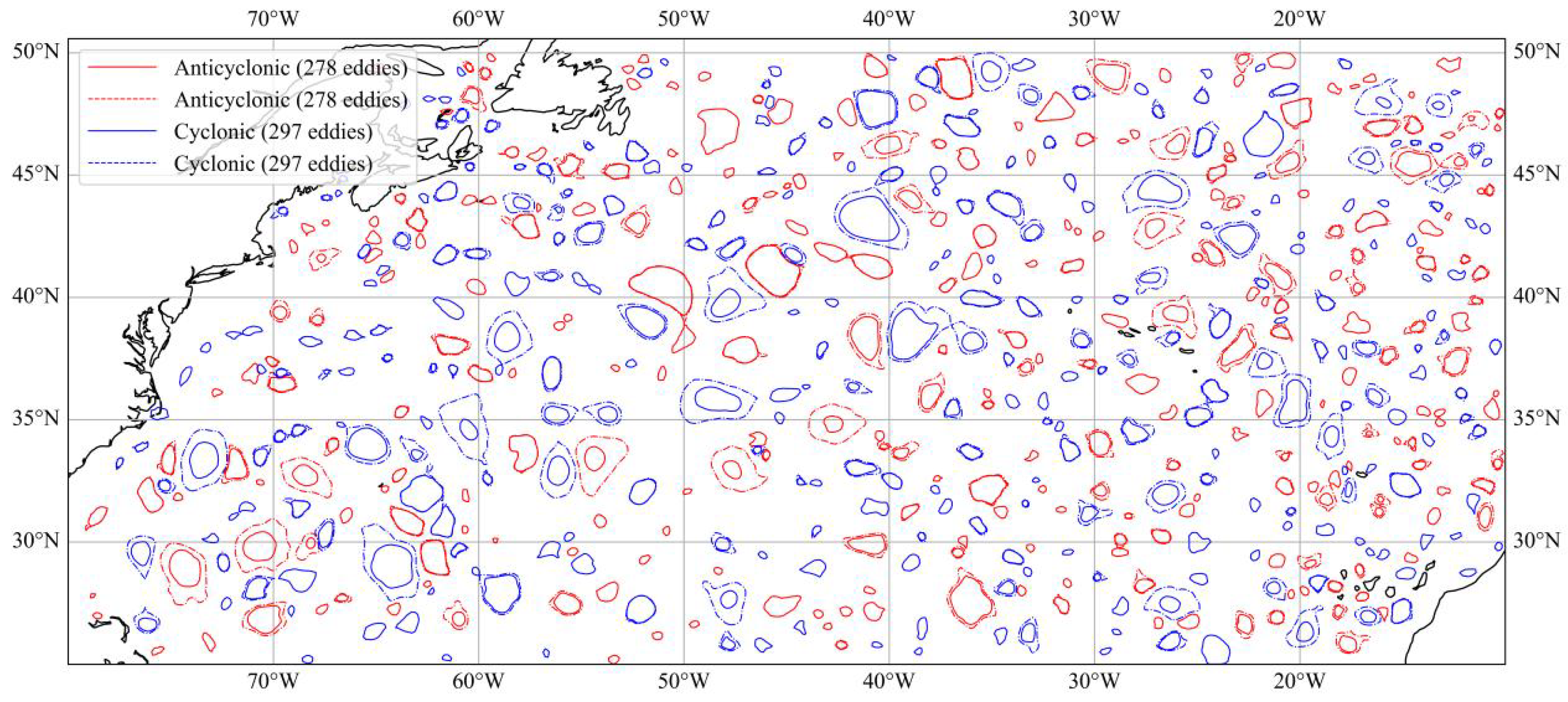
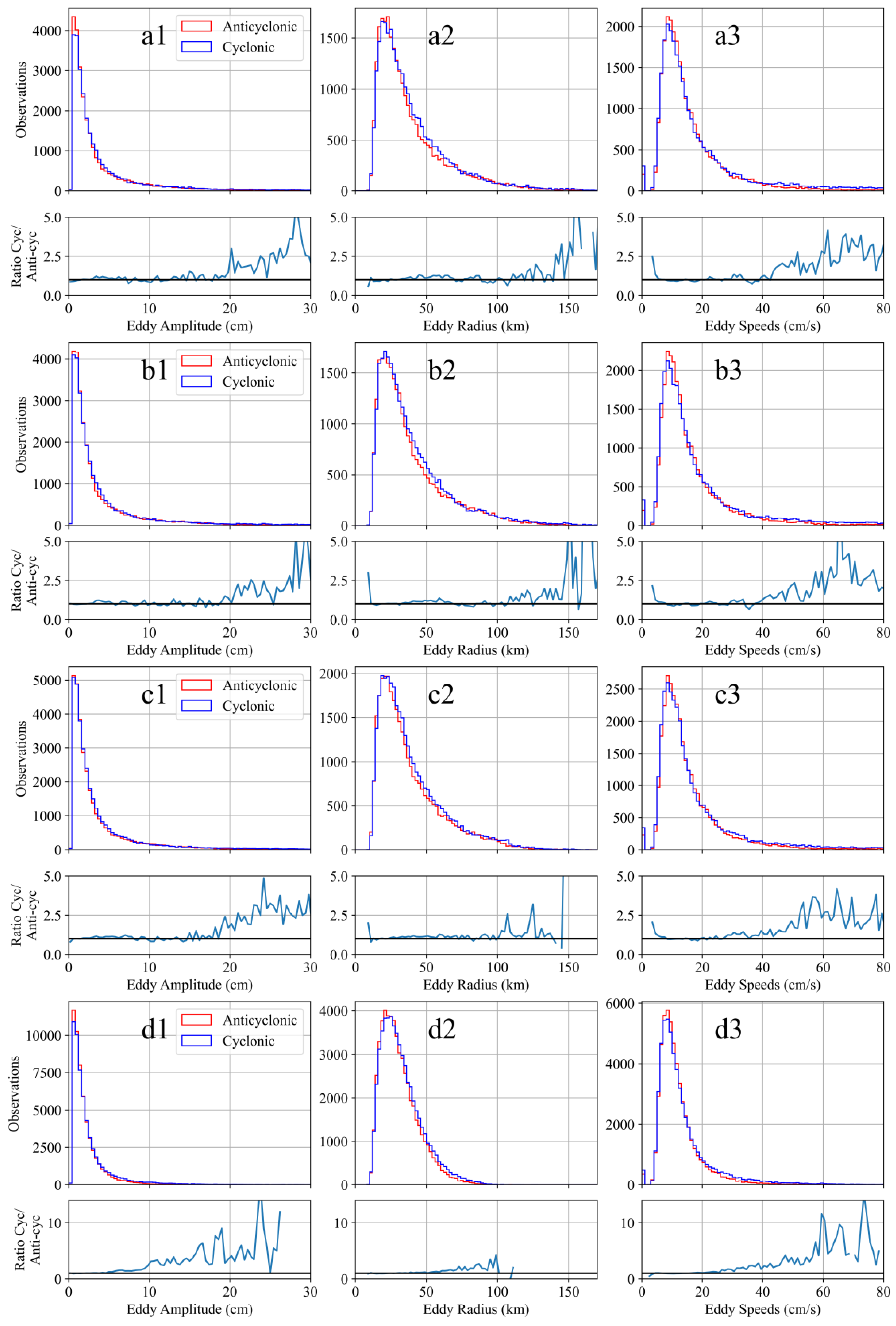
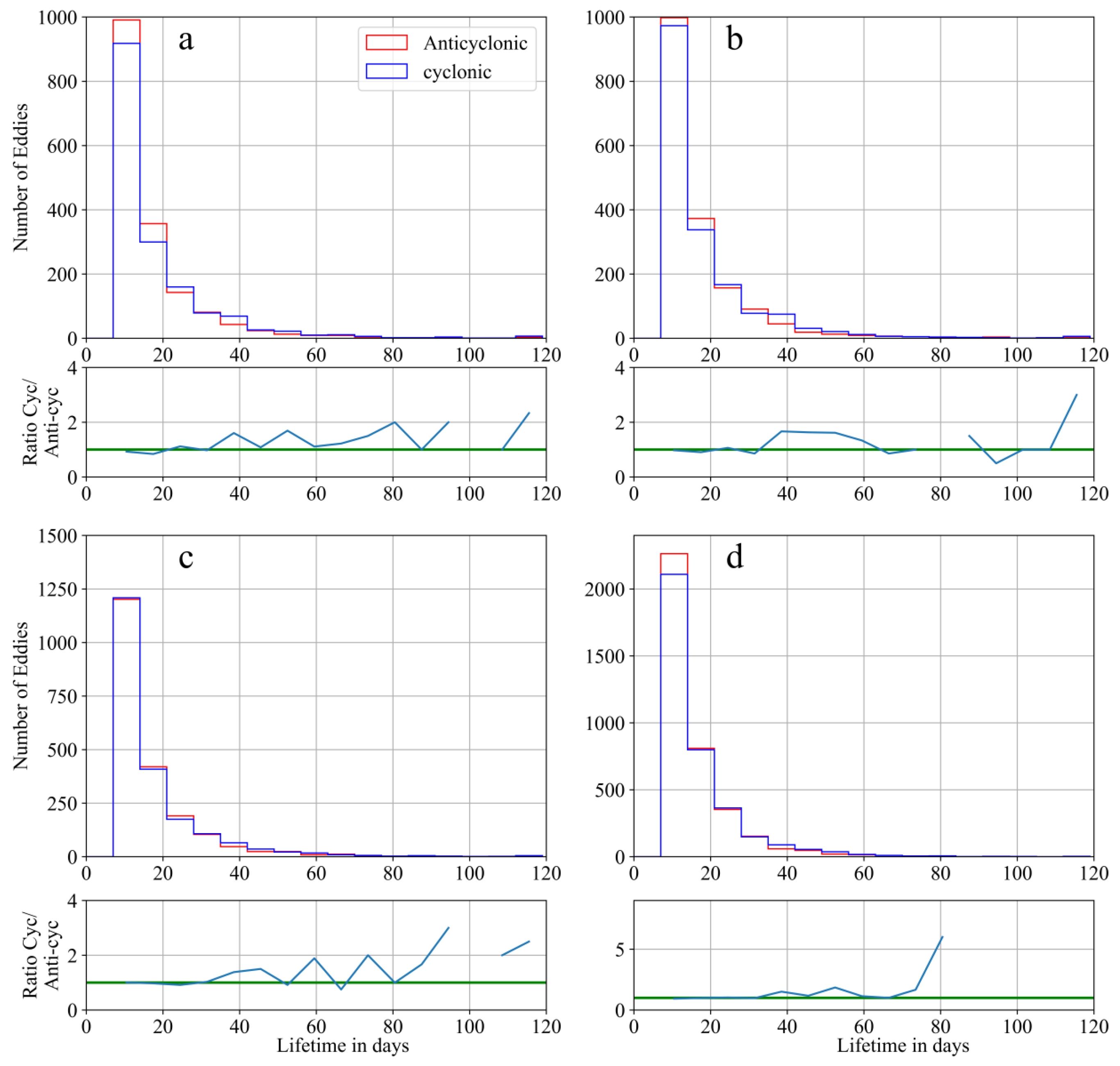



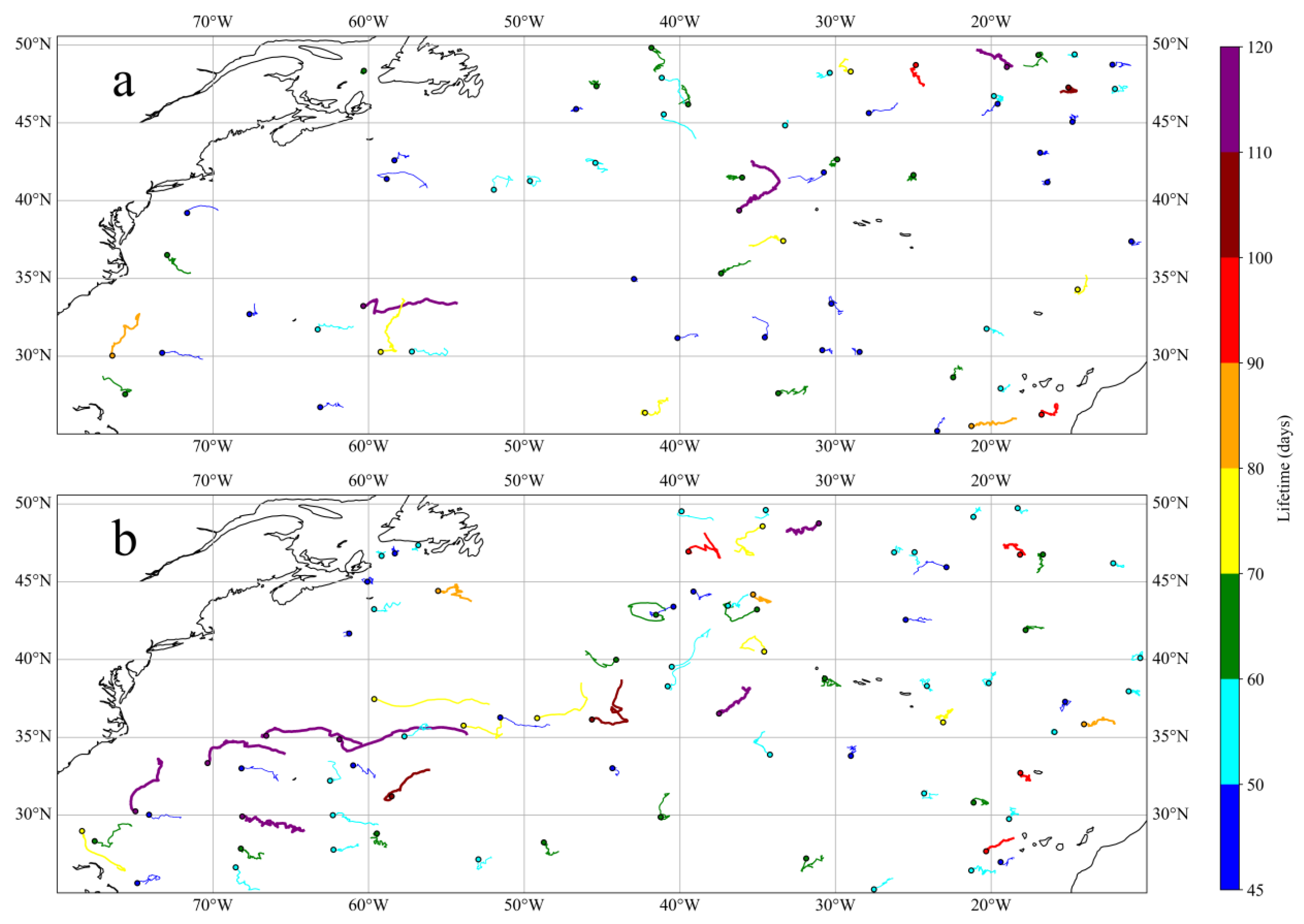


| Wavelength (km) | Eddy Type | Number | Mean Effective Radius (km) | Mean Rotational Speed (m/s) | Mean Amplitude (cm) |
|---|---|---|---|---|---|
| 800 | CE | 297 | 38 | 0.18 | 5 |
| AE | 278 | 37 | 0.15 | 4 | |
| 600 | CE | 307 | 39 | 0.18 | 5 |
| AE | 280 | 37 | 0.15 | 4 | |
| 400 | CE | 363 | 38 | 0.17 | 5 |
| AE | 328 | 37 | 0.15 | 3 | |
| 200 | CE | 585 | 32 | 0.13 | 3 |
| AE | 549 | 31 | 0.11 | 2 |
| Wavelength (km) | Eddy Type | Number | Percent of Observation |
|---|---|---|---|
| 800 | CE | 28,099 | 51.2 |
| AE | 26,733 | 48.8 | |
| 600 | CE | 29,386 | 51.5 |
| AE | 27,643 | 48.5 | |
| 400 | CE | 34,613 | 51.7 |
| AE | 32,344 | 48.3 | |
| 200 | CE | 57,339 | 51.1 |
| AE | 54,846 | 48.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, A.; Zhang, Z.; Yan, H.; Han, B. Spatial and Temporal Characteristics of Mesoscale Eddies in the North Atlantic Ocean Based on SWOT Mission. Remote Sens. 2025, 17, 1469. https://doi.org/10.3390/rs17081469
Cui A, Zhang Z, Yan H, Han B. Spatial and Temporal Characteristics of Mesoscale Eddies in the North Atlantic Ocean Based on SWOT Mission. Remote Sensing. 2025; 17(8):1469. https://doi.org/10.3390/rs17081469
Chicago/Turabian StyleCui, Aiqun, Zizhan Zhang, Haoming Yan, and Baomin Han. 2025. "Spatial and Temporal Characteristics of Mesoscale Eddies in the North Atlantic Ocean Based on SWOT Mission" Remote Sensing 17, no. 8: 1469. https://doi.org/10.3390/rs17081469
APA StyleCui, A., Zhang, Z., Yan, H., & Han, B. (2025). Spatial and Temporal Characteristics of Mesoscale Eddies in the North Atlantic Ocean Based on SWOT Mission. Remote Sensing, 17(8), 1469. https://doi.org/10.3390/rs17081469






