Application of Microwave Remote Sensing to Dynamic Testing of Stay-Cables

Abstract

Recent advances in radar techniques and systems have favoured the development of microwave interferometers, suitable for the non-contact vibration monitoring of large structures. The paper addresses the application of microwave remote sensing to the measurement of the vibration response in the stay-cables of cable-stayed bridges. The reliability and accuracy of the proposed technique were investigated by comparing the natural frequencies (and the cable tensions predicted from natural frequencies) identified from radar data and the corresponding quantities obtained using more conventional techniques. The investigation, carried out on the cables of two different cable-stayed bridges, clearly highlights: (a) the accuracy of the results provided by the microwave remote sensing; (b) the simplicity of use of the radar technique (especially when compared with conventional approaches) and its effectiveness to simultaneously measuring the dynamic response of all the stay-cables of an array.

1. Introduction

The development of innovative non-contact systems for vibration measurement has recently drawn the attention of several researchers. Examples of non-contact sensors include Laser Doppler Vibrometer (LDV) [1,2,3], Global Positioning Systems (GPS) [4,5] and vision-based systems using digital image processing techniques [6]. Furthermore, the microwave interferometry has recently emerged as a technology, suitable to the remote sensing of large structures [7,8,9,10]: a new radar sensor, based on high resolution waveform [11] and interferometric principles [12], was developed by the Italian company IDS (Ingegneria Dei Sistemi, Pisa, Italy), in collaboration with various partners [7]. The main characteristic of the microwave interferometer, named IBIS-S (Image By Interfeometric Survey of Structures), is the possibility of measuring the static or dynamic displacement at multiple locations within its applicable distance. From the technical standpoint, the sensor is a Stepped Frequency Continuous Wave (SF-CW), coherent radar, operating in the K_u frequency band.

After some preliminary tests on full-scale structures [7], a joint research started between IDS and the Dept. of Structural Engineering of Politecnico di Milano, mainly aimed at validating the results of the equipment and to assess its performance in ambient vibration tests (AVT) of bridges. The main results of these investigations are reported in [8,9,10] and included:

• establishing the actual displacement sensitivity of the equipment (0.01 ÷ 0.02 mm) through free vibration tests carried out in the laboratory on a simple spring-mass system [9];
• verifying the stability in long term functioning (both in the laboratory and on-site), required for effective employment in static and dynamic tests or in continuous dynamic monitoring [8,9,10];
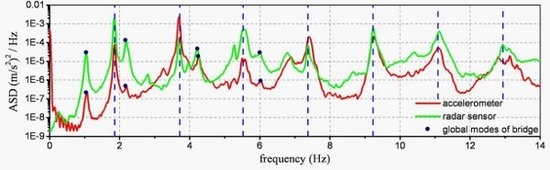
• AVT of a reinforced concrete bridge, using simple radar reflectors placed as close as possible to conventional sensors [8,9], in order to perform an extensive comparison between time-histories and modal properties (i.e., resonant frequencies and mode shapes) obtained from radar and traditional measurement techniques. In particular, the modal parameters of the bridge, that were identified from the radar signals, turned out to be as accurate as that obtained with traditional accelerometers;
• static testing of a steel-composite bridge [10], in order to directly compare the deflections provided by the microwave interferometer and conventional techniques.

The paper first describes the radar equipment and its technical characteristics in order to highlight advantages and potential issues of the new technology. Subsequently, the application of microwave remote sensing to the measurement of cable vibrations is addressed.

Periodic dynamic measurements on stay cables of cable-stayed bridges are currently performed to evaluate the global integrity and structural safety of a cable-stayed bridge by using accelerometers; these contact sensors need to be conveniently mounted on the external cable surface and the installation is generally difficult, time-consuming (especially when dealing with the large number of stay cables, common in modern cable-stayed bridges) and might subject the test crew to hazardous conditions, if the bridge is in service. Hence, microwave remote sensing seems especially promising in order to perform systematic dynamic assessment of stay-cables in a simple and quick way. In addition, the radar technique seems to exhibit various advantages, when compared to other techniques of remote sensing [1,2,3,4,5,6], such as: (a) possibility of use also in case of fog or rain; (b) higher accuracy; (c) possibility of simultaneously measuring the dynamic response of all cables belonging to an array.

The results of experimental tests, carried out on the longer stay-cables of two different cable-stayed bridges, are presented and discussed. In the first case study, the measurement of vibrations on one array of stay-cables was performed by simultaneously using conventional piezoelectric accelerometers and the radar sensor, in order to demonstrate the effectiveness of microwave remote sensing and its accuracy in terms of both natural frequencies and cable tensions. In the test of the second cable-stayed bridge, the two main arrays of bridge forestays were surveyed, with the aim of verifying also the operational simplicity provided by the microwave remote sensing.

2. The Microwave Measurement System

The radar sensor used in this work (IDS, IBIS-S system) is an industrially engineered micro-wave interferometer and consists of a sensor module, a control PC and a power supply unit. The sensor module (Figure 1) is a coherent radar (i.e., a radar preserving the phase information of the received signal) generating, transmitting and receiving the electromagnetic signals to be processed in order to provide the deflection measurements. The sensor, including two horn antennas, has a weight of 12 kg and is installed on a tripod equipped with a rotating head, so that it can be aligned in any desired direction (Figure 1).

Figure 1. View of the microwave interferometer (IDS, model IBIS-S).

Figure 1. View of the microwave interferometer (IDS, model IBIS-S).

The sensor unit consists of low frequency (LF), intermediate frequency (IF) and radio frequency (RF) sections. A fast frequency hopping signal is generated by a Direct Digital Synthesis device in the LF or base-band section; a tune-able sine wave is generated through a high-speed digital to analog converter, reading a sine look-up table in response to a digital tuning word and a precision clock source. In addition, the LF section receives the base-band signal and performs its analog to digital conversion. The IF and RF sections mainly perform amplification and frequency conversion operations (up-conversion in the transmitter chain and down-conversion in the receiving chain). The RF section radiates at a central frequency of 16.75 GHz with a maximum bandwidth of 300 MHz. The up and down frequency conversions are made by using the same internal reference signal in order to preserve the phase information of the signal. As in super heterodyne architecture radars, the conversion to and from the high frequency band is made in two steps: the first step is performed in the IF section and brings the signal to an intermediate frequency while the second step, performed into the RF section, converts the signal to the radio frequency band. A final calibration section provides the necessary phase stability; design specifications on phase uncertainty are suitable for measuring deflections with a range uncertainty lower than 0.01 mm.

The sensor unit is connected to the control PC by means of a standard USB 2.0 interface; the control PC is provided with the software for the system management and is used to configure the acquisition parameters, store the acquired signals, process the data and view the initial results in real time. Finally, the power supply unit provides power to the system through a 12 V battery unit.

The main functions of the equipment are the simultaneous detection of the position and deflection of different targets placed at different distances from the sensor. This performance is obtained by using two well-known radar techniques:

• he SF-CW technique (see e.g., [11]), adopted to resolve the scenario in the range direction, i.e., to detect the position of different target surfaces placed along the radar’s line of sight;
• he phase interferometry technique (see e.g., [12], implemented to compute the displacement of each target by comparing the phase information of the back-scattered electromagnetic waves collected at different times.

It should be noticed that a CW radar can reach the same far distance of a pulse radar by transmitting lower peak power so that SF-CW radars are generally included in the Short Range Device category as a license-free use equipments. Furthermore, SF modulated radars can transmit and receive signals with precise frequency control by using Direct Digital Synthesizer, an innovative up-to-date device for generating step-frequency signals.

According to the SF-CW technique, the radar continuously transmits bursts of N electromagnetic pulses, whose frequencies are increased from pulse to pulse by a constant frequency increment Δf; hence, a large effective bandwidth of B=(N − 1)Δf is attained. A large value of B is, in turn, highly desirable since the range resolution (i.e., the minimum separation that can be detected along the radar’s line of sight) Δr may be expressed as:

$$\Delta r=\frac{c}{2B}$$

(1)

where c is the speed of light in free space.

The SF-CW technique was implemented in the IBIS-S sensor to obtain a minimum range resolution of 0.50 m while the scenario is sampled at a rate ranging up to 200 Hz, that is an excellent performance since the significant frequency content of the deflection time-histories is generally in the frequency range 0−20 Hz for a large structure. In addition, sampling interval Δt = 0.005 s is in principle well suited to provide a good waveform definition of the acquired signals and a maximum.

The magnitude of the Inverse Discrete Fourier Transform (IDFT) of the received echoes at each time sample provides a synthetic image (range profile) of the scattering objects in the space illuminated by the antenna beam. A range profile (or synthetic image) is simply a map of the intensity of the received radar echoes in function of the distance of the objects that generated the echoes themselves; in other words, it represents a 1-D map of the scattering objects versus their distances.

It is worth underlining that the radar has only 1-D imaging capabilities, i.e., different targets can be individually detected only if they are separated in range; hence, measurement errors may arise from the multiplicity of contributions to the same range bin, coming from different points placed at the same distance from the radar but not lying on the same axis [8,9,10].

According to phase interferometry technique [12] in radar systems, two range profiles acquired at different time instants exhibit phase differences depending on the motion of the targets along the radar line-of-sight. Hence, the displacement along the radar line-of-sight d_r (or radial displacement) is simply computed from the phase shift Δϑ as:

$$d_r=-\frac{\lambda }{4\pi }\Delta \vartheta$$

(2)

where λ is the wavelength of the electromagnetic signal.

Since the interferometric technique, represented by Equation 2, provides a measurement of the radial displacement, the evaluation of the actual displacement requires the prior knowledge of the direction of motion. For many bridges (simple or continuous spans, frame or truss bridges), the displacement under traffic loads can be assumed as vertical and it can be easily evaluated by making straightforward geometric projections. For more complex bridges, such as arch bridges, this assumption is no longer verified [13].

3. Microwave Remote Sensing of Stay-cables

In order to investigate the global integrity and structural safety of cable-stayed bridges, periodic dynamic measurements on stay-cables are currently performed and generally aimed at: (1) identifying the local natural frequencies and damping ratios and; (2) evaluating the tension forces (that are predicted from natural frequencies) and monitoring the changes in these forces over time. If a linear correlation exists between the mode order n and the corresponding natural frequency f_n of a cable, the tension force T in this cable can be obtained from its natural frequencies using the taut string model [1,3,14]:

$$T=4\rho L^2{\left(\frac{f_n}{n}\right)}^2$$

(3)

where ρ is the mass per unit length and L is the effective length of the cable. For tension members that deviate from a taut string, still the cable forces can be predicted using the identified natural frequencies with reference to more advanced formulations (accounting for the effects of both the sag and the bending stiffness on the dynamic behavior of cables, see e.g., [3,15]).

The dynamic measurements on stay-cables are generally based on the use of that accelerometers, since these sensors are very accurate, relatively inexpensive and have adequate technical characteristics; on the other hand, the accelerometers need to be conveniently mounted on the external cable surface and the installation is generally uneasy, very time-consuming and might subject the test crew to hazardous conditions if the bridge is in service. Hence, it is of primary importance to develop and apply new measurement techniques, that enable accurate and systematic dynamic measurements on stay cables in a simple and safe way. Within this context, application of microwave remote sensing to the measurement of cable vibrations seems specially promising. Firstly, high accuracy has to be expected from radar-based measurements in terms of both natural frequencies [8,9,10] and cable tensions. Furthermore, the radar technique provides the deflection time-history of a cable, so that it could be used to directly evaluate the susceptibility of cables to large amplitude oscillations or the efficiency of devices (e.g., external dampers) adopted to prevent excessive vibrations. Finally, the microwave interferometry exhibits in principle some advantages with respect to other techniques of remote sensing [1,2,3,4,5,6], such as: (a) its reliability in case of fog or rain and in almost all weather conditions; (b) higher precision of the measured deflections; (c) possibility of simultaneously measuring the response of several cables.

The possible issues that may occur in the application of the radar technique to bridges and large structures (i.e., 1-D imaging capabilities and a priori knowledge of the direction of motion) do not affect the survey of an array of cables; peculiarly:

• the typical position of the sensor in the survey of an array of cables is inclined upward, as schematically shown in Figure 2(a); hence, the only targets encountered along the path of the electromagnetic waves are the stays itself, so that 1-D imaging capability is perfectly adequate to the test scenario;
• arrays of cables generally belong to a vertical plane, where the vibration of the cables mainly take place under the traffic loads. The in-plane motion of a cable can be assumed orthogonal to its axis, so that the actual deflection d can be obtained from the component d_r along the radar line of sight as:

  $$d=\frac{d_r}{\cos [\pi /2-({\alpha }_c+{\alpha }_s)]}$$

  (4)

  where α_c and α_s are the slope of the cable and of the sensor, respectively [Figure 2(a)]. Furthermore, if the radar line of sight belongs to the same plane of the array, only the in-plane component of the cable motion is measured, since the sensor only measures the deflections along its line of sight. In other words, the prior knowledge of the direction of motion is available for cable systems, so that it is possible to evaluate the actual displacement from the line-of-sight one.

Furthermore, Figure 2 shows that it is quite easy to predict the scenario under the radar beam when an array of cables is going to be tested: the inspection of the range profile (Figure 2b), performed on site, allows to quickly verify that the sensor positioning provides a correct image of the test scenario.

Figure 2. (a) Line-of-sight displacement versus actual (in-plane) displacement of a stay-cable, and (b) typical range profile expected for an array including two cables.

Figure 2. (a) Line-of-sight displacement versus actual (in-plane) displacement of a stay-cable, and (b) typical range profile expected for an array including two cables.

4. Application to Full-Scale Structures

4.1. Experimental Verification on a Single Stay-cable

As stated in Section 3, the main objective of dynamic testing stay-cables is the identification of the local natural frequencies. In order to evaluate the reliability and the accuracy of microwave remote sensing, the proposed technique was firstly applied to some cables [10] of a cable-stayed bridge by simultaneously using piezoelectric accelerometers and the radar system, for validation purposes.

The investigated cable-stayed bridge (Figure 3a) is a roadway bridge, which crosses the river Adda between the municipalities of Olginate and Calolziocorte (about 60 km northeast of Milan). The bridge, with a pre-stressed concrete deck, is formed by a central span of 110.0 m and two lateral spans of 55.0 m. The deck is suspended from 24 pairs of cable stays, arranged in a semi-fan and connected to two H-shaped reinforced concrete towers, reaching the height of about 38.0 m above the foundations. Elevation and typical cross-sections of the bridge are shown in Figure 3a.

Figure 3. (a) Elevation and typical cross-sections of the cable-stayed bridge over the river Adda. Accelerometer and radar position for dynamic testing of stay-cable S'₁₂; (b) View of the test scenario; (c) Range profile of the test scenario.

Figure 3. (a) Elevation and typical cross-sections of the cable-stayed bridge over the river Adda. Accelerometer and radar position for dynamic testing of stay-cable S'₁₂; (b) View of the test scenario; (c) Range profile of the test scenario.

Figure 4. (a) Typical deflection time-history measured by the radar sensor on the stay-cable S'₁₂; (b) Comparison between the acceleration obtained by accelerometer and radar sensors on the investigated cable.

Figure 4. (a) Typical deflection time-history measured by the radar sensor on the stay-cable S'₁₂; (b) Comparison between the acceleration obtained by accelerometer and radar sensors on the investigated cable.

The experimental tests were carried out at the end of the main phase of cable tensioning, so that the stay-cables were also instrumented with load cells, directly providing the value of the tension forces. Since the main objective of the tests was the evaluation of the global dynamic characteristics of the bridge [16] (in order to optimize the subsequent phase of adjustment of cable forces), ambient excitation was mainly provided by 2 two-axle trucks with 340 kN gross weight each, crossing the bridge with symmetric and eccentric passages and velocities in the range of 10 to 40 km/h.

Figure 3a,b show the accelerometer and radar position in the test of one cable, herein after referred to as stay-cable S'₁₂. The microwave interferometer was placed at base of the tower on the Calolziocorte side and inclined 55° upward; accelerometer and radar data were simultaneously acquired at rate of 200 Hz over a time windows of 1,700 s. The range profile of the test scenario is presented in Figure 3c; it is observed that, after some close and neighboring peaks around the range of 10.0 m (corresponding to the concrete transverse beam providing the anchorage for the cable closer to the sensor), five well defined peaks clearly identify the position of the other cables of the array, with the observed ranges being practically equal to the predictions previously made in the office.

The analysis of the results obtained by the radar sensor first included the qualitative inspection of the deflection measurements. Figure 4a shows an example of displacement time-history measured on the investigated stay-cable S'₁₂; it should be noticed that, as it has to be expected for a stay-cable, the fundamental period is clearly detected in the displacement signal. Although radar and conventional measurements refer to different points of the cable (Figure 3a), the comparison between the time-histories simultaneously recorded by the two measurement systems provides valuable information. An example of comparison is given in Figure 4b, where the acceleration computed by deriving twice the displacement obtained from the radar is compared to the one simultaneously recorded by the accelerometer. It can be observed that the two time series, which refer to two different points almost symmetrically placed with respect to the midpoint of the stay-cable, exhibit the same time evolution and very similar amplitudes.

Figure 5 shows the auto-spectral densities (ASD) of the ambient responses acquired, by using the two measurement systems, on the same cable S'₁₂. The ASDs were computed from the recorded time-histories using the modified periodogram method [17]: in the present application, each record was divided into 4,096-points Hanning-windowed periodograms, that are transformed and averaged with 66.7% overlapping, so that a total number of 124 spectral averages was obtained. Since the time interval is 0.005 s, the resulting frequency resolution is 1/(4,096 × 0.005) ≈ 0.0244 Hz.

Although the ASDs of Figure 5a,b are associated to different mechanical quantities measured (displacement and acceleration) and to different points of the stay cable, the spectral plots clearly highlight an excellent agreement in terms of local natural frequencies of the cable, marked with the vertical dashed lines, and are characterized by equally spaced and well-defined peaks in the investigated frequency range. Furthermore, some global natural frequencies of the bridge-identified in the bridge dynamic survey [16] and corresponding to peaks of the ASDs placed at 0.76, 1.25, 1.66, 1.90 and 2.78 Hz—are also apparent in Figure 5a,b.

Figure 5. Stay-cable S'₁₂: (a) Auto-spectrum of the displacement data measured by the radar; (b) Auto-spectrum of the acceleration data measured by the conventional sensor.

Figure 5. Stay-cable S'₁₂: (a) Auto-spectrum of the displacement data measured by the radar; (b) Auto-spectrum of the acceleration data measured by the conventional sensor.

Figure 5 also shows that a linear correlation exists between the mode order n and the corresponding natural frequency f_n of stay cable S'₁₂. Hence, the tension force T can be obtained from natural frequencies using Equation (3). The application of Equation (3) to the cable S'₁₂ (assuming L = 57.24 m and ρ = 36.51 kg/m) is summarized in Table 1 and highlights that the estimates of cable tension obtained from accelerometer and radar sensor are practically equal. Furthermore, the cable was also instrumented with a load cell and the tension force value measured by the load cell was 2,694 kN. Hence, the radar-based estimate of the cable tension turns out to be in excellent agreement also with the measurement provided by the load cell (with the maximum percentage difference being less than 0.6%).

Table 1. Tensions in cable S'₁₂ obtained from accelerometer and radar measurements.

Cable	Sensor	T(f1) (kN)	T(f2) (kN)	T(f3) (kN)	T(f4) (kN)	T(f5) (kN)	Average (kN)
S'12	Accelerometer	2,679	2,707	2,660	2,693	2,690	2,686
	Radar sensor	2,679	2,707	2,679	2,693	2,690	2,689

Table 1. Tensions in cable S'₁₂ obtained from accelerometer and radar measurements.

Cable	Sensor	T(f1) (kN)	T(f2) (kN)	T(f3) (kN)	T(f4) (kN)	T(f5) (kN)	Average (kN)
S'12	Accelerometer	2,679	2,707	2,660	2,693	2,690	2,686
	Radar sensor	2,679	2,707	2,679	2,693	2,690	2,689

4.2. Dynamic Measurements on the Forestays of the Cable-stayed Bridge over the River Oglio

Subsequently, microwave remote sensing was used to perform dynamic measurements on the arrays of forestays supporting the deck of the cable-stayed bridge crossing the river Oglio between the towns of Bordolano and Quinzano (Figure 6), about 70 km far from Milan.

The investigated bridge consists of a steel-composite deck, double-plane cables and two inclined concrete towers. Elevation and plan views of the bridge and typical cross-section are presented in Figure 6.

Figure 6. Elevation, plan and typical cross-sections of the cable-stayed bridge over the river Oglio (dimensions in m). Positions of the microwave sensor in the survey of the two arrays of forestays.

Figure 6. Elevation, plan and typical cross-sections of the cable-stayed bridge over the river Oglio (dimensions in m). Positions of the microwave sensor in the survey of the two arrays of forestays.

The deck, 70 m long, consists of a steel grid of 4 girders framed by 12 floor beams; girders and floor beams are all composite with a 30 cm reinforced concrete slab. The steel girders are 95 cm high and the outer girders are of box section while the inner ones are wide flange sections (Figure 6); similarly, the floor beams providing the anchorage of the forestays are of box section while the other ones are wide flange sections. The total width of the deck is 13.50 m, for two traffic lanes and two pedestrian walkways.

The cast-in-place concrete towers are 35.65 m high and each consists of an inclined, varying width, concrete leg bearing an upper steel device providing the upper anchorage for the stay-cables; two arrays of 3 forestays and 3 backstays converge at the top of each tower.

The dynamic characteristics of the bridge were well-known since ambient vibration tests were carried out in Spring 2004 by the Vibration Laboratory of L’Aquila University [18], using Sprengnether servo-accelerometers. During this test, 10 global modes of the bridge were identified in the frequency range 0−10 Hz and also the dynamic response of one cable (S_2U in Figure 6) has been recorded.

Figure 7. (a) Radar position in the survey of the upstream-side forestays; (b) Radar position in the survey of the downstream-side forestays; (c) Range profile of the test scenario on the upstream side; (d) Range profile of the test scenario on the downstream side.

Figure 7. (a) Radar position in the survey of the upstream-side forestays; (b) Radar position in the survey of the downstream-side forestays; (c) Range profile of the test scenario on the upstream side; (d) Range profile of the test scenario on the downstream side.

Figure 8. Deflection time-history measured by the radar sensor on the stay-cable S_2U.

Figure 8. Deflection time-history measured by the radar sensor on the stay-cable S_2U.

Figure 9. Comparison between the ASDs of cable S_2U obtained from conventional and radar sensor.

Figure 9. Comparison between the ASDs of cable S_2U obtained from conventional and radar sensor.

The deflection response of the two arrays of cables to wind and traffic excitation was quickly and safely acquired by positioning the microwave interferometer on the basement of the upstream-side and downstream-side tower, respectively (Figure 6).

Figure 7a,b show the radar positions on the upstream side and downstream side, respectively; the range profiles of the corresponding test scenarios are presented in Figure 7c,d. Since the test scenario on the two sides was practically the same, the radar image profiles are very similar and each range profile exhibits three well defined peaks, occurring at the expected distance from the sensor (Figure 6) and clearly identifying the position in range of the cables.

For each array, 3000 s of radar data were acquired at a rate of 200 Hz; the displacement time-history collected on stay-cable S_2U is shown in Figure 8. Furthermore, Figure 9 presents a direct comparison between: (1) the auto-spectrum of the acceleration measured on stay-cable S_2U by a conventional accelerometer in the test of Spring 2004 [18] and (2) the auto-spectrum of the acceleration obtained from the radar sensor (and computed by deriving the displacement data). The inspection of the spectral plots in Figure 9 clearly reveals that the values of the first seven natural frequencies of stay-cable S_2U, identified on the basis of the auto-spectra obtained using conventional and radar measurement systems are virtually coincident (1.84, 3.70, 5.53, 7.37, 9.24. 11.1 and 12.93 Hz in Figure 9). In addition, the peaks of the ASDs placed at 1.06, 2.18, 4.25 and 6.03 Hz correspond to the global natural frequencies of the bridge, identified in the previous dynamic survey of the bridge [18].

Figure 10 shows the ASDs of the deflection response of all forestay. The spectral plots in Figure 10 are a synthesis of the frequency content present on each cable and allowed the identification of several local resonant frequencies, marked with the vertical dashed lines, in the frequency range of analysis (0–25 Hz).

Figure 10. Auto-spectra of the displacement data measured by the radar on the forestays S_1U, S_1D, S_2U, S_2D, S_3U and S_3D.

Figure 10. Auto-spectra of the displacement data measured by the radar on the forestays S_1U, S_1D, S_2U, S_2D, S_3U and S_3D.

The inspection of the ASDs in Figure 10 clearly highlights that, as it has to be expected, the natural frequencies of the corresponding cables on the two opposite sides (S_1U–S_1D, S_2U–S_2D and S_3U–S_3D, see Figure 6) are almost equal. Furthermore, the response of all cables is characterized by a large number of equally spaced and well-defined peaks so that the tension forces can be computed from cable’s natural frequencies using the taut string model (3); application of this approach leads to values of cable tensions summarized in Table 2 and very close to the design values. Finally, Figure 11 shows how close the experimental resonant frequencies obtained from microwave remote sensing are to the predictions of taut string model.

Figure 11. Experimental and taut-string based natural frequencies of: (a) upstream-side forestays and (b) downstream-side forestays.

Figure 11. Experimental and taut-string based natural frequencies of: (a) upstream-side forestays and (b) downstream-side forestays.

Table 2. Radar-based tensions in the forestays of the cable-stayed bridge over the river Oglio.

Cable	T(f1) (kN)	T(f2) (kN)	T(f3) (kN)	T(f4) (kN)	T(f5) (kN)	Average (kN)
S1U	2,704	2,692	2,712	2,716	2,722	2,709
S1D	2,655	2,654	2,671	2,670	2,674	2,665
S2U	2,923	2,943	2,924	2,924	2,939	2,931
S2D	3,003	2,982	2,949	2,982	2,986	2,980
S3U	4,054	4,052	4,073	4,098	4,113	4,078
S3D	3,990	3,997	4,031	4,037	4,039	4,019

Table 2. Radar-based tensions in the forestays of the cable-stayed bridge over the river Oglio.

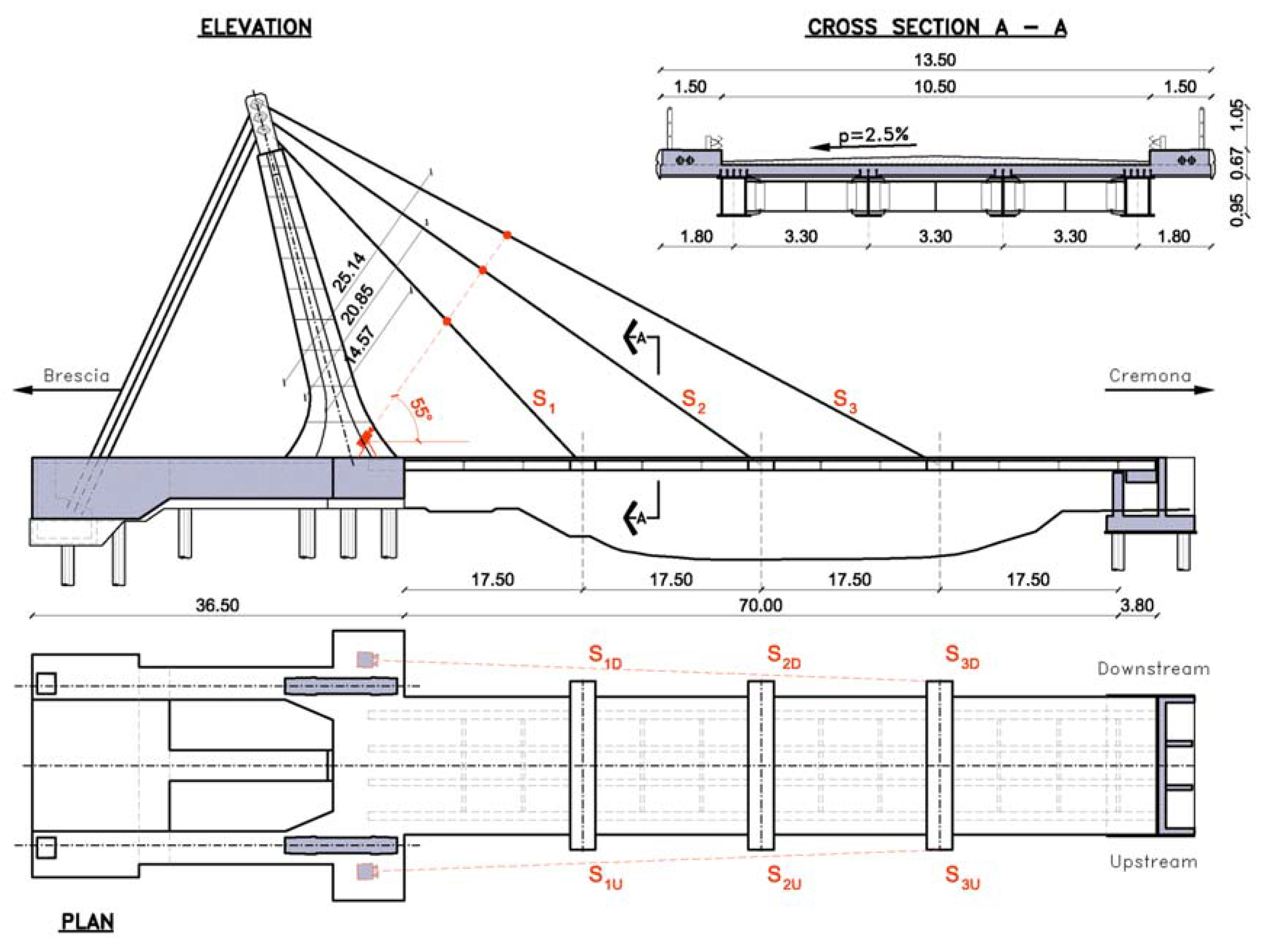
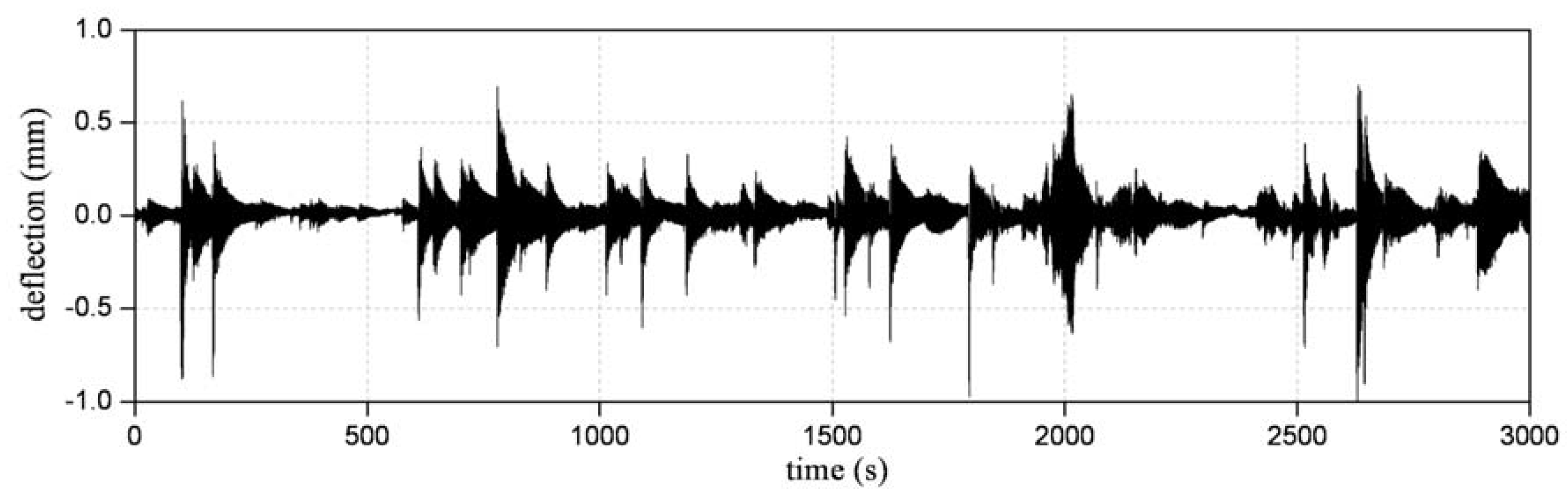
Cable	T(f1) (kN)	T(f2) (kN)	T(f3) (kN)	T(f4) (kN)	T(f5) (kN)	Average (kN)
S1U	2,704	2,692	2,712	2,716	2,722	2,709
S1D	2,655	2,654	2,671	2,670	2,674	2,665
S2U	2,923	2,943	2,924	2,924	2,939	2,931
S2D	3,003	2,982	2,949	2,982	2,986	2,980
S3U	4,054	4,052	4,073	4,098	4,113	4,078
S3D	3,990	3,997	4,031	4,037	4,039	4,019

5. Conclusions

The paper is focused on the application of microwave remote sensing to the measurement of dynamic deflections on the cables of two cable-stayed bridges. The radar technique exhibited excellent stability of functioning, when used on site for long time intervals, and turned out to be especially suitable to vibration survey of stay-cables; peculiarly, the microwave remote sensing allows to simultaneously measure the dynamic response of several stay-cables and provides a powerful and easy-to-use form of systematic and accurate evaluation of natural frequencies and cable tensions. More specifically, the results presented in the paper clearly highlight that:

• a large number of local resonant frequencies can be identified from radar data on each stay-cable of an array and these natural frequencies seems as accurate as that obtained with conventional accelerometers;
• in the investigated case studies, the number of frequencies identified from radar data was large enough to establish if the cables behave as a taut string or deviate from a taut string, so that accurate estimate of the cable tensions can be retrieved from the identified natural frequencies as well.

Furthermore, microwave remote sensing provides the deflection time-history of a stay-cable and could be used to directly evaluate the susceptibility of cables to large amplitude oscillations or the efficiency of devices (e.g., external dampers) adopted to prevent excessive vibrations.