Measurement of Surface Displacement and Deformation of Mass Movements Using Least Squares Matching of Repeat High Resolution Satellite and Aerial Images
Abstract
:1. Introduction
2. The Least Squares Matching Algorithm and Its Significance in Mass Movement Analysis
2.1. The Least Squares Matching Algorithm
2.2. The Least Squares Matching in Mass Movement Analysis
3. Methods
3.1. Image Datasets
3.2. Image Matching
3.2.1. Estimation of Initial Parameters
3.2.2. Least Squares Iteration
3.3. Computation of Displacement and Deformation
3.3.1. Horizontal Surface Displacement
3.3.2. Surface Strain and Rotation Rates
3.4. Performance Evaluation
4. Results
4.1. Horizontal Surface Displacements
4.2. Precision and Validity of the Displacement Data
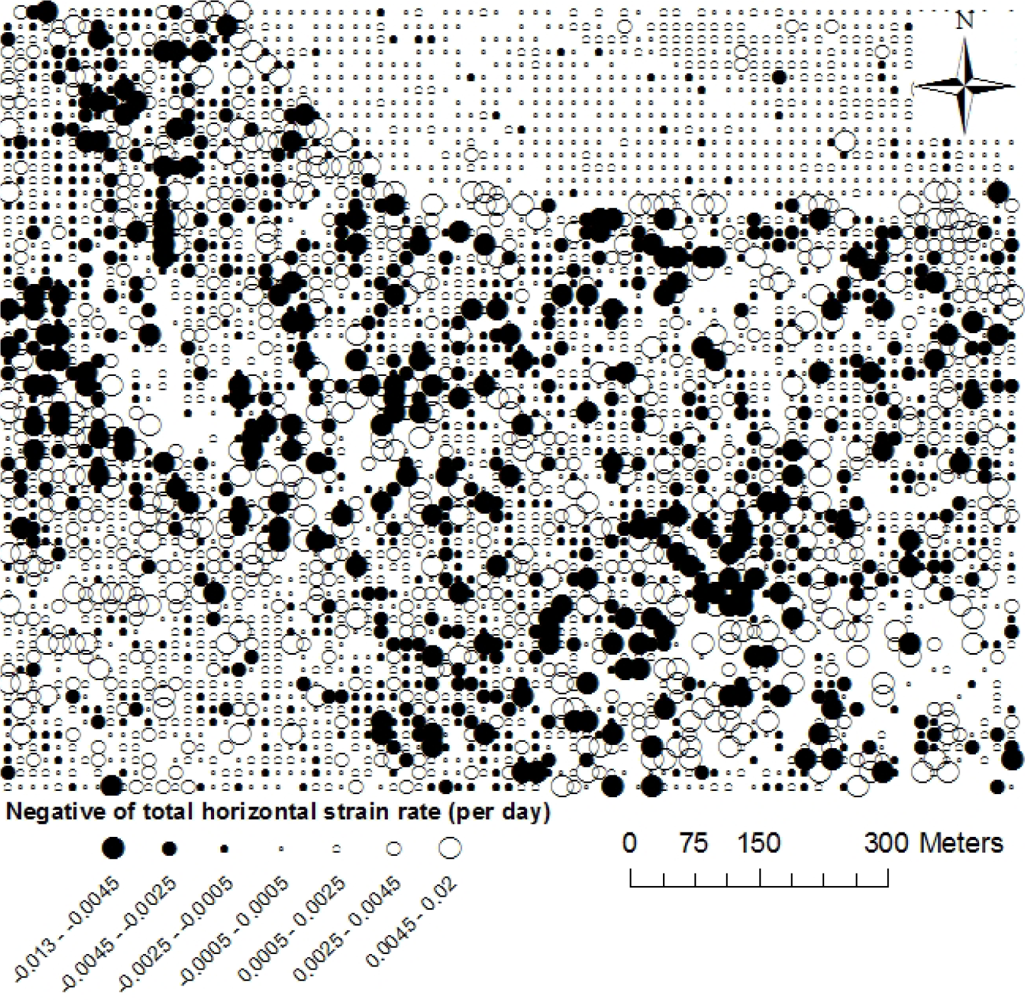
4.3. Surface Strain and Rotation Rates
4.3.1. The Muragl Rockglacier
4.3.2. The Nigardsbreen Glacier
4.3.3. The La Clapière Landslide
4.4. Precision and Validity of the Deformation Data
5. Discussion
5.1. Computed Displacements and Deformations
5.2. On the Precision of the Algorithm and Sources of Error
6. Conclusions and Outlook
Acknowledgments
References
- Kääb, A.; Haeberli, W.; Gudmundsson, G.H. Analysing the creep of mountain permafrost using high precision aerial photogrammetry: 25 years of monitoring Gruben rock glacier, Swiss Alps. Permafrost Periglac. Process 1997, 8, 409–426. [Google Scholar]
- Bindschadler, R.A.; Scambos, T.A. Satellite-image-derived velocity field of an Antarctic ice stream. Science 1991, 252, 242–246. [Google Scholar]
- Delacourt, C.; Allemand, P.; Casson, B.; Vadon, H. Velocity field of the “La Clapière” landslide measured by the correlation of aerial and Quickbird satellite images. Geophys. Res. Lett 2004, 31, 15–19. [Google Scholar]
- Rolstad, C.; Amlien, J.; Ove Hagen, J.; Lundén, B. Visible and near-infrared digital images for determination of ice velocities and surface elevation during a surge on Osbornebreen, a tidewater glacier in Svalbard. Ann. Glaciol 1996, 24, 255–261. [Google Scholar]
- Berthier, E.; Vadon, H.; Baratoux, D.; Arnaud, Y.; Vincent, C.; Feigl, K.L.; Remy, F.; Legresy, B. Surface motion of mountain glaciers derived from satellite optical imagery. Remote Sens. Environ 2005, 95, 14–28. [Google Scholar]
- De Matías, J.; De Sanjosé, J.; López-Nicolás, G.; Sagüés, C.; Guerrero, J. Photogrammetric methodology for the production of geomorphologic maps: Application to the Veleta rock glacier (Sierra Nevada, Granada, Spain). Remote Sens 2009, 1, 829–841. [Google Scholar]
- Zitová, B.; Flusser, J. Image registration methods: A survey. Image Vision Comput 2003, 21, 977–1000. [Google Scholar]
- Kääb, A.; Kaufmann, V.; Ladstadter, R.; Eiken, T. Rock Glacier Dynamics: Implications from High-Resolution Measurements of Surface Velocity Fields. Proceedings of the 8th International Conference on Permafrost, Zurich, Switzerland, 21–25 July 2003; pp. 501–506.
- Kääb, A. Remote Sensing of Mountain Glaciers and Permafrost Creep. 2005; p. 264. [Google Scholar]
- Brown, L.G. A survey of image registration techniques. ACM Comput. Surv 1992, 24, 325–376. [Google Scholar]
- Lewis, J.P. Fast normalized cross-correlation. Vision Interface 1995, 120–123. [Google Scholar]
- Debella-Gilo, M.; Kääb, A. Sub-pixel precision image matching for measuring surface displacements on mass movements using normalized cross-correlation. Remote Sens. Environ 2011, 115, 130–142. [Google Scholar]
- Förstner, W. On the Geometric Precision of Digital Image Correlation. Proceedings of the ISPRS Symposium Mathematical Models, Accuracy Aspects and Quality Control, Finland; 1982; pp. 176–189. [Google Scholar]
- Schenk, T. Digital Photogrammetry; TerraScience: Laurelville, OH, USA, 1999; Volume I, p. 428. [Google Scholar]
- Whillans, I.M.; Tseng, Y.H. Automatic tracking of crevasses on satellite images. Cold Reg. Sci. Technol 1995, 23, 201–214. [Google Scholar]
- Maas, H.G.; Casassa, G.; Schneider, D.; Schwalbe, E.; Wendt, A. Photogrammetric determination of spatio-temporal velocity fields at glaciar San Rafael in the northern Patagonian icefield. The Cryosphere Discuss 2010, 4, 2415–2432. [Google Scholar]
- Kaufmann, V.; Ladstädter, R. Quantitative Analysis of Rock Glacier Creep by Means of Digital Photogrammetry Using Multi-Temporal Aerial Photographs: Two Case Studies in the Austrian Alps. Proceedings of 8th International Conference on Permafrost, Zurich, Switzerland, 21–25 July 2003; pp. 525–530.
- Gruen, A. Least squares matching: A fundamental measurement algorithm. In Close Range Photogrammetry and Machine Vision; Atkinson, K.B., Ed.; Whittles Publ.: Caithness, Scotland, UK, 1996; pp. 217–255. [Google Scholar]
- Bethmann, F.; Luhmann, T. Least-Squares Matching with Advanced Geometric Transformation Models. In International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, Proceedings of ISPRS Commission V Mid-Term Symposium “Close Range Image Measurement Techniques”, Newcastle upon Tyne, UK, 21–24 June 2010; 2010. WG V/4:. pp. 86–91. [Google Scholar]
- Gruen, A.W.; Baltsavias, E.P. High-precision image matching for digital terrain model generation. Photogrammetria 1987, 42, 97–112. [Google Scholar]
- Rosenholm, D. Least squares matching method: Some experimental results. Photogramm. Rec 1987, 12, 493–512. [Google Scholar]
- Young, W.C.; Budynas, R.G.; Roark, R.J. Formulas for Stress and Strain; McGraw-Hill: New York, NY, USA, 2002; p. 852. [Google Scholar]
- Middleton, G.V.; Wilcock, P.R. Mechanics in the Earth and Environmental Sciences; Cambridge University Press: Cambridge, UK, 1994; p. 459. [Google Scholar]
- Hooke, R.L. Principles of Glacier Mechanics; Cambridge University Press: Cambridge, UK, 2005; p. 429. [Google Scholar]
- Haeberli, W.; Hallet, B.; Arenson, L.; Elconin, R.; Humlun, O.; Kääb, A.; Kaufmann, V.; Ladanyi, B.; Matsuoka, N.; Springman, S.; et al. Permafrost creep and rock glacier dynamics. Permafrost Periglac. Process 2006, 17, 189–214. [Google Scholar]
- Nye, J.F. The mechanics of glacier flow. J. Glaciol 1952, 2, 82–93. [Google Scholar]
- Nye, J.F. A method of determining the strain-rate tensor at the surface of a glacier. J. Glaciol 1959, 3, 409. [Google Scholar]
- Kääb, A.; Reichmuth, T. Advance mechanisms of rock glaciers. Permafrost Periglac Process 2005, 16, 187–193. [Google Scholar]
- Kneisel, C.; Kääb, A. Mountain permafrost dynamics within a recently exposed glacier forefield inferred by a combined geomorphological, geophysical and photogrammetrical approach. Earth Surf. Proc. Land 2007, 32, 1797–1810. [Google Scholar]
- Kääb, A.; Vollmer, M. Surface geometry, thickness changes and flow fields on creeping mountain permafrost: Automatic extraction by digital image analysis. Permafrost Periglac. Process 2000, 11, 315–326. [Google Scholar]
- Kääb, A. Monitoring high-mountain terrain deformation from repeated air- and spaceborne optical data: Examples using digital aerial imagery and ASTER data. ISPRS J. Photogramm 2002, 57, 39–52. [Google Scholar]
- Wangensteen, B.; Tønsberg, O.M.; Kääb, A.; Eiken, T.; Hagen, J.O. Surface elevation change and high resolution surface velocities for advancing outlets of Jostedalsbreen. Geografiska Annaler: Series A 2006, 88, 55–74. [Google Scholar]
- Casson, B.; Delacourt, C.; Baratoux, D.; Allemand, P. Seventeen years of the “La Clapière” landslide evolution analysed from ortho-rectified aerial photographs. Engineering Geology 2003, 68, 123–139. [Google Scholar]
- Lebourg, T.; Binet, S.; Tric, E.; Jomard, H.; El Bedoui, S. Geophysical survey to estimate the 3D sliding surface and the 4D evolution of the water pressure on part of a deep seated landslide. Terra Nova 2005, 17, 399–406. [Google Scholar] [Green Version]
- Chemenda, A.I.; Bois, T.; Bouissou, S.; Tric, E. Numerical modelling of the gravity-induced destabilization of a slope: The example of the La Clapière landslide, southern France. Geomorphology 2009, 109, 86–93. [Google Scholar]
- Keys, R.G. Cubic convolution interpolation for digital image processing. IEEE Trans. Acoust. Speech 1981, 29, 1153–1160. [Google Scholar]
- Dodgson, N.A. Image Resampling; University of Cambridge Computer Laboratory: London, UK, 1992; p. 264. [Google Scholar]
- Förstner, W. Reliability analysis of parameter estimation in linear models with applications to mensuration problems in computer vision. Comput. Vis. Graph 1987, 40, 273–310. [Google Scholar]
- Debella-Gilo, M.; Kääb, A. Locally adaptive template sizes for matching repeat images of earth surface mass movements. ISPRS J. Photogramm 2011. submitted.. [Google Scholar]
- Arenson, L.; Hoelzle, M.; Springman, S. Borehole deformation measurements and internal structure of some rock glaciers in Switzerland. Permafrost Periglac. Process 2002, 13, 117–135. [Google Scholar]
- Guglielmi, Y.; Cappa, F.; Binet, S. Coupling between hydrogeology and deformation of mountainous rock slopes: Insights from La Clapière area (southern alps, france). Comptes Rendus Geosciences 2005, 337, 1154–1163. [Google Scholar]
- Ackermann, F. Digital image correlation: Performance and potential application in photogrammetry. Photogramm. Rec 1984, 11, 429–439. [Google Scholar]
- Leprince, S.; Barbot, S.; Ayoub, F.; Avouac, J.P. Automatic and precise orthorectification, coregistration, and subpixel correlation of satellite images, application to ground deformation measurements. IEEE Trans. Geosci. Remote Sens 2007, 45, 1529–1558. [Google Scholar]









| Transformation Parameters of Equations (3) and (4) | Deformation Type Quantified | Visual Example | Significance in Mass Movement |
|---|---|---|---|
| p1 and p4 | Translation |  | Quantifies shift, creep, slip, and slide. Change in position disregarding shape and size. |
| p2 and p6 | Scaling |  | Measures change in length due to compressive/extending motion. Measures normal strain (elongation). |
| p3 and p5 | Shearing (and/or rotation) |  | The slippage of orthogonal masses in relation to one another (and/or rigid rotation of the mass). Measures shear strain and/or rotation angle. |
| Mass Movement | Muragl Rockglacier (ma−1) | Nigardsbreen Glacier (md−1) | La Clapière Landslide (ma−1) |
|---|---|---|---|
| Mean | 0.18 | 0.57 | 0.4 |
| Standard deviation | 0.09 | 0.32 | 0.32 |
| Maximum | 0.5 | 1.1 | 2.75 |
| Image Pair | Mean Precision of the Shift Parameters (Pixels) | |
|---|---|---|
| X-Shift (p1) | Y-Shift (p4) | |
| Muragl rockglacier creep | 0.07 | 0.06 |
| Nigardsbreen glacier flow | 0.11 | 0.12 |
| La Clapière landslide | 0.13 | 0.15 |
| Image Pair | MAD (in pixels) | Percent MAD | |
|---|---|---|---|
| NCC | LSM | Reduction by LSM | |
| Simulated (σ2n = 0.01) | 0.38 | 0.04 | 90 |
| Simulated (σ2n = 0.1) | 0.42 | 0.2 | 52 |
| Muragl rockglacier creep | 2.25 | 1.4 | 37 |
| Nigardsbreen glacier flow | 0.47 | 0.34 | 27 |
| La Clapière landslide | 2.5 | 2.01 | 19 |
| Deformation Parameter | Mean | Standard Deviation | Minimum | Maximum |
|---|---|---|---|---|
| Longitudinal strain rate (ma−1) | 0.00012 | 0.0018 | −0.0077 | 0.0085 |
| Transverse strain rate (a−1) | 0.00039 | 0.0016 | −0.0061 | 0.0077 |
| Shear strain rate (a−1) | 0.0015 | 0.0016 | 0 | 0.01 |
| Rotation rate (degrees a−1) | 0.068 | 0.066 | 0 | 0.44 |
| Deformation Parameter | Mean | Standard Deviation | Minimum | Maximum |
|---|---|---|---|---|
| Longitudinal strain rate (d−1) | −0.0003 | 0.0024 | −0.01 | 0.012 |
| Transverse strain rate (d−1) | −0.00067 | 0.002 | −0.01 | 0.007 |
| Shear strain rate (d−1) | 0.0017 | 0.002 | 0 | 0.019 |
| Rotation rate (degrees d−1) | 0.072 | 0.076 | 0 | 0.54 |
| Deformation Parameter | Mean | Standard Deviation | Minimum | Maximum |
|---|---|---|---|---|
| Longitudinal strain rate (a−1) | −0.0009 | 0.005 | −0.028 | 0.017 |
| Transverse strain rate (a−1) | −0.0007 | 0.005 | −0.01 | 0.017 |
| Shear strain rate (a−1) | 0.005 | 0.005 | 0 | 0.03 |
| Rotation rate (degrees a−1) | 0.15 | 0.13 | 0 | 0.7 |
| Mass Movement Type | Precision of the Parameters | |||
|---|---|---|---|---|
| Kp2 (p2 = 1 + εx) | Kp3 (P3 = γ1) | Kp5 (P5 = γ2) | Kp6 (P6 = 1 + εy) | |
| Muragl rockglacier creep | 0.002 (0.997) | 0.002 (0.021) | 0.002 (0.022) | 0.002 (0.998) |
| Nigardsbreen glacier flow | 0.003 (0.997) | 0.003 (0.013) | 0.003 (0.021) | 0.003 (0.999) |
| La Clapière landslide | 0.003 (1.001) | 0.003 (0.038) | 0.003 (0.044) | 0.003 (0.098) |
| Deformation Parameters | MAD | ||
|---|---|---|---|
| Nigardsbreen Glacier (d−1) | Muragl Rockglacier (a−1) | La Clapière Landslide (a−1) | |
| ɛ̇L | 0.0001 | 0.0005 | 0.006 |
| ɛ̇T | 0.0001 | 0.0006 | 0.002 |
| ɛ̇LT | 0.0002 | 0.001 | 0.005 |
| φ̇TL | 0.008 | 0.05 | 0.1 |
Share and Cite
Debella-Gilo, M.; Kääb, A. Measurement of Surface Displacement and Deformation of Mass Movements Using Least Squares Matching of Repeat High Resolution Satellite and Aerial Images. Remote Sens. 2012, 4, 43-67. https://doi.org/10.3390/rs4010043
Debella-Gilo M, Kääb A. Measurement of Surface Displacement and Deformation of Mass Movements Using Least Squares Matching of Repeat High Resolution Satellite and Aerial Images. Remote Sensing. 2012; 4(1):43-67. https://doi.org/10.3390/rs4010043
Chicago/Turabian StyleDebella-Gilo, Misganu, and Andreas Kääb. 2012. "Measurement of Surface Displacement and Deformation of Mass Movements Using Least Squares Matching of Repeat High Resolution Satellite and Aerial Images" Remote Sensing 4, no. 1: 43-67. https://doi.org/10.3390/rs4010043
APA StyleDebella-Gilo, M., & Kääb, A. (2012). Measurement of Surface Displacement and Deformation of Mass Movements Using Least Squares Matching of Repeat High Resolution Satellite and Aerial Images. Remote Sensing, 4(1), 43-67. https://doi.org/10.3390/rs4010043




