Abstract
Located within the Altiplano at 3,686 m above sea level, Lake Poopó is remarkably shallow and very sensitive to hydrologic recharge. Progressive drying has been observed in the entire Titicaca-Poopó-Desaguadero-Salar de Coipasa (TPDS) system during the last decade, causing dramatic changes to Lake Poopó’s surface and its regional water supplies. Our research aims to improve understanding of Lake Poopó water storage capacity. Thus, we propose a new method based on freely available remote sensing data to reproduce Lake Poopó bathymetry. Laser ranging altimeter ICESat (Ice, Cloud, and land Elevation Satellite) is used during the lake’s lowest stages to measure vertical heights with high precision over dry land. These heights are used to estimate elevations of water contours obtained with Landsat imagery. Contour points with assigned elevation are filtered and grouped in a points cloud. Mesh gridding and interpolation function are then applied to construct 3D bathymetry. Complementary analysis of Moderate Resolution Imaging Spectroradiometer (MODIS) surfaces from 2000 to 2012 combined with bathymetry gives water levels and storage evolution every 8 days.
1. Introduction
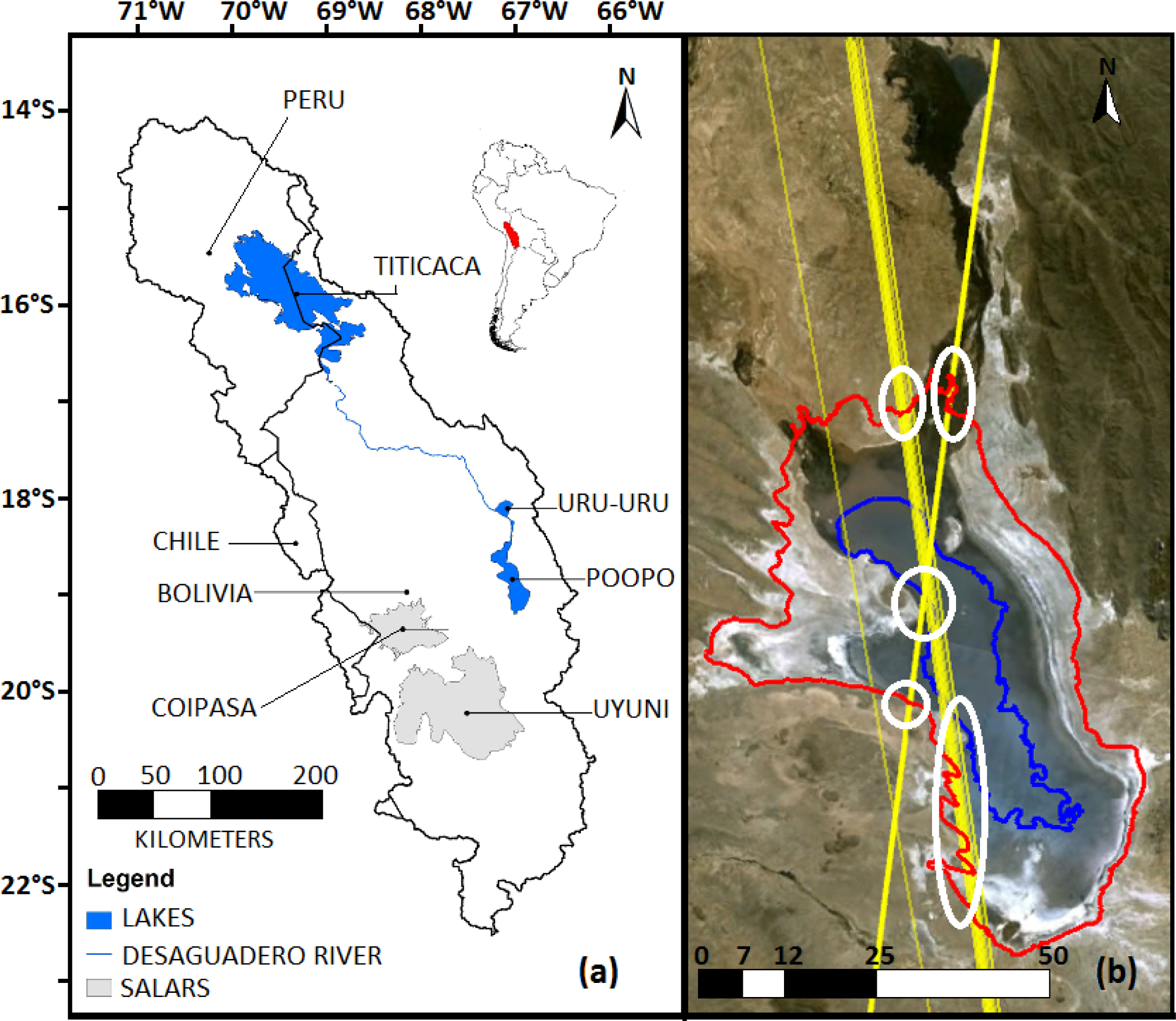
In the present study, we propose a new method of bathymetry restitution developed for the Lake Poopó in Bolivia. With this method we have recovered Lake Poopó water levels and storage time series which have remained unknown until now. The method is easy to implement and is based on freely available remote sensing data. Geographical applicability of our method is however limited to lakes situated in arid or semi-arid regions. Lake Poopó’s system (17°10′–19°53′S and 67°50′–66°24′W, at 3,686 m above sea level) is comprised of two interconnected lakes, Lake Uru-Uru and Lake Poopó (Figure 1a). Lake Poopó is remarkably shallow and sensitive to climate variations. Its shallow zone is seasonally dependent on hydrologic recharge during the wet season, which varies in extent from almost 0 to 3,000 km2 [1]. Lake Poopó is part of the Titicaca-Poopó-Desaguadero-Salar de Coipasa water system (TPDS) and plays an important role in the regional water budget. Unfortunately, Lake Poopó water levels and storage are not recorded. Previous works have attempted to correlate the dimensions of Lake Poopó with its depth in a relatively linear fashion [2,3], or have estimated Lake Poopó levels directly from Lake Titicaca level variations [2,4]. Accurate information about the water stage or water supplies was not available in these studies. Benefiting from years of experience, space borne altimetry offers the best solution for ungauged or difficult to access lakes and rivers. The usual approach consists in establishing remote sensed hypsometry of a lake, based on the simple assumption that every water level change induces a change of the water surface. If the water surface variation is large enough, it can be easily detected with multispectral high or medium resolution imagery [5–8]. When correlated with level variation time series or topographic measurements, the surface information can be converted into volume [3,6,9]. This technique was successfully applied in some studies [5,6] but unfortunately, Topex/Poseidon (T/P) is the only reliable radar altimeter satellite to cover Lake Poopó, and then only on its shallow western side, which is intermittently covered by water. While topographic, sonar and airborne lidar measurements are costly and difficult to obtain [3] it remains impossible to produce regular time series of Lake Poopó levels with radar altimetry. Nevertheless, several other methods and instruments can be used to create a lake bathymetry. One of these methods is very high resolution stereo imaging [10] but this method cannot be applied over flat and uniform surfaces of the lake bed. Photobathymetry [11,12] can be a solution for very shallow lakes. This method requires high resolution imaging and several assumptions about water turbidity and bottom reflectance. In the case of Lake Poopó these limitations can lead to a bathymetry with non-uniform and average vertical precision. We also examined the possibility of applying SAR imaging. However, this technique does not provide enough information in terms of vertical precision [13]. In looking for centimetric precision, we propose using the first laser-ranging instrument GLAS onboard the ICESat mission. ICESat provides even better accuracy than radar altimetry in non-clouded conditions [14–17] and has already been applied in lake surface/depth studies [18,19]. A rapid examination of ICESat tracks shows their perfect location just in the middle of Lake Poopó (Figure 1b). With a 91-day orbit it is possible to produce a limited time series between 2004 and 2009. In [16], the ICESat data have been validated over the Salar de Uyuni and it was found that the accuracy of laser ranging measurements is ±3 cm over dry land. Our research aims to exploit this laser-ranging high precision to estimate elevations of water contours obtained with Landsat imagery and transform them into isolines (isobaths). In another study, Abileah and Vignudelli [20] propose the combination of radar altimetry and imagery to calculate Lake Nasser levels and depth contours. In contrast, our method takes laser altimetry measurements directly over the bare ground when the lake reaches a very low stage. This approach avoids uncertainties due to wave height or wind direction because laser altimetry measures vertical height with high precision over dry land. Finally complementary analysis of Moderate Resolution Imaging Spectroradiometer (MODIS) surfaces from 2000 to 2012 combined with bathymetry gives water levels and storage evolution every 8-day. The article is organized as follows: Section 2 describes the data Section 3 describes the methodology for estimating contour elevations. Section 4 presents the results. Conclusions are drawn in Section 5.
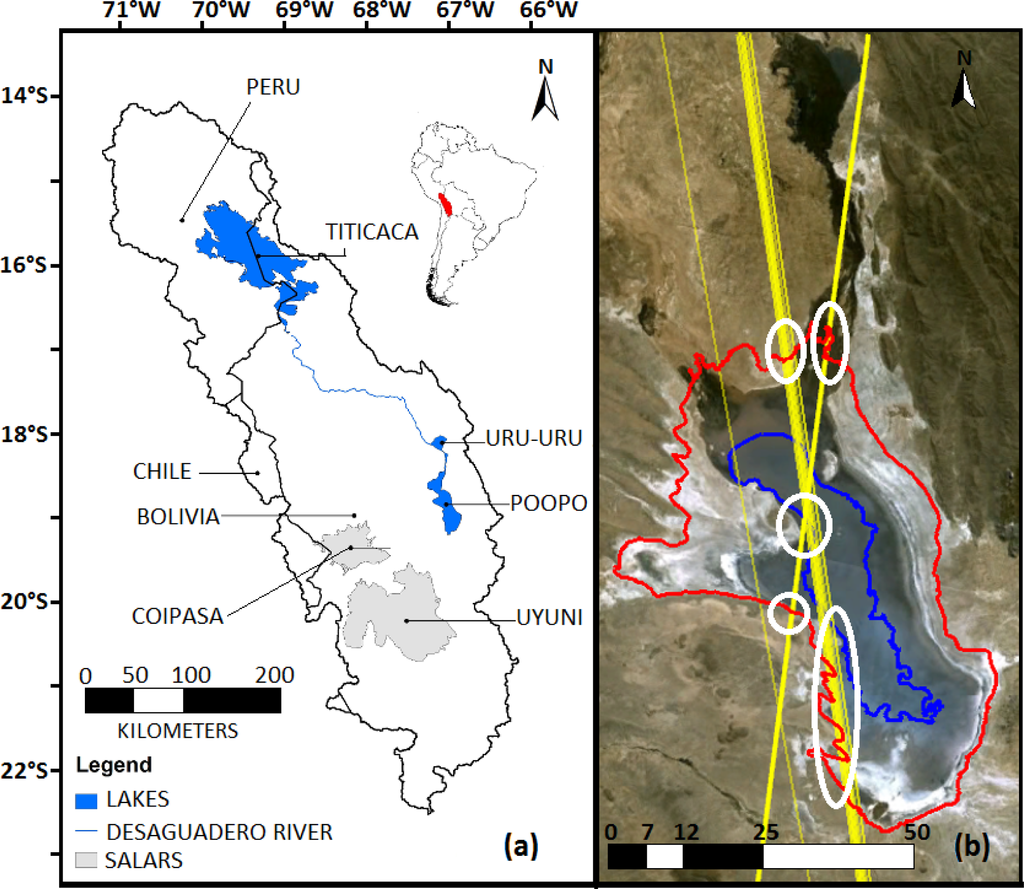
Figure 1.
Lake Poopó, (a) geographical overview, (b) Ice, Cloud, and land Elevation Satellite (ICESat) ascending and descending tracks (yellow lines) over Lake Poopó. White circles represent zones where ICESat elevation is intersected with water contours. Maximum (red) and minimal (blue) water extents of our bathymetry are shown.
2. Data
Through the USGS GLOVIS images archive [21] 18 cloud free scenes from Landsat 7 ETM+ and Landsat 5 TM were selected between 1999 and 2008 (Section 3.2). All selected Landsat scenes have Standard Terrain Correction (Level 1T). Image projection is UTM zone 19N, with 30 × 30 m of ground resolution. Since the first Landsat mission in 1972, there are over 150 suitable scenes now available at no cost through the Landsat archives. Terra Moderate Resolution Imaging Spectroradiometer (MODIS) was launched in 1999 on the Terra satellite. Between 2000 and 2012, 560 MODIS scenes were downloaded [22]. Data from the first laser-ranging instrument GLAS on board the ICESat 2003–2009 mission is used [23]. With a 91-day orbit, the ICESat GLA06 v33 [17] global elevation product is used, prior to the Correction to ICESat Data Product Surface Elevations announced in January 2013 [24]. It provides laser footprint geolocation and surface elevations determined with ice sheet specific algorithms [25]. Elevation values are referred to the T/P ellipsoid. GLA14 dataset showing only 1/3 of available flyovers was discarded.
3. Methodology
3.1. General Introduction
In this study, we use laser ranging information to convert water masks obtained with Landsat imagery (Section 3.2) into isolines (Section 3.4). Isolines (isobaths) are obtained by extracting water area contours and by interpolating ground elevation values in each location where water contours intersect with ICESat elevation profiles. Individual points from isolines are grouped in a cloud of 3D points and a bathymetry is created using grid meshing and interpolating function (Section 3.5). The bathymetry was created in the limits of existing ICESat profiles and depths below 3,685.70 m are not shown. Moreover, between 2000 and 2012, complementary analysis of variations of water area inferred from MODIS images classification (Section 3.2) was performed and linked to bathymetry through the Landsat/MODIS correlation curve. Lake Poopó water levels and storage are retrieved by combining bathymetry and MODIS surfaces time series.
3.2. Water Surface Masks for Bathimetry and Water Surface Area Variations
The Landsat 5 and Landsat 7 images selected for this study were strictly limited to cloud free and inundation free scenes in order to reduce difficulties in processing and interpretation. In order to extract water surfaces from Landsat images, digital numbers in each spectral band were converted to surface reflectance using the calibration coefficients provided in the image’s metadata. The water masks were obtained by combining supervised classification of the Normalized Difference Water Index (NDWI) [26], Modified Normalized Difference Water Index (MNDWI) [27], Weighted Water Index [28,29] and single band thresholding [30,31]. Since the threshold value of the NDWI for delineating open water features is known to vary in multi-temporal studies [27,32] we manually adjusted the NDWI threshold on a satellite-by-satellite basis. Manual adjustment of the threshold could achieve a more accurate result in the water delineation [27,33,34]. Co-registered water masks were sorted by decreasing surface order and then superposed. Any incoherencies between consecutive masks, e.g., when a lower surface contour exceeded a greater surface contour, were binary eroded to leave at least one pixel of spacing between masks. Contours from different images were converted into two datasets: one representing the main water body contours, the other representing major interior details such as islands or sandbars. Moreover, the MODIS instrument provides new remote sensing opportunities for global daily monitoring with improved spatial resolution for land observation at 250 and 500 m and improved spectral band placement [35]. The MODIS products include seven bands in the visible to middle infrared. Shallow depths such as those observed over the Lake Poopó; increase considerably the amount of solar energy reflected by a water body [36,37] showed that the strong water absorption at wavelength > 1 μm in MODIS bands (number 5, 6 and 7) does not allow illumination of the sediments in the water or at the shallow bottom of a water column. In this work a simple unsupervised classification based on threshold technique was performed on MODIS Band 5 to delineate the shallow, open water of the Lake Poopó. It has been assumed that for small value of surface reflectance allows characterizing open water, without any consideration on any normalized water index. This method was developed for floodplains in Arid zones [7] and has been tested and applied in other studies [1,38–42]. Surface analysis of a set of 550 8-day MODIS mosaics was strictly limited to the main water body. Flood plains and rivers outlets were ignored. Finally, as MODIS and Landsat images have different resolutions, we established link between MODIS surfaces and our bathymetry through Landsat/MODIS correlation curve in Section 4. Surfaces lower than 450 km2 are not used in this study, and are not shown on correlation and hypsometry curves.
3.3. ICESat Profiles Selection
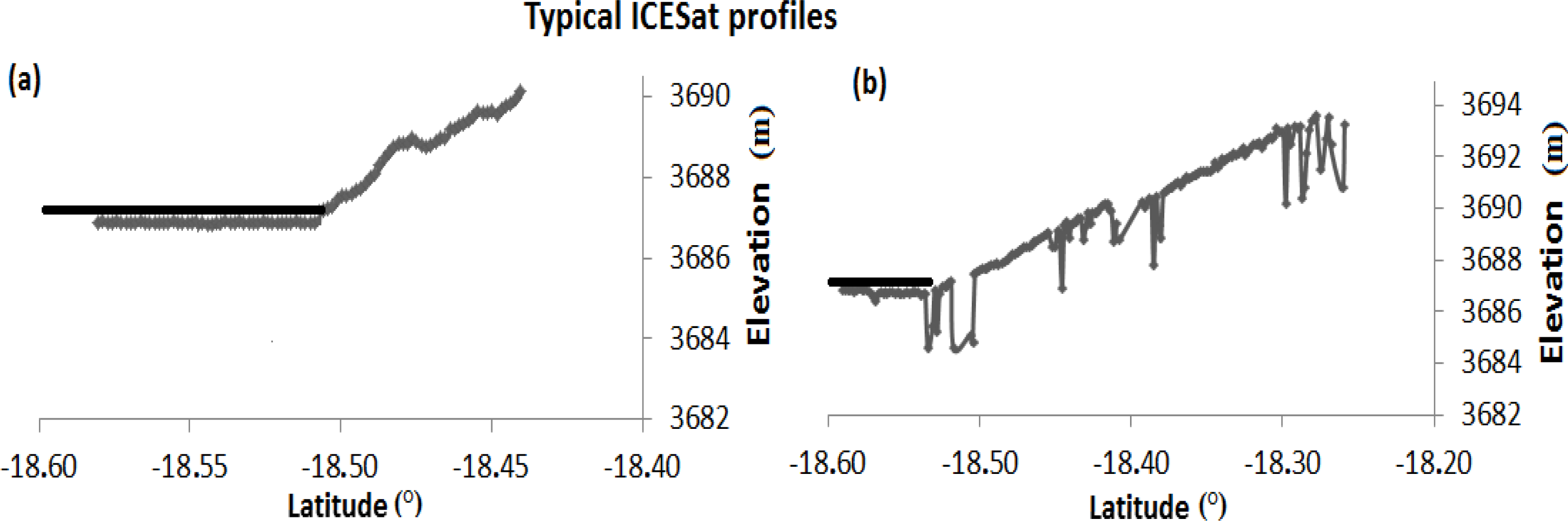
In Figure 2, typical ICESat profiles from the northern part of Lake Poopó are shown. Water surface can be identified in the lowest part of each profile. Several outliners’ points with differences of 20 to 40 cm to the water level can be attributed to waveform saturation [43].
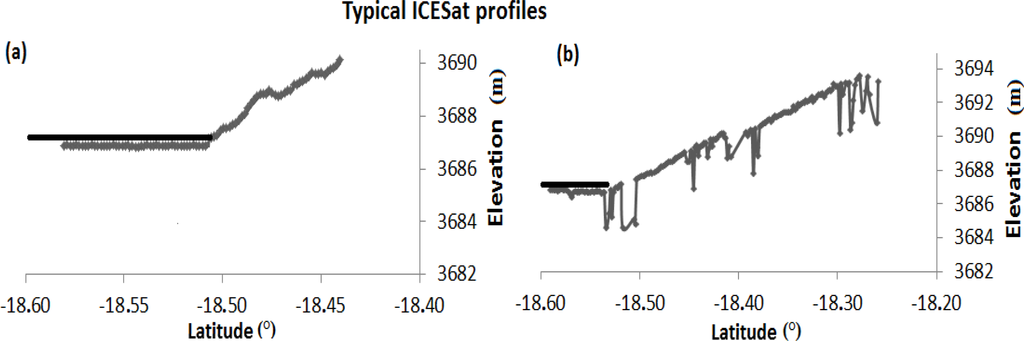
Figure 2.
Typical ICESat profiles from northern Lake Poopó. Threshold black line 5 cm above water surface helps to exclude all points taken over water. (a) Example of profile taken during dry period (b) This profile shows many saturated points on the lake slope, which suggest crossing over surface with different optical properties (i.e., water).
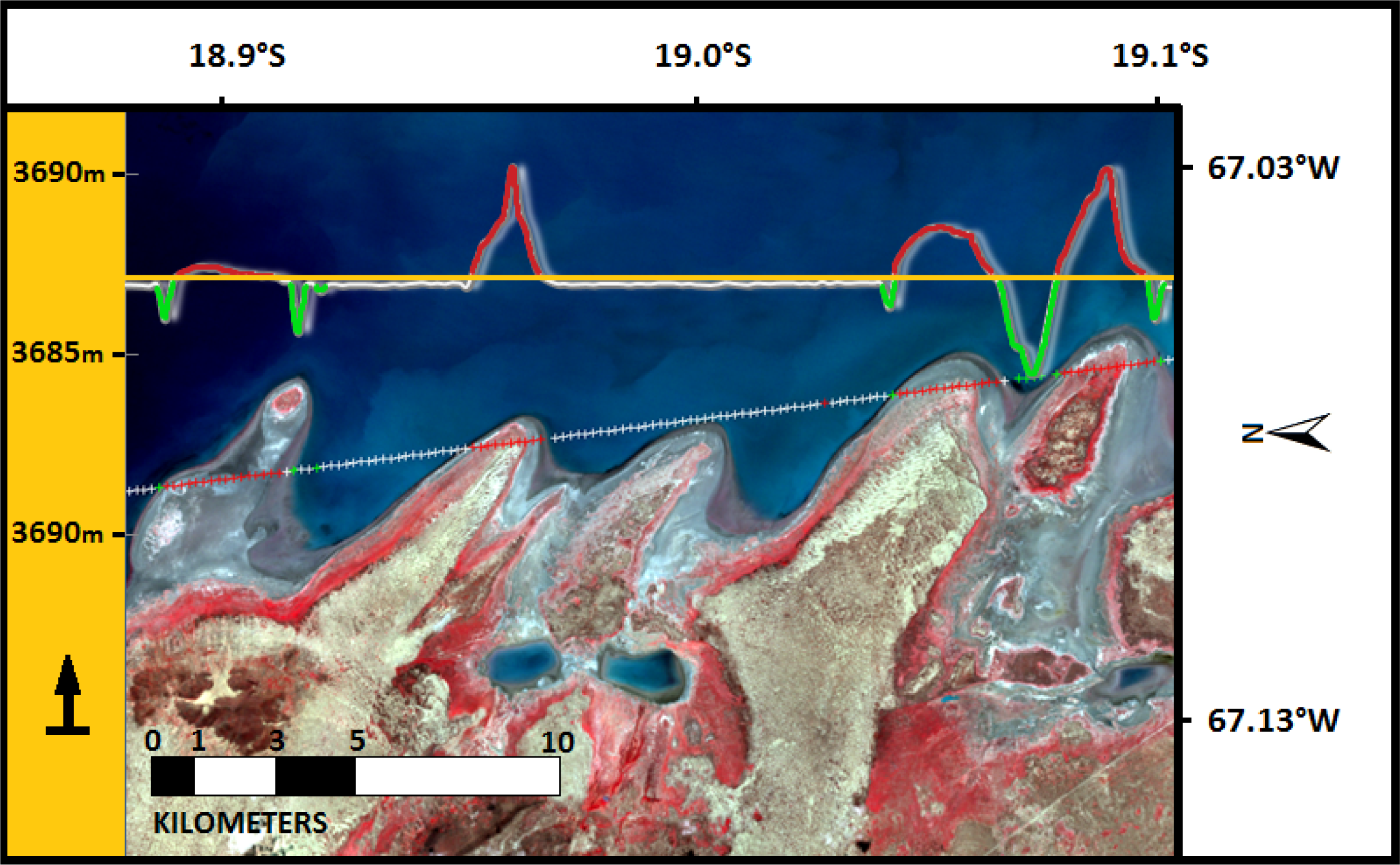
Further examination coupled with optical imagery permit to localize all saturated points in water-ground/mud transition zones (Figure 3). Saturation elevation correction (i_satElevCorr) as suggested by the GLAS Altimetry Data Dictionary [44] was applied. However, in transition zones this correction can produce sporadically underestimated elevations. All elevation profiles taken during or immediately after the February-March rain/flood season were rejected. These profiles can be easily identified by the presence of signal saturation zones (Figure 2b). The water stage of each ICESat profile is represented by a threshold value that lays 5 cm above the water surface (Figure 2a,b and Figure 3). This approach allows handling saturation problems occurring inside the main water body at the intersection of islands, dunes and capes. During processing, this threshold value is used to exclude from interpolation (in Section 3.4) all points that lay at the water level (points below threshold). Last, for all retained ICESat profiles (Table 1), elevation values referred to the T/P ellipsoid are converted to EGM2008 geoidal heights.
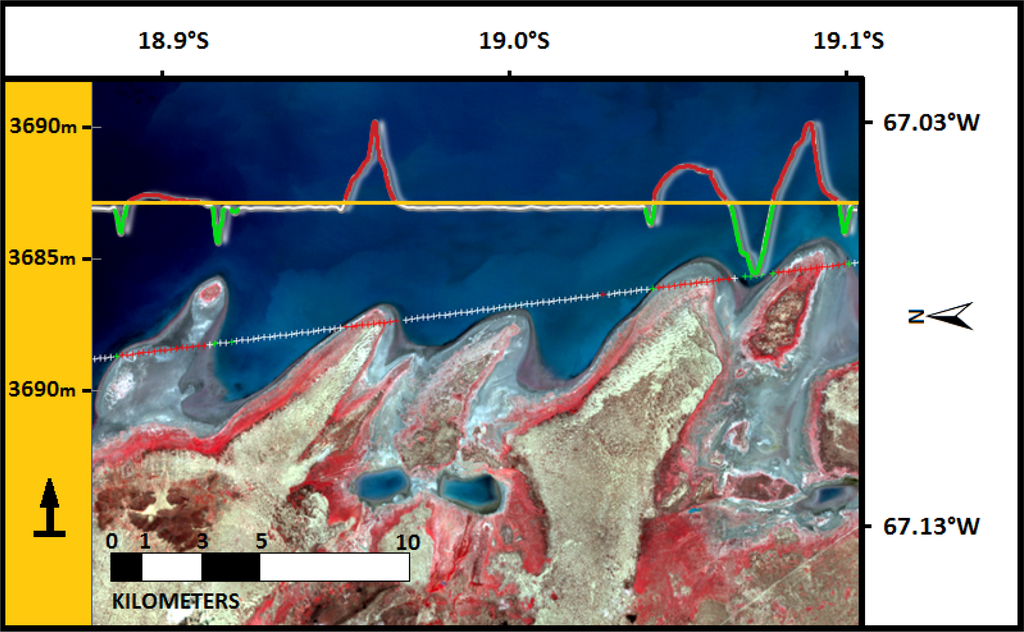
Figure 3.
ICESat profile is superposed on a Landsat image (white, red and green crosses). In addition, 2D plots show ICESat elevation values at corresponding latitudes. Water level is approximated by orange horizontal threshold line. Points above water (red) and saturated points below water (green) are shown.

Table 1.
List of ICESat profiles with no visible saturation problems.
3.4. Creating Isolines (Isobaths)
For each main water body contour, a simple algebraic method of line segment intersection [45,46] is used to determine geographic coordinates where water contour and ICESat elevation profiles intersect. For each intersection several elevation values are linearly interpolated using all ICESat profiles. If (for a given ICESat profile), at least one measurement lies above the “water” threshold, the interpolated value is kept. Using this approach, at least several elevation values can be obtained for each main water body contour. All elevation values obtained within one intersection were filtered to discard erroneous points. Lake Poopó is exceptionally shallow and given large values of possible outliers in relation to the small number of valid points, the median offers a more robust predictor than the mean. Thus the median value is retained as final isoline elevation, and is also assigned to all interior contours of the same layer. All isolines, except the bottom one, were obtained with previously described methodology. For the lowest stage of the lake we first identified 5 October 2009 ICESat flyover as the lowest valid elevation profile. We then extracted a water surface mask from Landsat 7 image taken on 2 October 2009 and we completed it with Landsat 5 image from 10 October 2009. The elevation for the lowest stage mask was obtained by calculating the median value of all ICESat elevation points lying within the body of water.
3.5. Bathymetry
The bathymetry reconstruction was performed with Matlab functions: TriScatteredInterp function [47], allowing interpolation on a regular grid from irregularly scattered points, and MeshGrid function for grid meshing [48]. A 5 × 5 pixel median filter was applied to smooth irregularities and remove artifacts. The bathymetry keeps the same pixel size as input Landsat images. For the purposes of comparison, Lake Poopó hypsometry is estimated directly from bathymetry using Heron’s formula [8]. The methodology presented above allowed us to calculate the Lake Poopo bathymetry and water storage variations as shown in the following section.
4. Results
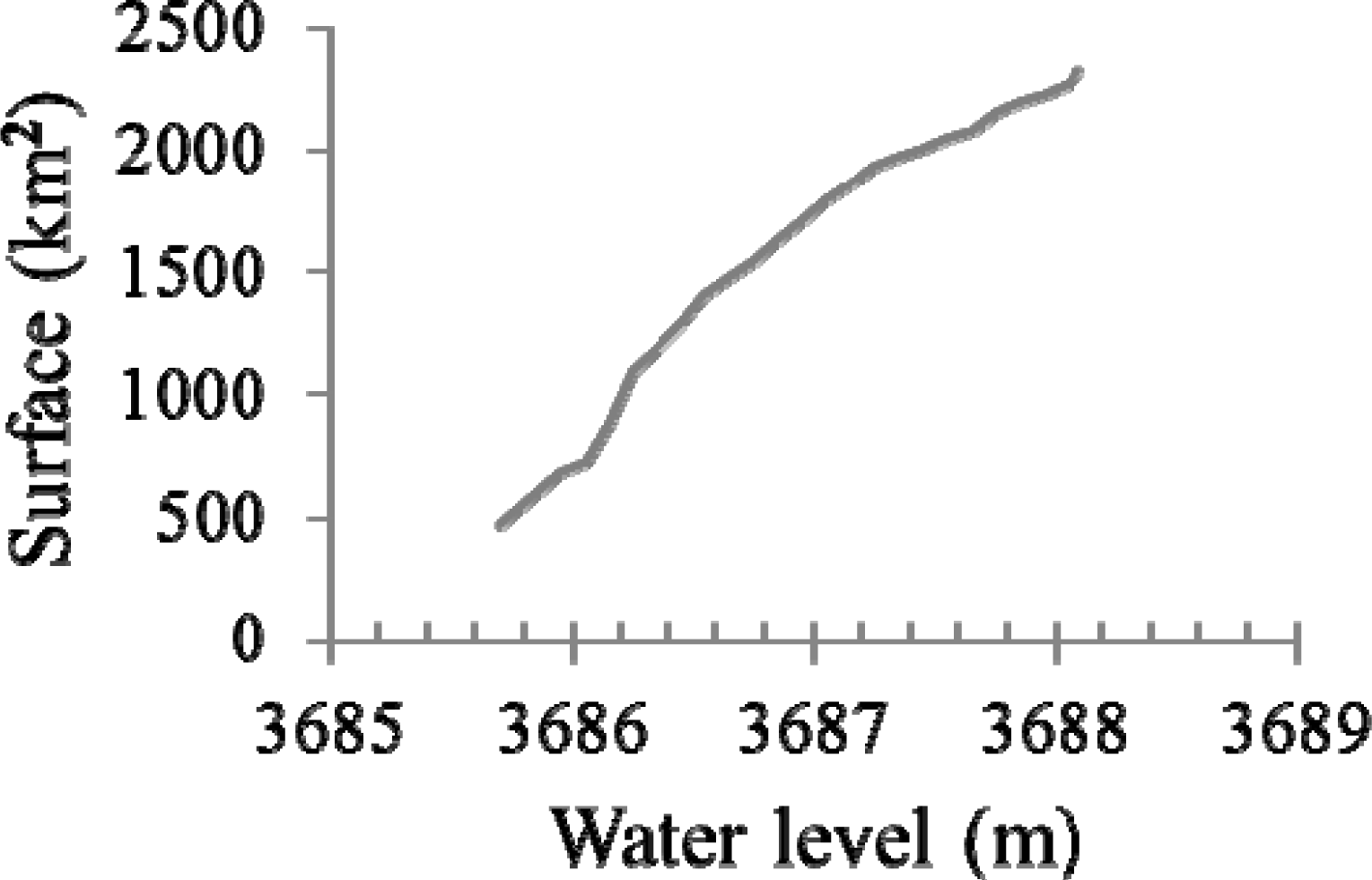
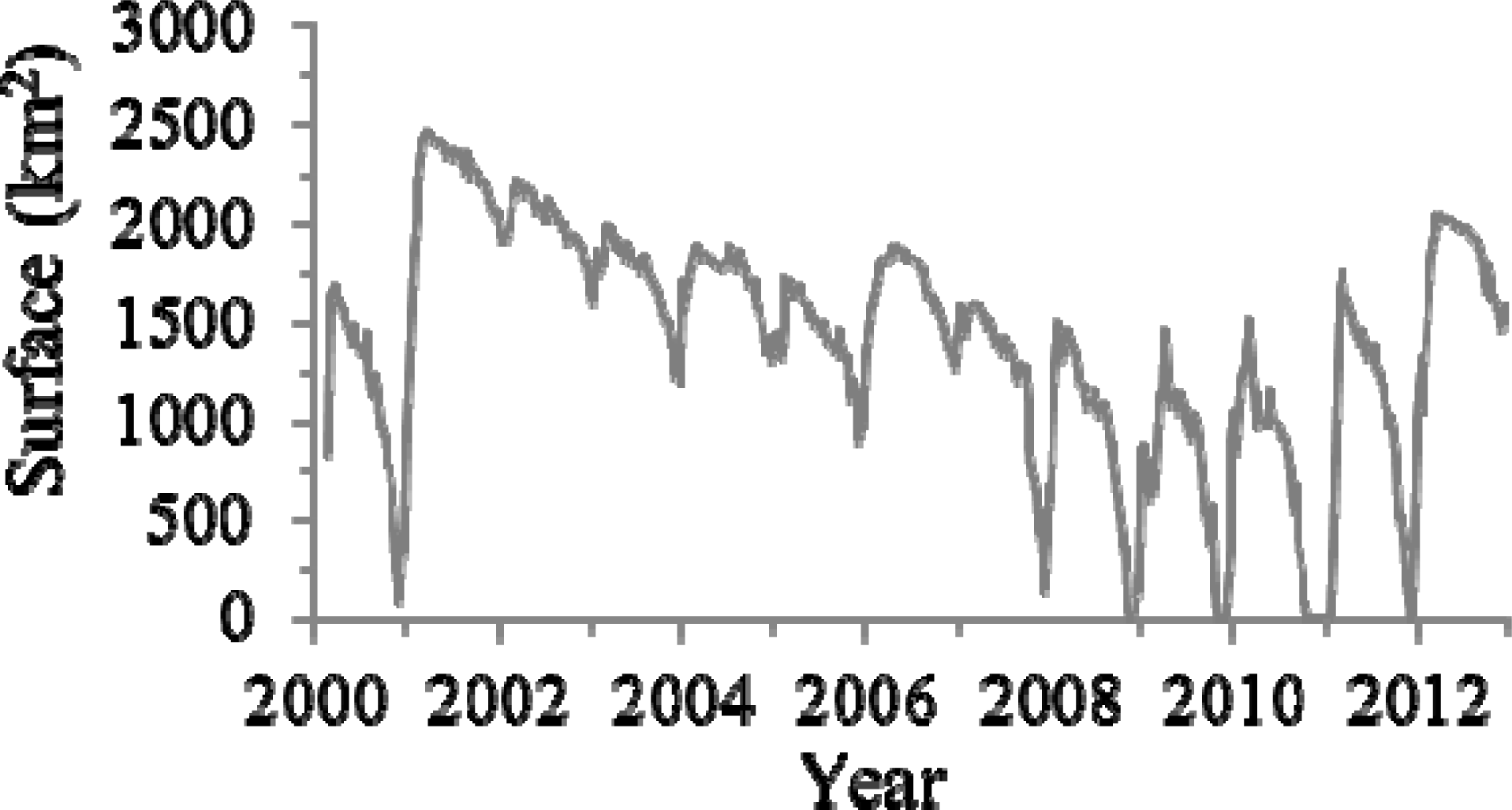
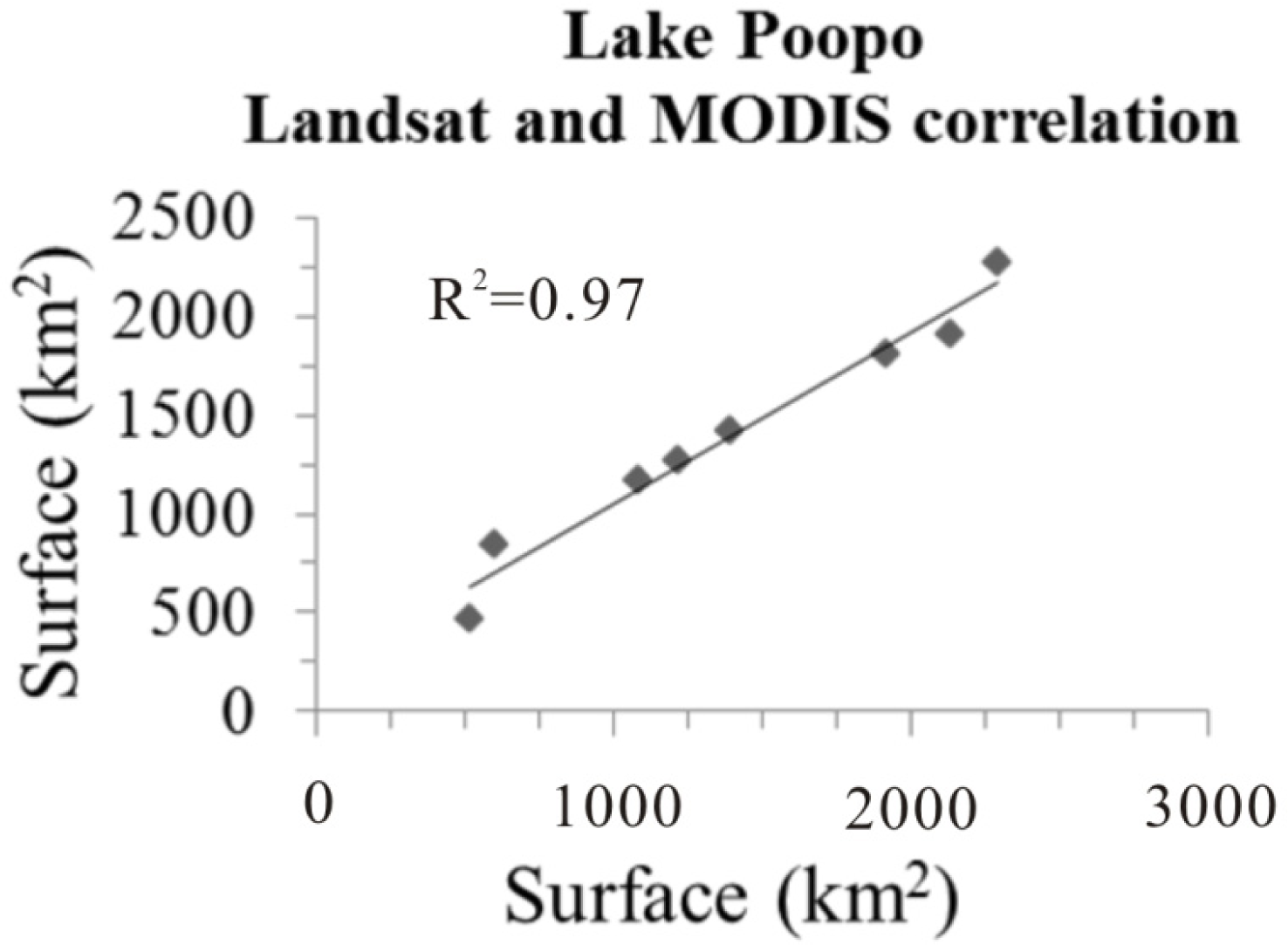
Lake Poopó hypsometry is presented on Figure 4. The lowest surface attributed to the 3,685.70 m elevation (ICESat 5 October 2009 flyover) is 467 km2 while the highest point on the curve has 3,688.10 m of elevation for a surface of 2,316 km2. The MODIS surfaces (Figure 5) are linked to bathymetry through the Landsat/MODIS calibration curve (Figure 6) and a correlation coefficient of R2 = 0.97 was obtained.
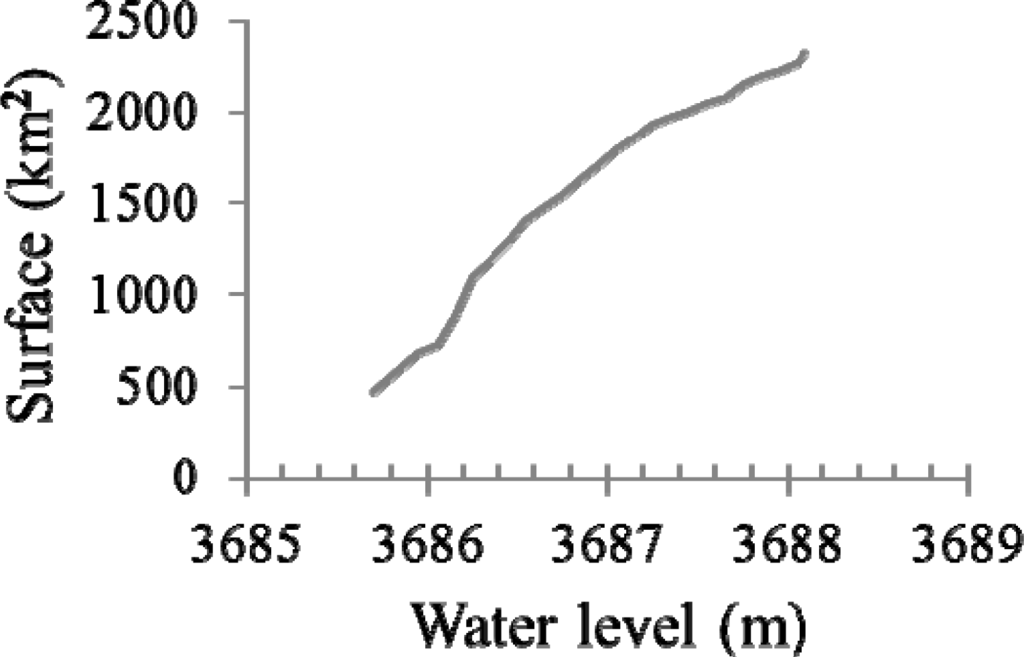
Figure 4.
Lake Poopó hypsometry.
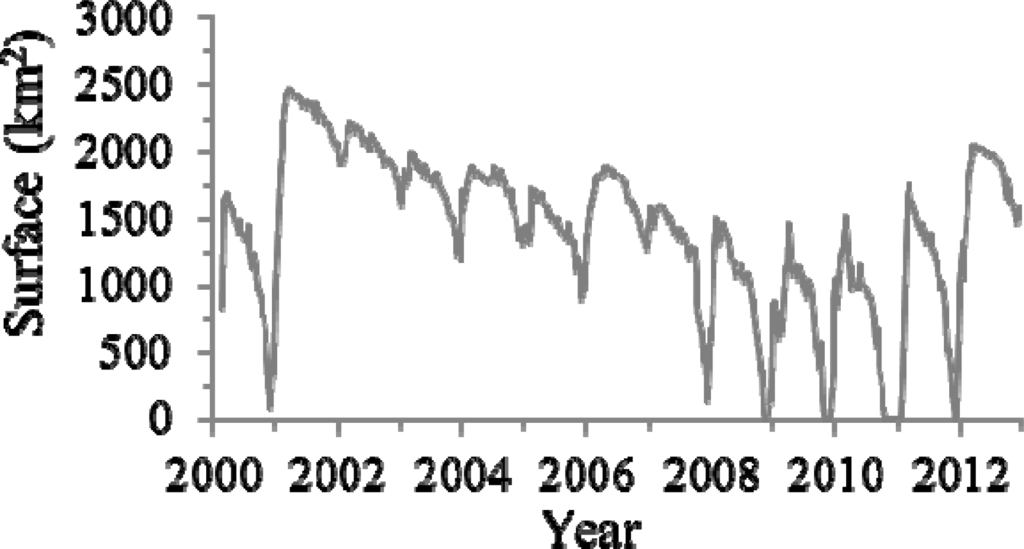
Figure 5.
Moderate Resolution Imaging Spectroradiometer (MODIS) surfaces between 2000 and 2012.
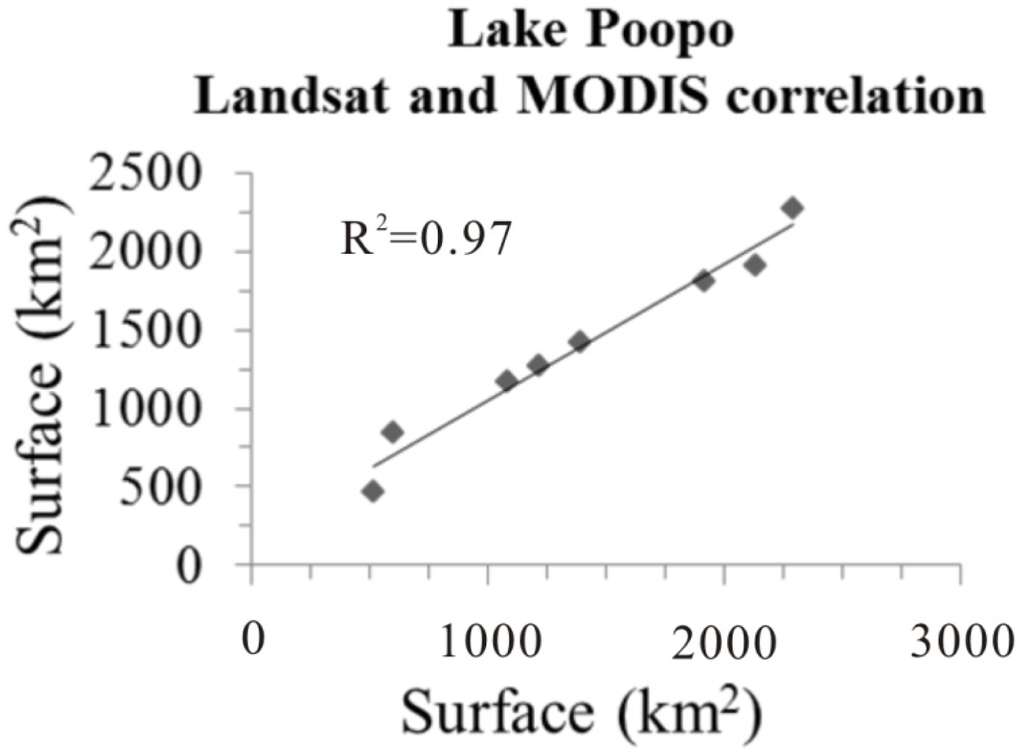
Figure 6.
Landsat/MODIS correlation curve.
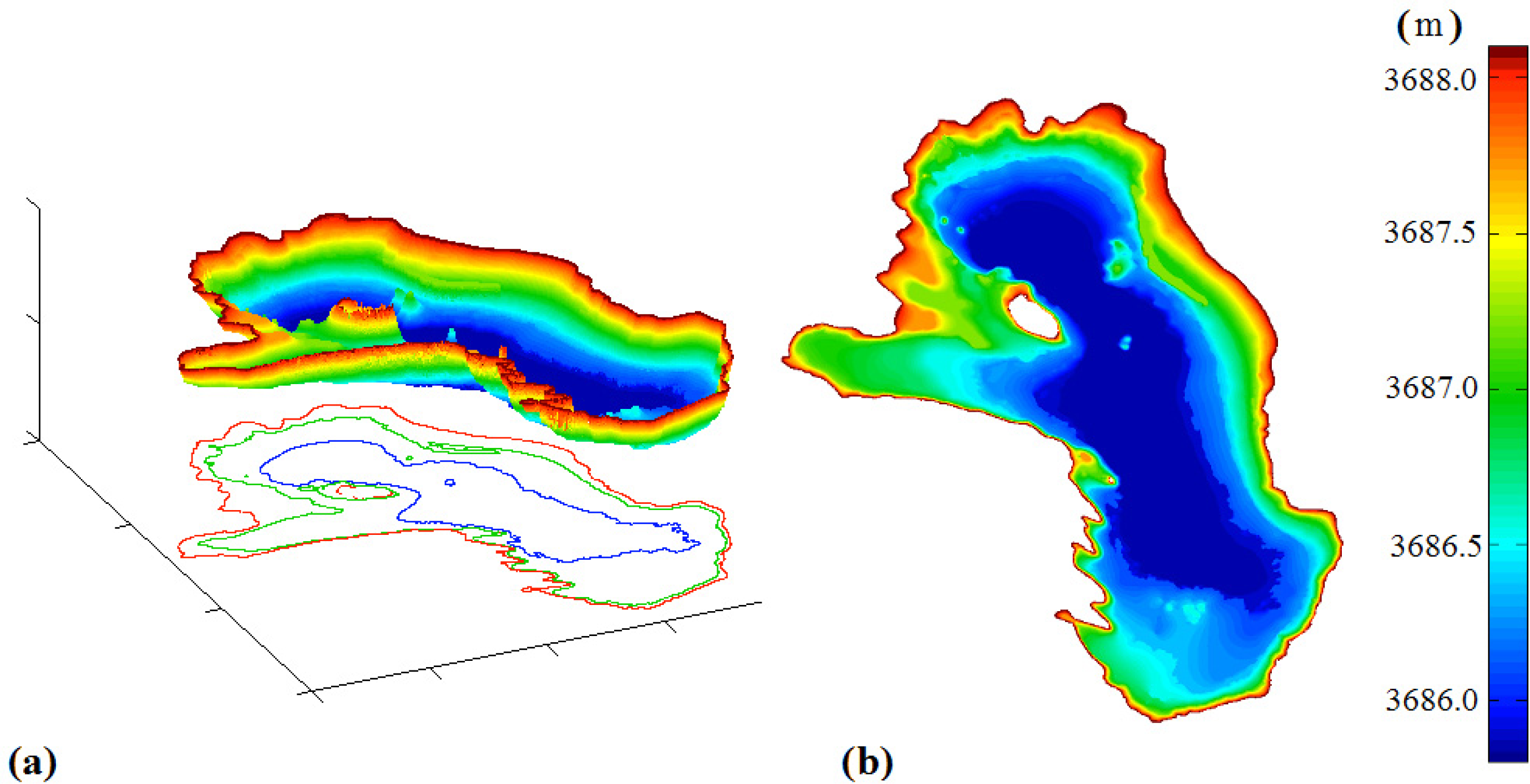
A top and inclined view of the final bathymetry is presented in Figure 7a,b. Table 2 shows relations between isolines vertical elevation, the elevation standard deviation (SD) and the number of profiles used for the calculation. The SD increases with the number of profiles and reaches 0.11 m for the highest contour. Vertical SD of the bottom mask calculated separately is 0.05 m. The precision of our method and repeatability has been confirmed by processing masks with similar water surface extension from images taken at different dates (a1–a2, b1–b2 in Table 2). In both cases, identical elevations were obtained. The bathymetry vertical resolution can be considered as decimetric.
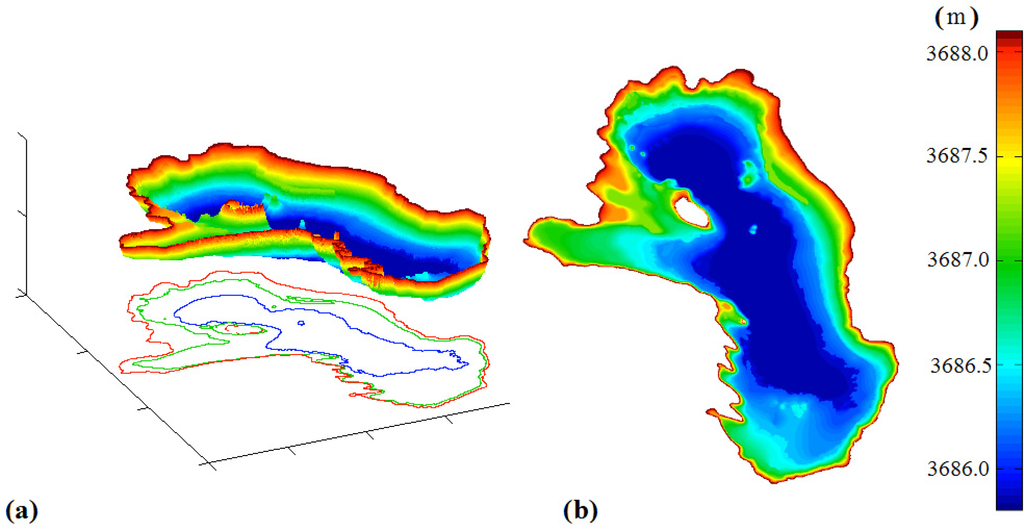
Figure 7.
Bathymetry of Lake Poopó (a) inclined view (b) viewed from top.

Table 2.
Landsat cloud free and inundation free images used to retrieve water contours (date in format: sat_yyyy_mm_dd). Water contour elevation, elevation standard deviation (SD) and number of ICESat profiles used to calculate each elevation are given.
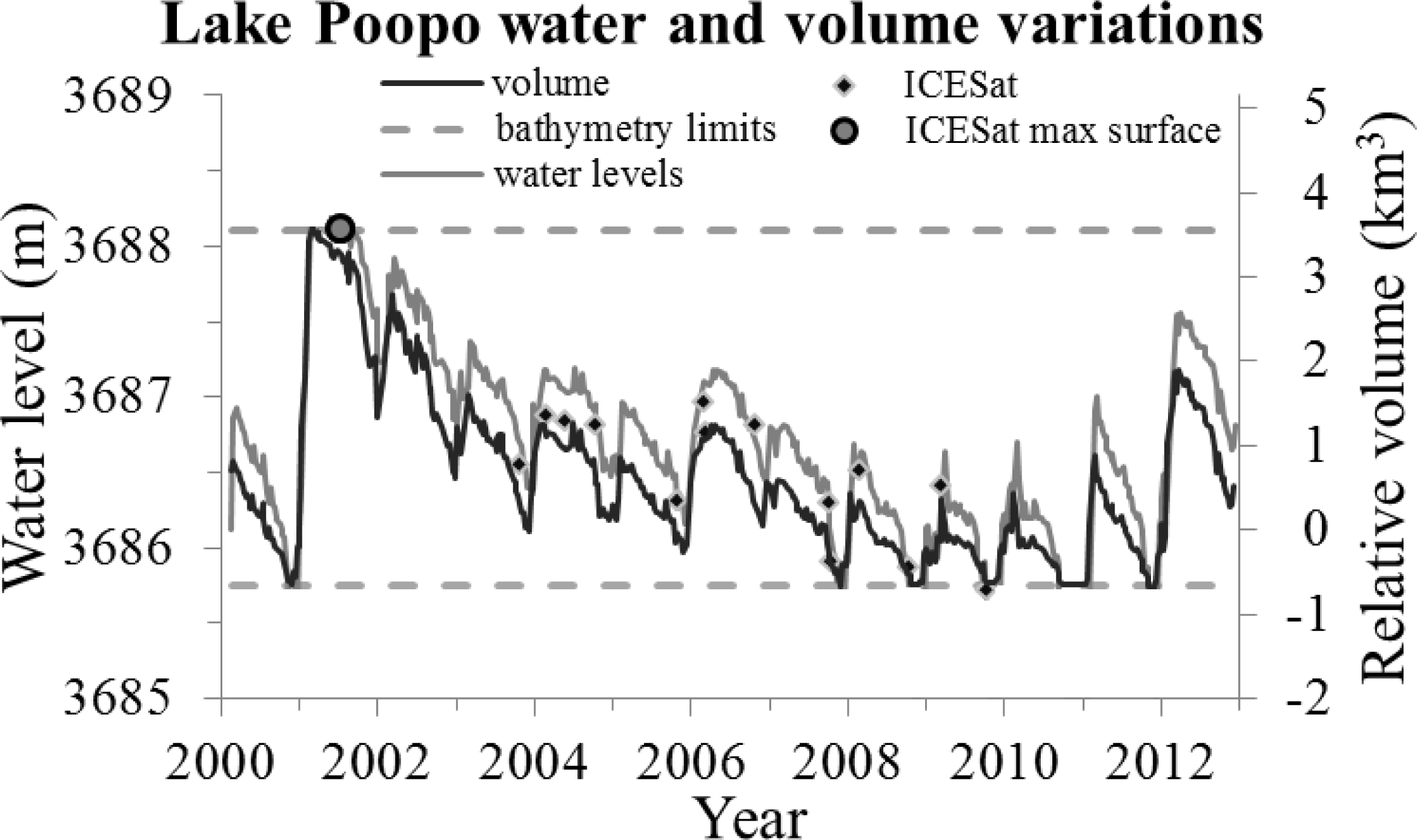
The bathymetry combined with MODIS time series is used to calculate Lake Poopó water levels and water storage (Figure 8). We can observe that lake maximum water storage is always reached between 1 March and 20 March each year. In March 2001 we observed the highest relative water storage. Minimum water storage can be observed at the beginning of November if only the water level in March is higher than 3,686.6 m (surface larger than 1,490 km2). When the water level in March was lower than 3,686.6 m then the minimum lake storage was reached during the 1st week of October as it has been observed in 2009, 2010 and 2011.
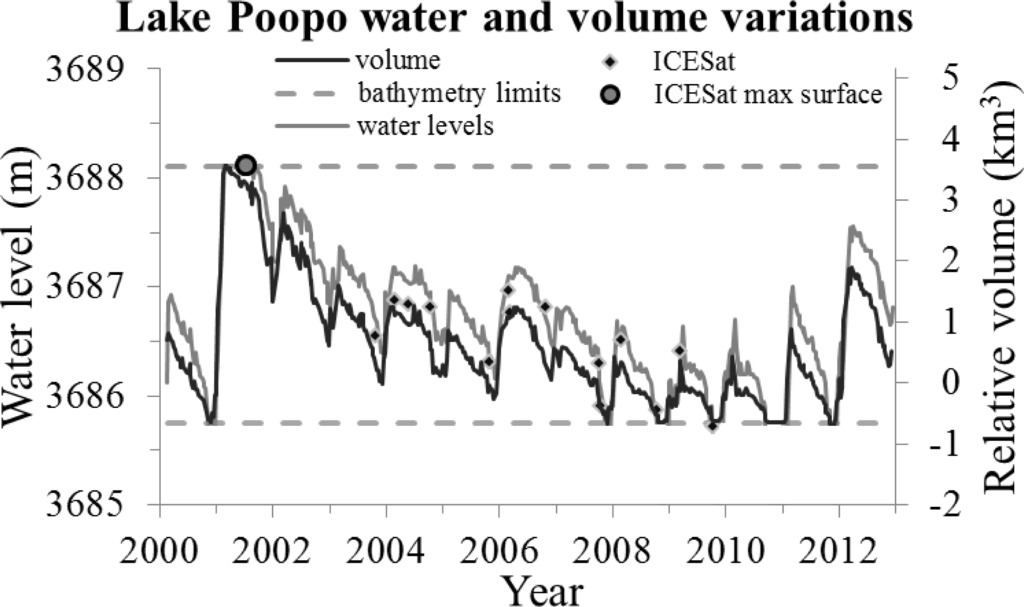
Figure 8.
Lake Poopó water and volumes reconstructed between 2000 and 2012.
From MODIS imagery (Figure 5) we can deduce that in 2009, 2010 and 2011 the water storage in October/November was close to zero. The bathymetry was created in the limits of existing ICESat profiles and depths below 3,685.70 m are not shown. We estimate that the missing part of the storage represents 10%–15% of the total volume.
5. Discussion and Perspectives
Our method uses exclusively freely available remote sensing data, and the vertical standard deviation of our estimates is ±10 cm. All major interior details of the lake, such as islands and sandbars, can be reproduced if needed. The method presented here is somewhat limited. Availability of appropriate images with visible water surface changes and accurate contour detection are prerequisite. The presence of an elevation profile that coincides with the lake minimum stage is the most important requirement. In Lake Poopó’s case the lowest ICESat profile was taken in October 2009. Later in November-December same year the lake dried out entirely (Figure 5). As for the method itself, the interpolation of elevation values in some regions of a lake can give incoherent results (sloped but flooded area seen from nadir, river path) and should be carefully analyzed. In our first attempt, we tried to split points into different zones (Figure 1b) and recommend this approach for future studies. In each zone, it is possible to have multiple intersections. For each contour, median values from different zones can be compared. Intersections on a sloping flooded area seen from nadir or in the river path can give values 1–3 m above the real water elevation. Those points should be rejected. Elevation values in opposite zones, i.e., south-north and east-west need to be checked. If the elevation values in opposite zones differ systematically from layer to layer in the same direction, this can be interpreted as a local geoid effect. If elevation values in opposite zones differ occasionally, the main water body contour may be affected by wind. In this case, it is advisable to retrieve the same contour from different images or to put more intermediary contours. From Landsat images collected in 1985 and 1986 we know that the water stage was higher than during the current decade but the method described here cannot be applied due to changes in dune and shoreline formation, which are inconsistent with the measure of ICESat during the last decade. These constraints and the need for close inspection may limit the applicability of this method, but in the case of Lake Poopó—with no gauging station and no radar altimetry coverage—even a partial bathymetry proves to be a major advancement. As expected, elevation precision seems to decrease (Table 2) with the number of profiles used in the calculations. It was not possible to compare absolute values of our hypsometry with previous works. Relative depth between surfaces of 500 km2 and 2,250 km2 in [3] seems to match the value of 2.25 m found in our study. Obtained volume and real water time series of Lake Poopó will greatly contribute to our understanding and knowledge of the changes occurring in the TPDS system. The outstanding vertical precision obtained in this study is mainly due to the total absence of vegetation close to the lake. This absence is due to water and terrain salinity and intense evaporation. In this study, only MODIS surfaces between 2000 and 2012 were used to retrieve continuous water storage time series, but there are 30 years of Landsat images in the archives that document past levels and storage variations. We believe that our method can be successfully applied in all similar regions with scarce vegetation, such as in the Middle East or for ephemeral lakes like Salar de Uyuni or Salar de Coipasa. As higher stages of the bathymetry can be easily approximated with existing DEM’s, future studies with different methods and other remote sensing instruments will be concentrated on the lower part of the bathymetry of Lake Poopó where the last 25% of surface variations occur. The bathymetry and further modifications will be available through the LEGOS HYDROWEB service [49].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Abarca Del Rio, R.; Crétaux, J.-F.; Berge-Nguyen, M.; Maisongrande, P. Does Lake Titicaca still control the Lake Poopó system water levels? An investigation using satellite altimetry and MODIS data (2000–2009). Remote Sens. Lett 2012, 3, 707–714. [Google Scholar]
- Pillco Zolá, R.; Bengtsson, L. Long-term and extreme water level variations of the shallow Lake Poopó, Bolivia. Hydrol. Sci. J 2006, 51, 98–114. [Google Scholar]
- Pillco Zolá, R.; Bengtsson, L. Three methods for determining the area-depth relationship of Lake Poopó, a large shallow lake in Bolivia. Lakes Reserv 2007, 12, 275–284. [Google Scholar]
- Condom, T.; Coudrain, A.; Dezetter, A.; Brunstein, D.; Delclaux, F.; Jean-Emmanuel, S. Transient modelling of lacustrine regressions: Two case studies from the Andean Altiplano. Hydrol. Process 2004, 18, 2395–2408. [Google Scholar]
- Crétaux, J.-F.; Calmant, S.; Abarca Del Rio, R.; Kouraev, A.; Bergé-Nguyen, M.; Maisongrande, P.; Rio, R.A. Lakes Studies from Satellite Altimetry. In Coastal Altimetry; Vignudelli, S., Kostianoy, A.G., Cipollini, P., Benveniste, J., Eds.; Springer: Berlin, German, 2011; pp. 509–533. [Google Scholar]
- Cretaux, J.F.; Jelinski, W.; Calmant, S.; Kouraev, A.; Vuglinski, V.; Berge-Nguyen, M.; Gennero, M.C.; Nino, F.; Abarca Del Rio, R.; Cazenave, A.; et al. SOLS: A lake database to monitor in the Near Real Time water level and storage variations from remote sensing data. Adv. Space. Res 2011, 47, 1497–1507. [Google Scholar]
- Cretaux, J.-F.; Berge-Nguyen, M.; Leblanc, M.; Abarca Del Rio, R.; Delclaux, F.; Mognard, N.; Lion, C.; Pandey, R.-K.; Tweed, S.; Calmant, S.; et al. Flood mapping inferred from remote sensing data. Int. Water Technol. J 2011, 1, 48–62. [Google Scholar]
- Abileah, R.; Vignudelli, S.; Scozzari, A. A completely remote sensing approach to monitoring reservoirs water volume. Int. Water Technol. J 2011, 1, 63–77. [Google Scholar]
- Sima, S.; Tajrishy, M. Using satellite data to extract volume-area-elevation relationships for Urmia Lake, Iran. J. Great Lakes Res 2013, 39, 90–99. [Google Scholar]
- Hobi, M.L.; Ginzler, C. Accuracy assessment of digital surface models based on WorldView-2 and ADS80 stereo remote sensing data. Sensors 2012, 12, 6347–6368. [Google Scholar]
- Huguenin, R.L.; Wang, M.H.; Biehl, R.; Stoodley, S.; Rogers, J.N. Automated subpixel photobathymetry and water quality mapping. Photogramm. Eng. Remote Sens 2004, 70, 111–123. [Google Scholar]
- Dekker, A.G; Phinn, S.R.; Anstee, J.; Bissett, P.; Brando, V.E.; Casey, B.; Fearns, P.; Hedley, J.; Klonowski, W.; Lee, Z.P.; et al. Intercomparison of shallow water bathymetry, hydro-optics, and benthos mapping techniques in Australian and Caribbean coastal environments. Limnol. Oceanogr. Methods 2011, 9, 396–425. [Google Scholar]
- Lee, I.; Chang, H.; Ge, L. GPS campaigns for validation of InSAR derived DEMs. Positioning 2005, 1–2, 82–87. [Google Scholar]
- Zwally, H.J.; Schutz, B.; Abdalati, W.; Abshire, J.; Bentley, C.; Brenner, A.; Bufton, J.; Dezio, J.; Hancock, D.; Harding, D.; et al. ICESat’s laser measurements of polar ice, atmosphere, ocean, and land. J. Geodyn 2002, 34, 405–445. [Google Scholar]
- Hien Phan, V.; Lindenbergh, R.; Menenti, M. ICESat derived elevation changes of Tibetan lakes between 2003 and 2009. Int. J. Appl. Earth Obs. Geoinf 2012, 17, 12–22. [Google Scholar]
- Fricker, H.A.; Borsa, A.; Minster, B.; Carabajal, C.; Quinn, K.; Bills, B. Assessment of ICESat performance at the Salar de Uyuni, Bolivia. Geophys. Res. Lett 2005, 32. [Google Scholar] [CrossRef]
- Zwally, H.J.R.; Schutz, C.; Bentley, J.; Bufton, T.; Herring, J.; Minster, J.; Spinhirne, R.T. GLAS/ICESat L1B Global Elevation Data, Version 33; National Snow & Ice Data Center: Boulder, CO, USA, 2003. [Google Scholar]
- Bills, B.G.; Borsa, A.A.; Comstock, R.L. MISR-based passive optical bathymetry from orbit with few-cm level of accuracy on the Salar de Uyuni, Bolivia. Remote Sens. Environ 2007, 107, 240–255. [Google Scholar]
- Zhang, G.; Xie, H.; Kang, S.; Yi, D.; Ackley, S.F. Monitoring lake level changes on the Tibetan Plateau using ICESat altimetry data (2003–2009). Remote Sens. Environ 2011, 115, 1733–1742. [Google Scholar]
- Abileah, R.; Vignudelli, S. Bathymetry from Fusion of Multi-Temporal Landsat and Radar Altimetery. Proceedings of the 6th International Workshop on the Analysis of Multi-temporal Remote Sensing Images (Multi-Temp), Trento, Italy, 12–14 July 2011; pp. 189–192.
- USGS Global Visualization Viewer. Available online: http://glovisusgs.gov/ (accessed on 31 July 2013).
- MODIS Land. Available online: http://modis-land.gsfc.nasa.gov/ (accessed on 31 July 2013).
- NASA. ICESat & ICESat-2. http://icesat.gsfc.nasa.gov/ (accessed on 31 July 2013).
- ICESat/GLAS Data Summaries. Available online: http://nsidc.org/data/icesat/correction-to-product-surface-elevations.html (accessed on 31 July 2013).
- Brenner, A.C.; Bentley, C.R.; Csatho, B.M.; Harding, D.J.; Hofton, M.A.; Minster, J.; Roberts, L.; Saba, J.L. Derivation of Range and Range Distributions from Laser Pulse Waveform Analysis for Surface Elevations, Roughness, Slope, and Vegetation Heights. Available online: http://www.csr.utexas.edu/glas/pdf/Atbd_20031224.pdf (accessed on 31 July 2013).
- McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens 1996, 17, 1425–1432. [Google Scholar]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens 2006, 27, 3025–3033. [Google Scholar]
- Polidorio, A.M.; Flores, F.C.; Franco, C.; Imai, N.N.; Tommaselli, A.M.G. Detecção Automática de Sombras e Nuvens em Imagens CBERS e Landsat 7 ETM; Anais XII Simpósio Brasileiro de Sensoriamento Remoto: Goiânia, Brazil, 2005. [Google Scholar]
- Polidorio, A.; Imai, N.; Tommaselli, A. Índice Indicador de Corpos d’ água Para Imagens Multispectrais 2004. Available online: http://www.ufpe.br/cgtg/ISIMGEO/CD/html/Fotogrametria%20e%20Sensoriamento%20Remoto/Artigos/f027.pdf (accessed on 31 July 2013).
- Jain, S.; Saraf, A.; Goswami, A.; Ahmad, T. Flood inundation mapping using NOAA AVHRR data. Water Resour. Manag 2006, 20, 949–959. [Google Scholar]
- Sethre, P.R.; Rundquist, B.C.; Todhunter, P.E. Remote detection of prairie pothole ponds in the Devils Lake Basin, North Dakota. GISci. Remote Sens 2005, 42, 277–296. [Google Scholar]
- Liu, Y.; Song, P.; Peng, J.; Ye, C. A physical explanation of the variation in threshold for delineating terrestrial water surfaces from multi-temporal images: Effects of radiometric correction. Int. J. Remote Sens 2012, 33, 5862–5875. [Google Scholar]
- Clemens, R.S.; Phinn, S.R.; Murray, N.J.; Roelfsema, C.M.; Fuller, R.A. Continental scale mapping of Tidal Flats across East Asia using the Landsat archive. Remote Sens 2012, 4, 3417–3426. [Google Scholar]
- Ji, L.; Zhang, L.; Wylie, B. Analysis of dynamic thresholds for the normalized difference water index. Photogramm. Eng. Remote Sens 2009, 75, 1307–1317. [Google Scholar]
- Justice, C.O.; Townshend, J.R.G.; Vermote, E.F.; Masuoka, E.; Wolfe, R.E.; El Saleous, N.; Roy, D.P.; Morisette, J.T. An overview of MODIS Land data processing and product status. Remote Sens. Environ 2002, 83, 3–15. [Google Scholar]
- Engman, E.T.; Gurney, R.J. Remote Sensing in Hydrology; Chapman and Hall: London, UK, 1991. [Google Scholar]
- Li, R.R.; Kaufman, Y.J.; Gao, B.-C.; Davis, C.O. Remote sensing of suspended sediments and shallow coastal waters. IEEE Trans. Geosci. Remote Sens 2003, 41, 559–566. [Google Scholar]
- Pedinotti, V.; Boone, A.; Decharme, B.; Crétaux, J.F.; Mognard, N.; Panthou, G.; Papa, F.; Tanimoun, B.A. Evaluation of the ISBA-TRIP continental hydrologic system over the Niger basin using in situ and satellite derived datasets. Hydrol. Earth Syst. Sci 2012, 16, 1745–1773. [Google Scholar]
- Pandey, R.K.; Cretaux, J.-F.; Berge-Nguyen, M.; Tiwari, V.M.; Drolon, V.; Calmant, S. Water level estimation by remote sensing for 2008 flood of Kosi. Int. J. Remote Sens 2013, in press. [Google Scholar]
- Crétaux, J.-F.; Létolle, R.; Calmant, S. Investigations on Aral Sea regressions from mirabilite deposits and remote sensing. Aquat. Geochem 2009, 15, 277–291. [Google Scholar]
- Yésou, H.; Huber, C.; Lai, X.; Averty, S.; Li, J.; Daillet, S.; Bergé-Nguyen, M.; Chen, X.; Huang, S.; James, B.; et al. Nine years of water resources monitoring over the middle reaches of the Yangtze River, with ENVISAT, MODIS, Beijing-1 time series, Altimetric data and field measurements. Lakes Reserv 2011, 16, 231–247. [Google Scholar]
- Aires, F.; Papa, F.; Prigent, C.; Crétaux, J.-F.; Berge-Nguyen, M. Characterization and space/time downscaling of the inundation extent over the Inner Niger Delta using GIEMS and MODIS data. J. Hydrometeorol 2013. [Google Scholar] [CrossRef]
- Baghdadi, N.; Lemarquand, N.; Abdallah, H.; Bailly, J.S. The relevance of GLAS/ICESat elevation data for the monitoring of river networks. Remote Sens 2011, 3, 708–720. [Google Scholar]
- GLAS Altimetry Data Dictionary. Available online: http://nsidc.org/data/docs/daac/glas_altimetry/data_dictionary.html (accessed on 31 July 2013).
- Antonio, F. Faster Line Segment Intersection. In Graphics Gems III; Kirk, D., Glassner, A., Eds.; Academic Press: San Diego, CA, USA, 1992; pp. 199–202. [Google Scholar]
- Cormen, T.; Leiserson, C.; Rivest, R.; Stein, C. Determining Whether any Pair of Segments Intersects: Section 33.2. In Introduction to Algorithms; Cormen, T., Leiserson, C., Rivest, R., Stein, C., Eds.; MIT Press: Cambridge, MA, USA, 2001; pp. 934–947. [Google Scholar]
- TriScatteredInterp in MathWorks MATLAB online Documentation Center. Available online: http://www.mathworks.fr/fr/help/matlab/ref/triscatteredinterp.html (accessed on 31 July 2013).
- Meshgrid in MathWorks MATLAB online Documentation Center. Available online: http://www.mathworks.fr/fr/help/matlab/ref/meshgrid.html (accessed on 31 July 2013).
- LEGOS HYDROWEB. Available online: http://www.legos.obs-mip.fr/soa/hydrologie/hydroweb/ (accessed on 31 July 2013).
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).