Next Article in Journal
A Procedure to Map Subsidence at the Regional Scale Using the Persistent Scatterer Interferometry (PSI) Technique
Previous Article in Journal
Monitoring the Fluctuation of Lake Qinghai Using Multi-Source Remote Sensing Data
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 6
Issue 11
10.3390/rs61110483
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

On the Downscaling of Actual Evapotranspiration Maps Based on Combination of MODIS and Landsat-Based Actual Evapotranspiration Estimates

by
Ramesh K. Singh
1,*,
Gabriel B. Senay
2,
Naga M. Velpuri
1,
Stefanie Bohms
3 and
James P. Verdin
2
1
ASRC Federal InuTeq, Contractor to the U.S. Geological Survey Earth Resources Observation and Science Center, 47914 252nd Street, Sioux Falls, SD 57198, USA
2
Geological Survey Earth Resources Observation and Science Center, 47914 252nd Street, Sioux Falls, SD 57198, USA
3
Stinger Ghaffarian Technologies Inc., Contractor to the U.S. Geological Survey Earth Resources Observation and Science Center, Sioux Falls, SD 57198, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2014, 6(11), 10483-10509; https://doi.org/10.3390/rs61110483
Submission received: 13 February 2014 / Revised: 16 October 2014 / Accepted: 21 October 2014 / Published: 30 October 2014
Browse Figures
Versions Notes

Abstract

:
Downscaling is one of the important ways of utilizing the combined benefits of the high temporal resolution of Moderate Resolution Imaging Spectroradiometer (MODIS) images and fine spatial resolution of Landsat images. We have evaluated the output regression with intercept method and developed the Linear with Zero Intercept (LinZI) method for downscaling MODIS-based monthly actual evapotranspiration (AET) maps to the Landsat-scale monthly AET maps for the Colorado River Basin for 2010. We used the 8-day MODIS land surface temperature product (MOD11A2) and 328 cloud-free Landsat images for computing AET maps and downscaling. The regression with intercept method does have limitations in downscaling if the slope and intercept are computed over a large area. A good agreement was obtained between downscaled monthly AET using the LinZI method and the eddy covariance measurements from seven flux sites within the Colorado River Basin. The mean bias ranged from −16 mm (underestimation) to 22 mm (overestimation) per month, and the coefficient of determination varied from 0.52 to 0.88. Some discrepancies between measured and downscaled monthly AET at two flux sites were found to be due to the prevailing flux footprint. A reasonable comparison was also obtained between downscaled monthly AET using LinZI method and the gridded FLUXNET dataset. The downscaled monthly AET nicely captured the temporal variation in sampled land cover classes. The proposed LinZI method can be used at finer temporal resolution (such as 8 days) with further evaluation. The proposed downscaling method will be very useful in advancing the application of remotely sensed images in water resources planning and management.

Graphical Abstract

1. Introduction

Evapotranspiration (ET), one of the major components of the hydrologic cycle, plays a key role in spatial and temporal distribution of water and energy under soil–plant–atmosphere continuum. Remote sensing techniques are increasingly used for accurately estimating ET at the field and regional scales. Availability of cost-free Landsat and Moderate Resolution Imaging Spectroradiometer (MODIS) images coupled with higher computing power has helped the modelers in quantifying ET using remotely sensed images. The actual ET (AET) maps derived using Landsat images have better spatial resolution (60 m vs. 1 km) than the maps created using MODIS images. However, creating seasonal/annual AET maps using MODIS images is simpler than using Landsat images due to the higher temporal resolution of MODIS (1 day vs. 16 days). Any presence of cloud makes less availability of usable Landsat images as compared to usable MODIS images. The trade-off between spatial and temporal resolution of MODIS and Landsat images presents a dilemma for the remote sensing community in general and ET modelers in particular. It is a natural tendency to try to make use of the best of all available remotely sensed images due to the complementary nature of various datasets [1,2,3]. Use of remotely sensed images having different spatial and temporal resolutions resulted in the development of downscaling and multi-sensor data fusion techniques. Some researchers have presented nice overview of the state of the art in data fusion [4,5]. Data fusion has been used in different forms and formats for a wide range of applications. Cliche et al. (1985) [6] used image fusion for integrating Systeme Pour I’Observation de la Terre (SPOT) panchromatic images with multispectral channels for image sharpness enhancement. The intensity-hue-saturation (IHS) transformation was applied for merging SPOT panchromatic images (10 m resolution) with simultaneously acquired SPOT multispectral images (20 m resolution) [7]. Comparison of three merging methods, Hue Intensity Saturation (HIS), Principal Component Analysis (PCA), and High Pass Filter (HPF), has shown that the HIS method distorted the spectral characteristics of the data the most, and HPF the least [1]. Price (1999) [8] used a band correlation method for merging high spatial resolution imagery with data from additional lower spatial resolution bands. An assessment criteria was proposed to evaluate the quality of merged products resulting from merging high spectral and high spatial resolution satellite data [9]. With the development of various fusion methods, Karathanassi et al. (2007) [10] evaluated different indicators to compare fusion methods and found that the peak signal-to-noise ratio indicator was the most appropriate for the evaluation of data fusion methods. Wavelet transform was used for merging SPOT panchromatic images with simultaneously acquired SPOT multispectral images [11]. The wavelet decomposition technique was used for merging Landsat Thematic Mapper (TM) images with the SPOT panchromatic images [12,13]. Gao et al. (2006) [14] used MODIS and Landsat images for predicting daily Landsat surface reflectance based on the Spatial and Temporal Adaptive Reflectance Fusion (STARFM) model. A semi-physical fusion approach used Landsat and MODIS images for relative radiometric normalization, cloud/cloud shadow and scan line corrector (SLC)-off gap filling, and predicting Landsat data [15]. Forest mapping has been carried out based on image fusion of Landsat and MODIS images [16]; fusion of multispectral/hyperspectral images and light detection and ranging (LiDAR) data [17]; and fusion of Landsat, Radarsat-1, and Phased Array L-band Synthetic Aperture Radar (PALSAR) [18]. Though image fusion has many advantages, it has some limitations too [19]. Furthermore, all of these applications do not include thermal bands.
AET estimation using energy balance methods involves thermal bands for land surface temperature (LST). Though LST using satellite data is frequently used in many disciplines including hydrology, there is limited literature available on the fusion of high spatial and temporal resolutions of thermal data. Earlier works on thermal data fusion used different terms, such as disaggregation [20,21,22], downscaling [23,24,25], enhancement [26,27,28], merging [28,29], and sharpening [30,31]. A few recent publications have presented a nice overview of the literature related to the remotely sensed LST disaggregation and its applications [32,33,34]. Ha et al. (2013) [32] broadly classified these techniques into two categories: downscaling, where images from a coarse spatial resolution is converted to fine resolution using statistically based models with regression or stochastic relationships among parameters without changing radiometric properties of the image; and fusion, where two or more images from the same sensor or different sensors are combined to obtain higher spectral and spatial resolution. Zhan et al. (2013) [34] identified thermal sharpening and temperature unmixing as two subtopics related to disaggregation of remotely sensed LST.
Disaggregation technique is based on fitting a statistical relationship between radiometric surface temperature (dependent variable) and the normalized difference vegetation index (independent variable) [22]. It is assumed that a unique functional relationship exists between radiometric surface temperature and vegetation indices at multiple spatial scales. However, there is further evidence that these statistical relationships are specific to different climatic and land use characteristics [31].
Thermal sharpening technique can be used for estimating surface temperature at higher resolutions (~250 m) using the visible/near infrared wavebands to obtain enough spatial details for discriminating AET from individual maize and soybean fields [35]. Hong et al. (2011) [36] compared input downscaling and output downscaling, each with two different disaggregation processes, subtraction and regression, for downscaling ET maps. They showed that output downscaling with regression (slope-intercept method) between Landsat and MODIS images is the most preferred scheme, while input downscaling with subtraction is the least preferred scheme. This was in part due to higher vulnerability caused by georeferencing disagreement between Landsat and MODIS images using the subtraction process than the regression process. Other than registration disagreement between Landsat and MODIS images, there are other sources of uncertainty, such as viewing and solar geometry, acquisition times, atmospheric correction, and emissivity estimation [3,37]. Furthermore, the application of regression will depend upon the geographical extent of the image similar to domain size effect on flux estimation [38].
Actual ET estimated using Landsat images is instantaneous and extrapolated to daily AET using different integration techniques (see Chavez et al. 2008 [39]). In this way, Landsat-based daily AET can be estimated for the day of satellite overpass. However, only a limited number of usable Landsat images can be obtained during a year because of cloud cover and the 16-day temporal resolution. It is reasonable to obtain annual AET based on a few daily AET estimates because any bias is compensated over a longer period of time [40,41,42]. However, it becomes challenging to obtain a representative monthly AET, particularly for a month when no Landsat scene is available. Downscaling becomes an attractive option to obtain Landsat-based monthly AET using annual Landsat AET and MODIS-based monthly AET.
In this paper we developed a novel methodology to downscale the MODIS-based monthly AET to Landsat-based monthly AET and validated the downscaled AET maps with field measurements. We also compared the newly developed method with the regression (slope-intercept) method and evaluated the validity of the slope-intercept method under a larger geographical extent in the Colorado River Basin in the western United States.

2. Study Area

This study was carried out in the Colorado River Basin (CRB), which has an area of about 630,000 km2. The Colorado River is one of the major rivers in the western United States. It flows about 2300 km through seven states (Wyoming, Colorado, Utah, New Mexico, Arizona, Nevada, and California) before draining into the Gulf of California (Figure 1). The annual flow of the river has ranged from 6.5 billion cubic meters (BCM) to 29.6 BCM during 1906–2000 [43]. The Colorado River supplies water to more than 25 million people and irrigates more than 12,000 km2 of cropland across the seven basin states [44]. The combined reservoir storage capacity (74.0 BCM) within the basin is about four times the long-term average annual flow (16.7 BCM). Based on the National Land Cover Database (NLCD, 2006) [45], shrubland (61%) is the most dominant land cover followed by evergreen forest (19%), grassland (8%), and deciduous forest (4%). Cropland and pasture/hay constitute about 2% of the CRB. The mean annual AET of shrubland, evergreen forest, grassland, and cropland during 2010 were 262 mm, 447 mm, 224 mm, and 538 mm, respectively [41]. Major crops grown in the CRB are forage, alfalfa, wheat, cotton, and vegetables. Hydrology of the CRB is mainly dependent on snow accumulation as the Colorado River is primarily a snowmelt-driven system. The large areal extent and relief of the basin results in substantial climate variability within the CRB. The reader can see Kumar and Duffy (2009) [46] for additional detail on geo-topographic and climatic conditions of the study area.

3. Method

3.1. Regression (Slope-Intercept) Method

Hong et al. (2011) [36] used linear regression to combine MODIS and Landsat imagery to generate slope and intercept values to obtain both high temporal and high spatial resolution. The regression method assumed that the linear relationship between coarse resolution images is valid between fine scale resolution imagery. Thus, for this output downscaling, a first order linear regression between two AET maps from MODIS images was calculated. Then, the regression was applied to the evapotranspiration map derived from the Landsat image to predict disaggregated AET map. We used their output regression method to compute slope and intercept values for downscaling monthly AET maps. Hong et al. (2011) [36] did not constrain the regression line to the zero intercept in order not to change the regression coefficient. We generated slope and intercept for each month based on MODIS monthly and annual AET using the 1st order regression analysis. Those slope and intercept values were used with the Landsat-based annual AET maps to generate monthly AET maps at the Landsat scale.
Remotesensing 06 10483 g001 1024
Figure 1. Location of the study area showing the Colorado River Basin with river network, sub-basin (Hydrologic Unit Code: HUC 8) boundaries, and validation flux towers.
Figure 1. Location of the study area showing the Colorado River Basin with river network, sub-basin (Hydrologic Unit Code: HUC 8) boundaries, and validation flux towers.
Remotesensing 06 10483 g001

3.2. Linear with Zero Intercept (LinZI) Method

Theoretically, AET estimated using Landsat images should be the same as AET estimated using MODIS images for homogeneous surfaces. However, there may be some differences due to spatial resolution, viewing and solar geometry, acquisition time, atmospheric correction, sensor bandwidth, geolocation error, and emissivity estimation. Since most of the pixels in an image may not be homogeneous, we hypothesize that it is simpler to express a linear relationship with zero intercept between Landsat and MODIS estimated AET as
L ( x i , y j , t k ) = α × M ( x i , y j , t k )
where L(xi, yj, tk) is AET using Landsat images for pixel location (xi, yj) and time domain tk (daily, monthly, seasonal, or annual), α is a multiplying factor, and M(xi, yj, tk) is AET using MODIS images for the same location and time domain. We have named this approach as linear with zero intercept (LinZI) method.
Thus, we can write annual AET using Landsat and MODIS images as
L ( x i , y j , t a ) = α × M ( x i , y j , t a )
where L(xi, yj, ta) is annual AET using Landsat images for pixel location (xi, yj), and M(xi, yj, ta) is annual AET using MODIS images for the same pixel location.
We assumed that the linear relationship between Landsat and MODIS-based AET is valid at different time scales. This assumption is reasonable as we are estimating the same process of water loss due to evaporation and transpiration, i.e., AET using two different data acquisition systems. Therefore, for monthly AET, we can write
L ( x i , y j , t m ) = α × M ( x i , y j , t m )
where L(xi, yj, tm) is monthly AET using Landsat images for pixel location (xi, yj), and M(xi, yj, tm) is monthly AET using MODIS images for the same pixel location. The physical significance of this equation is that there is a linear relationship between monthly AET estimated using MODIS and Landsat images.
By combining Equations (2) and (3), we have
L ( x i , y j , t m ) = M ( x i , y j , t m ) M ( x i , y j , t a ) × L ( x i , y j , t a )

4. Data

4.1. Landsat Data

We downloaded all the 328 cloud-free (less than 10% cloud) Landsat images (Thematic mapper and Enhanced thematic mapper plus) of the CRB for 2010 from EarthExplorer (http://earthexplorer.usgs.gov/). The CRB is covered by 44 different paths/rows ranging from path 33 to 40 and row 30 to 38. Landsat Thematic Mapper (TM) and Enhanced Thematic Mapper Plus (ETM+) data excluding the panchromatic band were used in the analysis. Total cloud-free images during 2010 for each path/row ranged from 5 to 11. The Operational Simplified Surface Energy Balance (SSEBop) model [41] algorithm was implemented with Landsat images using Model Maker in Erdas Imagine 2011 (version 11.0.4) (Intergraph Corporation, Huntsville, AL, USA) to compute daily AET on the day of the satellite overpass. We computed daily AET using instantaneous AET fraction as explained in Singh et al. (2014) [41]. The daily reference ET was computed using standardized equation [47]. Actual ET estimated on the day of the satellite overpass was used with reference ET to compute ET fraction, the ratio of AET to the reference ET. Finally, we upscaled daily AET to annual AET as follows:
E T a n n u a l = ∑ i = 1 n ( E T o i × E F f i )
where ETannual is the total annual AET (mm), EToi is the reference ET (mm) for period i (days), and EFfi is the representative ET fraction (–) for period i. This approach may not work for estimating monthly AET without a representative monthly ET fraction due to the limited number of usable Landsat images. However, it works well for estimating annual AET as any bias is compensated over a longer period of time [40,41,42]. Reader can refer to Singh et al. (2014) [41] for more details on the processing of the Landsat images used in this study.

4.2. MODIS Data

We used 16-day MODIS normalized difference vegetation index (MOD13A2.005) and 8-day LST and emissivity (MOD11A2.005) data for 2010 from the National Aeronautics and Space Administration (NASA) Land Processes Distributed Active Archive Center (https://lpdaac.usgs.gov/lpdaac/get_data; accessed on 18/01/2012). MOD13A2 products are computed from atmospherically corrected bidirectional surface reflectance acquired daily from the Terra satellite and provided every 16 days at 1-km spatial resolution. MOD11A2 products are derived as the average of daily acquired land surface temperature at 1-km spatial resolution from the Terra satellite over an 8-day period. We obtained monthly and annual AET after processing the MODIS data using the SSEBop model. Refer to Senay et al. (2013) [48] for the processing approach and data requirement.

4.3. Gridded FLUXNET Data

Jung et al. (2009) [49] created a global spatially and temporally explicit AET map based on upscaling of observations from the eddy covariance towers (FLUXNET) using the model tree ensemble approach. They used FLUXNET data, meteorological and remote sensing observations, and a machine learning algorithm to create gridded FLUXNET data. Their model tree ensemble approach provided a benchmark for the upscaling water fluxes from the FLUXNET sites to the global scale. This dataset is used as a reference dataset [50,51], so we used it to validate our newly created Landsat-based monthly AET data.

5. Evaluation of Downscaled Products

5.1. Validation Using Eddy Covariance Flux Towers

The downscaled monthly AET was compared with the eddy covariance measurements carried out at the eddy covariance measurement sites (Table 1). These sites are Flagstaff managed forest (FMF) [52], Flagstaff unmanaged forest (FUF) [52], Flagstaff wildfire (FWF) [52], Santa Rita Creosote (SRC) [53], Santa Rita Mesquite (SRM) [54], Kendall grassland (WKG) [55], and Charleston Mesquite (CMS) [56]. All of these sites, except for the Charleston Mesquite site, are part of FLUXNET [57]. The data used from the FLUXNET sites are Level 2 data, so they have data gaps ranging from about 7% (Flagstaff wildfire site) to 22% (Santa Rita Creosote site). The data collection and methodology for these sites are described in the respective references given in Table 1.
Eddy covariance flux measurements are representative of the weighted average of the fluxes from the upwind source areas. For comparison, we used the AET values of pixels that have a flux tower without any knowledge of the spatial extent and relative importance of upwind source areas (footprint). In general, the footprint of flux measurements depends upon the wind velocity and direction, surface roughness, measurement height, and atmospheric stability [58]. It should be also noted that there are systematic and random errors associated with the eddy covariance measurements resulting into lack of closure in the surface energy balance [59,60,61]. Thus, a part of uncertainty associated with the model evaluation also results due to uncertainty and bias associated with the flux measurement and overlook of the flux footprint.
Table
Table 1. Details of eddy covariance towers used for validating downscaled monthly actual evapotranspiration maps.
Table 1. Details of eddy covariance towers used for validating downscaled monthly actual evapotranspiration maps.
Sl. No.SiteLatitude (°)Longitude (°)Elevation (m)Tower Height (m)Land CoverLandsat Path/RowNo. of Cloud-Free ImagesReference
1Flagstaff managed forest35.1426−111.7273216023Ponderosa pine forest37/366Dore et al. (2012) [52]
2Flagstaff unmanaged forest35.089−111.762218023Ponderosa pine forest37/366Dore et al. (2012) [52]
3Flagstaff wildfire35.4454−111.771822704Ponderosa pine forest37/357Dore et al. (2012) [52]
4Santa Rita Creosote31.9083−110.83959914.25Open shrub land36/389Kurc and Benton (2010) [ 53]
5Santa Rita Mesquite31.8214−110.866111206.4Woody Savannas36/389Scott et al. (2009) [54]
6Kendall Grassland31.7365−109.941915316.4Grassland35/387Scott et al. (2010) [55]
7Charleston Mesquite31.6637−110.1776120014Riparian woodland35/387Scott et al. (2004) [56]

5.2. Evaluation Using Gridded FLUXNET Data

We compared our monthly AET maps at the Landsat scale with those of the gridded FLUXNET data (Jung et al. 2009) [49] at the subbasin level (Hydrologic Unit Code: HUC 8). The HUCs are based on a nationally consistent watershed dataset that divides the United States into six levels: region (HUC2), subregion (HUC4), basin (HUC6), subbasin (HUC8), watershed (HUC10), and subwatershed (HUC12). The area of subbasins within the CRB ranges from about 400 km2 to about 12,000 km2, with a mean of 4600 km2. We selected HUC8 for comparison based on the spatial resolution of the gridded fluxtnet data (≈50 km) and because runoff data are available at HUC8 levels. Many agencies including the United States Geological Survey (USGS) use the HUC system for assessing, developing, planning, and managing water resources in the United States.

5.3. Evaluation Using MODIS-Based AET

Senay et al. (2013) [48] used the SSEBop model to generate monthly and annual AET maps of the conterminous United States for 2000–2011 using MODIS data. Their validation using eddy covariance data from 45 Ameriflux stations corresponded well with the flux measurements; R2 values were up to 0.9 for individual flux towers with an overall R2 of 0.64 (N = 528) for all towers. Additional validation showed that these SSEBop model-based AET maps are of good accuracy over different land cover types, across a wide elevation range, and under various climatic zones [51]. They found overall root mean square error ranging from 26 to 32 mm/month which was attributed to random error due to pooling validation sites from different agro-ecological zones. We extracted monthly AET of the study area from these SSEBop model-generated AET maps and compared the downscaled AET maps.
A comparison was made using different statistical variables such as mean bias, mean absolute error (MAE), root mean square error (RMSE), and coefficient of determination (R2).

6. Results and Discussion

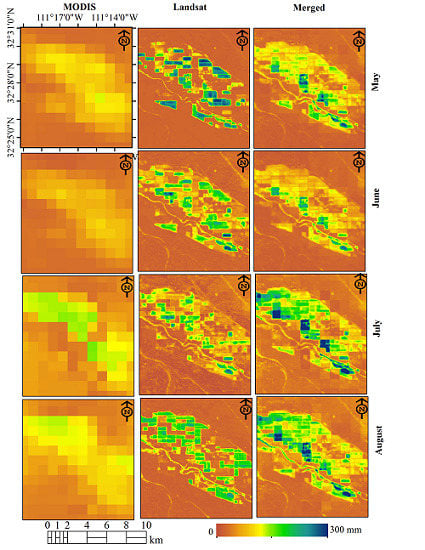
6.1. Monthly Evapotranspiration Using the Regression (Slope-Intercept) Method

Computed values of slope and intercept using the regression method have shown that their progression followed a distinct trend (Figure 2). Higher values of slope and lower values of intercept were found during the crop growing season (May–August), while lower values of slope and higher values of intercept were found during rest of the year. We used these monthly slope and intercept values to generate downscaled monthly AET maps for the Colorado River Basin (Figure 3). The spatial distribution of AET maps generated using the slope-intercept method are very different from that of the MODIS-based AET maps (Figure 4). MODIS-based monthly AET maps were derived using 8-day MODIS thermal data and other ancillary data. Since 8-day thermal data are based on daily acquired MODIS images, MODIS-based AET maps have better temporal representation. MODIS-based AET maps capture daily variability in water losses due to ET more precisely, so the spatial distribution of ET has higher confidence. On the other hand, slope-intercept method-based AET maps have very smooth ET variations except for the crop growing seasons (Figure 3, May–August). There are no similarities in spatial variation of monthly AET between MODIS-based AET (Figure 4) and regression (slope-intercept) based monthly AET (Figure 3). Computing slope and intercept values over a large area, such as the Colorado River Basin, dampens the vigor of this approach. In addition, the slope-intercept method is not effective if the areas under consideration are experiencing a dynamic change such as a rainfall event or a disturbance that happens over a very short period of time [16,36]. Since identification of a suitable area of interest for computing slope and intercept is subjective, it is more reasonable to limit the pixel-to-pixel localized relationship.

6.2. Monthly Evapotranspiration Using the LinZI Method

We computed monthly AET maps of the study area at the Landsat scale using the linear with zero intercept (LinZI) method as described in the methods Section 3.2. The monthly progression of AET showed a gradual increase in AET during the crop growing season and a subsequent decline with progress of the season (Figure 5). Though the maximum monthly AET during crop growing season exceeded 100 mm at some pixels (<0.01%), we have used 100 mm as upper limit only for map representation purpose so that there is more contrast in the AET variation from month to month. As presented under Section 4.1, we had only 5–11 cloud-free Landsat images for each path/row. Considering that cloud free Landsat images were not available for each month in the entire study area, it is impressive to see that the temporal and spatial variation of AET was nicely captured by these maps generated using LinZI method. For example, monthly AET progressions of three different land covers (irrigated cropland, evergreen forest, and shrubland) showed that the AET of shrubland mainly depends upon moisture variability caused by precipitation (Figure 6). The monthly AET of shrubland varies substantially from month to month depending upon the moisture availability from precipitation. On the other hand, irrigated cropland and evergreen forest have access to moisture mainly because of irrigation and groundwater, respectively. So monthly AET of irrigated cropland and deep rooted evergreen forest is not limited by the moisture availability but mainly by the atmospheric water demand.
Remotesensing 06 10483 g002 1024
Figure 2. Slope and intercept values using regression method for each month based on MODIS annual actual evapotranspiration and corresponding monthly actual evapotranspiration for the Colorado River Basin for 2010.
Figure 2. Slope and intercept values using regression method for each month based on MODIS annual actual evapotranspiration and corresponding monthly actual evapotranspiration for the Colorado River Basin for 2010.
Remotesensing 06 10483 g002
Remotesensing 06 10483 g003a 1024Remotesensing 06 10483 g003b 1024
Figure 3. Downscaled monthly actual evapotranspiration map of the Colorado River Basin using regression (slope-intercept) method for 2010.
Figure 3. Downscaled monthly actual evapotranspiration map of the Colorado River Basin using regression (slope-intercept) method for 2010.
Remotesensing 06 10483 g003aRemotesensing 06 10483 g003b
Remotesensing 06 10483 g004a 1024Remotesensing 06 10483 g004b 1024
Figure 4. Monthly actual evapotranspiration map of the Colorado River Basin using 8-day MODIS land surface temperature for 2010.
Figure 4. Monthly actual evapotranspiration map of the Colorado River Basin using 8-day MODIS land surface temperature for 2010.
Remotesensing 06 10483 g004aRemotesensing 06 10483 g004b
Remotesensing 06 10483 g005a 1024Remotesensing 06 10483 g005b 1024
Figure 5. Downscaled monthly actual evapotranspiration map of the Colorado River Basin for 2010 using linear with zero intercept (LinZI) method.
Figure 5. Downscaled monthly actual evapotranspiration map of the Colorado River Basin for 2010 using linear with zero intercept (LinZI) method.
Remotesensing 06 10483 g005aRemotesensing 06 10483 g005b
Table
Table 2. Evaluation statistics using mean bias, root mean square error (RMSE), and coefficient of determination (R2) for downscaled (LinZI method) monthly actual evapotranspiration against eddy covariance measured monthly actual evapotranspiration (N = 12).
Table 2. Evaluation statistics using mean bias, root mean square error (RMSE), and coefficient of determination (R2) for downscaled (LinZI method) monthly actual evapotranspiration against eddy covariance measured monthly actual evapotranspiration (N = 12).
SiteMean Bias (mm)RMSE (mm)R2
Flagstaff managed forest−8190.53
Flagstaff unmanaged forest22320.64
Flagstaff wildfire−16220.52
Santa Rita Creosote1100.61
Santa Rita Mesquite−2120.72
Kendall Grassland−9130.81
Charleston Mesquite7200.88

6.3. Comparison of Downscaled Monthly AET Maps with the Eddy Covariance Measurements

In general, the downscaled monthly AET using the LinZI method was in good agreement with the eddy covariance–measured monthly AET at the selected flux sites, except at the Flagstaff unmanaged forest and Flagstaff wildfire sites (Table 2, Figure 7). The mean monthly bias ranged from −16 mm (Flagstaff wildfire) to 22 mm (Flagstaff unmanaged forest), while R2 ranged from 0.52 (Flagstaff wildfire) to 0.88 (Charleston Mesquite). Both MODIS-based monthly AET and the LinZI downscaling method overestimated monthly AET compared to the field measurement at the Flagstaff unmanaged forest. In contrast, the LinZI downscaling method underestimated monthly AET compared to the field measurement at the Flagstaff wildfire. We had six cloud-free Landsat images for the Flagstaff unmanaged forest and seven for the Flagstaff wildfire sites (Table 1). The LinZI downscaling method captured the monthly variability well with the 6 Landsat scenes at the Flagstaff managed forest but not at the Flagstaff unmanaged forest. The wind rose diagram shows that more than 30% of the wind at the Flagstaff unmanaged forest site was from the northeast (Figure 8).
Remotesensing 06 10483 g006 1024
Figure 6. Monthly progression of actual evapotranspiration based on downscaled evapotranspiration maps using the LinZI method for sampled cropland, evergreen forest, and shrubland pixels (red star) for 2010. The background map shows the spatial distribution of actual evapotranspiration using LinZI method for July 2010 in the Colorado River Basin.
Figure 6. Monthly progression of actual evapotranspiration based on downscaled evapotranspiration maps using the LinZI method for sampled cropland, evergreen forest, and shrubland pixels (red star) for 2010. The background map shows the spatial distribution of actual evapotranspiration using LinZI method for July 2010 in the Colorado River Basin.
Remotesensing 06 10483 g006
Remotesensing 06 10483 g007a 1024Remotesensing 06 10483 g007b 1024
Figure 7. Progression of monthly actual evapotranspiration for 2010 at (a) Flagstaff managed forest; (b) Flagstaff unmanaged forest; (c) Flagstaff wildfire; (d) Santa Rita Creosote; (e) Santa Rita Mesquite; (f) Kendall Grassland; and (g) Charleston Mesquite sites.
Figure 7. Progression of monthly actual evapotranspiration for 2010 at (a) Flagstaff managed forest; (b) Flagstaff unmanaged forest; (c) Flagstaff wildfire; (d) Santa Rita Creosote; (e) Santa Rita Mesquite; (f) Kendall Grassland; and (g) Charleston Mesquite sites.
Remotesensing 06 10483 g007aRemotesensing 06 10483 g007b
Remotesensing 06 10483 g008a 1024Remotesensing 06 10483 g008b 1024
Figure 8. Wind rose diagram based on measured wind speed and wind direction for 2010 at the eddy covariance sites.
Figure 8. Wind rose diagram based on measured wind speed and wind direction for 2010 at the eddy covariance sites.
Remotesensing 06 10483 g008aRemotesensing 06 10483 g008b
The tower height at this site is 23 m, so considering the general “rule of thumb” of 1:100 height to fetch ratio [62], we can expect that the flux tower is actually looking toward the area circled in Figure 9a. The encircled area has some vegetation but also includes some unvegetated areas thus having low AET. This may explain the discrepancy between measured and downscaled AET at this site.
The majority of the wind at the Flagstaff wildfire site was from the south and southeast (Figure 8), where there is good forest cover within the footprint (Figure 9b). So the fluxes measured at this site are mostly some of eddies from the dense forest cover having higher AET values. The downscaled monthly AET at 30-m spatial resolution shows lower AET values than measured AET, while MODIS monthly AET at 1-km spatial resolution is in some agreement with the flux tower measurement at the Flagstaff wildfire site (Figure 7).
Most of the previous methods for enhancing the resolution quality of satellite images are limited to the visible and near infrared bands. Very limited works have been done for enhancing the data using thermal bands. Some of the previous works done using thermal data were constrained due to limited area specific computation. Our proposed methodology using the LinZI method in this manuscript is not limited by any such constraint and will be applicable to any geographical area of extent under different climatic conditions and land use characteristics. AET estimated using any energy balance based models or any other models can be used for downscaling using the LinZI method. Thus, the LinZI method will overcome many limitations of disaggregation technique based on statistical relationship [31].
Remotesensing 06 10483 g009 1024
Figure 9. False color composite (Band 4, 3, 2) of Landsat 5 Thematic Mapper showing (a) Flagstaff unmanaged forest flux tower location (image acquired on 26/06/2010); and (b) Flagstaff wildfire flux tower location (image acquired on 13/08/2010). The circled areas show the approximate footprint for majority of wind direction.
Figure 9. False color composite (Band 4, 3, 2) of Landsat 5 Thematic Mapper showing (a) Flagstaff unmanaged forest flux tower location (image acquired on 26/06/2010); and (b) Flagstaff wildfire flux tower location (image acquired on 13/08/2010). The circled areas show the approximate footprint for majority of wind direction.
Remotesensing 06 10483 g009

6.4. Comparison of Downscaled Monthly AET Maps with the Gridded FLUXNET Dataset

Comparison of downscaled monthly AET with the gridded FLUXNET dataset at the subbasin level (HUC8) shows that the LinZI method had performed better than the slope-intercept method during both non-growing and growing seasons (Table 3). In general, the slope-intercept method has very low R2 values (maximum R2 = 0.24), indicating a limitation of its applicability in larger study areas. When compared to the slope-intercept method, the LinZI method performed better throughout the year with lower mean bias and RMSE and higher R2. Although the LinZI method resulted in better performance when compared to the slope-intercept method, overall we found lower values of R2. This may be attributed to the very coarse resolution (≈50 km) of the gridded FLUXNET dataset. It was reported that good agreement in surface fluxes is limited when the length scale of surface heterogeneity is less than the mapping resolution [3]. Additionally, study has shown that there is a trade-off between spatial resolution and uncertainty of AET estimates, with lower uncertainty in the coarser resolution relative to higher uncertainty in the finer resolution AET estimates [63]. There is also a limitation in capturing spatial variability in soil moisture and therefore AET over large areas under extremely dry and wet conditions [64].
In general, the model output agreed better with the gridded FLUXNET data during the non-growing season than during the growing season. This was most likely due to less spatial variability in AET during the non-growing season, resulting in better agreement with coarser resolution of the gridded FLUXNET dataset. The resolution of gridded FLUXNET data is about 50 km, and the mean area of the subbasin (HUC 8) is only about 4600 km2. Depending upon the shape and size of subbasins within the study area, we had only from 0 to 6 pixels of gridded FLUXNET data in each subbasin. Zonal statistics computation of downscaled monthly AET maps for each subbasin resulted in the majority of the subbasins having only one pixel of the gridded FLUXNET data. In general, we found that a higher number of pixels of gridded FLUXNET data in a subbasin resulted in better correlation.
Table
Table 3. Comparison statistics using mean bias (MB), root mean square error (RMSE), and coefficient of determination (R2) for downscaled monthly AET maps against gridded FLUXNET dataset (N = 126).
Table 3. Comparison statistics using mean bias (MB), root mean square error (RMSE), and coefficient of determination (R2) for downscaled monthly AET maps against gridded FLUXNET dataset (N = 126).
MonthSlope-Intercept MethodLinZI Method
MB (mm)RMSE (mm)R2 (–)MB (mm)RMSE (mm)R2 (–)
January−360.01−460.75
February250.01080.53
March8100.084120.50
April690.05190.34
May24440.1418220.32
June21420.1310170.43
July13380.197200.23
August19400.2420260.20
September−5120.15−8120.45
October−890.25−10120.08
November−130.02−460.13
December−780.01−990.55
Remotesensing 06 10483 g010 1024
Figure 10. Comparison of mean monthly actual evapotranspiration at the subbasin (Hydrologic Unit Code: HUC 8) level within the Colorado River Basin using MODIS-based and linear with zero intercept (LinZI) method downscaled monthly actual evapotranspiration (N = 144).
Figure 10. Comparison of mean monthly actual evapotranspiration at the subbasin (Hydrologic Unit Code: HUC 8) level within the Colorado River Basin using MODIS-based and linear with zero intercept (LinZI) method downscaled monthly actual evapotranspiration (N = 144).
Remotesensing 06 10483 g010
Remotesensing 06 10483 g011 1024
Figure 11. Monthly actual evapotranspiration near Marana, Arizona, for May, June, July, and August 2010 using MODIS only, Landsat only, and MODIS and Landsat merged images.
Figure 11. Monthly actual evapotranspiration near Marana, Arizona, for May, June, July, and August 2010 using MODIS only, Landsat only, and MODIS and Landsat merged images.
Remotesensing 06 10483 g011

6.5. Comparison of the LinZI Method Monthly Evapotranspiration with Monthly MODIS AET Maps

There was very good agreement between downscaled monthly AET maps using the LinZI method and MODIS-based monthly AET maps at the subbasin level (Figure 10). The MAE ranged from 0 mm (December) to 10 mm (August), and RMSE varied between 1 mm (December) and 12 mm (August). The best agreement was observed in December (R2 = 0.96) while the least agreement was found in August (R2 = 0.61). This was due to low AET values for the month of December as a result of low atmospheric demand, and low agreement during peak crop growing season because of high water demand. Since downscaled monthly AET maps were derived using both Landsat and MODIS-based AET, it is expected that there will be good agreement between these maps. However, even independent estimation of annual AET using Landsat and MODIS-based images resulted in 1.06 slope with an R2 of 0.79 [41]. This result indicates that AET averaged over larger areas may be comparable when AET is estimated using either Landsat or MODIS images. Similar results were reported by other researchers [2,3,41,42].
Previous study has also shown that only MODIS-based AET maps cannot distinguish between maize and soybean fields [35]. The use of Landsat images for estimating AET has many advantages as most of the water management practices related to water application and conservation have to be implemented at the field scale. Individual fields can be identified in Landsat-based AET maps but cannot be clearly distinguished in MODIS-based AET maps (Figure 11). On the other hand, temporal progression of AET can be better captured using MODIS images due to its daily acquisition compared to the 16-day repeat cycle of Landsat images. For example, an AET map using only Landsat images for the month of May based on images acquired on 10 May and 3 June overestimates AET for the agricultural fields (Figure 11). Some of this bias was removed when the AET maps were downscaled by merging Landsat and MODIS-based AET maps as shown in Figure 11. Thus, downscaling using LinZI method captured the temporal progression of AET as well as maintained the spatial fidelity of monthly AET maps. This clearly demonstrates the advantages of downscaling using LinZI method for Landsat and MODIS-based AET maps.

7. Conclusions

Actual evapotranspiration estimation at finer temporal and spatial resolution can help immensely in water resources planning, assessment, development, and management. Limited availability of cloud-free Landsat images may be a constraint in estimating monthly AET using only Landsat images. If the time interval between two available cloud-free Landsat images is large, an irrigation/precipitation event may not be captured by the corresponding AET maps. Similarly, any water stress spell between two widely spaced cloud-free Landsat images will be missed in the respective AET maps. The combination of the better temporal resolution of MODIS and better spatial resolution of Landsat has many advantages. Our application of the output regression (slope-intercept) method (Hong et al. 2011) [36] for downscaling has shown that it has limitations when slope and intercept are computed over a large area. This method can work if slope and coefficients are based on a small area of interest or if the area is homogeneous.
We have demonstrated that the Linear with Zero Intercept (LinZI) method can be efficiently used for downscaling the Landsat-based annual AET to monthly AET using MODIS-based AET maps. Validation of LinZI method downscaled monthly AET using eddy covariance measurements at seven flux towers showed that the mean bias ranged from −16 mm/month to 22 mm/month while R2 varied from 0.52 to 0.88. Thus the LinZI method has great potential and capability for downscaling. The LinZI method was evaluated to downscale to a monthly time scale; further testing is needed to examine the validity of a finer time scale (such as 8 days). The LinZI method will be further evaluated for its performance at other geographical locations under more heterogeneous land cover conditions and ecosystems. The modeling framework will be developed to quantify the uncertainty and improvement in estimating AET compared to only Landsat or only MODIS-based AET maps.
This research can be viewed as a continuation of development approach for operationalization of the full potential of the energy balance method in water resources management. The successful application of the SSEBop model for estimating AET can be further extended to the next level where AET estimated from remotely sensed images at different spatial and temporal resolutions can be merged together using the LinZI method. Though we used SSEBop model for computing AET, the LinZI method can be used for merging AET maps from different sensors derived using any other AET models. This will be a great service to the hydrological community where AET estimates at different spatial and temporal resolutions are required. Such information can help water managers devise sustainable water use planning and management. This research is also relevant and timely in support of the U.S. Department of the Interior’s WaterSMART (Sustain and Manage America’s Resources for Tomorrow) initiative to achieve a sustainable water use strategy to meet the water needs of the nation and realize the vision of the National Water Census [65].

Acronyms and Abbreviations

AET
Actual evapotranspiration
BCM
Billion Cubic Meters
CMS
Charleston Mesquite
CRB
Colorado River Basin
ET
Evapotranspiration
ETM+
Enhanced Thematic Mapper Plus
FMF
Flagstaff Managed Forest
FUF
Flagstaff Unmanaged Forest
FWF
Flagstaff Wildfire
HIS
Hue-Intensity-Saturation
HPF
High Pass Filter
HUC
Hydrologic Unit Code
IHS
Intensity-hue-saturation
LiDAR
Light Detection And Ranging
LinZI
Linear with Zero Intercept
LST
Land Surface Temperature
MAE
Mean Absolute Error
MB
Mean Bias
MODIS
Moderate Resolution Imaging Spectroradiometer
NASA
National Aeronautics and Space Administration
NLCD
National Land Cover Database
PALSAR
Phased Array L-band Synthetic Aperture Radar
PCA
Principal Component Analysis
RMSE
Root Mean Square Error
SLC
Scan Line Corrector
SPOT
Systeme Pour I’Observation de la Terre
SRC
Santa Rita Creosote
SRM
Santa Rita Mesquite
SSEBop
Operational Simplified Surface Energy Balance
STARFM
Spatial and Temporal Adaptive Reflectance Fusion Model
TM
Thematic Mapper
USA
United States of America
USGS
United States Geological Survey
WaterSMART
Sustain and Manage America’s Resources for Tomorrow
WKG
Kendall Grassland

Acknowledgments

This work was performed under the United States Geological Survey (USGS) contract G13PC00028 and G10PC00044 in support of the WaterSMART program. Authors are grateful to Lei Ji for the internal review of the manuscript and to the anonymous reviewers for their valuable comments. We gratefully acknowledge the use of Ameriflux data and flux data supplied by Russell Scott, Agricultural Research Service, U.S. Department of Agriculture for our downscaling method validation. Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government.

Author Contributions

All authors contributed extensively to the work presented in this paper.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Chavez, P.S.; Sides, S.C.; Anderson, J.A. Comparison of three different methods to merge multiresolution and multispectral data: Landsat TM and SPOT panchromatic. Photogramm. Eng. Remote Sens. 1991, 57, 295–303. [Google Scholar]
  2. Long, D.; Singh, V.P. Integration of the GG model with SEBAL to produce time series of evapotranspiration of high spatial resolution at watershed scales. J. Geophys. Res.: Atmos. 2010. [Google Scholar] [CrossRef]
  3. McCabe, M.F.; Wood, E.F. Scale influences on the remote estimation of evapotranspiration using multiple satellite sensors. Remote Sens. Environ. 2006, 105, 271–285. [Google Scholar] [CrossRef]
  4. Hall, D.L.; Llinas, J. An introduction to multisensor data fusion. Proc. IEEE 1997, 85, 6–23. [Google Scholar] [CrossRef]
  5. Pohl, C.; van Genderen, J.L. Multisensor image fusion in remote sensing: Concepts, methods and applications. Int. J. Remote Sens. 1998, 19, 823–854. [Google Scholar] [CrossRef]
  6. Cliche, G.; Bonn, F.; Teillet, P. Integration of the SPOT panchromatic channel into its multispectral mode for image sharpness enhancement. Photogramm. Eng. Remote Sens. 1985, 51, 311–316. [Google Scholar]
  7. Carper, W.J.; Lillesand, T.M.; Kiefer, R.W. The use of intensity-hue-saturation transformations for merging SPOT panchromatic and multispectral image data. Photogramm. Eng. Remote Sens. 1990, 56, 459–467. [Google Scholar]
  8. Price, J.C. Combining multispectral data of differing spatial resolution. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1199–1203. [Google Scholar] [CrossRef]
  9. Wald, L.; Ranchin, T.; Mangolini, M. Fusion of satellite images of different spatial resolutions: Assessing the quality of resulting images. Photogramm. Eng. Remote Sens. 1997, 63, 691–699. [Google Scholar]
  10. Karathanassi, V.; Kolokousis, P.; Ioannidou, S. A comparison study on fusion methods using evaluation indicators. Int. J. Remote Sens. 2007, 28, 2309–2341. [Google Scholar] [CrossRef]
  11. Garguet-Duport, B.; Girel, J.; Chassery, J.M.; Pautou, G. The use of multiresolution analysis and wavelets transform for merging SPOT panchromatic and multispectral image data. Photogramm. Eng. Remote Sens. 1996, 62, 1057–1066. [Google Scholar]
  12. Yocky, D.A. Multiresolution wavelet decomposition image merger of Landsat Thematic Mapper and SPOT panchromatic data. Photogramm. Eng. Remote Sens. 1996, 62, 1067–1074. [Google Scholar]
  13. Nunez, J.; Otazu, X.; Fors, O.; Prades, A.; Pala, V.; Arbiol, R. Multiresolution-based image fusion with additive wavelet decomposition. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1204–1211. [Google Scholar] [CrossRef]
  14. Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar] [CrossRef]
  15. Roy, D.P.; Ju, J.; Lewis, P.; Schaaf, C.; Gao, F.; Hansen, M.; Lindquist, E. Multi-temporal MODIS-Landsat data fusion for relative radiometric normalization, gap filling, and prediction of Landsat data. Remote Sens. Environ. 2008, 112, 3112–3130. [Google Scholar] [CrossRef]
  16. Hilker, T.; Wulder, M.A.; Coops, N.C.; Linke, J.; McDermid, G.; Masek, J.G.; Gao, F.; White, J.C. A new data fusion model for high spatial and temporal resolution mapping of forest disturbance based on Landsat and MODIS. Remote Sens. Environ. 2009, 113, 1613–1627. [Google Scholar] [CrossRef]
  17. Dalponte, M.; Bruzzone, L.; Gianelle, D. Tree species classification in the southern Alps based on the fusion of very high geometrical resolution multispectral/hyperspectral images and LiDAR data. Remote Sens. Environ. 2012, 123, 258–270. [Google Scholar] [CrossRef]
  18. Wolter, P.T.; Townsend, P.A. Multi-sensor data fusion for estimating forest species composition and abundance in northern Minnesota. Remote Sens. Environ. 2011, 115, 671–691. [Google Scholar] [CrossRef]
  19. Zhang, Y. Understanding image fusion. Photogramm. Eng. Remote Sens. 2004, 70, 657–661. [Google Scholar]
  20. Kustas, W.; Norman, J.; Anderson, M.; French, A. Estimating subpixel surface temperatures and energy fluxes from the vegetation index-radiometric temperature relationship. Remote Sens. Environ. 2003, 85, 429–440. [Google Scholar] [CrossRef]
  21. Norman, J.M.; Anderson, M.C.; Kustas, W.P.; French, A.N.; Mecikalski, J.; Torn, R.; Diak, G.R.; Schmugge, T.J.; Tanner, B.C.W. Remote sensing of surface energy fluxes at 10-m pixel resolutions. Water Resour. Res. 2003. [Google Scholar] [CrossRef]
  22. Anderson, M.C.; Norman, J.M.; Mecikalski, J.R.; Torn, R.D.; Kustas, W.P.; Basara, J.B. A multiscale remote sensing model for disaggregating regional fluxes to micrometeorological scales. J. Hydrometeorol. 2004, 5, 343–363. [Google Scholar] [CrossRef]
  23. Kaheil, Y.H.; Rosero, E.; Gill, M.K.; McKee, M.; Bastidas, L.A. Downscaling and forecasting of evapotranspiration using a synthetic model of wavelets and support vector machines. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2692–2707. [Google Scholar] [CrossRef]
  24. Liu, D.S.; Pu, R.L. Downscaling thermal infrared radiance for subpixel land surface temperature retrieval. Sensors 2008, 8, 2695–2706. [Google Scholar] [CrossRef]
  25. Stathopoulou, M.; Cartalis, C. Downscaling AVHRR land surface temperatures for improved surface urban heat island intensity estimation. Remote Sens. Environ. 2009, 112, 2592–2605. [Google Scholar] [CrossRef]
  26. Tom, V.T.; Carlotto, M.J.; Scholten, D.K. Spatial resolution improvement of TM thermal band data. Proc. SPIE 1984. [Google Scholar] [CrossRef]
  27. Nishii, R.; Kusanobu, S.; Tanaka, S. Enhancement of low spatial resolution image based on high resolution bands. IEEE Trans. Geosci. Remote Sens. 1996, 34, 1151–1158. [Google Scholar] [CrossRef]
  28. Fasbender, D.; Tuia, D.; Bogaert, P.; Kanevski, M. Support-based implementation of Bayesian data fusion for spatial enhancement: Applications to ASTER thermal images. IEEE Geosci. Remote Sens. Lett. 2008, 5, 598–602. [Google Scholar] [CrossRef]
  29. Oki, K.; Omasa, K. A technique for mapping thermal infrared radiation variation within land cover. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1521–1524. [Google Scholar] [CrossRef]
  30. Lemeshewsky, G.P.; Schowengerdt, R.A. Landsat 7 thermal-IR image sharpening using an artificial neural network and sensor model. Proc. SPIE 2001. [Google Scholar] [CrossRef]
  31. Agam, N.; Kustas, W.P.; Anderson, M.C.; Li, F.Q.; Neale, C.M.U. A vegetation index based technique for spatial sharpening of thermal imagery. Remote Sens. Environ. 2007, 107, 545–558. [Google Scholar] [CrossRef]
  32. Ha, W.; Gowda, P.H.; Howell, T.A. A review of downscaling methods for remote sensing-based irrigation management: Part I. Irrig. Sci. 2013, 31, 831–850. [Google Scholar] [CrossRef]
  33. Ha, W.; Gowda, P.H.; Howell, T.A. A review of potential image fusion methods for remote sensing-based irrigation management: Part II. Irrig. Sci. 2013, 31, 851–869. [Google Scholar] [CrossRef]
  34. Zhan, W.; Chen, Y.; Zhou, J.; Wang, J.; Liu, W.; Voogt, J.; Zhu, X.; Quan, J.; Li, J. Disaggregation of remotely sensed land surface temperature: Literature survey, taxonomy, issues, and caveats. Remote Sens. Environ. 2013, 131, 119–139. [Google Scholar] [CrossRef]
  35. Kustas, W.P.; Li, F.; Jackson, T.J.; Prueger, J.H.; MacPherson, J.I.; Wolde, M. Effects of remote sensing pixel resolution on modeled energy flux variability of croplands in Iowa. Remote Sens. Environ. 2004, 92, 535–547. [Google Scholar] [CrossRef]
  36. Hong, S.; Hendrickx, J.M.H.; Borchers, B. Downscaling of SEBAL derived evapotranspiration maps from MODIS (250 m) to Landsat (30 m) scales. Int. J. Remote Sens. 2011, 32, 6457–6477. [Google Scholar] [CrossRef]
  37. Kim, J.; Hogue, T.S. Evaluation and sensitivity testing of a coupled Landsat-MODIS downscaling method for land surface temperature and vegetation indices in semi-arid regions. J. Appl. Remote Sens. 2012. [Google Scholar] [CrossRef]
  38. Long, D.; Singh, V.P.; Li, Z.L. How sensitive is SEBAL to changes in input variables, domain size and satellite sensor? J. Geophys. Res.: Atmos. 2011. [Google Scholar] [CrossRef]
  39. Chavez, J.L.; Neale, C.M.U.; Prueger, J.H.; Kustas, W.P. Daily evapotranspiration estimates from extrapolating instantaneous airborne remote sensing ET values. Irrig. Sci. 2008, 27, 67–81. [Google Scholar] [CrossRef]
  40. Singh, R.K.; Liu, S.; Tieszen, L.L.; Suyker, A.E.; Verma, S.B. Estimating seasonal evapotranspiration from temporal satellite images. Irrig. Sci. 2012, 30, 303–313. [Google Scholar] [CrossRef]
  41. Singh, R.K.; Senay, G.B.; Velpuri, N.M.; Bohms, S.; Scott, R.L.; Verdin, J.P. Actual evapotranspiration (water use) assessment of the Colorado River Basin at the Landsat resolution using the Operational Simplified Surface Energy Balance Model. Remote Sens. 2014, 6, 233–256. [Google Scholar] [CrossRef]
  42. Bastiaanssen, W.G.M.; Noordman, E.J.M.; Pelgrum, H.; Davids, G.; Thoreson, B.P.; Allen, R.G. SEBAL model with remotely sensed data to improve water-resources management under actual field conditions. J. Irrig. Drain. Eng. 2005, 131, 85–93. [Google Scholar] [CrossRef]
  43. Christensen, N.S.; Wood, A.W.; Voisin, N.; Lettenmaier, D.P.; Palmer, R.N. The effects of climate change on the hydrology and water resources of the Colorado River Basin. Clim. Chang. 2004, 62, 337–363. [Google Scholar] [CrossRef]
  44. Bruce, B.W. WaterSMART—The Colorado River Basin Focus Area Study; US Geological Survey: Washington, DC, USA, 2012. [Google Scholar]
  45. Fry, J.; Xian, G.; Jin, S.; Dewitz, J.; Homer, C.; Yang, L.; Barnes, C.; Herold, N.; Wickham, J. Completion of the 2006 national land cover database for the conterminous United States. Photogramm. Eng. Remote Sens. 2011, 77, 858–864. [Google Scholar]
  46. Kumar, M.; Duffy, C.J. Detecting hydroclimatic change using spatio-temporal analysis of time series in Colorado River Basin. J. Hydrol. 2009, 374, 1–15. [Google Scholar] [CrossRef]
  47. ASCE-EWRI. The ASCE standardized reference evapotranspiration equation. In Standardization of Reference Evapotranspiration Task Committee Final Report; Reston, V., Ed.; American Society of Civil Engineers (ASCE) Environmental and Water Resources Institute (EWRI): Reston, VA, USA, 2005. [Google Scholar]
  48. Senay, G.B.; Bohms, S.; Singh, R.K.; Gowda, P.H.; Velpuri, N.M.; Alemu, H.; Verdin, J.P. Operational evapotranspiration mapping using remote sensing and weather datasets: A new parameterization for the SSEB approach. J. Am. Water Resour. Assoc. 2013, 49, 577–591. [Google Scholar] [CrossRef]
  49. Jung, M.; Reichstein, M.; Bondeau, A. Towards global empirical upscaling of FLUXNET eddy covariance observations: Validation of a model tree ensemble approach using a biosphere model. Biogeosciences 2009, 6, 2001–2013. [Google Scholar] [CrossRef]
  50. Peters-Lidard, C.D.; Kumar, S.V.; Mocko, D.M.; Tian, Y. Estimating evapotranspiration with land data assimilation systems. Hydrol. Process. 2011, 25, 3979–3992. [Google Scholar] [CrossRef]
  51. Velpuri, N.M.; Senay, G.B.; Singh, R.K.; Bohms, S.; Verdin, J.P. A comprehensive evaluation of two MODIS evapotranspiration products over the conterminous United States: Using point and gridded FLUXNET and water balance ET. Remote Sens. Environ. 2013, 139, 35–49. [Google Scholar] [CrossRef]
  52. Dore, S.; Montes-Helu, M.; Hart, S.C.; Hungate, B.A.; Koch, G.W.; Moon, J.B.; Finkral, A.J.; Kolb, T.E. Recovery of ponderosa pine ecosystem carbon and water fluxes from thinning and stand-replacing fire. Glob. Chang. Biol. 2012, 18, 3171–3185. [Google Scholar] [CrossRef]
  53. Kurc, S.A.; Benton, L.M. Digital image-derived greenness links deep soil moisture to carbon uptake in a creosotebush-dominated shrubland. J. Arid Environ. 2010, 74, 585–594. [Google Scholar] [CrossRef]
  54. Scott, R.L.; Jenerette, G.D.; Potts, D.L.; Huxman, T.E. Effects of seasonal drought on net carbon dioxide exchange from a woody-plant-encroached semiarid grassland. J. Geophys. Res.: Biogeosci. 2009. [Google Scholar] [CrossRef]
  55. Scott, R.L.; Hamerlynck, E.P.; Jenerette, G.D.; Moran, M.S.; Barron-Gafford, G. Carbon dioxide exchange in a semidesert grassland through drought-induced vegetation change. J. Geophys. Res.: Biogeosci. 2010. [Google Scholar] [CrossRef]
  56. Scott, R.L.; Edwards, E.A.; Shuttleworth, W.J.; Huxman, T.E.; Watts, C.; Goodrich, D.C. Interannual and seasonal variation in fluxes of water and carbon dioxide from a riparian woodland ecosystem. Agric. For. Meteorol. 2004, 122, 65–84. [Google Scholar] [CrossRef]
  57. Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R.; et al. FLUXNET: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2431. [Google Scholar] [CrossRef]
  58. Leclerc, M.Y.; Thurtell, G.W. Footprint prediction of scalar fluxes using a Markovian analysis. Bound.-Lay. Meteorol. 1990, 52, 247–258. [Google Scholar] [CrossRef]
  59. Twine, T.E; Kustas, W.P.; Norman, J.M.; Cook, D.R.; Houser, P.R.; Meyers, T.P.; Prueger, J.H.; Starks, P.J.; Wesely, M.L. Correcting eddy covariance flux underestimates over a grassland. Agric. For. Meteorol. 2000, 103, 279–300. [Google Scholar] [CrossRef]
  60. Wilson, K.; Goldstein, A.; Falge, E.; Aubinet, M.; Baldocchi, D.; Berbigier, P.; Bernhofer, C.; Ceulemans, R.; Dolman, H.; Field, C.; et al. Energy balance closure at FLUXNET sites. Agric. For. Meteorol. 2002, 113, 223–243. [Google Scholar] [CrossRef]
  61. Hollinger, D.Y.; Richardson, A.D. Uncertainty in eddy covariance measurements and its application to physiological models. Tree Physiol. 2005, 25, 873–885. [Google Scholar] [CrossRef] [PubMed]
  62. Verma, S.B. Micrometeorological methods for measuring surface fluxes of mass and energy. Remote Sens. Rev. 1990, 5, 99–115. [Google Scholar] [CrossRef]
  63. Long, D.; Longuevergne, L.; Scanlon, B.R. Uncertainty in evapotranspiration from land surface modeling, remote sensing, and GRACE satellites. Water Resour. Res. 2014, 50, 1131–1151. [Google Scholar] [CrossRef] [Green Version]
  64. Long, D.; Singh, V.P. Assessing the impact of end-member selection on the accuracy of satellite-based spatial variability models for actual evapotranspiration estimation. Water Resour. Res. 2013, 49, 2601–2618. [Google Scholar] [CrossRef]
  65. US Department of the Interior (DOI). Fiscal year 2011 the interior budget in brief. In WaterSMART: Departmental Highlights; DOI: Washington, DC, USA, 2010; pp. 19–25. [Google Scholar]

Share and Cite

MDPI and ACS Style

Singh, R.K.; Senay, G.B.; Velpuri, N.M.; Bohms, S.; Verdin, J.P. On the Downscaling of Actual Evapotranspiration Maps Based on Combination of MODIS and Landsat-Based Actual Evapotranspiration Estimates. Remote Sens. 2014, 6, 10483-10509. https://doi.org/10.3390/rs61110483

AMA Style

Singh RK, Senay GB, Velpuri NM, Bohms S, Verdin JP. On the Downscaling of Actual Evapotranspiration Maps Based on Combination of MODIS and Landsat-Based Actual Evapotranspiration Estimates. Remote Sensing. 2014; 6(11):10483-10509. https://doi.org/10.3390/rs61110483

Chicago/Turabian Style

Singh, Ramesh K., Gabriel B. Senay, Naga M. Velpuri, Stefanie Bohms, and James P. Verdin. 2014. "On the Downscaling of Actual Evapotranspiration Maps Based on Combination of MODIS and Landsat-Based Actual Evapotranspiration Estimates" Remote Sensing 6, no. 11: 10483-10509. https://doi.org/10.3390/rs61110483

APA Style

Singh, R. K., Senay, G. B., Velpuri, N. M., Bohms, S., & Verdin, J. P. (2014). On the Downscaling of Actual Evapotranspiration Maps Based on Combination of MODIS and Landsat-Based Actual Evapotranspiration Estimates. Remote Sensing, 6(11), 10483-10509. https://doi.org/10.3390/rs61110483

Article Metrics

Back to TopTop