Evaluating Remotely Sensed Phenological Metrics in a Dynamic Ecosystem Model
Abstract
:1. Introduction
2. Method and Material
2.1. Agro-IBIS Model Description
2.2. Evaluation of Ground Phenology Observations
2.3. Evaluation of Remotely Sensed Phenological Metrics
2.4. Evaluation of the Propagation of Bias in Phenology
2.5. Errors in Simulated Productivities Caused by Biases in Phenology
3. Results
3.1. Ground Phenology Reference
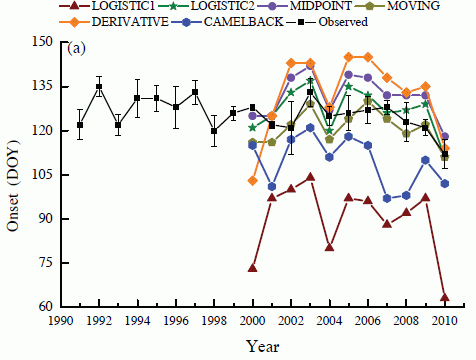
3.2. Remotely Sensed Phenological Metrics
3.3. The Propagation of Bias in Phenology
3.4. Impact of Bias in Phenology on Simulated Productivities
4. Discussion
4.1. Ground Phenology Reference and Agro-IBIS
4.2. Remotely Sensed Phenology
4.3. Modeled Phenology
4.4. Impact of Phenology on Simulated Productivities
4.5. Uncertainties in the Evaluation
5. Conclusions
Supplementary Information
remotesensing-06-04660-s001.pdfAcknowledgments
Conflicts of Interest
- Author ContributionsHong Xu and Tracy E. Twine designed the research. Hong Xu and Xi Yang performed data analysis and model simulations. All authors contributed with ideas, writing and discussions.
References
- Menzel, A.; Fabian, P. Growing season extended in Europe. Nature 1999, 397, 659. [Google Scholar]
- Myneni, R.B.; Keeling, C.D.; Tucker, C.J.; Asrar, G.; Nemani, R.R. Increased plant growth in the northern hight latitudes from 1981 to 1991. Nature 1997, 386, 698–702. [Google Scholar]
- Schwartz, M.D.; Reiter, B.E. Changes in north American spring. Int. J. Climatol 2000, 20, 929–932. [Google Scholar]
- Zhou, L.; Tucker, C.J.; Kaufmann, R.K.; Slayback, D.; Shabanov, N.V.; Myneni, R.B. Variation in northern vegetation activity inferred from satellite data of vegetation index during 1981 to 1999. J. Geophys. Res 2001, 106, 20069–20083. [Google Scholar]
- Zhu, W.; Tian, H.; Xu, X.; Pan, Y.; Chen, G.; Lin, W. Extension of the growing season due to delayed autumn over mid and high latitudes in north America during 1982–2006. Glob. Ecol. Biogeogr 2012, 21, 260–271. [Google Scholar]
- Menzel, A.; Sparks, T.H.; Estrella, N.; Koch, E.; Aasa, A.; Ahas, R.; Alm-Kubler, K.; Bissolli, P.; Braslavska, O.G.; Briede, A.; et al. European phenological response to climate change matches the warming pattern. Glob. Chang. Biol 2006, 12, 1969–1976. [Google Scholar]
- Peñuelas, J.; Filella, I. Phenology-responses to a warming world. Science 2001, 294, 793–795. [Google Scholar]
- Peñuelas, J.; Rutishauser, T.; Filella, I. Phenology feedbacks on climate change. Science 2009, 324, 887–888. [Google Scholar]
- Richardson, A.D.; Keenan, T.F.; Migliavacca, M.; Ryu, Y.; Sonnentag, O.; Toomey, M. Climate change, phenology, and phenological control of vegetation feedbacks to the climate system. Agric. For. Meteorol 2013, 169, 156–173. [Google Scholar]
- Richardson, A.D.; Anderson, R.S.; Arain, M.A.; Barr, A.G.; Bohrer, G.; Chen, G.; Chen, J.M.; Ciais, P.; Davis, K.J.; Desai, A.R.; et al. Terrestrial biosphere models need better representation of vegetation phenology: Results from the north American carbon program site synthesis. Glob. Chang. Biol 2012, 18, 566–584. [Google Scholar]
- Levis, S.; Bonan, G.B. Simulating springtime temperature patterns in the community atmosphere model coupled to the community land model using prognostic leaf area. J. Clim 2004, 17, 4531–4540. [Google Scholar]
- Migliavacca, M.; Sonnentag, O.; Keenan, T.F.; Cescatti, A.; O’Keefe, J.; Richardson, A.D. On the uncertainty of phenological responses to climate change, and implications for a terrestrial biosphere model. Biogeosciences 2012, 9, 2063–2083. [Google Scholar]
- Yang, X.; Mustard, J.F.; Tang, J.; Xu, H. Regional-scale phenology modeling based on meteorological records and remote sensing observations. J. Geophys. Res 2012, 117, G03029. [Google Scholar]
- Fisher, J.I.; Richardson, A.D.; Mustard, J.F. Phenology model from surface meteorology does not capture satellite-based greenup estimations. Glob. Chang. Biol 2007, 13, 707–721. [Google Scholar]
- De Beurs, K.M.; Henebry, G.M. Land surface phenology and temperature variation in the international geosphere-biosphere program high-latitude transects. Glob. Chang. Biol 2005, 11, 779–790. [Google Scholar]
- Liang, L.; Schwartz, M.D. Landscape phenology: An integrative approach to seasonal vegetation dynamics. Landsc. Ecol 2009, 24, 465–472. [Google Scholar]
- Zhang, X.; Tarpley, D.; Sullivan, J.T. Diverse responses of vegetation phenology to a warming climate. Geophys. Res. Lett 2007, 34, L19405. [Google Scholar]
- Botta, A.; Viovy, N.; Ciais, P.; Friedlingstein, P.; Monfray, P. A global prognostic scheme of leaf onset using satellite data. Glob. Chang. Biol 2000, 6, 7090–7725. [Google Scholar]
- White, M.A.; Thornton, P.E.; Running, S.W. A continental phenology model for monitoring vegetation responses to interannual climatic variability. Glob. Biogeochem. Cycles 1997, 11, 217–234. [Google Scholar]
- Balzter, H.; Gerard, F.; George, C.; Weedon, G.; Grey, W.; Combal, B.; Bartholomé, E.; Bartalev, S.; Los, S. Coupling of vegetation growing season anomalies and fire activity with hemispheric and regional-scale climate patterns in central and east Siberia. J. Clim 2007, 20, 3713–3729. [Google Scholar]
- De Beurs, K.M.; Henebry, G.M. Northern annular mode effects on the land surface phenologies of northern Eurasia. J. Clim 2008, 21, 4257–4279. [Google Scholar]
- Fisher, J.I.; Mustard, J.F.; Vadeboncoeur, M.A. Green leaf phenology at landsat resolution: Scaling from the field to the satellite. Remote Sens. Environ 2006, 100, 265–279. [Google Scholar]
- Reed, B.C.; Brown, J.F.; Vanderzee, D.; Loveland, T.R.; Merchant, J.W.; Ohlen, D.O. Measuring phenological variability from satellite imagery. J. Veg. Sci 1994, 15, 703–714. [Google Scholar]
- Tateishi, R.; Ebata, M. Analysis of phenological change patterns using 1982–2000 advanced very high resolution radiometer (AVHRR) data. Int. J. Remote Sens 2004, 25, 2287–2300. [Google Scholar]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.F.; Gao, F.; Reed, B.C.; Huete, A. Monitoring vegetation phenology using MODIS. Remote Sens. Environ 2003, 84, 471–475. [Google Scholar]
- Schwartz, M.D.; Reed, B.C.; White, M.A. Assessing satellite-derived start-of-season measures in the conterminous USA. Int. J. Climatol 2002, 22, 1793–1805. [Google Scholar]
- White, M.A.; de Beurs, K.M.; Didan, K.; Inouye, D.W.; Richardson, A.D.; Jensen, O.P.; O’Keefe, J.; Zhang, G.; Nemani, R.R.; van LEEUWEN, W.J.D.; et al. Intercomparison, interpretation, and assessment of spring phenology in north America estimated from remote sensing for 1982–2006. Glob. Chang. Biol 2009, 15, 2335–2359. [Google Scholar]
- Ahl, D.E.; Gower, S.T.; Burrows, S.N.; Shabanov, N.V.; Myneni, R.B.; Knyazikhin, Y.; Douglas, E.A. Monitoring spring canopy phenology of a deciduous broadleaf forest using MODIS. Remote Sens. Environ 2006, 104, 88–95. [Google Scholar]
- Foley, J.A.; Prentice, I.C.; Ramankutty, N.; Levis, S.; Pollard, D.; Sitch, S.; Haxeltine, A. An integrated biosphere model of land surface processes, terrestrial carbon balance, and vegetation dynamics. Glob. Biogeochem. Cycle 1996, 10, 603–628. [Google Scholar]
- Kucharik, C.J. Evaluation of a process-based agro-ecosystem model (Agro-IBIS) across the U.S. Corn belt: Simulations of the interannual variability in maize yield. Earth Interact 2003, 7, 1–33. [Google Scholar]
- Kucharik, C.J.; Foley, J.A.; Christine, D.; Fisher, V.A.; Coe, M.T.; Lenters, J.D.; Young-Molling, C.; Ramankutty, N.; Norman, J.M.; Gower, S.T. Testing the performance of a dynamic global ecosystem model: Water balance, carbon balance, and vegetation structure. Glob. Biogeochem. Cycle 2000, 14, 795–825. [Google Scholar]
- O’Keefe, J. Harvard Forest Data Archive: Hf003. Available online: http://harvardforest.fas.harvard.edu:8080/exist/xquery/data.xq?id=hf003 (accessed on 26 March 2014).
- Munger, J.W. Ameriflux: Harvard Forest. Available online: http://ameriflux.ornl.gov/fullsiteinfo.php?sid=50 (accessed on 26 March 2014).
- Kucharik, C.J.; Barford, C.C.; El Maayar, M.; Wofsy, S.C.; Monson, R.K.; Baldocchi, D.D. A multiyear evaluation of a dynamic global vegetation model at three ameriflux forest sites: Vegetation structure, phenology, soil temperature, and CO2 and H2O vapor exchange. Ecol. Modell 2006, 196, 1–31. [Google Scholar]
- Twine, T.E.; Kucharik, C.J. Evaluating a terrestrial ecosystem model with satellite information of greenness. J. Geophys. Res.-Biogeosci 2008, 113, G03027. [Google Scholar]
- Twine, T.E.; Kucharik, C.J. Climate impacts on net primary productivity trends in natural and managed ecosystems of the central and eastern United States. Agric. For. Meteorol 2009, 149, 2143–2161. [Google Scholar]
- Anderson-Teixeira, K.J.; Snyder, P.K.; Twine, T.E.; Cuadra, S.V.; Costa, M.H.; DeLucia, E.H. Climate-regulation services of natural and agricultural ecoregions of the Americas. Nat. Clim. Chang 2012, 2, 177–181. [Google Scholar]
- Motew, M.M.; Kucharik, C.J. Climate-induced changes in biome distribution, NPP, and hydrology in the upper midwest U.S.: A case study for potential vegetation. J. Geophys. Res.: Biogeosci 2013, 118, 248–264. [Google Scholar]
- Urbanski, S.; Barford, C.; Wofsy, S.; Kucharik, C.; Pyle, E.; Budney, J.; McKain, K.; Fitzjarrald, D.; Czikowsky, M.; Munger, J.W. Factors controlling CO2 exchange on timescales from hourly to decadal at harvard forest. J. Geophys. Res 2007, 112, G02020. [Google Scholar]
- The USGS Land Processes Distributed Active Archive Center. Available online: https://lpdaac.usgs.gov/ (accessed on 26 March 2014).
- Chen, J.; Jönsson, P.; Tamura, M.; Gu, Z.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky–Golay filter. Remote Sens. Environ 2004, 91, 332–344. [Google Scholar]
- Sarvas, R. Investigations on the annual cycle of development of forest trees: II. Autumn dormancy and winter dormancy. Commun. Instit. Forestalis Fenniae 1974, 84, 1–101. [Google Scholar]
- Delpierre, N.; Dufrene, E.; Soudani, K.; Ulrich, E.; Cecchini, S.; Boe, J.; Francois, C. Modelling interannual and spatial variability of leaf senescence for three deciduous tree species in France. Agric. For. Meteorol 2009, 149, 848–938. [Google Scholar]
- Hunter, A.F.; Lechowicz, M.J. Predicting the timing of budburst in temperate trees. J. Appl. Ecol 1992, 29, 597–604. [Google Scholar]
- Kramer, K. Selecting a model to predict the onset of growth of Fagus sylvatica. J. Appl. Ecol 1994, 31, 172–181. [Google Scholar]
- Campbell, G.S.; Norman, J.M. An Introduction to Environmental Biophysics; Springer: New York, NY, USA, 1998. [Google Scholar]
- Rob Dimeo’s IDL Programs. Available online: http://www.ncnr.nist.gov/staff/dimeo/idl_programs.html (accessed on 26 March 2014).
- Moffat, A.M.; Papale, D.; Reichstein, M.; Hollinger, D.Y.; Richardson, A.D.; Barr, A.G.; Beckstein, C.; Braswell, B.H.; Churkina, G.; Desai, A.R.; et al. Comprehensive comparison of gap-filling techniques for eddy covariance net carbon fluxes. Agric. For. Meteorol 2007, 147, 209–232. [Google Scholar]
- Richardson, A.D.; O’Keefe, J. Phenological Differences between Understory and Overstory: A Case Study Using the Long-Term Harvard Forest Records. In Phenology of Ecosystem Processes: Applications in Global Change Research; Noormets, A., Ed.; Springer: New York, NY, USA, 2009; pp. 87–117. [Google Scholar]
- Birky, A.K. NDVI a simple model of deciduous forest seasonal dynamics. Ecol. Modell 2001, 143, 43–58. [Google Scholar]
- Lüdeke, M.; Janecek, A.; Kohlmaier, G.H. Modelling the seasonal CO2 uptake by land vegetation using the global vegetation index. Tellus 1991, 43B, 188–196. [Google Scholar]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ 2002, 83, 195–213. [Google Scholar]
- Richardson, A.D.; Bailey, A.S.; Denny, E.G.; Martin, C.W.; O’Keefe, J. Phenology of a northern hardwood forest canopy. Glob. Chang. Biol 2006, 12, 1174–1188. [Google Scholar]
- Sonnentag, O.; Hufkens, K.; Teshera-Sterne, C.; Young, A.M.; Friedl, M.; Braswell, B.H.; Milliman, T.; O’Keefe, J.; Richardson, A.D. Digital repeat photography for phenological research in forest ecosystems. Agric. For. Meteorol 2012, 152, 159–177. [Google Scholar]
- Piao, S.; Friedlingstein, P.; Ciais, P.; Viovy, N.; Demarty, J. Growing season extension and its impact on terrestrial carbon cycle in the northern hemisphere over the past 2 decades. Glob. Biogeochem. Cycle 2007, 21, GB3018. [Google Scholar]
- Baldocchi, D. Turner review No. 15. ‘Breathing’ of the terrestrial biosphere: Lessons learned from a global network of carbon dioxide flux measurement systems. Austr. J. Bot 2008, 56, 1–26. [Google Scholar]
- Richardson, A.D.; Black, T.A.; Ciais, P.; Delbart, N.; Friedl, M.A.; Gobron, N.; Hollinger, D.Y.; Kutsch, W.L.; Longdoz, B.; Luyssaert, S.; et al. Influence of spring and autumn phenological transitions on forest ecosystem productivity. Philos. Transc. R. Soc. B 2010, 365, 3227–3246. [Google Scholar] [Green Version]








| Abbreviation | Description | Example | Source |
|---|---|---|---|
| MIDPOINT | VI is normalized to a range of 0–1. Onset is defined as the DOY when normalized VI exceeds 0.5 in the spring. Offset is defined as the DOY when normalized VI decreases below 0.5 in the autumn. |  | [19] |
| LOGISTIC1 | VI time series is fitted using logistic function. Then, the rate of change in curvature of fitted function is calculated. Onset is defined as the DOY when the rate of change in curvature reaches the first local maximum in the spring. Offset is defined as the DOY when the rate of change in curvature reaches the first local minimum in the autumn. |  | [25] |
| LOGISTIC2 | VI time series is fitted using logistic function. Onset is defined as the DOY when fitted VI exceeds 50% amplitude between the minimum and maximum in the spring. Offset is defined as the DOY when fitted VI decreases below 50% amplitude between the minimum and maximum in the autumn. |  | [22] |
| MOVING | A new VI curve is established from moving average models with an introduced time lag of 225-days. Onset is defined as the DOY when the original VI time series crosses the moving-average curve. Offset is defined the same way as onset with the VI time series reversed. |  | [23] |
| DERIVATIVE | The derivative of VI time series is derived by calculating the change in VI with a 20-day moving window. Onset is defined as the DOY when the maximal increase in VI is reached. Offset is defined as the DOY when the maximal decrease in VI is reached. |  | [24] |
| CAMELBACK | A moving window of 50 days (equivalent to the 5–10-day composite used in [20]) is passed over the VI time series. The slope of the regression of the VI against time within every window is calculated to establish the first order derivative time series. Then, the second order derivative is calculated using the same process and window. Onset is defined as the DOY when the second derivative time series reaches a local maximum and the slope is positive. Offset is determined at the time where the second order derivative reaches a local maximum and the slope is negative. |  | [20] |
| (%) | BBRK10 | BBRK20 | BBRK30 | BBRK40 | BBRK50 | BBRK60 | BBRK70 | BBRK80 | BBRK90 |
|---|---|---|---|---|---|---|---|---|---|
| LCOLOR10 | 10.46 | 10.69 | 10.51 | 10.79 | 10.92 | 11.04 | 11.03 | 11.31 | 11.45 |
| LCOLOR20 | 9.09 | 9.09 | 8.86 | 9.10 | 9.19 | 9.30 | 9.23 | 9.45 | 9.48 |
| LCOLOR30 | 9.45 | 9.53 | 9.28 | 9.51 | 9.61 | 9.72 | 9.63 | 9.83 | 9.84 |
| LCOLOR40 | 10.22 | 10.26 | 9.98 | 10.15 | 10.22 | 10.32 | 10.20 | 10.38 | 10.36 |
| LCOLOR50 | 11.38 | 11.40 | 11.11 | 11.30 | 11.35 | 11.45 | 11.31 | 11.46 | 11.41 |
| LCOLOR60 | 12.63 | 12.65 | 12.35 | 12.54 | 12.59 | 12.71 | 12.55 | 12.68 | 12.60 |
| LCOLOR70 | 14.21 | 14.22 | 13.91 | 14.10 | 14.15 | 14.26 | 14.10 | 14.21 | 14.11 |
| LCOLOR80 | 15.83 | 15.80 | 15.48 | 15.66 | 15.72 | 15.83 | 15.66 | 15.76 | 15.65 |
| LCOLOR90 | 17.98 | 17.92 | 17.59 | 17.76 | 17.82 | 17.93 | 17.75 | 17.85 | 17.71 |
| Leaf Onset | NDVI | EVI | ||
|---|---|---|---|---|
| RMSD | ρ | RMSD | ρ | |
| LOGISTIC1 | 36.1 | 0.06 | 13.8 | 0.44 |
| LOGISTIC2 | 6.3 | 0.31 | 13.3 | 0.80 |
| MIDPOINT | 9.2 | 0.42 | 13.1 | 0.54 |
| MOVING | 5.3 | 0.54 | 6.5 | 0.68 |
| DERIVATIVE | 14.5 | 0.28 | 14.7 | 0.51 |
| CAMELBACK | 16.5 | 0.30 | 12.2 | 0.48 |
| Leaf Offset | NDVI | EVI | ||
|---|---|---|---|---|
| RMSD | ρ | RMSD | ρ | |
| LOGISTIC1 | 20.6 | 0.53 | 45.3 | −0.25 |
| LOGISTIC2 | 21.1 | 0.38 | 5.2 | 0.02 |
| MIDPOINT | 21.8 | 0.32 | 9.8 | 0.17 |
| MOVING | 59.1 | 0.13 | 30.0 | 0.51 |
| DERIVATIVE | 29.4 | 0.03 | 17.0 | −0.38 |
| CAMELBACK | 36.4 | 0.30 | 39.3 | −0.33 |
| Leaf Offset | NDVI | EVI | ||
|---|---|---|---|---|
| RMSD | ρ | RMSD | ρ | |
| LOGISTIC1 | 34.5 | 0.20 | 12.2 | 0.31 |
| LOGISTIC2 | 5.7 | 0.63 | 12.5 | 0.68 |
| MIDPOINT | 10.2 | 0.72 | 12.5 | 0.68 |
| MOVING | 5.0 | 0.67 | 9.4 | 0.67 |
| DERIVATIVE | 11.3 | 0.65 | 13.5 | 0.80 |
| CAMELBACK | 17.4 | 0.30 | 13.3 | 0.32 |
| Leaf Offset | NDVI | EVI | ||
|---|---|---|---|---|
| RMSD | ρ | RMSD | ρ | |
| LOGISTIC1 | 18.1 | 0.53 | 49.5 | 0.50 |
| LOGISTIC2 | 17.1 | 0.47 | 3.4 | 0.40 |
| MIDPOINT | 18.1 | 0.50 | 9.6 | 0.04 |
| MOVING | 56.3 | 0.39 | 29.0 | 0.23 |
| DERIVATIVE | 22.6 | 0.52 | 10.3 | 0.02 |
| CAMELBACK | 34.1 | 0.50 | 37.3 | 0.35 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Xu, H.; Twine, T.E.; Yang, X. Evaluating Remotely Sensed Phenological Metrics in a Dynamic Ecosystem Model. Remote Sens. 2014, 6, 4660-4686. https://doi.org/10.3390/rs6064660
Xu H, Twine TE, Yang X. Evaluating Remotely Sensed Phenological Metrics in a Dynamic Ecosystem Model. Remote Sensing. 2014; 6(6):4660-4686. https://doi.org/10.3390/rs6064660
Chicago/Turabian StyleXu, Hong, Tracy E. Twine, and Xi Yang. 2014. "Evaluating Remotely Sensed Phenological Metrics in a Dynamic Ecosystem Model" Remote Sensing 6, no. 6: 4660-4686. https://doi.org/10.3390/rs6064660
APA StyleXu, H., Twine, T. E., & Yang, X. (2014). Evaluating Remotely Sensed Phenological Metrics in a Dynamic Ecosystem Model. Remote Sensing, 6(6), 4660-4686. https://doi.org/10.3390/rs6064660