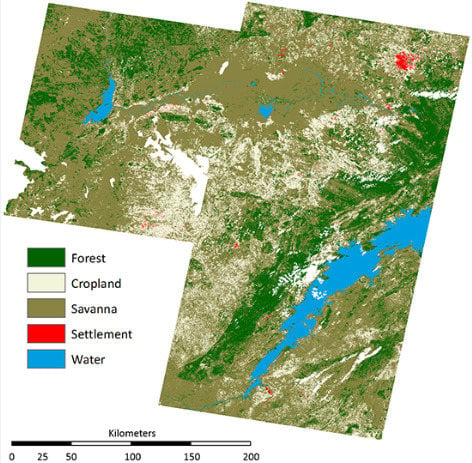
2.3. Analysis
Given the slight differences in image acquisition dates, and inherent difficulties related to normalizing reflectance among adjacent scenes, each footprint was classified independently. Land cover within the area delineated by the TM footprint at Path: 172; Row: 071 (WRS 2) was classified first. The method for classifying land cover in this footprint, and classification results, are presented in detail. Classification results from the two adjacent footprints are provided in the supplement.
To develop a training dataset, a clustering algorithm (ISODATA) in Erdas IMAGINE was applied to the multi-temporal spectral data to identify statistical patterns and segment pixels into natural occurring clusters. Utilizing a minimum spectral distance formula, pixels were grouped into ten clusters and randomly sampled, generating 75 points within each unsupervised cluster. Square buffers, delineating an area of 900 m
2, were constructed around sample points and a ground cover label assigned to each polygon through interpretation of high resolution Google Earth imagery [
22,
59,
60]. Training locations were coded with Google Earth imagery acquired between 2007 and 2010. Of the total sample of 750 points, 498 were interpretable and intersected with suitable land cover reference imagery. Training data were labeled as 1 of 5 primary land cover classes: (1)
forest; (2)
cropland; (3)
savanna; (4)
settlement; and (5)
water. The dominant land covers were adequately sampled by this scheme, however, the
settlement class was underrepresented so purposeful sampling was performed to supplement the training data for that category with an additional 25 points.
A processing diagram is provided to illustrate the workflow that follows (
Figure 2). As operations are described, text is provided directing to specific points in the diagram, e.g., “Operation 1,
Figure 2” refers to the operation icon in the workflow labeled “1” (hierarchical clustering of training signatures). Spectral signatures were extracted from the multi-temporal data at sample locations and imported into DataDesk statistical software [
61]. Because intra-class spectral variability was high, the compliment of signatures associated with each primary land cover category was grouped into spectrally similar subsets, or subgroups, using hierarchical clustering (Operation 1,
Figure 2). Mean subgroup signatures were produced by averaging signature values for each unique cluster of signatures.
Figure 2.
Classification workflow using objects and syntax analogous to the model builder in ERDAS Imagine. Note that reclassification iterations are performed by repeating the loop of Operations 5, 8–11 (in bold), the remaining operations are performed once. The dashed line, directing to Operation 5 in the diagram, represents data not used directly in the operation but rather to establish parameters for Operation 5.
Figure 2.
Classification workflow using objects and syntax analogous to the model builder in ERDAS Imagine. Note that reclassification iterations are performed by repeating the loop of Operations 5, 8–11 (in bold), the remaining operations are performed once. The dashed line, directing to Operation 5 in the diagram, represents data not used directly in the operation but rather to establish parameters for Operation 5.
Separability was tested among subgroup signatures, within primary categories, by calculating the Transformed Divergence (TD) [
62], merging signature pairs with a TD value less than 1700 [
63]. Spectral variability was high among all non-water categories. The greatest variability was observed in the cropland class where spectral signatures were partitioned into 10 clusters with minimal overlap (
Figure 3).
Figure 3.
Distribution of cropland clusters in T1TM3 (x-axis) and T2TM4 (y-axis) feature space. Dashed lines delineate the distribution of individual signatures that compose the respective cluster. TM3 is utilized to illustrate soil reflectance variability and TM4 to illustrate the variability in vegetation response. Surface reflectance is scaled to unsigned 8-bit.
Figure 3.
Distribution of cropland clusters in T1TM3 (x-axis) and T2TM4 (y-axis) feature space. Dashed lines delineate the distribution of individual signatures that compose the respective cluster. TM3 is utilized to illustrate soil reflectance variability and TM4 to illustrate the variability in vegetation response. Surface reflectance is scaled to unsigned 8-bit.
The bulk of training samples (~67%) was distributed among the cropland and savanna categories. Hierarchical clustering of training signatures produced 3 to 10 subgroups for non-water categories with cropland and savanna represented by the greatest number of subgroups (
Table 1). The mean signatures used to parameterize the initial classification represented the average spectral value of each of these subgroups. We categorized the spectral data in Erdas IMAGINE with a MLC, selecting all layers in the temporal dataset as input to the classifier and applying the 25 subgroup signatures (Operation 2,
Figure 2). The 25-category thematic output serves several purposes, namely: a mechanism for identifying and isolating commission error within spatially defined strata of primary land covers; a sampling template, and, a mask to spatially constrain pixel reclassification. The number of primary categories and breadth of training data dictates the quantity of subgroups and the number of classes in the thematic output. These parameters will vary by type of study and composition of landscape but the method of primary category stratification is certainly generalizable to a variety of studies, and equally, landscapes.
Table 1.
Primary category training data for footprint at Path: 172 Row: 071: category description, sample size, and number of subgroups. Column 3 indicates the total number of training samples for each primary category. Column 4 indicates the number of subgroups generated from the hierarchical clustering of training signatures.
Table 1.
Primary category training data for footprint at Path: 172 Row: 071: category description, sample size, and number of subgroups. Column 3 indicates the total number of training samples for each primary category. Column 4 indicates the number of subgroups generated from the hierarchical clustering of training signatures.
| Primary LC Category | Description | Sample Size | No. Subgroups |
|---|
| Forest | Tree assemblages ≥ 40% canopy closure | 88 | 5 |
| Cropland | Cultivated land for subsistence or commercial agriculture | 177 | 10 |
| Savanna | Savanna: grassland (woody canopy cover < 10%), bushland savanna (10% < bush cover < 40%), woodland savanna (10% < tree canopy < 40%) [55,56]. | 172 | 6 |
| Settlement | Urban areas, villages, and roads | 54 | 3 |
| Water | Lakes, rivers, streams, and seasonally inundated areas | 32 | 1 |
Proportional random sampling of the 25-category thematic map was used to generate validation points (Operation 3,
Figure 2). A total of 477 validation points were interpretable and intersected with suitable reference land cover imagery. Since classification accuracy in Erdas IMAGINE is evaluated within a 3-pixel by 3-pixel window, square buffers (8100 m
2) were constructed around the sample validation points and a land cover label assigned to each polygon through interpretation of Google Earth imagery.
Classification error was evaluated through an accuracy assessment of the 25-category (subgroup) thematic map (Operation 4,
Figure 2). The assessment allowed us to examine the distribution of error within strata of a primary category and identify the subgroup(s) where the greatest classification error resided. The largest detected commission errors were related to savanna misclassified as cropland and cropland as settlement. An examination of a portion of the error matrix, revealed error concentrated in the
cropland_3 and
cropland_4 subgroups and within the
settlement_2 and
settlement_3 subgroups (
Table 2)
.
Table 2.
Partial classification error matrix containing cropland and settlement subgroups. Rows represent the classified subgroup map categories and columns represent reference or validation data. High commission errors are indicated by asterisks.
Table 2.
Partial classification error matrix containing cropland and settlement subgroups. Rows represent the classified subgroup map categories and columns represent reference or validation data. High commission errors are indicated by asterisks.
| Subgroup | Forest | Cropland | Savanna | Settlement | Water |
|---|
| Cropland_1 | 0 | 27 | 0 | 0 | 0 |
| Cropland_2 | 0 | 32 | 0 | 0 | 0 |
| Cropland_3 | 0 | 28 | 13* | 0 | 0 |
| Cropland_4 | 0 | 6 | 28* | 0 | 0 |
| Cropland_5 | 0 | 2 | 0 | 0 | 0 |
| Cropland_6 | 0 | 1 | 0 | 0 | 0 |
| Cropland_7 | 0 | 1 | 0 | 0 | 0 |
| Cropland_8 | 0 | 33 | 0 | 0 | 0 |
| Cropland_9 | 0 | 4 | 0 | 0 | 0 |
| Cropland_10 | 0 | 2 | 0 | 0 | 0 |
| Settlement_1 | 0 | 1 | 0 | 2 | 0 |
| Settlement_2 | 0 | 8* | 0 | 37 | 0 |
| Settlement_3 | 0 | 7* | 0 | 1 | 0 |
Reclassification was iterative, each iteration addressing commission error within a particular high-error subgroup and restricted to the spatial extent of same. There were, overall, five subgroups reclassified within the footprint (Path: 172 Row: 071) but only four subgroups directly affected error in the primary cropland class: two cropland and two settlement. We limit our description of method and models to these subgroups, describing the approach to reclassification in detail using one of the cropland subgroups and one of the settlement groups as examples.
Commission error within the
cropland_3 class resulted in 13 known areas of savanna misclassified as cropland (
Table 2), indicating a data high degree of spectral confusion between savanna and cropland within this strata. We randomly sampled 200 locations within the
cropland_3 thematic subgroup and assigned a land cover label (Operation 5,
Figure 2). Land cover was interpreted for 176 observations with high confidence, the remainder were eliminated from the analysis.
The assessment indicated that classification error was distributed between two primary land cover categories (e.g., cropland and savanna) within subgroups; the binary outcome allowed us to use logistic regression to estimate the probability that one of the two particular land covers was present given a set of predictors. The binary logistic regression model has the form:
where p = probability of a case belonging to category 1; p/(1 – p) = odds; a = constant; n = number of predictors; b
1...b
n = regression coefficients; and bx
1...x
n = regression predictors.
Logit models are used as the basis for pixel reclassification for a number of reasons. First, logistic regression does not assume a linear relationship between predictors and the outcome variable. Second, accuracy assessment of the subgroup thematic map indicates that the dependent variable is dichotomous. Third, there are no predictor requirements for normality, linearity, or equal variance within primary categories of subgroups. Fourth, the primary categories are mutually exclusive and exhaustive. Last, logit models provide an efficient way of testing classification outcomes and offer a flexible interface for evaluating the contribution of any given predictor, or set of predictors.
Predictors for the logit model were generated from the original multi-spectral data, incorporating elements of phenology and sub-pixel composition of land cover. Multi-temporal data is utilized to capture variability in phenology which has been demonstrated to enhance differentiation between cropland and surrounding natural land cover [
59,
64,
65,
66] as well as among crop type [
67,
68]. Temporal intra-band differencing (e.g., B1
Ti–B1
T2) was adopted to measure change in phenological states within the unique spectral windows of each band, between date 1 (T
1) and date 2 (T
2) (Operation 6,
Figure 2). Quantitative subpixel information of surface components was estimated using SMA to spectrally unmix one image of the seasonal image pairs (Operation 7,
Figure 2). We selected the Landsat image acquired during the harvest season since spectral separation between cropland and the surrounding natural savanna was slightly greater than that found in the preseason scene. No discernible advantage in separation between cropland and settlement was detected between scenes. A Sequential Maximum Angle Convex Cone (SMACC) [
69], utilizing a residual minimization model, was used to identify a
pseudo set of image endmembers that were displayed in a scatterplot amongst all pixels in the TM image as reference locations that would guide endmember selection. The set of four endmembers used in this analysis was selected through iterative testing of candidate pixels at reference locations, representing photosynthetic vegetation (PV), soil, non-photosynthetic vegetation (NPV), and shade components (
Figure 4). Results of the constrained model showed few pixels with values below 0 or above 1 and a mean RMS error of 5.538 indicating that the selected endmembers effectively characterized the landscape. An inspection of RMS distribution revealed the highest error pixels concentrated in areas that seasonally inundate with water, however the magnitude of error was not considered serious enough to warrant modification of the model. The library of candidate predictors utilized in the logit model consisted of six difference variables (one for each band pair, 1–5, and 7) and four fraction images. Predictor values were extracted at the sampled locations and collated (Operation 8,
Figure 2).
Figure 4.
(Left): Location of selected endmembers in scatterplot where Landsat TM band 4 is assigned to the y-axis and band 7, the x-axis. Values of X and Y-Axes are at-surface reflectance. (Right): Endmember pixel boundaries mapped and overlaid on high-resolution imagery (Google Earth).
Figure 4.
(Left): Location of selected endmembers in scatterplot where Landsat TM band 4 is assigned to the y-axis and band 7, the x-axis. Values of X and Y-Axes are at-surface reflectance. (Right): Endmember pixel boundaries mapped and overlaid on high-resolution imagery (Google Earth).
The type of error that we detect within subgroups is always commission error. Our logit models are used to identify misclassified pixels of the commissioned category, assigning a value of 1 to cases associated with the latter category and 0 to cases associated with the primary category to which the subgroup has membership. For example, we wanted to identify misclassified savanna within the
cropland_3 subgroup, correcting the commissioning of savanna by cropland, so an outcome value of 1 was assigned to savanna cases and outcome value of 0 to cropland. The 10 candidate predictors were input to the logit model using backward stepwise selection (Operation 9,
Figure 2). The significance level for removal was set at 0.10 and classification cutoff at 0.5. Overall fit of the model was evaluated using scalar measures of fit, such as log-likelihood, as well as information based measures (70). The likelihood ratio test (
G2) compares the log likelihoods of the full and constrained model (
i.e., a model with all coefficients but the intercept constrained to zero), and is reported as a chi-square statistic, with degrees of freedom and a statistical significance level. The likelihood ratio test allowed us to test the hypothesis that all model coefficients except the intercept were zero. Common pseudo-R square measures, such as McKelvey and Zavoina’s R
2 and Nagelkerke R
2 were used to assess the adequacy of the model. We also used the Hosmer and Lemeshow's goodness-of-fit test to compare predicted to observed frequencies, whereby a test with a large p-value indicates a good fit between the model and the data. Finally, to compare full (non-nested) to nested models we employ information measures of fit. Comparisons were made between the full, or non-nested (10 predictor), and nested (4 predictor) models using the difference in the Bayesian Information Criterion (BIC) measures for the two models (where an absolute difference of 2–6 suggests positive evidence, 6–10 indicates strong evidence, and a difference greater than 10 suggests very strong evidence in favor of the nested model [
70]. Using Erdas IMAGINE’s
Model Builder, parameters returned from the nested logit model were applied to the predictor layers, utilizing the subgroup thematic map to restrict the operation to the spatial extent of the strata of interest (Operation 10,
Figure 2). Pixels within the subgroup were recoded to the appropriate land cover based on a threshold probability of 50% (Operation 11,
Figure 2). Operations 5, 8–11 (Figure 2) were repeated for the remainder of high error subgroups. Once all high error subgroups were addressed, validation was performed using the dataset generated in (Operation 3,
Figure 2).