Satellite and Ground Based Thermal Observation of the 2014 Effusive Eruption at Stromboli Volcano
Abstract
:1. Introduction
2. Thermal Observations of Active Volcanoes
2.1. Characteristics of Instruments Suitable for Observing Volcanic Thermal Anomalies
- high spatial resolution (width of an average lava flow <20 m),
- short revisit time (<15 min),
- numerous spectral channels, or at least an appropriate combination of channels [27],
- high radiometric accuracy (<0.1 K), and
- automatic adjustment of gain settings, i.e., being able to observe high and low temperature events using the same sensor.
2.2. TET-1
| Parameter | 1 VIS Camera | 2 IR Cameras |
|---|---|---|
| Wavelength | 460–560 nm 565–725 nm 790–930 nm | 3.4–4.2 μm 8.5–9.3 μm |
| Quantization | 14 bit | |
| Swath width | 192 km | 162 km |
| Spatial resolution | 40 m | 320 m |
| Ground sampling distance | 40 m | 160 m |
3. TET-1 Data Processing Chain

3.1. Pre-Processing
3.2. Co-Registration of MIR and TIR Channels
- combine VNIR data with MIR/TIR,
- preserve the radiometric values in MIR/TIR channels, and
- simultaneously preserve the geometry of MIR/TIR pixels.
3.3. Area, Temperature and Volcanic Radiant Power of Lava Flow
3.4. Time Averaged Lava Discharge Rate
4. Results
4.1. Field Observations
| A | B | C | D | |
|---|---|---|---|---|
| Longitude | 15°12′49.92″ E | 15°12′52.12″ E | 15°12′48.68″ E | 15°12′15″ E |
| Latitude | 38°48′18.58″ N | 38°48′13.52″ N | 38°48′26.68″ N | 38°48′59″ N |
| Observer elevation | 293 m | 372 m | 178 m | 0 m |
| Target mean elevation | 600 m | 700 m | 300 m | 500 m |
| Date (September 2014) | 10, 12, 15,17 | 16 | 18–24 | 20 (boat) |
| Mean dist. from the lava flow | 1100 m | 1100 m | 850 m | 2200 m |
| SWIR transmittance | - | 0.75 | 0.80 | - |
| MIR transmittance | 0.82 | 0.82 | 0.87 | 0.57 |
| TIR transmittance | 0.70 | 0.70 | 0.75 | 0.35 |

| Infratec ImageIR | Infratec VarioCam HR | |
|---|---|---|
| Spectral range | 2.0–5.5 μm | 7.5–14.0 μm |
| Central wavelengths | filter 1: 2.4 μm, filter 2: 3.9 μm | 10.3 μm |
| Detector type | Cooled InSB FPA | Uncooled micro bolometer FPA |
| Number of pixels | 640 × 512 | 640 × 480 |
| Temperature res. At 303 K | 0.02 K | 0.03 K |
| Accuracy | ±1% | ±1% |
| Dynamic range | 16 bit | 16 bit |
| Lenses focal length | 25 mm | 30 mm |
| Field of View | 21.7° × 17.5° | 30° × 23° |

| Date & Time | Maximal T (K) in | Remarks | ||
|---|---|---|---|---|
| TIR | MIR | SWIR | ||
| 2014/09/10; 17:45 | 699 | / | / | We could observe the area close to the vent with T > 670 K. Mid-flow was out of sight. The lowest part was visible, but significantly cooler with T ~430 K. |
| 2014/09/12; 10:30–13:00 | 767 | / | / | We could observe the area close to the vent with T ~750 K. T dropped between 10:30 and 10:40. First it dropped to 670 K and then it kept cooling, but remained above 570 K |
| 2014/09/15; 16:20–17:00 | 733 | 961 | / | We could observe the area close to the vent with T ~950 K (in MIR). First simultaneous observations in MIT and TIR band. |
| 2014/09/16; 10:30–11:20 | 758 | 923 | 806 | Only the area close to the vent was visible. First observations with SWIR filter. |
| 2014/09/17; 13:30 | 617 | / | / | We could observe only the area just below the vent, but not the vent itself. |
| 2014/09/17; 15:40 | 680 | / | / | We could observe the entire area with the exception of the vent. Considering the temperatures, it is likely that fresh lava remained under the crust. |
| 2014/09/18; 12:05–12:50 | 680 | 728 | / | The lava front extended between 12:09 and 12:12; it progressed by 220 m in 3 min (Figure 3). This was accompanied by a flow front brecciating and collapsing down the slope, with rocks having temperatures between 500 and 700 K and rolling down with velocities ~10 m/s. |
| 2014/09/19; 10:55–11:35 | 892 | / | / | The observed part of the flow reached T > 770 K (at 11:07), but the lava front did not advance down the slope. At 11:10, it started to cool down to 570 K. At 11:28, it heated up again and some material broke out for 10 s. |
| 2014/09/20; 15:50 | 668 | / | / | Short observation; we could observe only the lower part of the flow. |
| 2014/09/20; 19:35–19:55 | 831 | 1080 | Night observations were made from a boat at a distance to vents ~2.2 km. Lava front on the west side moved for 120 m in 5 min. | |
| 2014/09/20; 23:25–23:35 | 573 | 751 | 829 | Night observations; lava front was high on the slope. |
| 2014/09/21; 14:40–15:00 | 739 | Observations in SWIR exposed significant degassing. | ||
| 2014/09/21; 15:10-15:25 | 535 | / | / | The entire flow was visible below the vent. |
| 2014/09/21; 15:28–15:38 | 502 | 735 | / | Observations of the crater area revealed visible explosions shooting material up to 50 m above the terrain. |
| 2014/09/21; 15:40–16:40 | 529 | 702 | / | Lava front advanced three times: the first pulse was weak; the second one was stronger—it moved the lava front 240 m down the slope in 5 min; the third pulse moved the lava front with the same velocity over the same path as the second event. |
| 2014/09/22; 11:20–12:40 | 543 | 737 | / | Low temperatures and low activity with some rock-fall and some minor movements of the lava front. |
| 2014/09/23; 10:30–10:45 | 872 | 1112 | 977 | High temperatures were observed high on the slope and not on the lowest lava front. Some intense degassing (no ash) was visible above the crater. |
| 2014/09/24; 16:10 | 652 | Although the temperatures were relatively low, the lava flow almost reached the sea. | ||

| Min TADR (m3/s) | Max TADR (m3/s) | |
|---|---|---|
| ImageIR 3.9 μm | 0.189 | 0.409 |
| VarioCam | 0.190 | 0.343 |
| Teff (dual band) | 0.186 | 0.440 |
4.2. TET-1 Observations


| Parameter | Min TADR | Max TADR |
|---|---|---|
| Tamb ambient air temperature | 303 K | |
| Tcore lava core temperature | 1273 K | |
| Tbase flow base temperature | 773 K | |
| k lava thermal conductivity | 0 W/m2/K | 1.5 W/m2/K |
| hc convective heat transfer coefficients | 10 W/m2/K | 15 W/m2/K |
| ρ lava density | 2340 kg/m3 | 2030 kg/m3 |
| cp lava specific heat capacity | 1035 J/kg/K | 900 J/kg/K |
| ΔT temperature diff. between eruption and solidus temperature | 350 K | 200 K |
| f mass fraction of post eruption crystallization | 0.45 | |
| L latent crystallization heat | 3.5 × 105 J/m3 | |
| h thickness of thermal boundary layer | 1 m | |
4.3. MODIS Observations



5. Discussion
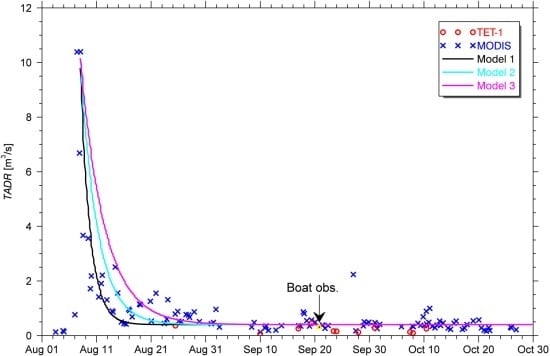
5.1. Simple Model for Waning Mass Flux

5.2. Added Value of TET-1 Data

| Date/Time | T (K) | A (Ha) | VRPDB (MV) | VRPW (MW) |
|---|---|---|---|---|
| 2014/08/25 10:49 | 572 | 3.2 | 182 | 187 |
| 2014/09/09 23:30 | 672 | 0.2 | 23 | 36 |
| 2014/09/16 23:32 | 587 | 1.7 | 105 | 155 |
| 2014/09/19 10:46 | 504 | 7.4 | 238 | 167 |
| 2014/09/23 10:33 | 583 | 1.3 | 78 | 90 |
| 2014/09/23 23:34 | 601 | 0.7 | 52 | 102 |
| 2014/09/27 23:21 | 966 | 0.1 | 62 | 94 |
| 2014/09/30 23:34 | 541 | 2.6 | 115 | 150 |
| 2014/10/07 10:33 | 724 | 0.3 | 49 | 95 |
| 2014/10/07 23:33 | 698 | 0.2 | 32 | 68 |
| 2014/10/10 10:45 | 539 | 2.7 | 117 | 124 |
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Blackburn, E.A.; Wilson, L.; Sparks, R.S.J. Mechanisms and dynamics of strombolian activity. J. Geol. Soc. 1976, 132, 429–440. [Google Scholar] [CrossRef]
- Chouet, B.; Hamisevicz, N.; McGetchin, T.R. Photoballistics of volcanic jet activity at Stromboli, Italy. J. Geophys. Res. 1974, 79, 4961–4976. [Google Scholar] [CrossRef]
- De Fino, M.; la Volpe, L.; Falsaperla, S.; Frazzetta, G.; Neri, G. The Stromboli eruption of December 6, 1985–April 25, 1986: Volcanological, petrological and seismological data. Rend. Soc. Ital. Miner. Pet. 1988, 43, 1021–1038. [Google Scholar]
- Calvari, S.; Spampinato, L.; Lodato, L.; Harris, A.J.L.; Patrick, M.R.; Dehn, J.; Burton, M.R.; Andronico, D. Chronology and complex volcanic processes during the 2002–2003 flank eruption at Stromboli volcano (Italy) reconstructed from direct observations and surveys with a handheld thermal camera. J. Geophys. Res. Solid Earth 2005, 110. [Google Scholar] [CrossRef]
- Harris, A.; Dehn, J.; Patrick, M.; Calvari, S.; Ripepe, M.; Lodato, L. Lava effusion rates from hand-held thermal infrared imagery: An example from the June 2003 effusive activity at Stromboli. Bull. Volcanol. 2005, 68, 107–117. [Google Scholar] [CrossRef]
- Calvari, S.; Lodato, L.; Steffke, A.; Cristaldi, A.; Harris, A.J.L.; Spampinato, L.; Boschi, E. The 2007 Stromboli eruption: Event chronology and effusion rates using thermal infrared data. J. Geophys. Res. Solid Earth 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Ripepe, M.; Delle Donne, D.; Lacanna, G.; Marchetti, E.; Ulivieri, G. The onset of the 2007 Stromboli effusive eruption recorded by an integrated geophysical network. J. Volcanol. Geotherm. Res. 2009, 182, 131–136. [Google Scholar] [CrossRef]
- Ripepe, M.; Donne, D.D.; Genco, R.; Maggio, G.; Pistolesi, M.; Marchetti, E.; Lacanna, G.; Ulivieri, G.; Poggi, P. Volcano seismicity and ground deformation unveil the gravity-driven magma discharge dynamics of a volcanic eruption. Nat. Commun. 2015, 6. [Google Scholar] [CrossRef] [PubMed]
- Tinti, S.; Maramai, A.; Armigliato, A.; Graziani, L.; Manucci, A.; Pagnoni, G.; Zaniboni, F. Observations of physical effects from tsunamis of 30 December 2002 at Stromboli volcano, southern Italy. Bull. Volcanol. 2005, 68, 450–461. [Google Scholar] [CrossRef]
- Tinti, S.; Pagnoni, G.; Zaniboni, F.; Bortolucci, E. Tsunami generation in Stromboli island and impact on the south-east Tyrrhenian coasts. Nat. Hazards Earth Syst. Sci. 2003, 3, 299–309. [Google Scholar] [CrossRef]
- Di Traglia, F.; Battaglia, M.; Nolesini, T.; Lagomarsino, D.; Casagli, N. Shifts in the eruptive styles at Stromboli in 2010–2014 revealed by ground-based InSAR data. Sci. Rep. 2015, 5. [Google Scholar] [CrossRef] [PubMed]
- Rizzo, A.L.; Federico, C.; Inguaggiato, S.; Sollami, A.; Tantillo, M.; Vita, F.; Bellomo, S.; Longo, M.; Grassa, F.; et al. The 2014 effusive eruption at Stromboli volcano (Italy): Inferences from soil CO2 flux and 3He/4He ratio in thermal waters. Geophys. Res. Lett. 2015, 42. [Google Scholar] [CrossRef]
- Simkin, T.; Siebert, L. Volcanoes of the World: A Regional Directory, Gazetteer, and Chronology of Volcanism during the Last 10,000 Years; Geoscience Press: Tucson, AZ, USA, 1994. [Google Scholar]
- Oppenheimer, C.; Francis, P. Remote sensing of heat, lava and fumarole emissions from Erta ’Ale volcano, Ethiopia. Int. J. Remote Sens. 1997, 18, 1661–1692. [Google Scholar] [CrossRef]
- Coppola, D.; Piscopo, D.; Staudacher, T.; Cigolini, C. Lava discharge rate and effusive pattern at Piton de la Fournaise from MODIS data. J. Volcanol. Geotherm. Res. 2009, 184, 174–192. [Google Scholar] [CrossRef]
- Dehn, J.; Dean, K.; Engle, K. Thermal monitoring of North Pacific volcanoes from space. Geology 2000, 28, 755–758. [Google Scholar] [CrossRef]
- Harris, A.J.L.; Swabey, S.E.J.; Higgins, J. Automated thresholding of active lavas using AVHRR—Data. Int. J. Remote Sens. 1995, 16, 3681–3686. [Google Scholar] [CrossRef]
- Lombardo, V.; Buongiorno, M.; Amici, S. Characterization of volcanic thermal anomalies by means of sub-pixel temperature distribution analysis. Bull. Volcanol. 2006, 68, 641–651. [Google Scholar] [CrossRef]
- Pergola, N.; Marchese, F.; Tramutoli, V. Automated detection of thermal features of active volcanoes by means of infrared AVHRR records. Remote Sens. Environ. 2004, 93, 311–327. [Google Scholar] [CrossRef]
- Rothery, D.A.; Francis, P.W.; Wood, C.A. Volcano monitoring using short wavelength infrared data from satellites. J. Geophys. Res. 1988, 93, 7993–8008. [Google Scholar] [CrossRef]
- Wright, R.; Flynn, L.; Garbeil, H.; Harris, A.; Pilger, E. Automated volcanic eruption detection using MODIS. Remote Sens. Environ. 2002, 82, 135–155. [Google Scholar] [CrossRef] [Green Version]
- Davies, A.G.; Calkins, J.; Scharenbroich, L.; Vaughan, R.G.; Wright, R.; Kyle, P.; Castańo, R.; Chien, S.; Tran, D. Multi-instrument remote and in situ observations of the Erebus Volcano (Antarctica) lava lake in 2005: A comparison with the Pele lava lake on the jovian moon Io. J. Volcanol. Geotherm. Res. 2008, 177, 705–724. [Google Scholar] [CrossRef]
- Harris, A.J.L.; Dehn, J.; Calvari, S. Lava effusion rate definition and measurement: A review. Bull. Volcanol. 2007, 70, 1–22. [Google Scholar] [CrossRef]
- Wright, R.; Pilger, E. Radiant flux from Earth’s subaerially erupting volcanoes. Int. J. Remote Sens. 2008, 29, 6443–6466. [Google Scholar] [CrossRef]
- Zakšek, K.; Shirzaei, M.; Hort, M. Constraining the uncertainties of volcano thermal anomaly monitoring using a Kalman filter technique. Geol. Soc. Lond. Spec. Publ. 2013, 380, 137–160. [Google Scholar] [CrossRef]
- Zakšek, K.; Pick, L.; Shirzaei, M.; Hort, M. Thermal monitoring of volcanic effusive activity: The uncertainties and outlier detection. Geol. Soc. Lond. Spec. Publ. 2015, 426. [Google Scholar] [CrossRef]
- Lombardo, V.; Musacchio, M.; Buongiorno, M.F. Error analysis of subpixel lava temperature measurements using infrared remotely sensed data. Geophys. J. Int. 2012, 191, 112–125. [Google Scholar] [CrossRef]
- ESA SMO FuegoTec Programme—GSP. Available online: http://gsp.esa.int/document-view/-/wcl/wlGiHTp4j7JC/10192/smo-fuegotec-programme (accessed on 11 August 2015).
- Schroeder, W.; Oliva, P.; Giglio, L.; Csiszar, I.A. The New VIIRS 375 m active fire detection data product: Algorithm description and initial assessment. Remote Sens. Environ. 2014, 143, 85–96. [Google Scholar] [CrossRef]
- Lorenz, E.; Mitchell, S.; Säuberlich, T.; Paproth, C.; Halle, W.; Frauenberger, O. Remote sensing of high temperature events by the FireBird mission. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, XL-7/W3, 461–467. [Google Scholar] [CrossRef]
- Briess, K.; Jahn, H.; Lorenz, E.; Oertel, D.; Skrbek, W.; Zhukov, B. Fire recognition potential of the bi-spectral Infrared Detection (BIRD) satellite. Int. J. Remote Sens. 2003, 24, 865–872. [Google Scholar] [CrossRef]
- Fischer, C.; Klein, D.; Kerr, G.; Stein, E.; Lorenz, E.; Frauenberger, O.; Borg, E. Data validation and case studies using the TET-1 Thermal Infrared Satellite System. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, XL-7/W3, 1177–1182. [Google Scholar] [CrossRef]
- Jahn, H.; Reulke, R. Staggered Line Arrays in Pushbroom Cameras: Theory and Application. Available online: http://elib.dlr.de/18149/ (accessed on 21 November 2015).
- DLR Firebird—Data Access and Products. Available online: http://www.dlr.de/firebird/en/desktopdefault.aspx/tabid-9090/17974_read-42458/ (accessed on 27 October 2015).
- Wright, R.; Flynn, L.P.; Garbeil, H.; Harris, A.J.L.; Pilger, E. MODVOLC: Near-real-time thermal monitoring of global volcanism. J. Volcanol. Geotherm. Res. 2004, 135, 29–49. [Google Scholar] [CrossRef]
- Berk, A.; Anderson, G.P.; Acharya, P.K.; Bernstein, L.S.; Muratov, L.; Lee, J.; Fox, M.; Adler-Golden, S.M.; Chetwynd, J.H., Jr.; Hoke, M.L.; et al. MODTRAN5: 2006 update. SPIE Proc. 2006, 6233. [Google Scholar] [CrossRef]
- Harris, A. Thermal Remote Sensing of Active Volcanoes: A User’s Manual; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Zhukov, B.; Lorenz, E.; Oertel, D.; Wooster, M.; Roberts, G. Spaceborne detection and characterization of fires during the bi-spectral infrared detection (BIRD) experimental small satellite mission (2001-2004). Remote Sens. Environ. 2006, 100, 29–51. [Google Scholar] [CrossRef]
- Lucy, L.B. An iterative technique for the rectification of observed distributions. Astron. J. 1974, 79, 745–749. [Google Scholar] [CrossRef]
- Richardson, W.H. Bayesian-based iterative method of image restoration. J. Opt. Soc. Am. 1972, 62, 55–59. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E. Pattern Classification and Scene Analysis; John Willey & Sons: New York, NY, USA, 1973. [Google Scholar]
- Xie, H.; Hicks, N.; Randy Keller, G.; Huang, H.; Kreinovich, V. An IDL/ENVI implementation of the FFT-based algorithm for automatic image registration. Comput. Geosci. 2003, 29, 1045–1055. [Google Scholar] [CrossRef]
- Steffke, A.; Harris, A. A review of algorithms for detecting volcanic hot spots in satellite infrared data. Bull. Volcanol. 2011, 73, 1109–1137. [Google Scholar] [CrossRef]
- Dozier, J. A method for satellite identification of surface temperature fields of subpixel resolution. Remote Sens. Environ. 1981, 11, 221–229. [Google Scholar] [CrossRef]
- Oppenheimer, C. Thermal distributions of hot volcanic surfaces constrained using three infrared bands of remote sensing data. Geophys. Res. Lett. 1993, 20, 431–434. [Google Scholar] [CrossRef]
- Mouginis-Mark, P.J.; Garbeil, H.; Flament, P. Effects of viewing geometry on AVHRR observations of volcanic thermal anomalies. Remote Sens. Environ. 1994, 48, 51–60. [Google Scholar] [CrossRef]
- Wright, R.; Rothery, D.A.; Blake, S.; Pieri, D.C. Improved remote sensing estimates of lava flow cooling: A case study of the 1991–1993 Mount Etna eruption. J. Geophys. Res. 2000, 105, 23681–23694. [Google Scholar] [CrossRef]
- Lombardo, V.; Buongiorno, M.F. Lava flow thermal analysis using three infrared bands of remote-sensing imagery: A study case from Mount Etna 2001 eruption. Remote Sens. Environ. 2006, 101, 141–149. [Google Scholar] [CrossRef]
- Vaughan, R.G.; Keszthelyi, L.P.; Davies, A.G.; Schneider, D.J.; Jaworowski, C.; Heasler, H. Exploring the limits of identifying sub-pixel thermal features using ASTER TIR data. J. Volcanol. Geotherm. Res. 2010, 189, 225–237. [Google Scholar] [CrossRef]
- Giglio, L.; Kendall, J.D. Application of the Dozier retrieval to wildfire characterization: A sensitivity analysis. Remote Sens. Environ. 2001, 77, 34–49. [Google Scholar] [CrossRef]
- Moré, J.J. The Levenberg-Marquardt algorithm: Implementation and theory. In Numerical Analysis; Watson, G.A., Ed.; Springer: Berlin, Germany, 1978; Volume 630, pp. 105–116. [Google Scholar]
- Markwardt, C.B. Non-linear least squares fitting in IDL with MPFIT. In Proceedings of the Astronomical Data Analysis Software and Systems (ADASS) XVII, Québec, QC, Canada, 2–5 November 2008.
- Glaze, L.; Francis, P.W.; Rothery, D.A. Measuring thermal budgets of active volcanoes by satellite remote sensing. Nature 1989, 338, 144–146. [Google Scholar] [CrossRef]
- Harris, A.J.L.; Blake, S.; Rothery, D.A.; Stevens, N.F. A chronology of the 1991 to 1993 Mount Etna eruption using advanced very high resolution radiometer data: Implications for real-time thermal volcano monitoring. J. Geophys. Res. 1997, 102, 7985–8003. [Google Scholar] [CrossRef]
- Wright, R.; Blake, S.; Harris, A.J.L.; Rothery, D.A. A simple explanation for the space-based calculation of lava eruption rates. Earth Planet. Sci. Lett. 2001, 192, 223–233. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Justice, C.O.; Flynn, L.P.; Kendall, J.D.; Prins, E.M.; Giglio, L.; Ward, D.E.; Menzel, W.P.; Setzer, A.W. Potential global fire monitoring from EOS-MODIS. J. Geophys. Res. 1998, 103, 32215–32238. [Google Scholar] [CrossRef]
- Murphy, S.W.; Oppenheimer, C.; de Souza Filho, C.R. Calculating radiant flux from thermally mixed pixels using a spectral library. Remote Sens. Environ. 2014, 142, 83–94. [Google Scholar] [CrossRef]
- Wooster, M.J.; Zhukov, B.; Oertel, D. Fire radiative energy for quantitative study of biomass burning: Derivation from the BIRD experimental satellite and comparison to MODIS fire products. Remote Sens. Environ. 2003, 86, 83–107. [Google Scholar] [CrossRef]
- Pieri, D.C.; Baloga, S.M. Eruption rate, area, and length relationships for some Hawaiian lava flows. J. Volcanol. Geotherm. Res. 1986, 30, 29–45. [Google Scholar] [CrossRef]
- Crisp, J.; Baloga, S. Estimating eruption rates of planetary lava flows. Icarus 1990, 85, 512–515. [Google Scholar] [CrossRef]
- Coppola, D.; Laiolo, M.; Piscopo, D.; Cigolini, C. Rheological control on the radiant density of active lava flows and domes. J. Volcanol. Geotherm. Res. 2013, 249, 39–48. [Google Scholar] [CrossRef]
- Wadge, G. The variation of magma discharge during basaltic eruptions. J. Volcanol. Geotherm. Res. 1981, 11, 139–168. [Google Scholar] [CrossRef]
- Harris, A.; Steffke, A.; Calvari, S.; Spampinato, L. Thirty years of satellite-derived lava discharge rates at Etna: Implications for steady volumetric output. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Allard, P.; Carbonnelle, J.; Métrich, N.; Loyer, H.; Zettwoog, P. Sulphur output and magma degassing budget of Stromboli volcano. Nature 1994, 368, 326–330. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zakšek, K.; Hort, M.; Lorenz, E. Satellite and Ground Based Thermal Observation of the 2014 Effusive Eruption at Stromboli Volcano. Remote Sens. 2015, 7, 17190-17211. https://doi.org/10.3390/rs71215876
Zakšek K, Hort M, Lorenz E. Satellite and Ground Based Thermal Observation of the 2014 Effusive Eruption at Stromboli Volcano. Remote Sensing. 2015; 7(12):17190-17211. https://doi.org/10.3390/rs71215876
Chicago/Turabian StyleZakšek, Klemen, Matthias Hort, and Eckehard Lorenz. 2015. "Satellite and Ground Based Thermal Observation of the 2014 Effusive Eruption at Stromboli Volcano" Remote Sensing 7, no. 12: 17190-17211. https://doi.org/10.3390/rs71215876
APA StyleZakšek, K., Hort, M., & Lorenz, E. (2015). Satellite and Ground Based Thermal Observation of the 2014 Effusive Eruption at Stromboli Volcano. Remote Sensing, 7(12), 17190-17211. https://doi.org/10.3390/rs71215876