1. Introduction
Hay meadows in Europe provide important services for humans mainly by providing fodder for animals. Furthermore, extensively used hay meadows bear high biodiversity values, they represent high nature value farmlands [
1] and when traditional practices were applied in rural landscapes, they provide great aesthetic values. All these services are critically dependent on specific agricultural management and particularly on regular cutting at a specific time of the season [
2]. This implies that hay meadows are very sensitive and of a dynamic nature because when proper management is neglected they decline from a good status quite fast [
3]. In Central Europe, a good historical example was the intensification of extensive hay meadows (both due to intensive cutting and grazing) during the Communist era [
4] and when collective farming collapsed, agriculture was abandoned followed by overgrowing and shrub encroachment [
5]. However, the traditional agricultural management of hay meadows is not very profitable and today subsides are needed from the EU’s Common Agricultural Policy (CAP) in order to sustain the good condition of hay meadows and the services they provide [
6]. In this respect, proper tools are needed in order to monitor hay meadow management in large areas with the aim of assessing the success of specific CAP-implemented measures. It is obvious that comprehensive, timely monitoring (e.g., on an annual basis) through field research is not feasible on a broader scale (e.g., national wide), when bearing in mind the costs and variability of cutting practices across such a large area. Therefore, remote sensing (RS) approaches need to be analyzed and tested in order to deliver consistent spatial information on proper hay meadow management practices in larger areas [
7].
Remote sensing (RS) approaches have been widely used mainly for mapping and classifying grasslands and for estimating the biomass they provide. However, grassland studies have seen variable success and depend mainly on site specific conditions, grassland types and the landscape’s spatial composition. In general, the more homogenous grassland landscape is, the better the classification success, which can be documented, for example, by relatively good grassland classification accuracy in the Netherlands [
8], as opposed to complicated detection of grasslands in the Carpathians [
9]. Use of multi-temporal classification approaches was found to be of essential help mainly when grasslands were found in complex agricultural areas [
10]. Furthermore, with the increased availability of vegetation indices (VI) time series (e.g., derived from AVHRR, MERIS, MODIS or Landsat archive), many studies demonstrated these products could be utilized for grassland studies, such as for mapping of specific grassland types [
11], characterizing their vegetation state [
12] or classifying their management practices [
13]. In the context of grassland management, these studies were mainly motivated by the identification of degraded grasslands due to overgrazing, for example in Southern Europe [
14], where grazing seems to be the main driver of good condition of grasslands. In Central Europe on the other hand, proper cut management of grasslands is an important driver specifically for hay meadows [
7]. However, with the use of RS approaches, cutting practices were identified mainly indirectly within the complex classification studies and they were inherently included in different categories, for instance in distinguishing managed and unmanaged agriculture classes [
15,
16], improved and unimproved grasslands [
17,
18], and conservation as opposed to moderately productive grasslands [
19]. To our knowledge, only three published studies were found by us that exactly analyzed RS approaches for detecting cut practices in European grasslands. Franke
et al. [
7] used indicators of proper cutting practices through Rapid Eye data time series in order to detect extensively used hay meadows in Germany. Schuster
et al. [
20] and Voormansik
et al. [
21] analyzed radar time series to detect local scale cutting in grasslands, resulting in completely opposite results. All the authors have suggested that high spatial resolution data are needed to detect grassland management as it is highly fragmented in Europe. However, Nitze
et al. [
17] used MODIS VI time series to distinguish improved and semi-improved grasslands in Ireland, and Alcantara
et al. [
16] used the coarser resolution MODIS data to differentiate active agriculture (including regularly cut grasslands) and abandoned agriculture (including unmanaged grasslands) in Central Europe, with both studies providing promising results. They documented that, besides specific classification algorithm, pre-processing of input data, use of a specific period and number of scenes and differences between EVI and NDVI vegetation indices should be considered when using multi-temporal classification for grassland studies.
Our study aims to analyze the potential of MODIS VI time series to detect cutting in hay meadows. We are aware of the spatial limitation in MODIS products for grassland studies in Central Europe, therefore we based our analysis on homogenous samples in order to minimize mixed pixel and MODIS gridding artifact effects. The main objective here is to set up a conceptual framework for analyzing annual VI time series, motivated by its potential utilization after MODIS-like data products become available with a higher spatial resolution (e.g., by combining of Sentinel2 and Landsat VI products). Therefore, we focused in addition to simple classification, on comparing specific VIs (NDVI vs. EVI), analyzing the optimal time period and number of scenes needed, the effect of smoothing and the added value of simple transformations (first difference series, seasonal statistics) for classification performance in order to suggest the proper way for using MODIS data to monitor cutting practices in hay meadows.
2. Study Area and Methods
The study area covers all of Slovakia, with quite a diverse landscape that reflects mainly heterogeneous geological formations, soils, elevations and terrain [
22]. The climate is also quite diverse, exemplified by the area covering four climate zones and nine European-based climatic strata [
23] with the continental zone having the biggest coverage. Grasslands in Slovakia are formed mainly as small scattered patches with a diverse spatial arrangement (
Figure 1).
Based on national agricultural statistics, the total coverage of grasslands (excluding natural alpine grasslands) is estimated to be approx. 15% of Slovakia and 30% of its agricultural landscape. Grassland vegetation types vary broadly based on nutrition, geological substrate, soils, hydrology and elevation. Land use is an important driver of grasslands, including cutting on meadows, grazing at different intensities on pastures or both (spring cutting and autumn grazing). A substantial proportion of grasslands were abandoned and became overgrown after socioeconomic changes in the early 1990s. Recently, agro-environmental subsidies have introduced special management in the most valuable semi-natural grasslands in Slovakia [
24]. This study focuses on “semi-natural” or extensively used grasslands with traditional grassland management practices and high biodiversity values. Of these, the great majority, evenly distributed in Slovakia, are mesophilous hay meadows, classified as Habitat 6510 (lowland hay meadows) under the EU Habitat Directive [
25]. A first cut (mainly in late June or early July) is the prerequisite for proper management in order to sustain the hay meadows in good condition. Optionally, either a second cut or soft grazing is undertaken in these grassland types [
26]. When these hay meadows are not cut, however, grassland values can be threatened and farmers are unable to obtain financial support from agro-environmental programmes. Because of CAP subsides, these grassland habitats were intensively mapped in Slovakia and registered in agricultural map portal (
www.podnemapy.sk). However, there is no information about the cutting management of the grasslands in Slovakia so we needed to gather ground truth data as follows. Firstly, we took 150 random locations within the grassland land cover class (Corine class 231) across Slovakia. These locations were visually inspected on Google Earth and agricultural map portal to obtain a homogenous uncut Natura 6510 habitat site that was closest to the randomly selected point in order to minimize mixed-pixel problems and gridding artifacts in the MODIS data [
27]. The absent cutting on these sites was preliminarily detected by visual interpretation of Landsat images series of 2012 (
Figure 2). Secondly, we took another 150 random locations and repeat the process for selection of 6510 habitat sites, where cutting was preliminarily detected (
Figure 2).
Sample sites varied in size and shape but only one MODIS pixel (approx. 250 × 240 m in native projection) was selected for each site (
Figure 3).
Figure 1.
Study area and sampled hay meadows (red dots) that were used for the analyses. Green areas represent all grasslands in Slovakia (Corine Land Cover class 231 [
28]).
Figure 1.
Study area and sampled hay meadows (red dots) that were used for the analyses. Green areas represent all grasslands in Slovakia (Corine Land Cover class 231 [
28]).
Figure 2.
Preliminary detection of cutting on selected sites. A. Cutting before 11.7.2012. B. and C. cutting between 11.7, and 27.7. 2012. D. No cutting in these periods.
Figure 2.
Preliminary detection of cutting on selected sites. A. Cutting before 11.7.2012. B. and C. cutting between 11.7, and 27.7. 2012. D. No cutting in these periods.
Figure 3.
Selection of MODIS homogenous pixels for analyses.
Figure 3.
Selection of MODIS homogenous pixels for analyses.
These 300 sites were randomly split into training set (200) and validation set (100) and monitored for other years (2013–2014) based on regular field visits and visual inspection of Landsat images in order to confirm the preliminarily estimated cutting per site. The field visit during this period included also consultation with local farmers about the cut management. Visual interpretation of Landsat images series helped in confirmation of permanent absence of cut management on site. Those sites where we were not sure about the cutting performed were masked for the analyses. Finally, the cutting treatment information from 2012 was used in analyses with final distribution of samples as it is listed in
Table 1.
Table 1.
Final proportion of treatments in training and validation data sets.
Table 1.
Final proportion of treatments in training and validation data sets.
| | Training Set | Validation Set |
|---|
| Cut (2012) | 84 | 46 |
| Uncut (2012) | 102 | 54 |
Annual series of EVI and NDVI vegetation indices for the period from 2012–2014 were extracted from MOD13Q1 and MYD13Q1 products (16 days, 250 meters) along with quality assurance information from the Land Processes Distributed Active Archived Center (LPDAAC,
https://lpdaac.usgs.gov/) for the area covered by the h19v04 MODIS grid tile. Data were downloaded using EarthExplorer (
http://earthexplorer.usgs.gov/) and re-projected to the native coordination system (Krovak projection, JTSK EastNorth coordination system). Only good quality pixels (VI usefulness index good and higher) were selected for analysis in order to minimize the negative effects of clouds, cloud shadows, aerosols, sun-sensor geometries and snow. There were a total of 46 VI images per year, and the data therefrom were lumped together using MOD13Q1 product as reference (e.g., MYD13Q1 product was used only when MOD13Q1 VI usefulness index was less than good) to obtain 23 images per year, which was thought to reflect vegetation development over a 16-day time span and increase availability of good quality data. No missing data interpolation was done for the period from Day of the Year (DOY) 97 to Julian Day 257. Temporal median substitution (for three years) of bad quality data followed by linear interpolation of three consecutive images was done for the winter and late autumn periods (DOY 1–97; DOY 273–365). The final analyses involved annual series from 2012 because that period had the highest good quality data available. Because of the analysis of the optimal period and number of images needed for classification performance, the series was split into sets with different temporal extents centered on the main harvesting period (3 July, DOY 184), resulting in 11 raw data NDVI series (RD NDVI) and 11 raw data EVI series (RD EVI). Later, we used simple transformations of the raw data series. The first transformation involved basic seasonal statistics such as the mean (MN), maximum (MAX), minimum (MIN), range (RG) and standard deviation (SD). These seasonal statistics were computed for entire seasons (23 images) and for different time spans centered on the main harvesting period (3 July, DOY 184), producing 11 NDVI seasonal statistics series (SS NDVI) and 11 EVI seasonal statistics series (SS EVI). The second transformation involved the so-called first difference series [
29], namely substituting the image value (in this case VI value) from the first consecutive image in the time series. Similarly, these transformation series were split into a set of the series with a different temporal extents centered on the main harvesting period (3 July, DOY 184), resulting in 11 first difference NDVI series (FD NDVI) and 11 first difference EVI series (FD EVI). The way how the different input variables were used and aggregated for respective periods is illustrated in
Figure 4.
Figure 4.
First difference transformation, notation and selection of input variables for the respective classification run. Solid line—raw data (RD), dotted line—first difference transformed data (FD).
Figure 4.
First difference transformation, notation and selection of input variables for the respective classification run. Solid line—raw data (RD), dotted line—first difference transformed data (FD).
Smoothing techniques based on Fourier adjustment [
30] was done using different levels of Fourier terms (2,3,4,5) in order to test the impact of smoothing on classification algorithms (
Figure 5).
Figure 5.
The effect of Fourier adjustments by using different levels of Fourier terms on temporal profile of VI.
Figure 5.
The effect of Fourier adjustments by using different levels of Fourier terms on temporal profile of VI.
Simple classification tree (CART) [
31] algorithm was used to classify cut and uncut meadows because of its simplicity and easy interpretation of classification logic, what allows production of simple set of rules (or production rules), which should be meaningful and could later serve as an input to knowledge based classification as it was suggested by [
32]. Specifically, we used C4.5 algorithm[
33], gini measure of purity as splitting rule [
34] and direct stopping rule for pruning the trees (not less than 5% proportion in node). Totally, we performed 90 classification runs with different periods and input variables as they are listed in
Table 2.
Table 2.
List of all classification runs with different data series. The best case series for different types of the data sets are marked in bold. RD—raw data, SS—seasonal statistics, FD—first difference, FA—Fourier adjustment.
Table 2.
List of all classification runs with different data series. The best case series for different types of the data sets are marked in bold. RD—raw data, SS—seasonal statistics, FD—first difference, FA—Fourier adjustment.
| Classification Run | VI | Type/Transformation | Period | Number of Input Variables |
|---|
| CT01 | NDVI | RD | 8 January–26 December 2012 | 23 |
| CT02 | NDVI | RD | 21 January–10 December 2012 | 21 |
| CT03 | NDVI | RD | 9 February–24 November 2012 | 19 |
| CT04 | NDVI | RD | 25 February–8 November 2012 | 17 |
| CT05 | NDVI | RD | 13 March–23 October 2012 | 15 |
| CT06 | NDVI | RD | 29 March–7 October 2012 | 13 |
| CT07 | NDVI | RD | 14 April–21 September 2012 | 11 |
| CT08 | NDVI | RD | 30 April–5 September 2012 | 9 |
| CT09 | NDVI | RD | 16 May–20 August 2012 | 7 |
| CT10 | NDVI | RD | 1 June–4 August 2012 | 5 |
| CT11 | NDVI | RD | 17 June–19 July 2012 | 3 |
| CT12 | NDVI | SS | 8 January–26 December 2012 | 5 |
| CT13 | NDVI | SS | 21 January–10 December 2012 | 5 |
| CT14 | NDVI | SS | 9 February–24 November 2012 | 5 |
| CT15 | NDVI | SS | February25–8 November 2012 | 5 |
| CT16 | NDVI | SS | 13 March13–23 October 2012 | 5 |
| CT17 | NDVI | SS | 29 March29–7 October 2012 | 5 |
| CT18 | NDVI | SS | 14 April–21 September 2012 | 5 |
| CT19 | NDVI | SS | 30 April–5 September 2012 | 5 |
| CT20 | NDVI | SS | 16 May–20 August 2012 | 5 |
| CT21 | NDVI | SS | 1 June–4 August 2012 | 5 |
| CT22 | NDVI | SS | 17 June–19 July 2012 | 5 |
| CT23 | NDVI | FD | 21 January–26 December 2012 | 22 |
| CT24 | NDVI | FD | 9 February–10 December 2012 | 20 |
| CT25 | NDVI | FD | 25 February–24 November 2012 | 18 |
| CT26 | NDVI | FD | 13 March–8 November 2012 | 16 |
| CT27 | NDVI | FD | 29 March–23 October 2012 | 14 |
| CT28 | NDVI | FD | 14 April–7 October 2012 | 12 |
| CT29 | NDVI | FD | 30 April–21 September 2012 | 10 |
| CT30 | NDVI | FD | 16 May–5 September 2012 | 8 |
| CT31 | NDVI | FD | 1 June–20 August 2012 | 6 |
| CT32 | NDVI | FD | 17 June–4 August 2012 | 4 |
| CT33 | NDVI | FD | 3 July–19 July 2012 | 2 |
| CT34 | NDVI | FA(2 harmonics) of the RD | 30 April–5 September 2012 | 9 |
| CT35 | NDVI | FA(3 harmonics) of the RD | 30 April–5 September 2012 | 9 |
| CT36 | NDVI | FA(4 harmonics) of the RD | 30 April–5 September 2012 | 9 |
| CT37 | NDVI | FA(5 harmonics) of the RD | 30 April–5 September 2012 | 9 |
| CT38 | NDVI | SS using FA(2 harmonics) instead of RD | 16 May–20 August 2012 | 5 |
| CT39 | NDVI | SS using FA(3 harmonics) instead of RD | 16 May–20 August 2012 | 5 |
| CT40 | NDVI | SS using FA(4 harmonics) instead of RD | 16 May–20 August 2012 | 5 |
| CT41 | NDVI | SS using FA(5 harmonics) instead of RD | 16 May–20 August 2012 | 5 |
| CT42 | NDVI | FD using FA(2 harmonics) instead of RD | 1 June–20 August 2012 | 6 |
| CT43 | NDVI | FD using FA(3 harmonics) instead of RD | 1 June–20 August 2012 | 6 |
| CT44 | NDVI | FD using FA(4 harmonics) instead of RD | 1 June–20 August 2012 | 6 |
| CT45 | NDVI | FD using FA(5 harmonics) instead of RD | 1 June–20 August 2012 | 6 |
| CT46 | EVI | RD | 8 January–26 December 2012 | 23 |
| CT47 | EVI | RD | 21 January–10 December 2012 | 21 |
| CT48 | EVI | RD | 9 February–24 November 2012 | 19 |
| CT49 | EVI | RD | 25 February–8 November 2012 | 17 |
| CT50 | EVI | RD | 13 March–23 October 2012 | 15 |
| CT51 | EVI | RD | 29 March–7 October 2012 | 13 |
| CT52 | EVI | RD | 14 April–21 September 2012 | 11 |
| CT53 | EVI | RD | 30 April–5 September 2012 | 9 |
| CT54 | EVI | RD | 16 May–20 August 2012 | 7 |
| CT55 | EVI | RD | 1 June–4 August 2012 | 5 |
| CT56 | EVI | RD | 17 June–19 July 2012 | 3 |
| CT57 | EVI | SS | 8 January–26 December 2012 | 5 |
| CT58 | EVI | SS | 21 January–10 December 2012 | 5 |
| CT59 | EVI | SS | 9 February–24 November 2012 | 5 |
| CT60 | EVI | SS | 25 February–8 November 2012 | 5 |
| CT61 | EVI | SS | 13 March–23 October 2012 | 5 |
| CT62 | EVI | SS | 29 March–7 October 2012 | 5 |
| CT63 | EVI | SS | 14 April–21 September 2012 | 5 |
| CT64 | EVI | SS | 30 April–5 September 2012 | 5 |
| CT65 | EVI | SS | 16 May– 20 August 2012 | 5 |
| CT66 | EVI | SS | 1 June–4 August 2012 | 5 |
| CT67 | EVI | SS | 17 June–19 July 2012 | 5 |
| CT68 | EVI | FD | 21 January–26 December 2012 | 22 |
| CT69 | EVI | FD | 9 February–10 December 2012 | 20 |
| CT70 | EVI | FD | 25 February–24 November 2012 | 18 |
| CT71 | EVI | FD | 13 March–8 November 2012 | 16 |
| CT72 | EVI | FD | 29 March–23 October 2012 | 14 |
| CT73 | EVI | FD | 14 April–7 October 2012 | 12 |
| CT74 | EVI | FD | 30 April–21 September 2012 | 10 |
| CT75 | EVI | FD | 16 May–5 September 2012 | 8 |
| CT76 | EVI | FD | 1 June–20 August 2012 | 6 |
| CT77 | EVI | FD | 17 June–4 August 2012 | 4 |
| CT78 | EVI | FD | 3 July–19 July 2012 | 2 |
| CT79 | EVI | FA(2 harmonics) of the RD | 14 April–21 September 2012 | 11 |
| CT80 | EVI | FA(3 harmonics) of the RD | 14 April–21 September 2012 | 11 |
| CT81 | EVI | FA(4 harmonics) of the RD | 14 April–21 September 2012 | 11 |
| CT82 | EVI | FA(5 harmonics) of the RD | 14 April–21 September 2012 | 11 |
| CT83 | EVI | SS using FA(2 harmonics) instead of RD | 1 June–4 August 2012 | 5 |
| CT84 | EVI | SS using FA(3 harmonics) instead of RD | 1 June–4 August 2012 | 5 |
| CT85 | EVI | SS using FA(4 harmonics) instead of RD | 1 June– 4 August 2012 | 5 |
| CT86 | EVI | SS using FA(5 harmonics) instead of RD | 1 June– 4 August 2012 | 5 |
| CT87 | EVI | FD using FA(2 harmonics) instead of RD | 16 May–5 September 2012 | 8 |
| CT88 | EVI | FD using FA(3 harmonics) instead of RD | 16 May–5 September 2012 | 8 |
| CT89 | EVI | FD using FA(4 harmonics) instead of RD | 16 May–5 September 2012 | 8 |
| CT90 | EVI | FD using FA(5 harmonics) instead of RD | 16 May–5 September 2012 | 8 |
Variable importance ranking was estimated based on summing the drop (delta) in node impurity for all predictors over all nodes in the trees and expressing these sums relative to the largest sum found over all predictors, as implemented in Statistica v. 9 software (StatSoft, Inc., Tulsa, OK, USA). The main criteria for classification performance were accuracy measures such as overall accuracy (OA), producer’s accuracy (PA), user’s accuracy (UA) and Cohen’s kappa [
35]. Significant differences between the classifications were subjected to McNemar tests, as suggested and described by Foody [
36].
3. Results
The seasonal profile of VI in grasslands exhibits a typical shape, which reflects green biomass development during the season, with a sharp increase in spring reaching the maximum in early summer and a smooth decrease thereafter until the end of the vegetation season (
Figure 6).
The small decrease visible after the period when the seasonal maximum is reached may be a response to summer drought and hay harvesting. The effect of grass cutting is more influential, which is apparent when cut and uncut meadows are plotted separately (
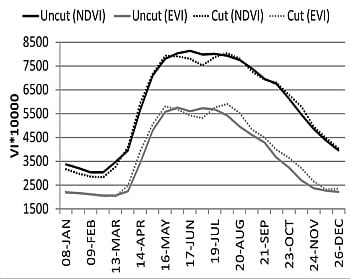
Figure 7). After the hay harvesting period, vegetation re-growth is evident, reaching the second VI peak in late summer. Variation of this profile is the highest during the spring vegetation increase, followed by the autumn and the harvesting period, which is the lowest during both vegetation peaks in late spring and late summer. Here, variation in late autumn and winter is not considered as this is largely affected by low data quality due to clouds or snow. The temporal EVI and NDVI patterns are similar. EVI bears constantly lower values and higher spatial variability throughout the season.
However, when the cut and uncut meadows are analyzed separately, the bigger difference appears. EVI bears higher values in cut meadows compared to uncut meadows over the entire season except for a short period after harvesting (
Figure 7). In contrast, NDVI is almost the same in cut and uncut meadows during the whole season except for more apparent difference occurring between the two vegetation peaks (16 May and 4 August).
Figure 6.
Temporal profile of NDVI and EVI (bars represent standard deviation) in all sampled hay meadows (286 sites).
Figure 6.
Temporal profile of NDVI and EVI (bars represent standard deviation) in all sampled hay meadows (286 sites).
Figure 7.
Temporal profile of NDVI and EVI in cut (dot line) and uncut (solid line) hay meadows.
Figure 7.
Temporal profile of NDVI and EVI in cut (dot line) and uncut (solid line) hay meadows.
The best case classifications from all the raw and transformed data sets are visible in
Figure 8 and accuracy measures for the best case classifications are reported in
Table 3,
Table 4,
Table 5,
Table 6,
Table 7 and
Table 8. In general, the best classification results yield first difference series followed by seasonal statistics series and raw data series. However, differences in the best case classifications were statistically significant only in NDVI at the 0.05 (FD NDVI
vs. SS NDVI) and 0.01 (FD NDVI
vs. RD NDVI) level, respectively. Moreover, the FD series classification trees were quite simple (5 rules/splits) compared to very complex trees composed of raw data series (9 splits) and seasonal statistics series (7–9 splits), making them difficult to interpret (
Table 7). When shorter periods centered on the harvesting date were used, better results were achieved (
Figure 4). This was consistent across all classifications, where the best results in the FD series were seen using the period between 16 May and 5 September (EVI) and between 1 June and 20 August (NDVI). The best classification in all types was compared to their smoothing counterparts using different numbers of harmonics in temporal Fourier analysis. By using smoothing series for all the best case classifications (RD, SS, FD), significantly lower accuracies were obtained, although this was not the case when five harmonics were used. Using raw VI and seasonal statistics, EVI series yield better classification accuracies than NDVI series, yet these were not statistically significant.
On the other hand, though not statistically significant, NDVI yielded consistently better accuracies than EVI in FD series classifications, where the best was for the period between 1 June and 20 August using two images less than the best FD EVI classification. User’s and producer’s accuracies were well balanced in the NDVI series (
Table 7) and cut detection using NDVI outperformed the EVI series, reaching producer’s accuracies of 85% in comparison to just 67% using the EVI series.
Table 3.
Confusion matrix and accuracies of raw NDVI data set (30 April to 5 September).
Table 3.
Confusion matrix and accuracies of raw NDVI data set (30 April to 5 September).
| Cut | Uncut | Total | User’s Accur. (%) |
|---|
| Cut | 31 | 14 | 45 | 68.89 |
| Uncut | 15 | 40 | 55 | 72.73 |
| Total | 46 | 54 | 100 | |
| Producer’s Accur. % | 67.39 | 74.07 | | |
| Overall Accur. % | 71 | | | |
| Cohen’s Kappa | 0.42 | | | |
Table 4.
Confusion matrix and accuracies of raw EVI data set (14 April to 21 September).
Table 4.
Confusion matrix and accuracies of raw EVI data set (14 April to 21 September).
| Cut | Uncut | Total | User’s Accur. (%) |
|---|
| Cut | 29 | 9 | 38 | 76.32 |
| Uncut | 17 | 45 | 62 | 72.58 |
| Total | 46 | 54 | 100 | |
| Producer’s Accur. % | 63.04 | 83.33 | | |
| Overall Accur. % | 74 | | | |
| Cohen’s Kappa | 0.46 | | | |
Figure 8.
Classification performance of the all tested data series with different periods used. (a) raw data series RD, (b) seasonal statistics series SS, (c) first difference series FD. NDVI—solid line, EVI—dot line. The best case series for each NDVI and EVI are marked with the value of Cohen`s kappa. Bold line indicated significant difference in comparison to the best case of relevant series. Filled boxes indicated significant difference between EVI vs. NDVI using the same data set.
Figure 8.
Classification performance of the all tested data series with different periods used. (a) raw data series RD, (b) seasonal statistics series SS, (c) first difference series FD. NDVI—solid line, EVI—dot line. The best case series for each NDVI and EVI are marked with the value of Cohen`s kappa. Bold line indicated significant difference in comparison to the best case of relevant series. Filled boxes indicated significant difference between EVI vs. NDVI using the same data set.
Table 5.
Confusion matrix and accuracies of NDVI seasonal statistics data set (16 May to 20 August).
Table 5.
Confusion matrix and accuracies of NDVI seasonal statistics data set (16 May to 20 August).
| Cut | Uncut | Total | User’s Accur. (%) |
|---|
| Cut | 33 | 12 | 45 | 73.33 |
| Uncut | 13 | 42 | 55 | 76.36 |
| Total | 46 | 54 | 100 | |
| Producer’s Accur. % | 71.74 | 77.78 | | |
| Overall Accur. % | 75 | | | |
| Cohen’s Kappa | 0.50 | | | |
Table 6.
Confusion matrix and accuracies of EVI seasonal statistics data set (1 June to 4 August).
Table 6.
Confusion matrix and accuracies of EVI seasonal statistics data set (1 June to 4 August).
| Cut | Uncut | Total | User’s Accur. (%) |
|---|
| Cut | 29 | 5 | 34 | 85.29 |
| Uncut | 17 | 49 | 66 | 74.24 |
| Total | 46 | 54 | 100 | |
| Producer’s Accur. % | 63.04 | 90.74 | | |
| Overall Accur. % | 78 | | | |
| Cohen’s Kappa | 0.54 | | | |
Table 7.
Confusion matrix and accuracies of first difference NDVI data set (1 June to 20 August).
Table 7.
Confusion matrix and accuracies of first difference NDVI data set (1 June to 20 August).
| Cut | Uncut | Total | User’s Accur. (%) |
|---|
| Cut | 39 | 8 | 47 | 82.98 |
| Uncut | 7 | 46 | 53 | 86.79 |
| Total | 46 | 54 | 100 | |
| Producer’s Accur. % | 84.78 | 85.19 | | |
| Overall Accur. % | 85 | | | |
| Cohen’s Kappa | 0.70 | | | |
Table 8.
Confusion matrix and accuracies of first difference EVI data set (16 May to 5 September).
Table 8.
Confusion matrix and accuracies of first difference EVI data set (16 May to 5 September).
| Cut | Uncut | Total | User’s Accur. (%) |
|---|
| Cut | 31 | 3 | 34 | 91.18 |
| Uncut | 15 | 51 | 66 | 77.27 |
| Total | 46 | 54 | 100 | |
| Producer’s Accur. % | 67.39 | 94.44 | | |
| Overall Accur. % | 82 | | | |
| Cohen’s Kappa | 0.63 | | | |
The logic behind the classifications could be partly explained by the analysis of variability importance. In the raw data EVI series, the most influential images for differentiation of cut and uncut meadows lay in late summer (with 20 August being the highest), followed by an image ranked far lower in importance after the harvest (3 July) and with the lowest importance for the images during the harvesting periods (
Figure 9).
When the NDVI series is used, despite the similar importance of late summer images, the high influence of images from the harvesting period (17 June and 1 June) for differentiating cut and uncut meadows is apparent. This reflects well the dissimilar pattern of the VI seasonal profile from EVI and NDVI in cut and uncut meadow values in these periods (
Figure 7). The importance of SS for classifying cut and uncut meadows is similar in NDVI and EVI, where range, minimum and standard deviation (
Figure 10) rank highest in importance.
Figure 9.
Variable importance for the best case classification of the raw data series (RD).
Figure 9.
Variable importance for the best case classification of the raw data series (RD).
Figure 10.
Variable importance for the best case classification of the seasonal statistics series (SS).
Figure 10.
Variable importance for the best case classification of the seasonal statistics series (SS).
In the FD EVI series (
Figure 11), several periods are comparably important for classification, namely late summer (20 August), which can reflect the higher increase (vegetation re-growth) in cut meadows compared to uncut meadows; after the harvest period (3 July), reflecting the removal of biomass after the harvest and before the harvest period (1 June), which may respond to dissimilarities in cut and uncut meadows at the vegetation biomass peak (
Figure 7). Contrarily, the FD NDVI series saw only a decrease after the harvest in different periods ranging from 3 July until 4 August, which is of comparably high importance for classification. The final classification trees for the best case FD series for EVI and NDVI are presented in
Figure 12. In both series, cutting is classified by 5 leaf paths (production rules) and uncut meadows only by one leaf path what reflects higher variability of cut meadows and cutting practices. Seventy-five percent (63 sites) of cut and 80% (82 sites) of uncut training sites in NDVI series and 62% (52 sites) of cut and 84% (86 sites) of uncut training sites in EVI series were used in the final pruned tree. Cutting was classified mainly by decision rules that reflect decrease in NDVI between consecutive 16 days periods (e.g., in 19 July, 17 June) and increase of EVI (e.g., 4 August, 20 August). Again, this could reflect the dissimilar pattern of VI seasonal profile of EVI and NDVI in cut and uncut meadows, which may lead to different ways of discriminating cut and uncut meadows using the EVI and NDVI FD series.
Figure 11.
Variable importance for the best case classification of the first difference series (FD).
Figure 11.
Variable importance for the best case classification of the first difference series (FD).
Figure 12.
Classification tree and splitting rules of the best case first difference series for EVI (a) and NDVI (b). Values are in VI × 10000. Percentages in parentheses represent the proportion of the classified sites of the respective leaf to the total amount of sites in that specific class. Thus, sum of these percentages represents proportion of sites from the respective class, which were used in the final pruned tree.
Figure 12.
Classification tree and splitting rules of the best case first difference series for EVI (a) and NDVI (b). Values are in VI × 10000. Percentages in parentheses represent the proportion of the classified sites of the respective leaf to the total amount of sites in that specific class. Thus, sum of these percentages represents proportion of sites from the respective class, which were used in the final pruned tree.
5. Conclusions
We reported here the possible usage of VI time series for detection of cut management in hay meadows. Transformation of raw series clearly helps, mainly FD, which decreases the complexity of the resulting classification trees. Specifically, FD series classification trees resulted in simple tree with 5 rules/splits compared to very complex trees composed of raw data series (9 splits) and seasonal statistics series (7–9 splits). We think that such simple rule-based algorithms should be better transferable than complex trees. However, this needs to be tested in different regions, grassland types and years. We do slightly consider regional differences here as the relatively large study area includes different bioregions, but we do not consider other grassland types and more importantly we do not consider climate variability between years. This needs to be tested in longer term case studies that may include anomaly years as well. NDVI slightly outperformed EVI in the best case FD classification. Specifically, the best case NDVI FD series classification yielded overall accuracy of 85%, EVI FD series yielded slightly lower values (82%), though not significantly different. Moreover, user’s and producer’s accuracies were well balanced in the NDVI series and cut detection using NDVI outperformed the EVI series, reaching producer’s accuracies of 85% in comparison to just 67% using the EVI series. This might be caused mainly by the higher variability of EVI and different VI response to cutting in the temporal profile, leading to different ways of discriminating cut and uncut meadows. All other differences were masked in the NDVI profile except the apparent biomass decrease after the harvest in different time periods. Contrary, EVI saw constantly higher values in cut meadows over a longer period and their higher variability may have caused the higher misclassification rates and omission errors of cut meadows. By using smoothing series for all the best case classifications (RD, SS, FD), significantly lower accuracies were obtained, although this was not the case when five harmonics were used. On the other hand, interpolation techniques followed by smoothing is a method commonly used and they could essentially improve the amount of useful input data, leading to more representative coverage of study areas and full coverage products. Therefore, proper analysis of the missing data effect and utilization of proper interpolation and smoothing techniques should be done in future grassland classification studies. There is no need to have the whole annual series in order to sufficiently detect cutting. In fact, the optimal period for detection lay between 1 June and 20 August. More importantly, the 16-day compositing period seemed to be enough for detection of cutting, which would be the time span that might be hopefully achieved by upcoming on-board HR sensors (e.g., Sentinel2), followed by combining them with existing platforms (e.g., Landsat). This looks promising when the possible usage of similar concepts at finer scales is borne in mind.