Incorporating Diversity into Self-Learning for Synergetic Classification of Hyperspectral and Panchromatic Images

Abstract

Derived from semi-supervised learning and active learning approaches, self-learning (SL) was recently developed for the synergetic classification of hyperspectral (HS) and panchromatic (PAN) images. Combining the image segmentation and active learning techniques, SL aims at selecting and labeling the informative unlabeled samples automatically, thereby improving the classification accuracy under the condition of small samples. This paper presents an improved synergetic classification scheme based on the concept of self-learning for HS and PAN images. The investigated scheme considers three basic rules, namely the identity rule, the uncertainty rule, and the diversity rule. By integrating the diversity of samples into the SL scheme, a more stable classifier is trained by using fewer samples. Experiments on three synthetic and real HS and PAN images reveal that the diversity criterion can avoid the problem of bias sampling, and has a certain advantage over the primary self-learning approach.

1. Introduction

Among all the remote sensing techniques, hyperspectral (HS) imaging is probably the most widely researched and applied one in earth observation, due to its powerful ability to recognize diverse land-covers and allow for the accurate analyses of terrestrial features. Classification, as an active area of research in HS data interpretation, has long attracted the attention of the remote sensing community, since classification results are the basis for many environmental and socioeconomic applications [1,2]. Conventional classification algorithms require a large number of labeled samples to training a stable classifier. Unfortunately, non-availability of a sufficient number of labeled samples is a general problem in pattern classification, and this is a more severe problem in remote sensing because it is extremely difficult and expensive to identify and label the samples, and sometimes it is not even feasible [3]. This observation has facilitated the idea of exploiting unlabeled samples to improve the capability of the classifiers.

Two popular machine learning approaches have been developed to solve this problem: semi-supervised learning (SSL) and active learning (AL) [4,5,6]. Semi-supervised algorithms incorporate the unlabeled samples and labeled samples to find a classifier with better boundaries [7,8]. The area of SSL has experienced a significant evolution in terms of the adopted models, which comprise complex generative models [9,10], self-training models, multi-view learning models, transductive support vector machines (TSVMs) [11], and graph-based methods [12]. A survey of SSL algorithms is available in [13].

Active learning, on the other hand, assumes that a few new samples can be labeled and added to the original training set, which means the training set can be iteratively expanded according to an interactive process that involves a supervisor who is able to assign the correct label to any queried samples [14]. AL has demonstrated its effectiveness when applied to large datasets needing an accurate selection of examples. The main challenge in AL is how to evaluate the information content of the unlabeled pixels. Generally, the selection criteria of uncertain samples can be grouped into three different families: (1) committee-based heuristics; (2) large margin–based heuristics [15,16]; (3) posterior probability–based heuristics [17]. An overview of the AL classification techniques can be found in [18]. Recently, another family of AL heuristics, cluster-based, has been proposed [19].

Conventional AL requires the interaction between the supervisor and machine to label the uncertain pixels. This is, however, sometimes difficult and time-consuming, especially for remote sensing applications when there is a dense distribution of ground objects. The authors of [20] proposed a semi-supervised self-learning (SL) algorithm which adopts standard AL approaches into a self-learning scenario. In this case, no extra cost is required for labeling the selected samples. In [21], a synergetic self-learning classification approach based on image segmentation and AL is proposed for HS and panchromatic (PAN) images, in which the algorithm automatically determines the labels of some unknown samples according to the classification result of the classifier and the corresponding segmentation map of the high-resolution PAN image. Since the PAN images usually have a higher resolution than HS images, a finer classification map can be obtained through this strategy. The segmentation-based self-learning is effective when the supervised classifier is not able to achieve a reliable result under the condition of small samples. In some cases, if the distribution of unlabeled samples in the feature space is quite different from the labeled samples, the optimization procedure is designed to keep its learning from fluctuation during the iterations. This may result in a lack of diversity between the selected samples.

Actually, the diversity criterion has already been applied in SSL or AL with the goal of improving the robustness of classifiers by using as few samples as possible [22,23], but it has never been incorporated with such self-learning scenarios. Therefore, the main contribution of this paper is to integrate diversity measures into the SL scheme to tackle this problem. Differing from most of those published studies, in this work, the diversity measures are applied only within the unlabeled samples rather than between the labeled and unlabeled samples. As an improved version, the presented SL strategy considers three basic rules: (1) the identity rule, namely the necessary condition, determines the candidate set in which the samples are allowed to be trained; (2) the uncertainty rule, namely the standard AL process, determines the informative samples that are helpful to the classifier among the candidate set; (3) the diversity rule, which refines the informative samples, aimed at enhancing the stability of the classifier while using the fewest samples.

The remainder of this paper is organized as follows. Section 2 describes the experimental data sets and gives a short review of the SL algorithm. Specifically, we focus on presenting three state-of-the-art diversity criteria and illustrating our strategy of the incorporation. Section 3 reports classification results using synthetic and real HS/PAN datasets. Finally, conclusions are given in Section 4.

2. Materials and Methodology

2.1. Data Sets

In this sub-section, we introduce three data sets, which are shown in Figure 1.

(1) Data set of San Diego. The first data set is a low-altitude AVIRIS HS image of a portion of the North Island of the U.S. Naval Air Station in San Diego, CA, USA. This HS image consists of 126 bands of size 400 × 400 pixels with a spatial resolution of 3.5 m per pixel. We use the average of bands 6–36 to synthesize a PAN image. Then the HS image is subsampled to a lower scale by a factor of 4 (i.e., a resolution of 14 m). The ground truth image has the same resolution as the original HS image with eight classes inside.

(2) Data set of Indian Pines. The second data set we used in our experiments is a well-known scene taken in 1992 by the AVIRIS sensor over the Indian Pines region in Northwestern Indiana [3]. It has 144 × 144 pixels and 200 spectral bands with a pixel resolution of 20 m. Nine classes including different categories of crops have been labeled in the ground truth image. Likewise, we simulate the low-resolution HS and high-resolution PAN images by spatial and spectral degradation of the original HS image.

(3) Data set of the University of Houston. The last data set includes an HS image provided by the 2013 IEEE GRSS Data Fusion Contest and a co-registered PAN image collected by the WorldView-II satellite. The HS image is collected over the University of Houston campus and the neighboring urban area, and consists of 144 bands with a spatial resolution of 2.5 m. For the sake of avoiding the registration error caused by a different platform, a subset of size 640 × 320 is used and subsampled by a factor of 4. The PAN image has a spatial resolution of 0.5 m, and is subsampled to the same scale as the original HS image. A ground truth image including 12 classes is also available and has the same size as the original HS image. All images have been radiometrically calibrated.

2.2. Related Work

In this sub-section, a brief review of the SL approach is presented. Unlike conventional multi-source classification techniques based on the feature level or decision level [24], SL can be considered as a new framework of synergetic processing for HS and high-resolution PAN images. It consists of two prevalent techniques, namely high-resolution image segmentation and active learning. The segmentation processing is applied on the high-resolution PAN image, which can be realized through any existing algorithms that consider spatial-spectral information [25,26,27,28]. Then for a given labeled sample, the pixels that locate in the same object can be labeled with high confidence as belonging to the same class (here we call it the object label) as this labeled sample [21]. Meanwhile, a spectral-based classification is conducted on the HS image to obtain the predicted labels for these pixels. Hence, those pixels that have identical object labels and predicted labels comprise the candidate set. Afterwards a typical AL method (e.g., margin sampling [15], etc.) is adopted to select informative samples. The main framework of the presented self-learning algorithm is shown in Figure 2. Obviously, the segmentation scale is quite crucial to the final result, and an over-segmentation would be preferred since it is necessary to ensure that the given samples with different class labels should not locate in a single object.

In order to avoid introducing mislabeled samples, and keep the iterations from fluctuation, an optimization processing of the candidate set can be appended to attain a steady result by involving a distance measure between the unknown samples and the training samples. See details in [21]. However, the determination of the distance threshold remains problematic. Meanwhile, a sub-optimal value will lead to a lack of diversity in the selected samples, as the isolated samples sometimes will also be helpful to the determination of the decision boundary. Thus, we can imagine that incorporating the diversity of samples should benefit the learning procedure, and enhance the classification result with fewer iterations.

The main idea of integrating diversity into AL is to select a batch of unknown samples that have low confidence (i.e., the most uncertain ones) and are diverse from each other simultaneously, hence finding more precise decision rules by using as few samples as possible [29]. In [30], the diversity of candidates is enforced by constraining the margin sampling (MS) solution to pixels associated with different closest support vectors. The authors of [22] proposed the kernel cosine angular as the similarity measure between samples in the kernel space. The authors of [31] proposed to integrate k-means clustering into the binary support vector machine (SVM) AL technique. The diversity criterion can also work in spatial domain, e.g., [32] formulated the spatial and spectral diversity as a multi-objective optimization problem, [33] proposed a region-based query-by-committee AL combined with two spatial diversity criteria, etc. In this paper, we take account of three state-of-the-art diversity criteria: (1) spatial Euclidean distance; (2) kernel cosine angle (KCA) [34]; and (3) kernel k-means clustering (KKM) [35]. Spatial Euclidean distance computes the Euclidean distance between the two-dimensional (2-D) coordinates of two candidates in the spatial domain of the image. In particular, the negative value is adopted to convert the maximization problem into a minimization one. KCA is a similarity measure in the spectral domain. Unlike the spectral angle mapping (SAM), KCA is the cosine angle distance defined in the kernel space,

$$\mathrm{KCA}=\frac{\varnothing \left(x_i\right)·\varnothing \left(x_j\right)}{\parallel \varnothing \left(x_i\right)\parallel ·\parallel \varnothing \left(x_j\right)\parallel }=\frac{k\left(x_i,x_j\right)}{\sqrt{k\left(x_i,x_i\right)·k\left(x_j,x_j\right)}}$$

(1)

where $x_i$ and $x_j$ represent two samples, $\varnothing (·)$ is a nonlinear mapping function and $k\left(·,·\right)$ is the kernel function. The angle between two samples is small if they are close to each other and vice versa.

Cluster-based techniques evaluate the distribution of the samples in a feature space and group the similar samples into the same cluster. The samples within the same cluster are usually correlated and provide similar information, so a representative sample is selected from each cluster. KKM works also in the kernel space. It starts with several initial clusters. Since the cluster centers in the kernel space cannot be expressed explicitly, several pseudocenters will be selected, and then the distance between each sample $\varnothing \left(x_i\right)$ and cluster center $\varnothing \left({\mu }_v\right)$, (${\mu }_v$ is the $v\mathrm{th}$ pseudocenter) in the kernel space can be computed [36]:

$$\begin{array}{ll}{D}^2\left(\varnothing \left(x_i\right),\varnothing \left({\mu }_v\right)\right)& =\parallel \varnothing \left(x_i\right)-\frac{1}{\left|C_v\right|}{\displaystyle {\displaystyle \sum }_{j=1}^m}\delta \left(\varnothing \left(x_j\right),C_v\right)\varnothing \left(x_j\right)\parallel \\ & =k\left(x_i,x_i\right)-\frac{2}{\left|C_v\right|}{\displaystyle {\displaystyle \sum }_{j=1}^m}\delta \left(\varnothing \left(x_j\right),C_v\right)k\left(x_i,x_j\right)\\ & +\frac{2}{{\left|C_v\right|}^2}{\displaystyle {\displaystyle \sum }_{j=1}^m}{\displaystyle {\displaystyle \sum }_{l=1}^m}\delta \left(\varnothing \left(x_j\right),C_v\right)\delta \left(\varnothing \left(x_l\right),C_v\right)k\left(x_i,x_l\right)\end{array}$$

(2)

where $m$ is the amount of samples, $\delta \left(\varnothing \left(x_j\right),C_v\right)=1$, if $x_j$ is assigned to $C_v$ ($C_v$ denotes the $v\mathrm{th}$ cluster); otherwise, $\delta \left(\varnothing \left(x_j\right),C_v\right)=0$. The algorithm is iterated until convergence as standard k-means clustering.

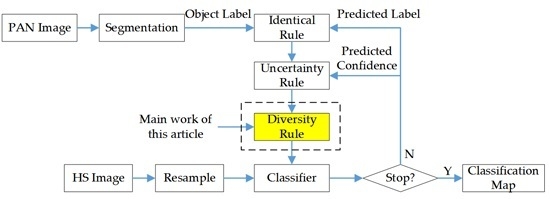
2.3. Implementation of Diversity Criteria within SL

In this paper, each diversity criterion is combined solely with SL procedure. Instead of considering the similarity between the unlabeled samples and training samples in [6] or [30], in this work, we take account of the similarity only within the unlabeled samples. Two different algorithms are presented here by taking the SVM algorithm, for example. First let us review the SVM algorithm [37,38] briefly. For a simple purpose, we first consider a binary classification problem.

Given a training set made up of n labeled samples, $X^L={\{\left(x_i^L,y_i\right)\}}_{i=1}^n$, in which $y_i\in \left\{+1,-1\right\}$ denotes the associated labels. Then the goal of a binary SVM is to find out an optimal hyperplane that separates the feature space into two classes as $w·x+b\ge +1,\left(y_i=+1\right)$ and $w·x+b\le -1,\left(y_i=-1\right)$. The points lying on the two hyperplanes, which are defined by $w·x+b=\pm 1$, are so-called support vectors (SV). The SVM approach is equal to solve the optimization problem that maximizes the distance between the closest training samples (the SVs) and the separating hyperplane.

In practical applications, the training data in two classes are not often completely separable. In this case, a hyperplane that maximizes the margin while minimizing the errors is desirable. Therefore, a slack variable ξ ≥ 0 may be introduced to allow for misclassification. Nonetheless, a more general situation is that the training data is nonlinearly separable. Then an effective way to improve the separation is to project the data onto another higher-dimensional space through a positive definite kernel, which is defined as $K\left(x_i,x\right)=\left(\mathsf{\Phi }\left(x_i\right),\mathsf{\Phi }\left(x\right)\right)$. A kernel that can be used to construct an SVM must meet Mercer’s condition, e.g., radial basis function, sigmoid kernel, polynomial kernel [39]. The binary SVM can be easily extended for multiple-class classification scenarios through two approaches, i.e., “one-against-all” and “one-against-one” [40,41]. Generally, we use the “one-against-one” approach in this paper.

Assume that a training set $X^{Train}=\left\{\left(x_k^{Train},y_k\right)|k\in \left\{1,2,\dots ,n\right\},y_k\in \left\{1,2,\dots ,C\right\}\right\}$ including $n$ labeled samples is available, in which each sample $x_k^{Train}$ belongs to an individual object $O_k$ that is obtained by image segmentation, $C$ is the number of classes. $O_k^U$ denotes the set of unlabeled samples inside $O_k$. Then the identity rule aims at collecting those samples that satisfy $\left\{x_i^U\right|x_i^U\in O_k^U\cap {\tilde{y}}_i=y_k\},$ where ${\tilde{y}}_i$ denotes the prediction labels of the spectral-based classifier. Therefore, the candidate set $X^{Cand}$ is made up of the unlabeled samples that have identical predicted labels with object labels. In addition, the informative sample set $X^I$ is made up of the samples selected by standard AL strategy. Assume that for each iteration, $N$ samples (denoted as $X^L$) will be picked out and appended to the training set, then we generalize the implementation of similarity measure-based diversity criteria, e.g., spatial Euclidean distance, KCA and as such, as follows (Algorithm 1, The source codes of proposed algorithms are provided as supplementary materials.):

Algorithm 1. AL combined with similarity measure–based diversity criterion

Input: Candidate set $X^{Cand}$, number of classes $C$, number of selected samples $N$;

Output: Totally $N$ samples included in $X^L={\cap }_{c=1}^C{X}_c^L$;

1. Select most informative samples via AL strategy, denoted as $X^I$;

For $c$ = 1 to $C$

2. Select the samples of $c\mathrm{th}$ class from $X^I$, denoted as $X_c^I$;

3. $X_c^L=\varnothing$;

4. If the number of samples in $X_c^I$ is less than $N/C$, then put them into $X_c^L$,

Otherwise:

5. Pick out the most uncertain sample from $X_c^I$, and put it into $X_c^L$;

6. For each sample $\left\{x_i|x_i\in X_c^I\cap x_i\notin X_c^L\right\}$, compute the mean value of distance (negative value of spatial distance or the KCA value) with the samples in $X_c^L$;

7. Pick out the sample that has minimum mean value, and put it into $X_c^L$;

8. Repeat steps 6 and 7 until $X_c^L$ has $N/C$ samples;

End for

whereas the cluster-based diversity criterion can be implemented via Algorithm 2.

Algorithm 2. AL combined with cluster-based diversity criterion

Input: Candidate set $X^{Cand}$, number of classes $C$, number of selected samples $N$;

Output: Total $N$ samples included in $X^L={\cap }_{c=1}^C{X}_c^L$;

1. Select most informative samples via AL strategy, denoted as $X^I$;

For $c$ = 1 to $C$

2. Select the samples of the $c\mathrm{th}$ class from $X^I$, denoted as $X_c^I$;

3. $X_c^L=\varnothing$;

4. If the number of samples in $X_c^I$ is less than $N/C$, then put them into $X_c^L$,

Otherwise:

5. Apply kernel k-means clustering to $X_c^I$, the cluster number is $N/C$;

6. Select the most uncertain sample of each cluster, and put it into $X_c^L$, until $X_c^L$ has $N/C$ samples;

End for

For the SVM classifier, only the samples inside the margins will be considered. In addition, for other probabilistic classifiers, a number of samples with lowest confidence will be considered. Figure 3 shows how the diversity criterion works. Figure 3a shows the primary hyperplane obtained by the training set (the labeled samples). Figure 3b shows the retrained hyperplane without considering the diversity rule. Two candidates per class are selected by the uncertainty rule. It can be seen that the AL heuristics only concentrate on the samples lying on the boundaries of different classes. Obviously, it is unsatisfactory as some samples have been misclassified. Figure 3c shows the retrained hyperplane with similarity measures. The first sample is selected according to its confidence, while the subsequent ones are selected according to their distance to the previous ones. Figure 3d shows the retrained hyperplane with sample clustering. The selected samples are picked from each cluster. By contrast, the diversity-based ALs not only focuses on the uncertainty, but also considers the similarity between the selected samples. Therefore, the selected samples scatter around the classes and can overcome the problem of bias sampling.

3. Experimental Results and Analyses

This section reports the experimental results and analyses conducted on the three data sets that are shown in Figure 1. To demonstrate the performance of our algorithms, we use very small labeled training sets, i.e., only 5, 10, and 15 samples per class will be selected randomly from the ground truth images at most. In addition, the remaining labeled samples are used for testing purposes. A segmentation operation based on edge detection and the full λ-schedule (FLS) algorithm [28] is first applied on high-resolution PAN images, and the probabilistic SVM with the Gaussian radial basis function (RBF) kernel [42] is used as the spectral-based classifier. The segmentation parameters contain a scale level and a merge level, which decide the edge intensity and merge cost, respectively. The parameters of the SVM model, i.e., the penalty factor and σ (the spread of the RBF kernel), are chosen by five-fold cross-validation and will be updated at each iteration of the AL procedure. The RBF kernel is also used in KCA and KKM with the same σ as is used in SVM. The classical modified breaking ties (MBT) and modified margin sampling (MMS) [21] methods will be used as AL strategies to test the algorithms. In all cases, we conduct 10 independent Monte Carlo runs with respect to the labeled training set from the ground truth images. All the graphics display the average values of 10 experiments. The maximum iteration is 20, and the within-class variance is used as the stop criterion of the learning procedure.

3.1. Experimental Results on Simulated Data Set

To better test our presented approaches, we first conduct experiments on the synthetic data sets of San Diego and the Indian Pines region. We compare the diversity-based SL methods with the primary SL method (i.e., segmentation-based self-learning, SBSL [21]) as well as neighbor-based self-learning (NBSL) [20]. As we have mentioned above, defining the optimal scale of image segmentation remains problematic. An over-segmentation would be preferable. Here, for the first data set, the segmentation parameters are set as 35.00 and 65.00, manually corresponding to the scale level and merge level, respectively. For the second data set, the scales are set as 20.00 and 65.00, respectively. Figure 4 and Figure 5 show the overall accuracies (OAs) with respect to the iterations. The experiments are conducted under different amounts of labeled (5, 10, and 15) and unlabeled samples. The first point on each curve represents the OA obtained by using the SVM algorithm alone, i.e., randomly using 5, 10, and 15 samples per class for training. The SBSL-SPA stands for the spatial Euclidean distance–based diversity criterion, and SBSL-KCA/SBSL-KKM stand for kernel cosine angle and kernel k-means clustering, respectively. Apart from the advantage of exploiting unlabeled samples as is shown by all of these SL approaches, the OAs increase as the number of training samples increases, and incline to converge after a small number of iterations. This deserves special attention since these samples are generated in a relatively lower-cost, easier, and, more importantly, self-learning fashion, i.e., no extra cost of human labeling or determination is required during the learning procedure.

For a clearer comparison,

Table 1. Overall accuracies of San Diego and the Indian Pines region data sets (%).

San Diego

5 Labeled Samples per Class, 40 Unlabeled Samples per Iteration

SVM

NBSL

SBSL

SBSL-SPA

SBSL-KCA

SBSL-KKM

MBT

MMS

MBT

MMS

MBT

MMS

MBT

MMS

MBT

MMS

OA

79.64 ± 4.59

89.13 ± 2.97

89.44 ± 2.59

91.24 ± 2.91

90.89 ± 2.06

91.72 ± 2.34

91.68 ± 2.60

90.74 ± 2.32

91.57 ± 2.23

91.89 ± 2.38

91.78 ± 2.95

Kappa

0.7591 ± 0.0528

0.8708 ± 0.0349

0.8743 ± 0.0305

0.8956 ± 0.0343

0.8914 ± 0.0244

0.9010 ± 0.0279

0.9006 ± 0.0310

0.8897 ± 0.0274

0.8995 ± 0.0263

0.9032 ± 0.0284

0.9019 ± 0.0351

10 labeled samples per class, 64 unlabeled samples per iteration

SVM

NBSL

SBSL

SBSL-SPA

SBSL-KCA

SBSL-KKM

MBT

MMS

MBT

MMS

MBT

MMS

MBT

MMS

MBT

MMS

OA

88.03 ± 1.70

92.24 ± 1.89

90.39 ± 2.02

92.47 ± 1.93

92.86 ± 2.73

93.36 ± 1.88

93.66 ± 2.03

92.81 ± 1.60

92.92 ± 2.70

93.95 ± 1.85

93.76 ± 2.24

Kappa

0.8575 ± 0.0202

0.9076 ± 0.0224

0.8850 ± 0.0240

0.9105 ± 0.0228

0.9150 ± 0.0322

0.9208 ± 0.0223

0.9243 ± 0.0240

0.9144 ± 0.0189

0.9158 ± 0.0318

0.9278 ± 0.0218

0.9256 ± 0.0265

15 labeled samples per class, 80 unlabeled samples per iteration

SVM

NBSL

SBSL

SBSL-SPA

SBSL-KCA

SBSL-KKM

MBT

MMS

MBT

MMS

MBT

MMS

MBT

MMS

MBT

MMS

OA

91.00 ± 1.70

93.48 ± 1.01

93.05 ± 1.60

94.38 ± 1.58

93.85 ± 2.45

94.35 ± 0.41

94.71 ± 0.97

93.73 ± 1.69

93.54 ± 1.16

95.29 ± 0.41

95.03 ± 0.83

Kappa

0.8927 ± 0.0200

0.9222 ± 0.0119

0.9172 ± 0.0189

0.9328 ± 0.0186

0.9265 ± 0.0287

0.9325 ± 0.0049

0.9369 ± 0.0115

0.9253 ± 0.0201

0.9230 ± 0.0137

0.9437 ± 0.0050

0.9406 ± 0.0099

Indian Pines

5 labeled samples per class, 27 unlabeled samples per iteration

SVM

NBSL

SBSL

SBSL-SPA

SBSL-KCA

SBSL-KKM

MBT

MMS

MBT

MMS

MBT

MMS

MBT

MMS

MBT

MMS

OA

51.85 ± 8.92

69.07 ± 5.39

66.78 ± 3.69

75.90 ± 4.71

77.14 ± 3.86

78.12 ± 4.57

77.47 ± 4.29

76.84 ± 5.08

77.46 ± 6.41

78.64 ± 4.72

78.17 ± 6.10

Kappa

0.4454 ± 0.0974

0.6410 ± 0.0604

0.6146 ± 0.0.415

0.7190 ± 0.0531

0.7322 ± 0.0445

0.7432 ± 0.0531

0.7361 ± 0.0494

0.7284 ± 0.0578

0.7359 ± 0.0733

0.7497 ± 0.0549

0.7446 ± 0.0697

10 labeled samples per class, 36 unlabeled samples per iteration

SVM

NBSL

SBSL

SBSL-SPA

SBSL-KCA

SBSL-KKM

MBT

MMS

MBT

MMS

MBT

MMS

MBT

MMS

MBT

MMS

OA

71.05 ± 4.42

80.17 ± 3.52

77.56 ± 2.89

85.07 ± 4.06

85.60 ± 3.22

84.75 ± 3.17

85.51 ± 3.08

87.83 ± 2.36

87.58 ± 2.41

87.09 ± 1.81

87.00 ± 3.02

Kappa

0.6644 ± 0.0457

0.7685 ± 0.0399

0.7387 ± 0.0325

0.8251 ± 0.0467

0.8311 ± 0.0370

0.8211 ± 0.0362

0.8301 ± 0.0353

0.8568 ± 0.0274

0.8538 ± 0.0280

0.8483 ± 0.0206

0.8473 ± 0.0348

15 labeled samples per class, 45 unlabeled samples per iteration

SVM

NBSL

SBSL

SBSL-SPA

SBSL-KCA

SBSL-KKM

MBT

MMS

MBT

MMS

MBT

MMS

MBT

MMS

MBT

MMS

OA

80.49 ± 2.80

84.09 ± 3.04

83.14 ± 3.24

89.00 ± 4.54

90.97 ± 1.90

91.15 ± 1.77

90.92 ± 1.54

91.45 ± 2.32

91.65 ± 2.40

91.53 ± 1.77

91.80 ± 1.73

Kappa

0.77150.0324

0.8132 ± 0.0353

0.8019 ± 0.0205

0.8705 ± 0.0525

0.8933 ± 0.0223

0.8954 ± 0.0208

0.8924 ± 0.0181

0.8987 ± 0.0271

0.9011 ± 0.0281

0.9015 ± 0.0209

0.9028 ± 0.0205

lists the final OAs and Kappa coefficients of each technique attained after 20 iterations. The first line in each cell is the average of 10 runs, while the second run represents the standard deviation (SD), which gives a brief comparison of the stability of these methods. From the table it can be seen that even though the supervised classification has terrible results sometimes (e.g., five labeled samples per class in Indian Pines data set), the SL has the ability to exploit the inherent information existing in the abundant unlabeled samples, thereby achieving a relatively satisfactory result. In most cases, the diversity-based SL approaches can attain higher accuracies. Besides, different AL heuristics show little discrimination of the final result. It can be seen that MBT generally performs a little better than MMS.

3.2. Experimental Results on Real Data Set

The experiment on the real data set is described in this part. This data set consists of a low-resolution airborne HS image and a high-resolution satellite PAN image. The number of labeled samples per class is also set to {5, 10, 15}. The segmentation scales are set as 35.00 and 70.00, respectively. Likewise, Figure 6 shows the comparison of OAs under different amounts of labeled and unlabeled samples. Furthermore, as a matter of fact, due to the complex and dense distribution of ground objects for urban areas, the segments on PAN images usually turn to be small and scattered. In such cases, the SL approaches seem to converge in much fewer iterations; for instance, KKM and KCA converge within only five iterations. This is quite meaningful since it takes a smaller computation cost.

4. Discussion

As we can see from these experiments, the accuracy of supervised classifiers (SVM algorithm) is only determined by the initial labeled samples, which can be easily observed from Table 1 (79.64%, 88.03%, and 91.00% corresponding to 5, 10, and 15 samples for the San Diego data set respectively, 51.85%, 71.05%, and 80.49% for the Indian Pines data set, respectively), while the unlabeled samples can provide useful information to construct stable classification rules during the learning procedure (for instance, the OA increases in Figure 4a and finally reaches 91.89% at most for the first group of experiments), and more importantly, since they exist in the local neighborhood of the labeled samples, their labels can be determined in an automatic and low-cost fashion.

Obviously, with the increment of initial labeled samples, the number of available unlabeled samples (namely the candidates) increases in the meantime theoretically for both NBSL and SBSL strategies, resulting in a continuous improvement of the final accuracy, which can also be observed from Table 1 (91.24%, 92.47%, and 94.38%, respectively, for the first data set, and 75.90%, 85.07%, and 89.00% for the second one using SBSL with MBT). It is also worth noting that the final classification accuracy after reaching convergence is more likely to be affected by the labeled samples rather than the unlabeled samples, since the quality and quantity of unlabeled samples are strongly related to the distribution of the labeled samples. A similar conclusion can also be observed from the third data set.

By comparing the five strategies in these figures, we can see that the SBSL approach is superior to NBSL. This is because compared with NBSL, SBSL aims at selecting those most informative samples in a single object (usually having a lower spectral similarity with the known sample), while NBSL selects the uncertain samples locating in the neighborhood of the labeled samples (generally having greater spectral similarity). Additionally, the diversity criteria have a further beneficial effect on the SL approach (91.89%, 93.95%, and 95.29% for the first data set, respectively, and 78.64%, 87.09%, and 91.53% for the second one using KKM with MBT, much higher than the corresponding results of NBSL and SBSL). Nevertheless, different diversity measures, as is shown in Figure 4 and Figure 5, usually lead to discrepant results for various data sets. For instance, the SPA-based SBSL performs well on the San Diego data set (91.68%, 93.66%, and 94.71% for the MMS strategy under different numbers of samples), but it is not satisfactory on the Indian Pines data set since it has little enhancement compared with the SBSL approach. On the contrary, the KCA-based approach performs better on the second and third data sets compared to the first one. This is possibly because the two approaches cannot balance the relation between the uncertainty and similarity of those selected samples. It seems that the cluster-based diversity criterion (SBSL-KKM) is an effective strategy for considering the redundancy between samples of a local region, i.e., it achieves higher accuracies for the same number of samples (or the same accuracy with less samples), and more importantly, achieves convergence in fewer iterations than the other techniques in most cases. The KCA-based approach also seems to be acceptable in a manner.

Apart from the accuracies observed in these figures, since the results are the average of 10 runs, the standard deviation also gives a brief comparison of the stability of these methods. Due to the random sampling of the initial training samples, the supervised algorithm has relatively higher standard deviations, which also leads to non-zero standard deviations for the self-learning results. Nevertheless, as is shown in Table 1, they are much lower than the initial SDs. This indicates the stability of these self-learning methods.

5. Conclusions

In this paper, the diversity problem between unlabeled samples is addressed in the framework of the self-learning strategy, which is developed for the synergetic classification of hyperspectral and panchromatic images, to further enhance the classification accuracy and stability. The presented self-learning strategy considers three criteria, namely the identity rule, the uncertainty rule, and the diversity rule. The identity rule considers the consistency between the object labels, which is obtained through the segmentation process, and the predicted labels, thereby improving the classification result by expanding the training set automatically. The uncertainty rule, namely the standard active learning algorithm, is applied to select the informative samples that are helpful to the classifier, hence greatly reducing the computation cost. In particular, the goal of the integration of diversity within SL is to require as little cost as possible to train a stable classifier and achieve a better classification result at the same time. Three state-of-the-art diversity criteria have been discussed and applied to three groups of synthetic and real remote sensing data sets. Theoretical analyses and experiments have demonstrated that an appropriate diversity criterion is beneficial to the SL algorithm at a limited increment of computation cost. Results show that the cluster-based diversity criterion significantly improves the performance of the SL algorithm, and surpasses the other state-of-the-art diversity approaches. It is also worth noting that the presented strategy does not need any additional parameters, except for the initial segmentation scales and the number of samples, and thus can be implemented in a much easier and automatic fashion. In future work, we will focus on the determination of the optimal segmentation scales as well as the number of samples.