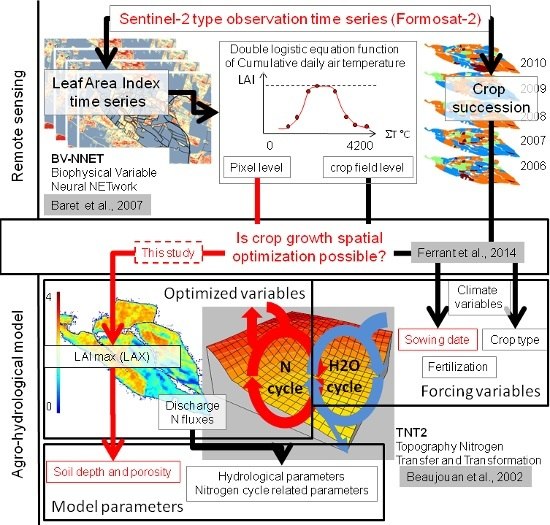
Extracting Soil Water Holding Capacity Parameters of a Distributed Agro-Hydrological Model from High Resolution Optical Satellite Observations Series
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site Description
2.1.1. Soil Type, Hydrological Characteristics and Spatial Heterogeneity
2.1.2. LAI Monitoring from Satellite
2.1.3. Maximal LAI (LAX) Estimated from F2 Series
2.2. TNT2 Model Description and Application in the Study Site
2.2.1. Spatial Water and Nitrogen Transfer Simulation
2.2.2. A-priori Soil Parameters
2.2.3. Model Application in the Study Site
2.3. SWHC Re-Estimation Based on LAX
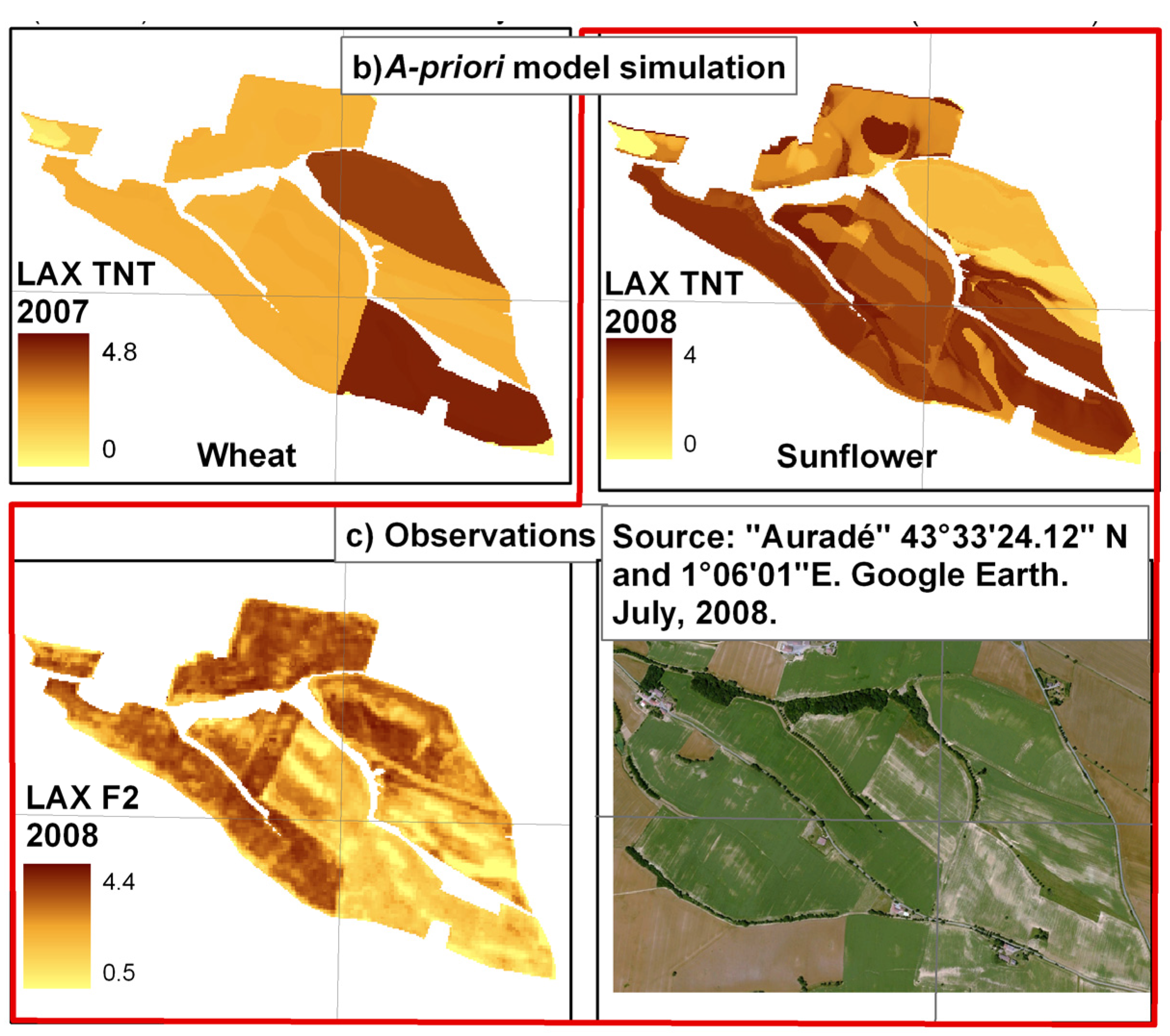
- Soil map does not represent the real heterogeneity. Soil units correspond to a mix of soil types, within which one soil type is dominant. Heterogeneity remains within soil units, especially soil depth.
- Soil parameters greatly impact the sunflower crop growth. Observed and simulated crop growth heterogeneity is highly influenced by soil parameters, especially for sunflower. Figure 2b shows that “a-priori” simulations from TNT2 lead to a lower heterogeneity of wheat LAX than sunflower. This heterogeneity is directly linked to the soil map delineation.
2.3.1. Generation of Synthetic LAX Based on SWHC
2.3.2. Spatial Sensitivity of LAX to Depth and Micmac
2.3.3. Selection Method for Numerical Best Solution of SWHC
3. Results
3.1. Crop Growth Sensitivity
3.1.1. Sensitivity of LAX and BiomaX to Soil Parameters and TSI
3.1.2. Spatial LAX Sensitivity
3.2. Inversion of SWHC with LAX
3.2.1. Best Numerical Solutions of SWHC for One Year
3.2.2. Multi-Year Best Numerical Solutions of SWHC
4. Discussion
4.1. Impacts of Spatial Patterns of Water and Nitrogen Uses
4.2. Limits and Improvements of the Model and Inversion Method
4.2.1. Realistic SWHC
4.2.2. Limitations of this Virtual Experiment
4.2.3. Spatial Interactions between Crop Growth and Hydrology
4.2.4. LAX and LAI Retrieval Uncertainty
5. Conclusions and Perspectives
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bongiovanni, R.; Lowenberg-Deboer, J. Precision Agriculture and Sustainability. Precis. Agric. 2004, 5, 359–387. [Google Scholar] [CrossRef]
- Robert, P.C. Precision Agriculture: A challenge for crop nutrition management. Plant Soil 2002, 247, 143–149. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Houlès, V.; Guérif, M.; Mary, B. Elaboration of a Nitrogen nutrition indicator for winter wheat based on Leaf Area Index and chlorophyll content for making nitrogen recommendations. Eur. J. Agron. 2007, 27, 1–11. [Google Scholar] [CrossRef]
- Launay, M.; Guerif, M. Assimilating remote sensing data into a crop model to improve predictive performance for spatial applications. Agric. Ecosyst. Environ. 2005, 111, 321–339. [Google Scholar] [CrossRef]
- Jégo, G.; Pattey, E.; Liu, J. Using Leaf Area Index, Retrieved from Optical Imagery, in the STICS Crop Model for Predicting Yield and Biomass of Field Crops. Field Crops Res. 2012, 131, 63–74. [Google Scholar] [CrossRef]
- Morel, J.; Bégué, A.; Todoroff, P.; Martiné, J.-F.; Lebourgeois, V.; Petit, M. Coupling a sugarcane crop model with the remotely sensed time series of fIPAR to optimise the yield estimation. Eur. J. Agron. 2014, 61, 60–68. [Google Scholar] [CrossRef]
- Varella, H.; Guérif, M.; Buis, S.; Beaudoin, N. Soil Properties estimation by inversion of a crop model and observations on crops improves the prediction of agro-environmental variables. Eur. J. Agron. 2010, 33, 139–147. [Google Scholar] [CrossRef]
- Hank, T.B.; Bach, H.; Mauser, W. Using a remote sensing-supported hydro-agroecological model for field-scale simulation of heterogeneous crop growth and yield: Application for wheat in central Europe. Remote Sens. 2015, 7, 3934–3965. [Google Scholar] [CrossRef]
- Ferrant, S.; Gascoin, S.; Veloso, A.; Salmon-Monviola, J.; Claverie, M.; Rivalland, V.; Dedieu, G.; Demarez, V.; Ceschia, E.; Probst, J.L.; et al. Agro-hydrology and multi temporal high resolution remote sensing: Toward an explicit spatial processes calibration. Hydrol. Earth Syst. Sci. 2014, 18, 5219–5237. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Batlivala, P.P.; Dobson, M.C. Microwave backscatter dependence on surface roughness, soil moisture, and soil texture: Part I-bare soil. IEEE Trans. Geosci. Electron. 1978, 16, 286–295. [Google Scholar] [CrossRef]
- Niang, M.A.; Nolin, M.C.; Jégo, G.; Perron, I. Digital Mapping of soil texture using RADARSAT-2 polarimetric synthetic aperture radar data. Soil Sci. Soc. Am. J. 2014, 78, 673–684. [Google Scholar] [CrossRef]
- Kruse, F.A. Use of airborne imaging spectrometer data to map minerals associated with hydrothermally altered rocks in the Northern Grapevine Mountains, Nevada, and California. Remote Sens. Environ. 1988, 24, 31–51. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Taylor, R.G.; Hill, J.; Demattê, J.A.M.; Whiting, M.L.; Chabrillat, S.; Sommer, S. Imaging spectrometry for soil applications. Adv. Agron. 2008, 97, 321–392. [Google Scholar]
- Zribi, M.; Hégarat-Mascle, S.; Ottlé, C.; Kammoun, B.; Guerin, C. Surface Soil moisture estimation from the synergistic use of the (multi-Incidence and Multi-Resolution) active microwave ERS wind scatterometer and SAR Data. Remote Sens. Environ. 2003, 86, 30–41. [Google Scholar] [CrossRef]
- Zribi, M.; Dechambre, M. A new empirical model to retrieve soil moisture and roughness from C-Band radar data. Remote Sens. Environ. 2003, 84, 42–52. [Google Scholar] [CrossRef]
- Sreelash, K.; Sekhar, M.; Ruiz, L.; Buis, S.; Bandyopadhyay, S. Improved modeling of groundwater recharge in agricultural watersheds using a combination of crop model and remote sensing. J. Indian Inst. Sci. 2013, 93, 189–207. [Google Scholar]
- Refsgaard, J.; Thorsen, M.; Jensen, J.; LKleeschulte, S.; Hansen, S. Large scale modelling of groundwater contamination from nitrate leaching. J. Hydrol. 1999, 211, 117–140. [Google Scholar] [CrossRef]
- Arnold, J.G.; Allen, P.M.; Bernhardt, G. A comprehensive surface-groundwater flow model. J. Hydrol. 1993, 142, 47–69. [Google Scholar] [CrossRef]
- Whitehead, P.; Wilson, E.; Butterfield, D. A semi-distributed integrated nitrogen model for multiple source assessment in catchment. Part 1. model structure and process equations. Sci. Total Environ. 1998, 210/211, 547–558. [Google Scholar] [CrossRef]
- Beaujouan, V.; Durand, P.; Ruiz, L.; Aurousseau, P.; Cotteret, G. A hydrological model dedicated to topography-based simulation of nitrogen transfer and transformation: Rationale and application to the geomorphology-denitrification relationship. Hydrol. Process. 2002, 16, 493–507. [Google Scholar] [CrossRef]
- Ledoux, E.; Gomez, E.; Monget, J.; Viavattene, C.; Viennot, P.; Ducharne, A.; Benoit, M.; Mignolet, C.; Schott, C.; Mary, B. Agriculture and groundwater nitrate contamination in the Seine Basin. The STICS-MODCOU modelling chain. Sci. Total Environ. 2007, 375, 33–47. [Google Scholar] [CrossRef] [PubMed]
- Viaud, V.; Durand, P.; Merot, P.; Sauboua, E.; Saadi, Z. Modeling the impact of the spatial structure of a hedge network on the hydrology of a small catchment in a temperate climat. Agric. Water Manag. 2005, 74, 135–163. [Google Scholar] [CrossRef]
- Ferrant, S.; Caballero, Y.; Perrin, J.; Gascoin, S.; Dewandel, B.; Aulong, S.; Dazin, F.; Ahmed, S.; Maréchal, J.C. Projected impacts of climate change on farmers’ extraction of groundwater from crystalline aquifers in South India. Sci. Rep. 2014, 4. [Google Scholar] [CrossRef] [PubMed]
- Perrin, J.; Ferrant, S.; Massuel, S.; Dewandel, B.; Marechal, J.C.; Aulong, S.; Ahmed, S. Assessing water availability in a semi-arid watershed of Southern India using a semi-distributed model. J. Hydrol. 2012, 460–461, 143–155. [Google Scholar] [CrossRef]
- Ferrant, S.; Oehler, F.; Durand, P.; Ruiz, L.; Salmon-Monviola, J.; Justes, E.; Dugast, P.; Probst, A.; Probst, J.L.; Sanchez-Perez, J.M. Understanding nitrogen transfer dynamics in a small agricultural catchment: Comparison of a distributed (TNT2) and a semi distributed (SWAT) modelling approaches. J. Hydrol. 2011, 406, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Cheema, M.J.M.; Immerzeel, W.W.; Bastiaanssen, W. Spatial Quantification of groundwater abstraction in the Irrigated Indus Basin. Groundwater 2014, 52, 25–36. [Google Scholar] [CrossRef] [PubMed]
- Immerzeel, W.W.; Gaur, A.; Zwart, S.J. Integrating Remote sensing and a process-based hydrological model to evaluate water use and productivity in South Indian Catchment. Agric. Water Manag. 2008, 95, 11–24. [Google Scholar] [CrossRef]
- Martin, E.; Gascoin, S.; Grusson, Y.; Murgue, C.; Bardeau, M.; Anctil, F.; Ferrant, S.; Lardy, R.; LeMoigne, P.; Leenhardt, D.; et al. On the use of hydrological models and satellite data to study the water budget of river basins affected by human activities: Examples from the Garonne Basin of France. Surv. Geophys. 2016, in press. [Google Scholar]
- Calvet, J.-C.; Noilhan, J.; Roujean, J.-L.; Bessemoulin, P.; Cabelguenne, M.; Olioso, A.; Wigneron, J.-P. An interactive vegetation SVAT model tested against data from six contrasting sites. Agric. For. Meteorol. 1998, 92, 73–95. [Google Scholar] [CrossRef]
- Canal, N.; Calvet, J.-C.; Decharme, B.; Carrer, D.; Lafont, S.; Pigeon, G. Evaluation of root water uptake in the ISBA-A-Gs land surface model using agricultural yield statistics over France. Hydrol Earth Syst Sci 2014, 18, 4979–4999. [Google Scholar] [CrossRef]
- Brisson, N.; Mary, B.; Ripoche, D.; Jeuffroy, H.; Ruget, F.; Nicollaud, B.; Gate, P.; Devienne-Barret, F.; Antonioletti, R.; Durr, C.; et al. Stics: A generic model for the simulation of crops and their water and nitrogen balances. I. Theory and parameterization applied to wheat and corn. Agron. Paris 1998, 18, 311–346. [Google Scholar] [CrossRef]
- Moreau, P.; Viaud, V.; Parnaudeau, V.; Salmon-Monviola, J.; Durand, P. An approach for global sensitivity analysis of a complex environmental model to spatial inputs and parameters: A case study of an agro-hydrological model. Environ. Model. Softw. 2013, 47, 74–87. [Google Scholar] [CrossRef]
- BVEA. Availabel oneline: http://www.ecolab.omp.eu/bvea/ (accessed on 14 February 2016).
- Béziat, P.; Ceschia, E.; Dedieu, G. Carbon balance of three crop succession over two cropland sites in South West of France. Agric. For. Meteorol. 2009, 149, 1628–1645. [Google Scholar] [CrossRef] [Green Version]
- Tallec, T.; Béziat, P.; Jarosz, N.; Rivalland, V.; Ceschia, E. Crop’s water use efficiencies in temperate climate: Comparison of stand, ecosystem and agronomical approaches. Agric. For. Meteorol. 2013, 168, 69–81. [Google Scholar] [CrossRef]
- Ferrant, S.; Laplanche, C.; Durbe, G.; Probst, A.; Dugast, P.; Durand, P.; Sanchez-Perez, J.M.; Probst, J.L. Continuous measurement of nitrate concentration in a highly event-responsive agricultural catchment in South-West of France: Is the gain of information useful? Hydrol. Proc. 2012, 12, 1751–1763. [Google Scholar] [CrossRef] [Green Version]
- Roussiez, V.; Probst, A.; Probst, J.-L. Significance of floods in metal dynamics and export in a small agricultural catchment. J. Hydrol. 2013, 499, 71–81. [Google Scholar] [CrossRef]
- Taghavi, L.; Probst, J.-L.; Merlina, G.; Marchand, A.-L.; Durbe, G.; Probst, A. Flood event impact on pesticide transfer in a small agricultural catchment (Montoussé at Auradé, South West France). Int. J. Environ. Anal. Chem. 2010, 90, 390–405. [Google Scholar] [CrossRef]
- Macary, F.; Almeida-Dias, J.; Uny, D.; Probst, A. Assessment of the Effects of best environmental practices on reducing pesticide contamination in surface water, using multi-criteria modelling combined with a GIS. Int. J. Multicriteria Decis. Mak. 2013, 3, 178–211. [Google Scholar] [CrossRef]
- Perrin, A.-S. Rôle Des Fertilisants Azotés Dans L’érosion Chimique Des Bassins Versants Carbonatées: Implication Dans La Consommation de CO2 et La Composition Chimique Des Eaux de Surface. Ph.D. Thesis, Université de Toulouse, Toulouse, France, March 2008. [Google Scholar]
- Chern, J.S.; Wu, A.M.; Lin, S.F. Lesson learned from Formosat-2 mission operations. Acta Astronaut. 2006, 59, 344–350. [Google Scholar] [CrossRef]
- Hagolle, O.; Dedieu, G.; Mougenot, B.; Debaeker, V.; Duchemin, B.; Meygret, A. Correction of aerosol effects on multi-temporal images acquired with constant viewing angles: Application to formoat-2 images. Remote Sens. Environ. 2008, 112, 1689–1701. [Google Scholar] [CrossRef] [Green Version]
- Hagolle, O.; Huc, M.; Pascual, D.V.; Dedieu, G. A multi-temporal method for cloud detection, applied to FORMOSAT-2, VENuS, LANDSAT and SENTINEL-2 Images. Remote Sens. Environ. 2010, 114, 1747–1755. [Google Scholar] [CrossRef] [Green Version]
- Claverie, M.; Demarez, V.; Duchemin, B.; Hagolle, O.; Ducrot, D.; Dejoux, J.F.; Huc, M.; Keravec, P.; Béziat, P.; Fieuzal, R.; et al. Maize and sunflower biomass estimation in Southwest France using high spatial and temporal resolution remote sensing data. Remote Sens. Environ. 2012, 124, 844–857. [Google Scholar] [CrossRef] [Green Version]
- Baret, F.; Hagolle, O.; Geiger, B.; Bicheron, P.; Miras, B.; Huc, M.; Berthelot, B.; Nino, F.; Weiss, M.; Samain, O.; et al. LAI, fAPAR and fCover CYCLOPES Global products derived from VEGETATION. Part 1: principles of the algorithm. Remote Sens. Environ. 2007, 3, 275–286. [Google Scholar] [CrossRef] [Green Version]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT + SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, 56–66. [Google Scholar] [CrossRef]
- Claverie, M.; Vermote, E.F.; Weiss, M.; Baret, F.; Hagolle, O.; Demarez, V. Validation of coarse spatial resolution LAI and FAPAR time series over cropland in Southwest France. Remote Sens. Environ. 2013, 139, 216–230. [Google Scholar] [CrossRef]
- Beven, K. Distributed modelling in hydrology: Applications of topmodel concept. Adv. Hydrol. Process. 1997, 350, 59–79. [Google Scholar]
- Burns, I. A model for predicting the redistribution of salts applied to fallow soils after excess of rainfall or evaporation. J. Soil Sci. 1974, 25, 165–178. [Google Scholar] [CrossRef]
- Sobol, I.M. Sensitivity estimates for non linear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Trnka, M.; Eitzinger, J.; Kapler, P.; Dubrovský, M.; Semerádová, D.; Žalud, Z.; Formayer, H. Effect of estimated daily global solar radiation data on the results of crop growth models. Sensors 2007, 7, 2330–2362. [Google Scholar] [CrossRef]
- Gmur, S.; Vogt, D.; Zabowski, D.; Moskal, L.M. Hyperspectral analysis of soil nitrogen, carbon, carbonate, and organic matter using regression trees. Sensors 2012, 12, 10639–10658. [Google Scholar] [CrossRef]
- Duchemin, B.; Maisongrande, P.; Boulet, G.; Benhadj, I. A Simple algorithm for yield estimates: evaluation for semi-arid irrigated winter wheat monitored with green Leaf Area Index. Environ. Model. Softw. 2008, 23, 876–892. [Google Scholar] [CrossRef]
- Claverie, M. Estimation spatialisee de la biomasse et des besoins en eau des cultures a l’aide de donnees satellitales a hautes resolutions spatiale et temporelle: Application Aux agrosystemes du sud-ouest de la France. Ph.D. Thesis, Université de Toulouse, Toulouse, France, 2012. [Google Scholar]
- Grabs, T.; Seibert, J.; Bishop, K.; Laudon, H. Modeling spatial patterns of saturated areas: A comparison of the topographic wetness index and a dynamic distributed model. J. Hydrol. 2009, 373, 15–23. [Google Scholar] [CrossRef] [Green Version]
- Saadi, S.; Simonneaux, V.; Boulet, G.; Raimbault, B.; Mougenot, B.; Fanise, P.; Ayari, H.; Lili-Chabaane, Z. Monitoring irrigation consumption using high resolution NDVI image time series: Calibration and validation in the Kairouan Plain (Tunisia). Remote Sens. 2015, 7, 13005–13028. [Google Scholar] [CrossRef]
- Baghdadi, N.; Aubert, M.; Zribi, M. Use of TerraSAR-X data to retrieve soil moisture over bare soil agricultural fields. IEEE Geosci. Remote Sens. Lett. 2012, 9, 512–516. [Google Scholar] [CrossRef] [Green Version]
- Demarez, V.; Duthoit, S.; Baret, F.; Weiss, M.; Dedieu, G. Estimation of leaf area and clumping indexes of crops with hemispherical photographs. Agric. For. Meteorol. 2008, 148, 644–655. [Google Scholar] [CrossRef] [Green Version]







| Soil Name | Surface Proportion (%) | Layers (cm) | Sand (%) | Silt (%) | Clay (%) | Organic Matter (%) | C/N | Apparent Density |
|---|---|---|---|---|---|---|---|---|
| Cambisol calcaric locally endostagnic (*) | 31.0 | 0–25 | 25.9 | 36.9 | 37.2 | 2 | 8.3 | 1.67 |
| 25–50 | 29 | 36.2 | 34.8 | 1.5 | 7.4 | 1.69 | ||
| 50–100 | 31.2 | 34.8 | 34 | 0.9 | 6.8 | 1.72 | ||
| >100 | 17 | 55.6 | 27.4 | 0.4 | 6.3 | - | ||
| Fluvic cambisol calcaric | 19.0 | 0–20 | 21.7 | 41.4 | 36.9 | 2.1 | 8.2 | 1.52 |
| 20–45 | 15.4 | 45.5 | 39.1 | 1.2 | 7 | 1.64 | ||
| 45–70 | 8.8 | 52.1 | 39.1 | 0.9 | 6.5 | 1.73 | ||
| 70–140 | 11.9 | 48.6 | 39.5 | 0.9 | 6.2 | 1.6 | ||
| 140–180 | 22 | 37.5 | 40.5 | 0.7 | 5.8 | 1.53 | ||
| Cambisol calcaric colluvic soil pit 1 | 10.0 | 0–25 | 23.3 | 37.9 | 38.8 | 1.7 | 7.9 | 1.58 |
| 25–65 | 19.7 | 36.5 | 43.8 | 0.4 | 4.5 | 1.7 | ||
| 65–120 | 19.4 | 36 | 44.6 | 0.2 | 3.1 | 1.76 | ||
| 120–130 | 39.1 | 29.2 | 31.7 | 0.1 | 2.6 | - | ||
| 130–160 | 52.3 | 28.9 | 18.8 | 0.1 | 1.7 | - | ||
| 160–200 | 75.9 | 16 | 8.1 | 0.2 | 5.8 | - | ||
| Cambisol calcaric colluvic soil pit 2 | Same soil than previous | 0–25 | - | - | - | - | - | 1.67 |
| 25–60 | 18.3 | 38.6 | 43.1 | 1.5 | 7.4 | 1.69 | ||
| 60–150 | 13.6 | 39.9 | 46.5 | 0.4 | 4 | 1.72 | ||
| Rendzic leptosol (molassic material) | 4.5 | 0–25 | 19 | 45.4 | 35.6 | 1.5 | 8.9 | 1.74 |
| 25–40 | 37.9 | 42.1 | 20 | 0.3 | 5.7 | - | ||
| 40–70 | 36.5 | 46.3 | 17.2 | 0.4 | 8.4 | - | ||
| >70 | 37.4 | 50.5 | 12.1 | 0.2 | 3.7 | - | ||
| Cambisol hypereutric (farmed) | 1.6 | 0–25 | 18 | 37.2 | 44.8 | 2.3 | 9 | 1.33 |
| 25–80 | 20.6 | 37.8 | 41.6 | 1.2 | 7.9 | 1.7 | ||
| 80–120 | 15.2 | 36 | 48.8 | 0.6 | 5.1 | - | ||
| 120–150 | 16.9 | 46.5 | 36.6 | 0.5 | 5.9 | - | ||
| Cambisol hypereutric (forested) | Same soil than previous | 0–15 | 20.6 | 36.7 | 42.7 | 5.3 | 12.2 | - |
| 15–50 | 18.7 | 36.2 | 45.1 | 1.5 | 8.4 | - | ||
| 50–100 | 13.7 | 35.3 | 51 | 0.7 | 5.6 | - | ||
| 100–150 | 11.4 | 35.7 | 52.9 | 0.3 | 3.2 | - | ||
| Rendzic leptosol | 0.9 | 0–20 | 70.4 | 24.7 | 14.9 | 2.1 | 10.1 | - |
| (calcaric material) | >20 | 63 | 23.6 | 13.4 | 1 | 8.9 | - | |
| Stagnic luvisol | 0.7 | 0–25 | 30.1 | 47.8 | 22.1 | 1.3 | 8.4 | - |
| 25–80 | 23.4 | 49.8 | 26.8 | 0.9 | 7.8 | - | ||
| 80–120 | 13 | 40.5 | 46.5 | 0.5 | 4.9 | - | ||
| Cambisol dystric episkeletic | 0.2 | 0–30 | 20.2 | 49.6 | 30.2 | 1.5 | 8.9 | - |
| 30–60 | 12.7 | 41.7 | 45.6 | 0.5 | 5.8 | - | ||
| 60–100 | 11.6 | 35.2 | 53.2 | 0.5 | 5.4 | - |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferrant, S.; Bustillo, V.; Burel, E.; Salmon-Monviola, J.; Claverie, M.; Jarosz, N.; Yin, T.; Rivalland, V.; Dedieu, G.; Demarez, V.; et al. Extracting Soil Water Holding Capacity Parameters of a Distributed Agro-Hydrological Model from High Resolution Optical Satellite Observations Series. Remote Sens. 2016, 8, 154. https://doi.org/10.3390/rs8020154
Ferrant S, Bustillo V, Burel E, Salmon-Monviola J, Claverie M, Jarosz N, Yin T, Rivalland V, Dedieu G, Demarez V, et al. Extracting Soil Water Holding Capacity Parameters of a Distributed Agro-Hydrological Model from High Resolution Optical Satellite Observations Series. Remote Sensing. 2016; 8(2):154. https://doi.org/10.3390/rs8020154
Chicago/Turabian StyleFerrant, Sylvain, Vincent Bustillo, Enguerrand Burel, Jordy Salmon-Monviola, Martin Claverie, Nathalie Jarosz, Tiangang Yin, Vincent Rivalland, Gérard Dedieu, Valerie Demarez, and et al. 2016. "Extracting Soil Water Holding Capacity Parameters of a Distributed Agro-Hydrological Model from High Resolution Optical Satellite Observations Series" Remote Sensing 8, no. 2: 154. https://doi.org/10.3390/rs8020154
APA StyleFerrant, S., Bustillo, V., Burel, E., Salmon-Monviola, J., Claverie, M., Jarosz, N., Yin, T., Rivalland, V., Dedieu, G., Demarez, V., Ceschia, E., Probst, A., Al-Bitar, A., Kerr, Y., Probst, J. -L., Durand, P., & Gascoin, S. (2016). Extracting Soil Water Holding Capacity Parameters of a Distributed Agro-Hydrological Model from High Resolution Optical Satellite Observations Series. Remote Sensing, 8(2), 154. https://doi.org/10.3390/rs8020154