The Impact of Forest Density on Forest Height Inversion Modeling from Polarimetric InSAR Data
Abstract
:1. Introduction
2. The Random-Volume-Over-Ground (RVoG) Model and Three-Stage Height Inversion Method
3. The Simulated Datasets and Real P-Band E-SAR Data
3.1. The Simulated Datasets
3.2. The Real P-Band ESAR Data
4. Experimental Results and Analysis
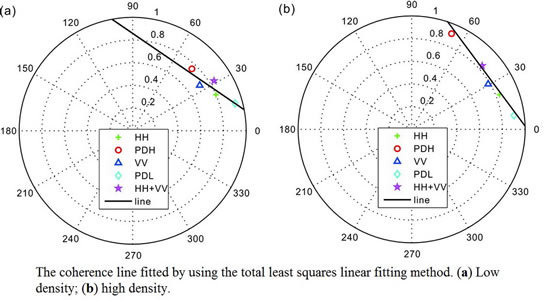
4.1. Results and Analysis of the Simulated Datasets
4.2. Results of P-Band E-SAR Datasets
4.3. The Ground Phase for Different Density
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fu, H.; Wang, C.; Zhu, J.; Xie, Q.; Zhao, R. Inversion of vegetation height from PolInSAR using complex least squares adjustment method. Sci. China Earth Sci. 2015, 58, 1018–1031. [Google Scholar] [CrossRef]
- Wu, Y.; Hong, W.; Wang, Y. Research status and edification for polarimetric SAR interferometry. J. Electron. Inf. Technol. 2007, 9, 1258–1263. [Google Scholar]
- Askne, J.; Dammert, P.; Ulander, L.; Smith, G. C-band repeat-pass interferometric SAR observations of the forest. IEEE Trans. Geosci. Remote Sens. 1997, 35, 25–35. [Google Scholar] [CrossRef]
- Askne, J.; Santoro, M.; Smith, G.; Fransson, J.E. Multitemporal repeat-pass SAR interferometry of boreal forests. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1540–1550. [Google Scholar] [CrossRef]
- Askne, J.; Santoro, M. Multitemporal repeat pass SAR interferometry of boreal forests. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1219–1228. [Google Scholar] [CrossRef]
- Treuhaft, R.N.; Madsen, S.N.; Moghaddam, M.; Zyl, J.J. Vegetation characteristics and underlying topography from interferometric radar. Radio Sci. 1996, 31, 1449–1485. [Google Scholar] [CrossRef]
- Treuhaft, R.N.; Cloude, S.R. The structure of oriented vegetation from polarimetric interferometry. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2620–2624. [Google Scholar] [CrossRef]
- Treuhaft, R.N.; Siqueira, P.R. Vertical structure of vegetated land surfaces from interferometric and polarimetric radar. Radio Sci. 2000, 35, 141–177. [Google Scholar] [CrossRef]
- Papathanassiou, K.P.; Cloude, S.R. Single-baseline polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Senci. 2001, 39, 2352–2362. [Google Scholar] [CrossRef]
- Mette, T.; Kugler, F.; Papathanassiou, K.; Hajnsek, I. Forest and the random volume over ground-nature and effect of 3 possible error types. In Proceedings of the EUSAR 2006—6th European Conference on Synthetic Aperture Radar, Dresden, Germany, 16–18 May 2006.
- Lavalle, M.; Solimini, D.; Pottier, E.; Desnos, Y.-L. The Dependence of the PolinSAR degree of coherence on forest parameters. In Proceedings of the PolInSAR Workshop 2009, Frascati, Italy, 26–30 January 2009.
- Zhou, Y.; Hong, W.; Cao, F. Investigation on volume scattering for vegetation parameter estimation of polarimetric SAR interferometry. PIERS Online 2009, 5, 1–5. [Google Scholar] [CrossRef]
- Ballester-Berman, J.D.; Vicente-Guijalba, F.; Lopez-Sanchez, J.M. A simple RVoG test for PolInSAR data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1028–1040. [Google Scholar] [CrossRef]
- Garestier, F.; Dubois-Fernandez, P.C.; Papathanassiou, K.P. Pine forest height inversion using single-pass X-band PolInSAR data. IEEE Trans. Geosci. Remote Sens. 2008, 46, 59–68. [Google Scholar] [CrossRef] [Green Version]
- Lopez-Martinez, C.; Alonso-Gonzalez, A. Assessment and estimation of the RVoG model in polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3091–3106. [Google Scholar] [CrossRef]
- Neumann, M.; Saatchi, S.S.; Ulander, L.M.; Fransson, J.E. Assessing performance of L-and P-band polarimetric interferometric SAR data in estimating boreal forest above-ground biomass. IEEE Trans. Geosci. Remote Sens. 2012, 50, 714–726. [Google Scholar] [CrossRef]
- Lei, Y.; Siqueira, P. Estimation of forest height using spaceborne repeat-pass L-Band InSAR correlation magnitude over the US State of maine. Remote Sens. 2014, 6, 10252–10285. [Google Scholar] [CrossRef]
- Lavalle, M.; Simard, M.; Pottier, E.; Solimini, D. PolInSAR forestry applications improved by modeling height-dependent temporal decorrelation. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 4772–4776.
- Lavalle, M.; Simard, M.; Solimini, D.; Pottier, E. Height-dependent temporal decorrelation for POLINSAR and TOMOSAR forestry applications. In Proceedings of the 8th European Conference on Synthetic Aperture Radar, Aachen, Germany, 7–10 June 2010; pp. 1–4.
- Lavalle, M.; Simard, M.; Hensley, S. A temporal decorrelation model for polarimetric radar interferometers. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2880–2889. [Google Scholar] [CrossRef]
- Ahmed, R.; Siqueira, P.; Hensley, S.; Chapman, B.; Bergen, K. A survey of temporal decorrelation from spaceborne L-Band repeat-pass InSAR. Remote Sens. Environ. 2011, 115, 2887–2896. [Google Scholar] [CrossRef]
- Simard, M.; Hensley, S.; Lavalle, M.; Dubayah, R.; Pinto, N.; Hofton, M. An empirical assessment of temporal decorrelation using the uninhabited aerial vehicle synthetic aperture radar over forested landscapes. Remote Sens. 2012, 4, 975–986. [Google Scholar] [CrossRef]
- Neumann, M. Remote Sensing of Vegetation Using Multi-Baseline Polarimetric SAR Interferometry: Theoretical Modeling and Physical Parameter Retrieval. Ph.D. Thesis, University de Rennes 1, Rennes France, 2009. [Google Scholar]
- Lu, H.; Suo, Z.; Guo, R.; Bao, Z. S-RVoG model for forest parameters inversion over underlying topography. Electron. Lett. 2013, 49, 618–620. [Google Scholar] [CrossRef]
- Xie, Q.; Wang, C.; Zhu, J.; Fu, H. Forest height inversion by combining S-RVOG Model with terrain factor and PD coherence optimization. Acta Geod. Cartogr. Sin. 2015, 44, 686–693. [Google Scholar]
- Lavalle, M.; Solimini, D.; Pottier, E.; Desnos, Y.L. PolinSAR for forest biomass retrieval: PALSAR observations and model analysis. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, IGARSS 2008, Boston, MA, USA, 7–11 July 2008; Volume 3, pp. 302–305.
- Cloude, S.R.; Papathanassiou, K.P. Three-stage inversion process for Polarimetric SAR Interferometry. IEEE Proc. Radar Sonar Navig. 2003, 150, 125–134. [Google Scholar] [CrossRef]
- Cloude, S.R.; Papathanassiou, K.P. Polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1551–1565. [Google Scholar] [CrossRef]
- Tabb, M.; Orrey, J.; Flynn, T.; Carande, R. Phase diversity: A decomposition for vegetation parameter estimation using polarimetric SAR interferometry. In Proceedings of the 4th European Conference on Synthetic Aperture Radar, Cologne, Germany, 4–6 June 2002; pp. 721–724.
- Pottier, E.; Ferro-Famil, L.; Allain, S.; Cloude, S.; Hajnsek, I.; Papathanassiou, K.P.; Moreira, A.; Williams, M.; Minchella, A.; Lavalle, M.; et al. Overview of the PolSARpro V4. 0 software. The open source toolbox for polarimetric and interferometric polarimetric SAR data processing. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, IGARSS 2009, Cape Town, South Africa, 12–17 July 2009; Volume 4, pp. 936–939.
- Ulander, L.M.; Gustavsson, A.; Dubois-Fernandez, P.; Dupuis, X.; Fransson, J.E.; Holmgren, J.; Wallerman, J.; Eriksson, L.; Sandberg, G.; Soja, M. BIOSAR 2010-A SAR campaign in support to the BIOMASS mission. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Vancouver, BC, Canada, 24–29 July 2011; pp. 1528–1531.
- Ulander, L.M.; Sandberg, G.; Soja, M.J. Biomass retrieval algorithm based on P-band biosar experiments of boreal forest. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Vancouver, BC, Canada, 24–29 July 2011; pp. 4245–4248.
- Tebaldini, S.; Rocca, F. Multibaseline polarimetric SAR tomography of a boreal forest at P-and L-bands. IEEE Trans. Geosci. Remote Sens. 2012, 50, 232–246. [Google Scholar] [CrossRef]
- Santi, E.; Pettinato, S.; Paloscia, S.; Castracane, P.; Di Giammatteo, U. CATARSI—Cap and trade assessment by remote sensing investigation: An algorithm for crop and forest biomass estimate. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, QC, Canada, 13–18 July 2014; pp. 733–736.
- Lee, S.K.; Kugler, F.; Papathanassiou, K.; Hajnsek, I. Polarimetric SAR interferometry for forest application at P-band: Potentials and challenges. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, IGARSS 2009, Cape Town, South Africa, 12–17 July 2009; Volume 4, pp. 13–16.
- Neumann, M.; Saatchi, S.S.; Ulander, L.M.; Fransson, J.E. Parametric and non-parametric forest biomass estimation from PolInSAR data. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Vancouver, BC, Canada, 24–29 July 2011; pp. 420–423.
- Freeman, A.; Durden, S. A three-component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef]
- Park, S.E.; Moon, W.M.; Pottier, E. Assessment of scattering mechanism of polarimetric SAR signal from mountainous forest areas. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4711–4719. [Google Scholar] [CrossRef]









| Platform Altitude | 3000 m |
|---|---|
| Horizontal Baseline | 10 m |
| Vertical Baseline | 1 m |
| Incidence Angle | 45° |
| Center Frequency | 1.5 GHz |
| Tree Species | Pine |
| Reference Height | 10 m, 14 m, and 18 m |
| Forest Stand Number | Forest Stand Density (stems/Ha) | Average Height from LiDAR(m) | Average Height from the Three-Stage Method (m) | RMSE (m) |
|---|---|---|---|---|
| 3689 | 633 | 20.71 | 16.39 | 4.56 |
| 4115 | 925 | 19.49 | 17.69 | 3.87 |
| 36169 | 1498 | 17.17 | 15.17 | 3.76 |
| 18147 | 1827 | 17.63 | 15.77 | 3.13 |
| Forest Stand Number | 3689 | 4115 | 36169 | 18147 |
|---|---|---|---|---|
| Forest Stand Density (stems/Ha) | 633 | 925 | 1498 | 1827 |
| RMSE (rad) | 0.26 | 0.22 | 0.15 | 0.14 |
| Forest Stand Number | 3689 | 4115 | 36169 | 18147 |
|---|---|---|---|---|
| Forest stand density (stems/Ha) | 633 | 925 | 1498 | 1827 |
| STD | 0.075 | 0.095 | 0.126 | 0.143 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Wang, L.; Fu, H.; Xie, Q.; Zhu, J. The Impact of Forest Density on Forest Height Inversion Modeling from Polarimetric InSAR Data. Remote Sens. 2016, 8, 291. https://doi.org/10.3390/rs8040291
Wang C, Wang L, Fu H, Xie Q, Zhu J. The Impact of Forest Density on Forest Height Inversion Modeling from Polarimetric InSAR Data. Remote Sensing. 2016; 8(4):291. https://doi.org/10.3390/rs8040291
Chicago/Turabian StyleWang, Changcheng, Lei Wang, Haiqiang Fu, Qinghua Xie, and Jianjun Zhu. 2016. "The Impact of Forest Density on Forest Height Inversion Modeling from Polarimetric InSAR Data" Remote Sensing 8, no. 4: 291. https://doi.org/10.3390/rs8040291
APA StyleWang, C., Wang, L., Fu, H., Xie, Q., & Zhu, J. (2016). The Impact of Forest Density on Forest Height Inversion Modeling from Polarimetric InSAR Data. Remote Sensing, 8(4), 291. https://doi.org/10.3390/rs8040291