Next Article in Journal
Simulation of Forest Carbon Fluxes Using Model Incorporation and Data Assimilation
Previous Article in Journal
PROBA-V Mission Exploitation Platform
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 8
Issue 7
10.3390/rs8070565
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Mapping Global Forest Aboveground Biomass with Spaceborne LiDAR, Optical Imagery, and Forest Inventory Data

by
Tianyu Hu
1,†,
Yanjun Su
1,2,†,
Baolin Xue
1,
Jin Liu
1,
Xiaoqian Zhao
1,
Jingyun Fang
1,3 and
Qinghua Guo
1,2,*
1
State Key Laboratory of Vegetation and Environmental Change, Institute of Botany, Chinese Academy of Sciences, Beijing 100093, China
2
Sierra Nevada Research Institute, School of Engineering, University of California at Merced, Merced, CA 95343, USA
3
Department of Ecology, College of Urban and Environmental Sciences, and Key Laboratory for Earth Surface Processes of the Ministry of Education, Peking University, Beijing 100871, China
*
Author to whom correspondence should be addressed.
†
These authors contributed equally to this work.
Remote Sens. 2016, 8(7), 565; https://doi.org/10.3390/rs8070565
Submission received: 28 February 2016 / Revised: 25 June 2016 / Accepted: 30 June 2016 / Published: 4 July 2016
Browse Figures
Versions Notes

Abstract

:
As a large carbon pool, global forest ecosystems are a critical component of the global carbon cycle. Accurate estimations of global forest aboveground biomass (AGB) can improve the understanding of global carbon dynamics and help to quantify anthropogenic carbon emissions. Light detection and ranging (LiDAR) techniques have been proven that can accurately capture both horizontal and vertical forest structures and increase the accuracy of forest AGB estimation. In this study, we mapped the global forest AGB density at a 1-km resolution through the integration of ground inventory data, optical imagery, Geoscience Laser Altimeter System/Ice, Cloud, and Land Elevation Satellite data, climate surfaces, and topographic data. Over 4000 ground inventory records were collected from published literatures to train the forest AGB estimation model and validate the resulting global forest AGB product. Our wall-to-wall global forest AGB map showed that the global forest AGB density was 210.09 Mg/ha on average, with a standard deviation of 109.31 Mg/ha. At the continental level, Africa (333.34 ± 63.80 Mg/ha) and South America (301.68 ± 67.43 Mg/ha) had higher AGB density. The AGB density in Asia, North America and Europe were 172.28 ± 94.75, 166.48 ± 84.97, and 132.97 ± 50.70 Mg/ha, respectively. The wall-to-wall forest AGB map was evaluated at plot level using independent plot measurements. The adjusted coefficient of determination (R2) and root-mean-square error (RMSE) between our predicted results and the validation plots were 0.56 and 87.53 Mg/ha, respectively. At the ecological zone level, the R2 and RMSE between our map and Intergovernmental Panel on Climate Change suggested values were 0.56 and 101.21 Mg/ha, respectively. Moreover, a comprehensive comparison was also conducted between our forest AGB map and other published regional AGB products. Overall, our forest AGB map showed good agreements with these regional AGB products, but some of the regional AGB products tended to underestimate forest AGB density.

Graphical Abstract

1. Introduction

Global forest ecosystems, which cover 30% of the land surface, play an important role in the global carbon cycle since they sequester atmospheric carbon dioxide and are able to mitigate global warming [1,2]. Aboveground biomass (AGB) is the total amount of biological material (usually based on a dry weight) presented above the ground in a specified area. Since approximately 50% of plant biomass is composed of carbon, accurate estimation of the total AGB in forest ecosystems is critical for carbon cycle studies from local to global scales [3]. For example, the amount and distribution of regional to global biomass can provide either initial conditions or validations for ecosystem and biogeochemical models [4,5,6,7], which simulate the exchange of carbon and energy between the atmosphere and biosphere. They can also provide the baseline of forest carbon stocks for calculating carbon fluxes from deforestation, land cover change, and other disturbances [8,9]. Moreover, biomass and its change also act as indicators of other ecosystem services, such as biodiversity [10]. Consequently, accurate estimations of the regional to global distribution of forest AGB are of great benefit to improve our understanding of carbon dynamics and quantify anthropogenic emissions caused by deforestation and forest degradation against the background of global climate change [11,12,13].
Generally, forest inventories are recognized as the most accurate method for providing information on biomass at local or regional scales [14,15]. However, these approaches are usually time-consuming and labor-intensive when applied to large areas, and also cannot provide spatially continuous AGB measurements [16]. Compared with traditional forest inventory methods, the availability of remote sensing techniques has greatly improved the efficiency and lowered the cost of forest AGB mapping, especially in remote areas [17,18]. Remote sensing techniques cannot directly acquire forest AGB measurements. Instead, they are used with regression models, which are built by linking ground measurements with remotely sensed data.
Currently, passive optical remote sensing, radar, and light detection and ranging (LiDAR) techniques are the three commonly used remotely sensed data sources for mapping forest AGB. Among these three techniques, passive optical remote sensing (e.g., Landsat Thematic Mapper data and MODIS (Moderate Resolution Imaging Spectroradiometer) data) and radar (e.g., phased array L-band Synthetic Aperture Radar (SAR)) are the more frequently used data sources because of their availability at regional to global scales [19,20,21]. However, many studies have demonstrated that approaches using optical remotely sensed data are limited by the saturation effect of optical sensors, and the saturation points can range from 15 to 150 Mg/ha depending on different sensors [22,23,24,25,26,27,28,29,30]. The saturation points for active SAR are higher than for optical sensors (ranging from 30 to over 300 Mg/ha based on the use of different frequencies and polarization methods), because SAR is more sensitive to forest spatial structures and standing biomass [31,32,33,34,35].
LiDAR, as an alternative active remote sensing technique, uses a focused short-wavelength laser pulse, which can penetrate the forest canopy more effectively [36]. With its ability to detect the vertical structures in forests, LiDAR has proved to be an efficient tool in the study of forest AGB estimation in a variety of forest environments [37,38,39,40,41]. Currently, the saturation phenomenon is rarely observed in the LiDAR approach, even in forests with high AGB levels; and the accuracy of forest AGB mapping can be significantly improved by using LiDAR, compared with optical passive and radar approaches [39,42,43]. However, LiDAR currently has disadvantages in temporal and spatial coverages, which has limited its application in global forest AGB estimation. Neither of the two major LiDAR platforms, airborne LiDAR and spaceborne LiDAR, can provide globally continuous LiDAR measurements. So far, airborne LiDAR data are only available in certain small areas because of the relatively high cost of airborne LiDAR flight missions [44,45]. The only available spaceborne LiDAR system, Geoscience Laser Altimeter System (GLAS) onboard the Ice, Cloud, and Land Elevation Satellite (ICESat), can provide worldwide LiDAR data. However, the density of the GLAS footprint is too low to directly produce a wall-to-wall forest AGB map [46].
Recently, many studies have tried to integrate multisource data to overcome the deficiencies of GLAS data and estimate regional- to continental-scale forest AGB. One of the major problems in these studies is how to build correlations between plot measurements and GLAS footprints considering the relatively low density of GLAS footprints. Generally, there are three ways to link forest inventories data and GLAS points [47]. (1) Direct links based on the geolocation [48,49,50]. Baccini et al. [49] used field data that were collected within the GLAS footprints to calibrate GLAS observations, and then used GLAS observations and other remote sensing data to generate a spatially continuous AGB in a pan-tropical forest; (2) The use of airborne LiDAR data as a medium [38]. Boudreau et al. [38] first used airborne LiDAR data to calibrate GLAS observations in parts of the study area, and then extrapolated GLAS observations using other remote sensing data to the whole study area in Québec, Canada; (3) Extrapolation of GLAS parameters [47,51]. Instead of linking ground measurements with GLAS data at the footprint level, Su et al. [47] first extracted GLAS full-waveform parameters and used statistical methods to extrapolate them into spatially continuous layers. Then, they used these extrapolated layers as predictors to build statistical models based on ground inventories, and estimated continuous forest AGB distribution in China. No matter which method is chosen, having a sufficient number of ground measurements that are well distributed across the world is a pre-requisite to estimate the distribution of global-scale forest AGB.
Although biomass maps based on multisource remote sensing data have recently become available in certain national [47,52], pan-tropical [48,49], circumboreal [53], and northern boreal and temperate forests [54], spatially explicit datasets on global forest AGB in a single product have been rarely seen up to now. In this study, our objective was to estimate global forest AGB using a combination of ground inventory data, spaceborne LiDAR, optical imagery, climate surfaces, and topographic data. Over 4000 plot measurements were collected from published literature to address this objective. This study selected extrapolation of GLAS parameters (the third method mentioned above) as the method to map global forest AGB [47] because there was only a low chance that the collected plot measurements would coincide with the GLAS footprints and sufficient airborne LiDAR data were not available. The resulting global wall-to-wall forest AGB map at 1-km resolution can be downloaded from web [55]. This new product can help to improve the accuracy of predictions of carbon dynamics and quantify the carbon fluxes from deforestation, land cover change, and other disturbances.

2. Materials and Methodology

As mentioned, this study chose the framework developed by Su et al. [47], which has been successfully used to estimate the nationwide forest AGB of China, to estimate global forest AGB. In line with the framework (Figure 1), we collected forest ground inventory, GLAS, Normalized Difference Vegetation Index (NDVI), topographic, climatic and land cover data (Table 1). Detailed descriptions of each dataset and a brief introduction to the AGB estimation methodology are given below.

2.1. Ground AGB Measurements

A sufficient amount of ground inventory data is fundamental to estimate forest AGB from remotely sensed data, no matter which methods are chosen. In this study, we collected 4090 records of plot measurements from papers published between 1990 and 2013. The allometric equations used in these literatures were based on either DBH (diameter at breast height) or DBH and tree height (Table S1). Some literatures directly provided the carbon density (Mg·C/ha) and we used a common factor of 2.0 to convert the carbon density to biomass density (Mg/ha) [14]. The stand origin (plantation or natural forest), plot size, measurement method, data publication year, and AGB value for each individual record are provided in the supplementary materials. To ensure the in-situ plot measurements were representative to the forest conditions of corresponding locations, the collected plot measurements were further filtered to ensure they were larger than 0.05 ha in size. The records measured through harvesting methods were also excluded from the AGB estimation procedures. In total, 3348 plot samples were retained in this study for the forest AGB mapping procedure (Figure 2; Table S2).

2.2. GLAS Data

The GLAS instrument was onboard the NASA (National Aeronautics and Space Administration) ICESat satellite, which was launched on 12 January 2003. It was equipped with three laser sensors, L1–L3, each of which has a 1064-nm laser channel for surface altimetry and dense cloud heights. The ellipsoidal footprints of ~65 m in diameter were spaced at 170 m along the track and at tens of kilometers across tracks [61]. In this study, we selected GLAS data from the operating periods L2B, L2C, and L3A (17 February 2004 to 9 November 2004) for the AGB mapping procedure. Three GLAS products, namely GLA01, GLA06, and GLA14, were downloaded from the ICESat/GLAS data pool. They respectively recorded the full-waveform, geolocation and data quality, and surface elevation information of each laser shot. These three products were linked by the combination of a unique record index (i_rec_ndx) and shot count (i_shot_count) for each shot.
To ensure the quality of the GLAS measurements, we further applied four criteria to filter the GLAS laser shots, namely: (1) should be cloud free (FRir_qa_flg = 15); (2) should have no saturation effects (i_satNdx <2); (3) should have high signal to noise ratios (i.e., >50); and (4) should not be significantly higher (i.e., <100 m) than the land surface elevation denoted by the Shuttle Radar Topography Mission (SRTM) data. Finally, 4,513,563 full-waveform records were retained in the final GLAS dataset. Working from the definitions of the waveform extent, leading edge extent, and trailing edge extent [62], we derived these three parameters from the full-waveform information of each laser shot. These variables have been shown to be highly correlated with canopy height, canopy height variability, and terrain slope, respectively [38,62,63,64].

2.3. NDVI Data

We selected MODIS-Terra MOD13A2 data as the source of NDVI data [58]. These data are computed from atmospherically corrected MODIS bi-directional surface reflectance data that have been masked for water, clouds, heavy aerosols, and cloud shadows. MOD13A2 data are provided every 16 days at 1-km spatial resolution in the sinusoidal projection. In this study, we collected global MOD13A2 data during 2004 from the Land Processes Distributed Active Archive Center (LP DAAC) data pool. Since cumulative NDVI from a time-series can increase the AGB estimation accuracy compared with the use of NDVI data from a single time period [45], we computed the cumulative NDVI from the sum of all NDVI data in the growing season of 2004 and used this as a predictor in forest AGB estimations.

2.4. Topographic Data

The elevation and slope were two important factors in the forest AGB mapping procedures proposed by Su et al. (2016) [47]. In this study, we chose the SRTM digital elevation model (DEM) data to obtain land surface elevation and slope information, which covers 99.97% of the Earth land surface from 56°S to 60°N [65,66]. We downloaded the 4.1 version of the SRTM data at a resolution of 90 m from the Consultative Group for International Agricultural Research-Consortium for Spatial Information (CGIAR-CSI) [57]. For consistency with other datasets, the SRTM DEM was resampled to 1-km resolution for further steps, and the slope product was derived from the resampled SRTM DEM.

2.5. Climatic Data

Climate conditions have a profound impact on the potential forest AGB [67,68]. We collected four bioclimatic variables between 1950 and 2000 from the WorldClim dataset, namely annual mean temperature, annual temperature seasonality, annual total precipitation, and annual precipitation seasonality [56]. These climate surfaces were provided in 1-km grids.

2.6. Land Cover Data

The global mosaics of the standard MODIS land cover type data product (MCD12Q1) in the IGBP Land Cover Type Classification was used in this study [59,60]. MCD12Q1 has provided an annual land cover map since 2001. For consistency with GLAS data, we downloaded a land cover map for 2004 from the Global Land Cover Facility.

2.7. Forest AGB Estimation Methods

As mentioned, this study used the AGB estimation framework developed by Su et al. (2016) [47] to estimate the global forest AGB. Detailed descriptions of the framework can be found in Su et al. (2016) [47]. As shown in Figure 1, the framework can generally be divided into four major steps.
First, the three discrete GLAS full-waveform parameters were extrapolated into spatial continuous layers using the random forest (RF) algorithm. Each of the three parameters were first aggregated into 1-km pixels using the average value of the corresponding parameter within each pixel. These 1-km pixels were used as training data to build the RF models to extrapolate the GLAS parameters based on prediction variables (i.e., cumulative NDVI, DEM, slope, climate surfaces, and land cover map).
Second, 100 sets of ground plot measurements with plot location uncertainty were generated. Most geolocations for the collected plots were accurate to 0.01° (corresponding to ~1 km), but some were only accurate to 0.1° (corresponding to ~10 km). As suggested by Su et al. (2016) [47], the plot location uncertainty may be too large and bring unneglectable error when linking the plots with other prediction variables. To minimize the influence of the plot location uncertainty on the forest AGB estimation, Su et al. (2016) [47] introduced an uncertainty field model into the forest AGB mapping procedure. This method assumed that the real plot center is randomly located within a circular buffer zone of the provided plot location. The radius of the buffer is determined by the uncertainty of the plot location (1 km or 10 km in this study). Then, a large number of plot measurements sets (i.e., 100 in this study) were randomly generated within these buffers using Monte-Carlo simulation.
Third, the initial global forest AGB distribution was mapped. Each set of the plot measurements with location uncertainty from the previous step was used as training data to estimate one global forest AGB distribution layer. The RF algorithm was used to build the regression models, and the three extrapolated GLAS parameters along with the eight parameters in Table 1 were used as explanatory variables. The initial global forest AGB map was computed as the average of the results from these 100 separate runs.
Finally, non-forested areas were masked to refine the forest AGB map. The initial global forest AGB map was further masked by the land cover map. The final global forest AGB map was obtained by setting the forest AGB density in areas without forest coverage as 0 Mg/ha.
The RF method for extrapolating the GLAS parameters and estimating forest AGB distribution was implemented using the randomForest R package [69]. The land cover map was used as a dummy variable in the RF regression procedures. Each land cover type was represented by a unique numerical identification number and fed into the RF regression tree models. Not all of the retained 3348 plots were used in the procedure of mapping global forest AGB distribution. Approximately 70% of the plots were randomly used to map the forest AGB and the other 30% were used to evaluate the forest AGB estimation result.

2.8. Accuracy Assessment

In this study, we used the adjusted coefficient of determination (R2) and root-mean-square error (RMSE) to evaluate the accuracy of the estimated global forest AGB at the plot level. The plot-level accuracy was assessed by directly comparing the estimated result with the independent validation ground inventory dataset. Moreover, the ecoregion-level AGB value was compared with the IPCC suggested value in each ecoregion.
We further conducted a comprehensive comparison between our estimated result and other published regional forest AGB products at the pixel level. Table 2 shows the regional forest AGB products that were used to make the comparison. As can be seen, most currently available published forest AGB products are concentrated in three regions, pan-tropical areas, boreal forest, and the continental U.S. The spatial similarity between our product and these other regional products was compared in two ways: direct pixel-level differencing and the use of the Fuzzy Numerical (FN) index map. The FN index map can measure the similarity of spatial patterns between two numerical raster maps at the pixel level [70,71]. The FN index, ranging between 0 (fully distinct maps) and 100 (fully identical maps), can be computed as the average of the numerical similarity s between each pair of corresponding cells (a and b) in two maps, which in turn can be computed cell-by-cell as follows:
s ( a , b ) = ( 1 − | a − b | max ( | a | , | b | ) ) × 100
where the cell values (a and b) are re-computed considering the neighboring cells within a specified window, such as 1 × 1 (in this study), 3 × 3, 5 × 5.

3. Results

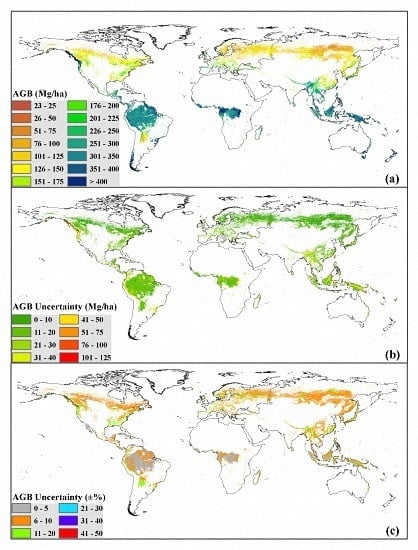
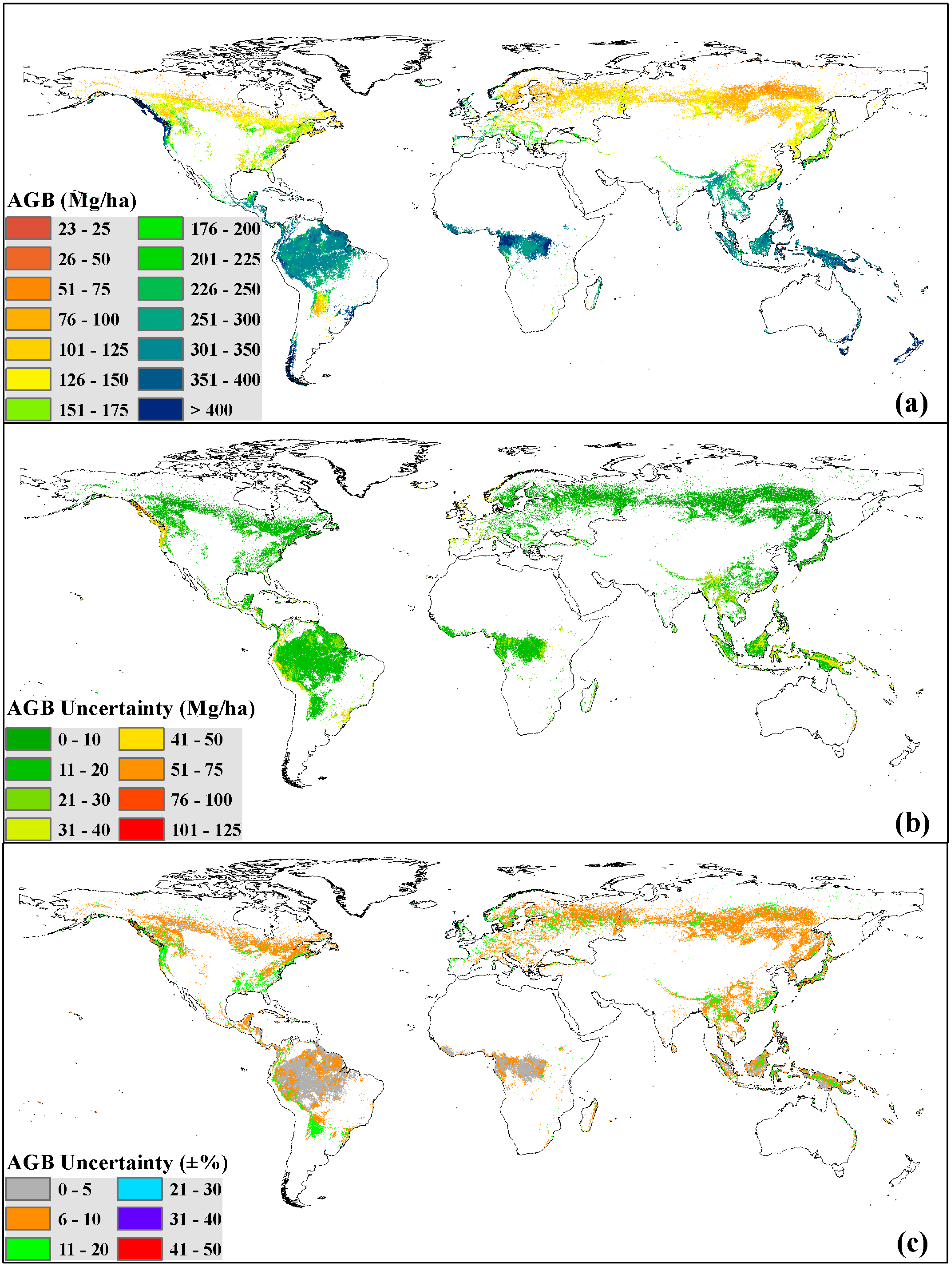
3.1. Wall-to-Wall Global Forest AGB Map

Figure 3 shows the distributions of the three extrapolated GLAS parameters. In general, the RF regression models explained 64.1%, 51.4%, and 55.1% of the variances in waveform extent, leading edge extent, and trailing edge extent, respectively. The mean root-mean-square residuals for the extrapolated waveform extent, leading edge extent, and trailing edge extent were 16.08 m, 12.8 m, and 4.7 m, respectively. These three extrapolated GLAS parameters along with the other eight collected predictors were used to estimate the global wall-to-wall forest AGB map. The resulting global wall-to-wall forest AGB map is shown in Figure 4 and can be downloaded from the web [55]. The RF regression tree model built from plot measurements without considering plot location uncertainty explained 61.21% of the variances in forest AGB and the root-mean-squared residual was 99.30 Mg/ha. The importance of each variables was provided in the Figure S1. The final global forest AGB result indicated that the mean AGB density for global forests was 210.09 Mg/ha with a standard deviation of 109.31 Mg/ha.
The forest AGB density gradually increased from the boreal forest area to the tropical forest area (Figure 4a). The boreal coniferous forests, which were mainly distributed in northern Europe, northern Asia, and northern North America, had relatively low average forest AGB densities (111.63, 97.49 and 126.80 Mg/ha, respectively). The internal variation of the forest AGB in these areas was also low (16, 20 and 18 Mg/ha, respectively). The temperate continental forests, which were mainly distributed in eastern Asia, western Europe, and eastern North America, had slightly higher forest AGB densities compared with the boreal coniferous forests (131.34, 120.70, and 155.85 Mg/ha on average, respectively). The temperate oceanic forests were mainly distributed in Eastern Europe with a few areas in western North America, southern South America, and New Zealand. The mean AGB density of temperate oceanic forest in Europe was 184.20 Mg/ha, which was lower than other temperate oceanic forests (North America 317.28 Mg/ha, South America 435.45 Mg/ha, and New Zealand 527.15 Mg/ha). The internal variations of the forest AGB in these areas were higher compared with the boreal areas: 80.01 Mg/ha in Europe, 109.71 Mg/ha in New Zealand, 98.47 Mg/ha in North America, and 84.56 Mg/ha in South America.
The subtropical dry forests (Mediterranean) were mainly distributed in Southern Europe (193.62 ± 51.85 Mg/ha) with a few areas in North America, South America (333.72 ± 55.95 Mg/ha), Asia (157.96 ± 19.91 Mg/ha), and Africa (242.90 ± 89.24 Mg/ha). Subtropical humid forests were mainly distributed in Asia, southern North America, and South America. The subtropical humid forest in South America had the highest AGB density (336.65 Mg/ha) and variation (101.15 Mg/ha) compared with those in Asia (171.41 ± 53.28 Mg/ha) and North America (141.43 ± 26.24 Mg/ha). Tropical rainforests are usually known for having the highest AGB density compared with other forests. The tropical rainforests in Africa had the highest mean AGB density (341.44 ± 51.14 Mg/ha) compared with those in South America (309.48 ± 30.26 Mg/ha) and Asia (305.17 ± 33.42 Mg/ha). Since they experienced 3–5 dry months in winter, the AGB density of tropical moist deciduous forests was lower than the tropical rainforest (Africa 240.16 ± 73.15 Mg/ha, Asia 259.15 ± 40.57 Mg/ha, and South America 258.36 ± 72.74 Mg/ha). Tropical dry forests had the lowest AGB density in the tropics. The tropical dry forest in South America had an AGB density of 138.93 ± 51.26 Mg/ha compared with Africa (178.57 ± 65.78 Mg/ha) and Asia (226.58 ± 59.68 Mg/ha).
At the continental level, South America forests had the highest AGB stock (188.68 Pg) since the high AGB density (301.68 ± 67.43 Mg/ha) and larger forest areas (608.6 Mha) (Table 3). The AGB stock in Asia, North America, Africa, and Europe was 143.14, 77.46, 64.65 and 40.83 Pg, respectively. Although Australia and Oceania had high average AGB density (415.66 and 424.30 Mg/ha, respectively), the total AGB in Australia and Oceania was low (8.69 and 9.30 Pg, respectively) since there are relatively small forest areas. At the national level, the Brazil forests had the highest AGB stock (97.44 Pg) since the high AGB density (306.79 ± 36.1 Mg/ha) and large forest areas (317.34 Mha). Russian Federation had the secondary AGB stock (59.87 Pg) since the largest forest cover (530.48 Mha), and forest AGB density and stock of other main countries in each continent were listed in Table 3 and Table S3.
The uncertainty in the AGB estimation introduced by the plot location for each pixel was evaluated using the standard deviation of the 100 sets of initial forest AGB estimation maps (Figure 4b,c). The mean uncertainty introduced by the plot location was 14.53 Mg/ha with a range of 3.75–127.69 Mg/ha. Most forests distributed in the European, North American, and Amazon areas had relatively low uncertainty values (<30 Mg/ha). In Southeast Asia, the influence of plot location uncertainty became larger, resulting in a forest AGB uncertainty of over 50 Mg/ha. The AGB estimation uncertainty introduced by the plot location was highest on the western coast of North America and central Papua New Guinea, reaching values of 100 Mg/ha.

3.2. Validation at Plot Level

The retained 30% of independent plot measurements were used to evaluate the forest AGB estimation result at the plot scale. As can be seen in Figure 5, the estimated forest AGB map showed good agreement with the field-measured AGB. The fitted line between the observed values and predicted values was close to the 1:1 line. The statistical parameters also show that the accuracy of the estimated global forest AGB map was satisfactory. The R2 between the observed and predicted AGB was 0.56 and the RMSE was 87.53 Mg/ha. However, the global forest AGB map had some limitations. It was inclined to overestimate forest AGB density in areas with low AGB density (<221 Mg/ha), and underestimate forest AGB density in areas with relatively high AGB density (>221 Mg/ha).
At the ecoregion zone level, the forest AGB map was compared with by the AGB density values of the eight ecological zones in different continents provided by the IPCC. As shown in Figure 6, the R2 and RMSE between the IPCC suggested values and the predicted AGB were 0.38 and 101.21 Mg/ha, respectively. However, there was a clear outlier where the predicted forest AGB density for the North America temperate oceanic forest was significantly lower than the value provided by the IPCC. When we removed this data point, the R2 increased to 0.56 and the RMSE decreased to 82.38 Mg/ha, which was very close to the plot-level validation results.

3.3. Comparisons with Published Regional Forest AGB Maps

3.3.1. Pan-Tropical Forests

Figure 7 shows the pixel-level differences between our forest AGB map and the products from Saatchi et al. (2011) [48], Baccini et al. (2012) [49], Avitabile et al. (2015) [72], and Ruesch & Gibbs (2008) [73]. In general, our forest AGB density values tended to be higher (80 Mg/ha on average) than those from Saatchi et al. (2011) [48] (Figure 7a), especially in the Amazon Basin and eastern Democratic Republic of Congo. In South and Southeast Asia, differences between the two products were mixed, with positive and negative values. The FN index map (Figure 8a) showed that the two products had high similarity in spatial patterns. Over 59% of the pixels had a FN index value larger than 70. The differences between our product and that from Baccini et al. (2012) [49] and Avitabile et al. (2015) [72] were similar (Figure 7b,c). Our product tended to be slightly higher than these two products, and the average differences were both around 65 Mg/ha. However, the standard deviation of differences between our product and that of Baccini et al. (2012) [49] was smaller than between our product and the product of Avitabile et al. (2015) [72], at 77.07 Mg/ha and 107.40 Mg/ha, respectively. The spatial similarity among these three products was also similar. The average FN index between our product and that from Baccini et al. (2012) [49] was 75.32, and the average FN index between our product and that from Avitabile et al. (2015) [72] was 65.80. However, the spatial similarity between our product and that from Avitabile et al. (2015) [72] was relatively poor in Central America and south of the Amazon Basin. Finally, our product tended to be lower than the product from Ruesch & Gibbs (2008) [73], especially in the Amazon Basin and the tropical areas of Central Africa. The average difference between the two products was −12 Mg/ha. The average value of the FN index was 76.37, which indicated these two products also had high spatial similarity. However, the spatial similarity in Southeast and South Asia was relatively poor compared with that in the Amazon Basin and Central Africa (Figure 8d).

3.3.2. Boreal Forests

In boreal forest areas, our wall-to-wall forest AGB map was compared with three products in northern America [54,73,74] and three products in northern Eurasia [54,73,75]. In northern America (Figure 9), our product tended to be higher than all three products, except for the difference between our product and that of Ruesch & Gibbs et al. (2008) [73] in the eastern U.S. The average differences between our product and the products of Margolis et al. (2015) [75], Thurner et al. (2014) [54], and Ruesch & Gibbs (2008) [73] were 56 Mg/ha, 96 Mg/ha and 75 Mg/ha, respectively. The average FN index for the product of Margolis et al. (2015) [75] was 55.76, which was the highest among the three products (Figure 10). The spatial similarity between our product and the products of Thurner et al. (2014) [54] and Ruesch & Gibbs (2008) [73] was relatively poor.
Our product also tended to be higher than all three products in northern Eurasia (Figure 11). The average differences between our product and the products of Neigh et al. (2015) [74], Thurner et al. (2014) [54], and Ruesch & Gibbs et al. (2014) [73] were 36 Mg/ha, 72 Mg/ha and 71 Mg/ha, respectively. Nearly all pixels had positive differences between our product and these three products, except those between our product and the product of Neigh et al. (2015) [74] in central northern Eurasian areas. Among these three products, the spatial similarity between our product and that from Neigh et al. (2015) [74] was the highest (Figure 12). The average FN index between these two products was 59.27. The spatial similarities between our product and the products from Thurner et al. (2014) [54] and Ruesch & Gibbs (2008) [73] were relatively poor. Over 83.24% pixels of the FN index map between our product and the product from Thurner et al. (2014) [54] were lower than 50. The FN index between our product and the product of Ruesch & Gibbs (2008) [73] was more unevenly distributed.

3.3.3. U.S. Forests

Our product was also compared with three nationwide forest AGB products [73,76,77] in the U.S. As can be seen in Figure 13, the average differences between our product and the product of Saatchi et al. (2005) [76] was the smallest among all three products. The differences were mixed with positive and negative values, and the average difference was 24 Mg/ha. The spatial similarity between these two products was also high (Figure 14b). Over 72.18% of pixels had an FN index higher than 50. Compared with the product of Blackard et al. (2005) [77], our product tended to be slightly higher. About 43.73% of pixels had differences ranging from 10 Mg/ha to 50 Mg/ha. The spatial similarity between these two products was the highest (the mean FN index = 67.55). The average differences between our product and that of Ruesch & Gibbs (2008) [73] were the highest among all three U.S. forest AGB products (the mean difference was 71 Mg/ha). The variation of differences between these two products was also very high. In the western and northeastern U.S., our product was around 107.60 Mg/ha higher than the product of Ruesch & Gibbs (2008) on average. However, in the southern eastern U.S., our product was around 42.03 Mg/ha lower than their product on average. The spatial similarity between these two products was also the lowest among all three U.S. forest AGB maps, especially in the western and northeastern U.S.

4. Discussion

The global wall-to-wall forest AGB map obtained from our analysis had good agreement with the independent plot measurements and IPCC-suggested AGB values at the ecoregion level. The trends of forest AGB density along latitude also similar to previous results [12] (Figure 15): the highest AGB density occurred in the temperate latitudes of the Southern hemisphere (southeastern Australia, New Zealand, and Chile), and AGB density decreased from the tropical latitudes to temperate and boreal latitudes of the Northern hemisphere. The high AGB density in the Pacific Northwest of North America brought a significant peak in the trend line of AGB density at the temperate latitudes of the Northern hemisphere (Figure 15). In this study, comparisons between our resulting new map and other published maps were mainly aimed to validate the spatial pattern and AGB level of our result. Therefore, we only conducted direct comparisons based on pixel-level differences. The systematic comparison results showed that our product also had good correspondence in spatial patterns and AGB levels with many of the published products (Table S4; Figure S2). However, our product still had differences with some products in certain areas.
Saatchi et al. (2011) [48] and Baccini et al. (2012) [49] produced the first two pan-tropical AGB maps using a similar method that integrated GLAS data, optical imagery, and plot data, and Avitabile et al. (2015) [72] fused these two products into a new pan-tropical AGB map using an independent reference dataset of field observations and locally calibrated high-resolution biomass maps. In the western Amazon Basin, our map tended to be slightly higher than the map from Saatchi et al. (2011) [48], but much lower than the map from Baccini et al. (2012) [49] and slightly lower than the map from Avitabile et al. (2015) [72] (Figure 7). In the center of the Amazon Basin, the difference maps were mixed with positive and negative values and our map in general tended to be higher than others (Figure 7). In the northeastern Amazon Basin, our map tended to be higher than Saatchi et al. (2011) [48] and Baccini et al. (2012) [49], but lower than Avitabile et al. (2015) [72] (Figure 7). The spatial difference in AGB in the Amazon Basin between our map and first two pan-tropic AGB maps (Saatchi et al. (2011) [48] and Baccini et al. (2012) [49]) concurred with the results found by Mitchard et al. (2014) [78], who compared these two maps with a map derived from kriging interpolation using 413 field plots. Mitchard et al. (2014) [78] thought that neglecting the regional variations of wood density or D:H (diameter at breast height:height) relationships that cannot be detected by remote sensing was the major reason. We think two factors may have reduced the loss in the information on regional variations of wood density or D:H relationships during our estimation process. First, we directly used the field data from the literature and did not carry out any conversion before the extrapolation, which may keep the potential variations of forest wood density. In contrast, both Saatchi et al. (2011) [48] and Baccini et al. (2012) [49] converted the field AGB into GLAS-derived AGB, which may lose the potential information of forest wood density contained in the plot data. Second, we used bioclimatic layers as inputs in our study, which could potentially be related to wood density [68] or D:H relationships [79] in tropical or global forest areas. The difference map between Avitabile et al. (2015) [72] and Saatchi et al. (2011) [48] or Baccini et al. (2012) [49] presented a similar pattern to ours and the map from Mitchard et al. (2014) [78] in the Amazon Basin, which may be benefitted from the fusion with an external field dataset.
Compared with the tropical forest area, most AGB products in the boreal forest areas tended to be lower than our AGB map. We think these differences may result from the following three reasons. First, the underestimation may be caused by the limitation of the remote sensing data used to predict AGB. Thurner et al. (2014) [54] only used the growing stock volume (GSV) product retrieved from SAR (Santoro et al., unpublished data) to predict biomass and their map was lower than other AGB maps in most boreal forest areas. Although Santoro et al. [80] reported GSV was mapped without saturation up to 300 m3/ha, which is suitable for the boreal forest, the predicted GSV was lower than the reference GSV in their study [80]. This may be the reason for the underestimation in the map from Thurner et al. (2014) [54]. Second, the differences may come from the extrapolation methods. Neigh et al. (2015) [53,74] and Margolis et al. (2015) [75] used the same method to map the boreal forest AGB in northern Eurasia and North America, respectively. They divided the forest AGB into different strata, e.g., conifer, hardwood, mixed wood, and wetlands, using Landsat and MODIS land cover products. The AGB value of each pixel was assigned by the ratio of different strata, the values of which were estimated by combining GLAS, airborne LiDAR and plot data. Since the mean AGB value of a stratum was used while assigning, this may tend to underestimate the AGB density in high AGB areas. Moreover, the strata also included non-forest areas and burned areas, which were not considered in our study. This could also introduce underestimation to their results. Third, the differences may be caused by insufficient number of plot data. In general, the map from Neigh et al. (2015) [74] had high spatial similarity in north Eurasia areas, except northwestern Russia (Figure 12a). This phenomenon may be caused by the AGB estimation model used by Neigh et al. (2015) [74] in the Scandinavian and Russian Taiga, which only linked the airborne LiDAR data with plots of conifer forest in southern Norway. According to the MODIS land cover map (Figure 2), the majority of northwestern Russia is covered by mixed forests and this would introduce an underestimation while applying an AGB model built for conifer forests to mixed forests.
Ruesch & Gibbs (2008) [73] presented the first global forest biomass map and provided important benchmarks for climate policy dialogues, but they tended to significantly overestimate AGB in tropical areas, and underestimate it in boreal forest areas compared with our product. The negative or positive values in the AGB difference map between Ruesch & Gibbs (2008) and our map tend to form large patches (Figure 7d and Figure 13c), which is different from other AGB difference maps. The method used by Ruesch & Gibbs may be the major reason for this phenomenon. Ruesch & Gibbs (2008) [73] used the global forest AGB default values provided by the IPCC to map forest AGB from a range of spatially explicit climate and vegetation datasets. All the pixels in each ecological zone used the same value, which could not reflect spatial variance in the same ecological zone. Moreover, according to the validation at the ecological zone level (Figure 6), our results were higher than the IPCC value in boreal forest and lower than the value in tropical forest, which was coincident with this phenomenon.
Although the global wall-to-wall forest AGB map has a good correspondence with the independent plot data and nine other published products (in spatial pattern and AGB level), there were deficiencies in this study. First of all, the uncertainty of the forest AGB map was not fully quantified. In this study, we only computed the uncertainty caused by the plot location uncertainty, but there are other error sources from the uncertainty of each prediction variables. Generally, the propagation of the uncertainty from each prediction variable to the final forest AGB estimation uncertainty was evaluated using the Monte Carlo simulation method assuming the influences of each variable are independent. However, to conduct this, thousands of RF runs need to be executed to estimate the uncertainty of the extrapolated GLAS parameters and the final forest AGB product. Each run will need to take a week to finish. Considering the time and computation cost, we only evaluated the uncertainty caused by plot location in the current study and other uncertainties will be fulfilled in the future study. Second, the quality of reference data still needs improvements in future research. Currently, temporal mismatch between our ground inventory data and remote sensing data was a potential error source. The collected ground plots were spanned from 1990 to 2013 while the prediction variables were collected in 2004. During this long time (up to 14 year) span, the condition in some plots would be changed due to the land cover/use change, forest growth, or heavy degradation. However, currently, we do not have enough ground plots from a single year (e.g., 2004) to build a robust global forest AGB estimated model. There is a tradeoff between temporal match and quantity control in current collected plots at the global scale. We will continue to work on collecting more ground measurements to address this issue. Moreover, there was also a deficiency to use plot AGB values to represent the biomass at 1 km resolution. The difference between the plot size and the resolution of prediction variables may be another source of error in the final result. Airborne LiDAR has been recognized as an important method to extrapolate plot biomass into grids with high accuracy [45]. In the future, it would be a practical option to first use airborne LiDAR to extrapolate plot measurements into regional scale and then use the airborne LiDAR derived AGB as the ground truth input of the proposed method in this study. Third, the seasonality of GLAS data should be considered in the further research. In the temperate deciduous forest, GLAS waveforms from the summer and early stage of autumn period can well capture the returns from forest canopy [81]. By contrast, data from other periods received less signals from forest canopy and did not effectively reflect forest height [81]. Since all GLAS data in 2004 were used in this study, it may introduce some uncertainty to the final AGB results in the temperate forest areas.
Global forest ecosystems are important land surface carbon sinks which greatly influence the global carbon cycle [1,2]. Since forest AGB is a direct measurement of the forest carbon stock, it is of great significance to accurately map the global forest AGB distribution. To the best of our knowledge, this study, for the first time, mapped the global continuous forest AGB distribution using remotely sensed observation data and a large amount of plot estimations. The resulting map can help researchers to improve the accuracy of global carbon cycle modelling, enhance our understanding on global carbon dynamics, and quantify anthropogenic carbon dioxide emissions.

5. Conclusions

This study produced a global wall-to-wall forest AGB map at a 1-km resolution for the first time, and this new product is available through the web [55]. This product was generated based on the framework proposed by Su et al. (2016) [46] and over 4000 plot measurement records collected from published literature. Based on this forest AGB product, the global forest AGB density was around 210 Mg/ha on average with a standard deviation of 109 Mg/ha. The uncertainty introduced by plot location was 14.53 Mg/ha on average with a range of 3.75–127.69 Mg/ha. This product was evaluated at the plot level and the result showed that our products had a good correspondence with the independent plot measurements (R2 = 0.56 RMSE = 87.53 Mg/ha). At the ecoregion level, values recommended by the IPCC were used to compare with this new map which also showed a good correspondence (R2 = 0.38 RMSE = 101.21 Mg/ha with one outlier, R2 = 0.56 RMSE = 82.38 Mg/ha after removing one outlier). Moreover, a systematic comparison between our product and other published regional products was conducted in pan-tropical areas, northern boreal forest areas, and the U.S. This comparison was aimed to compare the spatial similarity in AGB distribution and AGB level between our map and other published maps. The results indicated our product corresponded well with products obtained by integrating LiDAR data. Products generated using traditional optical passive remote sensing and radar data tended to underestimate forest AGB density. This new map is highly beneficial to global carbon assessments and biogeochemical modellings. Moreover, it can also help to quantify changes in forest biomass caused by deforestation or afforestation.

Supplementary Materials

The following are available online at www.mdpi.com/2072-4292/8/7/565/s1, Table S1: The main literature provided the AGB using allometry equation; Table S2: The distribution of plots in each continents and ecoregions; Table S3: The national level forest AGB density and biomass stock in this study; Table S4: The mean AGB and FN differences for each major region; Figure S1: The mean importance of variables for 100 runs AGB estimation RandomForest model, indicated by percentage increase of mean-squared error (%IncMSE) (left) and the increase in node purity (IncNodePurity) (right). le, we, te, prec_total, precp_s, tmean, T_s, ndvi, and landuse represent the leading edge extent, waveform extent, trailing edge extent, annual total precipitation, annual precipitation seasonality, annual mean temperature, annual temperature seasonality, cumulative NDVI, and landcover type, respectively; Figure S2: validation of AGB map at different ecoregions.

Acknowledgments

This study is supported by the National Key Basic Research Program of China (project number 2013CB956604), National Science Foundation of China (project numbers 41471363 and 31270563), and National Science Foundation (DBI 1356077). We thank the United States Geological Survey and National Aeronautics and Space Administration for providing the SRTM DEM products.

Author Contributions

Tianyu Hu, Yanjun Su and Qinghua Guo designed the experiment; Baolin Xue, Jin Liu and Xiaoqian Zhao collected the required data; Tianyu Hu and Yanjun Su performed the experiment; Tianyu Hu, Yanjun Su and Baolin Xue conducted the analysis of the results; Tianyu Hu, Yanjun Su, Jingyun Fang and Qinghua Guo contributed towards writing the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
AGBaboveground biomass
LiDARLight Detection and Ranging
GLASGeoscience Laser Altimeter System
ICESatIce, Cloud, and Land Elevation Satellite
R2adjusted coefficient of determination
RMSEroot-mean-square error
SARSynthetic Aperture Radar
NDVINormalized Difference Vegetation Index
LP DAACLand Processes Distributed Active Archive Center
SRTMShuttle Radar Topographic Mission
CGIAR-CSIConsultative Group for International Agricultural Research-Consortium for Spatial Information
DEMdigital elevation model
RFrandom forest
FNfuzzy numerical
Htree height
DBH,Ddiameter at breast height
GSVgrowing stock volume

References

  1. Arneth, A.; Harrison, S.P.; Zaehle, S.; Tsigaridis, K.; Menon, S.; Bartlein, P.J.; Feichter, J.; Korhola, A.; Kulmala, M.; O’donnell, D. Terrestrial biogeochemical feedbacks in the climate system. Nat. Geosci. 2010, 3, 525–532. [Google Scholar] [CrossRef]
  2. Bonan, G.B. Forests and climate change: Forcings, feedbacks, and the climate benefits of forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef] [PubMed]
  3. Drake, J.B.; Knox, R.G.; Dubayah, R.O.; Clark, D.B.; Condit, R.; Blair, J.B.; Hofton, M. Above-ground biomass estimation in closed canopy neotropical forests using lidar remote sensing: Factors affecting the generality of relationships. Glob. Ecol. Biogeogr. 2003, 12, 147–159. [Google Scholar] [CrossRef]
  4. Foley, J.A.; Prentice, I.C.; Ramankutty, N.; Levis, S.; Pollard, D.; Sitch, S.; Haxeltine, A. An integrated biosphere model of land surface processes, terrestrial carbon balance, and vegetation dynamics. Glob. Biogeochem. Cycle 1996, 10, 603–628. [Google Scholar] [CrossRef]
  5. Friend, A.; Stevens, A.; Knox, R.; Cannell, M. A process-based, terrestrial biosphere model of ecosystem dynamics (hybrid v3. 0). Ecol. Model. 1997, 95, 249–287. [Google Scholar] [CrossRef]
  6. Hurtt, G.C.; Moorcroft, P.; Pacala, S.W.; Levin, S.A. Terrestrial models and global change: Challenges for the future. Glob. Chang. Biol. 1998, 4, 581–590. [Google Scholar] [CrossRef]
  7. Potter, C.S. Terrestrial biomass and the effects of deforestation on the global carbon cycle results from a model of primary production using satellite observations. BioScience 1999, 49, 769–778. [Google Scholar] [CrossRef]
  8. Houghton, R.A. Tropical deforestation and atmospheric carbon dioxide. In Tropical Forests and Climate; Springer: Dordrecht, The Netherlands, 1992; pp. 99–118. [Google Scholar]
  9. Houghton, R.; Lawrence, K.; Hackler, J.; Brown, S. The spatial distribution of forest biomass in the brazilian amazon: A comparison of estimates. Glob. Chang. Biol. 2001, 7, 731–746. [Google Scholar] [CrossRef]
  10. Bunker, D.E.; DeClerck, F.; Bradford, J.C.; Colwell, R.K.; Perfecto, I.; Phillips, O.L.; Sankaran, M.; Naeem, S. Species loss and aboveground carbon storage in a tropical forest. Science 2005, 310, 1029–1031. [Google Scholar] [CrossRef] [PubMed]
  11. Galbraith, D.; Levy, P.E.; Sitch, S.; Huntingford, C.; Cox, P.; Williams, M.; Meir, P. Multiple mechanisms of amazonian forest biomass losses in three dynamic global vegetation models under climate change. New Phytol. 2010, 187, 647–665. [Google Scholar] [CrossRef] [PubMed]
  12. Keith, H.; Mackey, B.G.; Lindenmayer, D.B. Re-evaluation of forest biomass carbon stocks and lessons from the world’s most carbon-dense forests. Proc. Natl. Acad. Sci. USA 2009, 106, 11635–11640. [Google Scholar] [CrossRef] [PubMed]
  13. Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A large and persistent carbon sink in the world’s forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed]
  14. Fang, J.; Chen, A.; Peng, C.; Zhao, S.; Ci, L. Changes in forest biomass carbon storage in china between 1949 and 1998. Science 2001, 292, 2320–2322. [Google Scholar] [CrossRef] [PubMed]
  15. Malhi, Y.; Phillips, O.; Lloyd, J.; Baker, T.; Wright, J.; Almeida, S.; Arroyo, L.; Frederiksen, T.; Grace, J.; Higuchi, N. An international network to monitor the structure, composition and dynamics of amazonian forests (rainfor). J. Veg. Sci. 2002, 13, 439–450. [Google Scholar] [CrossRef]
  16. Houghton, R. Aboveground forest biomass and the global carbon balance. Glob. Chang. Biol. 2005, 11, 945–958. [Google Scholar] [CrossRef]
  17. Cohen, W.B.; Harmon, M.E.; Wallin, D.O.; Fiorella, M. Two decades of carbon flux from forests of the pacific northwest. BioScience 1996, 46, 836–844. [Google Scholar] [CrossRef]
  18. Running, S.; Baldocchi, D.; Turner, D.; Gower, S.; Bakwin, P.; Hibbard, K. A global terrestrial monitoring network integrating tower fluxes, flask sampling, ecosystem modeling and eos satellite data. Remote Sens. Environ. 1999, 70, 108–127. [Google Scholar] [CrossRef]
  19. Woodcock, C.E.; Collins, J.B.; Gopal, S.; Jakabhazy, V.D.; Li, X.; Macomber, S.; Ryherd, S.; Harward, V.J.; Levitan, J.; Wu, Y. Mapping forest vegetation using landsat tm imagery and a canopy reflectance model. Remote Sens. Environ. 1994, 50, 240–254. [Google Scholar] [CrossRef]
  20. Fazakas, Z.; Nilsson, M.; Olsson, H. Regional forest biomass and wood volume estimation using satellite data and ancillary data. Agric. For. Meteorol. 1999, 98, 417–425. [Google Scholar] [CrossRef]
  21. Foody, G.M.; Cutler, M.E.; Mcmorrow, J.; Pelz, D.; Tangki, H.; Boyd, D.S.; Douglas, I. Mapping the biomass of bornean tropical rain forest from remotely sensed data. Glob. Ecol. Biogeogr. 2001, 10, 379–387. [Google Scholar] [CrossRef]
  22. Sader, S.A.; Waide, R.B.; Lawrence, W.T.; Joyce, A.T. Tropical forest biomass and successional age class relationships to a vegetation index derived from landsat tm data. Remote Sens. Environ. 1989, 28, 143–198. [Google Scholar] [CrossRef]
  23. Baccini, A.; Laporte, N.; Goetz, S.; Sun, M.; Dong, H. A first map of tropical africa’s above-ground biomass derived from satellite imagery. Environ. Res. Lett. 2008, 3, 045011. [Google Scholar] [CrossRef]
  24. Luckman, A.; Baker, J.; Kuplich, T.M.; Yanasse, C.D.C.F.; Frery, A.C. A study of the relationship between radar backscatter and regenerating tropical forest biomass for spaceborne sar instruments. Remote Sens. Environ. 1997, 60, 1–13. [Google Scholar] [CrossRef]
  25. Toan, T.; Beaudoin, A.; Riom, J.; Guyon, D. Relating forest biomass to sar data. IEEE Trans. Geosci. Remote 1992, 30, 403–411. [Google Scholar] [CrossRef]
  26. Wagner, W.; Luckman, A.; Vietmeier, J.; Tansey, K. Large-scale mapping of boreal forest in siberia using ers tandem coherence and jers backscatter data. Remote Sens. Environ. 2003, 8, 125–144. [Google Scholar] [CrossRef]
  27. Sun, G.; Ranson, K.J.; Kharuk, V.I. Radiometric slope correction for forest biomass estimation from sar data in the western sayani mountains, siberia. Remote Sens. Environ. 2002, 79, 279–287. [Google Scholar] [CrossRef]
  28. Ranson, K.J.; Sun, G. Mapping biomass of a northern forest using multifrequency sar data. IEEE Trans. Geosci. Remote 1994, 32, 388–396. [Google Scholar] [CrossRef]
  29. Saatchi, S.; Halligan, K.; Despain, D.G.; Crabtree, R.L. Estimation of forest fuel load from radar remote sensing. IEEE Trans. Geosci. Remote 2007, 45, 1726–1740. [Google Scholar] [CrossRef]
  30. Cartus, O.; Santoro, M.; Kellndorfer, J. Mapping forest aboveground biomass in the northeastern united states with alos palsar dual-polarization l-band. Remote Sens. Environ. 2012, 124, 466–478. [Google Scholar] [CrossRef]
  31. Kasischke, E.S.; Melack, J.M.; Dobson, C.M. The use of imaging radars for ecological applications: A review. Remote Sens. Environ. 1997, 59, 141–156. [Google Scholar] [CrossRef]
  32. Lu, D. The potential and challenge of remote sensing-based biomass estimation. Int. J. Remote Sens. 2006, 27, 1297–1328. [Google Scholar] [CrossRef]
  33. Mitchard, E.; Saatchi, S.; Woodhouse, I.; Nangendo, G.; Ribeiro, N.; Williams, M.; Ryan, C.; Lewis, S.; Feldpausch, T.; Meir, P. Using satellite radar backscatter to predict above-ground woody biomass: A consistent relationship across four different african landscapes. Geophys. Res. Lett. 2009, 36, L23401. [Google Scholar] [CrossRef]
  34. Myneni, R.B.; Dong, J.; Tucker, C.J.; Kaufmann, R.K.; Kauppi, P.E.; Liski, J.; Zhou, L.; Alexeyev, V.; Hughes, M. A large carbon sink in the woody biomass of northern forests. Proc. Natl. Acad. Sci. USA 2001, 98, 14784–14789. [Google Scholar] [CrossRef] [PubMed]
  35. Woodhouse, I.H.; Mitchard, E.T.; Brolly, M.; Maniatis, D.; Ryan, C.M. Radar backscatter is not a ‘direct measure’ of forest biomass. Nat. Clim. Chang. 2012, 2, 556–557. [Google Scholar] [CrossRef]
  36. Su, Y.; Guo, Q. A practical method for srtm dem correction over vegetated mountain areas. ISPRS J. Photogramm. Remote Sens. 2014, 87, 216–228. [Google Scholar] [CrossRef]
  37. Clark, M.L.; Clark, D.B.; Roberts, D.A. Small-footprint lidar estimation of sub-canopy elevation and tree height in a tropical rain forest landscape. Remote Sens. Environ. 2004, 91, 68–89. [Google Scholar] [CrossRef]
  38. Boudreau, J.; Nelson, R.; Margolis, H.; Beaudoin, A.; Guindon, L.; Kimes, D. Regional aboveground forest biomass using airborne and spaceborne lidar in québec. Remote Sens. Environ. 2008, 112, 3876–3890. [Google Scholar] [CrossRef]
  39. Clark, M.L.; Roberts, D.A.; Ewel, J.J.; Clark, D.B. Estimation of tropical rain forest aboveground biomass with small-footprint lidar and hyperspectral sensors. Remote Sens. Environ. 2011, 115, 2931–2942. [Google Scholar] [CrossRef]
  40. Lefsky, M.A.; Harding, D.J.; Keller, M.; Cohen, W.B.; Carabajal, C.C.; Del Bom Espirito-Santo, F.; Hunter, M.O.; de Oliveira, R. Estimates of forest canopy height and aboveground biomass using icesat. Geophys. Res. Lett. 2005, 32, L22S02. [Google Scholar] [CrossRef]
  41. Popescu, S.C.; Zhao, K.; Neuenschwander, A.; Lin, C. Satellite lidar vs. Small footprint airborne lidar: Comparing the accuracy of aboveground biomass estimates and forest structure metrics at footprint level. Remote Sens. Environ. 2011, 115, 2786–2797. [Google Scholar] [CrossRef]
  42. Nelson, R.; Ranson, K.; Sun, G.; Kimes, D.; Kharuk, V.; Montesano, P. Estimating siberian timber volume using modis and icesat/glas. Remote Sens. Environ. 2009, 113, 691–701. [Google Scholar] [CrossRef]
  43. Swatantran, A.; Dubayah, R.; Roberts, D.; Hofton, M.; Blair, J.B. Mapping biomass and stress in the sierra nevada using lidar and hyperspectral data fusion. Remote Sens. Environ. 2011, 115, 2917–2930. [Google Scholar] [CrossRef]
  44. Asner, G.P.; Clark, J.K.; Mascaro, J.; García, G.G.A.; Chadwick, K.D.; Encinales, N.D.A.; Paez-Acosta, G.; Montenegro, C.E.; Kennedy-Bowdoin, T.; Duque, Á.; et al. High-resolution mapping of forest carbon stocks in the colombian amazon. Biogeosciences 2012, 9, 2683–2696. [Google Scholar] [CrossRef]
  45. Li, L.; Guo, Q.; Tao, S.; Kelly, M.; Xu, G. Lidar with multi-temporal modis provide a means to upscale predictions of forest biomass. ISPRS J. Photogramm. Remote Sens. 2015, 102, 198–208. [Google Scholar] [CrossRef]
  46. Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping forest canopy height globally with spaceborne lidar. J. Geophys. Res. Biogeosci. 2011, 116. [Google Scholar] [CrossRef]
  47. Su, Y.; Guo, Q.; Xue, B.; Hu, T.; Alvarez, O.; Tao, S. Spatial distribution of forest aboveground biomass in china: Estimation through combination of spaceborne lidar, optical imagery, and forest inventory data. Remote Sens. Environ. 2016, 173, 187–199. [Google Scholar] [CrossRef]
  48. Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.; Salas, W.; Zutta, B.R.; Buermann, W.; Lewis, S.L.; Hagen, S.; et al. Benchmark map of forest carbon stocks in tropical regions across three continents. Proc. Natl. Acad. Sci. USA 2011, 108, 9899–9904. [Google Scholar] [CrossRef] [PubMed]
  49. Baccini, A.; Goetz, S.; Walker, W.; Laporte, N.; Sun, M.; Sulla-Menashe, D.; Hackler, J.; Beck, P.; Dubayah, R.; Friedl, M. Estimated carbon dioxide emissions from tropical deforestation improved by carbon-density maps. Nat. Clim. Chang. 2012, 2, 182–185. [Google Scholar] [CrossRef]
  50. Zhang, Y.; Liang, S.; Sun, G. Forest biomass mapping of northeastern China using glas and modis data. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 140–152. [Google Scholar] [CrossRef]
  51. Zhang, G.; Ganguly, S.; Nemani, R.R.; White, M.A. Estimation of forest aboveground biomass in california using canopy height and leaf area index estimated from satellite data. Remote Sens. Environ. 2014, 151, 44–56. [Google Scholar] [CrossRef]
  52. Chi, H.; Sun, G.; Huang, J.; Guo, Z.; Ni, W.; Fu, A. National forest aboveground biomass mapping from icesat/glas data and modis imagery in China. Remote Sens. 2015, 7, 5534–5564. [Google Scholar] [CrossRef]
  53. Neigh, C.S.R.; Nelson, R.F.; Ranson, K.J.; Margolis, H.A.; Montesano, P.M.; Sun, G.; Kharuk, V.; Næsset, E.; Wulder, M.A.; Andersen, H.-E. Taking stock of circumboreal forest carbon with ground measurements, airborne and spaceborne lidar. Remote Sens. Environ. 2013, 137, 274–287. [Google Scholar] [CrossRef]
  54. Thurner, M.; Beer, C.; Santoro, M.; Carvalhais, N.; Wutzler, T.; Schepaschenko, D.; Shvidenko, A.; Kompter, E.; Ahrens, B.; Levick, S.R.; et al. Carbon stock and density of northern boreal and temperate forests. Glob. Ecol. Biogeogr. 2014, 23, 297–310. [Google Scholar] [CrossRef]
  55. Guo, Q. Global Forest Aboveground Biomass. Available online: http://guolablidar.com/ (accessed on 1 July 2016).
  56. Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
  57. Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole-Filled Srtm for the Globe Version 4. Available from the CGIAR-CSI SRTM 90 m Database. 2008. Available online: http://srtm.csi.cgiar.org (accessed on 1 May 2015).
  58. Carroll, M.; DiMiceli, C.; Sohlberg, R.; Townshend, J. 1 km Modis Normalized Difference Vegetation Index; University of Maryland: College Park, MA, USA, 2004. [Google Scholar]
  59. Channan, S.; Collins, K.; Emanuel, W. Global Mosaics of the Standard Modis Land Cover Type Data; University of Maryland and the Pacific Northwest National Laboratory: College Park, MA, USA, 2014. [Google Scholar]
  60. Friedl, M.A.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X. MODIS collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ. 2010, 114, 168–182. [Google Scholar] [CrossRef]
  61. Schutz, B.; Zwally, H.; Shuman, C.; Hancock, D.; DiMarzio, J. Overview of the icesat mission. Geophys. Res. Lett. 2005, 32, L21S01. [Google Scholar] [CrossRef]
  62. Lefsky, M.A.; Keller, M.; Pang, Y. Revised method for forest canopy height estimation from geoscience laser altimeter system waveforms. J. Appl. Remote Sens. 2007, 1, 013537. [Google Scholar]
  63. Lefsky, M.A. A global forest canopy height map from the moderate resolution imaging spectroradiometer and the geoscience laser altimeter system. Geophys. Res. Lett. 2010, 37, L15401. [Google Scholar] [CrossRef]
  64. Su, Y.; Guo, Q.; Ma, Q.; Li, W. Srtm dem correction in vegetated mountain areas through the integration of spaceborne lidar, airborne lidar, and optical imagery. Remote Sens. 2015, 7, 11202–11225. [Google Scholar] [CrossRef]
  65. Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef]
  66. Rabus, B.; Eineder, M.; Roth, A.; Bamler, R. The shuttle radar topography mission—A new class of digital elevation models acquired by spaceborne radar. ISPRS J. Photogramm. Remote Sens. 2003, 57, 241–262. [Google Scholar] [CrossRef]
  67. Takyu, M.; Aiba, S.-I.; Kitayama, K. Changes in biomass, productivity and decomposition along topographical gradients under different geological conditions in tropical lower montane forests on mount kinabalu, borneo. Oecologia 2003, 134, 397–404. [Google Scholar] [CrossRef] [PubMed]
  68. Malhi, Y.; Wood, D.; Baker, T.R.; Wright, J.; Phillips, O.L.; Cochrane, T.; Meir, P.; Chave, J.; Almeida, S.; Arroyo, L. The regional variation of aboveground live biomass in old-growth amazonian forests. Glob. Chang. Biol. 2006, 12, 1107–1138. [Google Scholar] [CrossRef]
  69. Liaw, A.; Wiener, M. Classification and regression by randomforest. R News 2002, 2, 18–22. [Google Scholar]
  70. Visser, H.; de Nijs, T. The map comparison kit. Environ. Model. Softw. 2006, 21, 346–358. [Google Scholar] [CrossRef]
  71. Avitabile, V.; Herold, M.; Henry, M.; Schmullius, C. Mapping biomass with Remote Sensing: A comparison of methods for the case study of uganda. Carbon Balance Manag. 2011, 6, 7. [Google Scholar] [CrossRef] [PubMed]
  72. Avitabile, V.; Herold, M.; Heuvelink, G.B.M.; Lewis, S.L.; Phillips, O.L.; Asner, G.P.; Armston, J.; Asthon, P.; Banin, L.F.; Bayol, N.; et al. An integrated pan-tropical biomass map using multiple reference datasets. Glob. Chang. Biol. 2016, 22, 1406–1420. [Google Scholar] [CrossRef] [PubMed]
  73. Ruesch, A.; Gibbs, H.K. New IPCC Tier-1 Global Biomass Carbon Map for the Year 2000; Carbon Dioxide Information Analysis Center, Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2008. [Google Scholar]
  74. Margolis, H.A.; Nelson, R.F.; Montesano, P.M.; Beaudoin, A.; Sun, G.; Andersen, H.-E.; Wulder, M.A. Combining satellite lidar, airborne lidar, and ground plots to estimate the amount and distribution of aboveground biomass in the boreal forest of north america. Can. J. For. Res. 2015, 45, 838–855. [Google Scholar] [CrossRef]
  75. Neigh, C.S.; Nelson, R.F.; Ranson, K.J.; Margolis, H.; Montesano, P.M.; Sun, G.; Kharuk, V.; Naesset, E.; Wulder, M.A.; Anderson, H. Lidar-Based Biomass Estimates, Boreal Forest Biome, Eurasia, 2005–2006; ORNL Distributed Active Archive Center: Oak Ridge, TN, USA, 2015. [Google Scholar]
  76. Blackard, J.A.; Finco, M.V.; Helmer, E.H.; Holden, G.R. Mapping us forest biomass using nationwide forest inventory data and moderate resolution information. Remote Sens. Environ. 2008, 112, 1658–1677. [Google Scholar] [CrossRef]
  77. Saatchi, S.; Yu, Y.; Alex, F.; Nuemann, M.; Chapman, B.; Nguyen; Nemani, R.; Ganguly, S.; Zhang, G.; et al. CMS US Forest Biomass Map. 2005. Available online: http://carbon.nasa.gov/cgi-bin/cms/inv_pgp.pl?pgid=582&format=1 (accessed on 1 July 2016). [Google Scholar]
  78. Mitchard, E.T.A.; Feldpausch, T.R.; Brienen, R.J.W.; Gonzalez, G.; Monteagudo, A.; Baker, T.R.; Lewis, S.L.; Lloyd, J.; Quesada, C.A.; Gloor, M. Markedly divergent estimates of amazon forest carbon density from ground plots and satellites. Glob. Ecol. Biogeogr. 2014, 23, 935–946. [Google Scholar] [CrossRef] [PubMed]
  79. Feldpausch, T.R.; Banin, L.; Phillips, O.L.; Baker, T.R.; Lewis, S.L.; Quesada, C.A.; Affum-Baffoe, K.; Arets, E.J.; Berry, N.J.; Bird, M. Height-diameter allometry of tropical forest trees. Biogeosciences 2011, 8, 1081–1106. [Google Scholar] [CrossRef] [Green Version]
  80. Santoro, M.; Beer, C.; Cartus, O.; Schmullius, C.; Shvidenko, A.; McCallum, I.; Wegmüller, U.; Wiesmann, A. Retrieval of growing stock volume in boreal forest using hyper-temporal series of envisat asar scansar backscatter measurements. Remote Sens. Environ. 2011, 115, 490–507. [Google Scholar] [CrossRef]
  81. Pang, Y.; Lefsky, M.; Sun, G.; Miller, M.; Li, Z. Temperate forest height estimation performance using ICESat GLAS data from different observation periods. Int. Arch. Photogram. Remote Sens. Spat. Inf. Sci. 2008, 37, 777–782. [Google Scholar]
Remotesensing 08 00565 g001 1024
Figure 1. The workflow for estimating global forest aboveground biomass (AGB) distribution from multisource remotely sensed data and ground inventory data.
Figure 1. The workflow for estimating global forest aboveground biomass (AGB) distribution from multisource remotely sensed data and ground inventory data.
Remotesensing 08 00565 g001
Remotesensing 08 00565 g002 1024
Figure 2. Geolocations of the collected ground inventory data. The background maps are the ecoregion zone map and land cover map from MODIS 2004.
Figure 2. Geolocations of the collected ground inventory data. The background maps are the ecoregion zone map and land cover map from MODIS 2004.
Remotesensing 08 00565 g002
Remotesensing 08 00565 g003 1024
Figure 3. Distributions of extrapolated GLAS-derived full-waveform parameters, (a) waveform extent; (b) leading edge extent; and (c) trailing edge extent. Note that non-forest coverage has been excluded from the maps.
Figure 3. Distributions of extrapolated GLAS-derived full-waveform parameters, (a) waveform extent; (b) leading edge extent; and (c) trailing edge extent. Note that non-forest coverage has been excluded from the maps.
Remotesensing 08 00565 g003
Remotesensing 08 00565 g004 1024
Figure 4. (a) The derived wall-to-wall map of global forest AGB in this study; (b) the absolute uncertainty induced by plot location uncertainty (estimated as the standard deviation of the 100 RF run results); and (c) the relative uncertainty induced by plot location uncertainty. The study region was bounded at 80° north latitude and 58° south latitude and from longitude −180° to 180°.
Figure 4. (a) The derived wall-to-wall map of global forest AGB in this study; (b) the absolute uncertainty induced by plot location uncertainty (estimated as the standard deviation of the 100 RF run results); and (c) the relative uncertainty induced by plot location uncertainty. The study region was bounded at 80° north latitude and 58° south latitude and from longitude −180° to 180°.
Remotesensing 08 00565 g004
Remotesensing 08 00565 g005 1024
Figure 5. Evaluation of predicted forest AGB using validation ground inventory dataset at the plot level. R2 represents the adjusted coefficient of determination, RMSE represents the root-mean-square error.
Figure 5. Evaluation of predicted forest AGB using validation ground inventory dataset at the plot level. R2 represents the adjusted coefficient of determination, RMSE represents the root-mean-square error.
Remotesensing 08 00565 g005
Remotesensing 08 00565 g006 1024
Figure 6. Comparison of the predicted forest AGB with IPCC suggested values at the ecological zone level. The outlier is the temperate oceanic forest in North America. R2 represents the adjusted coefficient of determination, and RMSE represents the root-mean-square error.
Figure 6. Comparison of the predicted forest AGB with IPCC suggested values at the ecological zone level. The outlier is the temperate oceanic forest in North America. R2 represents the adjusted coefficient of determination, and RMSE represents the root-mean-square error.
Remotesensing 08 00565 g006
Remotesensing 08 00565 g007 1024
Figure 7. The difference map between our global wall-to-wall forest AGB product and the products from (a) Saatchi et al. (2011) [48]; (b) Baccini et al. (2012) [49]; (c) Avitabile et al. (2015) [72]; and (d) Reusch & Gibbs (2008) [73] in pan-tropical forest areas.
Figure 7. The difference map between our global wall-to-wall forest AGB product and the products from (a) Saatchi et al. (2011) [48]; (b) Baccini et al. (2012) [49]; (c) Avitabile et al. (2015) [72]; and (d) Reusch & Gibbs (2008) [73] in pan-tropical forest areas.
Remotesensing 08 00565 g007
Remotesensing 08 00565 g008 1024
Figure 8. The spatial similarity map between our global wall-to-wall forest AGB product and the products from (a) Saatchi et al. (2011) [48]; (b) Baccini et al. (2012) [49]; (c) Avitabile et al. (2015) [72]; and (d) Reusch & Gibbs (2008) [73] in pan-tropical forest areas.
Figure 8. The spatial similarity map between our global wall-to-wall forest AGB product and the products from (a) Saatchi et al. (2011) [48]; (b) Baccini et al. (2012) [49]; (c) Avitabile et al. (2015) [72]; and (d) Reusch & Gibbs (2008) [73] in pan-tropical forest areas.
Remotesensing 08 00565 g008
Remotesensing 08 00565 g009 1024
Figure 9. The difference map between our global wall-to-wall forest AGB product and the products from (a) Margolis et al. (2015) [74]; (b) Thurner et al. (2014) [54]; and (c) Reusch & Gibbs (2008) [73] in the North America forest area.
Figure 9. The difference map between our global wall-to-wall forest AGB product and the products from (a) Margolis et al. (2015) [74]; (b) Thurner et al. (2014) [54]; and (c) Reusch & Gibbs (2008) [73] in the North America forest area.
Remotesensing 08 00565 g009
Remotesensing 08 00565 g010 1024
Figure 10. The spatial similarity map between our global wall-to-wall forest AGB product and the products from (a) Margolis et al. (2015) [74]; (b) Thurner et al. (2014) [54]; and (c) Reusch & Gibbs (2008) [73] in the North America boreal forest area.
Figure 10. The spatial similarity map between our global wall-to-wall forest AGB product and the products from (a) Margolis et al. (2015) [74]; (b) Thurner et al. (2014) [54]; and (c) Reusch & Gibbs (2008) [73] in the North America boreal forest area.
Remotesensing 08 00565 g010
Remotesensing 08 00565 g011 1024
Figure 11. The difference map between our global wall-to-wall forest AGB product and the products from (a) Neigh et al. (2015) [75]; (b) Thurner et al. (2014) [54]; and (c) Reusch & Gibbs (2008) [73] in the northern Eurasia boreal forest area.
Figure 11. The difference map between our global wall-to-wall forest AGB product and the products from (a) Neigh et al. (2015) [75]; (b) Thurner et al. (2014) [54]; and (c) Reusch & Gibbs (2008) [73] in the northern Eurasia boreal forest area.
Remotesensing 08 00565 g011
Remotesensing 08 00565 g012 1024
Figure 12. The spatial similarity map between our global wall-to-wall forest AGB product and the products from (a) Neigh et al. (2015) [75]; (b) Thurner et al. (2014) [54]; and (c) Reusch & Gibbs (2008) [73] in the northern Eurasia boreal forest area.
Figure 12. The spatial similarity map between our global wall-to-wall forest AGB product and the products from (a) Neigh et al. (2015) [75]; (b) Thurner et al. (2014) [54]; and (c) Reusch & Gibbs (2008) [73] in the northern Eurasia boreal forest area.
Remotesensing 08 00565 g012
Remotesensing 08 00565 g013 1024
Figure 13. The difference map between our global wall-to-wall forest AGB product and the products from (a) Blackard et al. (2008) [76]; (b) Saatchi et al. (2005) [77]; and (c) Reusch & Gibbs (2008) [73] in the U.S. forest area.
Figure 13. The difference map between our global wall-to-wall forest AGB product and the products from (a) Blackard et al. (2008) [76]; (b) Saatchi et al. (2005) [77]; and (c) Reusch & Gibbs (2008) [73] in the U.S. forest area.
Remotesensing 08 00565 g013
Remotesensing 08 00565 g014 1024
Figure 14. The spatial similarity map between our global wall-to-wall forest AGB product and the products from (a) Blackard et al. (2008) [76]; (b) Saatchi et al. (2005) [77]; and (c) Reusch & Gibbs (2008) [73] in the U.S. forest area.
Figure 14. The spatial similarity map between our global wall-to-wall forest AGB product and the products from (a) Blackard et al. (2008) [76]; (b) Saatchi et al. (2005) [77]; and (c) Reusch & Gibbs (2008) [73] in the U.S. forest area.
Remotesensing 08 00565 g014
Remotesensing 08 00565 g015 1024
Figure 15. The trend of global forest AGB density along the latitude. The line indicates the mean AGB and grey shadows show the stand deviation of AGB at corresponding latitude.
Figure 15. The trend of global forest AGB density along the latitude. The line indicates the mean AGB and grey shadows show the stand deviation of AGB at corresponding latitude.
Remotesensing 08 00565 g015
Table
Table 1. Variables used in the random forest method to model aboveground biomass of forests.
Table 1. Variables used in the random forest method to model aboveground biomass of forests.
VariableDatasetYearResolutionReference
Annual Mean Precipitation (mm)Worldclim1950–20001 kmHijmans et al., 2005 [56]
Precipitation Seasonality (Coefficient of Variation)Worldclim1950–20001 kmHijmans et al., 2005 [56]
Annual Mean Temperature (°C)Worldclim1950–20001 kmHijmans et al., 2005 [56]
Temperature Seasonality (standard deviation × 100)Worldclim1950–20001 kmHijmans et al., 2005 [56]
Elevation (m)SRTM20001 kmJarvis et al., 2008 [57]
SlopeSRTM20001 km
NDVIMOD13A220041 km[58]
Land CoverMCD12Q120041 km[59,60]
Waveform ExtentGLAS2004
Leading Edge ExtentGLAS2004
Trailing Edge ExtentGLAS2004
Table
Table 2. Main characteristics of the AGB maps used for the comparison in this study.
Table 2. Main characteristics of the AGB maps used for the comparison in this study.
AGB MapCoverageYearResolutionReference
Saatchi mapPan-tropic20001 km[48]
Baccini mapPan-tropic2007–2008500 m[49]
Avitabile mapPan-tropic~20001 km[72]
Ruesch & Gibbs mapGlobal20001 km[73]
Margolis mapNorth America2005–20061 km[74]
Thurner mapNorthern Hemisphere20101 km[54]
Neigh mapEuro-Asia2005–20061 km[75]
Blackard mapU.S.20011 km[76]
Saatchi mapU.S.~20051 km[77]
Table
Table 3. The continental-level and national-level forest AGB density and biomass stock in this study.
Table 3. The continental-level and national-level forest AGB density and biomass stock in this study.
ContinentMean AGB (Mg/ha)Forest Area (Mha)Total AGB (Pg)
Africa333.34 ± 63.80191.064.65
Asia172.28 ± 94.75762.2143.14
Australia415.66 ± 131.7520.38.69
North America166.48 ± 84.97459.177.46
Oceania424.30 ± 114.0321.99.30
South America301.68 ± 67.43608.6188.68
Europe132.97 ± 50.70310.140.83
CountryMean AGB (Mg/ha)Forest Area (Mha)Total AGB (Pg)
Australia415.85 ± 131.6920.288.68
Brazil306.79 ± 36.1317.3497.44
Canada141.38 ± 64.68268.8138.26
China160.74 ± 45.16101.3416.41
Democratic Republic of the Congo342.01 ± 49.17103.6635.52
Finland89.42 ± 7.9915.511.37
Indonesia328.25 ± 43.39102.7834.04
Japan175.78 ± 41.6922.834.03
New Zealand488.69 ± 107.9412.246.07
Norway210.15 ± 116.769.041.95
Russian Federation110.14 ± 23.48530.4859.87
Sweden108.11 ± 16.3926.322.82
United Kingdom265.09 ± 87.33.220.87
United States180.96 ± 92.44150.6127.71

Share and Cite

MDPI and ACS Style

Hu, T.; Su, Y.; Xue, B.; Liu, J.; Zhao, X.; Fang, J.; Guo, Q. Mapping Global Forest Aboveground Biomass with Spaceborne LiDAR, Optical Imagery, and Forest Inventory Data. Remote Sens. 2016, 8, 565. https://doi.org/10.3390/rs8070565

AMA Style

Hu T, Su Y, Xue B, Liu J, Zhao X, Fang J, Guo Q. Mapping Global Forest Aboveground Biomass with Spaceborne LiDAR, Optical Imagery, and Forest Inventory Data. Remote Sensing. 2016; 8(7):565. https://doi.org/10.3390/rs8070565

Chicago/Turabian Style

Hu, Tianyu, Yanjun Su, Baolin Xue, Jin Liu, Xiaoqian Zhao, Jingyun Fang, and Qinghua Guo. 2016. "Mapping Global Forest Aboveground Biomass with Spaceborne LiDAR, Optical Imagery, and Forest Inventory Data" Remote Sensing 8, no. 7: 565. https://doi.org/10.3390/rs8070565

APA Style

Hu, T., Su, Y., Xue, B., Liu, J., Zhao, X., Fang, J., & Guo, Q. (2016). Mapping Global Forest Aboveground Biomass with Spaceborne LiDAR, Optical Imagery, and Forest Inventory Data. Remote Sensing, 8(7), 565. https://doi.org/10.3390/rs8070565

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop