A Conversion Method to Determine the Regional Vegetation Cover Factor from Standard Plots Based on Large Sample Theory and TM Images: A Case Study in the Eastern Farming-Pasture Ecotone of Northern China
Abstract
:1. Introduction
2. Study Area
3. Materials and Methods
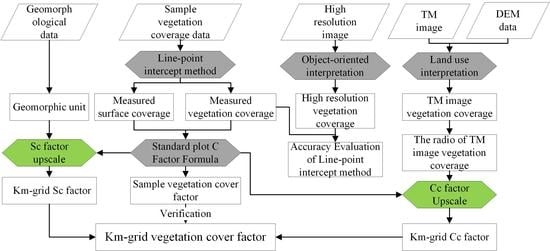
3.1. Basic Idea and Research Framework
3.2. Materials
3.3. Methods
3.3.1. Canopy Coverage Factor Upscaling
3.3.2. TM Image Land Use Interpretation
3.3.3. Surface Coverage Factor Upscaling
3.3.4. Regional Vegetation Cover Factor
4. Results
4.1. C Factor of the Survey Sample Area
4.2. Fractional Vegetation Cover (FVC) in the Study Area
4.3. C Factor in the Study Area
5. Discussion
5.1. Relationship between Line-Point Estimated Vegetation Coverage and Intercept Vegetation Coverage in the Km-Sized Grid
5.2. Comparison of Our Method and the C Factor Algorithm Based on Remote Sensing Vegetation Index
5.3. Uncertainties of the Calculated C Factors
5.3.1. The Empirical Parameters of the C Factor Need to Be Further Confirmed
5.3.2. Differences between the Remote Sensing Image Coverage and the Measured Coverage
5.3.3. The Accuracy of the TM Image Interpretation
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. The C Factor Algorithm Based on the Remote Sensing Vegetation Index
1. Calculate Vegetation Coverage Based on the Vegetation Index

| Different Geographical Elements | Dryness Degree | Sand Land or Not | Landform Type | Vegetation Type | |
|---|---|---|---|---|---|
| Pearson correlation | 0.386 * | −0.206 | 0.114 | −0.283 | |
| Significance (2-tail) | 0.012 | 0.190 | 0.473 | 0.069 | |
| Dryness Grade | Unstandardized Coefficient | Normalization Coefficient | t | Significance | ||
|---|---|---|---|---|---|---|
| B | Standard Error | Beta | ||||
| Dryness 1 | (constant) | 0.263 | 0.075 | 3.516 | 0.003 | |
| EVI coefficient | 0.938 | 0.201 | 0.780 | 4.667 | 0.000 | |
| Dryness 2 | (constant) | 0.548 | 0.046 | 11.903 | 0.000 | |
| EVI coefficient | 0.347 | 0.122 | 0.633 | 2.836 | 0.015 | |
| Dryness 3 | (constant) | 0.406 | 0.122 | 3.336 | 0.009 | |
| EVI coefficient | 1.009 | 0.356 | 0.687 | 2.839 | 0.019 | |
2. C Factor Based on the Vegetation Index

References
- European Environment Agency (EEA). Environment in the European Union at the Turn of the Century; European Environment Agency: Copenhagen, Denmark, 1999. [Google Scholar]
- Füssel, H.-M.; Jol, A. Climate Change, Impacts and Vulnerability in Europe 2012: An Indicator-Based Report; Publications Office of the European Union: Copenhagen, Denmark, 2012. [Google Scholar]
- Lin, D.; Guo, H.; Lian, F.; Gao, Y.; Yue, Y.; Wang, J.A. A Quantitative Method for Long-Term Water Erosion Impacts on Productivity with a Lack of Field Experiments: A Case Study in Huaihe Watershed, China. Sustainability 2016, 8, 675. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Poesen, J.; Ballabio, C.; Lugato, E.; Meusburger, K.; Montanarella, L.; Alewell, C. The new assessment of soil loss by water erosion in Europe. Environ. Sci. Policy 2015, 54, 438–447. [Google Scholar] [CrossRef]
- Panagos, P.; Ballabio, C.; Borrelli, P.; Meusburger, K. Spatio-temporal analysis of rainfall erosivity and erosivity density in Greece. Catena 2016, 137, 161–172. [Google Scholar] [CrossRef]
- Nachtergaele, F.; Petri, M.; Biancalani, R.; Van Lynden, G.; Van Velthuizen, H. An Information Database for Land Degradation Assessment at Global Level; Global Land Degradation Information System (GLADIS): Rome, Italy, 2010. [Google Scholar]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses—A Guide to Conservation Planning; U.S. Depatment of Agriculture: Washington, DC, USA, 1978.
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; McCool, D.K.; Yoder, D.C. Predicting Soil Erosion By Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE); United States Department of Agriculture: Washington, DC, USA, 1997; Volume 703.
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; Porter, J.P. RUSLE: Revised universal soil loss equation. J. Soil Water Conserv. 1991, 46, 30–33. [Google Scholar]
- Liu, B.; Zhang, K.; Xie, Y. An empirical soil loss equation. In Proceedings of the 12th International Soil Conservation Organization Conference, Beijing, China, 26–31 May 2002; Tsinghua University Press: Beijing, China, 2002; p. 15. [Google Scholar]
- Jones, C.; Lowe, J.; Liddicoat, S.; Betts, R. Committed terrestrial ecosystem changes due to climate change. Nat. Geosci. 2009, 2, 484–487. [Google Scholar] [CrossRef]
- Benkobi, L.; Trlica, M.; Smith, J.L. Evaluation of a refined surface cover subfactor for use in RUSLE. J. Range Manag. 1994, 47, 74–78. [Google Scholar] [CrossRef]
- Biesemans, J.; Van Meirvenne, M.; Gabriels, D. Extending the RUSLE with the Monte Carlo error propagation technique to predict long-term average off-site sediment accumulation. J. Soil Water Conserv. 2000, 55, 35–42. [Google Scholar]
- Risse, L.M.; Nearing, M.A.; Laflen, J.M.; Nicks, A.D. Error assessment in the universal soil loss equation. Soil Sci. Soc. Am. J. 1993, 57, 825–833. [Google Scholar] [CrossRef]
- Suriyaprasit, M.; Shrestha, D.P. Deriving Land Use and Canopy Cover Factor from Remote Sensing and Field Data in Inaccessible Mountainous Terrain for Use in Soil Erosion Modelling. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 1747–1750. [Google Scholar]
- Warren, S.D.; Mitasova, H.; Hohmann, M.G.; Landsberger, S.; Iskander, F.Y.; Ruzycki, T.S.; Senseman, G.M. Validation of a 3-D enhancement of the Universal Soil Loss Equation for prediction of soil erosion and sediment deposition. Catena 2005, 64, 281–296. [Google Scholar] [CrossRef]
- Wang, G.; Wente, S.; Gertner, G.; Anderson, A. Improvement in mapping vegetation cover factor for the universal soil loss equation by geostatistical methods with Landsat Thematic Mapper images. Int. J. Remote Sens. 2002, 23, 3649–3667. [Google Scholar] [CrossRef]
- Lu, D.; Li, G.; Valladares, G.S.; Batistella, M. Mapping soil erosion risk in Rondonia, Brazilian Amazonia: Using RUSLE, remote sensing and GIS. Land Degrad. Dev. 2004, 15, 499–512. [Google Scholar] [CrossRef] [Green Version]
- Patric, J.H. Soil erosion in the eastern forest. J. For. 1976, 74, 671–677. [Google Scholar]
- Gertner, G.; Wang, G.; Fang, S.; Anderson, A.B. Mapping and uncertainty of predictions based on multiple primary variables from joint co-simulation with Landsat TM image and polynomial regression. Remote Sens. Environ. 2002, 83, 498–510. [Google Scholar] [CrossRef]
- Fu, B.; Xu, Y.; Lv, Y. Scale Characteristics and Coupled Research of Landscape Pattern and Soil and Water Loss. Adv. Earth Sci. 2010, 25, 673–681. [Google Scholar]
- Lehmann, E.L. Elements of Large-Sample Theory; Springer Science & Business Media: Dordrecht, The Netherlands, 2004. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. ACM SIGMOBILE Mob. Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef]
- Ji, L.; Wang, J.; Geng, X.; Gong, P. Probabilistic graphical model based approach for water mapping using GaoFen-2 (GF-2) high resolution imagery and Landsat 8 time series. arXiv, 2016; arXiv:1612.07801. [Google Scholar]
- Floyd, D.A.; Anderson, J.E. A comparison of three methods for estimating plant cover. J. Ecol. 1987, 75, 221–228. [Google Scholar] [CrossRef]
- Godínez-Alvarez, H.; Herrick, J.E.; Mattocks, M.; Toledo, D.; Van Zee, J. Comparison of three vegetation monitoring methods: Their relative utility for ecological assessment and monitoring. Ecol. Indic. 2009, 9, 1001–1008. [Google Scholar] [CrossRef]
- Hanley, T.A. A comparison of the line-interception and quadrat estimation methods of determining shrub canopy coverage. J. Range Manag. 1978, 60–62. [Google Scholar] [CrossRef]
- Edwards, T.A. Monitoring Plant and Animal Populations. Pac. Conserv. Biol. 2002, 8, 219. [Google Scholar] [CrossRef]
- Duncan, J.; Stow, D.; Franklin, J.; Hope, A. Assessing the relationship between spectral vegetation indices and shrub cover in the Jornada Basin, New Mexico. Int. J. Remote Sens. 1993, 14, 3395–3416. [Google Scholar] [CrossRef]
- Purevdorj, T.; Tateishi, R.; Ishiyama, T.; Honda, Y. Relationships between percent vegetation cover and vegetation indices. Int. J. Remote Sens. 1998, 19, 3519–3535. [Google Scholar] [CrossRef]
- Chen, J.; Chen, J.; Liao, A.; Cao, X.; Chen, L.; Chen, X.; He, C.; Han, G.; Peng, S.; Lu, M.; et al. Global land cover mapping at 30 m resolution: A POK-based operational approach. ISPRS J. Photogramm. Remote Sens. 2015, 103, 7–27. [Google Scholar] [CrossRef]
- Gong, P.; Wang, J.; Yu, L.; Zhao, Y.; Zhao, Y.; Liang, L.; Niu, Z.; Huang, X.; Fu, H.; Liu, S. Finer resolution observation and monitoring of global land cover: First mapping results with Landsat TM and ETM+ data. Int. J. Remote Sens. 2013, 34, 2607–2654. [Google Scholar] [CrossRef]
- Liu, J.; Liu, M.; Tian, H.; Zhuang, D.; Zhang, Z.; Zhang, W.; Tang, X.; Deng, X. Spatial and temporal patterns of China’s cropland during 1990 2000: An analysis based on Landsat TM data. Remote Sens. Environ. 2005, 98, 442–456. [Google Scholar] [CrossRef]
- Jengo, C. Rulegen v1. 02 Extension in ENVI; ITT Visual Information Solutions User-Contributed Library: Boulder, Colorado, 2004. [Google Scholar]
- Zhao, Y.; Gong, P.; Yu, L.; Hu, L.; Li, X.; Li, C.; Zhang, H.; Zheng, Y.; Wang, J.; Zhao, Y. Towards a common validation sample set for global land-cover mapping. Int. J. Remote Sens. 2014, 35, 4795–4814. [Google Scholar] [CrossRef]
- Bollinne, A. Adjusting the universal soil loss equation to use in Western Europe. In Soil Erosion and Conservation Society of America; El-Swaify, S.A., Moldenhauer, W.C., Lo, A., Eds.; Soil Conservation Society of America: Ankeny, LA, USA, 1985; pp. 206–213. [Google Scholar]
- Jin, Z.; Shi, P.; Hou, F. Soil Erosion System Model and Control Model in Huangfuchuan Watershed of the Yellow River; Ocean Press: Beijing, China, 1992. [Google Scholar]
- Jiang, Z.; Wang, Z.; Liu, Z. Quantitative study on spatial variation of soil erosion in a small watershed in the loess hilly region. J. Soil Eros. Soil Conserv. 1996, 2, 1–9. [Google Scholar]
- Liu, B. Soil Loss Equation of Beijing; Science Press: Beijing, China, 2010. [Google Scholar]
- Landis, J.R.; Koch, G.G. Measurement of observer agreement for categorical data. Biometrics 1977, 33, 159–174. [Google Scholar] [CrossRef] [PubMed]










| Sample ID | Longitude | Latitude | County | Measuring Point | Geomorphic Unit * |
|---|---|---|---|---|---|
| 1 | 115°6′55″E | 41°40′57″N | Taibus Banner | 1983 | Wavy High Plains |
| 2 | 115°14′3″E | 42°0′40″N | Taibus Banner | 2012 | Wavy High Plains |
| 3 | 115°54′25″E | 42°16′53″N | Zhenglan Banner | 2002 | Rising hills |
| 4 | 114°39′9″E | 42°11′33″N | Hua De County | 1936 | Layered high plain |
| 5 | 113°54′48″E | 41°55′2″N | Hua De County | 1953 | Wavy High Plains |
| 6 | 113°30′56″E | 41°32′14″N | Shangdu County | 1996 | Wavy High Plains |
| 7 | 113°16′26″E | 41°13′44″N | Qahar Right Wing Rear Banner | 1989 | Layered high plain |
| 8 | 111°16′16″E | 39°55′19″N | Jungar Banner | 1985 | Rising hills |
| 9 | 113°7′22″E | 40°51′6″N | Qahar Right Wing Front Banner | 2008 | Layered high plain |
| 10 | 113°55′3″E | 40°53′12″N | Xinghe County | 1995 | Rising hills |
| 11 | 118°50′4″E | 42°11′30″N | Hongshan District | 2006 | Rising hills |
| 12 | 118°48′29″E | 42°19′21″N | Hongshan District | 2000 | Rising hills |
| 13 | 119°39′56″E | 42°27′48″N | Aohan Banner | 1990 | Rising hills |
| 14 | 120°49′5″E | 42°47′45″N | Naiman banner | 1999 | Sandy land |
| 15 | 122°13′59″E | 43°19′28″N | Horqin Left Wing Rear Banner | 1985 | Sandy land |
| 16 | 122°2′13″E | 44°9′47″N | Horqin Left Wing Middle Banner | 2000 | Sandy land |
| 17 | 121°45′36″E | 44°56′28″N | Horqin Right Wing Middle Banner | 1988 | Sandy land |
| 18 | 122°9′22″E | 46°9′38″N | Horqin Right Wing Front Banner | 2015 | Sandy land |
| 19 | 120°9′48″E | 49°9′29″N | Evenki Autonomous Banner | 2000 | Valley plain |
| 20 | 119°30′58″E | 49°19′55″N | Chen Barag Banner | 2008 | Layered high plain |
| 21 | 118°25′21″E | 49°28′49″N | Chen Barag Banner | 2008 | Wavy High Plains |
| Sample ID | Cropland (%) | Grassland (%) | Litter Cover (%) | Fecal Cover (%) | Gravel Cover (%) | Wood Land (%) | Bareland (%) | Road (%) | Built-up Land (%) | Water (%) | Sc Ratio (%) | C |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1A | 0.00 | 49.55 | 4.41 | 2.71 | 4.51 | 0.10 | 42.53 | 0.70 | 0.00 | 0.00 | 11.63 | 0.34 |
| 1B | 32.76 | 24.14 | 2.13 | 4.46 | 0.81 | 0.00 | 35.50 | 1.01 | 0.00 | 0.00 | 7.40 | 0.55 |
| 2A | 1.30 | 16.62 | 0.50 | 1.00 | 4.70 | 1.80 | 28.23 | 9.71 | 37.54 | 0.00 | 6.21 | 0.69 |
| 2B | 27.44 | 34.16 | 4.94 | 1.28 | 6.02 | 0.39 | 30.11 | 6.42 | 0.00 | 0.00 | 12.24 | 0.48 |
| 3A | 0.00 | 55.60 | 4.60 | 1.00 | 3.80 | 0.00 | 35.20 | 3.20 | 0.40 | 0.00 | 9.40 | 0.31 |
| 3B | 0.00 | 59.38 | 6.39 | 3.89 | 9.88 | 0.00 | 27.74 | 0.00 | 2.59 | 0.00 | 20.16 | 0.22 |
| 4A | 56.57 | 8.79 | 0.10 | 0.00 | 7.47 | 0.00 | 30.30 | 4.24 | 0.00 | 0.00 | 7.58 | 0.37 |
| 4B | 20.51 | 28.96 | 1.16 | 0.00 | 20.08 | 1.27 | 42.39 | 5.71 | 0.00 | 0.00 | 21.25 | 0.42 |
| 5A | 8.95 | 20.95 | 19.05 | 0.11 | 8.53 | 0.84 | 48.42 | 1.68 | 0.00 | 0.00 | 27.68 | 0.40 |
| 5B | 0.00 | 5.48 | 17.05 | 0.80 | 5.68 | 2.09 | 71.19 | 3.39 | 0.00 | 0.00 | 23.53 | 0.50 |
| 6A | 0.50 | 26.03 | 14.47 | 0.00 | 4.92 | 0.70 | 35.78 | 10.45 | 12.06 | 0.00 | 19.40 | 0.44 |
| 6B | 0.00 | 36.66 | 12.59 | 0.20 | 7.99 | 4.90 | 43.06 | 2.60 | 0.00 | 0.00 | 20.78 | 0.36 |
| 7A | 0.00 | 33.64 | 5.56 | 0.71 | 21.31 | 1.01 | 54.75 | 4.34 | 0.00 | 0.00 | 27.58 | 0.32 |
| 7B | 0.00 | 30.03 | 0.00 | 1.00 | 25.13 | 0.00 | 54.75 | 0.90 | 13.31 | 0.00 | 26.13 | 0.35 |
| 8A | 6.29 | 18.58 | 27.01 | 0.00 | 0.00 | 7.82 | 30.05 | 9.64 | 0.61 | 0.00 | 27.01 | 0.37 |
| 8B | 7.30 | 25.20 | 14.20 | 0.00 | 1.50 | 3.80 | 18.70 | 2.50 | 28.30 | 0.00 | 15.70 | 0.50 |
| 9A | 2.78 | 33.53 | 9.42 | 0.10 | 0.89 | 2.48 | 46.23 | 1.79 | 1.39 | 2.28 | 10.42 | 0.50 |
| 9B | 2.80 | 48.60 | 8.80 | 0.30 | 1.50 | 5.00 | 32.80 | 1.70 | 0.00 | 0.00 | 10.60 | 0.38 |
| 10A | 16.38 | 38.69 | 7.34 | 0.50 | 4.32 | 9.05 | 24.02 | 4.02 | 0.00 | 0.00 | 12.16 | 0.44 |
| 10B | 12.80 | 35.60 | 1.40 | 0.00 | 8.50 | 8.50 | 22.90 | 2.30 | 7.50 | 9.00 | 9.90 | 0.48 |
| 11A | 0.00 | 43.60 | 7.00 | 0.10 | 0.10 | 5.00 | 34.70 | 4.20 | 5.40 | 0.00 | 7.20 | 0.44 |
| 11B | 1.19 | 29.03 | 11.93 | 0.10 | 0.20 | 26.64 | 21.77 | 9.34 | 0.00 | 0.00 | 12.23 | 0.28 |
| 12A | 0.00 | 25.20 | 7.30 | 0.20 | 0.00 | 28.60 | 24.50 | 2.80 | 11.50 | 0.00 | 7.50 | 0.29 |
| 12B | 15.40 | 24.30 | 6.60 | 0.00 | 2.10 | 35.70 | 11.40 | 3.00 | 3.60 | 0.00 | 8.70 | 0.32 |
| 13A | 77.34 | 8.26 | 0.20 | 0.00 | 0.91 | 1.31 | 7.15 | 2.82 | 2.92 | 0.00 | 1.11 | 0.24 |
| 13B | 75.83 | 13.24 | 0.00 | 0.00 | 0.00 | 3.91 | 4.81 | 1.91 | 0.30 | 0.00 | 0.00 | 0.30 |
| 14A | 0.00 | 7.34 | 3.22 | 0.00 | 0.00 | 54.33 | 35.11 | 0.00 | 0.00 | 0.00 | 3.22 | 0.10 |
| 14B | 0.00 | 42.99 | 6.87 | 0.00 | 0.00 | 31.44 | 18.71 | 0.00 | 0.00 | 0.00 | 6.87 | 0.26 |
| 15A | 0.00 | 35.36 | 14.08 | 0.20 | 0.00 | 19.05 | 31.31 | 0.00 | 0.00 | 0.00 | 14.29 | 0.31 |
| 15B | 0.00 | 39.78 | 13.03 | 0.20 | 0.00 | 24.85 | 22.14 | 0.00 | 0.00 | 0.00 | 13.23 | 0.27 |
| 16A | 0.00 | 19.10 | 24.40 | 0.00 | 0.00 | 31.90 | 23.30 | 1.30 | 0.00 | 0.00 | 24.40 | 0.17 |
| 16B | 0.00 | 38.30 | 3.10 | 0.60 | 0.30 | 0.40 | 52.40 | 0.00 | 0.00 | 5.20 | 4.00 | 0.52 |
| 17A | 0.00 | 5.38 | 29.51 | 0.00 | 0.10 | 35.60 | 28.90 | 0.61 | 0.00 | 0.00 | 29.61 | 0.07 |
| 17B | 12.57 | 27.05 | 2.79 | 0.00 | 0.10 | 33.23 | 21.96 | 2.40 | 0.00 | 0.00 | 2.89 | 0.38 |
| 18A | 0.00 | 38.08 | 16.13 | 0.00 | 9.52 | 22.14 | 20.94 | 2.71 | 0.00 | 0.00 | 25.65 | 0.21 |
| 18B | 19.08 | 18.58 | 3.93 | 0.00 | 0.39 | 22.62 | 31.27 | 4.52 | 0.00 | 0.00 | 4.33 | 0.46 |
| 19A | 0.00 | 47.50 | 45.60 | 0.10 | 0.00 | 0.00 | 6.80 | 0.00 | 0.00 | 0.00 | 45.70 | 0.16 |
| 19B | 0.00 | 39.10 | 29.60 | 2.30 | 0.80 | 1.70 | 23.00 | 0.80 | 0.00 | 0.00 | 32.70 | 0.26 |
| 20A | 0.00 | 49.30 | 50.70 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 50.70 | 0.14 |
| 20B | 0.00 | 47.22 | 43.06 | 0.30 | 0.00 | 4.76 | 1.59 | 0.00 | 0.00 | 2.88 | 43.35 | 0.18 |
| 21A | 0.00 | 13.66 | 38.19 | 1.89 | 0.10 | 1.60 | 37.89 | 1.89 | 4.89 | 0.00 | 40.18 | 0.32 |
| 21B | 0.00 | 28.16 | 41.79 | 0.70 | 0.10 | 2.29 | 25.37 | 1.69 | 0.00 | 0.00 | 42.59 | 0.25 |
| N | Correlation | Significance | |
|---|---|---|---|
| Interpretation & measured Vegetation coverage | 63 | 0.760 | 0.000 |
| Paired Differences | t | df | Significance (2-Tail) | |||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std. Deviation | Std. Error Mean | 95% Confidence Interval of the Difference | |||||
| Lower | Upper | |||||||
| Interpretation & measured coverage | −0.03 | 0.12 | 0.02 | −0.06 | −0.002 | −0.03 | 0.12 | 0.038 |
| True Surface | ||||||||
|---|---|---|---|---|---|---|---|---|
| Water Body | Built-up Land | Grassland | Cropland | Woodland | Unused Land | User’s Accuracy (%) | ||
| Land use classification results | Water body | 40 | 0 | 1 | 4 | 1 | 1 | 85.1 |
| Built-up land | 0 | 61 | 7 | 17 | 8 | 5 | 62.24 | |
| Grassland | 1 | 9 | 551 | 120 | 41 | 61 | 70.37 | |
| Cropland | 0 | 10 | 53 | 443 | 60 | 18 | 75.86 | |
| Woodland | 0 | 3 | 39 | 49 | 234 | 10 | 69.85 | |
| Unused land | 0 | 3 | 14 | 14 | 4 | 111 | 76.03 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, D.; Gao, Y.; Wu, Y.; Shi, P.; Yang, H.; Wang, J. A Conversion Method to Determine the Regional Vegetation Cover Factor from Standard Plots Based on Large Sample Theory and TM Images: A Case Study in the Eastern Farming-Pasture Ecotone of Northern China. Remote Sens. 2017, 9, 1035. https://doi.org/10.3390/rs9101035
Lin D, Gao Y, Wu Y, Shi P, Yang H, Wang J. A Conversion Method to Determine the Regional Vegetation Cover Factor from Standard Plots Based on Large Sample Theory and TM Images: A Case Study in the Eastern Farming-Pasture Ecotone of Northern China. Remote Sensing. 2017; 9(10):1035. https://doi.org/10.3390/rs9101035
Chicago/Turabian StyleLin, Degen, Yuan Gao, Yaoyao Wu, Peijun Shi, Huiming Yang, and Jing’ai Wang. 2017. "A Conversion Method to Determine the Regional Vegetation Cover Factor from Standard Plots Based on Large Sample Theory and TM Images: A Case Study in the Eastern Farming-Pasture Ecotone of Northern China" Remote Sensing 9, no. 10: 1035. https://doi.org/10.3390/rs9101035
APA StyleLin, D., Gao, Y., Wu, Y., Shi, P., Yang, H., & Wang, J. (2017). A Conversion Method to Determine the Regional Vegetation Cover Factor from Standard Plots Based on Large Sample Theory and TM Images: A Case Study in the Eastern Farming-Pasture Ecotone of Northern China. Remote Sensing, 9(10), 1035. https://doi.org/10.3390/rs9101035