The Geometry of Large Tundra Lakes Observed in Historical Maps and Satellite Images
Abstract
:1. Introduction
- To develop image-processing routines that segment historical topographic maps and recent satellite images, and allow us to visualize tundra lakes in binary (black and white) images.
- To calculate area–perimeter values for each of the individual lakes in our two sources of data.
- To measure the geometrical properties of the tundra lakes in our two sources of data by calculating their fractal dimension.
2. Materials and Methods
2.1. Detection of Lakes in Historical Maps
2.2. Detection of Lakes in Google Earth Engine Images
2.3. Calculating the Geometrical Properties of Lakes
3. Results
3.1. Geometrical Properties of Tundra Lakes in Historical Maps and Satellite Imagery
3.2. Statistical Properties of Tundra Lakes Distribution in Historical Maps and Satellite Imagery
4. Discussion
4.1. Image Analysis Effectiveness and Changes in Lake Size over Time
4.2. Phase Transitions and the Complex Geometry of Tundra Lake Patterns
5. Conclusions
- (1)
- An image processing strategy that combines color thresholding and region growing allows us to segment historical maps and satellite images. This isolates lakes from other information in these images. In the case of historical maps, this other information includes the distribution of wetlands, and in the case of satellite images includes vegetation, soil and other components of the land surface.
- (2)
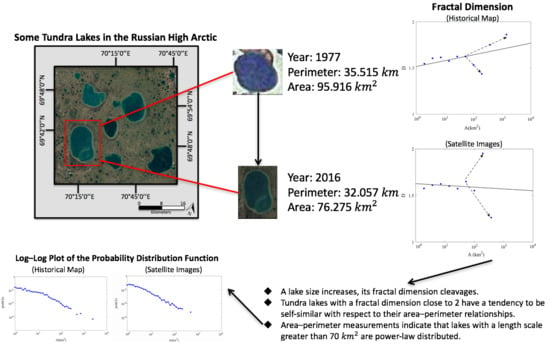
- The fractal dimension of lakes within the size range 1–70 km observed in historical maps is on average (Figure 6a). However, the fractal dimension of lakes larger than 100 km displays bifurcating behavior: the fractal dimension of some of these large lakes is and the fractal dimension of some of these large lakes is (Figure 6a).
- (3)
- (4)
- Area–perimeter measurements for each of the individual lakes in our analyses show that, for lakes in our historical maps, those with a length scale larger than 100 km are power-law distributed with a tail exponent (). For lakes in the satellite images we have analyzed, those with a length scale larger than 70 km are also power-law distributed with a tail exponent (). Similar exponents have been observed for other lakes on the Earth surface [30].
- (5)
- We have undertaken a preliminary analysis of the changes in lake size that have taken place in the 39 year interval between the production of the historical map we have used and the satellite images we have examined. We find that some lakes in our study region have increased in size over time, whereas others have decreased in size over time. Changes in lake size during this time interval can be up to half the size of the lake as recorded in the historical map.
Acknowledgments
Author Contributions
Conflicts of Interest
References and Notes
- Duarte, C.M.; Lenton, T.M.; Wadhams, P.; Wassmann, P. Abrupt climate change in the Arctic. Nat. Clim. Change 2012, 2, 60–62. [Google Scholar] [CrossRef]
- Hinzman, L.D.; Deal, C.J.; McGuire, A.D.; Mernild, S.H.; Polyakov, I.V.; Walsh, J.E. Trajectory of the Arctic as an integrated system. Ecol. Appl. 2013, 23, 1837–1868. [Google Scholar] [CrossRef] [PubMed]
- Lenton, T.M.; Held, H.; Kriegler, E.; Hall, J.W.; Lucht, W.; Rahmstorf, S.; Schellnhuber, H.J. Tipping elements in the Earth’s climate system. Proc. Natl. Acad. Sci. USA 2008, 105, 1786–1793. [Google Scholar] [CrossRef] [PubMed]
- Schuur, E.A.G.; McGuire, A.D.; Schadel, C.; Grosse, G.; Harden, J.W.; Hayes, D.J.; Hugelius, G.; Koven, C.D.; Kuhry, P.; Lawrence, D.M.; et al. Climate change and the permafrost carbon feedback. Nature 2015, 520, 171–179. [Google Scholar] [CrossRef] [PubMed]
- Hope, C.; Schaefer, K. Economic impacts of carbon dioxide and methane released from thawing permafrost. Nat. Clim. Change 2016, 6, 56–59. [Google Scholar] [CrossRef]
- Wik, M.; Ruth, K.V.; Anthoney, K.W.; MacIntyre, S.; Bastviken, D. Climate-sensitive northern lakes and ponds are critical components of methane release. Nat. Geosci. 2016, 9, 99–105. [Google Scholar] [CrossRef]
- Walter, K.M.; Zimov, S.A.; Chanton, J.P.; Verbyla, D.; Chapin, F.S., III. Methane bubbling from Siberian thaw lakes as positive feedback to climate warming. Nature 2006, 443, 71–75. [Google Scholar] [CrossRef] [PubMed]
- Golubyatnikov, L.L.; Kazantsev, V.S. Contribution of tundra lakes in Western Siberia to the atmospheric methane budget. Izv. Atmos. Ocean. Phys. 2013, 49, 395–403. [Google Scholar] [CrossRef]
- Andresen, C.G.; Lougheed, V.L. Disappearing Arctic tundra ponds: Fine-scale analysis of surface hydrology in drained thaw lake basins over a 65 year period (1948–2013). J. Geophys. Res. Biogeosci. 2015, 120, 1–14. [Google Scholar] [CrossRef]
- Legleiter, C.J.; Tedesco, M.; Smith, L.C.; Arp, C.D.; Behar, A.E.; Overstreet, B.T. Mapping the bathymetry of supraglacial lakes and streams on the Greenland ice sheet using field measurements and high-resolution satellite images. Cryosphere 2014, 8, 215–228. [Google Scholar] [CrossRef]
- Hohenegger, C.; Alali, B.; Steffen, K.R.; Perovich, D.K.; Golden, K.M. Transition in the fractal geometry of Arctic melt ponds. Cryosphere 2013, 6, 1157–1162. [Google Scholar] [CrossRef] [Green Version]
- Karlsson, J.M.; Lyon, S.W.; Destouni, G. Temporal behavior of lake size-distribution in a thawing permafrost landscape in northwestern Siberia. Remote Sens. 2014, 6, 621–636. [Google Scholar] [CrossRef]
- Polishchuk, Y.M.; Bryksina, N.A.; Polishchuk, V.Y. Remote analysis of changes in the number of small thermokarst lakes and their distribution with respect to their sizes in the cryolithozone of Western Siberia. Izv. Atmos. Ocean. Phys. 2015, 51, 999–1006. [Google Scholar] [CrossRef]
- Nitze, I.; Grosse, G.; Jones, B.M.; Arp, C.D.; Ulrich, M.; Fedorov, A.; Veremeeva, A. A Landsat based trend analysis of lake dynamics across northern permafrost regions. Remote Sens. 2017, 9, 640. [Google Scholar] [CrossRef]
- Mander, L.; Dekker, S.C.; Li, M.; Mio, W.; Punyasena, S.W.; Lenton, T.M. A morphometric analysis of vegetation patterns in dryland ecosystems. R. Soc. Open Sci. 2017, 4. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.J.; Jung, H.S. Melt Pond mapping with high-resolution SAR: The first view. Proc. IEEE. 2013, 101, 748–758. [Google Scholar] [CrossRef]
- Polishchuk, Y.M.; Bogdanov, A.N.; Polishchuk, V.Y.; Manasypov, R.M.; Shirokova, L.S.; Kirpotin, S.N.; Pokrovsky, O.S. Size distribution, surface coverage, water, carbon, and metal storage of thermokarst lakes in the permafrost zone of the Western Siberia lowland. Water 2017, 9, 228. [Google Scholar] [CrossRef]
- Karlsson, J.M.; Lyon, S.W.; Destouni, G. Temporal behavior of lake size-distribution in a thawing permafrost landscape in northwestern Siberia. Remote Sens. 2014, 6, 621–636. [Google Scholar]
- Romanova, E.A. Tipologicheskaya Karta Bolot Zapadno-Sibirskoi Ravniny. [Typological Map of the Wetlands of the West Siberian Plain]; The State Hydrological Institute: Leningrad, Russia, 1977. (In Russian) [Google Scholar]
- Ivanov, K.E.; Novikov, S.M. Bolota Zapadnoi Sibiri, Ikh Stroenie I Gidrologicheskiy Rezhim. [Bogs of West Siberia, their Structure and Hydrology]; Gidrometeoizdat: Leningrad, Russia, 1976. (In Russian) [Google Scholar]
- Romanova, E.A. Deshifrirovaniye aerofotosnimkov i sostavleniye krupnomasshtabnykh tipologicheskikh kart bolot Zapadnoy Sibiri. [Decoding of aerial photographs and creation of large-scale typological maps of bogs in the Western Siberia]. In Krupnomasshtabnoye Kartografirovaniye Rastitel’nosti. [Large-Scale Vegetation Mapping]; Nauka: Novosibirsk, Russia, 1970; pp. 118–123. (In Russian) [Google Scholar]
- The Imagery of the Western Siberia (70°24′27.16″ N and 71°53′11.70″ E). Google Earth Engine. Issued 30 December 2016. (accessed on August 2017).
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Remote sensing of environment Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017. [Google Scholar] [CrossRef]
- Deines, J.M.; Kendall, A.D.; Hyndman, D.W. Annual Irrigation Dynamics in the U.S. Northern High Plains Derived from Landsat Satellite Data. Geophys. Res. Lett. 2017. [Google Scholar] [CrossRef]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A training algorithm for optimal margin classifiers. In Proceedings of the Fifth Annual ACM Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Kroon, D. Region Growing Code. Available online: https://www.mathworks.com/matlabcentral/fileexchange/19084-region-growing (accessed on 1 June 2017).
- Dillencourt, M.B.; Samet, H.; Tamminen, M. A general approach to connected-component labeling for arbitrary image representations. J. ACM 1992, 39, 253–280. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Fractals: Form, Chance and Dimension; W.H. Freeman and Company: San Francisco, CA, USA, 1977. [Google Scholar]
- Cael, B.B.; Seekell, D.A. The size-distribution of Earth’s lakes. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed]
- Balkhanov, V.K.; Lukhneva, O.F.; Kusner, Y.S.; Bashkuyev, Y.B. Fractal dimensionality of the Lena river delta and tundra lakes in Yakutia. Geogr. Nat. Resour. 2008, 2, 153–157. [Google Scholar]
- Kirpotin, S.; Polishchuk, Y.; Zakharova, E.; Shirokova, L.; Pokrovsky, O.; Kolmakova, M.; Dupre, B. One of possible mechanisms of thermokarst lakes drainage in West-Siberian North. Int. J. Environ. Stud. 2008, 65, 631–635. [Google Scholar] [CrossRef]
- Van Huissteden, J.; Berrittella, C.; Parmentier, F.J.W.; Mi, Y.; Maximov, T.C.; Dolman, A.J. Methane emissions from permafrost thaw lakes limited by lake drainage. Nat. Clim. Change 2011, 1, 119–123. [Google Scholar] [CrossRef]
- Sudakov, I.; Vakulenko, S.A. A mathematical model for a positive permafrost carbon-climate feedback. IMA J. Appl. Math. 2015, 80, 811–824. [Google Scholar] [CrossRef]
- Stepanenkova, V.M.; Machulskaya, E.E.; Glagolev, M.V.; Lykossov, V.N. Numerical modeling of methane emissions from lakes in the permafrost zone. Izv. Atmos. Ocean. Phys. 2011, 47, 252–264. [Google Scholar] [CrossRef]
- Tan, Z.; Zhuang, Q. Arctic lakes are continuous methane sources to the atmosphere under warming conditions. Environ. Res. Lett. 2015, 10. [Google Scholar] [CrossRef]









| Historical Map | Google Earth Engine | ||||||
|---|---|---|---|---|---|---|---|
| Original Image | Binary Image | Area (km) | Perimeter (km) | Original Image | Binary Image | Area (km) | Perimeter (km) |
 |  | 116.883 | 48.309 |  |  | 98.920 | 41.899 |
 |  | 95.916 | 35.515 |  |  | 76.275 | 32.057 |
 |  | 52.416 | 30.615 |  |  | 117.316 | 47.914 |
 |  | 478.553 | 115.059 |  |  | 159.262 | 53.789 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sudakov, I.; Essa, A.; Mander, L.; Gong, M.; Kariyawasam, T. The Geometry of Large Tundra Lakes Observed in Historical Maps and Satellite Images. Remote Sens. 2017, 9, 1072. https://doi.org/10.3390/rs9101072
Sudakov I, Essa A, Mander L, Gong M, Kariyawasam T. The Geometry of Large Tundra Lakes Observed in Historical Maps and Satellite Images. Remote Sensing. 2017; 9(10):1072. https://doi.org/10.3390/rs9101072
Chicago/Turabian StyleSudakov, Ivan, Almabrok Essa, Luke Mander, Ming Gong, and Tharanga Kariyawasam. 2017. "The Geometry of Large Tundra Lakes Observed in Historical Maps and Satellite Images" Remote Sensing 9, no. 10: 1072. https://doi.org/10.3390/rs9101072
APA StyleSudakov, I., Essa, A., Mander, L., Gong, M., & Kariyawasam, T. (2017). The Geometry of Large Tundra Lakes Observed in Historical Maps and Satellite Images. Remote Sensing, 9(10), 1072. https://doi.org/10.3390/rs9101072