1. Introduction
Accurate quantification of precipitation events is directly related to the temporal and spatial sampling of the observing system. A robust sensor with complete spatial coverage (e.g., radar or satellite) should be able to capture both temporal and spatial patterns of a precipitation system through its high spatiotemporal sampling. However, in practice, spatiotemporal sampling of observing systems is often limited and thus can result in errors in quantification of precipitation events.
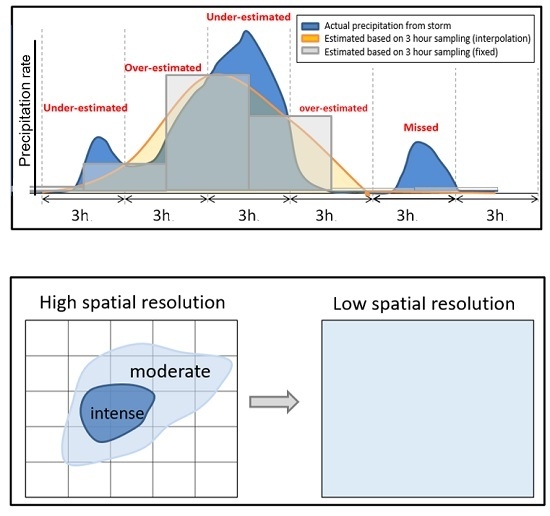
Figure 1 shows a schematic representation of temporal and spatial errors resulting from poor temporal (
Figure 1a) and spatial (
Figure 1b) sampling. In
Figure 1a a hypothetical precipitation event (shown in blue curve) is sampled every three hours, which has been a common temporal sampling for satellite precipitation products (e.g., the Tropical Rainfall Measuring Mission (TRMM) 3B42 product [
1]). Over- and under-estimation errors can be defined as the difference between the actual precipitation rate (blue curve) and precipitation rate from that can be approximated from the three-hour sampling (e.g., using linear interpolation or fixed values shown in yellow and gray color, respectively).
Figure 1b shows an example of error resulting from poor spatial sampling (shown on the right) of a hypothetical precipitation event with regions of moderate and intense precipitation (shown on the left).
While both temporal and spatial sampling can result in errors, their magnitude can depend on the type of precipitation system. For example, precipitation from an isolated convective system may be more sensitive to the spatial and temporal sampling than precipitation from a stratiform system. The relative magnitude of temporal errors compared to spatial errors can also be different depending on precipitation environment and geographical conditions. For example, sampling errors associated with a fast-moving frontal system are expected to be larger than errors from a similar but slower-moving system. Furthermore, one can expect larger sampling errors over mountainous regions (e.g., due to sharp intensity gradient caused by orographic lifting) than a flat region.
The quantification of errors resulting from poor spatial and temporal sampling is important as they can largely affect several studies such as hydrologic simulations and applications. Nijssen and Lettenmaier [
2] studied the effect of error in accumulated precipitation, due to periodic sampling of the precipitation rate, and found that streamflow errors were large for small drainage areas but decreased rapidly for drainage areas larger than about 50,000 km
2. Steiner et al. [
3] used ground radar data set over the Great Plains in the United States and evaluated the sampling-related uncertainty of rainfall estimate as a function of rainfall rate, domain size, accumulation period, and sampling period. Furthermore, in evaluation studies, precipitation products are often mapped onto a common spatiotemporal resolution prior to cross-comparison of products. What is often not carefully considered is that by smoothening of the higher resolution products, errors are added to the estimates that may lead to an unfair assessment of the high resolution products.
Here we quantify and examine the precipitation spatiotemporal sampling errors over global land and ocean and compare their relative magnitudes in different regions and seasons. This global analysis is not feasible using ground stations or radars, but has become possible through recent precipitation estimates from space that offer higher accuracy and spatiotemporal sampling than before.
3. Results
Figure 2a–c show maps of annual, winter, and summer mean precipitation rates for IMERG at a 0.1° × 0.1° resolution. Maps of percent relative-error for the different resolution-scenarios (described in
Section 2.2) are shown in
Figure 2d–o. The three-hour and six-hour scenarios are referred to in T3 and T6, respectively. The 0.5° × 0.5° is about five times coarser than IMERG original resolution in each dimension and hereafter is referred to as S5. Similarly, we refer to 1.0° × 1.0° as S10. To reduce redundancies we did not report the results of the 0.25° × 0.25° experiment. T3 shows that by degrading the temporal resolution of IMERG from 0.5 h to three hours, relative error exceed 30% in most regions. The errors are generally larger over land than ocean, especially over mountainous regions such as the Rocky Mountains in western North America, the Andes along the western edge of South America, and the Tibetan Plateau. By degrading the temporal resolution to six hours (T6), the errors will further increase, but the general pattern remains similar to T3. Large errors over ocean (e.g., over the Southern Ocean) are also observed, which is likely related to the fast moving precipitation systems affected by the polar and subtropical jet streams. The impact of spatial resolution degradation are displayed in the bottom two rows (
Figure 2j–o): (a) land and mountainous region generally show higher relative errors than ocean, and (b) smaller relative error for both S5 and S10 are observed in high latitudes compared to the lower latitudes. This could be related to the fact that tropical regions contain a higher fraction of convective and small scale precipitation than higher latitudes [
10]. Furthermore, there is a tendency towards less convective and more cellular cloud structures in high latitudes, resulting from cold air advection over warmer ocean surfaces [
11], and thus precipitation in high latitudes might be less sensitive to changes in spatial resolution of the products. It should be noted that part of the observed zonal dependence of the results could be related to the use of equal latitude–longitude grids in IMERG, so a grid in lower latitudes covers a larger area than a grid in higher latitudes.
Figure 2 suggests that spatial and temporal relative errors can have different patterns. This can be better seen in the scatter plots of different pairs of relative errors (e.g., S5, S10, T3, and T6) shown in
Figure 3. The Pearson correlation coefficients (CC) between the pairs are also shown in each panel to quantify the relationships. Overall, higher correlations between the spatial and temporal relative errors are observed over land than over ocean. This might be partly related to the fact that, over some regions (e.g., topographically complex areas), both spatial and temporal degradation cause large errors (see
Figure 3).
We recognized that, even after removing areas with low mean precipitation rate, some regions display large relative errors mainly due to dividing the errors by small mean precipitation rates (e.g., regions around tropical subsidence zone). In order to mitigate this effect we also plotted ratios of relative errors that are shown in
Figure 4. As expected T6 shows higher relative error than T3, and S10 shows higher relative error than S5. In fact, these ratios (T6/T3 and S10/S5) are fairly uniform across land and ocean and for different seasons. The ratios between temporal and spatial relative errors are especially interesting as T3/S5 suggests that relative error of T3 is larger than S5 over high latitudes, but is equal or less in lower latitudes. Even T3/S10 shows that the relative error of T3 exceeds S10 over ocean between latitudes 50° and 60° in both hemispheres. It was found that T6/S5 is always greater than one over land and ocean and across all seasons, while in large regions over tropical ocean, and over land T6 and S10 show similar error ratios.
Figure 4 provides insights on how relative errors due to degradation of temporal and spatial resolution are compared globally. While seasonal differences exist, they are not easily observed in
Figure 4. The differences can be better seen in zonal mean plots of the relative-error ratios shown separately over land (
Figure 5) and ocean (
Figure 6).
Figure 5a shows that relative error of T6 is almost 20% larger than T3 over tropical land and gradually decreases to about 10% in higher latitudes. This ratio is also larger in warm seasons than cold seasons.
Figure 6a shows a similar pattern over ocean, but ratios are about 10% larger than over land (e.g., ~30% instead of 20% and 20% instead of 10%). Over land, relative error of S10 is about 20–25% larger than S5 within 40°S–40°N (
Figure 5b). Poleward of 40°N this ratio increases in winter (30%), but remains almost the same in summer. The results over land area south of 40° S is unstable due to limited land areas. Over ocean relative error of S10 is about 25% larger than S5 in the tropics and gradually increases by moving towards higher latitudes (e.g., ~40% near 60° S).
Figure 5 shows that over land relative error of T6 is larger than S5 across all latitudes, while T6 has larger relative error than S10 only poleward of ~20°S/N. Similarly, the relative error of T3 exceeds S5 poleward of ~20°S/N, but does not exceed S10, except at very high latitudes. Similar results are also seen over ocean, but the ratios are generally larger and less sensitive to seasonal changes (See
Figure 6c,d).
Figure 5 and
Figure 6 also show that the seasonal sensitivity of the results is generally larger over tropical land than tropical ocean, which can be inferred from the wider spread of the winter, summer, and all-season plots. In higher latitudes, the effect of seasonal differences is large over both land and ocean. This suggests that, in order to accurately account for spatiotemporal errors, it is important to perform the analyses by region and season, separately over land and ocean.
4. Summary and Concluding Remarks
In this study, the errors resulted from temporal and spatial sampling of precipitation events were investigated using the latest version (V4) of IMERG, providing precipitation estimates at 0.1° × 0.1° resolution every 30 min within the latitude band 60°N–60°S since spring of 2014. RMSE divided by mean precipitation was used to calculate climatology errors at 0.1° × 0.1° every 0.5 h between the degraded (temporally and spatially) and original IMERG products. The temporal and spatial degradation was performed by producing three hour (T3), six-hour (T6), 0.5° × 0.5° (S5), and 1.0° × 1.0° (S10) maps from IMERG. To enhance the stability of results, regions with annual or seasonal mean precipitation less than 0.5 mm/day were excluded from comparisons. The study was conducted using two years (2015–2016) of data, separately for all seasons, winter, and summer months. The results generally show larger errors over land than ocean, especially over mountainous regions. The relative error of T6 is almost 20% larger than T3 over tropical land and gradually decreases to about 10% in higher latitudes. Over land relative error of T6 is larger than S5 across all latitudes, while T6 has larger relative error than S10 only poleward of ~20°S/N. Similarly, the relative error of T3 exceeds S5 poleward of ~20°S/N, but does not exceed S10, except at very high latitude. Similar results are also seen over ocean, but the ratios are generally larger and less sensitive to seasonal changes (see
Figure 6c,d). Furthermore, we found that the spatial and temporal relative errors are not necessarily correlated. Overall, lower correlations between the spatial and temporal relative errors are observed over ocean than over land.
We would like to emphasize that in addition to product-specific algorithmic errors, in practice [
2,
12] one should consider errors that can be originated from differences in spatiotemporal resolutions of products. For example, in mountainous basins, products that offer coarse spatiotemporal resolution may result in large errors in hydrologic simulations, despite the accuracy of the retrieval method used in these products. Even a spatial resolution of 0.1° × 0.1° may not be sufficient in such regions. Nevertheless, it is important to recognize that creating gridded products with finer spatial resolution than what input level-two products offer may not be suitable. While in this study we limited our analysis to few popular spatial and temporal resolutions, further analysis can include other resolutions and can be performed over a specific region [
13], watershed, or at an event scale. Such analyses can provide additional insights on the type of observing systems or products needed for various studies.