Potential of Spaceborne Lidar Measurements of Carbon Dioxide and Methane Emissions from Strong Point Sources

Abstract

Emissions from strong point sources, primarily large power plants, are a major portion of the total CO₂ emissions. International climate agreements will increasingly require their independent monitoring. A satellite-based, double-pulse, direct detection Integrated Path Differential Absorption (IPDA) Lidar with the capability to actively target point sources has the potential to usefully complement the current and future GHG observing system. This initial study uses simple approaches to determine the required Lidar characteristics and the expected skill of spaceborne Lidar plume detection and emission quantification. A Gaussian plume model simulates the CO₂ or CH₄ distribution downstream of the sources. A Lidar simulator provides the instrument characteristics and dimensions required to retrieve the emission rates, assuming an ideal detector configuration. The Lidar sampling frequency, the footprint distance to the emitting source and the error of an individual measurement are of great importance. If wind speed and direction are known and environmental conditions are ideal, an IPDA Lidar on a 500-km orbit with 2 W average power in the 1.6 µm CO₂ absorption band, 500 Hz pulse repetition frequency, 50 m footprint at sea level and 0.7 m telescope diameter can be expected to measure CO₂ emission rates of 20 Mt/a with an average accuracy better than 3% up to a distance of 3 km away from the source. CH₄ point source emission rates can be quantified with comparable skill if they are larger than 10 kt/a, or if the Lidar pulse repetition frequency is augmented.

1. Introduction

The actual implementation of the Paris Agreement (COP21) will rely on an independent, global measurement system of greenhouse gas emissions, in particular of CO₂, to verify and complement national inventories and reports. Emissions from large power plants are a major portion of the total CO₂ emissions. They account for up to 56% of the national anthropogenic CO₂ emissions in some countries, and for 34% of all anthropogenic emissions on a global average [1]. Power plants, industrial, fracking or mining regions, and cities may contain one or more large point sources. Likewise, high scientific and societal interest exists in monitoring emissions from carbon sequestration sites, for example [2], biomass burning regions [3], volcanoes [4] and other anthropogenic and natural point sources. Actually, CO₂ point sources are causing significant uncertainties in emission inventories due to imprecise emission magnitude and location [5], which in turn leads to discrepancies between atmospheric transport models which are needed to assess the fluxes on a regional to global scale [6]. In addition, point sources are the fraction most responsive to independent monitoring and a target of mitigation initiatives or emission commitments [7,8]. For CH₄ the situation is similarly pressing due to a higher anthropogenic share [9]. Coalmine and stable ventilation installations, and leaks in oil and gas production infrastructure constitute major CH₄ point sources [10].

Emissions from strong point sources increase the ambient CO₂ or CH₄ abundance by an amount significantly larger than the variability from surrounding natural sources and sinks. Despite their importance, point sources are sparsely sampled by the ground-based network which calls for more measurements, whereby satellite remote sensors offer global cover. Several comprehensive studies assess emissions from localized CO₂ and CH₄ sources using passive remote sensors [11,12,13,14]. Recently, the Carbon Monitoring Satellite (CarbonSat) was proposed to the European Space Agency (ESA) to retrieve city emissions globally [15]. In addition, airborne imaging spectroscopy is able to see the full extent of the plume yet has difficulties to quantify the concentration enhancements of CO₂ [16] or CH₄ plumes [10] with sufficient accuracy. Finally, ground-based or airborne in-situ instruments can measure concentrations along a line in time or space, respectively, and provide validation opportunities for satellite observations. Airborne instruments can validate space observations by means of vertical profiling and can bridge inconsistencies between satellite and ground-based in-situ measurements by quasi-simultaneous overflights of the site at multiple heights with a flight track oriented along the satellite footprint. The dependency on enough sunlight is a serious limitation to passive sensors operating in the NIR and SWIR spectral domains, mainly in the Northern Hemisphere, where substantial emissions occur particularly in winter, but also in other seasons. In contrast, Integrated Path Differential Absorption (IPDA) Lidar measurements are largely immune to these limitations and initial results from airborne IPDA-Lidar applications look promising [17,18]. Installed on-board an aircraft or a satellite, such an active remote sensor uses laser signals scattered back from Earth’s surface to measure the weighted vertical column concentrations (XCO₂, XCH₄) with a small and well-defined field-of-view. A single plume overpass in the lee of the point source, within distances between a few hundred meters and a few km away from the source, yields measurements of the XCO₂ or XCH₄ plume enhancement which is directly proportional to the emission rate [18]. The plume has to be sampled in its full cross sectional extension but need not necessarily be overflown in direction perpendicular to its alignment along the wind.

First airborne IPDA Lidar measurements of individual CO₂ and CH₄ plumes from power plants and a coalmine ventilation shaft were reported recently, and emission rates could successfully be estimated from the measured column concentration enhancements generated by the plumes [17,18]. It is appropriate now to assess the feasibility of global Lidar observations of point sources that could complement the current and future observation systems, and to discuss the implications for a novel space-borne IPDA Lidar which goes beyond the systems currently being designed and developed [19,20,21,22,23]. In this initial feasibility study we first introduce the IPDA method focusing on plume detection sensitivity in Section 2, and use a Lidar performance model to assess the required size of a satellite Lidar for plume detection in Section 3. A Gaussian plume model is applied in Section 4 to simulate the CO₂ or CH₄ distribution downstream of large point sources. The plume model and a mass budget approach are finally used in Section 5 to quantify the uncertainties to be expected in the emission rates retrieved from measurements of a future space Lidar.

2. Methodology: Integrated-Path Differential-Absorption Lidar

An IPDA Lidar sends laser pulses from an airborne or spaceborne platform towards the Earth’s surface at two distinct but close wavelengths where the trace gas of interest absorbs (online), and where quasi no atmospheric absorption occurs (offline). Unlike atmospheric backscatter Lidar, IPDA Lidar uses only the stronger surface or cloud top backscatter signals to obtain total vertical column concentrations. The main advantage is a considerable gain in measurement accuracy and precision, while keeping the instrument at an affordable size. More details on the IPDA methodology are found in [18,24,25,26]. We focus here on particularities of the method regarding plume measurements from an air- or spacecraft, and apply the formalism introduced by [25]. The logarithm of the ratio of the off- and online backscattered signals P_off and P_on normalized by the corresponding ratio of pulse energies that also have to be measured for each Lidar pulse, yields the (unit-less) Differential Absorption Optical Depth (DAOD). The DAOD likewise expresses Lambert–Beer’s law of extinction, whereby n_gas (in m⁻³) is the CO₂ or CH₄ molecule number density and ∆σ = σ_on − σ_off (in m²) the pressure and temperature dependent differential absorption cross section of CO₂ or CH₄ between the scattering surface (SFC) and the top of the atmosphere (TOA):

$$DAO{D}_{gas}={\displaystyle \underset{z=z_{SFC}}{\overset{z_{TOA}}{\int }}{n}_{gas}\left(z\right)\cdot \Delta {\sigma }_{gas}\left(p\left(z\right),T\left(z\right)\right)\cdot dz}=\frac{1}{2}\cdot \ln \left(\frac{P_{off}\cdot E_{on}}{P_{on}\cdot E_{off}}\right)$$

(1)

IPDA needs a pair of on- and offline laser wavelengths for which only the atmospheric trace gas of interest, here CO₂ or CH₄, contributes to this differential absorption. Under this condition the weighted average of the trace gas dry-air volume mixing ratio along the probed column, denoted by the prefix “X”, here exemplified for CH₄, is directly proportional to the DAOD:

$$\mathrm{X}\mathrm{C}{\mathrm{H}}_4=\frac{DAO{D}_{\mathrm{C}{\mathrm{H}}_4}}{{\displaystyle \underset{p=0}{\overset{p_{SFC}}{\int }}W{F}_{\mathrm{C}{\mathrm{H}}_4}\left(p\right)\cdot dp}}$$

(2)

The denominator is the integral of the so-called weighting function (WF) along the probed column, determined by spectroscopic and atmospheric parameters ([25] Equation (A5)):

$$W{F}_{\mathrm{C}{\mathrm{H}}_4}\left(p\right)=\frac{\Delta {\sigma }_{\mathrm{C}{\mathrm{H}}_4}\left(p,T\left(p\right)\right)}{g\cdot \left(m_{dry-air}+m_{{\mathrm{H}}_2\mathrm{O}}\cdot vm{r}_{{\mathrm{H}}_2\mathrm{O}}\left(p\right)\right)}$$

(3)

Here, m_dry-air and m_H2O are the molecular weights of dry air and water, vmr_H2O is the dry-air volume mixing ratio of water vapor, and g is Earth’s gravitational acceleration. The WF is obtained from spectroscopic measurements and from pressure, temperature and humidity profiles from meteorological (re-)analyses, likely the best data available yet still not perfect. Sensitivity studies have shown that, among all auxiliary atmospheric parameters required, uncertainties in surface pressure (p_SFC), which varies with surface height (z_SFC) and meteorological conditions, have the largest impact on IPDA measurements: 1 hPa error in p_SFC results in a XCO₂ or XCH₄ bias of ~0.1% [24,25]. Uncertainties in atmospheric temperature and humidity have smaller influence thanks to the particularly low sensitivities of the selected absorption lines of

Table 1. On- and offline space Lidar wavenumber positions selected for CO₂ and CH₄. The lower rotational level denotes the selected molecular absorption lines. The most recent HITRAN 2016 spectroscopic data [28] were used to calculate the differential absorption cross section ∆σ_sfc at mean sea level. The total columnar one-way DAOD is determined by Equation (1) using the environmental parameters of Table 2.

Species	Wavelength Region	Online Wave-Number in cm−1	Off-Line Wave-Number in cm−1	Lower Rotational Level	∆σsfc in m²	DAOD
CO2	1.57 µm	6361.23	6356.50	R18	6.81 × 10−27	0.84
CO2	2.05 µm	4875.65	4875.22	R30	2.25 × 10−26	1.17
CH4	1.65 µm	6076.99	6075.90	R6	1.59 × 10−24	0.53
References		[24,25]		[28]		Table 2

. They generate a bias on the order of only 0.1% in the extreme case of a 200 m thick hot (370 K) and humid (70 g/kg) exhaust plume. A first order error propagation of Equation (2) relates the relative single-measurement uncertainty on XCH₄ to the relative measurement uncertainties of backscattered optical power P and pulse energy E:

$$\frac{\delta \mathrm{X}\mathrm{C}{\mathrm{H}}_4}{\mathrm{X}\mathrm{C}{\mathrm{H}}_4}=\frac{1}{2\cdot DAOD}\cdot \sqrt{{\left(\frac{\delta P_{on}}{P_{on}}\right)}^2+{\left(\frac{\delta P_{off}}{P_{off}}\right)}^2+{\left(\frac{\delta E_{on}}{E_{on}}\right)}^2+{\left(\frac{\delta E_{off}}{E_{off}}\right)}^2}$$

(4)

All terms in the square root represent noise-to-signal ratios of signals incident onto the detector, major noise sources being the laser signals and the solar background radiation both governed by Poisson statistics (where the noise δP ~ $\sqrt{P}$), the detector and amplifier chain, speckle effects, and on-/offline overlap inaccuracies [24,25]. In practice, the measurement of the pulse energies can be made as precisely as necessary by splitting out a sufficient fraction of the emitted laser energy, so that the two last terms under the square root can be neglected with respect to the two first terms. Optimum for near-surface plume measurements is high sensitivity at high pressure close to the surface and no or low sensitivity aloft. Figure 1 illustrates that this can be obtained by positioning the online wavelength in the wing of the absorption line, where the WF peaks at surface pressure values, as first discussed in [24]. Figure 1 also shows that a wing position considerably lowers the value of the WF, or measurement sensitivity, so that this idea can only be applied in the vicinity of sufficiently strong absorption lines, found for CO₂ in the 2.05 µm band, and used for example by [17,26].

To assess the IPDA altitude sensitivity more quantitatively, we investigate which impact a hypothetical doubling of the CO₂ or CH₄ mixing ratio within a layer at a certain altitude has on the total columnar XCO₂ or XCH₄ mixing ratio while keeping the rest of the column at constant standard concentrations. We use a standard atmosphere going up to 62 km (~0.2 hPa) with 410 ppmv CO₂ mixing ratio throughout, and 1.8 ppmv CH₄ [9] constant up to 8 km asl. and decreasing above following a climatological average. We use two different suitable CO₂ absorption line positions that were selected for the ESA A-SCOPE IPDA Lidar satellite mission [27], and the CH₄ line position foreseen for the upcoming MERLIN mission [20,25], all listed in Table 1. We investigated possible interference by other plume exhaust gases by scanning the HITRAN database [28] for the occurrence of absorption lines of other gases in the vicinity of the wavenumbers of Table 1. We found one CO line close to our 1.57 µm CO₂ line with an absorption cross section of about a factor 4 smaller than the CO₂ line at our online position. CO emissions from power plants are about 100 times weaker than the CO₂ emissions [1] making the influence of this CO line significantly smaller than our measurement accuracy and thus negligible.

We partly modify the gas number density profile n_gas to obtain the relative column differences between a profile with a modified (here: doubled) mixing ratio within a 100-m layer at a particular height and an unperturbed atmosphere, integrated after Equation (1). Since n_gas decreases exponentially with altitude and ∆σ is a nonlinear function of the altitude (see Figure 1 and Equation (3)), the IPDA measurement sensitivity as defined in this way is strongly dependent on the altitude in which the perturbation occurs. All curves in Figure 2 show maximum variation or sensitivity at sea level and low sensitivity above the tropopause as desired, yet with a large spread in the lower troposphere, owing to the different distances between the online position and the corresponding absorption line center. Doubling the mixing ratio is just an expressive example. The curves’ shapes are invariant to the amount of mixing ratio change in a particular layer, and the impact on the total column is proportional to this amount. For example, doubling the thickness of the layer doubles the relative column difference. IPDA measurements at 2.05 µm have a factor of >2 higher sensitivity than at 1.57 µm below altitudes of 1 km where most CO₂ sources and sinks are located. The CH₄ position ranges in the middle because its line center distance also ranges in between that of both CO₂ options. We find a significant advantage for the 2 µm CO₂ option arising from spectroscopic and atmospheric conditions that we will have to balance later with instrumental constraints in this wavelength range.

3. Instrument: Space IPDA Lidar Setup for Plume Measurements

This section describes a realizable IPDA Lidar configuration for assessing emission rates from point sources with acceptable accuracy, putting the focus on the basic instrument dimensioning requirements and less on technological issues. It is obvious that such a Lidar will have to be operated in a pointing mode with active laser beam and receiver field of view steering, targeting the individual plumes in direct proximity to previously specified point sources. As an example, the Fourier transform spectrometer on the Greenhouse Gas Observing Satellite (GOSAT; [29,30]) uses an agile pointing mechanism which allows for along-track and cross-track pointing of about ±20°. However, its aperture is only 68 mm in diameter and additionally, as a passive instrument, there is no need to simultaneously steer a laser beam. For the larger Lidar apertures on the order of 0.5 to 1 m the implementation of reflective or refractive scanners appears difficult due to size and weight restrictions. Alternative means to simultaneously steer both laser and receiver FOV are via the attitude control system of the satellite platform (the steering wheels), or using other technologies already in place for optical inter-satellite [31] or free-space communication. Finally, a promising technique may consist of a roving-fovea approach [32] with an oversized spherical primary mirror and a fast steering secondary mirror used for example for precision tracking and imaging of orbital debris.

We limit our Lidar sizing analysis to pulsed, direct detection systems with two wavelengths (on- and offline), using knowledge gained during the planning and design phase of airborne [18] and spaceborne IPDA Lidars [20,24,25,27,33]. Alternative Lidar methodologies might likewise be applicable [19,22,34]. Plume detection from quickly moving platforms such as satellites, however, requires high spatial resolution, which will only be achievable with a small laser footprint, a high laser pulse repetition frequency (PRF) and a single-measurement (non-averaged) retrieval. These requirements are realizable with a two-wavelength pulsed system. A small surface footprint generally poses certain challenges, as it goes along with high speckle noise [24] and on-/offline overlap uncertainty [35]. A high PRF implies that there is less energy per pulse available for a given average laser power which mainly drives performance, cost and complexity. As detailed below and based on our airborne experience [18,35] we choose as compromise a PRF of 500 Hz (double-pulse, on-/offline) and a footprint of 50 m diameter, corresponding to a laser beam divergence of 0.1 mrad. This yields overlapping footprints separated by 14 m for a low-earth orbit with typical satellite velocity v_SAT ≈ 7 km/s, as the separation between two footprints equals the ratio v_SAT/PRF. We use a model developed and described in [25,33] to assess the performance of IPDA Lidar for a baseline set of instrument, platform and environmental parameters listed in

Table 2. Instrument, platform and environmental parameters used for the space Lidar simulations.

Instrument		References
Laser pulse energy	2 mJ
Average output power, on-/offline	2 W
Double-pulse repetition frequency	500 Hz
Footprint diameter at sea level, FWHM	50 m
Telescope diameter	0.7 m
Transmitter and receiver optical efficiency	0.65	[27]
Receiver filter bandwidth	1 nm	[24]
Detector dark noise	zero, ideal detector
Platform		[27]
Orbit type	polar
Orbit altitude	500 km
Footprint velocity	7 km/s
Footprint spacing	14 m
Environment
Pressure, temperature	standard atmosphere
CO2 concentration	410 ppm
CH4 concentration	1.8 ppm	[9]
Aerosol profile, ESA median, total columnar optical depth	0.1	[24]
Solar background radiation	5 mW m−2 nm−1 sr−1	[25]
Surface reflectance, vegetation	0.10 sr−1 at 1.57 and 1.65 µm	[23]
	0.03 sr−1 at 2.05 µm	[22]

that influence the precision (random instrument noise; Equation (4)) of space-based Lidar measurements. Use of the standard atmosphere described in Section 2 simplifies the simulations, making the weighting function (Equation (3)) as well as its vertical integral (Equation (2)) a constant only dependent on the selected on-/offline pair from Table 1. Typical variations in aerosol load and climate conditions have minor influence on the IPDA Lidar performance [24], in the absence of clouds [33]. Our analysis does not include systematic errors (measurement biases), extensively discussed in [24] and found to be sufficiently smaller than the single-measurement noise errors presented here below.

We run the IPDA Lidar performance model for each online option of Table 1 using the instrument, platform and environmental parameters listed in Table 2. Key performance parameters are average laser power, telescope size, orbit altitude, surface reflectance and detector dark noise [25]. Concerning the latter, the new development and first airborne tests of a HgCdTe APD for NIR applications looks very promising despite the need for cooling it down to 110 K [36,37]. Our simulations show that this new detector outperforms state-of-the-art InGaAs APDs of current IPDA Lidar systems by about a factor of 2 in terms of SNR or precision due to its NEP which is ~20 times lower in a comparable optical setup. As development is ongoing with technological details of future space realisations still open, we assume in our simulations an ideal detector with zero dark noise. The HgCdTe APD used by [36] is about a factor 1.4 worse than our ideal detector, in terms of measurement precision, which we think justifies selecting an ideal detector in this initial study on point source emission quantification. An average total power of 2 W is comparable to the actual airborne system CHARM-F [18] and about four times larger than the MERLIN laser.

Figure 3 shows the resulting precisions for simulated single-shot, non-averaged XCO₂ and XCH₄ measurements as function of the altitude of the surface (target) from where most of the laser radiation is scattered back. The curves vary owing to different DAOD values and line-wing positions. Their minima lie between 0 and 2 km, as the on-/offline wavelength positions were optimized for this range. The 2 µm CO₂ option is penalized due to a three times smaller reflectance from vegetated surfaces, which were chosen as being most representative for surfaces surrounding large point sources, and ranging between brighter semi-arid and darker water or snow surfaces [22,23]. The CH₄ option is performing worse due to a slightly sub-optimal DAOD, selected because its particular online position in between several strong lines considerably relaxes the requirement for the wavelength stability of the MERLIN laser. The precision loss for both the 2 µm CO₂ and the CH₄ option is a factor of ~1.4 compared with CO₂ at 1.57 µm, which shows a random noise level of 5%. We continue with plume modeling in the next section under use of this value.

Figure 4 gives an overview on the effect of varying the key instrument parameters “average power” and “telescope size” for the 1.6 µm CO₂ and CH₄ options. It can help finding an optimal Lidar design by trading off performance, here in terms of the precision, size and cost of the instrument. The omitted 2 µm CO₂ option is close to the green CH₄ lines (see Figure 3). For powers below 1 W the precision is mainly limited by noisy solar background and Lidar backscatter signals incident on the detector (Equation (4)). This is the high-noise regime. In the low-noise regime above 1 W, the improvement of precision is limited by speckle noise which is independent of laser power. Following [24] the speckle noise floor in Figure 4 is 2.5% for a 50-m diameter footprint and a 0.7 m telescope diameter, and increases to about 10% if the footprint were reduced to 10 m. Thus, speckle noise becomes the main issue when reducing the footprint size to obtain better spatial resolution, key to observing point source plumes. In addition, increasing the PRF in the attempt of gaining better spatial resolution by denser samples, without augmenting size and cost of the instrument by keeping the average laser power constant (P = 2 W) also comes at the price of a degrading precision (Figure 5). The degradation of precision with PRF is due to decreasing SNR as the pulse energies E = P/(2PRF) decrease from 40 mJ at 25 Hz, and 2 mJ at 500 Hz (the baseline; Table 2), to 1 mJ at 1000 Hz. Keeping the 50 m footprint size constant implies that the overlap between adjacent footprints increases with the PRF, starting at a PRF of 140 Hz where overlap begins. According with [25] the curves in Figure 5 can be interpreted by the following power-law relationship: precision ~E^−0.3. To conclude, a system with reasonable cost and complexity will be limited in its spatial resolution, both concerning the footprint size and the PRF. As a compromise, a footprint of 50 m and a PRF of 500 Hz are selected for the Lidar baseline. This configuration yields considerable overlap (correlation) between adjacent footprints (measurement samples) which is beneficial to the methods described next.

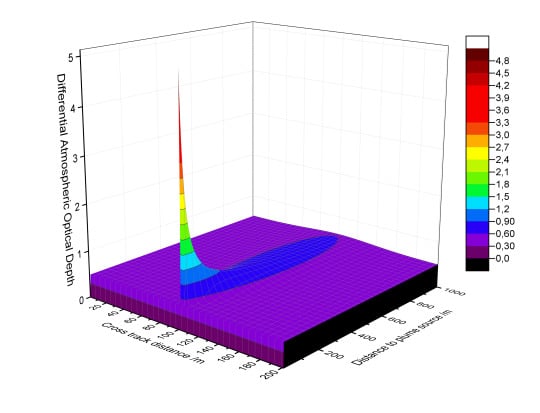
4. Model: CO₂ and CH₄ Point Source Plumes

Exhaust plumes from point sources have, in good approximation, Gaussian shapes in cross-wind horizontal and vertical dimensions and increase in size with distance x from the source, depending on the intensity of atmospheric turbulence ([38];

Table 3. Gaussian plume dimensions in the horizontal (σ_y, across mean wind direction) and vertical (σ_z), as function of point source distance x and strength of atmospheric turbulence, after [38].

Distance from the Point Source	Moderately Unstable		Slightly Unstable		Neutral Atmosphere
	σy/m	σz/m	σy/m	σz/m	σy/m	σz/m
x = 0.5 km	84	53	55	32	36	18
1.0 km	157	109	105	61	69	30
1.5 km	226	169	152	88	100	41
2.0 km	292	230	197	115	130	50
2.5 km	356	293	241	141	159	58
3.0 km	419	358	284	167	187	66

). In direction parallel with the wind, along the X-axis in Figure 6, the initial concentration injected by the source decreases with increasing plume size, until turbulence and diffusion in the surface or boundary layer have mixed the plume down to insignificant background anomalies. We limit this first Lidar plume detection study to situations where the plume is still “visible” as a positive anomaly in the IPDA DAOD signals, i.e., where its contrast with the background is above a certain threshold, defined below. We simulate emission rates typical for large point sources, listed in [11]. We further limit our approach to cloud-free situations over flat terrain with constant wind speed and direction. Wind speed is decisive for the concentration levels within the plume and consequently the DAOD contrast. We use 3 m/s throughout our analysis, which is close to a climatological mean [11] for locations of major point sources and also close to the measurement examples provided by [18]. Our artificial background signal is flat, exempt of regional gradients, air-mass boundaries, frontal zones or plumes from neighboring sources. We finally assume that the geographical positions of the source and of the Lidar footprint are known such that the distance between source and footprint can be determined with sufficient accuracy. We choose this simple approach to obtain a first overview on how far in distance from the source we can measure its emissions.

Following [18], the point source emission rate or flux q_gas in g/s can be extracted from a spatial series of DAOD measurements (Equation (1)) during the overpass of a plume using the following simple expression:

$$q_{gas}=\frac{M_{gas}}{\Delta {\sigma }_{gas}}\cdot A_y\cdot u_x$$

(5)

The expression is valid if the DAOD enhancement due to the plume is sampled both horizontally and vertically in its full extent. A_y is the integral of the DAOD anomaly above the background DAOD, in a plane normal to the mean wind u_x (see Figure 6). For airborne IPDA, the requirement is to fly well above the plume, with a flight direction different from the wind direction but not necessarily perpendicular to u_x. M_gas is the molecular mass of CO₂ or CH₄, and ∆σ_gas the altitude-dependent differential absorption cross section for altitudes within the plume for the selected on-/offline wavelength pair. For all pairs of Table 1 (which lists the sea-level, surface values ∆σ_sfc) ∆σ_gas varies with altitudes below 500 m by <6%. Our simple forward model uses the Gaussian plume approach of Seinfeld and Pandis ([38]; Table 3) to simulate the CO₂ or CH₄ distribution downstream of a point source, and Equation (5) to compute the resulting DAOD enhancement with Gaussian shape, as exemplified in Figure 7. Equation (5) is not exclusively limited to Gaussian plumes but valid also for other shapes, for example distorted plumes. In addition, the background DAOD need not necessarily be constant if it is varying on larger spatial scales, and if it is well distinguishable from the plume and quantifiable on both sides of the plume. Table 3 is adapted to space Lidar, applicable in particular to our horizontal resolution of 14 m, defined in Section 3. It does not cover stable atmospheric situations where turbulent diffusion is so weak that the plumes are too small to be detected from space. Due to very few Lidar footprints sampling these plumes, distances <1 km to the source will be challenging, as well as stable atmospheric situations without turbulence. The first airborne IPDA Lidar measurements of plumes had horizontal plume extents of 50 to several hundreds of meters, i.e., were located relatively close to the sources, sampling with horizontal resolutions of 15 m [17] and 4 m [18]. Such small plumes will be challenging to target and to quantify from space, because the airborne resolution will be out of reach.

Equation (5) shows that the integral of the DAOD enhancement A_y is mainly dependent on the ratio of emission rate to wind velocity, while ∆σ varies only slightly with pressure and temperature. A_y is independent of the distance x to the source, and of the atmospheric turbulence strength. This enables independent assessments of both the emission rate, and the turbulence strength, using Table 3 as a lookup table if the distance x is known. Furthermore, knowing x and the turbulence strength, the vertical extent σ_z of the plume (Figure 6) can be estimated from Table 3. Finally, in the above-described ideal situation with, in particular, flat background concentrations, Equation (1) yields the CO₂ or CH₄ concentration change ∆n_gas inside the plume using the measured DAOD enhancement and the plume thickness σ_z. Such derived products are valuable for cross-comparisons with in-situ sensors measuring the concentrations directly within the plume.

Based on the expected measurement precision from the previous section, Gaussian noise with a standard deviation of 5% of the mean DAOD is added to the artificial plumes and to the flat background DAOD to simulate a realistic satellite IPDA Lidar system. To find out the skill and limits of plume detection and quantification for the (best) case of undistorted Gaussian plumes, we retrieve the emission rates backward by fitting the sum of a Gaussian function and a constant background to the noisy signals, as illustrated in Figure 7. We apply a nonlinear least-squares fit that returns independent estimates for the background DAOD level and the integral of the Gaussian DAOD enhancement A_y’, proportional to the emission rate.

5. Results: Skill and Limits of Space Lidar Plume Detection and Quantification

For the above-described idealized scenario with a Gaussian plume on a flat background in a well-known wind field, we now assess how well the fit retrieves the original emission rate from the artificial, noisy Lidar signals. Using the space Lidar configuration from Section 3 with 5% random noise and assuming constant wind speed, Equation (5) yields an estimate of the emission rate q’ from the fit results A_y’. The relative difference between the original (forward, q) and retrieved (backward model, q’) emission rates for many different noise realizations yields the expected uncertainties and potential SNR-dependent biases of plume detection and emission rate quantification within a pure mathematical-statistical frame. The Gaussian fit accuracy in

Table 5. Skill of space IPDA Lidar emission rate quantification as function of distance from the source for an ideal scenario. Plume contrast is the ratio between the maximum DAOD enhancement in the middle of the plume and the noisy background. Accuracy is the median of (A_y’ − A_y)/A_y. Fail rate indicates how often the retrieval fails to find the correct location of the plume, or does not converge (in case of Gaussian fit only). Modeling environment conditions are taken from Table 4.

Distance from CO2 Point Source	Lidar Samples within Plume	Plume Contrast	Gaussian Fit		Budget Approach
			Accuracy	Fail Rate	Accuracy	Fail Rate
1 km	10	14%	2.0%	0.5%	0.2%	0.0%
2 km	19	7.3%	−2.1%	2.2%	0.5%	0.1%
3 km	27	5.1%	−2.3%	3.9%	1.1%	0.9%

represents the median relative differences (A_y’ − A_y)/A_y or biases of 10⁵ different 5% noise realizations for the conditions of

Table 4. Assumed emission rates, typical for large point sources, and auxiliary parameters used for plume modeling.

Plume Modeling Parameters	CO2	CH4	Reference
IPDA Lidar wavelength range	1.57 µm	1.65 µm	Table 1
Emission rate q	20 Mt/a, 634 kg/s	10 kt/a, 317 g/s	[11]
Mean wind speed ux	3.0 m/s	3.0 m/s	[11]
∆σsfc	6.81 × 10−27 m²	1.59 × 10−24 m²	Table 1
Integral of the DAOD enhancement Ay	20 m	6.3 m	Equation (5); Figure 7
Background mixing ratio	410 ppmv	1.8 ppmv	Table 2
Background DAOD	0.84	0.53	Table 1
Gaussian noise level, 1-σ	5%	5%	Section 3
Measurement length	10 km	10 km
Atmospheric stability	neutral	neutral	Table 3; [38]

. An alternative method, termed budget approach by [18], consists of integrating the noisy DAOD series across the plume extent, and subtracting the background, to obtain estimates of A_y. This simple approach has the advantage that it can include non-Gaussian shaped plumes, e.g., distorted by wind shear, for which Equation (5) is also valid. It can also be considered as a straightforward application of Equation (5) without the complexity and potential ambiguity inherent to any fit or inversion retrieval. This approach shows a slightly better skill, likely attributable to the low number of Lidar samples within the plume (<30) that inhibits the Gaussian fit routine to work efficiently. At 3 km distance, the plume contrast is about equal to the noise level of 5%. Here, the plume is hardly visible “by eye”, which in real measurements would entail plume location misinterpretations due to errors in the wind direction, expressed by the fail rate in Table 5. This sets a limit to our idealized and simplified approach. Overall, we find low biases when repeating the experiment many times within this distance limit. We conclude that both the Gaussian fit and the budget approach are basically apt to retrieve the original emission rates without significant noise-induced biases. Note however that the numbers presented here do not include real-world biases which will be mainly due to uneven background signals, overlap by other plumes upstream, or overlooked details of the local wind field.

CO₂ plumes are better detected than CH₄ plumes because the assumed CO₂ emission rates in our experiment are stronger. More precisely, the term A_y which basically characterizes the plume detection sensitivity (Equation (5)) is more than three times larger in Table 4. CH₄ emission rates would either need to be higher than 10 kt/a, or another stronger absorption line should be selected, or the Lidar instrument would need to be more performant than our baseline. For example, it should run at a higher PRF to obtain enough samples across fresh plumes located closer than 1 km to the source where the concentrations are higher. Concerning CO₂ plume measurements at 2 µm we obtain, under consideration of the ∆σ_sfc ratio of 3.3 between both wavelength options from Table 1, a term A_y larger by a factor of 3.3 compared to CO₂ at 1.57 µm, albeit at the cost of a precision loss factor of ~1.4 as documented in Figure 3. The overall advantage factor of 3.3/1.4 = 2.4 for 2 µm measurements at sea level appears very attractive, but is not yet exploitable given the overall lower Lidar technology readiness level at 2 µm. Efforts for improving CO₂ systems at 2 µm are ongoing [17,22]. This initial study favored a more cautious approach with 1.6 µm technology where more experience and heritage exists from space Lidar missions such as MERLIN.

6. Discussion

The skill to retrieve emission rates relies equally on accurate wind speed and Lidar absorption measurements. Lack of wind measurements within the plumes, complex orography, local secondary circulations or weather model inaccuracies may lead to substantial wind speed and direction uncertainties. Furthermore, in dependence of the flow regime within the surface layer or, for larger plumes, the boundary layer, wind speed and direction may vary with altitude, which has to be considered, as the plume extends vertically as a function of distance from the source (Table 3; Figure 6). Because the possibilities to improve the wind observations are limited in this complex small-scale context, it is essential to obtain Lidar absorption measurements with high accuracy, in order to keep the wind-induced error propagated onto the emission rate (Equation (5)) within acceptable bounds. We are aware that the fail rate of individual point source overpasses may be high, mainly due to uncertainties in the wind field and the background concentrations. Clouds in the Lidar field of view are a further issue, yet can be unambiguously identified and flagged by analyzing the backscatter profiles. The aggregation of subsequent overpasses of specific sites will have to bring the required accuracy. The local time of satellite overpass may also play a role if power plants emit less overnight or on weekends. Overlapping plumes from adjacent point sources, for example in cities and in oil, gas or coal mining regions are a further considerable challenge. High Lidar accuracy is again essential in this context to better discriminate the different plumes from each other, as well as from the background. In addition, complementary observations from spaceborne imaging spectroscopy may help separate the different plumes. The modeling examples given by [15] show that, in Central Europe, plumes from large cities and industrial regions are separated by extended regions with background GHG concentration levels. The satellite Lidar cross sections in between the point source targets will hopefully provide robust background measurements over such regions that show less or no local emissions.

The knowledge about the abundance of CH₄ point sources is lower. For example, in a high-resolution (1.5 km) emission data base that separates sources at the surface from sources at altitudes higher than 52 m asl., i.e., emissions at the top of tall chimneys, the ratio of point source emissions over total emissions for Germany is 50.98% for CO₂ and 0.67% for CH₄ (Christoph Gerbig, MPI for Biogeochemistry, personal communication, 2017). While the CO₂ ratio fairly agrees with the 48.1% reported for German power plants by [1], the CH₄ ratio is biased low by the fact that CH₄ does not emanate from tall chimneys. In addition, CH₄ plumes from sources covering a small area fraction (quasi point sources) like landfills are not taken into account. A related question, to be addressed by future airborne Lidar and modeling experiments, is how well emissions from such small-area sources can be quantified. For CO₂, relevant quasi-point sources are regions with intense extra-urban traffic such as dense highways, shipping routes, or airports. Their independent monitoring may gain high importance in the future. Finally, prominent natural point sources are related to volcanic activity, leading to elevated plumes, but also to plumes from low-altitude small-area sources such as mud volcanoes. All types of volcanoes are generally difficult to access, so that spaceborne remote sensing with high accuracy and spatial resolution is a promising complement to the common in-situ observations.

The success of the presented approach not only relies on knowledge of wind and clouds, but also on the clear identification of unfavorable environmental situations such as for example the absence of turbulence or the presence of upper-level CO₂ or CH₄ gradients. The results will have to be flagged using thresholds in parameters describing these conditions that can be obtained from airborne precursor experiments. Fortunately, active remote sensing for plume emission quantification is largely insensitive to a number of environmental conditions perturbing other methods, such as the likely presence of aerosol, high temperature and humidity in the plumes, distortions of the plume, or CO₂ plume density heterogeneities due to other reasons. Generally, our approach is robust with respect to variations in the extent, height and density of the plume, under the only conditions that the signal of an individual plume is clearly distinguishable from the surrounding CO₂ or CH₄ background, and that the full horizontal and vertical extent of the plume is covered by the Lidar curtain.

7. Conclusions

First airborne integrated-path differential-absorption (IPDA) Lidar measurements of individual CO₂ and CH₄ plumes from anthropogenic point sources such as power plants and coalmines with successful retrieval of emission rates have been reported recently [17,18]. Plume detection from space Lidar with pointing capability should consequently be envisaged and assessed, because international climate agreements will increasingly require independent global monitoring. Leaving the details of instrument and pointing for future more technology-oriented studies, we used an instrument model with an ideal detector to assess the size required for such a Lidar. We find that an instrument with reasonable size will be able to usefully complement the existing and future observing systems with new, independent emission measurements from important CO₂ point sources. Concerning CH₄, a stronger absorption line or a higher Lidar PRF would be needed to fulfill the more demanding observational constraints. Spaceborne active remote sensing is technologically more challenging and expensive than other methods but provides global cover at high spatial resolution and high accuracy. Major advantages include insensitivity to aerosol, temperature, humidity, and CO₂ or CH₄ density heterogeneity in the plumes. In a next more realistic simulation step, the impact of plume shape and CO₂ or CH₄ background concentration heterogeneities should be addressed. One may push the limits of plume detection further by combining the error statistics on turbulence and wind provided by the weather models with the measurement uncertainties using an optimal estimation retrieval framework. In parallel, more airborne feasibility experiments are needed. In 2018, the flight campaign CoMet (carbon dioxide and methane mission) will combine several active, passive and in-situ instruments on board the German HALO research aircraft, including the DLR IPDA Lidar CHARM-F.