RapidScat Cross-Calibration Using the Double Difference Technique
Abstract
:1. Introduction
2. Materials and Methods
2.1. RapidScat and QuikScat Datasets
2.2. Ancillary Data Sources
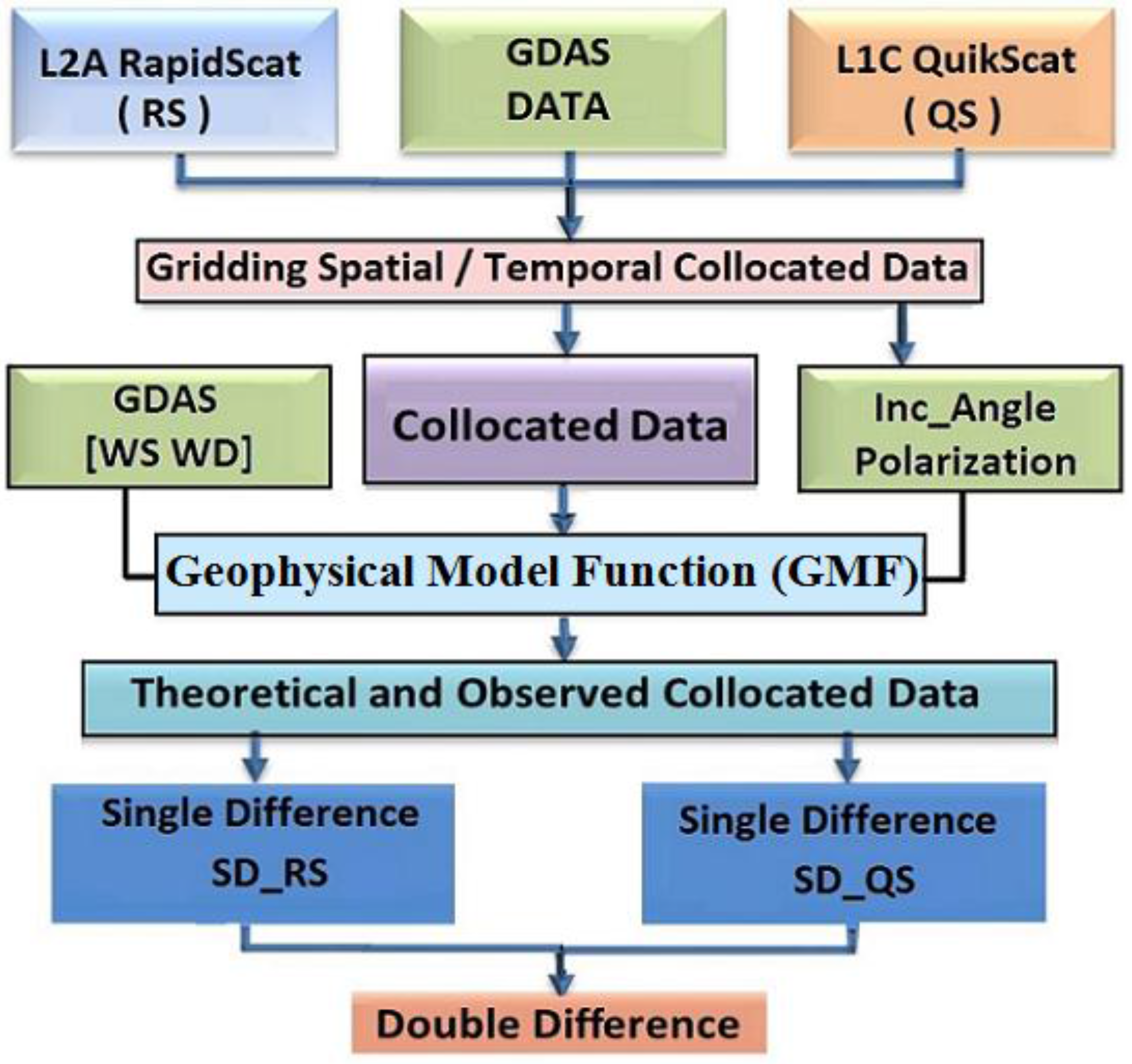
2.3. Calibration Method
3. Results
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Alsabah, R.; Al-Sabbagh, A.; Zec, J. Calibration of RapidScat Scatterometer. In Proceedings of the IEEE 5th Microwaves, Radar and Remote Sensing Symposium, Kiev, Ukraine, 29–31 August 2017. [Google Scholar]
- Chander, G.; Tim, J.; Hewison, N.F.; Wu, X.; Xiong, X.; Blackwell, W.J. Overview of intercalibration of satellite instruments. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1056–1108. [Google Scholar] [CrossRef]
- Paget, C.A.; Long, G.D.; Madsen, N.M. RapidScat Diurnal Cycles Over Land. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3336–3344. [Google Scholar]
- Rodriguez, E. The NASA ISS-RapidScat mission (Invited). Presented at the American Geophysical Union Fall Meeting, San Francisco, CA, USA, 9–13 December 2013. Paper U23A-03. [Google Scholar]
- Madsen, M.N.; Long, D.G. Calibration and validation of the RapidScat scatterometer using tropical rainforests. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2846–2854. [Google Scholar]
- Biswas, K.S.; Farrar, S.; Gopalan, K.; Santos-Garcia, A.; Jones, W.L.; Bilanow, S. Intercalibration of microwave radiometer brightness temperatures for the global precipitation measurement mission. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1465–1477. [Google Scholar]
- Katsaros, B.K.; Mitnik, L.; Black, P. Microwave instruments for observing tropical cyclones. In Typhoon Impact and Crisis Management; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Zhu, J.; Dong, X.; Yun, R. Calibration and validation of the HY-2 scatterometer backscatter measurements over ocean. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014. [Google Scholar]
- Shen, Y. ISS-RapidSca. 2015. Available online: https://www.nasa.gov/mission_pages/station/research/experiments/1067.html (accessed on 20 July 2016).
- RapidScat Project. RapidScat Level 2A Surface Flagged Sigma-0 and Attenuations in 12.5Km Swath Grid Version 1.2. Ver. 1.2. PO.DAAC, CA, USA. 2016. Available online: http://dx.doi.org/10.5067/RSX12-L2A12 (accessed on 20 July 2016).
- Climate Prediction Center. National Centers for Environmental Prediction. National Oceanic and Atmospheric Administration (NOAA). Available online: http://www.ncep.noaa.gov/ (accessed on 20 July 2016).
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef]
- Crofton, S. Validation of Wideband Ocean Emissivity Radiative Transfer Model. Master’s Thesis, University of Central Florida, Orlando, FL, USA, 2010. [Google Scholar]
- Ghazi, Z. Conae Microwave Radiometer (MWR) Counts to Brightness Temperature Algorithem. Ph.D. Thesis, University of Central Florida, Orlando, FL, USA, 2014. [Google Scholar]
- Ricciardulli, L.; Wentz, F. Progress and future plans on an ocean vector wind climate record. In Proceedings of the IOVWST Meeting, Brest, France, 2–4 June 2014. [Google Scholar]
- Jones, W.L.; Zec, J. Evaluation of Rain Effects on NSCAT Wind Retrievals. Presented at the Oceans 96 Conference, Ft. Lauderdale, FL, USA, 23–26 September 1996. [Google Scholar]
- Jones, W.L.; Park, J.D.; Donnelly, W.J.; Carswell, J.R.; McIntosh, R.E.; Zec, J.; Yueh, S. An improved NASA scatterometer geophysical model function for tropical cyclones. In Proceedings of the 1998 IEEE International Geoscience and Remote Sensing (IGARSS’98), Seattle, WA, USA, 6–10 July 1998; Volume 4, pp. 1994–1997. [Google Scholar]
- Lucrezia, R.; Wentz, F.J. A scatterometer geophysical model function for climate-quality winds: QuikScat Ku-2011. J. Atmos. Ocean. Technol. 2015, 32, 1829–1846. [Google Scholar]
- Ricciardulli, L.; Meissner, T.; Wentz, F.J. Building a Climate Data Record for Ocean Vector Winds. Presented at the American Geophysical Union Fall Meeting, California, CA, USA, 15–19 December 2014. paper OS51D-02. [Google Scholar]
- Ebrahimi, H.; Datta, S.; Santos-Garcia, A.; Jones, L. Radiometric inter-calibration of SAPHIR using the Microwave Humidity Sounders. In Proceedings of the 13th Specialist Meeting on Microwave Radiometry and Remote Sensing of the Environment (MicroRad), Pasadena, CA, USA, 24–27 March 2014; pp. 211–214. [Google Scholar]
- Ebrahimi, H.; Datta, S.; Jones, W.L. Investigation of radiative transfer model effect on radiometric inter-calibration of GPM sounder channels. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015. [Google Scholar]
- Gopalan, K.; Jones, W.L.; Biswas, S.; Bilanow, S.; Wilheit, T.; Kasparis, T. A time-varying radiometric bias correction for the TRMM microwave imager. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3722–3730. [Google Scholar] [CrossRef]
- Kroodsma, R.; McKague, D.; Ruf, C. Robustness of the vicarious cold calibration algorithm in the double difference method for GPM inter-calibration. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011. [Google Scholar]
- Linwood, J.; Datta, S.; Santos-Garcia, A.; Wang, J.R.; Payne, V.; Viltard, N.; Wilheit, T. Radiometric intercalibration of the Microwave Humidity Sounder on NOAA-18, MetOp-A, and NOAA-19 using SAPHIR on Megha-Tropiques. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Melbourne, Australia, 21–26 July 2013; pp. 1151–1154. [Google Scholar]









| Months | January 2015 | February 2015 | March 2015 | April 2015 | May 2015 | June 2015 | July 2015 | August 2015 | September 2015 | October 2015 | November 2015 | January 2016 | February 2016 | March 2016 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HH-POL | SD | −0.18 | −0.55 | −0.6 | −0.12 | −0.26 | −0.7 | −0.63 | −0.26 | 0.34 | 0.15 | 0.53 | 0.79 | 0.5 | 2.14 |
| DD | Non | Non | −0.45 | −0.2 | 0.41 | 0.12 | −0.34 | −0.09 | 0.18 | 0.19 | 0.86 | Non | 0.85 | Non | |
| VV-POL | SD | −0.7 | −0.75 | −0.79 | −0.26 | −0.36 | −0.77 | −0.83 | −0.51 | 0.06 | −0.36 | −0.21 | 0.09 | −0.26 | 1.05 |
| DD | 0.02 | 0.06 | Non | 0.48 | −0.11 | −0.01 | 0.11 | −0.23 | 1.11 | 0.4 | Non | 1.83 | 1.37 | 1.52 | |
| January 2015 | February 2015 | March 2015 | April 2015 | May 2015 | June 2015 | July 2015 |
| 2.0645 | 2.4209 | 2.097 | 3.5033 | 2.28 | 2.2547 | 2.1804 |
| August 2015 | September 2015 | October 2015 | November 2015 | January 2016 | February 2016 | March 2016 |
| 2.5195 | 3.677 | 2.7371 | 2.0645 | 3.3369 | 3.101 | 5.515 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zec, J.; Jones, W.L.; Alsabah, R.; Al-Sabbagh, A. RapidScat Cross-Calibration Using the Double Difference Technique. Remote Sens. 2017, 9, 1160. https://doi.org/10.3390/rs9111160
Zec J, Jones WL, Alsabah R, Al-Sabbagh A. RapidScat Cross-Calibration Using the Double Difference Technique. Remote Sensing. 2017; 9(11):1160. https://doi.org/10.3390/rs9111160
Chicago/Turabian StyleZec, Josko, W. Linwood Jones, Ruaa Alsabah, and Ali Al-Sabbagh. 2017. "RapidScat Cross-Calibration Using the Double Difference Technique" Remote Sensing 9, no. 11: 1160. https://doi.org/10.3390/rs9111160
APA StyleZec, J., Jones, W. L., Alsabah, R., & Al-Sabbagh, A. (2017). RapidScat Cross-Calibration Using the Double Difference Technique. Remote Sensing, 9(11), 1160. https://doi.org/10.3390/rs9111160





