Local Deep Hashing Matching of Aerial Images Based on Relative Distance and Absolute Distance Constraints

Abstract

Aerial images have features of high resolution, complex background, and usually require large amounts of calculation, however, most algorithms used in matching of aerial images adopt the shallow hand-crafted features expressed as floating-point descriptors (e.g., SIFT (Scale-invariant Feature Transform), SURF (Speeded Up Robust Features)), which may suffer from poor matching speed and are not well represented in the literature. Here, we propose a novel Local Deep Hashing Matching (LDHM) method for matching of aerial images with large size and with lower complexity or fast matching speed. The basic idea of the proposed algorithm is to utilize the deep network model in the local area of the aerial images, and study the local features, as well as the hash function of the images. Firstly, according to the course overlap rate of aerial images, the algorithm extracts the local areas for matching to avoid the processing of redundant information. Secondly, a triplet network structure is proposed to mine the deep features of the patches of the local image, and the learned features are imported to the hash layer, thus obtaining the representation of a binary hash code. Thirdly, the constraints of the positive samples to the absolute distance are added on the basis of the triplet loss, a new objective function is constructed to optimize the parameters of the network and enhance the discriminating capabilities of image patch features. Finally, the obtained deep hash code of each image patch is used for the similarity comparison of the image patches in the Hamming space to complete the matching of aerial images. The proposed LDHM algorithm evaluates the UltraCam-D dataset and a set of actual aerial images, simulation result demonstrates that it may significantly outperform the state-of-the-art algorithm in terms of the efficiency and performance.

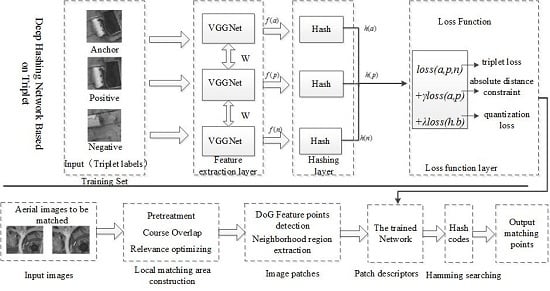
1. Introduction

With the rapid development of aerial photographing technology and the development of high-resolution aerial remote sensing cameras, aerial images have been widely used in emergency rescue, environmental monitoring, digital city construction, and other sectors [1,2]. A key premise for the processing of aerial images is to obtain the physical and geometric information of images, namely the corresponding image features. The extraction and matching of aerial images’ feature points are the basis for image analysis, image fusion, change detection, and stereo matching, which plays a crucial role in the field of aerial photography.

Based on image content and features, texture, and structure that the gray level information carries on the corresponding relation, consistency, and similarity analysis, image matching has been developed as a method for fast seeking of similar image targets in two images to be matched. According to the approaches used in image matching, it can be divided into two categories: one is gray-based image matching, the other is feature-based image matching. Recently, the feature-based matching algorithms have gradually become a major research orientation, e.g., SIFT [3], BRIEF (Binary Robust Independent Elementary Features) [4], ORB (Oriented FAST and Rotated BRIEF) [5], and SURF [6]. An efficient feature extraction and matching implementation for large images in large-scale aerial photogrammetry was proposed in Yanbiao Sun etc. [7]. The demand of the original SIFT algorithm for memory was reduced by designing the SIFT blocks, and a “Red-Black” tree data structure was proposed to reduce the searching complexity at the time of matching. In order to match the features for registering dynamic aerial images, a robust feature point matching method was proposed [8], which combines the SIFT and the Support Vector Machine (SVM) experimental results, showing that such an algorithm has a higher accuracy even with an image with a large number of outliers. The ABRISK (Accelerated Binary Robust Invariant Scalable Keypoints) algorithm was proposed by Chung-Hsien Tsai etc. [9], and the images are registered by analyzing the corresponding control points and those irrelevant matching point pairs are filtered by a “sorting ring” as soon as possible to accelerate the matching process. As an efficient algorithm, three sets of local features are extracted by SIFT and then k-means clustering is performed to achieve accurate matching in Amin Sedaghat etc. [10]. Furthermore, an accurate method for remote sensing image registration with different viewpoint was proposed in Kun Yang etc. [11], which constructs a finite mixture model, then three features were combined and substituted into the mixture model to form a feature complementation. However, the above matching methods are based on histogram of gradient, comparison of intensity, and other image operations, which rely heavily on human experience and lack the ability of self-study.

With the development of deep learning (DL), the deep semantic features of images extracted by neural networks [12,13,14] show better characterization and have been applied in image classification [15], image retrieval [13], and object detection [16]. The established model is made to directly learn the image features, substantially reducing the error due to the manual extraction of image features. A framework for the extraction of image features was firstly proposed in Alex Krizhevsky etc. [12], in which the feature vectors in the seventh layer of the network are used for image retrieval and show prominent performance in the ImageNet dataset, but the convolutional neural network (CNN) features have 4096 dimensions and the efficiency will be low if the similarity of features is retrieved directly in the Euclidean space. With respect to the high dimensionality of CNN features, the dimensions were reduced via learning a low-rank projection matrix W in Artem Babenko etc. [17] so that the CNN features with reduced dimensions improve the retrieval efficiency. Additionally, many deep learning methods spring up for road detection; a siamesed FCN (Fully Convolutional Network) was proposed to extract high-level features [16], which is able to consider RGB-channel images, semantic contours, and location priors simultaneously to segment the road region elaborately. These methods use the whole image as the input of the network, and learned feature descriptors can only be used to retrieve similar images, and cannot achieve the purpose of image matching.

The learning of patch-based image descriptors has been widely used in computer vision, such as image matching, image stitching, or classification. A unified standard framework was constructed in Xufeng Han etc. [18], where the features of image patches are extracted and the similarity of the extracted features is calculated by the deep convolution neural network and three fully connected layers, respectively. The overfitting is suppressed by adding artificial samples in the standard dataset, which not only improves the accuracy, but also reduces the storage needs. A triplet network was given in Vassileios Balntas etc. [19] and improved the loss function, finding that the matching time of the 128-dimension descriptor can be compared with the binary descriptor, such as BRIEF or ORB, when running on a GPU.

Although the above algorithms have better results in respect of feature description and matching performance, as the amount of image data and higher dimensions increase, dimension reduction has become the main solution to this problem, for example, Principal Component Analysis (PCA) [20], Locally Linear Embedding (LLE) [21], and methods based on subspace learning [22,23,24,25]. LADA (Locality Adaptive Discriminant Analysis) is a novel dimensionality reduction method [22], which focuses on data points with a close relationship both in spectral and spatial domains, has been successfully applied to his (Hyperspectral Image) classification. An unsupervised subspace learning method, PCE (Principal Coefficients Embedding), was proposed in Xi Peng etc. [25], which can automatically determine the optimal dimension of feature space and obtain the low-dimensional representation of a given dataset. However, the calculating workload for the distance of floating-point descriptors in the Euclidean space is relatively high, and given that all the data is saved in binary form in the computer memory, the computational burden and storage space will be significantly reduced by constructing a suitable hash function to generate the binary descriptors and calculating in the Hamming space. Hash technology has been extensively used in computer vision, machine learning, information retrieval, and other related fields. The vast majority of previous hashing methods learn the hash function by projecting randomly, based on the manually-based features, the construction of features, and the process of hash coding, are relatively independent from each other, resulting in the acquired features possibly not being compatible with the coding process. To overcome the deficiencies of such hash algorithms, the learning-based hashing algorithm has been proposed, the ideal precision can be assured only by using hash codes with shorter bits, so as to further improve the retrieval and learning efficiency [26]. The existing hashing learning models can be divided into unsupervised models, semi-supervised models, and supervised models based on whether any supervision information of the sample is used in the learning model. The unsupervised hashing methods do not take the label information into account, including isotropic hashing [27], spectral hashing [28], or iterative quantization [29]; the semi-supervised hashing methods partly take account of the similarity information, such as SSH (Semi-Supervised Hashing) [30]; and the supervised hashing methods use the label information or similar point pairs as the supervised information, such as supervised discrete hashing [31] and supervised hashing with kernels [32].

Due to the superiority in feature learning of deep convolutional neural networks and the superiority in retrieval calculating speed and storage space of hashing methods, deep convolution neural networks and hash methods have been combined with each other over many years, which can be divided into two stages. One is the “two-stage” network form: a supervised hashing algorithm was proposed in Rongkai Xia etc. [33] that combines a CNN and a hashing algorithm that firstly uses the data similarity information to construct a similar matrix, then uses the learned matrix as the network input, and learns the representation of the image and hash function, but such a method does not incorporate the process of generating the hash code into the network, which cannot gradually optimize the network through back propagation, with poor effect. The other is the “one-stage” network form: Lai et al. modified a CNNH (Convolutional Neural Network Hashing) algorithm and the proposed DNNH (Deep Neural Network Hashing) algorithm, which incorporate the process of generating the hash code into the network framework, performed the image feature learning and hash function learning simultaneously in the network, and optimized the overall performance through feedback. Compared to the “two-stage” deep hash algorithms, such a method often yields a better effect [34].

Aerial images are usually rich in edges and texture information, and the number of feature points of aerial images are much greater than general images. Therefore, traditional matching methods are usually not suitable. Additionally, most deep hash algorithms are developed only for image retrieval, but not available for aerial matching. According to the characteristics of aerial images and combining the advantages of deep convolutional neural networks with hashing algorithms, we propose an algorithm for learning binary image patch hash coding by a deep convolution neural network based on the local region of aerial images, and the learned binary descriptor can be used for high-resolution aerial image matching. The basic contribution of this paper is given as follows: (1) optimize the overlapping region according to the course overlap rate of aerial images and obtain the local region of aerial images; (2) construct the local deep hashing network to mine the deep features and generate binary hash codes of image patches; (3) optimize the network through adding the absolute distance constraints in the triplet loss and incorporating the quantization error into the objective function; and (4) use the approximate nearest neighbor search strategy for feature point matching.

2. Proposed Method

Based on the extracted local region of aerial images, this paper uses the triplet-based deep hashing method to achieve the fast matching of high-definition aerial images. In the construction of local regions, the local region of aerial images is obtained for matching, based on the course overlap rate of aerial images and relevance optimizing is implemented. At the stage of feature point description, this paper uses a “one-stage” framework based on the VGG-Net (VGG-Network) model, in which the neighborhood patch of feature points is used as the network input, which can simultaneously learn the feature representation of aerial image patches and hash function. The framework for the proposed method is as shown in Figure 1. The input of this model is an aerial image patch, the binary hash code representation is obtained by the pre-trained deep network model, and the aerial image matching is completed through Hamming searching. This network model mainly comprises three parts: (1) a feature extraction layer: learning the image representation; (2) a hashing layer: learning the hash function and map the learned feature to a binary hash code; and (3) a loss function layer: utilizing triplet loss to optimize the network, adding the constraints of the absolute distance from positive sample pairs and the quantization loss to improve the hashing quality.

3. Construction of the Local Matching Region

An aerial image has a high resolution and large size, which contains a variety of detail information. There are a great deal of redundant calculations if the feature points of the whole aerial image are extracted and matched, thereby reducing the matching efficiency of aerial images. To improve the matching efficiency, a local matching region extraction algorithm for aerial images is proposed. In other words, the local matching region is constructed according to the overlap rate of aerial images and the feature points are extracted and matched only in the region, to avoid any calculating redundancy for the extraction of the whole image, and improve the matching efficiency.

3.1. Construction of Initial Local Region

According to the UAV (Unmanned Aerial Vehicle) aerial photographing requirements, the course overlap rate is 60% in photographing, the minimum threshold shall not be less than 53%, and the lateral overlap rate is given as 30%, the minimum shall not be less than 15%. Due to the impact of weather and other factors when photographing, the actual course overlap rate should be higher than 60%. Therefore, the aerial photographing matching efficiency will be improved by extracting the overlapping region of aerial images to match. Firstly, the number of spaces of the image to be matched N is calculated according to the course overlap rate of aerial images, and the local region is estimated according to the overlap rate requirement. The value of N is defined as:

$$N=\lfloor l{g}_{{\alpha }_0}^{{\alpha }_1}\rfloor =\lfloor \frac{lg{\alpha }_1}{lg{\alpha }_0}\rfloor$$

(1)

In Equation (1), ${\alpha }_0$ is the course overlap rate of aerial images, ${\alpha }_1$ means the optimum overlap rate of aerial images in the actual application, $\lfloor \rfloor$ represents rounding down. According to Equation (1), every N images will be selected, its overlap rate with the adjacent image in the image subset will be: $1-N(1-{\alpha }_0)$, and the rectangular matching region is constructed according to the new overlap rate.

3.2. Local Region Optimization

Since a UAV may be easily susceptible to external interference during a high-altitude flight, the flight direction may shift and the course overlap rate will be subject to certain deviation. If the extracted local region is matched directly in accordance with Section 3.1, some matching regions will get lost and the redundant region will be added. Therefore, in this paper, we optimize the initial local region and search for the optimal local matching region, as shown in Figure 2:

The $i\mathrm{th}$ frame and the $(N+i)\mathrm{th}$ frame image to be matched in the image subset are denoted as $I_1$ and $I_2$ respectively, their respective overlapping region is $A$ and $B$, in which $I_2$ is the image with an ideal overlap rate, while the actually obtained images are often as shown in ${I_2}^{\prime }$ or ${I_2}^{″}$. Assume the horizontal and vertical difference of the image ${I_2}^{\prime }$ from $I_2$ as $a$ and $b$, respectively, the correlation between the overlapping regions of the two images is calculated according to Equation (2):

$$\rho =\frac{{\displaystyle \sum _m{\displaystyle \sum _n(A(m+a,n+b)-{\overline{A}}_{m+a,n+b})}}(B(m+a,n+b)-{\overline{B}}_{m+a,n+b})}{\sqrt{{\displaystyle \sum _m{\displaystyle \sum _n{(A(m+a,n+b)-{\overline{A}}_{m+a,n+b})}^2{(B(m+a,n+b)-{\overline{B}}_{m+a,n+b})}^2}}}}$$

(2)

where $\overline{A}$, $\overline{B}$ are the mean values for the local region $A$, $B$, respectively; $m$, $n$ are the horizontal and vertical coordinate variables of the local region, respectively; $a$, $b$ are the lateral and longitudinal step lengths of this region, respectively, $A(m+a,n+b)$, $B(m+a,n+b)$ are the pixel gray values corresponding to the new n. The correlation of $A$, $B$ after each shift is calculated by laterally and longitudinally transforming the ideal overlapping region when it reaches the maximum value, that is, the actual overlapping region of two aerial images influenced by external factors, the extraction and matching calculation of feature points in the irrelevant regions can be avoided, and the aerial photographing matching efficiency will be improved if the images are matched in the local region. The specific process as shown in Algorithm 1:

Algorithm 1: Construction of the local matching region of aerial images.

Input: ${\alpha }_0$, ${\alpha }_1$, image sequence $I_i,(i=1,2,\cdots \mathrm{g})$, lateral shift step length $a$, longitudinal shift step length $b$, number of iterations $t_m$ and $t_m$, ${\rho }_{\max }=0$

Output: The $\rho (t_m,t_n)$ corresponding to maximum value ${\rho }_{\max }$ is the actual overlapping region to be solved

Step1 Calculate the number of intervals N according to Equation (1)   Step2 Denote the two aerial images to be matched $I_i$, $I_{i+N}$ as $I_1$ and $I_2$ respectively, calculate the overlapping rate of the two images is $1-N(1-{\alpha }_0)$   Step3 According the new overlap rate, calculate the ideal overlapping region of $I_1$ and $I_2$, denoted as $A$ and $B$, the pixel size is $m\times n$   Step4 Optimize local region   For $m$ From $m-t_m\times a$ To $m+t_m\times a$    For $n$ From $n-t_n\times b$ To $n+t_n\times b$     According to Equation(2), calculate $\rho (t_m,t_n)$, ${\rho }_{\max }$ = max(${\rho }_{\max }$, $\rho (t_m,t_n)$)    End   End

4. Deep Hash Network Structure with Distance Constraint and Quantization Loss

Given N training sample image patches $S=\{S_1,S_2,\cdots ,S_N\}$ and M triplets of training examples $\Gamma =\{(a_1,p_1,n_1),(a_2,p_2,n_2),\cdots (a_M,p_M,n_M)\}$, in which the $a_m\in \{1,2,\cdots N\}$ is a reference image patch, which is more similar to the positive sample image patch $p_m\in \{1,2,\cdots N\}$, but not similar to the negative sample image bock $n_m\in \{1,2,\cdots N\}$, that is to say $a_m$, $p_m$ means the same feature point, while $n_m$ does not.

Each image patch is entered to the convolutional neural network (CNN), the descriptor is obtained in the fully connected layer through nonlinear change. Image patch $x\in R^{n\times n}$ is the network input, while $f\left(x\right)\in R^D$ as the network output, which is a D-dimension descriptor, $f(\cdot )$ means the nonlinear transformation of the neural network. The goal is to obtain the transformation $f(\cdot )$, so that ${\Vert f\left(x_1\right)-f\left(x_2\right)\Vert }_2$ is the smallest possible when $x_1$ and $x_2$ are entered as the same feature point, while the greatest as possible when entering them as different feature points.

It is shown in Hanjiang Lai etc. [34] that a convolution layer with a larger convolution kernel replaced by a convolution layer with multiple smaller convolution kernels may not only reduce the number of parameters, but also create more nonlinear mappings and enhance the expression ability of the network. In this paper, the VGG-16 (VGG Network with 16 layers) model is treated as the basic framework, and three same VGG-16 network structures are used to comprise a feature extraction network. Due to the sharing of parameters among the three networks, the number of parameters is reduced and the training process of the network is accelerated. Three image patches are entered into the three VGG-16s to output the feature expression, and the loss is calculated at the loss layer. The network parameters and the hash function are trained simultaneously by using a back propagation algorithm. The VGG-16 network consists of 13 convolutional layers (Conv1–Conv13), two fully-connected layers (Fc1-Fc2), and an output layer, which performs the calculation with a smaller convolution kernel (3 × 3).

4.1. Independent Hashing Layer

A larger calculating cost will be incurred when using floating-point descriptors, while the binary descriptor completes the matching of image patches by performing simple XOR operation in the Hamming space, so as to greatly improve the matching efficiency. In order to obtain the hash code of the image patches, the output layer of VGG-16 is replaced as the hashing layer for learning the hash function. As shown in Figure 3, in order to obtain a separate hash code, this hash sub-network firstly equalizes the D-dimension feature representation at the Layer Fc15 into q sub-features $\{f_1(x),f_2(x)\cdots f_q(x)\}$, each sub-feature representation at the Layer Fc15, $f_i(x)(i=1,2,\cdots q)$ is mapped through the activation function $sigmoid(x)=\frac{1}{1+exp(-\beta x)}$ to the output value in $\left[0,1\right]$:

$$h_i(x)=sigmoid(W_h^T{f}_i(x)+v_h)=\frac{1}{1+exp(-\beta (W_h^T{f}_i(x)+v_h))}$$

(3)

In Equation (3), $f_i(x)$ represents the output of the feature extraction network, $W_h$ and $v_h$ are the hash layer parameters means the weight and bias respectively, $\beta$ is a hyper-parameter that controls the smoothness of the activation function. The hash code $h_i(x)$ obtained by the activation function is a continuous real value between 0 and 1, the threshold function is used to obtain the binary hash code $b_i(x)=\frac{1}{2}\left[sgn(h_i(x)-0.5)+1\right],\mathrm{i}=1,\cdots q$, in which $sgn(\cdot )$ is the sign function, if the bracketed is greater than 0, it will be 1, otherwise it will be −1. The q-dimension hash codes, ${\{0,1\}}^q$, is obtained through the fully-connected layer. The independent hash codes are constructed with hashing layer, in which the weight matrix $W_h$ and $v_h$ is learned only related to the sub-features, so as to obtain better hashing functions and hash codes with better expression ability. In this part, other architectures, like the divide-and-encode module proposed by Karen Simonyan etc. [35] can also be applied here. We do not focus on this in this work and leave this for future study.

4.2. New Objective Function

The loss layer comprises of the Softmax loss and the quantization loss. Since the relative position information of the triplet is only considered in the traditional classification loss, such as in Zishun Liu etc. [36] proposed to train Euclidean and Hamming embedding for image patch description with triplet convolutional networks. This paper proposes optimizing the network through adding the absolute distance constraints in the classification loss. Without considering the absolute position information among positive sample pairs, in order to further increase the precision to classify and obtain a more representative feature descriptor.

4.2.1. Classification Loss Based on the Absolute Distance Constraint

All the early local feature descriptors relying on deep learning are based on the Siamese network, which is composed of two of the same convolution neural networks in the form of shared parameters. The input is a pair of image patches and the supervised information is the similarity label for these two image patches.

It is given in Elad Hoffer etc. [37] that the triplet-based learning image representation has a performance better than the pairwise-based result, given the same deep neural network. Therefore, this paper replaces the original loss function with the triplet loss function. The hashing layer maps the image patch feature $f(\cdot )$ into the binary coding $b(\cdot )$. In order to retain the semantic similarity, the constructed hash layer needs to satisfy that the Hamming distance of positive samples $b(a)$ and $b(p)$ re smaller to the extent possible, while that of negative samples $b(a)$ and $b(n)$ are larger to the extent possible. Therefore, the loss function is defined as Equation (4):

$$loss(r)={\displaystyle \sum _{M}max(0,\alpha -{\Vert b(a)-b(n)\Vert }_H+{\Vert b(a)-b(p)\Vert }_H)}$$

(4)

where $b(a),b(p),b(n)\in {\{0,1\}}^q$, ${\Vert \cdot \Vert }_H$ means the Hamming distance, $\alpha$ is a parameter that denotes the margin. From Equation (4), when the difference between the negative sample pair and the positive sample pair ${\Vert b(a)-b(n)\Vert }_H-{\Vert b(a)-b(p)\Vert }_H$, is greater than the margin $\alpha$, $loss(r)=0$, this loss function will not optimize the network. In order to solve this problem, It was proposed to utilize triplets of training samples together with in-triplet mining of hard negatives [38], which ensures that the hardest negative inside the triplet is used for back propagation by swapping anchor and positive samples. In addition, unlike the pairwise-based loss, the triplet loss focuses on the relative position relation among triplets, while the pairwise loss focuses on the position relation among similar (dissimilar) image pairs. According to Fatih Cakir etc. [39], to obtain a better retrieval performance, it is wrong to make the distance among dissimilar images to the greatest extent possible. Therefore, this paper proposes a new loss function, considering the relative distance constraint between the positive and negative sample pairs in triplet loss and the absolute distance constraint of the positive sample in pairwise loss at the same time, which not only improves the expression ability of features, but also overcomes the deficiency that the network cannot be optimized separately using triplet loss at $loss(r)=0$. Therefore, the loss function mentioned here is as shown in Equation (5), where $\gamma$ is the weight:

$$\begin{array}{ll}loss& =loss(r)+\gamma loss(a)\\ & ={\displaystyle \sum _{M}max(0,\alpha -{\Vert b(a)-b(n)\Vert }_H+{\Vert b(a)-b(p)\Vert }_H)+}\gamma {\displaystyle \sum _M{\Vert b(a)-b(p)\Vert }_H}\end{array}$$

(5)

Since $b(\cdot )\in {\{0,1\}}^q$ is a discrete value in $\{0,1\}$, the optimization may be not easily done if the Hamming distance is used for back propagation. In order to obtain a differentiable loss function, the binary hash code $b(\cdot )\in {\{0,1\}}^q$ at the threshold layer is replaced by the activation layer output $h(\cdot )\in {\left[0,1\right]}^q$, and the Hamming distance is replaced by the Euclidean distance. The new loss function will be:

$$los{s}^{\ast }={\displaystyle \sum _M(max(0,\alpha -{\Vert h(a)-h(n)\Vert }_2^2+{\Vert h(a)-h(p)\Vert }_2^2)+\gamma {\Vert h(a)-h(p)\Vert }_2^2})$$

(6)

4.2.2. Quantization Loss

In the section of classification loss, to obtain a differentiable loss function, the continuous value at the activation layer $h_i(x)$ replaces the discrete value at the threshold layer $b_i(x)$. In the objective function, the loss between the continuous values coding in $\left[0,1\right]$ that is obtained from the activation layer and the hash code output from the threshold layer, namely the quantization loss, will be expressed as follows:

$$loss(q)={\displaystyle \sum _M\frac{1}{2}{\displaystyle \sum _x{\Vert h(x)-b(x)\Vert }_2^2},x\in \{a,p,n\}}$$

(7)

where $h(x)=\{h_1(x),h_2(x)\cdots h_q(x)\}$, $b(x)=\{b_1(x),b_2(x)\cdots b_q(x)\}$. The objective of this loss function is to obtain the output value of the activation layer closest to the quantization value 0 and 1 by learning, so as to reduce the loss caused by setting up a threshold. The whole objective function of the proposed framework is obtained by combining the loss function of the Softmax loss and the quantization loss:

$$Loss=los{s}^{\ast }+\lambda loss(q)$$

(8)

where $\lambda$ is the weight, which controls the important ratio of the classification loss and the quantization loss. The loss function of the whole framework is differentiable. Thus, the network is trained using a back propagation algorithm, so as to minimize the loss function.

In this paper, the proposed algorithm is implemented in open source Caffe, and the learning process of the proposed LDHM algorithm is explained in Algorithm 2. The proposed network is trained by stochastic gradient descent and back propagation to optimize the parameters, the training is conducted in batches, each batch is 256, with the training rate: 0.1, momentum: 0.98, and weight decay: 10⁻⁶. The balance parameters $\lambda$ and $\gamma$ in our loss are initialized as 0.2 and 0.5.

Algorithm 2: LDHM algorithm

Input: Image training set $\Gamma =\{a_i,p_i,n_i\}$, hash code dimension $q=128$, number of iterations $T$, weight $\gamma$, $\lambda$   Output: The network matrix and the hash layer parameter, $w$, $v$

Step1 (Initialization) Use the VGG-Net model pre-trained in ImageNet to initialize the network, initialize the Hash Layer by randomly sampling from a Gaussian distribution with mean $0$ and variance $0.01$;

Step2 According to the network structure, calculate the deep feature representation $f(x_i)$;   Step3 Calculate $h_i(x)=sigmoid(W_h^T{f}_i(x)+v_h)$;   Step4 Calculate the binary Hash code $b_i(x)=\frac{1}{2}\left[sgn(h_i(x)-0.5)+1\right]$;   Step5 Calculate the derivative of the objective function (8), update the parameter $w$, $v$ and the network matrix by back propagation;   Step6 Repeat Step2~Step5 until the parameter value is invariable

When the parameters in the network are learned through back propagation, every image patche can be represented by compact binary hash codes, and then, in the matching stage, the fast matching can be achieved by comparing the Hamming distance between hash codes. The matching steps based on the Hamming space are as follows:

• Step 1: Local matching regions $A^{\prime }$ and $B^{\prime }$ are obtained from two aerial images to be matched $I_1$ and $I_2$ by Algorithm 1, as described in Section 3.
• Step 2: The DoG algorithm is used to detect the feature point in the local matching regions $A^{\prime }$ and $B^{\prime }$, then the neighborhood patch of feature points is constructed with a size of 64 × 64 pixels.
• Step 3: According to Section 4, each image patch will be inputted to the trained network and represented by a binary hash code with better characterization and discrimination.
• Step 4: All feature patches in two local matching regions are represented by binary hash codes: for any feature in $A^{\prime }$, its corresponding matching point in $B^{\prime }$ will be found by the approximate nearest neighbor search algorithm in the Hamming space, realizing the matching of aerial images.

5. Discussions

All the experiments for deep learning-based algorithms are carried out in the context of GPU processing with the configuration of an NVIDIA GTX TITAN X GPU, while the non-learning matching algorithms are implemented only in the context of CPU processing with the configuration of an Intel Xeon E5-2650 CPU.

5.1. Experimental Sample Dataset

In order to measure the matching performance of the proposed LDHM algorithm for different image types, three groups of image sets photographed by UltraCam-D aerial cameras at Tehran, Iran in 2005 are used as the dataset to evaluate different algorithms, as shown in

Table 1. UltraCam-D dataset.

Name	Image Pairs	Resolution (Pixel)	GSD (m)	Number (Ten Thousand)	Patch Size (Pixel)
Group 1	UltraCam-D	1256 × 1278	0.10	15	64 × 64
	UltraCam-D	1256 × 1278	0.10		64 × 64
Group 2	UltraCam-D	1161 × 1169	0.10	12	64 × 64
	UltraCam-D	1161 × 1169	0.10		64 × 64
Group 3	UltraCam-D	1197 × 1203	0.10	13	64 × 64
	UltraCam-D	1197 × 1203	0.10		64 × 64

[10]. Such image pairs in the dataset obtained from different viewpoints, all are ultra-high resolution aerial images of 1256 × 1278, 1161 × 1169, and 1197 × 1203 pixels, respectively, which cover different texture features. In order to obtain the image patches for neural network training, the feature points of each group of images are detected by the difference of Gaussian algorithm, and the neighborhood image patches of feature points are extracted with a size of 64 × 64 pixels, where 50% for matching were extracted from the corresponding feature points and the other 50% for non-matching pairs were randomly extracted from non-corresponding feature points. In order to construct a triplet, the matched image patches of the same feature point are randomly selected as the reference image and the positive sample image, and the image patches of different feature points are randomly selected as the negative sample image. In the course of the experiment, we resized each image patch from 64 × 64 pixels to 32 × 32 pixels, and all patches are smoothed by a Gaussian kernel with standard deviation of 0. In addition, the actual UAV aerial images were used for the matching experiment, with a resolution of 2048 × 2048 pixels. The algorithms which are used for comparison with the proposed algorithm including: SIFT [3], MatchNet [18], DeepCompare [40], Deep Desc [41], PN-Net [19], and CovexOpt [42].

5.2. Evaluation Criterion

Three image sets with different resolutions photographed by the UltraCam-D aerial camera are denoted as Group 1, Group 2, and Group 3, in the course of the experiment, different datasets are used as the training test and testing set, respectively, in order to compare the performance of the proposed algorithm, six training sets and test sets are divided: (1) Testing Set Group 1, Training Set Group 2; (2) Testing Set Group 1, Training Set Group 3; (3) Testing Set Group 2, Training Set Group 1; (4) Testing Set Group 2, Training Set Group 3; (5) Testing Set Group 3, Training Set Group 1; and (6) Testing Set Group 3, Training Set Group 2.

5.2.1. Precision Rate

The precision rate is evaluated by the receiver operating characteristics (ROC) curve, which describes the relationship between the true positive (matching patch pairs) rate and false positive (non-matching patching pairs) rate. The performance of the proposed algorithm is compared with the other algorithms, in addition to the current state-of-the-art algorithms (see Figure 4).

From Figure 4, the proposed LDHM algorithm achieves the best results when used for experiments in different training sets and test sets, and compared with manual features-based SIFT algorithm, all learning-based algorithms achieve better performance. Compared with the other algorithms, the performance of the triplet loss-based PN-Net algorithm is the closest to that of the proposed algorithm, and it is superior to the other algorithms based on pairwise loss.

5.2.2. Performance of the 95% Error Rate

In the experiments, we use a false positive rate at 95% recall to evaluate our algorithm, which refers to the percentage of incorrect matches obtained when 95% of true matches are found. It is also shown that the lower the error rate is, the better the performance of the descriptor is. The 95% error rate is calculated using the six groups of training sets and testing sets, respectively. The experimental results are as shown in

Table 2. Performance of the 95% error rate.

Training Set	Group 2	Group 3	Group 1	Group 3	Group 1	Group 2	Average
Testing Set	Group 1		Group 2		Group 3		95% ERR
SIFT	26.76		20.76		23.74		23.75
Deep Desc	7.93		5.64		14.05		9.21
MatchNate	7.93	12.32	5.35	8.65	12.63	10.06	9.49
DeepCompare	12.24	16.35	7.51	9.47	18.84	14.79	13.2
PN-Net	7.58	8.76	4.78	5.33	8.39	6.63	6.91
CovexOpt	10.72	13.68	7.24	8.27	10.37	9.24	9.92
Proposed	7.14	7.56	4.68	5.40	7.96	6.24	6.50

.

As shown in Table 2, the error rate of 95% of the proposed algorithm is compared with other algorithms in different training sets and testing sets, and the last column in

Table 3. Performance of the matching score.

Algorithm	SIFT	BRIEF	PN-Net	DeepCompare	MatchNet	Proposed
Group 1	0.301	0.194	0.322	0.313	0.247	0.329
Group 2	0.294	0.184	0.310	0.304	0.238	0.322
Group 3	0.281	0.171	0.289	0.293	0.225	0.305
Average	0.292	0.183	0.307	0.303	0.237	0.319

indicates the average of 95% error rate for each algorithm. From the average 95% error rates listed in Table 3, the error rate of the proposed algorithm is 6.50%, 17.25% lower than the SIFT algorithm, and other algorithms are at least 10.55% higher than the SIFT algorithm. These data shows that the learning-based matching algorithm has a better accuracy than the manual features-based matching algorithm. Among the learning-based matching algorithms, PN-Net is just second to the proposed algorithm, while the other algorithms have similar error rates. The absolute distance constraint of similar samples is added to the triplet loss in the proposed algorithm, which makes the deep features of the images obtain a better characterization and discrimination, and the error matching rate is reduced, so the error rate is the lowest.

5.2.3. Performance of the Matching Score

The matching score refers to the ratio of ground truth corresponding over the number of features. This criterion measures the overall performance of feature descriptors, and a higher matching score means better performance. The matching score is evaluated on the three groups of datasets, respectively, the results are given in the Table 3, and the last row gives the mean matching score

As shown in Table 3, the difference in matching scores for the same algorithm in different datasets is relatively small. In the same dataset, the matching score of the proposed algorithm is the highest, which means the matching score is 0.319, while the mean matching score of the BRIEF algorithm with a simple binary descriptor is the lowest, only at 0.183, 0.136 lower than the proposed algorithm. As the learning-based matching algorithms, the matching scores of PN-Net and DeepCompare are similar, 0.012 and 0.016 lower than the proposed algorithm, respectively, while that of MatchNet is relatively small, 0.082 lower than the proposed algorithm. However, the mean matching score of the SIFT algorithm with manual features is higher than that of MatchNet, but lower than any of the other learning-based algorithms.

5.2.4. Comparison of the Matching Results

In order to verify the efficiency of the proposed algorithm, the proposed LDHM algorithm is compared with the manual features-based floating-point feature matching algorithm SURF, the binary feature matching algorithm BRIEF, and the learning-based matching algorithm MatchNet, the experimental results based on three aerial images are given in Figure 5, Figure 6 and Figure 7.

According to the experimental results, the proposed LDHM algorithm achieves better matching results with respect to the three aerial images. SURF is a modified version of the classical SIFT algorithm in terms of the matching efficiency, which has a higher stability, but the feature descriptor is inaccurate and increases the error matching rate because it depends heavily on the gradient direction of the local regional pixels when seeking its main direction. BRIEF makes a binary description of its neighborhood based on the detection of feature points, but it is more sensitive to scale and the noise, with relatively poor matching results as shown in Figure 5b and Figure 6b. MatchNet uses the learned descriptor for matching, which shows a better matching effect compared to the manual features-based matching algorithm. The proposed algorithm not only detects a large number of feature points, but also has a higher matching accuracy, because the proposed algorithm performs detection and matching of feature points in the local region of aerial image, and the feature point descriptor with strong discriminating ability that is obtained from the deep learning network, reduces the occurrence of mismatching.

5.2.5. Comparison of Algorithm Efficiency

As shown in

Table 4. Time consumption.

Algorithm	SIFT	BRIEF	PN-Net	DeepCompare	MatchNet	Proposed
Time (ms)	0.51	0.013	0.021	0.049	0.624	0.018

, BRIEF is the fastest and makes a binary description of the feature points through the value of pixels, while SIFT performs matching with the 128-dimension floating-point descriptor, which has a lower efficiency. Among the deep learning-based matching algorithms, PN-NET achieves faster matching by reducing the dimensions of feature descriptor, while MatchNet performs matching with the 512-dimension descriptor, so it takes the longest time. The proposed LDHM that is implemented by GPU processing performs detection of feature points in the local region of the aerial images and adds the hashing layer into the network to construct the binary descriptor, its matching time gets closer to BRIEF, which is implemented by CPU processing, and can meet the real-time needs when processing an aerial image with large amounts of data.

6. Conclusions

In this manuscript, a hashing matching algorithm for aerial images based on relative distance and absolute distance constraints is proposed which is suitable for real-time matching of aerial images for its low complexity and fast matching speed. Within the proposed framework, firstly, the local matching region of an aerial image is extracted according to the overlap rate, which not only improves the matching efficiency, but also reduces the occurrence of mismatching. Secondly, the feature point descriptor of local region is learned by the triplet network structure which using VGG-Net as the basic framework, the output layer is replaced by the hashing layer with the constraint of independence. Finally, the absolute position information of the positive sample pair is included, and the quantization error is incorporated into the objective function when the network is optimized with the traditional triplet loss at the loss function layer and obtaining a binary hash code with better expressions. Compared with any modern aerial image matching algorithms, the proposed algorithm shows better matching efficiency and better matching accuracy.