Ocean Wind and Current Retrievals Based on Satellite SAR Measurements in Conjunction with Buoy and HF Radar Data
Abstract
:1. Introduction
2. Data and Methods
2.1. Satellite, Buoy, and High-Frequency Radar Data
2.2. Retrieval Method of Winds from Radarsat-2 SAR Images
2.3. Validation Method for the Effect of Ocean Currents on the Winds Retrieved from SAR
- (1)
- RADARSAT-2 fine quad-polarization mode SLC SAR data are characterized by a nominal spatial resolution of 8.0 in azimuth and range and the pixel spacing in range and azimuth directions is about 5 m. We make a 20 20 pixel boxcar average on the NRCS, in each polarization, so that the resampled pixel spacing is 100 m.
- (2)
- Extract geophysical parameters and SAR system information from quad-polarization RADARSAT-2 SAR images, such as longitude, latitude, incident angles, and other information for each pixel, track angle, radar look direction.
- (3)
- Use MATLAB to obtain the NRCS for VV, VH polarization images, and complex backscattering coefficients S_VV, S_VH for each pixel, for each SAR image.
- (4)
- Firstly, we use the NRCS for VH polarization data to calculate wind speed at 10-m reference height () from Equation (4). Secondly, we use the NRCS for VV data to calculate wind direction with ambiguities from Equation (5). Finally, using the directional ambiguity removal criteria previously mentioned, the final wind directions are obtained without ambiguities.
- (5)
- Collect ocean currents from HF radar and observed wind fields from NDBC buoys in the same location and time as the SAR images.
- (6)
- Analyze two groups of experiments. In the first group, directly retrieved winds (including wind speed and directions) from SAR are compared to the winds obtained from the corresponding buoy data and the errors are calculated. In the second group, the ocean current information (including the current speeds and directions), are overlaid on wind fields retrieved from SAR images, again compared with the corresponding winds observed by buoys, and the errors are calculated. By comparing the errors calculated in both groups, the impact of ocean currents on the winds retrieved from SAR images at the sea surface can be estimated.
3. Results and Discussion
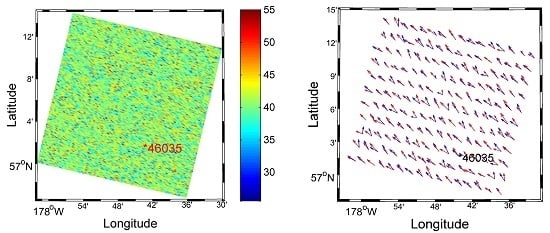
3.1. Effect of Ocean Currents on the Retrieval of Sea Surface Wind from SAR
3.2. Ocean Current Vector Retrieval from Empirical Formulae
3.2.1. Empirical Formulae of Ocean Currents and DWF Vector
3.2.2. Cases of Retrieved Ocean Currents
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Klemas, V. Remote Sensing of Coastal and Ocean Currents: An Overview. J. Coast. Res. 2012, 28, 576–586. [Google Scholar] [CrossRef]
- Zuckerman, S.; Anderson, S.P.; Stuart, G.; Cooper, C. Real-time Ocean Surface current measurements in the Gulf of Mexico. IEEE Oceans 2015, 1–6. [Google Scholar] [CrossRef]
- Paduan, J.D.; Washburn, L. High-Frequency Radar Observations of Ocean Surface Currents. Annu. Rev. Mar. Sci. 2013, 5, 115–136. [Google Scholar] [CrossRef] [PubMed]
- Romeiser, R.; Breit, H.; Eineder, M.; Runge, H.; Flament, P. Current measurements by sar along-track interferometry from a space shuttle. IEEE Trans. Geosci. Remote Sens. 2005, 10, 2315–2324. [Google Scholar] [CrossRef]
- Hansen, M.W.; Collard, F.; Dagestad, K.-F.; Johannessen, J.; Fabry, P.; Chapron, B. Retrieval of Sea Surface Range Velocities from Envisat ASAR Doppler Centroid Measurements. IEEE Geosci. Remote Sens. 2011, 49, 3582–3592. [Google Scholar] [CrossRef]
- Toporkov, J.V.; Hwang, P.A.; Sletten, M.A.; Farquharson, G.; Perkovic, D.; Frasier, S.J. Surface Velocity Profiles in a Vessel’s Turbulent Wake Observed by a Dual-Beam Along-Track Interferometric SAR. IEEE Geosci. Remote Sens. Lett. 2011, 8, 602–606. [Google Scholar] [CrossRef]
- Qazi, W.A.; Emery, W.J.; Fox-Kemper, B. Computing Ocean Surface Currents over the Coastal California Current System Using 30-Min-Lag Sequential SAR Images. IEEE Geosci. Remote Sens. 2014, 52, 7559–7580. [Google Scholar] [CrossRef]
- Perrie, W.; He, Y.; Li, H.; Fang, H.; Zhao, S.; Yu, W. Ocean surface wave measurements from fully polarimetric SAR imagery. Sci. China Earth Sci. 2015, 10, 1849–1861. [Google Scholar]
- Perrie, W.; Xie, T. Gulf Stream thermal fronts detected by synthetic aperture radar. In Proceedings of the IEEE International Geoscience & Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010. [Google Scholar]
- Kuang, H.; Perrie, W.; Xie, T. Retrievals of sea surface temperature fronts from SAR imagery. J. Geophys. Res. Lett. 2012, 10, 1–7. [Google Scholar] [CrossRef]
- Kelly, K.A.; Dickinson, S.; Mcphaden, M.J.; Johnson, G.C. Ocean currents evident in satellite wind data. J. Geophys. Res. Lett. 2001, 28, 2469–2472. [Google Scholar] [CrossRef]
- Zhang, F.W.; Drennan, W.M.; Haus, B.K. On wind-wave-current interactions during the Shoaling Waves Experiment. J. Geophys. Res. Oceans 2009, 14, 287–295. [Google Scholar] [CrossRef]
- Small, R.J.; Richards, K.J.; Xie, S.P. Damping of Tropical Instability Waves caused by the action of surface currents on stress. J. Geophys. Res. 2009, 114, 553–556. [Google Scholar] [CrossRef]
- O’Neill, L.W.; Chelton, D.B.; Esbensen, S.K. High-Resolution Satellite Measurements of the Atmospheric Boundary Layer Response to SST Variations along the Agulhas Return Current. J. Clim. 2005, 14, 2706–2723. [Google Scholar] [CrossRef]
- Xie, T.; Zhao, D.; Perrie, W.; Fang, H. Electromagnetic backscattering from one-dimensional drifting fractal sea surface I: Wave-current coupled model. Chin. Phys. B 2016, 4, 79–102. [Google Scholar] [CrossRef]
- Xie, T.; Perrie, W.; Zhao, D.; Fang, H. Electromagnetic backscattering from one-dimensional drifting fractal sea surface II: Electromagnetic backscattering model. Chin. Phys. B 2016, 6, 64–101. [Google Scholar] [CrossRef]
- MacDonald, Dettwiler and Associates (MDA). Radarsat-2 Product Description; MDA: Richmond, BC, Canada, 2015. [Google Scholar]
- Kohut, J.T.; Glenn, S.M.; Chant, R.J. Seasonal current variability on the New Jersey inner Shelf. J. Geophys. Res. 2013, 109. [Google Scholar] [CrossRef]
- Emery, B.M.; Washburn, L.; Harlan, J.A. Evaluating radial current measurements from CODAR High-frequency radars with moored current meters. J. Atmos. Ocean. Technol. 2004, 21, 1259–1271. [Google Scholar] [CrossRef]
- Liu, Y.; Weisberg, R.H.; Merz, C.R. Assessment of CODAR and WERA HF radars in mapping currents on the West Florida Shelf. J. Atmos. Ocean. Technol. 2014, 31, 1363–1382. [Google Scholar] [CrossRef]
- Shen, Z.; Wu, X.; Lin, H.; Chen, X.; Xu, X.; Li, L. Spatial Distribution Characteristics of Surface Tidal Currents in the Southwest of Taiwan Strait. J. Ocean Univ. China 2014, 13, 971–978. [Google Scholar] [CrossRef]
- Harlan, J.; Terrill, E.; Hazard, L.; Otero, M.; Roarty, H. The Integrated Ocean Observing System HF radar network. In Proceedings of the IEEE Washington OCEANS’15 MTS, Washington, DC, USA, 19–22 October 2015. [Google Scholar]
- Temll, E.; Otero, M.; Hazard, L.; Conlee, D.; Harlan, J.; Kohut, J.; Reuter, P.; Cook, T.; Harris, T. Lindquist. Data Management and Real-time Distribution in the HF-Radar National Network. In Proceedings of the IEEE Oceans, Boston, MA, USA, 18–21 September 2006. [Google Scholar]
- Hwang, P.A.; Zhang, B.; Toporkov, J.V.; Perrie, W. Comparison of composite Bragg theory and quad-polarization radar backscatter from RADARSAT-2: With application radar backscatter from RADARSAT-2: With applications to wave breaking and high wind retrieval. J. Geophys. Res. 2010, C8, 246–255. [Google Scholar]
- Vachon, P.W.; Wolfe, J. C-Band Cross-Polarization Wind Speed Retrieval. IEEE Geosci. Remote Sens. Lett. 2011, 3, 456–459. [Google Scholar] [CrossRef]
- Zhang, B.; Perrie, W. Cross-Polarized Synthetic Aperture Radar: A New Potential Measurement Technique for Hurricanes. Bull. Am. Meteorol. Soc. 2012, 93, 531–541. [Google Scholar] [CrossRef]
- Hersbach, H. Comparison of C-band scatterometer CMOD5.N equivalent neutral winds with ECMWF. J. Atmos. Ocean. Technol. 2010, 4, 721–736. [Google Scholar] [CrossRef]
- Yueh, S.H.; Kwok, R.; Nghiem, S.V. Polarimetric scattering and emission properties of targets with reflection symmetry. J. Radio Sci. 2016, 29, 1409–1420. [Google Scholar] [CrossRef]
- Yueh, S.H. Modeling of Wind Direction Signals in Polarimetric Sea Surface Brightness Temperatures. J. IEEE Geosci. Remote Sens. 1995, 35, 1400–1418. [Google Scholar] [CrossRef]
- Tsai, W.Y.; Nghiem, S.V.; Huddleston, J.N. Polarimetric scatterometry: A promising technique for improving ocean surface wind measurements from space. J. IEEE Geosci. Remote Sens. 2000, 38, 1903–1921. [Google Scholar] [CrossRef]
- Zhang, B.; Perrie, W.; Vachon, P.W. Ocean Vector Winds Retrieval from C-Band Fully Polarimetric SAR Measurements. IEEE Geosci. Remote Sens. 2012, 11, 4252–4261. [Google Scholar] [CrossRef]









| SAR Image | Buoy Data | HF Radar | Retrieval Currents | |
|---|---|---|---|---|
| Time | 03:52 | 03:50 | 04:00 | 03:50 |
| Site | 57.036° N 177.64° W | 57.026° N 177.74° W | 57.020° N 177.68° W | 57.026° N 177.74° W |
| Wind/current speed | Wind speed 9.85 m/s | Wind speed 11.5 m/s | Current speed 0.478 m/s | Current speed 0.406 m/s |
| Wind/current direction | Wind direction 252° | Wind direction 266° | Current direction 323.4° | Current direction 317.6° |
| Sar Image | Buoy Data | Hf Radar | Retrieval Currents | |
|---|---|---|---|---|
| Time | 02:12 | 02:12 | 04:00 | 03:50 |
| Site | 26.602° N 80.145° W | 26.613° N 80.034° W | 26.587° N 80.098° W | 26.613° N 80.034° W |
| Wind/current speed | Wind speed 10.52 m/s | Wind speed 8.9 m/s | Current speed 0.465 m/s | Current speed 0.380 m/s |
| Wind/current direction | Wind direction 41° | Wind direction 57° | Current direction 177.2° | Current direction 171° |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, H.; Xie, T.; Perrie, W.; Zhao, L.; Yang, J.; He, Y. Ocean Wind and Current Retrievals Based on Satellite SAR Measurements in Conjunction with Buoy and HF Radar Data. Remote Sens. 2017, 9, 1321. https://doi.org/10.3390/rs9121321
Fang H, Xie T, Perrie W, Zhao L, Yang J, He Y. Ocean Wind and Current Retrievals Based on Satellite SAR Measurements in Conjunction with Buoy and HF Radar Data. Remote Sensing. 2017; 9(12):1321. https://doi.org/10.3390/rs9121321
Chicago/Turabian StyleFang, He, Tao Xie, William Perrie, Li Zhao, Jingsong Yang, and Yijun He. 2017. "Ocean Wind and Current Retrievals Based on Satellite SAR Measurements in Conjunction with Buoy and HF Radar Data" Remote Sensing 9, no. 12: 1321. https://doi.org/10.3390/rs9121321
APA StyleFang, H., Xie, T., Perrie, W., Zhao, L., Yang, J., & He, Y. (2017). Ocean Wind and Current Retrievals Based on Satellite SAR Measurements in Conjunction with Buoy and HF Radar Data. Remote Sensing, 9(12), 1321. https://doi.org/10.3390/rs9121321