Comparison of Passive Microwave-Derived Early Melt Onset Records on Arctic Sea Ice
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Passive Microwave Algorithm
2.2. The Advanced Horizontal Range Algorithm
2.3. Tbs and Calibration
2.4. Methodology for Original MO Date Comparison
2.5. Methodology for Adjusted MO Date Comparisons
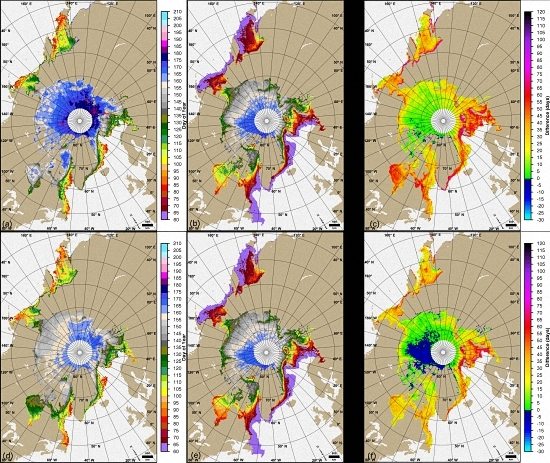
3. Results
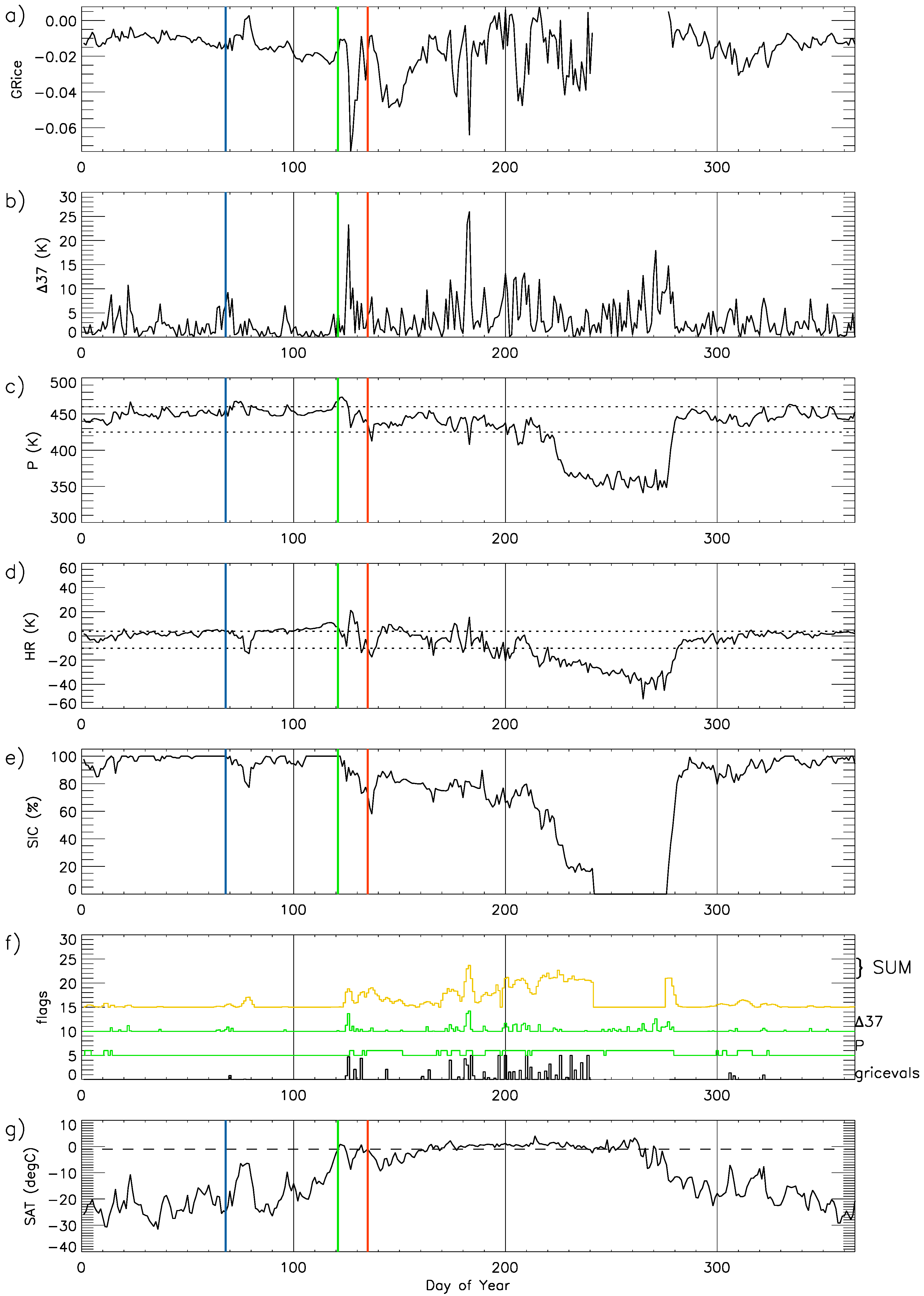
3.1. Examples of Algorithm Sensitivity
3.1.1. The Barents Sea
3.1.2. Laptev Sea
3.1.3. Central Arctic
3.1.4. Case Studies Summary
3.2. Comparison of Original and Adjusted MO Dates
3.3. Trend and Average Offset Comparisons
3.3.1. Original AHRA and PMWC Trend Comparison
3.3.2. Adjusted AHRA-A and PMWC-A Trend Comparison
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gloersen, P.; Campbell, W.J.; Cavalieri, D.J.; Comiso, J.C.; Parkinson, C.L.; Zwally, H.J. Satellite passive microwave observations and analysis of Arctic and Antarctic sea ice, 1978–1987. Ann. Glaciol. 1993, 17, 149–154. [Google Scholar] [CrossRef]
- Comiso, J.C.; Parkinson, C.L.; Gersten, R.; Stock, L. Accelerated decline in the Arctic sea ice cover. Geophys. Res. Lett. 2008, 35, L01703. [Google Scholar] [CrossRef]
- Cavalieri, D.J.; Parkinson, C.L. Arctic sea ice variability and trends, 1979–2010. Cryosphere 2012, 6, 881–889. [Google Scholar] [CrossRef]
- Belchansky, G.I.; Douglas, D.C.; Platonov, N.G. Duration of the Arctic sea ice melt season: Regional and interannual variability, 1979–2001. J. Clim. 2004, 17, 67–80. [Google Scholar] [CrossRef]
- Markus, T.; Stroeve, J.C.; Miller, J. Recent changes in Arctic sea ice melt onset, freezeup, and melt season length. J. Geophys. Res. Oceans 2009, 114, C12024. [Google Scholar] [CrossRef]
- Parkinson, C.L. Spatially mapped reductions in the length of the Arctic sea ice season. Geophys. Res. Lett. 2014, 41, 4316–4322. [Google Scholar] [CrossRef] [PubMed]
- Perovich, D.K.; Nghiem, S.V.; Markus, T.; Schweiger, A. Seasonal evolution and interannual variability of the local solar energy absorbed by the Arctic sea ice-ocean system. J. Geophys. Res. Oceans 2007, 112, C03005. [Google Scholar] [CrossRef]
- Persson, P.O.G. Onset and end of the summer melt season over sea ice: Thermal structure and surface energy perspective from SHEBA. Clim. Dyn. 2012, 39, 1349–1371. [Google Scholar] [CrossRef]
- Crane, R.G.; Anderson, M.R. Springtime microwave emissivity changes in the southern Kara Sea. J. Geophys. Res. Oceans 1994, 99, 14303–14309. [Google Scholar] [CrossRef]
- Curry, J.A.; Schramm, J.L.; Ebert, E.E. Sea-ice albedo climate feedback mechanism. J. Clim. 1995, 8, 240–247. [Google Scholar] [CrossRef]
- Drobot, S.D.; Anderson, M.R. Comparison of interannual snowmelt-onset dates with atmospheric conditions. Ann. Glaciol. 2001, 33, 79–84. [Google Scholar] [CrossRef]
- Bliss, A.C.; Anderson, M.R. Daily area of snow melt onset on Arctic sea ice from passive microwave satellite observations 1979–2012. Remote Sens. 2014, 6, 11283–11314. [Google Scholar] [CrossRef]
- Mortin, J.; Svensson, G.; Graversen, R.G.; Kapsch, M.-L.; Stroeve, J.C.; Boisvert, L.N. Arctic sea ice controlled by atmospheric moisture transport. Geophys. Res. Lett. 2016, 43, 6636–6642. [Google Scholar] [CrossRef]
- Smith, D.M. Observation of perennial Arctic sea ice melt and freeze-up using passive microwave data. J. Geophys. Res. Oceans 1998, 103, 27753–27769. [Google Scholar] [CrossRef]
- Drobot, S.D.; Anderson, M.R. An improved method for determining snowmelt onset dates over Arctic sea ice using Scanning Multichannel Microwave Radiometer and Special Sensor Microwave/Imager data. J. Geophys. Res. Atmos. 2001, 106, 24033–24049. [Google Scholar] [CrossRef]
- Belchansky, G.I.; Douglas, D.C.; Mordvintsev, I.N.; Platonov, N.G. Estimating the time of melt onset and freeze onset over Arctic sea-ice area using active and passive microwave data. Remote Sens. Environ. 2004, 92, 21–39. [Google Scholar] [CrossRef]
- Winebrenner, D.P.; Nelson, E.D.; Colony, R.; West, R.D. Observation of melt onset on multiyear Arctic sea ice using the ERS 1 synthetic aperture radar. J. Geophys. Res. 1994, 99, 22425–22441. [Google Scholar] [CrossRef]
- Kwok, R.; Cunningham, G.F.; Nghiem, S.V. A study of the onset of melt over the Arctic ocean in RADARSAT synthetic aperture radar data. J. Geophys. Res. Oceans 2003, 108, 3363. [Google Scholar] [CrossRef]
- Mahmud, M.S.; Howell, S.E.L.; Geldsetzer, T.; Yackel, J. Detection of melt onset over the northern Canadian Arctic Archipelago sea ice from RADARSAT, 1997–2014. Remote Sens. Environ. 2016, 178, 59–69. [Google Scholar] [CrossRef]
- Forster, R.R.; Long, D.G.; Jezek, K.C.; Drobot, S.D.; Anderson, M.R. The onset of Arctic sea-ice snowmelt as detected with passive- and active-microwave remote sensing. Ann. Glaciol. 2001, 33, 85–93. [Google Scholar] [CrossRef]
- Wang, L.; Wolken, G.J.; Sharp, M.J.; Howell, S.E.L.; Derksen, C.; Brown, R.D.; Markus, T.; Cole, J. Integrated pan-Arctic melt onset detection from satellite active and passive microwave measurements, 2000–2009. J. Geophys. Res. Atmos. 2011, 116, D22103. [Google Scholar] [CrossRef]
- Wang, L.; Derksen, C.; Brown, R.; Markus, T. Recent changes in pan-arctic melt onset from satellite passive microwave measurements. Geophys. Res. Lett. 2013, 40, 522–528. [Google Scholar] [CrossRef]
- Bliss, A.C.; Anderson, M.R. Arctic sea ice melt onset from passive microwave satellite data: 1979–2012. Cryosphere 2014, 8, 2089–2100. [Google Scholar] [CrossRef]
- Stroeve, J.C.; Markus, T.; Boisvert, L.; Miller, J.; Barrett, A. Changes in Arctic melt season and implications for sea ice loss. Geophys. Res. Lett. 2014, 41, 1216–1225. [Google Scholar] [CrossRef]
- NASA National Snow and Ice Data Center Distributed Active Archive Center. Documentation: Polar Stereographic Projection and Grid. Available online: https://nsidc.org/data/polar-stereo/ps_grids.html (accessed on 22 September 2016).
- Gloersen, P. Nimbus-7 SMMR Polar Gridded Radiances and Sea Ice Concentrations; Version 1; NASA DAAC at the National Snow and Ice Data Center: Boulder, CO, USA, 2006. [Google Scholar]
- Livingstone, C.E.; Singh, K.P.; Gray, A.L. Seasonal and regional variations of active/passive microwave signatures of sea ice. IEEE Trans. Geosci. Remote Sens. 1987. [Google Scholar] [CrossRef]
- Eppler, D.T.; Farmer, L.D.; Lohanick, A.W.; Anderson, M.R.; Cavalieri, D.J.; Comiso, J.; Gloersen, P.; Garrity, C.; Grenfell, T.C.; Hallikainen, M.; et al. Passive microwave signatures of sea ice. In Microwave Remote Sensing of Sea Ice; American Geophysical Union: Washington, DC, USA, 1992; pp. 47–71. [Google Scholar]
- Anderson, M.R.; Drobot, S.D. Spatial and temporal variability in snowmelt onset over arctic sea ice. Ann. Glaciol. 2001, 33, 74–78. [Google Scholar] [CrossRef]
- Cavalieri, D.J.; Gloersen, P.; Campbell, W.J. Determination of sea ice parameters with the NIMBUS 7 SMMR. J. Geophys. Res. Atmos. 1984, 89, 5355–5369. [Google Scholar] [CrossRef]
- Markus, T.; Cavalieri, D.J. Snow depth distribution over sea ice in the Southern Ocean from satellite passive microwave data. In Antarctic Sea Ice: Physical Processes, Interactions and Variability; Jeffries, M.O., Ed.; American Geophysical Union: Washington, DC, USA, 1998; pp. 19–39. [Google Scholar]
- Meier, W.; Fetterer, F.; Savoie, M.; Mallory, S.; Duerr, R.; Stroeve, J. NOAA/NSIDC Climate Data Record of Passive Microwave Sea Ice Concentration; Version 2; NASA DAAC at the National Snow and Ice Data Center: Boulder, CO, USA, 2013. [Google Scholar]
- Peng, G.; Meier, W.N.; Scott, D.J.; Savoie, M.H. A long-term and reproducible passive microwave sea ice concentration data record for climate studies and monitoring. Earth Syst. Sci. Data 2013, 5, 311–318. [Google Scholar] [CrossRef]
- Jezek, K.C.; Merry, C.; Cavalieri, D.; Grace, S.; Bedner, J.; Wilson, D.; Lampkin, D. Comparison between SMMR and SSM/I Passive Microwave Data Collected over the Antarctic Ice Sheet; BPRC Technical Report; Byrd Polar Research Center: Columbus, OH, USA, 1991. [Google Scholar]
- Abdalati, W.; Steffen, K.; Otto, C.; Jezek, K.C. Comparison of brightness temperatures from SSMI instruments on the DMSP F8 and F11 satellites for Antarctica and the Greenland ice sheet. Int. J. Remote Sens. 1995, 16, 1223–1229. [Google Scholar] [CrossRef]
- Stroeve, J.; Maslanik, J.; Xiaoming, L. An intercomparison of DMSP F11- and F13-derived sea ice products. Remote Sens. Environ. 1998, 64, 132–152. [Google Scholar] [CrossRef]
- Cavalieri, D.J.; Parkinson, C.L.; Digirolamo, N.; Ivanoff, A. Intersensor calibration between F13 SSMI and F17 SSMIS for global sea ice data records. IEEE Geosci. Remote Sens. Lett. 2012, 9, 233–236. [Google Scholar] [CrossRef]
- Maslanik, J.; Stroeve, J. DMSP SSM/I-SSMIS Daily Polar Gridded Brightness Temperatures; Version 4; NASA DAAC at the National Snow and Ice Data Center: Boulder, CO, USA, 2004. [Google Scholar]
- Cavalieri, D.J.; Gloersen, P.; Zwally, H.J. Near-Real-Time DMSP SSM/I-SSMIS Daily Polar Gridded Brightness Temperatures; Version 1; Maslanik, J., Stroeve, J., Eds.; NASA DAAC at the National Snow and Ice Data Center: Boulder, CO, USA, 1999. [Google Scholar]
- Rigor, I.G.; Colony, R.L.; Martin, S. Variations in surface air temperature observations in the Arctic. J. Clim. 2000, 13, 896–914. [Google Scholar] [CrossRef]
- Anderson, M.R.; Bliss, A.C.; Drobot, S.D. Snow Melt Onset over Arctic Sea Ice from SMMR and SSM/I-SSMIS Brightness Temperatures; Version 3; NASA DAAC at the National Snow and Ice Data Center: Boulder, CO, USA, 2014. [Google Scholar]
- Cavalieri, D.J.; Parkinson, C.L.; Gloersen, P.; Comiso, J.C.; Zwally, H.J. Deriving long-term time series of sea ice cover from satellite passive-microwave multisensor data sets. J. Geophys. Res. 1999, 104, 15803–15814. [Google Scholar] [CrossRef]
- Kwok, R.; Cunningham, G.F.; Wensnahan, M.; Rigor, I.; Zwally, H.J.; Yi, D. Thinning and volume loss of the Arctic ocean sea ice cover: 2003–2008. J. Geophys. Res. Oceans 2009, 114, C07005. [Google Scholar] [CrossRef]
- Parkinson, C.L.; di Girolamo, N.E. New visualizations highlight new information on the contrasting Arctic and Antarctic sea-ice trends since the late 1970s. Remote Sens. Environ. 2016, 183, 198–204. [Google Scholar] [CrossRef]
- Comiso, J.C. Large decadal decline of the Arctic multiyear ice cover. J. Clim. 2012, 25, 1176–1193. [Google Scholar] [CrossRef]
- Nghiem, S.V.; Rigor, I.G.; Perovich, D.K.; Clemente-Colón, P.; Weatherly, J.W.; Neumann, G. Rapid reduction of Arctic perennial sea ice. Geophys. Res. Lett. 2007, 34, L19504. [Google Scholar] [CrossRef]
- Tschudi, M.; Fowler, C.; Maslanik, J.; Stroeve, J. Tracking the movement and changing surface characteristics of Arctic sea ice. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 536–540. [Google Scholar] [CrossRef]






| AHRA | PMW | |
|---|---|---|
| Algorithm starting day of year | 61 (2 March) | 76 (17 March) |
| Passive microwave channels | 19/18H and 37H GHz | 19/18V and 37V GHz |
| Melt criteria | HR = Tb(19H) − Tb(37H) | Δ37V = |Tb(37V)(i − 1) − Tb(37V)(i)|; ΔGRice = GRice(i) − GRice(i + 1), where GRice = (Tbice(37V) − Tbice(19V))/(Tbice(37V) + Tbice(19V)); P = Tb(19V) + 0.8Tb(37V) |
| Time series testing method | 20-day window | Parameter weighting of melt criteria equations and neighborhood test for consistency |
| Sea ice masking method | 50% sea ice concentration on one of first two days of March | Pixels with 80% sea ice concentration for at least 5 days of the year (NASA Team) |
| Region | AHRA v3 | PMW Combined | Mean Diff. | ||||
|---|---|---|---|---|---|---|---|
| Mean | St. Dev. | Trend | Mean | St. Dev. | Trend | (PMW–AHRA) | |
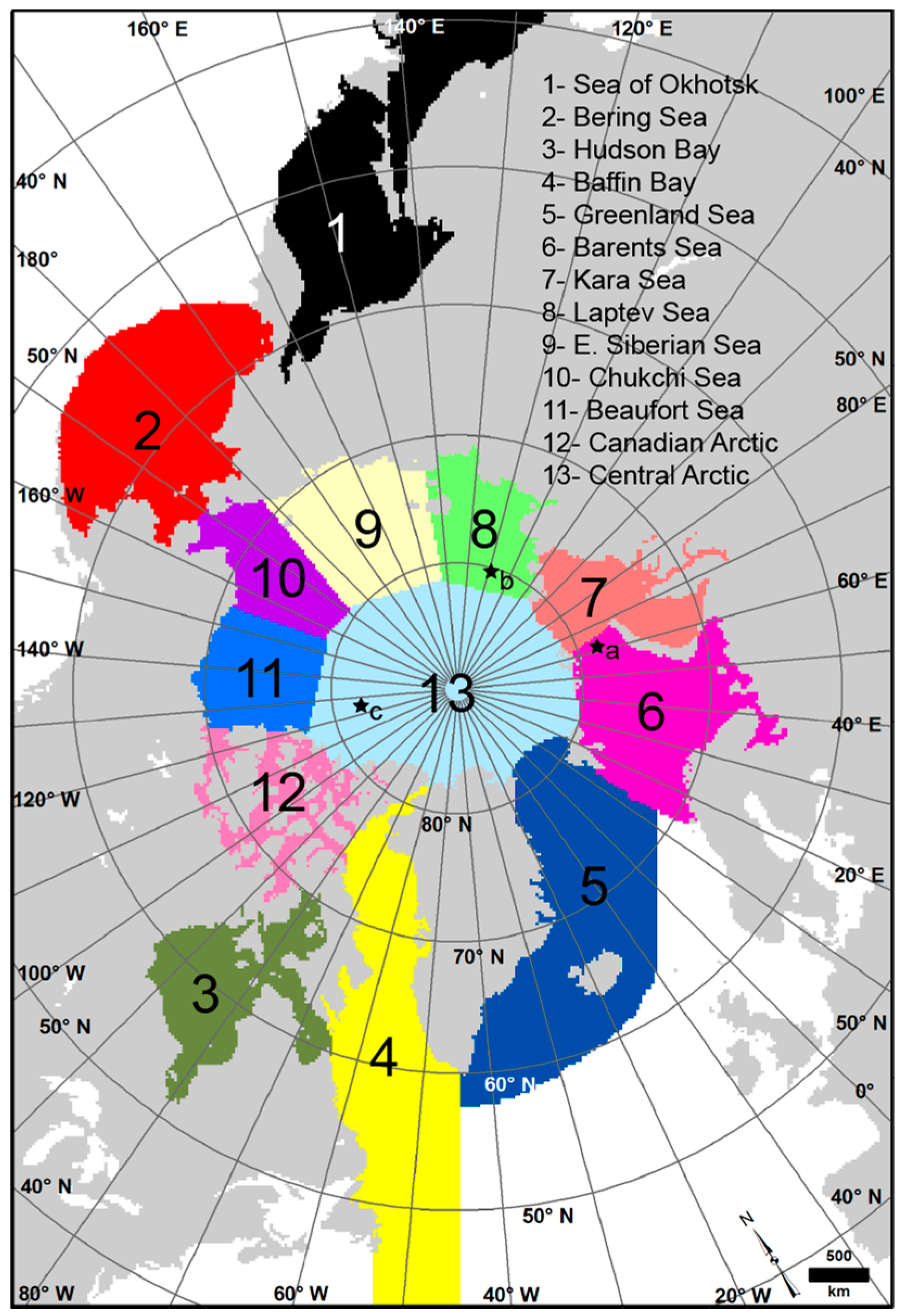
| Arctic-All | 121.9 | 5.2 | −4.5 * | 142.1 | 3.6 | −1.6 | 20.2 |
| Sea of Okhotsk | 74.1 | 3.9 | −1.0 | 110.0 | 6.3 | 2.4 | 35.9 |
| Bering Sea | 72.7 | 4.6 | 1.7 | 106.4 | 6.9 | −0.4 | 33.7 |
| Hudson Bay | 106.6 | 8.6 | −2.8 | 126.8 | 8.7 | −4.5 | 20.2 |
| Baffin Bay | 101.8 | 5.7 | −0.3 | 131.9 | 7.2 | −1.5 | 30.1 |
| Greenland Sea | 98.0 | 7.6 | 0.8 | 133.5 | 8.6 | −3.4 | 35.5 |
| Barents Sea | 84.3 | 10.4 | −7.5 * | 122.6 | 12.6 | −6.7 | 38.3 |
| Kara Sea | 128.9 | 12.9 | −9.3 * | 148.4 | 10.1 | −5.9 * | 19.5 |
| Laptev Sea | 145.0 | 11.7 | −8.2 * | 156.7 | 8.0 | −3.0 | 11.7 |
| East Siberian Sea | 150.1 | 14.5 | −11.8 * | 153.4 | 5.6 | −1.4 | 3.3 |
| Chukchi Sea | 136.3 | 12.7 | −8.3 * | 144.8 | 8.2 | −2.1 | 8.5 |
| Beaufort Sea | 148.2 | 9.9 | −7.2 * | 151.8 | 7.5 | −2.5 | 3.6 |
| Canadian Archipelago | 149.2 | 7.7 | −4.6 * | 152.9 | 6.0 | −2.0 | 3.7 |
| Central Arctic | 159.6 | 9.3 | −8.1 * | 160.7 | 5.2 | −2.7 | 1.1 |
| AHRA v. PMWC Comparison | AHRA-A v. PMWC-A Comparison | |||||||
|---|---|---|---|---|---|---|---|---|
| Region | AHRA Trend | PMWC Trend | Avg. Offset | Slopes Equal? (Y/N) | AHRA-A Trend | PMWC-A Trend | Avg. Offset | Slopes Equal? (Y/N) |
| Arctic-All | −4.5 * | −1.6 | 20.2 | N | −2.2 * | −3.7 * | 24.1 | N |
| Sea of Okhotsk | −1.0 | 2.4 | 35.9 | N | 1.4 | 0.8 | 38.6 | Y |
| Bering Sea | 1.7 | −0.4 | 33.7 | Y | 2.6 | −2.1 | 35.9 | Y |
| Hudson Bay | −2.8 | −4.5 | 20.2 | Y | 4.0 | −4.0 | 27.4 | N |
| Baffin Bay | −0.3 | −1.5 | 30.1 | Y | 0.9 | −3.3 | 33.6 | Y |
| Greenland Sea | 0.8 | −3.4 | 35.5 | N | 2.3 | −6.2 * | 39.4 | N |
| Barents Sea | −7.5 * | −6.7 | 38.3 | Y | −6.0 * | −9.7 * | 42.4 | Y |
| Kara Sea | −9.3 * | −5.9* | 19.5 | Y | −8.6 * | −6.0 * | 21.4 | Y |
| Laptev Sea | −8.2 * | −3.0 | 11.7 | N | −7.2 * | −3.9 | 14.2 | Y |
| East Siberian Sea | −11.8 * | −1.4 | 3.3 | N | −9.6 * | −2.7 | 5.8 | N |
| Chukchi Sea | −8.3 * | −2.1 | 8.5 | N | −6.7 * | −2.8 | 10.4 | Y |
| Beaufort Sea | −7.2 * | −2.5 | 3.6 | N | −6.3 * | −4.2 * | 4.8 | Y |
| Canadian Archipelago | −4.6 * | −2.0 | 3.7 | Y | −2.8 | −2.4 | 6.5 | Y |
| Central Arctic | −8.1 * | −2.7 | 1.1 | N | −5.2 * | −4.5 * | 4.9 | Y |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bliss, A.C.; Miller, J.A.; Meier, W.N. Comparison of Passive Microwave-Derived Early Melt Onset Records on Arctic Sea Ice. Remote Sens. 2017, 9, 199. https://doi.org/10.3390/rs9030199
Bliss AC, Miller JA, Meier WN. Comparison of Passive Microwave-Derived Early Melt Onset Records on Arctic Sea Ice. Remote Sensing. 2017; 9(3):199. https://doi.org/10.3390/rs9030199
Chicago/Turabian StyleBliss, Angela C., Jeffrey A. Miller, and Walter N. Meier. 2017. "Comparison of Passive Microwave-Derived Early Melt Onset Records on Arctic Sea Ice" Remote Sensing 9, no. 3: 199. https://doi.org/10.3390/rs9030199
APA StyleBliss, A. C., Miller, J. A., & Meier, W. N. (2017). Comparison of Passive Microwave-Derived Early Melt Onset Records on Arctic Sea Ice. Remote Sensing, 9(3), 199. https://doi.org/10.3390/rs9030199