Spectral-Spatial Response for Hyperspectral Image Classification

Abstract

This paper presents a hierarchical deep framework called Spectral-Spatial Response (SSR) to jointly learn spectral and spatial features of Hyperspectral Images (HSIs) by iteratively abstracting neighboring regions. SSR forms a deep architecture and is able to learn discriminative spectral-spatial features of the input HSI at different scales. It includes several existing spectral-spatial-based methods as special scenarios within a single unified framework. Based on SSR, we further propose the Subspace Learning-based Networks (SLN) as an example of SSR for HSI classification. In SLN, the joint spectral and spatial features are learned using templates simply learned by Marginal Fisher Analysis (MFA) and Principal Component Analysis (PCA). An important contribution to the success of SLN is the exploitation of label information of training samples and the local spatial structure of HSI. Extensive experimental results on four challenging HSI datasets taken from the Airborne Visible-Infrared Imaging Spectrometer (AVIRIS) and Reflective Optics System Imaging Spectrometer (ROSIS) airborne sensors show the implementational simplicity of SLN and verify the superiority of SSR for HSI classification.

1. Introduction

Hyperspectral Image (HSI) classification has recently gained in popularity and attracted interest in many fields, including assessment of environmental damage, growth regulation, land use monitoring, urban planning, reconnaissance, etc. [1,2,3,4,5]. Although high spectral resolution opens the door to many applications, the high dimensionality poses new challenges for HSI classification [3].

In the past few years, many methods have been proposed to perform the HSI classification. In order to deal with the problems arising as the data dimensionality increases, many Dimensionality Reduction (DR) methods [4,6,7,8,9,10] have been adopted for HSI classification. These methods fall into three categories: unsupervised, supervised and semi-supervised. Additionally, they can ameliorate statistically ill-posed problems and improve the classification performance [2]. Michele et al. proposed a semi-supervised multiview feature extraction method based on the multiset regularized kernel canonical correlation analysis for the classification of HSI [11,12]. Apart from feature extraction, designing an effective classifier is also an important way to promote the classification accuracy. For example, Support Vector Machine (SVM) and Relevance Vector Machine (RVM) have been successfully used for HSI classification [13,14]. Recently, Kernel-based Extreme Learning Machine (KELM) [15,16] was also applied to HSI classification [17], where KELM uses an idea to train a single-hidden layer feed forward neural network; that is, the hidden-node parameters are randomly generated based on certain probability distributions. This idea was originally proposed in [18] and further developed in [19,20]. A similar idea randomly generating the node parameters based on sparse representation has also been investigated in the matching problem, such as in [21,22]. The neural network is an important machine learning method, which has attracted more and more attention recently [23]. However, conventional methods only exploit the spectral information of HSIs, and the spatial structure is ignored. Their classification results may contain noise, like salt-and-pepper [24].

Recently, spectral-spatial-based methods have attracted great interests and improved the HSI classification accuracy significantly [25,26,27,28,29,30,31]. Camps-Valls et al. [32] proposed a Composite Kernel (CK) that easily combines spatial and spectral information to enhance the classification accuracy of HSIs. Li et al. extended CK to a generalized framework, which exhibits the great flexibility of combining the spectral and spatial information of HSIs [33]. Fauvel et al. introduced the Morphological Profile (MP), which is widely used for modeling structural information [34]. Li et al. proposed the Maximizer of the Posterior Marginal by Loopy Belief Propagation (MPM-LBP) [35]. It exploits the marginal probability distribution from both the spectral and spatial information. Zhong et al. developed a discriminant tensor spectral-spatial feature extraction method for HSI classification [24]. Kang et al. [36] proposed a spectral-spatial classification framework based on Edge-Preserving Filtering (EPF), where the filtering operation achieves a local optimization of the probabilities. Two-dimensional Gabor features extracted from selected bands and the Local Binary Pattern (LBP) were introduced for extracting local spatial features of HSIs in [37] and [38], respectively. Li et al. proposed to combine LBP and ELM (LBP-ELM) for HSI classification [38]. Feng et al. [25] defined Discriminate Spectral-Spatial Margins (DSSMs) to reveal the local information of hyperspectral pixels and explore the global structures of both labeled and unlabeled data via low-rank representation. Zhou et al. proposed a Spatial and Spectral Regularized Local Discriminant Embedding (SSRLDE) method for DR of HSIs [2]. He et al. proposed Spatial Translation-invariant Wavelet (STIW)-based Sparse Representation (STIW-SR) for extracting spectral-spatial features [39]. STIW can reduce the spectral observation noise and the spatial nonstationarity while maintaining the class-specific truth spectra. Soltani-Farani et al. presented the Spatially-Aware Dictionary Learning [40] (SADL) method, which is a structured dictionary-based model for hyperspectral data incorporating both spectral and contextual characteristics of spectral samples. Sun et al. presented the Sparse Multinomial Logistic Regression and Spatially-Adaptive Total Variation (SMLR-SpATV) classifier [41] using the SpATV regularization to enforce spatial smoothness. These methods have achieved promising results [1,2,3,27,28,42]. Furthermore, Li et al. proposed the Multiple Feature Learning (MFL) framework with state-of-the-art performance [30,43]. However, most of these extract spectral-spatial features using a shallow architecture and yield limited complexity and non-linearity.

In [44], a deep learning-based HSI classification method was proposed, where spectral and spatial information is extracted separately and then processed via stacked autoencoders. Similarly, Li et al. proposed to use Deep Belief Networks (DBN) for HSI classification [45]. Yue et al. explored both spatial and spectral features in higher levels by using a deep CNN framework for the possible classification of hyperspectral images [46]. Unsupervised sparse features were learned via deep CNN in a greedy layer-wise fashion for pixel classification in [47], and CNN was utilized to automatically find spatial-related features at high levels from a subspace after local discriminant embedding [48]. Very recently, a regularized deep Feature Extraction (FE) method was presented for Hyperspectral Image (HSI) classification using a Convolutional Neural Network (CNN) [49]. These works demonstrate that deep learning opens a new window for future research, showcasing the deep learning-based methods’ huge potential. However, how to design a proper deep net is still an open area in the machine learning community [50,51]. Generally, HSI classification aims at classifying each pixel to its correct class. However, pixels in smooth homogeneous regions usually have high within-class spectral variations. Consequently, it is crucial to exploit the nonlinear characteristics of HSIs and to reduce intraclass variations. The difference between natural image classification and HSI classification lies in that the former learns a valid representation for each image, while the latter learns an effective representation for each pixel in an HSI. However, with the high dimensionality of HSIs in the spectral domain, theoretical and practical problems arise. Furthermore, each pixel in an HSI will likely share similar spectral characteristics or have the same class membership as its neighboring pixels. Using spatial information can reduce the uncertainty of samples and suppress salt-and-pepper noise in the classification results. In order to make use of the nature of HSIs, we intend to learn the discriminative spectral-spatial features using the hierarchical deep architecture in this paper. More specifically, we learn effective spectral-spatial features by iteratively abstracting neighboring regions. In this way, the intraclass variations can be reduced, and the classification maps become more smooth. Meanwhile, label information of the training samples can also be used to learn discriminative spectral features at different scales [44,52,53,54,55,56].

Consequently, this paper proposes a hierarchical deep learning framework, called Spectral-Spatial Response (SSR), for HSI classification. SSR can jointly extract spectral-spatial features by iteratively abstracting neighboring regions and recomputing representations for new regions. It can exploit different spatial structures from varied spatial sizes. Using SSR, we develop a novel spectral-spatial-based method, Subspace Learning-based Networks (SLN), for HSI classification. It utilizes Marginal Fisher Analysis (MFA) and Principal Component Analysis (PCA) to learn discriminative spectral-spatial features. The main difference between the proposed framework and the general deep learning framework is that discriminative convolutional filters are learned directly from the images rather than learned by the stochastic gradient descent method that is used in the general deep learning method. Moreover, there are several advantages to be highlighted as follows:

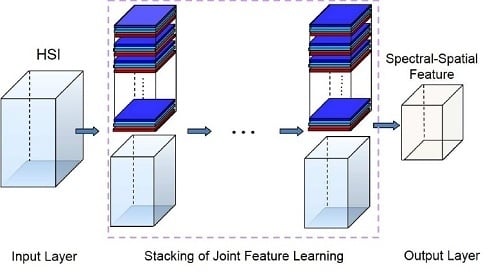
• SSR provides a new way to simultaneously exploit discriminative spectral and spatial information in a deep hierarchical fashion. The stacking of joint spectral-spatial feature learning units can produce intrinsic features of HSIs.
• SSR is a unified framework of designing new joint spectral-spatial feature learning methods for HSI classification. Several existing spectral-spatial-based methods are its special cases.
• As an implementation example of SSR, SLN is further introduced for HSI classification with a small number of training samples. It is easy to implement and has low sample complexity.

The remainder of this paper is organized as follows. In Section 2, the general framework SSR is presented, and the relationship with other methods is given. A new implementation of SSR called SLN is presented in detail in Section 3. Section 4 provides the experimental evaluations of the proposed framework by using four widely-used HSI datasets respectively collected by the Airborne Visible-Infrared Imaging Spectrometer (AVIRIS) and the Reflective Optics System Imaging Spectrometer (ROSIS). The comparison results with state-of-the-art methods are also reported. Finally, Section 5 concludes with some remarks and possible future research directions.

2. Spectral-Spatial Response

The proposed framework aims at learning effective features that maximize the difference between classes and minimize the difference within the class. The learned features are expected to be more discriminative for classification. In fact, spatial adjacent pixels usually share similar spectral characteristics and have the same label, and using spatial information can reduce the uncertainty of samples and suppress the salt-and-pepper noise of classification results [57]. Furthermore, recent studies have found that a higher layer of the deep hierarchical model produces increasingly abstract representations and is increasingly invariant to some transformations [58,59]. Consequently, we present a new framework that jointly learns the spectral-spatial features via a deep hierarchical architecture. Using this architecture, the spectral-spatial features can be learned recursively.

2.1. Definition of Spectral-Spatial Response

To define SSR, we need two ingredients as follows:

• A finite number of nested cubes to define the hierarchical architecture (see Figure 1). The SSRs on different layers can be learned from different cubes. The sizes of cubes determine the sizes of neighborhoods in the original HSI.
• A set of templates (or filters) that extract the spectral and spatial features. These templates can be learned from the training samples or the cubes centered at positions of the training samples.

The hierarchical architecture is composed of n cubes $H_1$, $H_2$, ⋯, $H_n$, as shown in Figure 1. In this section, the definition of the SSR based on three cubes ($H_1$, $H_2$ and $H_3$) is given as an illustrative example, where $H_1$ corresponds to a small cube in the HSI, $H_2$ is a larger cube and $H_3$ represents the whole HSI. Let $\mathbb{I}\in R^{m^{\prime }\times n^{\prime }\times d}$ be an HSI to be processed, where $m^{\prime }$, $n^{\prime }$ and d are the height of the HSI, the width of the HSI and the number of the spectral bands, respectively. The construction of SSR is given in a bottom-up fashion.

(1)

The first layer SSR:

The computation procedure of the first layer SSR is shown in Figure 2. Let ${\mathbb{I}}_{i,j}$ be the central pixel of $H_1$, then the spectral-spatial feature of ${\mathbb{I}}_{i,j}$ can be jointly learned as follows.

First, the spectral features can be learned from each pixel. The reproducing kernel, denoted by $K_1({\mathbb{I}}_{ii,jj},{\widehat{\mathit{t}}}_l^1)$, can be used to learn the spectral features, where ${\mathbb{I}}_{ii,jj}$ is a pixel in $H_1$ and ${\widehat{\mathit{t}}}_l^1$ is the l-th spectral template in ${\widehat{T}}_1$. The reproducing kernel can produce the spectral features by encoding the pixel by a set of learned templates. For example, one could choose the simple linear kernel, namely:

$${\widehat{K}}_1({\mathbb{I}}_{ii,jj},{\widehat{\mathit{t}}}_l^1)=\langle {\mathbb{I}}_{ii,jj},{\widehat{\mathit{t}}}_l^1\rangle .$$

(1)

The spectral templates are spectral feature extractors learned from training pixels. This operation intends to reduce the spectral redundancy. In this way, pixel ${\mathbb{I}}_{ii,jj}$ can be transformed into a $|{\widehat{T}}_1|$-dimensional feature vector,

$$\begin{array}{c}\hfill F_1\left({\mathbb{I}}_{ii,jj}\right)=\left(\begin{array}{c}{\widehat{K}}_1({\mathbb{I}}_{ii,jj},{\widehat{\mathit{t}}}_1^1)\\ {\widehat{K}}_1({\mathbb{I}}_{ii,jj},{\widehat{\mathit{t}}}_2^1)\\ ⋮\\ {\widehat{K}}_1({\mathbb{I}}_{ii,jj},{\widehat{\mathit{t}}}_{|{\widehat{T}}_1|}^1)\end{array}\right),\end{array}$$

(2)

where $|{\widehat{T}}_1|$ is the cardinality of the ${\widehat{T}}_1$ and $|{\widehat{T}}_1|<d$. Similarly, pixels in $H_1\in R^{v_1\times v_1\times d}$ (the pixel ${\mathbb{I}}_{i,j}$ and its neighborhoods) can be transformed to a new cube in $R^{v_1\times v_1\times \left|{\widehat{T}}_1\right|}$, where $v_1\times v_1$ is the size of the neighborhoods. In this cube, there are $|{\widehat{T}}_1|$ matrices of size $v_1\times v_1$. Here, these matrices are called the first layer spectral feature maps, denoted by ${\mathit{g}}_i^1$ $(i=1,2,\cdots ,|{\widehat{T}}_1\left|\right)$. Note that at this stage, we can move $H_1$ pixel by pixel.

Second, we learn the spatial features based on the outputs of the previous stage ${\mathit{g}}_i^1$ $(i=1,2,\cdots ,|{\widehat{T}}_1\left|\right)$. In this stage, our objective is to incorporate spatial contextual information within the neighbor into the processing pixel. We have:

$$\begin{array}{c}\hfill R_1\left({\mathbb{I}}_{i,j}\right)\left({\tilde{\mathit{t}}}_l^1\right)=\left(\begin{array}{c}{\tilde{K}}_1({\mathit{g}}_1^1,{\tilde{\mathit{t}}}_l^1)\\ {\tilde{K}}_1({\mathit{g}}_2^1,{\tilde{\mathit{t}}}_l^1)\\ ⋮\\ {\tilde{K}}_1({\mathit{g}}_{|{\widehat{T}}_1|}^1,{\tilde{\mathit{t}}}_l^1)\end{array}\right),\end{array}$$

(3)

where:

$${\tilde{K}}_1({\mathit{g}}_i^1,{\tilde{\mathit{t}}}_l^1)=\langle {\mathit{g}}_i^1,{\tilde{\mathit{t}}}_l^1\rangle$$

(4)

and spatial template ${\tilde{\mathit{t}}}_l^1$ can be learned from the first layer spectral feature maps of the training samples. In this way, for each ${\mathbb{I}}_{i,j}$, we can obtain a new feature vector:

$$\begin{array}{c}\hfill R_1\left({\mathbb{I}}_{i,j}\right)=\left(\begin{array}{c}{R}_1\left({\mathbb{I}}_{i,j}\right)\left({\tilde{\mathit{t}}}_1^1\right)\\ R_1\left({\mathbb{I}}_{i,j}\right)\left({\tilde{\mathit{t}}}_2^1\right)\\ ⋮\\ R_1\left({\mathbb{I}}_{i,j}\right)\left({\tilde{\mathit{t}}}_{|{\tilde{T}}_1|}^1\right)\end{array}\right),\end{array}$$

(5)

where $R_1\left({\mathbb{I}}_{i,j}\right)$ is called the first layer SSR of ${\mathbb{I}}_{i,j}$. This operation can be considered as the “convolution” in the conventional deep learning model. In this way, the spatial information of the local region can be learned. Consequently, the first layer SSR is obtained by jointly exploiting both spectral and spatial information of the HSI.

Finally, we concatenate $R_1\left({\mathbb{I}}_{i,j}\right)$ and ${\mathbb{I}}_{i,j}$ into a new spectral-spatial feature vector (see Figure 3). It can provide more spectral information. In this way, the spectral feature can be enhanced, and the oversmooth problem can be overcome. We processed all of the pixels in $\mathbb{I}\in R^{m^{\prime }\times n^{\prime }\times d}$, then a new feature cube denoted by ${\mathbb{I}}^{\prime }$ can be obtained. Note that each feature vector in ${\mathbb{I}}^{\prime }$ is learned from a cube with size of $H_1$ in the original HSI.

(2)

The second layer SSR:

Similarly, we can define the second layer SSR on a region corresponding to $H_2$ in the original image $\mathbb{I}$. In this case, two template sets are denoted by ${\widehat{T}}_2$ and ${\tilde{T}}_2$, respectively. For each ${\mathbb{I}}_{ii,jj}^{\prime }$, we have:

$$\begin{array}{c}\hfill F_2\left({\mathbb{I}}_{ii,jj}^{\prime }\right)=\left(\begin{array}{c}{\widehat{K}}_2({\mathbb{I}}_{ii,jj}^{\prime },{\widehat{\mathit{t}}}_1^2)\\ {\widehat{K}}_2({\mathbb{I}}_{ii,jj}^{\prime },{\widehat{\mathit{t}}}_2^2)\\ ⋮\\ {\widehat{K}}_2({\mathbb{I}}_{ii,jj}^{\prime },{\widehat{\mathit{t}}}_{|{\widehat{T}}_2|}^2)\end{array}\right),\end{array}$$

(6)

where:

$${\widehat{K}}_2({\mathbb{I}}_{ii,jj}^{\prime },{\widehat{\mathit{t}}}_l^2)=\langle {\mathbb{I}}_{ii,jj}^{\prime },{\widehat{\mathit{t}}}_l^2\rangle .$$

(7)

${\widehat{K}}_2({\mathbb{I}}_{ii,jj}^{\prime },{\widehat{\mathit{t}}}_l^2)$ can be regarded as the pooling operation over all spectral bands. The outputs of this operation on all positions are called the second layer spectral feature maps denoted by ${\mathit{g}}_i^2$ $(i=1,2,\cdots ,|{\widehat{T}}_2\left|\right)$. Then, these maps can be convoluted by the learned templates (or filters) ${\tilde{\mathit{t}}}_i^2$ ($i=1,2,\cdots ,|{\tilde{T}}_2|$). For the position $(i,j)$, we have:

$$\begin{array}{c}\hfill R_2\left({\mathbb{I}}_{i,j}^{\prime }\right)\left({\tilde{\mathit{t}}}_l^2\right)=\left(\begin{array}{c}{\tilde{K}}_2({\mathit{g}}_1^2,{\tilde{\mathit{t}}}_l^2)\\ {\tilde{K}}_1({\mathit{g}}_2^2,{\tilde{\mathit{t}}}_l^2)\\ ⋮\\ {\tilde{K}}_1({\mathit{g}}_{|{\widehat{T}}_2|}^2,{\tilde{\mathit{t}}}_l^2)\end{array}\right),\end{array}$$

(8)

Consequently, the second layer SSR on position $(i,j)$ can be defined by:

$$\begin{array}{c}\hfill R_2\left({\mathbb{I}}_{i,j}^{\prime }\right)=\left(\begin{array}{c}{R}_2\left({\mathbb{I}}_{i,j}^{\prime }\right)\left({\tilde{\mathit{t}}}_1^2\right)\\ R_2\left({\mathbb{I}}_{i,j}^{\prime }\right)\left({\tilde{\mathit{t}}}_2^2\right)\\ ⋮\\ R_2\left({\mathbb{I}}_{i,j}^{\prime }\right)\left({\tilde{\mathit{t}}}_{|{\tilde{\mathbf{T}}}_{\mathbf{2}}|}^{\mathbf{2}}\right)\end{array}\right).\end{array}$$

(9)

where ${\tilde{\mathit{t}}}_2$ can be learned from all feature maps ${\mathit{g}}_i^2$ of training samples. Similarly, the final output is obtained by concatenating $R_2\left({\mathbb{I}}_{i,j}^{\prime }\right)$ and ${\mathbb{I}}_{i,j}$ into a new spectral-spatial feature.

(3)

Extend to n layers:

The output of the previous step is a new feature cube. Similarly, the definition given above can be easily generalized to an n layer architecture defined by sub-cubes $H_1\subset H_2\subset \cdots \subset H_{n-1}\subset H_n\subset H_{n+1}$.

Based on the above descriptions, the flowchart of the proposed deep hierarchical framework can be shown in Figure 4, where the SSRs are concatenated with the normalized HSI to prevent from oversmoothing. It is composed of stacked joint feature learning units. Once a stacked architecture has been built, its highest level spectral-spatial features can be used as the input of a supervised learning algorithm, for example SVM or a KELM. The framework can learn substantially more efficient features with increasing depth. Different layers of SSRs are defined in different “receptive fields”. From the definition of the SSR, we can find that different learning methods can be flexibly applied to the templates’ learning modules. Consequently, we can design different algorithms based the proposed framework. The advantage of the hierarchical framework is that it can effectively learn spectral-spatial features layer by layer.

As mentioned above, the framework can be extended to deep layers by defining the SSR on the new feature cube. If we denote the original HSI as the first “feature cube”, then the new feature cube obtained by concatenating the first layer SSR and normalized HSI can be denoted as the second one, and so on. Then, the proposed framework can be reformulated from the perspective of the kernel.

Proposition 1.

Let ${\mathit{I}}^n=\{{\mathit{x}}_1^n,\cdots ,{\mathit{x}}_l^n\}$ be l feature vectors (corresponding to l pixels in the original HSI) from a sub-cube in the n-th feature cube, then we have:

$$\begin{array}{c}\hfill R_n={\tilde{K}}_n({\widehat{K}}_n({\widehat{T}}_n^T,{\mathit{I}}^n),{\tilde{T}}_n)\end{array}$$

(10)

where:

$$\begin{array}{c}\hfill {\widehat{T}}_n^T={\left(\begin{array}{c}{\widehat{\mathit{t}}}_1^n,{\widehat{\mathit{t}}}_2^n,\cdots ,{\widehat{\mathit{t}}}_{|{\widehat{T}}_n|}^n\end{array}\right)}^T\end{array}$$

(11)

is the n-th spectral template set,

$$\begin{array}{c}\hfill {\tilde{T}}_n=\left(\begin{array}{c}{\tilde{\mathit{t}}}_1^n,{\tilde{\mathit{t}}}_2^n,\cdots ,{\tilde{\mathit{t}}}_{|{\tilde{T}}_n|}^n\end{array}\right),\end{array}$$

(12)

is the n-th spatial template set, $n=1,2,3,4,\cdots$, ${\widehat{K}}_n$ is the kernel function on spectral domain, ${\tilde{K}}_n$ is the kernel function on spatial domain and $R_n$ is the n-th layer SSR.

Proof. 

As can be seen, we only need to prove the case of $n=1$ and generalize it to $R_n$. First, we have a pixel group $\{{\mathit{x}}_1^1,\cdots ,{\mathit{x}}_l^1\}$, which are centered at ${\mathit{x}}_i\in \{{\mathit{x}}_1^1,\cdots ,{\mathit{x}}_l^1\}$. Then, the first layer spectral feature maps can be obtained by:

$$\begin{array}{c}\hfill F_1=\left(\begin{array}{ccc}{\widehat{K}}_1({\widehat{\mathit{t}}}_1^1,{\mathit{x}}_1^1)& \dots & {\widehat{K}}_1({\widehat{\mathit{t}}}_1^1,{\mathit{x}}_l^1)\\ {\widehat{K}}_1({\widehat{\mathit{t}}}_2^1,{\mathit{x}}_1^1)& \dots & {\widehat{K}}_1({\widehat{\mathit{t}}}_2^1,{\mathit{x}}_l^1)\\ ⋮\\ {\widehat{K}}_1({\widehat{\mathit{t}}}_{|{\mathbf{T}}_1|}^1,{\mathit{x}}_1^1)& \dots & {\widehat{K}}_1({\widehat{\mathit{t}}}_{|{\mathbf{T}}_1|}^1,{\mathit{x}}_l^1)\end{array}\right)={\widehat{K}}_1({\widehat{T}}_1^T,{\mathit{I}}^1).\end{array}$$

(13)

In this case, each row of $F_1$ is a vectorized local feature map. Then, we can obtain the first layer SSR based on ${\tilde{T}}_1$. That is:

$$\begin{array}{c}\hfill R_1={\tilde{K}}_1(F_1,{\tilde{T}}_1)={\tilde{K}}_1({\widehat{K}}_1({\widehat{T}}_1^T,{\mathit{I}}^1),{\tilde{T}}_1).\end{array}$$

(14)

In a similar way, we can prove that:

$$\begin{array}{c}\hfill {\tilde{K}}_n({\widehat{K}}_n({\widehat{T}}_n^T,{\mathit{I}}^n),{\tilde{T}}_n)=R_n\end{array}$$

where $n=2,3\cdots$ and ${\mathit{x}}_i^n$ $(i=1,\cdots ,l)$ come from the n-th feature cube obtained by concatenating the $(n-1)$-th layer SSR and normalized HSI. ☐

This proposition indicates that SSRs are obtained by abstracting the features from the previous layer, where transform matrices are learned from the training data on each layer. The kernel computes the inner product in the induced feature space. There are many kernels that can be used, and the linear kernel is the simplest one. The following conclusions can be made for Proposition 1:

• The proposed framework shares similarities with deep learning models. If kernel functions ${\widehat{K}}_1$ and ${\tilde{K}}_1$ jointly learn spectral-spatial features on the first layer, then the iterated mapping in Equation (10) demonstrates the multilayer feature learning in the deep model. Consequently, with the increase of the depth, the receptive field becomes larger and larger. In this way, the hierarchical architecture could propagate local information to a broader region. Thus, this framework can learn spectral-spatial features of the HSI with multiple levels of abstractions.
• The proposed framework is designed for HSI classification. This shows that ${\widehat{K}}_n$ and ${\tilde{K}}_n$ can learn spectral and spatial features jointly. They are not considered in the conventional deep learning models, which are very popular in the computer vision community. These kernel functions can be viewed as inducing a nonlinear mapping from inputs to feature vectors. ${\widehat{K}}_n$ can learn spectral features and overcome the high-dimension problem. Additionally, ${\tilde{K}}_n$ can learn spatial features and decrease the intraclass variations. Consequently, the proposed SSR is suitable for the nature of the HSIs.

Remarks:

• An HSI usually contains homogeneous regions. Consequently, we assume that each pixel in an HSI will likely share similar spectral characteristics or have the same class membership as its neighboring pixels. This is the reason why the spatial information can be used in the proposed framework SSR.
• In SSR, the template plays an important role, and it could be a filter or an atom of the dictionary. Consequently, constructing the template sets is an interesting problem to be further investigated.
• Stacking joint spectral-spatial feature learning leads to a deep architecture. Different feature learning methods (linear and nonlinear) can be embedded into the proposed SSR. The flexibility offers the possibility to systematically and structurally incorporate prior knowledge; for example, MFA can be used to learn discriminative features.

2.2. Special Scenarios

SSR is a spectral-spatial-based deep learning framework to deal with the HSI classification. Moreover, several existing spectral-spatial-based HSI classification methods can be derived from SSR. As discussed above, we can use different methods to obtain the template sets. For example, we can learn a set of spectral templates by using techniques, such as PCA and Linear Discriminant Analysis (LDA). In this way, we can remove the spectral redundancy of the HSI and obtain the spectral feature fitting for classification. Similarly, spatial templates can have different forms, such as Principle Components (PCs), which can learn the spatial feature of the HSI.

2.2.1. PCA+Gabor

If the PCs and Gabor filters are selected as ${\widehat{T}}_1$ and ${\tilde{T}}_1$, respectively, SSR becomes the method proposed by Chen et al. [42]. That is, the image pixels are firstly processed by PCA, then the two-dimensional Gabor filter [37,42,60] is used to extract the spatial information in the PCA-projected subspace. Finally, the spatial feature and spectral feature are concatenated. In this case, we have:

$${\tilde{\mathit{t}}}_j^1=exp\left(-\frac{(x_0^2+{\gamma }^2{y}_0^2)}{2{\delta }^2}\right)exp\left(i(2\pi \frac{x_0}{\lambda })+\psi \right),$$

(15)

where:

$$x_0=xcos\theta +ysin\theta ,$$

(16)

$$y_0=-xsin\theta +ycos\theta ,$$

(17)

λ, θ, δ, γ and ψ are the wavelength, orientation, standard derivation of the Gaussian envelope, aspect ratio and phase offset, respectively.

2.2.2. Edge-Preserving Filtering

If we set the templates in ${\widehat{T}}_1$ as the SVM classifiers and the templates in ${\tilde{T}}_1$ as the edge-preserving filters, SSR reverts to Kang’s spectral-spatial method with EPF [36]. In this method, each pixel is firstly classified by a classifier, e.g., SVM, to generate multiple probability maps. The edge-preserving filtering is then applied to each map with the help of a guidance image. Finally, the classification of each pixel is determined by the maximum probability of filtered probability maps. In this case, we have:

$${\widehat{\mathit{t}}}_j^1=\sum _{i=1}^b{\alpha }_i{\widehat{y}}_i{\widehat{\mathit{x}}}_i,$$

(18)

where ${\widehat{\mathit{x}}}_i$, ${\widehat{y}}_i$, ${\alpha }_i$ and b are the i-th support vector, label, i-th Lagrange multiplier and the number of the support vectors, respectively. Note that the output of each pixel has only one non-zero number.

In summary, SSR provides us with a unified framework to treat existing shallow spectral-spatial methods in practice as a change of templates for feature learning at each layer. More importantly, SSR provides guidance for designing new hierarchical deep learning methods. As an example, we will present an implementation of SSR in Section 3.

3. Subspace Learning-Based Networks

Because using different template learning methods in SSR can lead to different algorithms, there are many ways to implement the SSR (as mentioned in Section 2.2). In this section, we proposed SLN as an implementation example of SSR. SLN uses the subspace learning methods (MFA and PCA) to learn the templates and KELM as the classifier to further promote the classification performance. SLN maximizes the spectral difference between classes using MFA and considers spatial information during the feature learning step using PCA. They are quite effective for HSI classification. Consequently, the proposed method is suitable for HSI classification.

Let ${\mathit{I}}_{tr}=\{{\mathit{I}}_1,{\mathit{I}}_2,\cdots ,{\mathit{I}}_N\}$ be the training set, where ${\mathit{I}}_i\in R^d$ $(i=1,2,\cdots ,N)$, and they belong to $\mathfrak{C}$ classes. For simplicity, SLN with one joint feature learning unit is presented here. It performs a normalization to the image, uses MFA to learn discriminative spectral templates, employs PCA [61] to learn spatial templates and then uses KELM to assign a label to each pixel. The detailed description of SLN is given as follows.

(1)

Preprocessing

The image preprocessing is to normalize the data values into $[0,1]$ by:

$${\tilde{\mathit{I}}}_{ij}\left(m\right)=\frac{{\mathit{I}}_{ij}\left(m\right)-M_x}{M_x-M_n},$$

(19)

where $M_x=max\left(\mathbb{I}(:)\right)$, $M_n=min\left(\mathbb{I}(:)\right)$ and ${\mathit{I}}_{ij}\left(m\right)$ is the m-th band of pixel ${\mathit{I}}_{ij}$. The normalized HSI is denoted as $\tilde{\mathit{I}}$.

(2)

Joint spectral-spatial feature learning:

First, the discriminative spectral features are desired for classification. Consequently, the label information of the training samples can be used. In SLN, a supervised subspace learning method, MFA [62], is used to construct ${\widehat{T}}_1$. MFA aims at searching for the projection directions on which the marginal sample pairs of different classes are far away from each other while requiring data points of the same class to be close to each other [63]. Here, the projection directions of MFA are taken as the templates in ${\widehat{T}}_1$. Assume that there are $|{\widehat{T}}_1|$ templates and ${\widehat{T}}_1\in R^{d\times |{\widehat{T}}_1|}$ is the template set. The spectral templates are the $|{\widehat{T}}_1|$ eigenvectors corresponding to a number of the largest eigenvalues of:

$${\tilde{\mathit{I}}}_{tr}\mathit{L}{\tilde{\mathit{I}}}_{tr}^T{\widehat{t}}^1=\lambda {\tilde{\mathit{I}}}_{tr}\mathit{B}{\tilde{\mathit{I}}}_{tr}^T{\widehat{t}}^1,$$

(20)

where ${\tilde{\mathit{I}}}_{tr}$ is the normalized training set, $\mathit{L}$ is the Laplacian matrix and $\mathit{B}$ is the constraint matrix (refer to [62]). Once the templates are given, the normalized HSI can be projected to the templates pixel by pixel. As described in Section 2, each template produces a feature map. In this way, we can obtain $|{\widehat{T}}_1|$ spectral feature maps.

Second, spatial information within the neighbor is expected to be incorporated into the processing pixel. In SLN, PCA as a linear autoencoder has been used to construct ${\tilde{T}}_1$. In this way, the template learning method is simple and fast. The templates in ${\tilde{T}}_1$ can be learned as follows.

We crop $v_1\times v_1$ image patches centered at each training sample in the i-th spectral feature map. Because there are N training samples, we can collect N patches from each map. These cropped patches are vectorized and form a matrix $\mathit{X}$. Matrix $\tilde{\mathit{X}}$ is then obtained after removing mean values. The construction of the template set is an optimization problem:

$${\tilde{t}}_{*}^1=argmax\frac{{\left({\tilde{t}}^1\right)}^T{\tilde{\mathit{X}}}^T\tilde{\mathit{X}}{\tilde{t}}^1}{{\left({\tilde{t}}^1\right)}^T{\tilde{t}}^1},$$

(21)

where ${\tilde{t}}^1$ is the spatial template; that is, to find the $|{\tilde{T}}_1|$ principal eigenvectors of $\tilde{\mathit{X}}{\tilde{\mathit{X}}}^T$ [64]. The patches cropped from each band of the training samples can be encoded by the $|{\tilde{T}}_1|$ templates. In this way, a feature cube can be obtained, where the number of its feature maps is $|{\tilde{T}}_1|\times |{\widehat{T}}_1|$. After that, we concatenate the obtained feature cube and normalized HSI into a new feature cube, where the height of the new feature cube is $|{\tilde{T}}_1|\times |{\widehat{T}}_1|+d$. Similarly, higher layer features can be obtained by extending this architecture to n. Consequently, SLN can extract deep hierarchical features.

(3)

Classification based on KELM:

After L alternations of the joint spectral-spatial feature learning processes, SLN obtains spectral-spatial features that are then classified by the KELM classifier [15,17,65].

Let the features of training samples be $\{{\mathit{x}}_i,{\mathit{y}}_i\}$($i=1,\cdots ,N$), where ${\mathit{x}}_i\in R^{|{\tilde{T}}_L|\times |{\widehat{T}}_L|+d}$ and ${\mathit{y}}_i=(y_{i,1},\cdots ,y_{i,\mathfrak{C}})\in R^{\mathfrak{C}}$ indicate $\mathfrak{C}$ classes and:

$${\mathit{y}}_{i,j}=\left\{\begin{array}{cc}1,\hfill & {\mathit{x}}_i\mathrm{belongs}\mathrm{to}\mathrm{the}j-\mathrm{th}\mathrm{class};\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(22)

The output of the KELM classifier is:

$$\begin{array}{c}\hfill f\left({\mathit{x}}_t\right)={\left(\begin{array}{c}K({\mathit{x}}_t,{\mathit{x}}_1)\\ ⋮\\ K({\mathit{x}}_t,{\mathit{x}}_N)\end{array}\right)}^T{\left(\frac{\mathit{I}}{\rho }+K(\mathit{X},\mathit{X})\right)}^{-1}\mathit{Y},\end{array}$$

(23)

where ${\mathit{x}}_t$ is the feature of the test sample, $\mathit{Y}={\left(\begin{array}{c}{\mathit{y}}_1{\mathit{y}}_2\cdots {\mathit{y}}_N\end{array}\right)}^T$ and K is the kernel function (this paper uses the Radial Basis Function (RBF) kernel). Finally, the class of the test sample is determined by the index of the output node with the highest output value [65].

Algorithm 1 SLN: training procedure.

Require:  ${I}\in R^{m^{\prime }\times n^{\prime }\times d}$, ${\mathit{I}}_{tr}=\left[{\mathit{I}}_1\dots {\mathit{I}}_N\right]$. 1:   Ensure:  ${\tilde{T}}_l$, ${\widehat{T}}_l$ (l = 1,...,L) and KELM classifier. 2:   3: Image preprocessing. 4:   5: for $l=1:L$ do 6:   7:  Obtain spectral template set ${\widehat{T}}_l$ by MFA. 8:   9:  for $i=1:m$ do 10:   11:   for $j=1:n$ do 12:   13:    Using ${\widehat{T}}_l$ to process the i-th row and j-th column of the input image. 14:   15:   end for 16:   17:  end for 18:   19:  $\mathit{X}=\left[\right]$ 20:   21:  for $i=1:N$ do 22:   23:   for $j=1:|{\widehat{T}}_l|$ do 24:   25:    Crop a neighboring region for the i-th training pixel on the j-th map and vectorize them, ${\mathit{x}}_{ij}$. 26:   27:    $\mathit{X}=\left[\mathit{X}{\mathit{x}}_{ij}\right]$. 28:   29:   end for 30:   31:  end for 32:   33:  Obtain spatial template set ${\tilde{T}}_l$ by PCA. 34:   35:  for $j=1:|{\widehat{T}}_l|$ do 36:   37:   Crop a neighboring region for the each pixel on the j-th map and process them using ${\tilde{T}}_j$. 38:   39:  end for 40:   41:  Concatenating the l-th SSRs with the normalized pixels. 42:   43: end for 44:   45: Training KELM classifier. 46:

Algorithm 2 SLN: test procedure

Require:  $\mathbb{I}\in R^{m^{\prime }\times n^{\prime }\times d}$. 1:   Ensure:  $y_t$. 2:   3: Image preprocessing. 4:   5: for $l=1:L$ do 6:   7:  for $i=1:m^{\prime }$ do 8:   9:   for $j=1:n^{\prime }$ do 10:   11:    Process the pixel in the i-th row and j-th column by learned ${\widehat{T}}_l$. 12:   13:   end for 14:   15:  end for 16:   17:  for $j=1:|{\widehat{T}}_l|$ do 18:   19:   Crop a neighboring region for each pixel on the j-th map and process them using learned ${\tilde{T}}_l$. 20:   21:  end for 22:   23:  Concatenating the l-th SSRs with the normalized pixels. 24:   25: end for 26:   27: Feed the output to the KELM. 28:

The pseudocodes of the training and testing procedures of SLN are given in Algorithms 1 and 2, respectively. In Algorithm 2, $y_t$ is the predicted class label of the test sample. In SLN, MFA is used to maximize the difference between classes and to minimize the difference within the class. Pixels with the same labels may occur in spatially-separated locations, and MFA can decrease this type of intraclass variation. The effects of spatial feature learning (PCA is used in SLN) can reduce the intraclass variations while making use of the local structure information. Moreover, the learning methods in SLN are adopted according to the nature of the HSI.

Remarks:

• As one implementation of SSR, SLN is a deep learning method. Similarly, other hierarchical methods can be obtained when applying different kinds of templates and kernels in SSR.
• The templates in SLN are learned by MFA and PCA, which are simple and have better performance in feature learning. Consequently, SLN is a simple and efficient method to jointly learn the spectral-spatial features of HSIs.

4. Experimental Results and Discussions

In this section, we provide an experimental evaluation for the presented framework and SLN using four real HSIs. In our experiments, the classification results are compared visually and quantitatively, where the quantitative comparisons are based on the class-specific accuracy, overall accuracy (OA), average accuracy (AA) and the κ coefficient [66]. Note that the kernel parameters in the KELM are set to 0.1. In our study, all experiments are performed using MATLAB R2014a on an Intel i7 quad-core 2.10-GHz machine with 8 GB RAM.

4.1. Datasets and Experimental Setups

Four HSI datasets, including AVIRIS Indian Pines, ROSIS University of Pavia, ROSIS Center of Pavia and Kennedy Space Center (KSC), are employed to evaluate the effectiveness of the proposed method.

• The Indian Pines dataset was acquired by the AVIRIS sensor over the Indian Pines test site in 1992 [67]. The image scene contains $145\times 145$ pixels and 220 spectral bands. The ground truth available is designated into 16 classes. In the experiments, the number of bands has been reduced to 200 due to atmospheric effects. This scene is challenging because of the significant presence of mixed pixels and the unbalanced number of available labeled pixels in each class [35]. A three-band false color image and the ground-truth image are shown in Figure 5.
• The second dataset was gathered by the ROSIS sensor over Pavia, Italy. This image has 610 × 340 pixels (covering the wavelength range from 0.4 to 0.9 $\mathsf{\mu }$m) and 115 bands. In our experiments, 12 bands are removed due to the noise. Therefore, there are 103 bands retained. There are nine ground-truth classes, in total 43,923 labeled samples. Figure 6 shows a three-band false color image and the ground-truth map.
• The third dataset was acquired by the ROSIS-3 sensor in 2003, with a spatial resolution of 1.3 m and 102 spectral bands. This image has nine ground-truth classes and consists of $1096\times 492$ pixels. The number of samples of each class ranges from 2152 to 65,278. There are 5536 training samples and 98,015 testing samples. Note that these training samples are out of the testing samples. A three-band false color image and the ground-truth map are shown in Figure 7.
• The last dataset was also acquired by the AVIRIS, but over the Kennedy Space Center, Florida, in 1996. Due to water absorption and the existence of low signal-noise ratio channels, 176 of them were used in our experiments. There are 13 land cover classes with 5211 labeled pixels. A three-band false color image and the ground-truth map are shown in Figure 8.

4.2. Experiments with the AVIRIS Indian Pines Dataset

For the first dataset, we randomly select 10% of labeled samples from each class for training and the rest for testing.

Table 1. Class-specific classification accuracies (in percentage), OA (in percentage), AA (in percentage) and kappa coefficient for the Aviris Indian Pines dataset. (The best results are highlighted in bold typeface).

Class Name	SVM	MH-KELM	PCA+Gabor	EPF	MPM-LBP	SADL	MFL	LBP-ELM	SC-MK	SLN
Alfalfa	42.71$\pm$14.38	98.12$\pm$2.07	96.46$\pm$2.95	100.0$\pm$0.00	78.33$\pm$9.68	89.58$\pm$10.67	86.46$\pm$7.30	97.71$\pm$2.07	98.78$\pm$1.29	95.00$\pm$3.83
Corn-notill	74.95$\pm$2.57	98.05$\pm$1.14	96.04$\pm$1.27	97.38$\pm$1.12	93.31$\pm$2.73	95.18$\pm$0.55	91.99$\pm$1.98	97.76$\pm$0.84	96.83$\pm$1.03	98.63$\pm$0.69
Corn-mintill	67.52$\pm$3.28	97.96$\pm$1.57	95.15$\pm$1.36	97.40$\pm$1.61	89.80$\pm$8.17	96.48$\pm$1.77	93.73$\pm$1.69	97.91$\pm$1.07	96.04$\pm$1.95	99.23$\pm$0.64
Corn	52.14$\pm$6.37	96.71$\pm$2.13	94.90$\pm$3.80	89.86$\pm$5.52	94.24$\pm$7.13	87.86$\pm$5.10	87.33$\pm$6.34	97.76$\pm$4.66	95.07$\pm$2.98	99.05$\pm$1.27
Grass-pasture	90.49$\pm$1.07	97.25$\pm$1.68	94.03$\pm$2.08	98.79$\pm$1.02	96.24$\pm$2.01	97.61$\pm$1.75	91.88$\pm$1.63	97.40$\pm$2.11	95.23$\pm$3.88	97.02$\pm$2.29
Grass-trees	94.39$\pm$0.94	99.76$\pm$0.26	99.54$\pm$0.43	94.84$\pm$3.05	99.05$\pm$0.87	99.06$\pm$0.64	98.38$\pm$0.76	99.14$\pm$0.63	99.09$\pm$1.18	99.90$\pm$0.28
Grass-pasture-mowed	77.39$\pm$9.35	91.74$\pm$7.23	98.26$\pm$2.25	100.0$\pm$0.00	92.17$\pm$12.43	100.0$\pm$0.00	87.83$\pm$6.42	94.35$\pm$11.24	90.40$\pm$8.68	99.96$\pm$4.12
Hay-windrowed	96.48$\pm$2.09	100.0$\pm$0.00	99.11$\pm$1.57	97.93$\pm$2.70	99.64$\pm$0.22	100.0$\pm$0.00	99.64$\pm$0.32	99.91$\pm$0.16	100.0$\pm$0.00	100.0$\pm$0.00
Oats	36.11$\pm$19.64	93.89$\pm$5.52	91.11$\pm$17.41	30.00$\pm$48.30	52.78$\pm$36.59	84.44$\pm$32.79	48.33$\pm$13.62	92.22$\pm$9.15	100.0$\pm$0.00	96.11$\pm$12.30
Soybean-notill	74.95$\pm$3.26	97.97$\pm$1.17	95.64$\pm$2.59	94.94$\pm$3.44	94.45$\pm$3.35	95.89$\pm$2.21	93.79$\pm$1.79	99.05$\pm$0.58	94.68$\pm$2.19	99.10$\pm$0.83
Soybean-mintill	83.43$\pm$1.38	99.23$\pm$0.25	98.13$\pm$0.57	90.22$\pm$4.04	97.43$\pm$1.50	98.27$\pm$1.24	98.14$\pm$0.68	99.23$\pm$0.52	98.90$\pm$0.52	99.59$\pm$0.36
Soybean-clean	65.72$\pm$2.20	98.41$\pm$0.71	92.34$\pm$2.54	95.50$\pm$3.11	96.96$\pm$1.49	94.58$\pm$2.53	91.70$\pm$3.86	96.59$\pm$1.36	95.65$\pm$1.76	98.10$\pm$1.54
Wheat	95.68$\pm$2.87	99.32$\pm$1.45	99.32$\pm$0.56	100.0$\pm$0.00	99.58$\pm$0.22	98.89$\pm$0.76	99.42$\pm$0.17	99.21$\pm$1.78	99.57$\pm$0.23	99.11$\pm$0.66
Woods	95.37$\pm$1.31	100.0$\pm$0.00	98.54$\pm$0.59	95.55$\pm$2.14	97.78$\pm$1.56	98.53$\pm$1.48	99.39$\pm$0.34	99.88$\pm$0.27	99.95$\pm$0.14	99.86$\pm$0.21
Buildings-Grass-Trees-Drives	50.91$\pm$4.91	98.45$\pm$0.60	93.30$\pm$5.27	92.70$\pm$2.37	90.70$\pm$4.40	98.74$\pm$1.60	92.84$\pm$2.73	98.77$\pm$2.46	98.21$\pm$0.75	99.06$\pm$0.79
Stone-Steel-Towers	85.76$\pm$6.45	87.06$\pm$7.72	95.18$\pm$3.06	95.09$\pm$2.61	89.76$\pm$11.63	97.76$\pm$2.11	86.24$\pm$6.84	94.00$\pm$4.52	97.59$\pm$0.57	94.71$\pm$3.34
OA	80.43$\pm$0.54	98.65$\pm$0.22	96.75$\pm$0.51	94.46$\pm$1.45	95.61$\pm$1.32	97.12$\pm$0.49	95.39$\pm$0.44	98.63$\pm$0.34	97.68$\pm$0.37	99.12$\pm$0.19
AA	74.00$\pm$1.75	97.12$\pm$0.97	96.06$\pm$1.07	91.89$\pm$2.84	91.39$\pm$3.01	95.81$\pm$2.01	90.44$\pm$1.26	97.56$\pm$1.28	97.25$\pm$0.72	98.21$\pm$0.64
κ	0.776$\pm$0.006	0.985$\pm$0.003	0.963$\pm$0.006	0.937$\pm$0.017	0.950$\pm$0.015	0.967$\pm$0.006	0.947$\pm$0.005	0.984$\pm$0.004	0.974$\pm$0.004	0.990$\pm$0.002

shows the class-specific accuracies, OAs, AAs and κ coefficients of different methods, where MH-KELM is the Multi-Hypothesis-based KELM [42,68] and SC-MK is the Superpixel-based Classification via Multiple Kernels [69]. PCA+Gabor, EPF, MH-KELM, MPM-LBP, LBP-ELM, MFL, SC-MK and SADL are spatial-based methods. SVM only uses the spectral information. The experimental results given in Table 1 are averaged over 10 runs, where the proposed SLN has five layer SSRs. The summary of some important parameters is given in

Table 2. Summary of the parameters on different datasets.

Data Set	AVIRIS Indian Pines					Pavia University		Pavia University (Fixed Training Set)		Center of Pavia		KSC
i	1	2	3	4	5	1	2	1	2	1	2	1	2	3	4	5
$|{\widehat{T}}_i|$	55	55	55	55	55	15	20	15	20	70	80	80	40	40	40	40
$|{\tilde{T}}_i|$	25	25	25	25	25	5	5	5	5	7	7	6	6	6	6	6
$v_i$	19	11	11	11	11	17	17	17	17	7	7	13	13	13	13	13

, where $v_i$ is the spatial size in the i-th layer. These parameters are determined experimentally. In the proposed method, $\rho =$ 100,000. For PCA+Gabor, $\gamma =0.5$, $\lambda =26$, $\delta =14.6$, $\theta =\{0^0,{22.5}^0,{45}^0,{67.5}^0,{90}^0,{112.5}^0,{135}^0,{157.5}^0\}$ and $\psi =0$. Experimental results given in Table 1 show that methods making use of the spectral-spatial information perform better than spectral-based methods. This is consistent with previous studies, demonstrating the advantage of exploiting spatial information in HSI classification. Another interesting observation is that MFL performs poorly on the oats class. The reason for this may be the unbalanced training samples (three samples were used for training). It is easy to find that SLN performs the best on this dataset. This is due to the hierarchical joint spectral-spatial feature learning in the SLN. The κ coefficient is a robust measure that takes into account the possibility of good classification due to random chance. To statistically test the significance of the accuracy differences, we conducted a t-test (at the level of $95\%$) between the κ coefficients of each pair of compared classification results.

Table 3. p-values corresponding to different methods for the Indian Pines dataset.

Method	p-Values
SVM	1.594$\times {10}^{-14}$
MH-KELM	6.999$\times {10}^{-4}$
PCA+Gabor	5.238$\times {10}^{-7}$
EPF	2.585$\times {10}^{-6}$
MPM-LBP	1.703$\times {10}^{-5}$
SADL	7.860$\times {10}^{-7}$
MFL	4.265 $\times {10}^{-9}$
SC-MK	1.005 $\times {10}^{-7}$
LBP-ELM	3.400$\times {10}^{-3}$

shows the p-values corresponding to different methods. Based on the results given in Table 3, we can conclude that the increases are statistically significant.

In real applications, the users are usually interested in the full classification map of the scene rather than the ground truth, which is already known. Consequently, Figure 9 illustrates full classification maps obtained by different methods. Each map is obtained from one of the random runs conducted on the Indian Pines dataset. As can be seen from Figure 9, SLN gives satisfactory results on smooth homogeneous regions by making use of the spatial information hierarchically. We can also see that the maps obtained by SVM and KELM have heavy noisy appearance. One of possible reasons for this may be that the spectral-based methods cannot make use of the spatial correlation of the HSI. Although MH-KELM, PCA+Gabor, EPF, MPM-LBP, MFL and SADL show improvements on the classification results, their classification maps still present noise. Further proven by the results in Table 1, the proposed SLN not only reduces noise, but also provides higher OA than other methods. Although LBP-ELM achieves high OA, it leads to oversmoothing.

Next, we show how the number of training samples affects the accuracy of different methods. In each test, we randomly select 2% to 10% of the labeled samples from each class to form the training set, and the remainder forms the test set. The quantitative results averaged over 10 runs for various methods are given in Figure 10. As can be seen, OAs increase monotonically as the percentage of training samples increases. With relatively limited training samples (2% of the ground truth), SLN can obtain an OA over 92%, which is around 4% higher than that obtained by the MH-KELM method. In this case, the proposed method obtains effective features using the hierarchical spectral-spatial learning model.

Finally, the resulting features of different steps are also given in Figure 11, where false color images are formed by the first three feature maps. Figure 11 shows that the discriminability of the learned features becomes stronger as the layer increases. Note that the learned spectral templates can produce feature maps that preserve the edges, and spatial templates can lead to feature maps that are smoother in the homogeneous regions. With the increase of depth, the local regions with pixels belonging to the same class become smoother while edges are preserved. Therefore, the proposed deep model can abstract intrinsic features from the HSI. This also reveals why the deep architecture can make the proposed method fit for HSI classification.

4.3. Experiments with the ROSIS University of Pavia Dataset

First, for each of the nine classes, 1% of the labeled pixels were randomly sampled for training, while the remaining 99% were used for testing. The experiment is repeated 10 times using different randomly-chosen training sets to avoid any bias induced by random sampling. In the proposed method, $\rho =100$.

Table 4. Class-specific classification accuracies (in percentage), OA (in percentage), AA (in percentage) and kappa coefficient for the Pavia University dataset. (The best results are highlighted in bold typeface).

Class Name	SVM	MH-KELM	PCA+Gabor	EPF	MPM-LBP	SADL	MFL	LBP-ELM	SC-MK	SLN
Asphalt	86.72$\pm$2.59	95.57$\pm$1.34	91.54$\pm$2.13	93.05$\pm$2.57	97.38$\pm$1.08	92.66$\pm$1.85	98.05$\pm$0.81	86.34$\pm$1.42	96.59$\pm$1.61	96.63$\pm$0.91
Meadows	96.71$\pm$0.66	99.77$\pm$0.22	99.05$\pm$0.57	95.37$\pm$1.80	99.45$\pm$0.58	98.92$\pm$0.46	99.61$\pm$0.15	99.23$\pm$0.49	98.63$\pm$1.07	99.64$\pm$0.62
Gravel	64.41$\pm$7.13	89.15$\pm$5.29	80.63$\pm$4.61	96.87$\pm$3.67	79.02$\pm$3.13	74.65$\pm$6.71	74.35$\pm$6.36	90.21$\pm$2.60	96.98$\pm$1.01	90.72$\pm$4.19
Trees	84.93$\pm$1.70	90.41$\pm$2.99	91.25$\pm$1.97	99.46$\pm$0.82	90.62$\pm$3.28	93.50$\pm$1.60	89.78$\pm$2.21	61.44$\pm$3.86	89.39$\pm$5.88	92.86$\pm$1.20
Painted metal sheets	98.51$\pm$0.80	45.62$\pm$6.49	97.39$\pm$0.62	98.09$\pm$3.84	97.52$\pm$0.98	99.38$\pm$0.39	98.45$\pm$0.86	94.33$\pm$6.23	99.13$\pm$0.52	99.73$\pm$0.18
Bare Soil	77.70$\pm$4.00	97.25$\pm$1.42	90.27$\pm$3.96	98.52$\pm$0.90	93.37$\pm$3.30	94.57$\pm$1.81	95.04$\pm$1.26	99.02$\pm$0.83	98.26$\pm$1.44	97.38$\pm$1.74
Bitumen	80.37$\pm$5.24	99.25$\pm$0.89	85.80$\pm$3.88	99.54$\pm$1.09	82.95$\pm$9.74	77.26$\pm$6.75	94.12$\pm$0.86	87.85$\pm$7.17	93.79$\pm$8.28	93.63$\pm$5.32
Self-Blocking Bricks	83.74$\pm$3.46	93.26$\pm$2.60	91.55$\pm$3.85	87.63$\pm$6.06	91.52$\pm$4.53	77.73$\pm$2.84	93.11$\pm$1.86	92.47$\pm$2.36	95.51$\pm$2.48	95.83$\pm$1.00
Shadows	95.15$\pm$6.08	97.30$\pm$0.76	98.26$\pm$0.61	96.88$\pm$0.83	98.94$\pm$0.70	99.14$\pm$0.45	91.54$\pm$6.32	47.09$\pm$7.74	93.69$\pm$6.53	87.94$\pm$6.41
OA	88.77$\pm$0.43	95.21$\pm$0.37	94.18$\pm$0.33	95.06$\pm$1.16	95.42$\pm$0.62	93.28$\pm$0.50	95.83$\pm$0.46	91.47$\pm$0.74	96.94$\pm$0.66	97.14$\pm$0.57
AA	85.36$\pm$0.65	89.73$\pm$0.97	91.75$\pm$0.45	96.16$\pm$0.75	92.31$\pm$1.06	89.76$\pm$0.92	92.67$\pm$0.99	84.22$\pm$1.87	95.78$\pm$1.68	94.93$\pm$1.27
κ	0.851$\pm$0.006	0.937$\pm$0.005	0.923$\pm$0.004	0.935$\pm$0.016	0.940$\pm$0.008	0.912$\pm$0.007	0.945$\pm$0.006	0.887$\pm$0.010	0.960$\pm$0.009	0.962$\pm$0.008

shows the averaged OAs, AAs, κs and individual class accuracies obtained in our comparisons (see the parameters in Table 2). As we can observe, SVM obtains poor results because it only uses the spectral information. Table 4 also shows that the proposed SLN outperforms other compared methods. It demonstrates that SLN can make use of the spatial information effectively. Figure 12 shows the full classification maps obtained by different methods. Again, we can find that the proposed SLN leads to a better classification map and LBP-ELM leads to the oversmooth problem. We further perform the paired t-test for κ coefficients between the SLN and other compared methods. The obtained p-values in

Table 5. p-values corresponding to different methods for the University of Pavia dataset.

Method	p Values
SVM	1.604$\times {10}^{-10}$
MH-KELM	8.565$\times {10}^{-6}$
PCA+Gabor	1.696$\times {10}^{-8}$
EPF	7.901$\times {10}^{-4}$
MPM-LBP	5.475$\times {10}^{-6}$
SADL	1.173$\times {10}^{-8}$
MFL	4.330$\times {10}^{-4}$
SC-MK	5.162 $\times {10}^{-1}$
LBP-ELM	3.394$\times {10}^{-8}$

demonstrate the effectiveness of the proposed method.

Second, the effect of the number of training samples on the classification accuracy for different methods is presented. In this experiment, we randomly select 1% to 3% (with a step of 0.5%) of the labeled samples from each class to form the training set, and the remainder forms the testing set. The experimental results are given in Figure 13, where the given accuracies are obtained by averaging over 10 runs. Similarly, the experimental results show that the proposed SLN outperforms other methods with a small number of training samples. Figure 13 also shows that the spectral-spatial-based methods significantly outperform the spectral-based methods.

Finally, we use about 9% of all data for training (3921 samples) and the rest for testing (40,002 samples). The sample distributions can be found in Figure 14, where the training set is provided by Prof. P.Gamba. The fixed training set is challenging because it is made up of small patches, and most of the patches in an HSI contain no training samples. The proposed method is compared with SVM with Composite Kernel (SVM-CK) [70], SADL [40], Simultaneous Orthogonal Matching Pursuit (SOMP) [70], Learning Sparse-Representation-based Classification with Kernel-smoothed regularization (LSRC-K) [26], MPM-LBP and SMLP-SpATV. The experimental results are given in

Table 6. Class-specific classification accuracies (in percent), OA (in percent), AA (in percent) and kappa coefficient for the Pavia University dataset with the fixed training and testing set. CK, Composite Kernel; SOMP, Simultaneous Orthogonal Matching Pursuit; LSRC-K, Learning Sparse-Representation-based Classification with Kernel-smoothed regularization; SMLR-SpATV, Sparse Multinomial Logistic Regression and Spatially-Adaptive Total Variation. (The best results are highlighted in bold typeface).

Method	SVM [70]	SVM-CK [70]	SADL [40]	SOMP [70]	LSRC-K [26]	MPM-LBP	SMLR-SpATV	SLN
Asphalt	84.30	79.85	79.17	59.33	93.86	81.66	94.57	92.48
Meadows	67.01	84.86	93.06	78.15	84.56	67.14	82.56	94.40
Gravel	68.43	81.87	85.41	83.53	74.05	74.60	81.13	76.91
Trees	97.80	96.36	95.32	96.91	98.90	95.54	95.01	96.50
Painted metal sheets	99.37	99.37	99.11	99.46	100.0	99.28	100.0	98.83
Bare Soil	92.45	93.55	92.34	77.41	88.21	93.22	100.0	91.99
Bitumen	89.91	90.21	83.00	98.57	90.93	87.87	99.17	93.78
Self-Blocking Bricks	92.42	92.81	92.61	89.09	97.86	90.81	98.45	97.27
Shadows	97.23	95.35	98.29	91.95	97.99	97.48	95.45	95.47
OA	79.15	87.18	90.60	79.00	88.98	78.81	90.01	93.55
AA	87.66	90.47	90.92	86.04	91.82	87.51	94.04	93.07
κ	0.737	0.833	0.875	0.724	0.855	0.732	0.872	0.914

, where some results come from the related references (parameters are given in the forth column of the Table 2). The proposed method has significant gains in the OA and κ and has high accuracy on the meadows class. We can conclude that SLN can make full use of the limited spatial information. This further demonstrates the advantage of SLN.

4.4. Experiments with the ROSIS Center of Pavia Dataset

In this experiment, our method is evaluated by using the ROSIS Center of Pavia dataset and compared with the state-of-the-art methods mentioned above. There are 5536 samples for training and the rest for testing, where the training set is provided by Prof. P. Gamba, as well. In the proposed method, $\rho =$ 1000,000. In this dataset, the distributions of the training samples are relative centralism, and less discriminative position information can be used, as well. Experimental results in

Table 7. Class-specific classification accuracies (in percentage), OA (in percentage), AA (in percentage) and kappa coefficient for the Center of Pavia dataset with the fixed training and testing Set. (The best results are highlighted in bold typeface).

Method	SVM	MH-KELM	PCA+Gabor	EPF	MPM-LBP	SADL	MFL	LBP-ELM	SC-MK	SLN
Water	98.77	97.29	98.50	100.0	99.10	98.79	99.43	86.79	96.07	99.31
Trees	91.94	96.87	92.21	99.39	94.57	92.66	87.02	86.55	87.49	98.86
Meadow	95.21	99.95	96.44	86.78	95.83	96.63	95.83	92.22	99.38	99.72
Brick	80.62	99.70	84.58	98.28	81.94	98.32	99.46	93.28	99.88	99.16
Bare Soil	93.84	98.67	99.42	96.64	97.75	97.91	99.43	74.92	98.99	98.97
Asphalt	95.22	99.93	98.00	77.48	95.21	95.51	95.05	83.74	95.05	98.99
Bitumen	95.88	98.24	98.60	95.29	94.51	98.24	96.39	94.75	96.22	98.04
Tiles	99.79	99.38	99.21	100.0	99.62	98.76	99.34	90.27	99.03	99.86
Shadow	99.95	100.0	99.95	100.0	100.0	100.0	97.23	65.99	100.0	92.69
OA	97.31	97.81	97.93	97.08	97.85	98.08	98.01	86.31	95.98	99.23
AA	94.58	98.89	96.32	94.87	95.39	97.42	96.47	85.39	96.90	98.90
κ	0.951	0.961	0.963	0.948	0.961	0.965	0.964	0.772	0.929	0.986

show that SLN performs the best in terms of the OA and κ (parameters are shown in Table 2). This proves that SSR is an effective strategy to learn spectral-spatial features.

Finally, the full classification maps of the methods listed in Table 7 are illustrated in Figure 15. From the visual inspection of the maps, we find that the proposed SLN outperforms other methods because its resulting classification map is smoother (with reduced salt-and-pepper classification noise). We also note that LBP-ELM not only obtains lower accuracy, but also leads to a serious oversmoothing problem.

4.5. Experiments with the Kennedy Space Center Dataset

First, we randomly chose 25 samples for each class as training samples, and the remaining samples composed the test set. In the proposed method, $\rho =$ 10,000. Experimental results in

Table 8. Class-specific classification accuracies (in percentage), OA (in percentage), AA (in percentage) and kappa coefficient for the KSC dataset. (The best results are highlighted in bold typeface).

Method	SVM	MH-KELM	PCA+Gabor	EPF	MPM-LBP	SADL	MFL	LBP-ELM	SC-MK	SLN
Scrub	88.40$\pm$2.57	98.76$\pm$1.49	98.30$\pm$0.79	99.96$\pm$0.13	97.84$\pm$1.20	95.00$\pm$1.60	94.20$\pm$1.80	95.30$\pm$4.03	92.84$\pm$3.23	99.95$\pm$0.13
Willow swamp	85.00$\pm$4.27	98.07$\pm$1.24	96.83$\pm$1.71	99.66$\pm$0.32	91.51$\pm$7.18	96.83$\pm$3.29	93.07$\pm$1.17	94.40$\pm$7.44	91.19$\pm$5.49	99.31$\pm$0.39
Cabbage palm hammock	90.74$\pm$2.53	99.31$\pm$0.47	95.45$\pm$2.70	100.0$\pm$0.00	98.48$\pm$0.55	95.41$\pm$1.76	96.28$\pm$1.02	99.48$\pm$0.67	97.84$\pm$1.26	99.74$\pm$0.55
Cabbage palm/oak hammock	71.85$\pm$4.62	88.11$\pm$6.22	77.09$\pm$5.67	92.42$\pm$5.20	76.83$\pm$12.01	87.14$\pm$4.94	88.19$\pm$5.64	95.95$\pm$4.36	91.01$\pm$6.54	98.15$\pm$2.45
Slash pine	66.47$\pm$2.82	97.35$\pm$2.97	88.16$\pm$4.06	98.89$\pm$2.16	79.93$\pm$7.87	93.31$\pm$3.85	94.78$\pm$4.47	100.0$\pm$0.00	93.01$\pm$8.69	100.0$\pm$0.00
Oak/broadleaf hammock	59.56$\pm$6.81	99.95$\pm$0.16	90.49$\pm$4.61	98.75$\pm$2.44	93.63$\pm$5.96	95.10$\pm$3.84	97.79$\pm$1.75	99.41$\pm$1.32	95.39$\pm$3.01	100.0$\pm$0.00
Hardwood swamp	90.37$\pm$5.04	100.0$\pm$0.00	99.38$\pm$1.21	88.12$\pm$12.43	99.88$\pm$0.40	100.0$\pm$0.00	99.75$\pm$0.53	100.0$\pm$0.00	98.88$\pm$0.71	100.0$\pm$0.00
Graminoid marsh	90.59$\pm$2.84	99.33$\pm$0.72	94.48$\pm$2.07	95.70$\pm$3.05	99.33$\pm$1.33	97.09$\pm$1.76	94.46$\pm$2.11	93.25$\pm$9.56	96.63$\pm$2.91	99.85$\pm$0.24
Spartina marsh	92.36$\pm$3.30	100.0$\pm$0.00	99.92$\pm$0.26	99.82$\pm$0.22	93.47$\pm$6.40	98.97$\pm$1.69	99.78$\pm$0.18	98.40$\pm$1.73	99.41$\pm$0.37	100.0$\pm$0.00
Cattail marsh	88.58$\pm$2.66	94.12$\pm$0.81	96.02$\pm$1.53	99.95$\pm$0.11	95.25$\pm$2.72	91.53$\pm$1.83	86.75$\pm$2.28	99.26$\pm$1.61	99.74$\pm$0.00	97.63$\pm$1.91
Salt marsh	95.66$\pm$1.68	99.90$\pm$0.18	98.86$\pm$1.00	95.45$\pm$2.77	98.32$\pm$4.00	95.84$\pm$4.68	95.30$\pm$4.26	99.82$\pm$0.42	98.27$\pm$1.25	100.0$\pm$0.00
Mud flats	84.23$\pm$3.97	92.74$\pm$2.15	95.61$\pm$2.63	99.89$\pm$0.27	89.21$\pm$4.82	92.01$\pm$2.27	88.72$\pm$3.77	97.89$\pm$1.92	96.95$\pm$2.38	96.80$\pm$3.06
Water	98.19$\pm$0.51	98.03$\pm$0.29	98.59$\pm$0.69	100.0$\pm$0.00	98.71$\pm$0.61	98.82$\pm$0.80	98.17$\pm$0.38	100.0$\pm$0.00	100.0$\pm$0.00	98.96$\pm$0.84
OA	88.39$\pm$0.40	97.47$\pm$0.43	96.03$\pm$0.41	98.45$\pm$0.62	94.81$\pm$0.84	95.56$\pm$0.38	94.52$\pm$0.71	97.80$\pm$1.11	96.81$\pm$0.48	99.16$\pm$0.23
AA	84.77$\pm$0.61	97.36$\pm$0.47	94.55$\pm$0.67	97.59$\pm$1.27	93.26$\pm$1.27	95.16$\pm$0.37	94.40$\pm$0.73	97.94$\pm$1.08	96.24$\pm$0.56	99.26$\pm$0.19
κ	0.871$\pm$0.44	0.972$\pm$0.005	0.956$\pm$0.005	0.983$\pm$0.007	0.942$\pm$0.009	0.950$\pm$0.004	0.939$\pm$0.008	97.55$\pm$0.012	0.964$\pm$0.005	0.991$\pm$0.003

show that SLN performs the best. Note that SVM performs poorly on this dataset. This experiment shows that SLN can lead to a high classification accuracy even when the distributions of the training samples are relative centralism, and less discriminative position information can be used. The same conclusion can be drawn as on Center of Pavia dataset. p-values in

Table 9. p-values corresponding to different methods for the KSC dataset.

Method	p Values
SVM	1.768$\times {10}^{-10}$
MH-KELM	7.688$\times {10}^{-6}$
PCA+Gabor	7.769$\times {10}^{-6}$
EPF	1.086$\times {10}^{-2}$
MPM-LBP	1.074$\times {10}^{-7}$
SADL	8.553$\times {10}^{-10}$
MFL	6.556$\times {10}^{-9}$
SC-MK	4.398 $\times {10}^{-7}$
LBP-ELM	5.888$\times {10}^{-3}$

also demonstrate that the improvement is significant.

Second, the full classification maps of the methods in Table 8 are given in Figure 16. The advantages of the proposed framework can be visually appreciated in the maps in Figure 16. Although LBP-ELM obtains high OA, AA and κ (see Table 8), its classification map is oversmooth. Figure 16f shows that MH-KELM performs poorly on the water class.

Finally, we perform an experiment to examine how the number of training samples affects the results of our method compared to other methods. Here, we randomly chose five to 25 of the labeled samples from each class to form the training set, and the remainder forms the testing set. The experimental results are given in Figure 17, where the accuracies are obtained by averaging over 10 runs. Similarly, the experimental results show that the proposed SLN outperforms other methods with a small number of training samples.

4.6. Discussion

In order to further analyze the proposed SLN, we test its performance on more experiments. In this section, the experimental results on the Indian Pines dataset are reported. We can make the same conclusions on the other datasets.

First, the comparisons with multiple-class SVM and the soft-max classifier are given in

Table 10. Comparisons of different classifiers on the Indian Pines dataset.

Method	Softmax	SVM	KELM
Accuracy (%)	97.65	98.93	99.12
Training Time (S)	19.54	0.5565	0.0754

. As shown in the table, KELM achieves higher classification accuracy and is fast. Consequently, KELM is used in the final stage of SLN. However, the SVM can obtain comparable results.

Second, we show the effects of the depth on the classification accuracy. A series of SLNs with different depths were trained, and their experimental results are shown in Figure 18. It can be observed that more layers usually lead to a higher classification accuracy. However, this does not mean the deeper the better. This helps us to determine how many layers are needed to obtain higher classification accuracy. The number of layers is related to the dataset. It is an open problem to determine the number of the layers. In this paper, it was determined experimentally.

Third, we compare the SLN with the recently-proposed deep learning-based methods [49,71]. The experimental results are reported in

Table 11. Comparisons of different deep learning-based on the Indian Pines dataset. (The best results are highlighted in bold typeface).

Method	3D-CNN-LR [49]	SDAE [71]	SSDCNN [72]	SSDL [73]	Deep${}_{\mathit{o}}$ [72]	SLN
Percent of the training samples	22%	10%	10%	10%	10%	10%
OA	97.56	98.61	96.02	91.60	97.45	99.12
AA	99.23	98.20	93.59	93.96	95.91	98.21
κ	0.970	0.982	0.947	90.43	0.964	0.990

, where SSDCNN is the Spectral-Spatial Deep Convolutional Neural Network, Deep${}_o$ is deep features with orthogonal matching pursuit and SSDL is Low Spatial Sampling Distance. From the results, we can see that the classification accuracy values of the proposed method in terms of OA and the κ coefficient are higher than those of other deep learning-based classification methods. We also note that 3D-CNN-LRhas higher sample complexity.

Finally, we show the effects of different spatial filters in the proposed SLN. In this paper, the Gabor filter (12 directions were used) was used for the baseline. The experimental results are given in Figure 19. These results show that the learned filters can achieve better classification accuracy in most cases. However, the SLN using learned filters performs worse than that using predefined filters when the number of the training sample is 2%. The reason may be that PCA cannot learn effective filters from a small number of training samples. However, we can also find that these two cases can perform better than the other contrastive methods shown in Figure 10. This phenomenon can demonstrate the effectiveness of the proposed framework.

5. Conclusions and Future Work

In this paper, a novel framework, called SSR, has been proposed for HSI classification. A main contribution of the presented framework is using hierarchical deep architecture to learn joint spectral-spatial features, which are suitable for the nature of HSI. It uses a new strategy to learn the spectral-spatial features of HSIs. Other deep learning-based HSI classification methods usually need to learn more parameters and have high sample complexity. SSR can overcome these problems. In addition, SSR is designed according to the characters of the HSI, other than directly using the conventional deep learning models like some other methods. Consequently, it can jointly learn spectral and spatial features of HSIs. Furthermore, a hierarchical spectral-spatial-based HSI classification method called SLN has been presented as an implementation example of SSR. SLN uses templates learned directly from HSIs to learn discriminative features. In SLN, the discriminative spectral-spectral features on each scale are learned by MFA and PCA. KELM is also embedded into SLN. Extensive experiments on four HSI datasets have validated the effectiveness of SLN. The experimental results also show that the hierarchical spectral-spatial feature learning is useful for classification, and SLN is promising for the classification of HSIs with a small number of training samples. The experimental results of SLN also verify the effectiveness of the proposed SSR. Our future research will follow three directions:

• In SSR, the spectral-spatial features are jointly learned through the template matching. Different template sets may lead to different features. Consequently, it is interesting to design new template learning methods.
• As shown in Section 3, SSR exploits the spatial information by matching each feature map using the two-dimensional templates. This operation will lead to high dimensional features. We will study a tensor SSR that replaces the two-dimensional templates with tensor-like templates [53,74].
• SLN achieves a high classification accuracy by stacking the joint spectral-spatial feature learning units. It is interesting to mathematically analyze and justify its effectiveness according to SSR.