A Comparison of Stand-Level Volume Estimates from Image-Based Canopy Height Models of Different Spatial Resolutions

Abstract

Digital aerial photogrammetry has recently attracted great attention in forest inventory studies, particularly in countries where airborne laser scanning (ALS) technology is not available. Further research, however, is required to prove its practical applicability in deriving three-dimensional (3D) point clouds and canopy surface and height models (CSMs and CHMs, respectively) over different forest types. The primary aim of this study is to investigate the applicability of image-based CHMs at different spatial resolutions (1 m, 2 m, 5 m) for use in stand-level forest inventory, with a special focus on estimation of stand-level merchantable volume of even-aged pedunculate oak (Quercus robur L.) forests. CHMs are generated by subtracting digital terrain models (DTMs), derived from the national digital terrain database, from corresponding digital surface models (DSMs), derived by the process of image matching of digital aerial images. Two types of stand-level volume regression models are developed for each CHM resolution. The first model is based solely on stand-level CHM metrics, whereas in the second model, easily obtainable variables from forest management databases are included in addition to CHM metrics. The estimation accuracies of the stand volume estimates based on stand-level metrics (relative root mean square error RMSE_% = 12.53%–13.28%) are similar or slightly higher than those obtained from previous studies in which stand volume estimates were based on plot-level metrics. The inclusion of stand age as an independent variable in addition to CHM metrics improves the accuracy of the stand volume estimates. Improvements are notable for young and middle-aged stands, and negligible for mature and old stands. Results show that CHMs at the three different resolutions are capable of providing reasonably accurate volume estimates at the stand level.

1. Introduction

As the most widely distributed terrestrial ecosystem on Earth, forests provide many direct and indirect benefits to human well-being [1,2]. Sustainable management of forests for the realization of their multiple functions and services requires spatially explicit information about their state and development [3], which is usually acquired through forest inventories. Although traditional field-based forest inventory can provide relatively accurate information, the process is time-consuming and labor intensive, and in some cases, access to certain areas is not possible [4]. Therefore, the potential of remote sensing application in forest inventory has long been recognized by both researchers and practicing foresters [5]. Over the last few decades, a rapid development of different remote sensing instruments has resulted in the development of various methods and techniques for retrieval of forest information from remote sensing data [6,7].

Airborne laser scanning (ALS) technology has been a focus of much research in the last twenty years, thus becoming an integral part of operational forest inventories in a number of developed countries (e.g., Scandinavian countries, Canada, and USA) [6,8,9,10]. Highly accurate, three-dimensional (3D) point clouds and canopy height models (CHMs) from ALS enable the derivation of various forest metrics (e.g., height metrics, canopy cover or density metrics, etc.) and characterization of vertical forest structure [11]. In combination with field reference data and established prediction models, ALS metrics could serve for the estimation of various tree and forest inventory attributes (e.g., height, basal area, volume, biomass, etc.) [10,11,12,13,14,15,16]. Generally, there are two main approaches to derive forest information from ALS data: the area-based approach (ABA) and the individual‑tree-based approach (ITBA). The ABA uses point cloud or CHM metrics of the sampled area (e.g., plot) as input to statistical models for forest attributes estimation [10,11,12,13,14,15,16]. On the other hand, the ITBA uses ALS metrics of the individual trees that are previously delineated using segmentation methods for derivation of tree height and crown dimensions, which are then used for calculation of other single-tree attributes (e.g., diameter at breast height, tree volume, biomass, etc.) [13,17]. Unlike the ABA, the ITBA is not used operationally yet, primarily due to difficulties in individual tree detection [7,18].

Another promising remote sensing method for deriving 3D point clouds and CHMs, which recently gained attention in forestry research, is digital aerial photogrammetry (DAP) [7,10,19]. Although aerial images have long been widely used in forest inventory (e.g., for visual interpretation of tree and stand attributes or delineation of forest stands) [20], the recent advancements and improvements in image quality (e.g., radiometric and geometric resolutions), image matching algorithms, computing power and hardware sizing and capacity have promoted their comeback in forest inventory research [3,10]. Compared to ALS, photogrammetric aerial surveys have lower costs [21] and, in many European countries including Croatia, aerial images are usually updated on a regular basis for topographic purposes [22]. By image matching of aerial stereo images, digital surface models (DSMs) of similar quality and accuracy to ALS-based DSMs can be derived [21,23]. To obtain a normalized point cloud (height above ground) or a CHM, ground elevation data (i.e., digital terrain model (DTM)) of a high spatial resolution is required. Unlike the ALS technology, which can penetrate through the forest canopy and derive an accurate DTM of high spatial resolution, DAP is unable to determine ground elevation information under the dense forest canopy. When a DTM is available, primarily from the ALS technology or stereo-photogrammetry, cartography, and/or field surveys, the normalized point clouds or CHMs are generated by subtracting DTMs from corresponding DSMs or point clouds. The normalized image-based point clouds and CHMs can then serve as a basis for deriving various forest attributes in the same manner as ALS data by using ABA or ITBA approaches.

A number of recent studies emphasized the great potential of dense point clouds and DSMs derived by image matching of digital aerial stereo images in combination with accurate DTMs for the CHMs and forest attributes estimation [3,19,22,24,25,26,27]. Moreover, comparison studies which evaluated different remote sensing data considered this image-based approach as a cost-effective alternative to ALS in forest inventory applications [10,11,12,28,29,30,31,32,33,34]. Most of the studies where the accuracy of forest attributes estimation is critical were evaluated mainly at the plot level. To date, only several studies published in peer-reviewed literature [3,10,24,30,34] evaluated forest attributes at the stand level (

Table 1. Description and results of previous studies dealing with estimation of volume at the stand level using normalized point clouds or canopy height models (CHMs) derived from digital aerial images and airborne laser scanning (ALS) based digital terrain model (DTM).

Reference	Bohlin et al. 2012 [24]			Rahlf et al. 2014 [10]	Gobakken et al. 2015 [30]	Stepper et al. 2015 [3]		Puliti et al. 2016 [34]
Study location	Southern Sweden			Southern Norway	South-eastern Norway	South-central Germany		South-eastern Norway
Dominant tree species	Picea abies, Pinus sylvestris, Betula spp.			P. abies, P. sylvestris, Betula spp.	P. abies, P. sylvestris, Betula spp.	Fagus sylvatica, Quercus petraea, P. sylvestris		P. abies, P. sylvestris, Betula spp.
Camera type	DMC			UltracamX	UltracamXp	UltracamXp		UltracamXp
GSD (m)	0.48	0.48	0.12	0.20	0.17	0.20		0.17
Overlap (%)	60/30	80/30	80/60	60/20	80/30	75/30		80/30	60/30
Matching software	Match-T DSM	Match-T DSM	Match-T DSM	NGATE (SocetSet)	Match-T DSM	Remote Sensing Software Package Graz		Agisoft PhotoScan	Agisoft PhotoScan
Regression type	Multiple linear	Multiple linear	Multiple linear	Linear mixed effects	Multiple linear	Multiple linear	Random forests	Multiple linear	Multiple linear
Type of independent variables	H, CC, T	H, CC, T	H, CC	H, CC	H, CC	H, V, CC, SP	H, V, CC, SP	H	H
Validation method	Cross	Cross	Cross	Cross	Independent	Cross	Cross	Independent	Independent
MD (m3∙ha−1)	3.6	1.7	−1.8	-	-	2.9	−8.2	−0.9	1.5
MD% (%)	1.4	0.7	−0.7	-	-	0.9	−2.6	−0.4	0.6
RMSE (m3∙ha−1)	32.8	32.6	36.2	33.8	-	46.7	43.9	31.2	35.9
RMSE% (%)	13.1	13.0	14.5	18.1	13.1–17.4	14.8	13.9	13.4	15.4

GSD: Ground Sampling Distance; RMSE: root mean square error; RMSE_%: relative root mean square error; MD: mean difference; MD_%: relative mean difference; H: height metrics; CC: canopy cover (density) metrics; T: texture metrics; SP: spectral metrics derived from orthoimages.

). Mainly, the stand level attributes were calculated by averaging plot level attributes in other studies. There were several studies where the satellite retrievals at stand level were used in assessment of forest attributes (e.g., [35,36]); however, to the best of the authors’ knowledge, no previous studies dealing with image matching of digital aerial images used the metrics of an entire stand for the estimation of forest attributes at the stand level. In addition, further research over different forest types is needed to prove the applicability of DAP in forest attributes estimation. While several studies [10,24,30,34] were conducted in boreal forests of Northern Europe with more uniform and consistent properties, only one study was conducted [3] in mixed, broadleaf-dominated forests of Central Europe (Germany).

The goal of the present study is to investigate the applicability of image-based CHM for forest attributes estimation and forest inventory at the stand level, with a special focus on the estimation of stand-level merchantable volume of even-aged pedunculate oak (Quercus robur L.) forests. The stand-level approach enables the use of information from existing forest management plans for model selection and parameterization, thus overcoming the need for field measurements and additional costs. The method that we present in this study can be universally applied, provided that aerial surveys and forest inventory surveys were conducted simultaneously, which usually is the case (e.g., if forest inventory interval is 10 years, it usually means that approximately 10% of the area of managed forests is measured each year). The impact of different spatial resolutions of CHM (1 m, 2 m, and 5 m) on the stand-level volume estimates is evaluated based on the ground reference data. For that purpose, the stand-level volume estimation models based on CHM metrics of the entire stand are generated. In addition, the inclusions of several variables obtained from forest management plans (stand age, soil type, site index, and phytocenological type) in the volume estimation models are examined. Stand volume is one of the most important inventory attributes and is crucial for understanding the dynamics and productive capacity of forest stands, as well as to manage their use within the limits of sustainability [37,38]. Pedunculate oak is a key tree species of European forests [39], and yet, it has not been the subject of previous similar studies. Overall, this study attempts to provide fast, simple and low-cost photogrammetric approach for stand-level volume estimation based on existing data (aerial images, DTM data, field data).

2. Materials and Methods

2.1. Study Area

The research was conducted in the state-owned managed forests of Spačva basin located in eastern Croatia (Figure 1). Covering the total area of approximately of 40,000 ha, Spačva basin is one of the largest coherent complexes of lowland pedunculate oak forests in Europe [40]. Even-aged pedunculate oak forests of different age classes ranging from 0 to 160 years are the main forest type, which together occupy 96% of the forest area of Spačva basin [41]. The oak stands of the area are less often pure and mainly mixed with other tree species (Fraxinus angustifolia Vahl., Alnus glutinosa (L.) Geartn., Carpinus betulus L.) The stands are of high quality with site index I or II and they are actively managed for sustained timber in 140-year rotations, ending with two or three regeneration fellings during the last 10 years of the rotation. The regeneration fellings are implemented when old stands produce seeds from which future young stands are raised. After successful natural regeneration and stand establishment, silvicultural treatments are carried out throughout the rotation.

The study area is characterized by flat terrain, with ground elevations ranging from 77 to 91 m a.s.l. The hydromorphic soils (pseudogley, hypogley, humogley, and semigley) prevail, while automorphic soils (luvisol) occur only on micro-elevations. According to Köppen classification, the climate of the area is temperate and warm rainy with a mean annual temperature of 10.2 °C and a precipitation of 709 mm·y⁻¹ [42].

2.2. Field Reference Data

Out of 13 management units in the Spačva basin, 6 management units with a total of 548 even-aged pedunculate oak stands covering the area of 11,261.85 ha were selected for this research (Figure 1). In order to enable comparison between field data and estimates from CHMs, the idea was to select those stands, i.e., management units, in which the regular forest inventories (field measurements) were conducted within one year of the image acquisition (2010–2012).

The field data used in this study were collected according to the Regulation on Forest Management (Official Gazette 111/06, 141/08) during the period 2010–2012 as part of the regular forest inventories conducted by national forestry company (Croatian Forests Ltd.). All stands above 20 years of age were systematically sampled with circular plots and minimum sampling intensity of 5%. The circular sample plots had an area of 500 m² (radius = 12.62 m), thus, at least, two plots were established per ha. Old stands, which were prescribed for the regeneration felling in the following ten years, were measured with 100% intensity (i.e., all trees in the stand). Diameter at breast height (dbh) on the trees in the sampled plots, and in the old stands, was measured for all trees with dbh ≥ 10 cm. At least 5 to 10 tree heights per a dbh class (5 cm gradation) were measured for each species in each group of stands. The stands’ grouping was based on site index and stand age. The site index, which presents potential productivity of forest stands, was determined for each stand using Croatian growth-yield tables [44], which included stand age and mean tree height as entries. Based on tree height and dbh measurements, the species-specific height curves (i.e., height–dbh models) were constructed by fitting Michailloff’s function [45]. The merchantable tree volume (up to a diameter of 7 cm overbark) of each sampled tree was calculated from field-measured dbh and tree height estimated from species-specific height curves using the Schumacher–Hall equation [46] and parameters from Croatian two-entry (dbh and height) volume tables [47,48,49,50]. The mean dbh and mean height for each forest stand were calculated by averaging data of all sampled trees in the stand, whereas stand density, basal area, and stand volume were calculated by summing the tree data and dividing them by the total area of all plots within the stand. To reduce possible uncertainties due to the time span between the field measurements and the aerial surveys, which was for some parts of the study area up to one year, it was decided to exclude the stands younger than 30 years from further analyses. Namely, very young stands have a significant share of trees with dbh thinner than the taxation limit (dbh ≥ 10 cm), and one-year ingrowth in those stands can considerably contribute to the stand volume [51].

A summary of the calculated stand-level forest attributes is presented in

Table 2. Descriptive statistics of the stand-level forest attributes for 548 selected even-aged pedunculate oak stands of Spačva basin.

Forest Attribute	Minimum	Maximum	Mean	SD
Age (years)	30.0	146.0	102.8	25.7
Mean dbh (cm)	14.1	58.9	32.7	6.5
Mean height (m)	14.3	33.6	25.3	3.0
Stand density (trees∙ha−1)	68.0	1195.0	372.0	185.7
Basal area (m2∙ha−1)	12.2	45.0	27.6	4.6
Volume (m3∙ha−1)	98.1	713.2	419.2	101.4

. Stand-level merchantable volume was used in the models development and validation as a ground-truth reference data. For those stands which were inventoried in 2010, the stand volume in 2011 was calculated by adding an annual increment to volume from 2010. The stand volume in 2011 of stands inventoried in 2012 was calculated by subtracting annual increment from volume measured in 2012. Fellings did not occur within selected stands for the period from 2010 to 2012, and therefore were not included in the stand volume calculation.

2.3. Photogrammetric Data

Photogrammetric data, aerial images, and digital terrain data were provided by the Croatian State Geodetic Administration (CSGA) and were used to develop DSM and DTM, respectively.

The color infrared (CIR) 8-bit digital aerial images were acquired using the Intergraph Z/I Imaging Digital Mapping Camera (DMC) system [52] as part of the regular national topographic survey in August 2011. The study area was represented by 157 images with the ground sampling distance (GSD) of approximately 30 cm. The images were collected in 11 flight lines with forward overlaps of 60% and side overlaps of 30%. The images were block-triangulated, using the bundle adjustment method, and post-processed, including radiometric and geometric corrections, as well as pan-sharpening. This was done by the contractor (Geodetski zavod Ltd. Osijek, Croatia) according to the rules of the CSGA (Product Specification 301D130). The horizontal (x, y) and vertical (z) accuracies of the processed images were validated with ground control points (root mean square error (RMSE) < 0.25 m and < 0.30 m, respectively).

The digital terrain data (breaklines, formlines, spot heights and mass points), used to generate DTM, were collected according to the rules of the CSGA (Product Specifications 301D150). The main method for national digital terrain data collection is aerial stereo photogrammetry (aerial images of GSD ≤ 30 cm), supported with vectorization of existing maps and field data collection (especially for unreliable areas, which are not visible from aerial images). Data density is dependent of terrain type, slope and surface roughness. The average distance between points in breaklines and formlines is recommended to be 25 m, while the average distance between mass points is recommended to be 70–90 m. For flat areas, or areas covered by vegetation, the distance can be larger but not more than 120 m. For the flat terrain, which correspond to the terrain type of the research area, (Spačva basin), the required number of points in breaklines and formlines is 400–800 points∙km², while the required number of mass points and spot heights is 100–150 points∙km². The required absolute accuracy of digital terrain data (including both horizontal and vertical accuracy) validated with ground control points is < ±1 m of the standard deviation for the well-defined details and < ±2 m for not well-defined details.

2.4. Photogrammetric Processing (CHM Generation)

The photogrammetric data processing, which included the generation of DSMs, DTMs, and CHMs, was performed using the PHOTOMOD 5.24 digital photogrammetric system (Racurs Co., Moscow, Russia).

DSMs were generated using the Dense DTM algorithm of PHOTOMOD DTM module. Dense DTM is an area-based image matching algorithm that calculates the coordinates of conjugate points between overlapping images for each pixel of the selected area using the cross-correlation approach. The spatial resolution (pixel size) of the resulting DSM thus corresponds to the image pixel size (0.30 m × 0.30 m). A detailed description of the procedure of the DSM generation using Dense DTM, as well as parameters settings, can be found in Balenović et al. [53]. Matching errors, i.e., spikes (points above or below the surface) were removed from DSM using the DSM filters. The resulting gaps (null cells) were then filled by a Smooth interpolation method. Finally, the initial raster DSM of 0.30 m resolution (DSM_0.3) was then resampled to DSMs of 1 m, 2 m, and 5 m resolutions (hereinafter referred to as DSM₁, DSM₂, and DSM₅). The resampling was conducted by: (a) converting the initial DSM from raster to point format; (b) reducing the number of points by using the “thin-out” coefficient of 3, 6 and 16; (c) creating the triangular irregular networks (TINs) from corresponding reduced points; and (d) generating raster DSMs of 1 m, 2 m, and 5 m resolutions from corresponding TINs. In the recently published study by Balenović and Marjanović [54], the vertical accuracy of DMSs of different spatial resolutions (DSM₁, DSM₂, and DSM₅) generated from the same aerial images, was evaluated by comparing manually stereo measured elevations of 294 tree tops with the elevations of planimetrically corresponding DSM’s points. The RMSE values for the DSM₁, DSM₂, and DSM₅ generated for the part of the Spačva basin (1869.33 ha) that was also included in the present study were 0.76 m, 0.84 m, and 1.31 m, respectively.

For the DTMs generation, national digital terrain data were used. First, a TIN was created from the digital terrain data, which was then converted through the linear interpolation into a raster DTMs of 1 m, 2 m, and 5 m resolutions.

A raster CHMs of 1 m, 2 m, and 5 m resolutions (hereinafter referred to as CHM₁, CHM₂, and CHM₅) of the research area was generated by subtracting ground from surface elevation data, i.e., by subtracting DTMs from corresponding DSMs. All pixels with heights above 45 m in CHMs were considered as outliers and were filtered (removed). The maximum threshold of 45 m was defined based on the maximum tree heights in the study area. The resulting gaps were then filled using a Smooth interpolation method. Prior to the metrics extraction (explained below), and in accordance with other similar studies [3,34], a minimum threshold of 5 m was applied to remove ground and understorey vegetation (e.g., shrubs, small trees with dbh < 10 cm). The minimum threshold of 5 m was defined based on the minimum height of trees with dbh ≥ 10 cm. In other words, all trees with dbh ≥ 10 cm at the study area have heights above 5 m.

2.5. CHM Metrics

In other studies [3,10,24,30], the height and density metrics extracted from CHMs have proven to be good predictors of various forest attributes. To extract the stand-level metrics from CHMs, the boundaries of the selected forest stands were overlaid on CHMs. For each forest stand, both height metrics and density metrics were extracted and calculated from each CHM. In total, 24 CHM metrics were extracted and considered in the statistical modeling (i.e., for development of stand-level volume models) as potential independent variables. The CHM metrics with corresponding description and explanation of the calculation are summarized in

Table 3. Metrics extracted from CHMs, calculated for each stand and used as potential independent variables in statistical analysis (development of stand-level volume model).

CHM Metrics		Description and Explanation
Height metrics	hmean (m)	Arithmetic mean of pixels height
	hSD (m)	Standard deviation of pixels height
	hmode (m)	Mode height
	hmax (m)	Maximum height
	hmin (m)	Minimum height
	p5, p10, p20, p25, p30, p40, p50, p60, p70, p75, p80, p90, p95, p99 (m)	Height percentiles (5th, 10th, 20th, 25th, 30th, 40th, 50th, 60th, 70th, 75th, 80th, 90th, 95th, 99th)
Density (cover) metrics	CC10, CC20, CC30, CC40	Ratio between area of canopy above certain height threshold (10 m, 20 m, 30 m, 40 m) and stand area
	k3D	Ratio between 3D canopy surface model area and ground area

.

2.6. Variables from Forest Management Plans

In addition to extracted CHM metrics, several existing and easily obtainable stand variables from Forest management plans (FMP variables) were considered in statistical modeling as potential independent variables (

Table 4. Existing stand variables from Forest management plans (FMP variables) used as potential independent variables in statistical analysis (development of stand-level volume models).

Variable	Description and Explanation
SA	Stand age (from 30 to 146)
ST	Soil type (pseudogley, hypogley, humogley, semigley, luvisol)
SI	Site index (I, II)
PT	Phytocenological type (Genisto elatae-Quercetum roburis caricetosum remotae, Genisto elatae-Quercetum roburis aceretosum tatarici, Carpino betuli-Quercetum roburis "typicum")

).

2.7. Development of the Stand-Level Volume Models and Validation

A multivariate linear regression approach, as explained in Bohlin et al. [24], Straub et al. [22] and Montealegre et al. [16], was applied to develop the stand-level volume models. In total, 548 forest stands were used in the statistical analyses, out of which 274 were selected for the models’ development and the other 274 stands for the models’ validation. To reduce bias in stands’ selection, they were categorized according to age from youngest to oldest, and then ranked. Every odd-numbered stand was selected in the modeling while every even-numbered stand was selected in the validation. This way, both datasets contained stands of similar ages. All the statistical analyses were performed using the program STATISTICA 11 [55].

Prior to the modeling, the potential independent variables were selected based on Pearson correlation coefficient (r). Among a number of potential predictors (CHM metrics and FMP variables), only variables that were highly correlated with field estimated stand volume (r ≥ ±0.5) were included in the backward stepwise regression. This type of regression is commonly used for linear modeling of forest attributes based on either image-based [22,24] or ALS-based [16,56] metrics. To justify the use of linear regression models, four principal statistical assumptions [57] were tested: (i) linearity and additivity of the relationship between dependent and independent variables (scatterplots of predicted vs. observed values and predicted values vs. residuals); (ii) homoscedasticity (scatterplots of predicted values vs. residuals and residuals vs. independent variables); (iii) normality of the error distribution (Shapiro–Wilk test [58]); and (iv) independence (auto-correlation) of the errors (Durbin–Watson test [59]). To meet the above-mentioned conditions and achieve a linear relationship, the dependent variable (stand volume) was logarithmically transformed, which is in agreement with other similar studies [24,34]. By applying backward stepwise regressions and Akaike information criterion value [60], two the-best-fit models were developed and selected for each CHM (CHM₁, CHM₂, CHM₅) using the modeling dataset. The first model was developed solely from CHM metrics, whereas the second model was developed from both CHM metrics and FMP variables. The multivariate log-linear models had the following form:

$$\ln \left(V_m\right)={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+\dots +{\beta }_n{X}_n$$

(1)

where $V_m$ is the predicted stand volume (m³∙ha⁻¹); ${\beta }_0$ is intercept; ${\beta }_1$, ${\beta }_2$, …, ${\beta }_n$ are regression coefficients; and $X_1$, $X_2$, $X_3$, …, $X_n$ are independent variables (CHM metrics, and FMP variables).

In order to account for the bias in log-normal linear regression, bias correction ratio (CR, Equation (2)) proposed by Snowdon [61] was calculated for each model. Several methods for correcting bias introduced by logarithmic transformation described in literature [61,62,63,64] were considered. Snowdon’s CR was selected as the most suitable for application in this research. CR was calculated as the ratio of the mean of the observed stand volumes ($\overline{V}$) and the mean of the predicted stand volumes (${\overline{V}}_m$, Equation (2)). Bias corrected volume ($V^{\prime }$), was calculated using Equation (3).

$$CR=\frac{\overline{V}}{{\overline{V}}_m}$$

(2)

$$V^{\prime }=V_m\times CR$$

(3)

The models were validated using the independent validation dataset. The stand-level volume estimates were compared with the corresponding field data (stand volume from field inventories). The goodness-of-fit of the stand-level volume models was evaluated by the adjusted coefficient of determination (R²_adj) calculated using raw (log-transformed) data and graphical analyses (observed vs. predicted values, residuals vs. independent variables). To evaluate the accuracy of the models’ estimates, the root mean square error (RMSE) (Equation (4)) and relative root mean square error (RMSE_%) (Equation (5)), as well as the mean difference (MD) (Equation (6)) and relative mean difference (MD_%) (Equation (7)) were calculated:

$$RMSE=\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^n{\left(V{\text{'}}_i-V_i\right)}^2}{n}}$$

(4)

$$RMS{E}_{\%}=\frac{RMSE}{\overline{V}}\times 100$$

(5)

$$MD=\frac{{{\displaystyle \sum }}_{i=1}^n\left(V{\text{'}}_i-V_i\right)}{n}$$

(6)

$$M{D}_{\%}=\frac{MD}{\overline{V}}\times 100$$

(7)

where $V{\text{'}}_i$ is the predicted volume of stand i, $V_i$ is the observed (field estimated) volume of stand i, n is the number of stands, and $\overline{V}$ is the mean of the observed values.

The accuracy measures were calculated for the entire modeling and validation datasets as well as for each stand development stage. According to the Regulation on Forest Management (Official Gazette 111/06, 141/08), stands of the research area were classified as young (30–70-year-old), middle-aged (71–93-year-old), mature (94–120-year-old), and old stands (≥121-year-old).

Additionally, the performance of the regression models with double-log transformation, i.e., with logarithmically transformed dependent and independent variables, was also evaluated.

3. Results

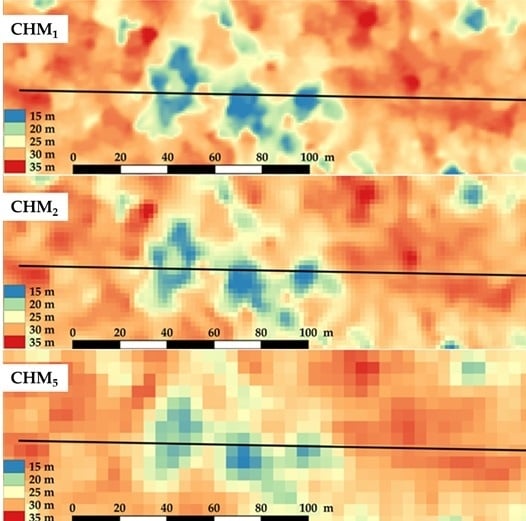
Examples of the generated CHMs for a sample area of 1.74 ha are given in Figure 2a–c. As expected, CHM₁ provides the highest discrimination of details. While all three CHMs enable visualization of larger gaps in the canopy, the smaller gaps cannot be determined by CHM₅ (Figure 2a–c). This is also evident in Figure 2d which shows a comparison of CHMs’ profiles through exemplary forest stand (marked with black lines in Figure 2a–c). CHM₂ provides a very similar profile with some minor differences from CHM₁ at the peak values. On the other hand, CHM₅ notably differ from CHM₁ and CHM₂. Namely, the areas of forest surface with greater heights are underestimated, while the areas of lower heights are considerably overestimated by CHM₅.

Table 5. Pearson correlation coefficients (r) between the potential predictors (CHM metrics and FMP variables) and stand volume from field measurements calculated on the modeling dataset.

Variable		Stand Volume (m3∙ha−1)
		CHM1	CHM2	CHM5
CHM metrics	hmean (m)	0.83 *	0.83 *	0.83 *
	hSD (m)	0.42 *	0.42 *	0.39 *
	hmode (m)	0.83 *	0.83 *	0.84 *
	hmax (m)	0.66 *	0.67 *	0.70 *
	hmin (m)	0.13 *	0.13 *	0.13 *
	p5 (m)	0.43 *	0.43 *	0.47 *
	p10 (m)	0.59 *	0.59 *	0.62 *
	p20 (m)	0.73 *	0.73 *	0.74 *
	p25 (m)	0.76 *	0.76 *	0.77 *
	p30 (m)	0.78 *	0.79 *	0.79 *
	p40 (m)	0.82 *	0.82 *	0.82 *
	p50 (m)	0.84 *	0.84 *	0.83 *
	p60 (m)	0.84 *	0.84 *	0.84 *
	p70 (m)	0.84 *	0.84 *	0.84 *
	p75 (m)	0.84 *	0.84 *	0.84 *
	p80 (m)	0.84 *	0.84 *	0.84 *
	p90 (m)	0.83 *	0.83 *	0.83 *
	p95 (m)	0.83 *	0.83 *	0.83 *
	p99 (m)	0.80 *	0.81 *	0.81 *
	CC10	0.17 *	0.17 *	0.18 *
	CC20	0.79 *	0.79 *	0.79 *
	CC30	0.54 *	0.54 *	0.51 *
	CC40	0.07 ns	0.07 ns	0.04 ns
	k3D	0.40 *	0.40 *	0.36 *
FMP variables	SA (years)	0.77 *	0.77 *	0.77 *
	ST	−0.19 *	−0.19 *	−0.19 *
	SI	0.09 ns	0.09 ns	0.09 ns
	PT	0.17 *	0.17 *	0.17 *

* Correlations are significant at p < 0.05; ns: not significant correlations (p ≥ 0.05).

shows the Pearson correlation coefficients (r) between stand volume from measurements from field inventories and potential predictors (i.e., stand-level metrics extracted from each CHM and variables obtained from FMPs), whereas the correlation coefficients between the potential predictors (independent variables) are presented in

Table A1. Pearson correlation coefficients (r) between the independent variables (CHM metrics and FMP variables) calculated on the modeling dataset for the each CHM resolution (1 m—CHM₁, 2 m—CHM₂, 5 m—CHM₅). Correlations marked with * are significant at p < 0.05.

CHM1

hmean

hSD

hmode

hmax

hmin

p5

p10

p20

p25

p30

p40

p50

p60

p70

p75

p80

p90

p95

p99

CC10

CC20

CC30

CC40

k3D

SA

ST

SI

PT

hmean

1.00

0.36 *

0.95 *

0.82 *

0.15 *

0.63 *

0.80 *

0.93 *

0.96 *

0.97 *

0.99 *

0.99 *

0.99 *

0.98 *

0.97 *

0.97 *

0.95 *

0.94 *

0.92 *

0.29 *

0.92 *

0.70 *

0.14 *

0.37 *

0.80 *

−0.26 *

0.14 *

0.19 *

hSD

1.00

0.57 *

0.60 *

−0.32 *

−0.42 *

−0.24 *

0.03

0.12

0.20 *

0.33 *

0.42 *

0.49 *

0.54 *

0.56 *

0.57 *

0.61 *

0.62 *

0.64 *

−0.45 *

0.24 *

0.51 *

0.37 *

0.93 *

0.60 *

−0.36 *

0.13 *

0.26 *

hmode

1.00

0.85 *

0.05

0.44 *

0.62 *

0.80 *

0.85 *

0.88 *

0.94 *

0.97 *

0.98 *

0.98 *

0.98 *

0.98 *

0.97 *

0.97 *

0.95 *

0.16 *

0.85 *

0.73 *

0.20 *

0.56 *

0.84 *

−0.32 *

0.16 *

0.22 *

hmax

1.00

−0.11

0.32 *

0.48 *

0.65 *

0.70 *

0.74 *

0.80 *

0.83 *

0.85 *

0.86 *

0.87 *

0.87 *

0.88 *

0.89 *

0.90 *

0.08

0.69 *

0.73 *

0.32 *

0.64 *

0.78 *

−0.35 *

0.14 *

0.23 *

hmin

1.00

0.40 *

0.31 *

0.22 *

0.19 *

0.17 *

0.13 *

0.11

0.09

0.08

0.07

0.07

0.06

0.05

0.03

0.31 *

0.18 *

0.03

−0.11

−0.24 *

0.01

−0.02

−0.10

−0.02

p5

1.00

0.93 *

0.79 *

0.74 *

0.70 *

0.63 *

0.57 *

0.52 *

0.49 *

0.47 *

0.46 *

0.43 *

0.41 *

0.38 *

0.71 *

0.66 *

0.28 *

−0.14 *

−0.33 *

0.29 *

−0.01

0.02

−0.01

p10

1.00

0.94 *

0.91 *

0.88 *

0.81 *

0.75 *

0.71 *

0.67 *

0.65 *

0.64 *

0.61 *

0.59 *

0.56 *

0.63 *

0.79 *

0.42 *

−0.07

−0.19 *

0.45 *

−0.06

0.06

0.05

p20

1.00

0.99 *

0.98 *

0.95 *

0.91 *

0.87 *

0.84 *

0.83 *

0.81 *

0.78 *

0.76 *

0.74 *

0.49 *

0.89 *

0.56 *

0.03

0.05

0.63 *

−0.13 *

0.11

0.10

p25

1.00

0.99 *

0.97 *

0.94 *

0.91 *

0.88 *

0.87 *

0.86 *

0.83 *

0.81 *

0.79 *

0.44 *

0.90 *

0.60 *

0.07

0.13 *

0.68 *

−0.16 *

0.12 *

0.12 *

p30

1.00

0.99 *

0.96 *

0.94 *

0.92 *

0.91 *

0.89 *

0.87 *

0.86 *

0.83 *

0.40 *

0.91 *

0.64 *

0.09

0.21 *

0.72 *

−0.18 *

0.13 *

0.14 *

p40

1.00

0.99 *

0.98 *

0.97 *

0.96 *

0.95 *

0.93 *

0.92 *

0.90 *

0.31 *

0.92 *

0.69 *

0.13 *

0.33 *

0.78 *

−0.23 *

0.14 *

0.17 *

p50

1.00

0.99 *

0.99 *

0.98 *

0.98 *

0.97 *

0.95 *

0.93 *

0.26 *

0.91 *

0.72 *

0.17 *

0.42 *

0.82 *

−0.27 *

0.15 *

0.19 *

p60

1.00

0.99 *

0.99 *

0.99 *

0.98 *

0.97 *

0.96 *

0.22 *

0.90 *

0.73 *

0.19 *

0.49 *

0.84 *

−0.30 *

0.15 *

0.21 *

p70

1.00

0.99 *

0.99 *

0.99 *

0.99 *

0.97 *

0.18 *

0.88 *

0.74 *

0.20 *

0.54 *

0.85 *

−0.32 *

0.15 *

0.22 *

p75

1.00

0.99 *

0.99 *

0.99 *

0.98 *

0.16 *

0.88 *

0.74 *

0.21 *

0.56 *

0.85 *

−0.33 *

0.15 *

0.23 *

p80

1.00

0.99 *

0.99 *

0.98 *

0.15 *

0.87 *

0.75 *

0.22 *

0.58 *

0.86 *

−0.34 *

0.15 *

0.24 *

p90

1.00

0.99 *

0.99 *

0.12 *

0.86 *

0.75 *

0.23 *

0.61 *

0.86 *

−0.35 *

0.15 *

0.24 *

p95

1.00

0.99 *

0.10

0.84 *

0.76 *

0.23 *

0.63 *

0.86 *

−0.37 *

0.15 *

0.25 *

p99

1.00

0.08

0.82 *

0.76 *

0.26 *

0.65 *

0.86 *

−0.39 *

0.14 *

0.25 *

CC10

1.00

0.34 *

0.05

−0.09

−0.39 *

0.04

0.06

0.02

−0.08

CC20

1.00

0.40 *

0.04

0.25 *

0.76 *

−0.08

0.19 *

0.13 *

CC30

1.00

0.28 *

0.52 *

0.55 *

−0.49 *

−0.03

0.21 *

CC40

1.00

0.40 *

0.18 *

−0.18 *

−0.04

0.19 *

k3D

1.00

0.61 *

−0.41 *

0.10 *

0.29 *

SA

1.00

−0.23 *

0.37 *

0.21 *

ST

1.00

0.04

−0.30 *

SI

1.00

−0.16 *

PT

1.00

CHM2

hmean

hSD

hmode

hmax

hmin

p5

p10

p20

p25

p30

p40

p50

p60

p70

p75

p80

p90

p95

p99

CC10

CC20

CC30

CC40

k3D

SA

ST

SI

PT

hmean

1.00

0.35 *

0.95 *

0.82 *

0.15 *

0.63 *

0.80 *

0.93 *

0.96 *

0.97 *

0.99 *

0.99 *

0.99 *

0.98 *

0.97 *

0.97 *

0.96 *

0.94 *

0.93 *

0.29 *

0.92 *

0.70 *

0.12 *

0.36 *

0.80 *

−0.26 *

0.14 *

0.19 *

hSD

1.00

0.56 *

0.60 *

−0.34 *

−0.42 *

−0.24 *

0.03

0.12

0.19 *

0.32 *

0.41 *

0.48 *

0.53 *

0.55 *

0.56 *

0.60 *

0.62 *

0.64 *

−0.44 *

0.24 *

0.50 *

0.33 *

0.93 *

0.59 *

−0.35 *

0.13 *

0.26 *

hmode

1.00

0.86 *

0.06

0.45 *

0.63 *

0.81 *

0.86 *

0.89 *

0.94 *

0.97 *

0.98 *

0.99 *

0.99 *

0.98 *

0.98 *

0.97 *

0.96 *

0.17 *

0.85 *

0.73 *

0.20 *

0.54 *

0.84 *

−0.32 *

0.15 *

0.22 *

hmax

1.00

−0.09

0.33 *

0.49 *

0.66 *

0.71 *

0.74 *

0.80 *

0.83 *

0.85 *

0.87 *

0.87 *

0.88 *

0.89 *

0.89 *

0.91 *

0.09

0.69 *

0.73 *

0.30 *

0.63 *

0.79 *

−0.35 *

0.15 *

0.24 *

hmin

1.00

0.43 *

0.33 *

0.22 *

0.19 *

0.17 *

0.13 *

0.11

0.09

0.08

0.07

0.07

0.06

0.05

0.04

0.33 *

0.18 *

0.03

−0.10

−0.24 *

0.02

−0.02

−0.10

−0.02

p5

1.00

0.94 *

0.79 *

0.74 *

0.70 *

0.63 *

0.57 *

0.53 *

0.50 *

0.48 *

0.47 *

0.44 *

0.42 *

0.39 *

0.71 *

0.66 *

0.28 *

−0.12

−0.33 *

0.30 *

−0.01

0.04

−0.02

p10

1.00

0.94 *

0.90 *

0.87 *

0.80 *

0.75 *

0.71 *

0.67 *

0.66 *

0.64 *

0.61 *

0.59 *

0.56 *

0.65 *

0.79 *

0.41 *

−0.07

−0.19 *

0.45 *

−0.07

0.07

0.04

p20

1.00

0.99 *

0.98 *

0.95 *

0.91 *

0.88 *

0.85 *

0.83 *

0.82 *

0.79 *

0.77 *

0.74 *

0.50 *

0.89 *

0.56 *

0.02

0.04

0.63 *

−0.14 *

0.11

0.10

p25

1.00

0.99 *

0.97 *

0.94 *

0.92 *

0.89 *

0.88 *

0.86 *

0.84 *

0.82 *

0.79 *

0.45 *

0.90 *

0.60 *

0.05

0.12 *

0.68 *

−0.16 *

0.12 *

0.12 *

p30

1.00

0.99 *

0.97 *

0.94 *

0.92 *

0.91 *

0.90 *

0.87 *

0.86 *

0.83 *

0.41 *

0.91 *

0.63 *

0.08

0.19 *

0.72 *

−0.19 *

0.13 *

0.14 *

p40

1.00

0.99 *

0.98 *

0.97 *

0.96 *

0.95 *

0.93 *

0.92 *

0.90 *

0.32 *

0.92 *

0.68 *

0.11

0.31 *

0.78 *

−0.23 *

0.14 *

0.17 *

p50

1.00

0.99 *

0.99 *

0.98 *

0.98 *

0.97 *

0.95 *

0.93 *

0.26 *

0.91 *

0.71 *

0.14 *

0.40 *

0.81 *

−0.27 *

0.15 *

0.19 *

p60

1.00

0.99 *

0.99 *

0.99 *

0.98 *

0.97 *

0.96 *

0.22 *

0.90 *

0.72 *

0.16 *

0.47 *

0.83 *

−0.30 *

0.15 *

0.21 *

p70

1.00

0.99 *

0.99 *

0.99 *

0.99 *

0.97 *

0.19 *

0.89 *

0.73 *

0.18 *

0.52 *

0.85 *

−0.32 *

0.15 *

0.22 *

p75

1.00

0.99 *

0.99 *

0.99 *

0.98 *

0.17 *

0.88 *

0.74 *

0.19 *

0.54 *

0.85 *

−0.33 *

0.15 *

0.23 *

p80

1.00

0.99 *

0.99 *

0.98 *

0.15 *

0.87 *

0.74 *

0.19 *

0.56 *

0.86 *

−0.33 *

0.15 *

0.23 *

p90

1.00

0.99 *

0.99 *

0.13 *

0.86 *

0.74 *

0.20 *

0.59 *

0.86 *

−0.35 *

0.15 *

0.24 *

p95

1.00

1.00

0.11

0.85 *

0.75 *

0.21 *

0.61 *

0.86 *

−0.37 *

0.15 *

0.25 *

p99

1.00

0.09

0.82 *

0.76 *

0.23 *

0.64 *

0.86 *

−0.39 *

0.14 *

0.25 *

CC10

1.00

0.34 *

0.06

−0.07

−0.39 *

0.04

0.05

0.02

−0.08

CC20

1.00

0.40 *

0.03

0.24 *

0.77 *

−0.08

0.20 *

0.13 *

CC30

1.00

0.25 *

0.51 *

0.55 *

−0.49 *

−0.03

0.20 *

CC40

1.00

0.35 *

0.16 *

−0.17 *

−0.04

0.17 *

k3D

1.00

0.60 *

−0.41 *

0.09

0.29 *

SA

1.00

−0.23 *

0.37 *

0.21 *

ST

1.00

0.04

−0.30 *

SI

1.00

−0.16 *

PT

1.00

CHM5

hmean

hSD

hmode

hmax

hmin

p5

p10

p20

p25

p30

p40

p50

p60

p70

p75

p80

p90

p95

p99

CC10

CC20

CC30

CC40

k3D

SA

ST

SI

PT

hmean

1.00

0.30 *

0.96 *

0.85 *

0.17 *

0.69 *

0.84 *

0.95 *

0.97 *

0.98 *

0.99 *

0.99 *

0.99 *

0.98 *

0.98 *

0.97 *

0.96 *

0.95 *

0.93 *

0.30 *

0.92 *

0.67 *

0.05

0.26 *

0.80 *

−0.26 *

0.14 *

0.19 *

hSD

1.00

0.49 *

0.56 *

−0.40 *

−0.42 *

−0.24 *

0.01

0.09

0.16 *

0.28 *

0.36 *

0.42 *

0.47 *

0.49 *

0.51 *

0.54 *

0.56 *

0.58 *

−0.45 *

0.20 *

0.44 *

0.15 *

0.91 *

0.55 *

−0.34 *

0.12 *

0.25 *

hmode

1.00

0.88 *

0.07

0.52 *

0.69 *

0.84 *

0.88 *

0.91 *

0.95 *

0.97 *

0.98 *

0.98 *

0.98 *

0.98 *

0.97 *

0.97 *

0.95 *

0.20 *

0.86 *

0.70 *

0.11

0.44 *

0.83 *

−0.30 *

0.15 *

0.22 *

hmax

1.00

−0.04

0.42 *

0.57 *

0.71 *

0.75 *

0.78 *

0.83 *

0.86 *

0.88 *

0.89 *

0.90 *

0.90 *

0.91 *

0.92 *

0.94 *

0.14 *

0.72 *

0.74 *

0.15 *

0.52 *

0.79 *

−0.38 *

0.12 *

0.25 *

hmin

1.00

0.46 *

0.35 *

0.24 *

0.21 *

0.19 *

0.15 *

0.13 *

0.11

0.10

0.09

0.08

0.07

0.06

0.05

0.37 *

0.20 *

0.04

−0.03

−0.30 *

0.03

−0.02

−0.09

−0.03

p5

1.00

0.95 *

0.82 *

0.78 *

0.74 *

0.68 *

0.63 *

0.59 *

0.56 *

0.54 *

0.53 *

0.50 *

0.48 *

0.46 *

0.68 *

0.69 *

0.32 *

−0.03

−0.37 *

0.35 *

−0.04

0.06

0.01

p10

1.00

0.95 *

0.92 *

0.89 *

0.84 *

0.79 *

0.76 *

0.72 *

0.71 *

0.69 *

0.66 *

0.64 *

0.62 *

0.62 *

0.81 *

0.44 *

−0.01

−0.24 *

0.50 *

−0.09

0.08

0.07

p20

1.00

0.99 *

0.99 *

0.96 *

0.93 *

0.90 *

0.87 *

0.86 *

0.85 *

0.82 *

0.80 *

0.77 *

0.48 *

0.89 *

0.56 *

0.01

−0.02

0.65 *

−0.15 *

0.11

0.12 *

p25

1.00

0.99 *

0.98 *

0.95 *

0.93 *

0.91 *

0.89 *

0.88 *

0.86 *

0.84 *

0.81 *

0.44 *

0.90 *

0.59 *

0.03

0.06

0.69 *

−0.18 *

0.12 *

0.13 *

p30

1.00

0.99 *

0.97 *

0.95 *

0.93 *

0.92 *

0.91 *

0.89 *

0.87 *

0.85 *

0.41 *

0.91 *

0.62 *

0.03

0.12 *

0.72 *

−0.19 *

0.13 *

0.15 *

p40

1.00

0.99 *

0.98 *

0.97 *

0.96 *

0.96 *

0.94 *

0.92 *

0.90 *

0.33 *

0.91 *

0.65 *

0.05

0.23 *

0.78 *

−0.23 *

0.14 *

0.17 *

p50

1.00

0.99 *

0.99 *

0.98 *

0.98 *

0.97 *

0.95 *

0.93 *

0.28 *

0.91 *

0.68 *

0.06

0.31 *

0.81 *

−0.26 *

0.15 *

0.19 *

p60

1.00

0.99 *

0.99 *

0.99 *

0.98 *

0.97 *

0.96 *

0.24 *

0.90 *

0.69 *

0.07

0.37 *

0.83 *

−0.29 *

0.15 *

0.20 *

p70

1.00

0.99 *

0.99 *

0.99 *

0.99 *

0.97 *

0.20 *

0.89 *

0.70 *

0.08

0.42 *

0.84 *

−0.31 *

0.15 *

0.22 *

p75

1.00

0.99 *

0.99 *

0.99 *

0.98 *

0.19 *

0.89 *

0.70 *

0.09

0.44 *

0.85 *

−0.32 *

0.15 *

0.22 *

p80

1.00

0.99 *

0.99 *

0.98 *

0.17 *

0.88 *

0.71 *

0.09

0.46 *

0.85 *

−0.33 *

0.15 *

0.23 *

p90

1.00

0.99 *

0.99 *

0.14 *

0.86 *

0.71 *

0.09

0.50 *

0.86 *

−0.35 *

0.15 *

0.24 *

p95

1.00

0.99 *

0.13 *

0.85 *

0.72 *

0.10

0.53 *

0.86 *

−0.36 *

0.14 *

0.24 *

p99

1.00

0.12 *

0.82 *

0.73 *

0.10

0.55 *

0.85 *

−0.38 *

0.13 *

0.25 *

CC10

1.00

0.35 *

0.07

0.01

−0.44 *

0.05

0.05

0.03

−0.07

CC20

1.00

0.37 *

0.02

0.17 *

0.77 *

−0.09

0.20 *

0.13 *

CC30

1.00

0.11

0.42 *

0.51 *

−0.48 *

−0.05

0.19 *

CC40

1.00

0.15 *

0.07

−0.09

−0.06

0.14 *

k3D

1.00

0.52 *

−0.38 *

0.06

0.25 *

SA

1.00

−0.23 *

0.37 *

0.21 *

ST

1.00

0.04

−0.30 *

SI

1.00

−0.16 *

PT

1.00

. Among 24 considered CHM metrics, for all CHMs, the same 18 metrics (h_mean, h_mode, h_max, p₁₀, p₂₀, …, p₉₉, CC₂₀, CC₃₀) fulfill required criteria (p < 0.05, r ≥ ±0.5) for entering the further modeling. Out of four FMP variables, a strong correlation with stand volume is identified only for stand age (SA). All selected variables result in very similar, almost identical r values for all CHMs. Accordingly, for each CHM, 19 identical potential independent variables (18 CHM metrics and one FMP variable) are selected and included in the backward stepwise regression.

For each CHM, two best fit stand-level volume models were developed and selected based on the backward stepwise regression and Akaike information criterion (

Table A2. Description (selected independent variables, estimated parameters, standard errors and significance values) of six selected stand-level volume models, including Snowdon’s correction ratio (CR) for bias correction (Equations (2) and (3)). Two models were selected for each CHM resolution (1 m—CHM₁, 2 m—CHM₂, 5 m—CHM₅). In the model name, number denotes a CHM resolution for which the model was developed, whereas letter denotes whether the model was derived solely from CHM metrics as independent variables (A), or from both CHM metrics and FMP variables (B).

Model	Equation	Parameters
		Symbol	Value	Standard Error	p Value
1-A	ln(Vm) = β0 + β1 × hmax + β2 × p80 + β3 × CC30	β0	3.88550	0.07654	<0.00001
		β1	−0.01524	0.00332	<0.00001
		β2	0.09532	0.00392	<0.00001
		β3	−0.45408	0.05968	<0.00001
		CR	1.00769
1-B	ln(Vm) = β0 + β1 × hmax + β2 × p80 + β3 × CC30 + β4 × SA	β0	4.06198	0.08733	<0.00001
		β1	−0.01789	0.00320	<0.00001
		β2	0.08348	0.00488	<0.00001
		β3	−0.38302	0.06098	<0.00001
		β4	0.00241	0.00062	<0.00001
		CR	1.00731
2-A	ln(Vm) = β0 + β1 × hmax + β2 × p50 + β3 × p95 + β4 × CC30	β0	3.08080	0.07612	<0.00001
		β1	−0.01737	0.00346	<0.00001
		β2	0.03844	0.00641	<0.00001
		β3	0.06154	0.00729	<0.00001
		β4	−0.45780	0.05839	<0.00001
		CR	1.00750
2-B	ln(Vm) = β0 + β1 × hmax + β2 × p70 + β3 × CC30 + β4 × SA	β0	4.10954	0.08453	<0.00001
		β1	−0.01720	0.00322	<0.00001
		β2	0.08093	0.00462	<0.00001
		β3	−0.35325	0.05892	<0.00001
		β4	0.00293	0.00059	<0.00001
		CR	1.00716
5-A	ln(Vm) = β0 + β1 × hmax + β2 × p30 + β3 × p90 + β4 × CC30	β0	3.89013	0.08219	<0.00001
		β1	−0.01848	0.00463	0.00008
		β2	0.01605	0.00441	0.00033
		β3	0.08180	0.00622	<0.00001
		β4	−0.40899	0.00581	<0.00001
		CR	1.00778
5-B	ln(Vm) = β0 + β1 × hmax + β2 × p25 + β3 × p90 + β4 × CC30 + β5 × SA	β0	4.07798	0.09199	<0.00001
		β1	−0.02041	0.00451	<0.00001
		β2	0.01747	0.00392	0.00001
		β3	0.06718	0.00697	<0.00001
		β4	−0.33150	0.05942	<0.00001
		β5	0.00262	0.00063	0.00005
		CR	1.00742

V_m: stand volume prior to correction for Snowdon’s correction ratio; h_max: maximum height; p₂₅: 25th height percentile; p₃₀: 30th height percentile; p₅₀: 50th height percentile; p₇₀: 70th height percentile; p₈₀: 80th height percentile; p₉₀: 90th height percentile; p₉₅: 95th height percentile; CC₃₀: the ratio between the area of canopy with height greater than 30 m and the stand area; SA: stand age; β₀: intercept; β₁, β₂, β₃, β₄, and β₅: regression coefficients; CR: Snowdon’s correction ratio.

). Development of the first model was based only on previously selected CHM metrics (h_mean, h_mode, h_max, p₁₀, p₂₀, …, p₉₉, CC₂₀, CC₃₀), whereas in the development of the second model SA was also included. All models and their parameters exhibit highly significant results (p < 0.001). A similar set of independent variables was included in all models. Namely, in all models one or two height percentiles were included, along with h_max and CC₃₀.

Table 6. Results of stepwise regression (modeling dataset) and validation results (validation dataset) for six selected stand-level volume models described in Table A2.

Model	Variables Included	Modeling Dataset					Validation Dataset
		R2adj	RMSE (m3∙ha−1)	RMSE% (%)	MD (m3∙ha−1)	MD% (%)	R2adj	RMSE (m3∙ha−1)	RMSE% (%)	MD (m3∙ha−1)	MD% (%)
1-A	hmax, p80, CC30	0.83	52.01	12.48	0.00	0.00	0.82	55.40	13.14	−3.75	−0.89
1-B	hmax, p80, CC30, SA	0.84	50.84	12.20	0.00	0.00	0.83	53.08	12.59	−4.10	−0.97
2-A	hmax, p50, p95, CC30	0.83	51.59	12.38	0.00	0.00	0.81	56.00	13.28	−3.29	−0.78
2-B	hmax, p70, CC30, SA	0.84	50.10	12.02	0.00	0.00	0.84	52.83	12.53	−3.86	−0.92
5-A	hmax, p30, p90, CC30	0.83	51.60	12.38	0.00	0.00	0.81	55.92	13.26	−3.96	−0.94
5-B	hmax, p25, p90, CC30, SA	0.84	50.26	12.06	0.00	0.00	0.83	53.31	12.64	−4.12	−0.98

R²_adj: adjusted coefficient of determination; RMSE: root mean square error; RMSE_%: relative root mean square error; MD: mean difference; MD_%: relative mean difference.

shows results of stepwise regression and validation for six selected stand-level volume models. The R²_adj for the modeling dataset for the first (1-A, 2-A, 5-A; hereinafter referred to as A models) and second (1-B, 2-B, 5-B; hereinafter referred to as B models) group of models is 0.83 and 0.84, respectively, indicating a good model fit (Table 6). For the validation dataset, both groups of models exhibit just slightly lower R²_adj values than for modeling dataset. R²_adj for modeling and validation dataset differ by <0.01 (model 2-B) or by only 0.01 (models 1-A, 1-B, 5-B) and 0.02 (models 2-A, 5-A). In addition, the accuracy measures (RMSE, RMSE_%, MD, MD_%) calculated for the validation dataset show just slightly less accurate volume estimates than for the modeling dataset. The differences between the RMSE_% values calculated for the modeling and validation datasets range from 0.39% to 0.90%, whereas the differences between the MD_% values for the two datasets range from −0.78% to −0.98%. A good agreement between the results obtained for the modeling and validation datasets indicates that the regression models provide reliable predictions.

According to the validation results (Table 6), the best performing model is model 2-B (R²_adj = 0.84, RMSE_% = 12.53%) with metrics extracted from CHM₂ (h_max, p₇₀, CC₃₀) and SA as independent variables. The worst performing model is model 2-A (R²_adj = 0.81, RMSE_% = 13.28%) with metrics extracted from CHM₂ (h_max, p₅₀, p₉₅, CC₂₀) as only independent variables. The same trend is also confirmed in the scatterplots (Figure 3), where it can be seen that model 2-B produces the smallest, and model 2-A the largest deviations from the fitted line. Furthermore, the MD and MD_% values are negative for all models and range from −0.78% to −0.98% indicating that the stand volume is on average slightly underestimated. According to Figure 3, the negative MD and MD_% values result from several larger residuals in the stands with the observed volume >500 m³∙ha⁻¹. To further characterize models’ performance and relationships between dependent and independent variables, scatterplots of residuals vs. independent variables are given in Appendix B (Figure A1).

Observed by models’ type, it can be noted that models developed solely from CHM metrics (A models) produce slightly less precise volume estimates than the models developed from both CHM metrics and SA (B models) (Table 6). This can be observed for all CHMs. Compared to models 1-A, 2-A, and 5-A, the R²_adj values for models 1-B, 2-B, and 5-B are increased by 0.1, 0.3, and 0.2, respectively, whereas the RMSE_% values are decreased by 0.55%, 0.75%, and 0.62%, respectively. However, compared to models 1-A, 2-A, and 5-A, the MD_% values for models 1-B, 2-B, and 5-B are increased by −0.08, −0.14, and −0.04, respectively.

The obtained results are similar for all three CHM resolutions (1 m—CHM₁, 2 m—CHM₂, and 5 m—CHM₅) (Table 6). For instance, the differences between the RMSE_% for the best performing model 2-B derived using metrics extracted from CHM₂, and models derived using metrics extracted from CHM₁ (model 1-B) and CHM₅ (model 5-B) are 0.06% and 0.11%, respectively.

Figure 4 shows validation results by stand development stages. Overall, the highest RMSEs_% are calculated for young stands (16.69%–20.65%), followed by mature (12.86%–13.45%) and middle-aged stands (10.82%–12.73%), whereas the lowest RMSE_%, i.e., the highest accuracy, are calculated for old stands (10.30%–11.42%). Except for the young stands, for which somewhat greater differences between RMSE_% of A and B models can be noticed (3.35%–3.96%), the differences between A and B models for all other development stages are considerably smaller (middle-aged: 0.87%–1.45%, mature: 0.26%–0.50%, old: 0.55%–0.84%). Similar to the complete dataset analyses, the differences between the CHM datasets of different resolutions (1 m, 2 m, and 5 m) for each development stage are negligible.

Unlike the RMSE_% values, the MD_% values vary noticeably for different development stages, as well as for different models’ types within each development stage. For the young stands, the values are overestimated for both models, ranging from 3.83% to 5.08% and from 0.84% to 1.93% for the A and B models, respectively. For the middle-aged stands, the MD_% values are also overestimated for the A models ranging between 4.02% to 4.86%, while the MD_% values for the B models are very close to 0, ranging from −0.56% to 0.27%. For these two development stages (young, middle-aged) it is evident that the inclusion of SA into the B models considerably decreases the models’ bias (underestimations). On the other hand, for the mature stands, both model types result in underestimated MD_% values with a similar range. The MD_% values for the A and B models range from −1.66% to −2.06% and from −1.57% to −1.99%, respectively. Furthermore, for the old stands, A models produce the underestimated values (−1.10% to −2.87%), whereas the inclusion of SA into the B models results in decreased MD_% values, ranging from −0.64% to 1.07%.

In general, the regression models with the double-log transformation used to model stand-level volume do not yield any better results than the log-linear regression models. Detailed results of the double-log analysis can be found in Appendix C (

Table A3. Results of the stepwise regression (on the modeling dataset) and of the validation (on the validation dataset) for the six selected stand-level volume models (double-log models, i.e., models with the logarithmically transformed dependent and independent variables).

Model	Variables Included	Modeling Dataset					Validation Dataset
		R2adj	RMSE (m3∙ha−1)	RMSE% (%)	MD (m3∙ha−1)	MD% (%)	R2adj	RMSE (m3∙ha−1)	RMSE% (%)	MD (m3∙ha−1)	MD% (%)
1-A′	hmax, p80, CC20	0.83	52.02	12.48	0.00	0.00	0.81	56.08	13.30	−3.13	−0.74
1-B′	hmax, p80, CC20, SA	0.84	50.28	12.07	0.00	0.00	0.83	52.93	12.55	−3.76	−0.89
2-A′	hmax, p40, p50, CC30	0.83	52.32	12.56	0.00	0.00	0.80	57.39	13.61	−4.29	−1.02
2-B′	hmax, p25, p40, p50, SA	0.85	49.70	11.93	0.00	0.00	0.83	53.24	12.63	−4.71	−1.12
5-A′	hmax, p80, CC30	0.82	52.46	12.59	0.00	0.00	0.81	56.74	13.46	−4.81	−1.14
5-B′	hmax, p25, p90, SA	0.84	50.97	12.23	0.00	0.00	0.83	53.04	12.58	−4.65	−1.10

R²_adj: adjusted coefficient of determination; RMSE: root mean square error; RMSE_%: relative root mean square error; MD: mean difference; MD_%: relative mean difference.

and

Table A4. Description (selected independent variables, estimated parameters, standard errors and significance values) of six selected stand-level volume models (double-log models, i.e., models with the logarithmically transformed dependent and independent variables), including Snowdon’s correction ratio (CR) for bias correction (Equations (2) and (3)). Two models were selected for each CHM resolution (1 m—CHM₁, 2 m—CHM₂, 5 m—CHM₅). In the model name, number denotes a CHM resolution for which the model was developed, whereas letter denotes whether the model was derived solely from CHM metrics as independent variables (A′), or from both CHM metrics and FMP variables (B′).

Model	Equation	Parameters
		Symbol	Value	Standard Error	p Value
1-A′	ln(Vm) = β0 + β1 × hmax + β2 × p80 + β3 × CC20	β0	2.47009	0.31889	<0.00001
		β1	−0.45194	0.11086	0.00006
		β2	1.46944	0.15866	<0.00001
		β3	0.42649	0.09907	0.00002
		CR	1.00789
1-B′	ln(Vm) = β0 + β1 × hmax + β2 × p80 + β3 × CC20 + β4 × SA	β0	2.55290	0.30744	<0.00001
		β1	−0.50482	0.10729	<0.00001
		β2	1.16292	0.16587	<0.00001
		β3	0.32178	0.09789	0.00115
		β4	0.25905	0.05470	<0.00001
		CR	1.00761
2-A′	ln(Vm) = β0 + β1 × hmax + β2 × p40 + β3 × p50 + β4 × CC30	β0	2.65916	0.34331	<0.00001
		β1	−0.42496	0.10948	0.00013
		β2	−2.23820	0.49331	<0.00001
		β3	3.70810	0.56427	<0.00001
		β4	0.07661	0.01840	0.00004
		CR	1.00817
2-B′	ln(Vm) = β0 + β1 × hmax + β2 × p25 + β3 × p40 + β4 × p50 + β5 × SA	β0	1.85652	0.18705	<0.00001
		β1	−0.60472	0.10253	<0.00001
		β2	1.72442	0.47945	0.00038
		β3	−6.93192	1.65233	0.00004
		β4	6.61737	1.24758	<0.00001
		β 5	0.35602	0.05236	<0.00001
		CR	1.00700
5-A′	ln(Vm) = β0 + β1 × hmax + β2 × p80 + β3 × CC30	β0	2.26908	0.34361	<0.00001
		β1	−0.44165	0.13458	0.00117
		β2	1.58609	0.16020	<0.00001
		β3	0.05308	0.01528	0.00060
		CR	1.00837
5-B′	ln(Vm) = β0 + β1 × hmax + β2 × p25 + β3 × p90 + β4 × SA	β0	1.61421	0.21136	<0.00001
		β1	−0.55506	0.12936	0.00003
		β2	0.35404	0.08479	0.00004
		β3	1.11244	0.18175	<0.00001
		β4	0.31759	0.05466	<0.00001
		CR	1.00745

V_m: stand volume prior to correction for Snowdon’s correction ratio; h_max: maximum height; p₂₅: 25th height percentile; p₄₀: 40th height percentile; p₅₀: 50th height percentile; p₈₀: 80th height percentile; p₉₀: 90th height percentile; CC₃₀: the ratio between the area of canopy with height greater than 30 m and the stand area; SA: stand age; β₀: intercept, β₁, β₂, β₃, β₄, and β₅: regression coefficients; CR: Snowdon’s correction ratio.

, Figure A2 and Figure A3).

4. Discussion

Despite the proven applicability of ALS technology for operational forest inventory, the high-cost of ALS surveys is a limiting factor that impedes its widespread use. In many countries, including Croatia, the national ALS surveys have not been conducted yet. Thus, aerial images, which are regularly updated in many European countries [22], present an alternative to ALS technology. The digital terrain data (breaklines, formlines, spot heights and mass points) used to generate DTM in this study present the national standard and they are the only available DTM data for Croatia. It is well known that the photogrammetrically-based (stereo-mapping) DTM of forested areas has a lower accuracy than ALS-based DTM because of the ground being obscured by vegetation [12,21]. However, since the research area in this study is characterized by flat terrain, it can be assumed that DTM derived from digital terrain data could be of satisfactory accuracy. Nevertheless, many countries may benefit from studies like this one where the main concern is to explore the applicability of the existing photogrammetric data to generate CHM and to estimate stand volume of different forest types.

Previous studies [3,10,24,30,34], regardless of the data used (ALS or aerial images), mostly utilized plot-level metrics to estimate volume at stand level, while in this study we have estimated the stand volume based on the stand-level metrics. To the best of the authors’ knowledge, this research is the first that has focused on stand-level metrics extracted from the image-based CHM, i.e., from CHM that is completely derived from photogrammetric data. Since it is completely based on existing data (aerial images, DTM data, field data), this approach is considered as a low-cost alternative. As such, the study serves as a basis for other studies where ALS technology is limited (i.e., in countries and regions which do not have access to ALS data, and will probably not have access in the near future either). Furthermore, to apply this stand-level approach, the acquisition of precise location (which is not an easy task in dense forests) of the reference field plots is not necessary. This presents an additional benefit for inventories of large areas to be completed in a short period of time. It should be emphasized that the aim of this approach is not to replace field inventories or plot-level remote sensing inventories which also requires a certain amount of field reference data collected at the same time as remote sensing data. As already noted, regular field forest inventories are usually conducted at 10-year intervals, whereas aerial images in Croatia and many other European countries are regularly updated every 3–5 years. Therefore, provided that aerial survey and regular forest inventory of some specific area (forest type) were conducted simultaneously (which was the case for the part of the Spačva basin in 2011), stand-level models could be derived using image-based CHM metrics and existing field inventory data. This approach, i.e., these models could be then used to estimate stand volume on other sites of the same forest type or for the same area after next aerial survey. Concretely, for the Spačva basin, the stand-level approach could be applied using new images from 2016, which will be available from CSGA soon. This means that fast and reasonably accurate stand volume estimates for Spačva basin could be obtained five years before regular forest inventory (2021–2022). Such more frequently updated information on forests could serve as a great support to practical management activities, as well as for monitoring of forest state and condition.

Regardless of the spatial resolution of the CHM datasets, the metrics extracted from each CHM exhibit a similar, almost identical correlation with the stand volume derived from field measurements (Table 5). This leads to the conclusion that the uncertainties involved in the modeling of forest surface, namely under- and overestimations obtained for CHM₅, are consistent throughout the area. As a result, by applying the backward stepwise regression, the similar set of independent variables are successfully selected and included in the stand-level volume models for all CHM resolutions (Table A2). As previously mentioned, the CHM metrics (e.g., height metrics, and canopy cover metrics) selected and included in the final stand-level modeling are similar to metrics used for predicting plot-level volume in other studies [3,10,24,30,34]. However, while in the present study the SA has been used in B models, variables in other studies, such as texture metrics derived from CHM rasters [24] or spectral metrics derived from orthoimage [3], were used in addition to height and canopy cover metrics extracted from CHMs.

This study (Table 6, Figure 3) suggests that models with CHM metrics and SA as independent variables (B models) have slightly better performance overall than models based solely on CHM metrics (A models). The inclusion of SA, in addition to CHM metrics, decreased RMSE_% by 0.55% (1-B), 0.75% (2-B), and 0.62% (5-B). This step of the research is of particular importance because the SA is, for even-aged stands, usually known, or easily obtainable variable, from the existing forest management plans. Therefore, it may be considered as an additional predictor of stand volume in future studies.

Among all tested models, model 2-B, with metrics extracted from CHM₂ and SA as independent variables, exhibits the best performance (RMSE_% = 12.53%). On the other hand, the worst performance is observed for model 5-A (RMSE_% = 13.28%) with metrics extracted from CHM₂ as only independent variables, which is in agreement with other studies [3,10,24,30,34]) where the estimated stand volume using image-based point clouds or CHMs had RMSE_% from 13.0% to 18.1%. Due to a number of differences between studies (e.g., site characteristics, forest structure, camera and image characteristics, matching software, etc.), precise comparison of the results is not possible. The agreement between the results of this and previous studies [3,10,24,30,34] suggests that the stand-level metrics extracted from the image-based CHMs can be used for the estimation of stand volume with similar or even slightly better accuracy than plot-level metrics. Moreover, the obtained results are also in agreement with the recent studies based on ALS data. For example, Rahlf et al. [10], Gobakken et al. [30], and Puliti et al. [34] estimated volume at stand level using ALS data with RMSE_% of 12.4%, 11.6%, and 13.3%, respectively.

Concerning the different resolutions (1 m, 2 m, 5 m) of CHMs used in this research, very similar results were obtained for all three CHMs (CHM₁, CHM₂, CHM₅) (Table 6, Figure 3). This implies that stand-level metrics extracted from all observed CHM resolutions (1 m, 2 m, 5 m) can provide reasonably accurate stand volume estimates. Similarly, Bohlin et al. [24] did not find improvements in estimation accuracy of forest stand attributes using point clouds derived from images of lower GSD (Table 1). Although the increase in resolution may result in better accuracy [30], CHMs of lower spatial resolution facilitate faster data manipulation and processing, especially for larger areas. Images of lower spatial resolutions or point clouds of lower densities, together with the lower amount of extracted metrics, occupy a smaller storage size than CHMs of high spatial resolution or very dense point clouds. Therefore, the trade-off between spatial resolution and required accuracy for a given area should be identified.

With respect to the stand development stages, the highest accuracy is obtained for old stands and the lowest accuracy for young stands (Figure 4). Although one could consider such a trend as the uncertainty of the proposed approach, it is in accordance with the findings of Gobakken et al. [30]. Namely, young stands of the research area are very dense with homogeneous structure and mostly without the presence of gaps in crowns. Therefore, the independent variable CC₃₀, which describes density (cover) of stands, has a less significant role in the performance of A models for young stands, resulting in the stand volume estimates of lower accuracy. This confirms our findings that the inclusion of SA as additional predictors in B models considerably improves estimation accuracy in young and middle-aged stands (Figure 4).

5. Conclusions

This research confirmed the great potential of digital aerial photogrammetry for stand-level forest inventory when fast, simple and low-cost approach based on existing data is needed. Image matching of existing digital aerial images from a national topographic survey, as well as interpolation of existing DTM data, were successfully applied to generate CHMs of different spatial resolutions (1 m, 2 m, and 5 m) for the area of even-aged pedunculate oak forests. For the first time, the stand-level metrics extracted from image-based CHMs were used to estimate the stand volume. The estimation accuracies were similar or even slightly better compared to those obtained from previous studies in which stand volume estimates were based on plot-level metrics. The validation results showed that the inclusion of stand age as an independent variable in addition to CHM metrics slightly improved the accuracy of stand volume estimates. Observed by stand development stages, these improvements were considerable for young and middle-aged stands, and they were negligible for mature and old stands. As stand age is an easily obtainable variable, it is recommended to use it for volume estimation, at least for young and middle-aged stands. The comparison between the different CHM’s resolutions (1 m, 2 m, 5 m) used for metrics extraction and volume estimation, showed that all observed CHM resolutions were capable of providing reasonably accurate volume estimates at the stand level. Additionally, this research revealed that in the absence of ALS-based DTM data, the existing digital terrain data, commonly collected by stereo mapping and field survey, could be readily used for DTM and CHM generation for flat terrains and lowland forests. This research serves as a basis for future studies where the applicability of the stand-level CHM approach should be tested for estimating other important forest stand attributes such as mean tree height, mean dbh, stand density, basal area, and biomass, across different forest types. The prediction potential of other variables obtainable from aerial images (e.g., color information/spectral metrics) and CHMs (e.g., texture metrics) should be examined.