Comparison of Multiple Linear Regression, Cubist Regression, and Random Forest Algorithms to Estimate Daily Air Surface Temperature from Dynamic Combinations of MODIS LST Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Weather Station Data
2.2. Data
2.2.1. MODIS LST
2.2.2. MODIS Land Cover
2.3. Methods
2.3.1. Calculating LST of Weather–Station–Location
- A total of 3652 MODIS images (MOD11A1 and MYD11A1, h27v06, Collection 5, from 1 January 2009 to 31 December 2013, over northern Vietnam) in HDF (Hierarchical Data Format) format were reprojected to WGS_1984_UTM_zone_48N using the nearest neighbor resampling method with the MODIS Re-Projection Tool. The corresponding layers (LST_Day_1km, LST_Night_1km, Daytime LST observation time, and Nighttime LST observation time) were extracted in TIF format. However, Daytime and Nighttime LST observation time were used in order to identify the approximate overpass time of MODIS at local time.
- MODIS LST data for the pixels in which the weather stations are located are extracted from 7304 TIF format MODIS images (3652 daytime and 3652 nighttime images) using batch processing of extract multi value to points in ArcGIS 10.3.
- All these LST data (DN value) were converted to Celsius temperature using the following equation:where °C is the Celsius temperature and 0.02 is the scale factor of the MODIS LST product.°C = 0.02 * DN − 273.15,
- Removing outlier data: MODIS LST products are not available for a location (pixel) if clouds are present [27]. However, there are some pixels that are lightly covered or contaminated by clouds. These pixels are not removed because the contamination is very small and cannot be detected by the cloud-removing mask algorithm [33,34]. To avoid this kind of data, we studied and developed a similar method that was used in [35]. This approach includes two steps: First, we simply filter and remove all unrealistic LST data that had values greater than 100 °C and/or below −50 °C. Second, we calculated the difference between Ta-max versus LST daytime and Ta-min versus LST nighttime. Then, we applied statistical outlier removal based on these differences’ histograms to detect and remove data with unusually large differences (the histogram does not follow a normal distribution).
2.3.2. Estimation Air Temperature Using MODIS LST Data
- Dynamic Combination of MODIS LST data
- Algorithms used
2.3.3. Comparison of Different Combination and Algorithms
- Assessment Criteria
- Comparison
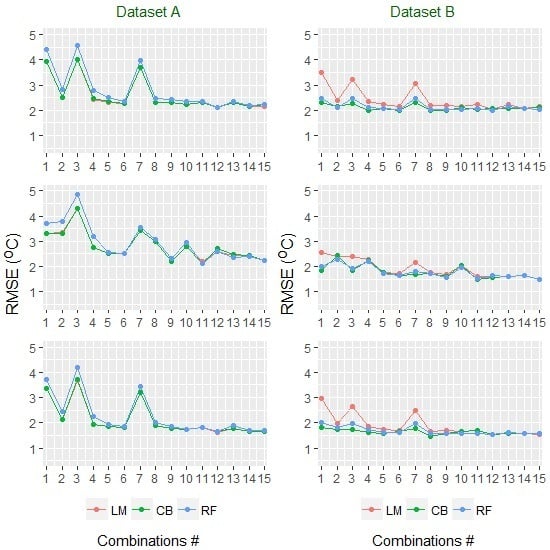
3. Results
3.1. The Relationship between Ta and LST MODIS
3.2. Different Combinations of MODIS LST for Ta Estimation
3.2.1. Combinations Using One LST Variable
3.2.2. Combinations Using Two-LST Variables
3.2.3. Combinations Using Three-LST Variables
3.2.4. Combinations Using Four-LST Variables
4. Discussion
4.1. Model Calibration and Validation
4.2. Effects of Different Combinations and Statistical Model Applications
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Combination | a0 | a1 | a2 | a3 | a4 | |
|---|---|---|---|---|---|---|
| Ta-min Estimation | C01 | −0.4567 | 0.6037 | |||
| C02 | −0.2678 | 1.0020 | ||||
| C03 | −1.1905 | 0.7170 | ||||
| C04 | −1.7601 | 1.0184 | ||||
| C05 | 0.1561 | −0.0656 | 1.0647 | |||
| C06 | −3.6700 | 0.0382 | 1.0329 | |||
| C07 | −4.1084 | 0.4906 | 0.2442 | |||
| C08 | −1.4168 | 1.0031 | 0.0277 | |||
| C09 | −2.1783 | −0.0425 | 1.0769 | |||
| C10 | −2.2857 | 0.4799 | 0.5784 | |||
| C11 | −2.8733 | −0.0336 | 0.0347 | 1.0349 | ||
| C12 | −2.4495 | 0.5464 | −0.0378 | 0.5552 | ||
| C13 | −1.0977 | −0.0344 | 0.9997 | 0.0496 | ||
| C14 | −0.5283 | −0.1538 | 0.6645 | 0.5408 | ||
| C15 | −1.6045 | −0.0714 | 0.6659 | −0.0020 | 0.4556 | |
| Ta-max Estimation | C01 | 0.7418 | 0.9849 | |||
| C02 | 8.4402 | 1.1748 | ||||
| C03 | 6.1865 | 0.9026 | ||||
| C04 | 5.8675 | 1.2125 | ||||
| C05 | −0.0367 | 0.5587 | 0.7505 | |||
| C06 | 4.3759 | 0.1263 | 1.1694 | |||
| C07 | −0.0708 | 1.0098 | −0.0068 | |||
| C08 | 8.5918 | 1.1432 | 0.0458 | |||
| C09 | −0.7751 | 0.4757 | 0.8778 | |||
| C10 | 5.5651 | 0.3821 | 0.9083 | |||
| C11 | 1.0850 | 0.5573 | −0.2434 | 0.9824 | ||
| C12 | 7.5080 | 0.4518 | −0.1274 | 0.9481 | ||
| C13 | 3.7089 | 0.6542 | 0.8513 | −0.3246 | ||
| C14 | −1.1526 | 0.4704 | 0.3212 | 0.6027 | ||
| C15 | 3.2723 | 0.5978 | 0.4074 | −0.4465 | 0.7015 | |
| Ta-mean Estimation | C01 | −0.3329 | 0.7579 | |||
| C02 | 3.0973 | 1.0630 | ||||
| C03 | 0.9103 | 0.8154 | ||||
| C04 | 1.1378 | 1.0888 | ||||
| C05 | −0.4702 | 0.2122 | 0.9074 | |||
| C06 | −1.6236 | 0.1523 | 1.0316 | |||
| C07 | −3.2005 | 0.6693 | 0.1964 | |||
| C08 | 1.3821 | 1.0028 | 0.1121 | |||
| C09 | −2.2374 | 0.1935 | 0.9691 | |||
| C10 | 0.7231 | 0.4639 | 0.6828 | |||
| C11 | −2.3500 | 0.2016 | 0.0036 | 0.9516 | ||
| C12 | −0.0214 | 0.5094 | 0.0377 | 0.6325 | ||
| C13 | −0.2995 | 0.2344 | 0.8818 | −0.0172 | ||
| C14 | −1.5659 | 0.1396 | 0.5060 | 0.5450 | ||
| C15 | −1.1587 | 0.1968 | 0.5392 | −0.0702 | 0.4952 |
Appendix B
| Combination | a0 | a1 | a2 | a3 | a4 | Elevation | Julian Day | |
|---|---|---|---|---|---|---|---|---|
| Ta-min Estimation | C01 | 4.1126 | 0.4728 | −0.0029 | 0.0066 | |||
| C02 | 0.3258 | 0.9505 | −0.0008 | 0.0057 | ||||
| C03 | 3.1331 | 0.6298 | −0.0042 | 0.0046 | ||||
| C04 | −1.6854 | 0.9873 | −0.0005 | 0.0050 | ||||
| C05 | 0.4293 | −0.0318 | 0.9822 | −0.0007 | 0.0050 | |||
| C06 | −4.5116 | 0.1075 | 0.9595 | −0.0006 | 0.0053 | |||
| C07 | 1.7992 | 0.0921 | 0.5553 | −0.0041 | 0.0042 | |||
| C08 | −1.4452 | 0.9067 | 0.0887 | −0.0009 | 0.0054 | |||
| C09 | −2.3238 | 0.0098 | 0.9868 | −0.0007 | 0.0049 | |||
| C10 | −2.7464 | 0.4843 | 0.5678 | −0.0003 | 0.0056 | |||
| C11 | −3.0229 | −0.0266 | 0.1405 | 0.8891 | −0.0011 | 0.0045 | ||
| C12 | −3.2945 | 0.5450 | −0.0031 | 0.5286 | −0.0003 | 0.0053 | ||
| C13 | −0.7924 | −0.0512 | 0.8894 | 0.1366 | −0.0010 | 0.0044 | ||
| C14 | −0.7538 | −0.1054 | 0.6304 | 0.4971 | −0.0005 | 0.0044 | ||
| C15 | −1.8881 | −0.0530 | 0.6303 | 0.0650 | 0.3815 | −0.0007 | 0.0041 | |
| Ta-max Estimation | C01 | 10.4393 | 0.7387 | −0.0043 | 0.0007 | |||
| C02 | 18.4850 | 0.8308 | −0.0045 | −0.0048 | ||||
| C03 | 15.9842 | 0.7267 | −0.0066 | −0.0048 | ||||
| C04 | 13.5620 | 0.9526 | −0.0032 | −0.0040 | ||||
| C05 | 10.5450 | 0.4115 | 0.5496 | −0.0038 | −0.0010 | |||
| C06 | 12.3927 | 0.3408 | 0.6526 | −0.0044 | −0.0055 | |||
| C07 | 11.3235 | 0.3628 | 0.4616 | −0.0058 | −0.0027 | |||
| C08 | 16.0125 | 0.5685 | 0.3214 | −0.0052 | −0.0056 | |||
| C09 | 6.3793 | 0.4536 | 0.6361 | −0.0031 | −0.0007 | |||
| C10 | 15.0605 | 0.3058 | 0.6539 | −0.0038 | −0.0045 | |||
| C11 | 8.8810 | 0.2941 | 0.1853 | 0.5654 | −0.0041 | −0.0032 | ||
| C12 | 15.3856 | 0.3071 | 0.2084 | 0.4250 | −0.0048 | −0.0060 | ||
| C13 | 13.7642 | 0.1994 | 0.4982 | 0.2098 | −0.0049 | −0.0043 | ||
| C14 | 8.8056 | 0.3859 | 0.2534 | 0.4067 | −0.0037 | −0.0008 | ||
| C15 | 12.8016 | 0.2253 | 0.3015 | 0.1265 | 0.3065 | −0.0047 | −0.0044 | |
| Ta-mean Estimation | C01 | 5.4211 | 0.6044 | −0.0030 | 0.0035 | |||
| C02 | 6.6191 | 0.9322 | −0.0017 | 0.0003 | ||||
| C03 | 7.1288 | 0.6996 | −0.0048 | −0.0001 | ||||
| C04 | 3.4497 | 1.0007 | −0.0011 | 0.0006 | ||||
| C05 | 2.4255 | 0.1864 | 0.8229 | −0.0013 | 0.0016 | |||
| C06 | 0.6160 | 0.2471 | 0.8388 | −0.0016 | 0.0003 | |||
| C07 | 4.1489 | 0.2239 | 0.5289 | −0.0043 | 0.0007 | |||
| C08 | 3.8781 | 0.7786 | 0.2243 | −0.0020 | −0.0002 | |||
| C09 | −0.5674 | 0.2103 | 0.8726 | −0.0011 | 0.0019 | |||
| C10 | 3.1115 | 0.4446 | 0.6126 | −0.0011 | 0.0004 | |||
| C11 | −0.1692 | 0.1288 | 0.1705 | 0.7716 | −0.0016 | 0.0009 | ||
| C12 | 2.0954 | 0.4650 | 0.1490 | 0.4676 | −0.0015 | −0.0002 | ||
| C13 | 2.9232 | 0.0875 | 0.7353 | 0.1781 | −0.0019 | 0.0001 | ||
| C14 | 0.6955 | 0.1371 | 0.4779 | 0.4833 | −0.0011 | 0.0014 | ||
| C15 | 1.5190 | 0.0943 | 0.4956 | 0.1184 | 0.3575 | −0.0016 | 0.0001 |
References
- De Wit, A.J.W.; van Diepen, C.A. Crop growth modelling and crop yield forecasting using satellite-derived meteorological inputs. Int. J. Appl. Earth Obs. 2008, 10, 414–425. [Google Scholar] [CrossRef]
- Daly, C. Guidelines for assessing the suitability of spatial climate data sets. Int. J. Climatol. 2006, 26, 707–721. [Google Scholar] [CrossRef]
- Stahl, K.; Moore, R.D.; Floyer, J.A.; Asplin, M.G.; McKendry, I.G. Comparison of approaches for spatial interpolation of daily air temperature in a large region with complex topography and highly variable station density. Agric. For. Meteorol. 2006, 139, 224–236. [Google Scholar] [CrossRef]
- Izady, A.; Davary, K.; Alizadeh, A.; Ziaei, A.N.; Akhavan, S.; Alipoor, A.; Joodavi, A.; Brusseau, M.L. Groundwater conceptualization and modeling using distributed SWAT-based recharge for the semi-arid agricultural Neishaboor plain. Iran. Hydrogeol. J. 2015, 23, 47–68. [Google Scholar] [CrossRef]
- Smith, W.L.; Leslie, L.M.; Diak, G.R.; Goodman, B.M.; Velden, C.S.; Callan, G.M.; Raymond, W.; Wade, G.S. The integration of meteorological satellite imagery and numerical dynamical forecast models. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1988, 324, 317–323. [Google Scholar] [CrossRef]
- Christiansen, B. Downward propagation and statistical forecast of the near-surface weather. J. Geophys. Res. 2005, 110, D14104. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2007: The Physical Science Basis: Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Lofgren, B.M.; Hunter, T.S.; Wilbarger, J. Effects of using air temperature as a proxy for evapotranspiration in climate change scenarios of Great Lakes basin hydrology. J. Gt. Lakes Res. 2011, 37, 744–752. [Google Scholar] [CrossRef]
- Stisen, S.; Sandholt, I.; Nørgaard, A.; Fensholt, R.; Eklundh, L. Estimation of diurnal air temperature using MSG SEVIRI data in West Africa. Remote Sens. Environ. 2007, 110, 262–274. [Google Scholar] [CrossRef]
- Nieto, H.; Sandholt, I.; Aguado, I.; Chuvieco, E.; Stisen, S. Air temperature estimation with MSG-SEVIRI data: Calibration and validation of the TVX algorithm for the Iberian Peninsula. Remote Sens. Environ. 2011, 115, 107–116. [Google Scholar] [CrossRef]
- Zhu, W.; Lű, A.; Jia, S. Estimation of daily maximum and minimum air temperature using MODIS land surface temperature products. Remote Sens. Environ. 2013, 130, 62–73. [Google Scholar] [CrossRef]
- Sun, Y.J.; Wang, J.F.; Zhang, R.H.; Gillies, R.R.; Xue, Y.; Bo, Y.C. Air temperature retrieval from remote sensing data based on thermodynamics. Theor. Appl. Climatol. 2005, 80, 37–48. [Google Scholar] [CrossRef]
- Mostovoy, G.V.; King, R.L.; Reddy, K.R.; Kakani, V.G.; Filippova, M.G. Statistical estimation of daily maximum and minimum air temperatures from MODIS LST data over the state of Mississippi. GISci. Remote Sens. 2006, 43, 78–110. [Google Scholar] [CrossRef]
- Vancutsem, C.; Pietro, C.; Tufa, D.; Stephen, J.C. Evaluation of MODIS land surface temperature data to estimate air temperature in different ecosystems over Africa. Remote Sens. Environ. 2010, 114, 449–465. [Google Scholar] [CrossRef]
- Benali, A.; Carvalho, A.C.; Nunes, J.P.; Carvalhais, N.; Santos, A. Estimating air surface temperature in Portugal using MODIS LST data. Remote Sens. Environ. 2012, 124, 108–121. [Google Scholar] [CrossRef]
- Good, E. Daily minimum and maximum surface air temperatures from geostationary satellite data. J. Geophys. Res. Atmos. 2015, 120, 2306–2324. [Google Scholar] [CrossRef]
- Noi, P.T.; Kappas, M.; Degener, J. Estimating daily maximum and minimum land air surface temperature using MODIS land surface temperature data and ground truth data in Northern Vietnam. Remote Sens. 2016, 8, 1002. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, F.; Ye, M.; Che, T.; Zhang, G. Estimating daily air temperatures over the Tibetan Plateau by dynamically integrating MODIS LST data. J. Geophys. Res. Atmos. 2016, 121, 11425–11441. [Google Scholar] [CrossRef]
- Wloczyk, C.; Borg, E.; Richter, R.; Miegel, K. Estimation of instantaneous air temperature above vegetation and soil surfaces from Landsat 7 ETM+ data in northern Germany. Int. J. Remote Sens. 2011, 32, 9119–9136. [Google Scholar] [CrossRef]
- Ho, H.C.; Knudby, A.; Sirovyak, P.; Xu, Y.; Hodul, M.; Henderson, S.B. Mapping maximum urban air temperature on hot summer days. Remote Sens. Environ. 2014, 154, 38–45. [Google Scholar] [CrossRef]
- Prince, S.D.; Goetz, S.J.; Dubayah, R.O.; Czajkowski, K.P.; Thawley, M. Inference of surface and air temperature, atmospheric precipitable water and vapor pressure deficit using advanced very high-resolution radiometer satellite observations: Comparison with field observations. J. Hydrol. 1998, 213, 230–249. [Google Scholar] [CrossRef]
- Shen, S.-H.; Leptoukh, G.-G. Estimation of surface air temperature over central and eastern Eurasia from MODIS land surface temperature. Environ. Res. Lett. 2011, 6, 045206. [Google Scholar] [CrossRef]
- Zeng, L.; Wardlow, B.D.; Tadesse, T.; Shan, J.; Hayes, M.J.; Li, D.; Xiang, D. Estimation of daily air temperature based on MODIS land surface temperature products over the corn belt in the US. Remote Sens. 2015, 7, 951–970. [Google Scholar] [CrossRef]
- Emamifar, S.; Rahimikhoob, A.; Noroozi, A. Daily mean temperature estimation from MODIS land surface temperature. Int. J. Climatol. 2013, 33, 3174–3181. [Google Scholar] [CrossRef]
- Xu, Y.; Knudby, A.; Ho, H.C. Estimating daily maximum air temperature from MODIS in British Columbia, Canada. Int. J. Remote Sens. 2014, 35, 8108–8121. [Google Scholar] [CrossRef]
- Meyer, H.; Katurji, M.; Appelhans, T.; Müller, M.U.; Nauss, T.; Roudier, P.; Zawar-Reza, P. Mapping daily air temperature for Antarctica based on MODIS LST. Remote Sens. 2016, 8, 732. [Google Scholar] [CrossRef]
- Wan, Z. New refinements and validation of the MODIS land-surface temperature/emissivity products. Remote Sens. Environ. 2008, 112, 59–74. [Google Scholar] [CrossRef]
- The U.S. Geological Survey. MODIS LST Data. Available online: http://earthexplorer.usgs.gov (accessed on 1 October 2016).
- Colombi, A.; De Michele, C.; Pepe, M.; Rampini, A. Estimation of daily mean air temperature from MODIS LST in Alpine areas. EARSeL eProc. 2007, 6, 38–46. [Google Scholar]
- Land Processes Distributed Active Archive Center. Available online: https://lpdaac.usgs.gov/dataset_discovery/modis/modis_products_table/mcd12q1 (accessed on 18 October 2016).
- Liang, D.; Zuo, Y.; Huang, L.; Zhao, J.; Teng, L.; Yang, F. Evaluation of the consistency of MODIS Land Cover Product (MCD12Q1) based on Chinese 30 m GlobeLand30 datasets: A case study in Anhui Province, China. ISPRS Int. J. Geo-Inf. 2015, 4, 2519–2541. [Google Scholar] [CrossRef]
- Land Quality Assessment Site of NASA. Julian Day. Available online: http://landweb.nascom.nasa.gov/browse/calendar.html (accessed on 2 December 2016).
- Ackerman, S.A.; Holz, R.E.; Frey, R.; Eloranta, E.W.; Maddux, B.C.; McGill, M. Cloud detection with MODIS. Part II: Validation. J. Atmos. Ocean. Technol. 2008, 25, 1073–1086. [Google Scholar]
- Williamson, S.N.; Hik, D.S.; Gamon, J.A.; Kavanaugh, J.L.; Koh, S. Evaluating cloud contamination in clear-sky MODIS Terra daytime land surface temperatures using ground-based meteorology station observations. J. Clim. 2013, 26, 1551–1560. [Google Scholar] [CrossRef]
- Williamson, S.N.; Hik, D.S.; Gamon, J.A.; Jarosch, A.H.; Anslow, F.S.; Clarke, G.K.C.; Rupp, T.S. Spring and summer monthly MODIS LST is inherently biased compared to air temperature in snow covered sub-Arctic mountains. Remote Sens. Environ. 2017, 189, 14–24. [Google Scholar] [CrossRef]
- Huang, R.; Zhang, C.; Huang, J.; Zhu, D.; Wang, L.; Liu, J. Mapping of daily mean air temperature in agricultural regions using daytime and nighttime land surface temperatures derived from TERRA and AQUA MODIS data. Remote Sens. 2015, 7, 8728–8756. [Google Scholar] [CrossRef]
- Shi, L.; Liu, P.; Kloog, I.; Lee, M.; Kosheleva, A.; Schwartz, J. Estimating daily air temperature across the Southeastern United States using high-resolution satellite data: A statistical modeling study. Environ. Res. 2016, 146, 51–58. [Google Scholar] [CrossRef] [PubMed]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling, 1st ed.; Springer: New York, NY, USA, 2013. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning: With Applications in R, 1st ed.; Springer: New York, NY, USA, 2013. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Quinlan, J.R. Learning with continuous classes. In Proceedings of the 5th Australian Joint Conference on Artificial Intelligence, Hobart, Tasmania, 16–18 November 1992; pp. 343–348. [Google Scholar]
- Quinlan, J.R. Combining instance-based and model-based learning. In Proceedings of the Tenth International Conference on Machine Learning, Amherst, MA, USA, 27–29 June 1993; pp. 236–243. [Google Scholar]
- Quinlan, J.R. C4.5: Programs For Machine Learning; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1993. [Google Scholar]
- Appelhans, T.; Mwangomo, E.; Hardy, D.R.; Hemp, A.; Nauss, T. Evaluating machine learning approaches for the interpolation of monthly air temperature at Mt. Kilimanjaro, Tanzania. Spat. Stat. 2015, 14, 91–113. [Google Scholar] [CrossRef]
- Walton, J.T. Subpixel urban land cover estimation: Comparing cubist, random forests, and support vector regression. Photogram. Eng. Remote Sens. 2008, 74, 1213–1222. [Google Scholar] [CrossRef]
- Kuhn, M.; Weston, S.; Keefer, C.; Coulter, N. Cubist: Rule- and Instance-Based Regression Modeling; R Package Version 0.0.13; CRAN: Wien, Austria, 2013. [Google Scholar]
- Zhang, W.; Huang, Y.; Yu, Y.Q.; Sun, W.J. Empirical models for estimating daily maximum, minimum and mean air temperatures with MODIS land surface temperatures. Int. J. Remote Sens. 2011, 32, 9415–9440. [Google Scholar] [CrossRef]
- Peón, J.; Recondo, C.; Calleja, J.F. Improvements in the estimation of daily minimum air temperature in peninsular Spain using MODIS land surface temperature. Int. J. Remote Sens. 2014, 35, 5148–5166. [Google Scholar] [CrossRef]
- Janatian, N.; Sadeghi, M.; Sanaeinejad, S.H.; Bakhshian, E.; Farid, A.; Hasheminia, S.; Ghazanfari, S. A statistical framework for estimating air temperature using MODIS land surface temperature data. Int. J. Climatol. 2016, 37, 1181–1194. [Google Scholar] [CrossRef]
- Jin, M.; Dickinson, R.E. Land surface skin temperature climatology: Benefitting from the strengths of satellite observations. Environ. Res. Lett. 2010, 5, 041002. [Google Scholar] [CrossRef]
- Shreve, C. Working towards a community-wide understanding of satellite skin temperature observations. Environ. Res. Lett. 2010, 5, 044004. [Google Scholar] [CrossRef]
- Fu, G.; Shen, Z.; Zhang, X.; Shi, P.; Zhang, Y.; Wu, J. Estimating air temperature of an alpine meadow on the Northern Tibetan Plateau using MODIS land surface temperature. Acta Ecol. Sin. 2011, 31, 8–13. [Google Scholar] [CrossRef]












| No. | Station | Lat (°) | Long (°) | Elevation (m) | Land Cover |
|---|---|---|---|---|---|
| 1 | Sin Ho | 22.37 | 103.25 | 1534 | Forest |
| 2 | Dien Bien | 21.37 | 103.00 | 475 | Crop land |
| 3 | Lai Chau | 22.07 | 103.15 | 243 | Forest |
| No. | Combination | SinHo | DienBien | LaiChau | Total | |||
|---|---|---|---|---|---|---|---|---|
| C01 | LSTad | 488 | 572 | 571 | 1631 | |||
| C02 | LSTan | 420 | 321 | 261 | 1002 | |||
| C03 | LSTtd | 427 | 500 | 507 | 1434 | |||
| C04 | LSTtn | 562 | 593 | 528 | 1683 | |||
| C05 | LSTad | +LSTan | 254 | 219 | 190 | 663 | ||
| C06 | LSTtd | +LSTtn | 255 | 286 | 298 | 839 | ||
| C07 | LSTad | +LSTtd | 297 | 318 | 348 | 963 | ||
| C08 | LSTan | +LSTtd | 231 | 193 | 176 | 600 | ||
| C09 | LSTad | +LSTtn | 283 | 348 | 340 | 971 | ||
| C10 | LSTan | +LSTtn | 294 | 224 | 193 | 711 | ||
| C11 | LSTtd | +LSTtn | +LSTad | 195 | 200 | 229 | 624 | |
| C12 | LSTtd | +LSTtn | +LSTan | 176 | 132 | 131 | 439 | |
| C13 | LSTad | +LSTan | +LSTtd | 184 | 138 | 137 | 459 | |
| C14 | LSTad | +LSTan | +LSTtn | 198 | 159 | 143 | 500 | |
| C15 | LSTad | +LSTan | +LSTtd | +LSTtn | 141 | 92 | 100 | 333 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noi, P.T.; Degener, J.; Kappas, M. Comparison of Multiple Linear Regression, Cubist Regression, and Random Forest Algorithms to Estimate Daily Air Surface Temperature from Dynamic Combinations of MODIS LST Data. Remote Sens. 2017, 9, 398. https://doi.org/10.3390/rs9050398
Noi PT, Degener J, Kappas M. Comparison of Multiple Linear Regression, Cubist Regression, and Random Forest Algorithms to Estimate Daily Air Surface Temperature from Dynamic Combinations of MODIS LST Data. Remote Sensing. 2017; 9(5):398. https://doi.org/10.3390/rs9050398
Chicago/Turabian StyleNoi, Phan Thanh, Jan Degener, and Martin Kappas. 2017. "Comparison of Multiple Linear Regression, Cubist Regression, and Random Forest Algorithms to Estimate Daily Air Surface Temperature from Dynamic Combinations of MODIS LST Data" Remote Sensing 9, no. 5: 398. https://doi.org/10.3390/rs9050398
APA StyleNoi, P. T., Degener, J., & Kappas, M. (2017). Comparison of Multiple Linear Regression, Cubist Regression, and Random Forest Algorithms to Estimate Daily Air Surface Temperature from Dynamic Combinations of MODIS LST Data. Remote Sensing, 9(5), 398. https://doi.org/10.3390/rs9050398