Better Estimated IEM Input Parameters Using Random Fractal Geometry Applied on Multi-Frequency SAR Data
Abstract
:1. Introduction
2. The IEM Backscattering Model
2.1. The IEM Validity Region
2.2. Conventional Inputs for IEM
3. Power-Law Inputs for the IEM
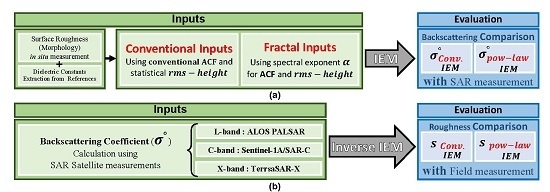
4. Implementation and Evaluation
4.1. Geometric Parameters Analysis
4.2. Evaluation of Backscattering and Surface Roughness Simulation
5. Discussion
6. Conclusions
Acknowledgments
Author Contribution
Conflicts of Interest
References
- Panciera, R.; Tanase, M.A.; Lowell, K.; Walker, J.P. Evaluation of iem, dubois, and oh radar backscatter models using airborne l-band sar. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4966–4979. [Google Scholar] [CrossRef]
- Rodrigues, F.Á.; Neto, J.R.; Marques, R.P.; de Medeiros, F.S.; Nobre, J.S. Sar image segmentation using the roughness information. IEEE Geosci. Remote Sens. Lett. 2016, 13, 132–136. [Google Scholar] [CrossRef]
- Zhu, L.; Walker, J.P.; Ye, N.; Rudiger, C. The effect of radar configuration on effective correlation length. In Proceedings of the 2016 International Conference on Electromagnetics in Advanced Applications (ICEAA), Cairns, Australia, 19–23 September 2016; pp. 820–823. [Google Scholar]
- Baghdadi, N.; Zribi, M.; Paloscia, S.; Verhoest, N.E.; Lievens, H.; Baup, F.; Mattia, F. Semi-empirical calibration of the integral equation model for co-polarized l-band backscattering. Remote Sens. 2015, 7, 13626–13640. [Google Scholar] [CrossRef]
- Gorrab, A.; Zribi, M.; Baghdadi, N.; Mougenot, B.; Chabaane, Z.L. Potential of x-band terrasar-x and cosmo-skymed sar data for the assessment of physical soil parameters. Remote Sens. 2015, 7, 747–766. [Google Scholar] [CrossRef]
- Martínez-Agirre, A.; Álvarez-Mozos, J.; Lievens, H.; Verhoest, N.E.; Giménez, R. Sensitivity of c-band backscatter to surface roughness parameters measured at different scales. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 700–703. [Google Scholar]
- Ulaby, F.T.; Long, D.G. Microwave Radar and Radiometric Remote Sensing; University of Michigan Press: Ann Arbor, MI, USA, 2014; pp. 425–445. [Google Scholar]
- Baghdadi, N.; Cresson, R.; Pottier, E.; Aubert, M.; Mehrez, M.; Jacome, A.; Benabdallah, S. A potential use for the c-band polarimetric sar parameters to characterize the soil surface over bare agriculture fields. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3844–3858. [Google Scholar] [CrossRef]
- Zribi, M.; Gorrab, A.; Baghdadi, N. A new soil roughness parameter for the modelling of radar backscattering over bare soil. Remote Sens. Environ. 2014, 152, 62–73. [Google Scholar] [CrossRef]
- Fung, A.K. Microwave Scattering and Emission Models and Their Applications; Artech House: Norwood, MA, USA, 1994. [Google Scholar]
- Fung, A.K.; Li, Z.; Chen, K. Backscattering from a randomly rough dielectric surface. IEEE Trans. Geosci. Remote Sens. 1992, 30, 356–369. [Google Scholar] [CrossRef]
- Hajnsek, I. Inversion of Surface Parameters Using Polarimetric Sar. Ph.D. Thesis, Friedrich-Schiller-Universität Jena, Jena, Germany, 2001. [Google Scholar]
- Franceschetti, G.; Riccio, D. Scattering, Natural Surfaces, and Fractals; Academic Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Martinez, A.; Byrnes, A.P. Modeling Dielectric-Constant Values of Geologic Materials: An Aid to Ground-Penetrating Radar Data Collection and Interpretation; Kansas Geological Survey, University of Kansas: Lawrence, KS, USA, 2001. [Google Scholar]
- Mazaheri Tehrani, H. Soil Moisture Estimation with Polarimetric Sar Data. Ph.D. Thesis, University of Calgary, Calgary, AL, Canada, 2014. [Google Scholar]
- Fung, A.K.; Chen, K.S. An update on the iem surface backscattering model. IEEE Geosci. Remote Sens. Lett. 2004, 1, 75–77. [Google Scholar] [CrossRef]
- Baghdadi, N.; Holah, N.; Zribi, M. Calibration of the integral equation model for sar data in c-band and hh and vv polarizations. Int. J. Remote Sens. 2006, 27, 805–816. [Google Scholar] [CrossRef]
- Barrett, B.W.; Dwyer, E.; Whelan, P. Soil moisture retrieval from active spaceborne microwave observations: An evaluation of current techniques. Remote Sens. 2009, 1, 210–242. [Google Scholar] [CrossRef]
- Chen, K.; Kao, W.; Tzeng, Y. Retrieval of surface parameters using dynamic learning neural network. Remote Sens. 1995, 16, 801–809. [Google Scholar] [CrossRef]
- Sahebi, M.R.; Bonn, F.; Bénié, G.B. Neural networks for the inversion of soil surface parameters from synthetic aperture radar satellite data. Can. J. Civ. Eng. 2004, 31, 95–108. [Google Scholar] [CrossRef]
- Dierking, W. Quantitative roughness characterization of geological surfaces and implications for radar signature analysis. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2397–2412. [Google Scholar] [CrossRef]
- Álvarez-Mozos, J.; Verhoest, N.E.; Larrañaga, A.; Casalí, J.; González-Audícana, M. Influence of surface roughness spatial variability and temporal dynamics on the retrieval of soil moisture from sar observations. Sensors 2009, 9, 463–489. [Google Scholar] [CrossRef] [PubMed]
- Choker, M.; Baghdadi, N.; Zribi, M.; El Hajj, M.; Paloscia, S.; Verhoest, N.E.; Lievens, H.; Mattia, F. Evaluation of the oh, dubois and iem backscatter models using a large dataset of sar data and experimental soil measurements. Water 2017, 9, 38. [Google Scholar] [CrossRef]
- Verhoest, N.E.; Lievens, H.; Wagner, W.; Álvarez-Mozos, J.; Moran, M.S.; Mattia, F. On the soil roughness parameterization problem in soil moisture retrieval of bare surfaces from synthetic aperture radar. Sensors 2008, 8, 4213–4248. [Google Scholar] [CrossRef] [PubMed]
- Ghafouri, A.; Amini, J.; Dehmollaian, M.; Kavoosi, M. Measuring surface roughness of geological rock surfaces in sar data using fractal geometry. C. R. Geosci. 2017, 11, 327–338. [Google Scholar]
- Baghdadi, N.; Chaaya, J.A.; Zribi, M. Semiempirical calibration of the integral equation model for sar data in c-band and cross polarization using radar images and field measurements. IEEE Geosci. Remote Sens. Lett. 2011, 8, 14–18. [Google Scholar] [CrossRef]
- Western, A.W.; Bloschl, G.; Grayson, R.B. How well do indicator variograms capture the spatial connectivity of soil moisture? Hydrol. Process. 1998, 12, 1851–1868. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; Macmillan Publishers: London, UK, 1983. [Google Scholar]
- Durst, P.J.; Mason, G.L.; McKinley, B.; Baylot, A. Predicting rms surface roughness using fractal dimension and psd parameters. J. Terramech. 2011, 48, 105–111. [Google Scholar] [CrossRef]
- Martino, G.D.; Franceschetti, G.; Riccio, D.; Zinno, I. Spectral processing for the extraction of fractal parameters from sar data. In Proceedings of the 2011 17th International Conference on Digital Signal Processing (DSP), Corfu, Greece, 6–8 July 2011; pp. 1–7. [Google Scholar]
- Yordanov, O.; Atanasov, I. Self-affine random surfaces. Eur. Phys. J. B 2002, 29, 211–215. [Google Scholar] [CrossRef]
- Yordanov, O.; Ivanova, K. Description of surface roughness as an approximate self-affine random structure. Surf. Sci. 1995, 331, 1043–1049. [Google Scholar] [CrossRef]
- Rasigni, G.; Llebaria, A.; Lafraxo, M.; Buat, V.; Rasigni, M.; Abdellani, F. Autoregressive process for characterizing statistically rough surfaces. J. Opt. Soc. Am. A 1993, 10, 1257–1262. [Google Scholar] [CrossRef]
- Roomi, S.; Kalaiyarasi, D.; Rangan, N.K. Discrete wavelet transform based despeckling for sar images. In Proceedings of the 2011 World Congress on Information and Communication Technologies, Mumbai, India, 11–14 December 2011; pp. 373–378. [Google Scholar]
- Wang, F.; Zhang, B.; Yang, D.; Li, W.; Zhu, Y. Sea-state observation using reflected beidou geo signals in frequency domain. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1656–1660. [Google Scholar] [CrossRef]
- Fadzal, C.C.W.; Mansor, W.; Khuan, L.; Mohamad, N.; Mahmoodin, Z.; Mohamad, S.; Amirin, S. Welch power spectral density of eeg signal generated from dyslexic children. In Proceedings of the 2014 IEEE Region 10 Symposium, Kuala Lumpur, Malaysia, 14–16 April 2014; pp. 560–562. [Google Scholar]
- Ghafouri, A.; Amini, J.; Dehmollaian, M.; Kavoosi, M. Random fractals geometry in surface roughness modeling of geological formations using synthetic aperture radar images. J. Geomat. Sci. Technol. Iran. Soc. Surv. Geomat. Eng. 2015, 5, 97–108. [Google Scholar]
- Di Martino, G.; Iodice, A.; Riccio, D.; Ruello, G.; Zinno, I. On the fractal nature of volcano morphology detected via sar image analysis: The case of somma-vesuvius volcanic complex. Eur. J. Remote Sens. 2012, 45, 177–187. [Google Scholar] [CrossRef]
- Zribi, M. Développement de Nouvelles Méthodes de Modélisation de la Rugosité Pour la Rétrodiffusion Hyperfréquence de la Surface Du Sol. Ph.D. Thesis, Université Paul Sabatier, Toulouse, France, 1998. [Google Scholar]
- Franceschetti, G.; Iodice, A.; Maddaluno, S.; Riccio, D. A fractal-based theoretical framework for retrieval of surface parameters from electromagnetic backscattering data. IEEE Trans. Geosci. Remote Sens. 2000, 38, 641–650. [Google Scholar] [CrossRef]
- Franceschetti, G.; Iodice, A.; Migliaccio, M.; Riccio, D. Scattering from natural rough surfaces modeled by fractional brownian motion two-dimensional processes. IEEE Trans. Antennas Propag. 1999, 47, 1405–1415. [Google Scholar] [CrossRef]
- Zribi, M.; Ciarletti, V.; Taconet, O.; Paillé, J.; Boissard, P. Characterisation of the soil structure and microwave backscattering based on numerical three-dimensional surface representation: Analysis with a fractional brownian model. Remote Sens. Environ. 2000, 72, 159–169. [Google Scholar] [CrossRef]














| Geological Formation | Geological Period | General Morphology Appearance |
|---|---|---|
| Asmari (As) | Oligocene to Lower Miocene | Rough |
| Gachsaran (Gs) | early Miocene | Moderate |
| Pabdeh (Pd) | Paleocene to early Miocene | Smooth |
| Satellite/Antenna | Acquisition Mode | Band | Freq. (GHz) | Incidence Angle/Pass/Look |
|---|---|---|---|---|
| ALOS–Palsar-2 | Spot-light | L | 1.200 | 32.3°/Ascending/Left |
| Sentinel-1A | Strip Map Mode | C | 5.405 | 38.1°/Ascending/Right |
| TerraSAR-X | Staring Spot-Light | X | 9.650 | 22.7°/Descending/Left |
| Site No. | Dominant Geological Formation | rms-Height (cm) | Corr. Length (cm) | |
|---|---|---|---|---|
| Site 1 | As | 6.02 | 81.07 | 1.5345 |
| Site 2 | Gs | 2.2 | 45.3 | 1.7112 |
| Site 3 | As-Gs | 4.64 | 54.07 | 1.6865 |
| Site 4 | Pd | 1.11 | 14.9 | 1.7923 |
| Site 5 | Pd | 1.21 | 18.03 | 1.8825 |
| Site 6 | Gs | 1.98 | 40.71 | 1.8817 |
| Site 7 | As | 4.97 | 74.38 | 1.5349 |
| Site 8 | Gs | 1.66 | 19.31 | 1.7501 |
| Site 9 | Gs | 2.86 | 50.9 | 1.7709 |
| Site 10 | Qu | 1.76 | 31.31 | 1.7472 |
| Geological Formation | L-Band | C-Band | X-Band | ||||||
|---|---|---|---|---|---|---|---|---|---|
| (5a) | (5b) | (5c) | (5a) | (5b) | (5c) | (5a) | (5b) | (5c) | |
| Asmari Fm. | √ | √ | √ | √ | √ | √ | × | × | × |
| Gachsaran Fm. | √ | × | √ | √ | √ | √ | √ | × | √ |
| Pabdeh Fm. | √ | × | √ | √ | √ | √ | √ | √ | √ |
| Geological Formation | L-Band | C-Band | X-Band | ||||||
|---|---|---|---|---|---|---|---|---|---|
| As. | Gs. | Pd. | As. | Gs. | Pd. | As. | Gs. | Pd. | |
| Inputs using the Conventional Geometry1 | 1.049 | 0.919 | 0.873 | 0.352 | 0.378 | 0.505 | 0.207 | 0.239 | 0.341 |
| Inputs using the Conventional Geometry2 | 0.985 | 0.799 | 0.834 | 0.375 | 0.309 | 0.506 | 0.232 | 0.283 | 0.355 |
| Inputs using the Power-law Geometry | 0.839 | 0.721 | 0.970 | 0.326 | 0.370 | 0.512 | 0.224 | 0.240 | 0.285 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghafouri, A.; Amini, J.; Dehmollaian, M.; Kavoosi, M.A. Better Estimated IEM Input Parameters Using Random Fractal Geometry Applied on Multi-Frequency SAR Data. Remote Sens. 2017, 9, 445. https://doi.org/10.3390/rs9050445
Ghafouri A, Amini J, Dehmollaian M, Kavoosi MA. Better Estimated IEM Input Parameters Using Random Fractal Geometry Applied on Multi-Frequency SAR Data. Remote Sensing. 2017; 9(5):445. https://doi.org/10.3390/rs9050445
Chicago/Turabian StyleGhafouri, Ali, Jalal Amini, Mojtaba Dehmollaian, and Mohammad Ali Kavoosi. 2017. "Better Estimated IEM Input Parameters Using Random Fractal Geometry Applied on Multi-Frequency SAR Data" Remote Sensing 9, no. 5: 445. https://doi.org/10.3390/rs9050445
APA StyleGhafouri, A., Amini, J., Dehmollaian, M., & Kavoosi, M. A. (2017). Better Estimated IEM Input Parameters Using Random Fractal Geometry Applied on Multi-Frequency SAR Data. Remote Sensing, 9(5), 445. https://doi.org/10.3390/rs9050445