Slope-Restricted Multi-Scale Feature Matching for Geostationary Satellite Remote Sensing Images
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
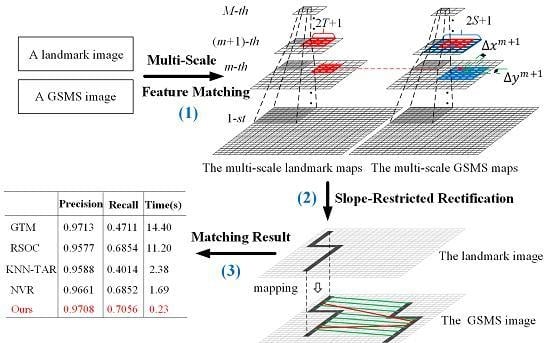
2.2. Multi-Scale Feature Matching
| Algorithm 1 Multi-Scale Feature Matching. |
| Input: The multi-scale landmark maps, the multi-scale feature maps and the multi-scale edge probability maps; Output: The matched pair set ; 1: for m from M to 1 do 2: for point in the m-th landmark map do 3: Determine the center of the searching window with Equations (6) and (7); 4: Seek the matched pair with local feature matching and add it into ; 5: end for 6: if m is larger than 1 then 7: Calculate the medians and from the offsets between the matched pairs in with Equations (8) and (9); 8 else 9: return as the matching result C; 10 end if 11: end for |
2.3. Slope-Restricted Rectification
| Algorithm 2 Slope-Restricted Rectification (SRR). |
| Input: The matched pair set C and the slope set ; Output: The rectification set ; 1: for n from 1 to N do 2: Select the K-nearest neighbor set and matched pair set for landmark ; 3: Calculate from the slopes relative to ; 4: for j from 1 to J do 5: if then 6: Find the matched pairs whose connections have slopes are equal to and add these pairs into ; 7: end if 8: end for 9: if is not null then 10: Calculate ; 11: if then 12: Add the matched pair into ; 13: else 14: Calculate and add the rectified pair into ; 15: end if 16: end if 17: end for |
3. Experimental Results and Discussion
3.1. Initial Matching Result Based on Multi-Scale Feature Matching
3.1.1. Parameter Setting
3.1.2. Comparative Analysis
3.2. Outliers Rectifying Based on SRR
3.2.1. Parameter Setting
3.2.2. Performance Analysis
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cheng, S.; Qiguang, M.; Pengfei, X. A novel algorithm of remote sensing image fusion based on Shearlets and PCNN. Neurocomputing 2013, 117, 47–53. [Google Scholar] [CrossRef]
- Ghahremani, M.; Ghassemian, H. Remote sensing image fusion using ripplet transform and compressed sensing. IEEE Geosci. Remote Sens. Lett. 2015, 12, 502–506. [Google Scholar] [CrossRef]
- Chen, L.; Ma, Y.; Liu, P.; Wei, J.; Jie, W.; He, J. A review of parallel computing for large-scale remote sensing image mosaicking. Clust. Comput. 2015, 18, 517–529. [Google Scholar] [CrossRef]
- Gong, M.; Zhou, Z.; Ma, J. Change detection in synthetic aperture radar images based on image fusion and fuzzy clustering. IEEE Trans. Image Process. 2012, 21, 2141–2151. [Google Scholar] [CrossRef] [PubMed]
- GJia, L.; Li, M.; Wu, Y.; Zhang, P.; Liu, G.; Chen, H.; An, L. SAR image change detection based on iterative label-information composite kernel supervised by anisotropic texture. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3960–3973. [Google Scholar]
- Li, X.; Shen, H.; Zhang, L.; Li, H. Sparse-based reconstruction of missing information in remote sensing images from spectral/temporal complementary information. ISPRS J. Photogramm. Remote Sens. 2015, 106, 1–15. [Google Scholar] [CrossRef]
- Díaz-Varela, R.A.; de la Rosa, R.; León, L.; Zarco-Tejada, P.J. High-resolution airborne UAV imagery to assess olive tree crown parameters using 3D photo reconstruction: Application in breeding trials. Remote Sens. 2015, 7, 4213–4232. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Zheng, L.; Wang, S.; Liu, Z.; Tian, Q. Packing and padding: Coupled multi-index for accurate image retrieval. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 July 2014; pp. 1939–1946. [Google Scholar]
- Zheng, L.; Wang, S.; Tian, Q. Coupled binary embedding for large-scale image retrieval. IEEE Trans. Image Process. 2014, 23, 3368–3380. [Google Scholar] [CrossRef] [PubMed]
- Sedaghat, A.; Mokhtarzade, M.; Ebadi, H. Uniform robust scale-invariant feature matching for optical remote sensing images. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4516–4527. [Google Scholar] [CrossRef]
- Qiu, P.; Liang, Y. The improved algorithm of remote sensing image registration based on SIFT and Contourlet transform. In Proceedings of the 2013 4th IEEE International Conference on Software Engineering and Service Science (ICSESS), Beijing, China, 23–25 May 2013; pp. 906–909. [Google Scholar]
- Fan, B.; Huo, C.; Pan, C.; Kong, Q. Registration of optical and SAR satellite images by exploring the spatial relationship of the improved SIFT. IEEE Geosci. Remote Sens. Lett. 2013, 10, 657–661. [Google Scholar] [CrossRef]
- Sedaghat, A.; Ebadi, H. Distinctive Order Based Self-Similarity descriptor for multi-sensor remote sensing image matching. ISPRS J. Photogramm. Remote Sens. 2015, 108, 62–71. [Google Scholar] [CrossRef]
- Belongie, S.; Malik, J.; Puzicha, J. Shape matching and object recognition using shape contexts. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 509–522. [Google Scholar] [CrossRef]
- Huang, L.; Li, Z.; Zhang, R. SAR and optical images registration using shape context. In Proceedings of the 2010 IEEE International Conference on Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25–30 July 2010; pp. 1007–1010. [Google Scholar]
- Shi, Q.; Ma, G.; Zhang, F.; Chen, W.; Qin, Q.; Duo, H. Robust image registration using structure features. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2045–2049. [Google Scholar]
- Gu, Y.; Ren, K.; Wang, P.; Gu, G. Polynomial fitting-based shape matching algorithm for multi-sensors remote sensing images. Infrared Phys. Technol. 2016, 76, 386–392. [Google Scholar] [CrossRef]
- Jiang, J.; Shi, X. A Robust Point-Matching Algorithm Based on Integrated Spatial Structure Constraint for Remote Sensing Image Registration. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1716–1720. [Google Scholar] [CrossRef]
- Le Moigne, J.; Campbell, W.J.; Cromp, R.F. An automated parallel image registration technique based on the correlation of wavelet features. IEEE Geosci. Remote Sens. Lett. 2002, 40, 1849–1864. [Google Scholar] [CrossRef]
- Le Moigne, J.; Zavorin, I.; Stone, H.S. On the use of wavelets for image registration. SPIE 2011, 99. [Google Scholar] [CrossRef]
- Murphy, J.M.; Le Moigne, J. Shearlet features for registration of remotely sensed multitemporal images. In Proceedings of the 2015 IEEE Conference on International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 1084–1087. [Google Scholar]
- Murphy, J.M.; Le Moigne, J.; Harding, D.J. Automatic image registration of multimodal remotely sensed data with global shearlet features. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1685–1704. [Google Scholar] [CrossRef]
- Szeliski, R. Computer Vision: Algorithms and Applications; Springer Science & Business Media: New York, NY, USA, 2010. [Google Scholar]
- Brodu, N.; Lague, D. 3D terrestrial lidar data classification of complex natural scenes using a multi-scale dimensionality criterion: Applications in geomorphology. ISPRS J. Photogramm. Remote Sens. 2012, 68, 121–134. [Google Scholar] [CrossRef]
- Huang, X.; Yang, W.; Zhang, H.; Xia, G. Automatic ship detection in SAR images using multi-scale heterogeneities and an a contrario decision. Remote Sens. 2015, 7, 7695–7711. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Wu, Y.; Ma, W.; Gong, M.; Su, L.; Jiao, L. A novel point-matching algorithm based on fast sample consensus for image registration. IEEE Geosci. Remote Sens. Lett. 2015, 12, 43–47. [Google Scholar] [CrossRef]
- Aguilar, W.; Frauel, Y.; Escolano, F.; Martinez-Perez, M.E.; Espinosa-Romero, A.; Lozano, M.A. A robust graph transformation matching for non-rigid registration. Image Vis. Comput. 2009, 27, 897–910. [Google Scholar] [CrossRef]
- Liu, Z.; An, J.; Jing, Y. A simple and robust feature point matching algorithm based on restricted spatial order constraints for aerial image registration. IEEE Trans. Geosci. Remote Sens. 2012, 50, 514–527. [Google Scholar] [CrossRef]
- Zhang, K.; Li, X.Z.; Zhang, J.X. A robust point-matching algorithm for remote sensing image registration. IEEE Geosci. Remote Sens. Lett. 2014, 11, 469–473. [Google Scholar] [CrossRef]
- Zeng, D.; Zhang, T.; Fang, R.; Shen, W.; Tian, Q. Neighborhood geometry based feature matching for geostationary satellite remote sensing image. Neurocomputing 2017, 236, 65–72. [Google Scholar] [CrossRef]
- National Satellite Meteorological Center. Available online: http://satellite.nsmc.org.cn/portalsite/default.aspx (accessed on 8 April 2017).
- Wessel, P.; Smith, W.H.F. A global, self-consistent, hierarchical, high-resolution shoreline. J. Geophys. Res. 1996, 101, 8741–8743. [Google Scholar] [CrossRef]
- Dollár, P.; Zitnick, C.L. Fast edge detection using structured forests. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1558–1570. [Google Scholar] [CrossRef] [PubMed]









| [15] | ||
|---|---|---|
| precision (%) | 59.87 | 93.31 |
| recall (%) | 53.24 | 76.65 |
| time (s) | 4920.79 | 1509.18 |
| precision (%) | 97.13 | 95.77 | 95.88 | 96.61 | 97.08 |
| recall (%) | 47.11 | 68.54 | 40.14 | 68.52 | 70.56 |
| time (s) | 14.40 | 11.20 | 2.38 | 1.69 | 0.23 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, D.; Wu, L.; Chen, B.; Shen, W. Slope-Restricted Multi-Scale Feature Matching for Geostationary Satellite Remote Sensing Images. Remote Sens. 2017, 9, 576. https://doi.org/10.3390/rs9060576
Zeng D, Wu L, Chen B, Shen W. Slope-Restricted Multi-Scale Feature Matching for Geostationary Satellite Remote Sensing Images. Remote Sensing. 2017; 9(6):576. https://doi.org/10.3390/rs9060576
Chicago/Turabian StyleZeng, Dan, Lidan Wu, Boyang Chen, and Wei Shen. 2017. "Slope-Restricted Multi-Scale Feature Matching for Geostationary Satellite Remote Sensing Images" Remote Sensing 9, no. 6: 576. https://doi.org/10.3390/rs9060576
APA StyleZeng, D., Wu, L., Chen, B., & Shen, W. (2017). Slope-Restricted Multi-Scale Feature Matching for Geostationary Satellite Remote Sensing Images. Remote Sensing, 9(6), 576. https://doi.org/10.3390/rs9060576