Exploiting Deep Matching and SAR Data for the Geo-Localization Accuracy Improvement of Optical Satellite Images
Abstract
:1. Introduction
1.1. Background and Motivation
1.2. Related Work
2. Deep Learning for Image Matching
2.1. Dilation
2.2. Network Architecture
2.3. SAR Image Pre-Processing
2.4. Matching Point Generation
2.5. Geo-Localization Accuracy Improvement
3. Experimental Evaluation and Discussion
3.1. Dataset Generation
3.2. Training Parameters
3.3. Influence of Speckle Filtering
3.4. Comparison of Network Architectures
3.5. Comparison to Baseline Methods
3.6. Outlier Removal
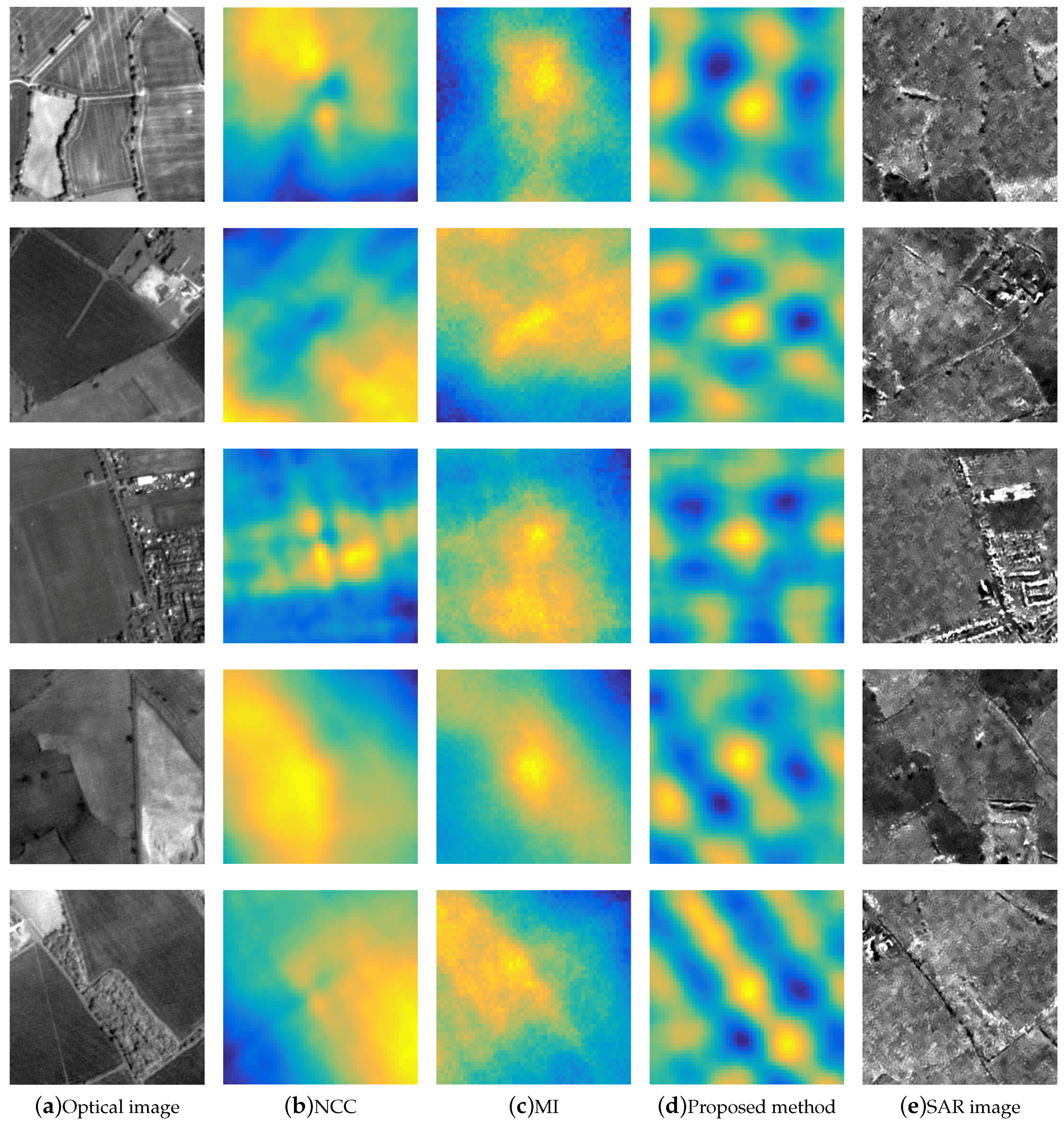
3.7. Qualitative Results
3.8. Limitations
3.9. Strengths
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Werninghaus, R.; Buckreuss, S. The TerraSAR-X Mission and System Design. IEEE Trans. Geosci. Remote Sens. 2010, 48, 606–614. [Google Scholar] [CrossRef]
- Eineder, M.; Minet, C.; Steigenberger, P.; Cong, X.; Fritz, T. Imaging Geodesy- Toward Centimeter-Level Ranging Accuracy with TerraSAR-X. IEEE Trans. Geosci. Remote Sens. 2011, 49, 661–671. [Google Scholar] [CrossRef]
- Cumming, I.; Wong, F. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation; Number Bd. 1 in Artech House Remote Sensing Library; Artech House: Boston, MA, USA; London, UK, 2005. [Google Scholar]
- Auer, S.; Gernhardt, S. Linear Signatures in Urban SAR Images—Partly Misinterpreted? IEEE Geosci. Remote Sens. Lett. 2014, 11, 1762–1766. [Google Scholar] [CrossRef]
- Reinartz, P.; Müller, R.; Schwind, P.; Suri, S.; Bamler, R. Orthorectification of VHR Optical Satellite Data Exploiting the Geometric Accuracy of TerraSAR-X Data. ISPRS J. Photogramm. Remote Sens. 2011, 66, 124–132. [Google Scholar] [CrossRef]
- Merkle, N.; Müller, R.; Reinartz, P. Registration of Optical and SAR Satellite Images based on Geometric Feature Templates. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, International Conference on Sensors & Models in Remote Sensing & Photogrammetry, Kish Island, Iran, 25–27 February 2015; Volume XL-1/W5, pp. 23–25. [Google Scholar]
- Perko, R.; Raggam, H.; Gutjahr, K.; Schardt, M. Using Worldwide Available TerraSAR-X Data to Calibrate the Geo-location Accuracy of Optical Sensors. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, IGARSS 2011, Vancouver, BC, Canada, 24–29 July 2011; pp. 2551–2554. [Google Scholar]
- Shi, W.; Su, F.; Wang, R.; Fan, J. A Visual Circle Based Image Registration Algorithm for Optical and SAR Imagery. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 2109–2112. [Google Scholar]
- Siddique, M.A.; Sarfraz, M.S.; Bornemann, D.; Hellwich, O. Automatic Registration of SAR and Optical Images Based on Mutual Information Assisted Monte Carlo. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 1813–1816. [Google Scholar]
- Suri, S.; Reinartz, P. Mutual-Information-Based Registration of TerraSAR-X and Ikonos Imagery in Urban Areas. IEEE Trans. Geosci. Remote Sens. 2010, 48, 939–949. [Google Scholar] [CrossRef]
- Hasan, M.; Pickering, M.R.; Jia, X. Robust Automatic Registration of Multimodal Satellite Images Using CCRE with Partial Volume Interpolation. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4050–4061. [Google Scholar] [CrossRef]
- Inglada, J.; Giros, A. On the Possibility of Automatic Multisensor Image Registration. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2104–2120. [Google Scholar] [CrossRef]
- Liu, X.; Lei, Z.; Yu, Q.; Zhang, X.; Shang, Y.; Hou, W. Multi-Modal Image Matching Based on Local Frequency Information. EURASIP J. Adv. Signal Process. 2013, 2013, 1–11. [Google Scholar] [CrossRef]
- Li, Q.; Qu, G.; Li, Z. Matching Between SAR Images and Optical Images Based on HOG Descriptor. In Proceedings of the IET International Radar Conference, Xi’an, China, 14–16 April 2013; pp. 1–4. [Google Scholar]
- Ye, Y.; Shen, L. HOPC: A Novel Similarity Metric Based on Geometric Structural Properties for Multi-modal Remote Sensing Image Matching. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, III-1, 9–16. [Google Scholar] [CrossRef]
- Hong, T.D.; Schowengerdt, R.A. A Robust Technique for Precise Registration of Radar and Optical Satellite Images. Photogramm. Eng. Remote Sens. 2005, 71, 585–593. [Google Scholar] [CrossRef]
- Li, H.; Manjunath, B.S.; Mitra, S.K. A Contour-Based Approach to Multisensor Image Registration. IEEE Trans. Image Process. 1995, 4, 320–334. [Google Scholar] [CrossRef] [PubMed]
- Pan, C.; Zhang, Z.; Yan, H.; Wu, G.; Ma, S. Multisource Data Registration Based on NURBS Description of Contours. Int. J. Remote Sens. 2008, 29, 569–591. [Google Scholar] [CrossRef]
- Dare, P.; Dowmanb, I. An Improved Model for Automatic Feature-Based Registration of SAR and SPOT Images. ISPRS J. Photogramm. Remote Sens. 2001, 56, 13–28. [Google Scholar] [CrossRef]
- Long, T.; Jiaoa, W.; Hea, G.; Zhanga, Z.; Chenga, B.; Wanga, W. A Generic Framework for Image Rectification Using Multiple Types of Feature. ISPRS J. Photogramm. Remote Sens. 2015, 102, 161–171. [Google Scholar] [CrossRef]
- Fan, B.; Huo, C.; Pan, C.; Kong, Q. Registration of Optical and SAR Satellite Images by Exploring the Spatial Relationship of the Improved SIFT. IEEE Geosci. Remote Sens. Lett. 2013, 10, 657–661. [Google Scholar] [CrossRef]
- Xu, C.; Sui, H.; Li, H.; Liu, J. An Automatic Optical and SAR Image Registration Method with Iterative Level Set Segmentation and SIFT. Int. J. Remote Sens. 2015, 36, 3997–4017. [Google Scholar] [CrossRef]
- Sui, H.; Xu, C.; Liu, J.; Hua, F. Automatic Optical-to-SAR Image Registration by Iterative Line Extraction and Voronoi Integrated Spectral Point Matching. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6058–6072. [Google Scholar] [CrossRef]
- Han, Y.; Byun, Y. Automatic and Accurate Registration of VHR Optical and SAR Images Using a Quadtree Structure. Int. J. Remote Sens. 2015, 36, 2277–2295. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep Learning-Based Classification of Hyperspectral Data. Sel. Top. Appl. Earth Obs. Remote Sens. IEEE J. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Liang, H.; Li, Q. Hyperspectral Imagery Classification Using Sparse Representations of Convolutional Neural Network Features. Remote Sens. 2016, 8, 99. [Google Scholar] [CrossRef]
- Wang, Q.; Lin, J.; Yuan, Y. Salient Band Selection for Hyperspectral Image Classification via Manifold Ranking. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1279–1289. [Google Scholar] [CrossRef] [PubMed]
- Mnih, V.; Hinton, G.E. Learning to Detect Roads in High-Resolution Aerial Images. In Proceedings of the 11th European Conference on Computer Vision, Heraklion, Crete, Greece, 5–11 September 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 210–223. [Google Scholar]
- Matthyus, G.; Wang, S.; Fidler, S.; Urtasun, R. HD Maps: Fine-grained Road Segmentation by Parsing Ground and Aerial Images. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Las Vegas, NV, USA, 27–30 June 2016; pp. 3611–3619. [Google Scholar]
- Geng, J.; Fan, J.; Wang, H.; Ma, X.; Li, B.; Chen, F. High-Resolution SAR Image Classification via Deep Convolutional Autoencoders. Geosci. Remote Sens. Lett. IEEE 2015, 12, 2351–2355. [Google Scholar] [CrossRef]
- Masi, G.; Cozzolino, D.; Verdoliva, L.; Scarpa, G. Pansharpening by Convolutional Neural Networks. Remote Sens. 2016, 8, 594. [Google Scholar] [CrossRef]
- Luo, W.; Schwing, A.G.; Urtasun, R. Efficient Deep Learning for Stereo Matching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Zbontar, J.; LeCun, Y. Stereo Matching by Training a Convolutional Neural Network to Compare Image Patches. J. Mach. Learn. Res. 2016, 17, 1–32. [Google Scholar]
- Bai, M.; Luo, W.; Kundu, K.; Urtasun, R. Exploiting Semantic Information and Deep Matching for Optical Flow. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 8–16 October 2016. [Google Scholar]
- Weinzaepfel, P.; Revaud, J.; Harchaoui, Z.; Schmid, C. DeepFlow: Large Displacement OpticalFlow with Deep Matching. In Proceedings of the IEEE Intenational Conference on Computer Vision (ICCV), Sydney, Australia, 1–8 December 2013. [Google Scholar]
- Altwaijry, H.; Trulls, E.; Hays, J.; Fua, P.; Belongie, S. Learning to Match Aerial Images with Deep Attentive Architectures. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Lin, T.Y.; Cui, Y.; Belongie, S.; Hays, J. Learning Deep Representations for Ground-to-Aerial Geolocalization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 5007–5015. [Google Scholar]
- Altwaijry, H.; Veit, A.; Belongie, S. Learning to Detect and Match Keypoints with Deep Architectures. In Proceedings of the British Machine Vision Conference (BMVC), York, UK, 19–22 September 2016. [Google Scholar]
- Bromley, J.; Guyon, I.; LeCun, Y.; Säckinger, E.; Shah, R. Signature Verification using a “Siamese” Time Delay Neural Network. In Proceedings of the Conference on Neural Information Processing Systems (NIPS), Denver, CO, USA, 28 November–1 December1994. [Google Scholar]
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P.A. Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion. J. Mach. Learn. Res. 2010, 11, 3371–3408. [Google Scholar]
- Fischer, A.; Igel, C. An Introduction to Restricted Boltzmann Machines. In Progress in Pattern Recognition, Image Analysis, Computer Vision, and Applications, Proceedings of the 17th Iberoamerican Congress, CIARP 2012, Buenos Aires, Argentina, 3–6 September 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 14–36. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–8 December 2012. [Google Scholar]
- Han, X.; Leung, T.; Jia, Y.; Sukthankar, R.; Berg, A.C. MatchNet: Unifying Feature and Metric Learning for Patch-Based Matching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Zagoruyko, S.; Komodakis, N. Learning to Compare Image Patches via Convolutional Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Simo-Serra, E.; Trulls, E.; Ferraz, L.; Kokkinos, I.; Fua, P.; Moreno-Noguer, F. Discriminative Learning of Deep Convolutional Feature Point Descriptors. In Proceedings of the International Conference on Computer Vision (ICCV), Santiago, Chile, 11–18 December 2015. [Google Scholar]
- Yu, F.; Koltun, V. Multi-Scale Context Aggregation by Dilated Convolutions. In Proceedings of the International Conference on Learning Representations (ICCV), San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the 32nd International Conference on Machine Learning (ICML-15), Lille, France, 6–11 July 2015. [Google Scholar]
- Deledalle, C.; Denis, L.; Tupin, F. Iterative Weighted Maximum Likelihood Denoising with Probabilistic Patch-Based Weights. IEEE Trans. Image Process. 2009, 18, 2661–2672. [Google Scholar] [CrossRef] [PubMed]
- Buades, A.; Coll, B. A Non-Local Algorithm for Image Denoising. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), San Diego, CA, USA, 20–26 June 2005. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014. [Google Scholar]
- Müller, R.; Krauß, T.; Schneider, M.; Reinartz, P. Automated Georeferencing of Optical Satellite Data with Integrated Sensor Model Improvement. Photogramm. Eng. Remote Sens. 2012, 78, 61–74. [Google Scholar] [CrossRef]
- Schneider, M.; Müller, R.; Krauss, T.; Reinartz, P.; Hörsch, B.; Schmuck, S. Urban Atlas—DLR Processing Chain for Orthorectification of PRISM and AVNIR-2 Images and TerraSAR-X as possible GCP Source. In Proceedings of the International Proceedings: 3rd ALOS PI Symposium, Kona, HI, USA, 9–13 November 2009. [Google Scholar]
- Bossard, M.; Feranec, J.; Otahel, J. CORINE Land Cover Technical Guide—Addendum 2000; European Environmental Agency: Copenhagen, Denmark, 2000. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving Deep Into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 11–18 December 2015. [Google Scholar]
- Burger, W.; Burge, M.J. Principles of Digital Image Processing: Core Algorithms, 1st ed.; Springer Publishing Company: London, UK, 2009. [Google Scholar]
- Walters-Williams, J.; Li, Y. Estimation of Mutual Information: A Survey. In Rough Sets and Knowledge Technology, Proceedings of the 4th International Conference, RSKT 2009, Gold Coast, Australia, 14–16 July 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 389–396. [Google Scholar]






| Methods | Matching Accuracy | Matching Precision | |||
|---|---|---|---|---|---|
| <2 pixels | <3 pixels | <4 pixels | avg (pixel) | (pixel) | |
| NCC | 2.94% | 7.92% | 13.01% | 9.92 | 4.04 |
| MI | 18.18% | 38.60% | 51.99% | 4.89 | 3.64 |
| CAMRI [10] | 33.55% | 57.06% | 79.93% | 2.80 | 2.86 |
| Ours | 25.40% | 49.60% | 64.28% | 3.91 | 3.17 |
| Ours (score) | 49.70% | 82.80% | 94.70% | 1.91 | 1.14 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Merkle, N.; Luo, W.; Auer, S.; Müller, R.; Urtasun, R. Exploiting Deep Matching and SAR Data for the Geo-Localization Accuracy Improvement of Optical Satellite Images. Remote Sens. 2017, 9, 586. https://doi.org/10.3390/rs9060586
Merkle N, Luo W, Auer S, Müller R, Urtasun R. Exploiting Deep Matching and SAR Data for the Geo-Localization Accuracy Improvement of Optical Satellite Images. Remote Sensing. 2017; 9(6):586. https://doi.org/10.3390/rs9060586
Chicago/Turabian StyleMerkle, Nina, Wenjie Luo, Stefan Auer, Rupert Müller, and Raquel Urtasun. 2017. "Exploiting Deep Matching and SAR Data for the Geo-Localization Accuracy Improvement of Optical Satellite Images" Remote Sensing 9, no. 6: 586. https://doi.org/10.3390/rs9060586
APA StyleMerkle, N., Luo, W., Auer, S., Müller, R., & Urtasun, R. (2017). Exploiting Deep Matching and SAR Data for the Geo-Localization Accuracy Improvement of Optical Satellite Images. Remote Sensing, 9(6), 586. https://doi.org/10.3390/rs9060586







