Geometry-Based Global Alignment for GSMS Remote Sensing Images
Abstract
:1. Introduction
2. Materials and Methods
2.1. Local Feature Matching by Geometric Coding
| Algorithm 1: Local feature matching. |
 |
2.2. Feature Refinement with Neighborhood Spatial Consistent Matching (NSCM)
2.3. Pixel Alignment Based on Polynomial Fitting
3. Results and Discussion
3.1. Dataset and Evaluation Criteria
3.2. Local Feature Matching by Geometric Coding
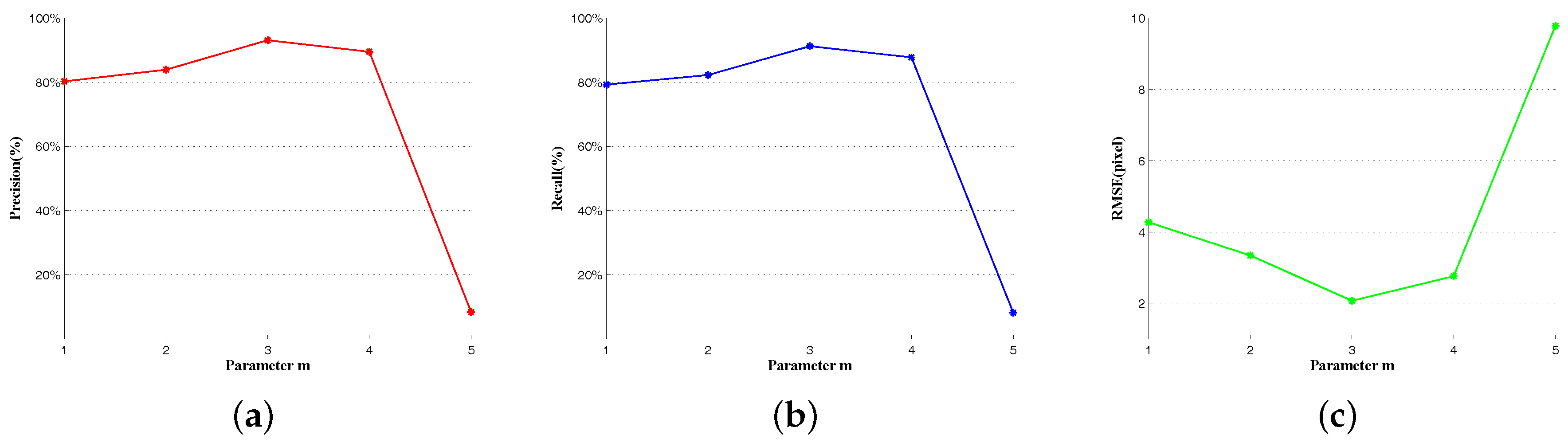
3.3. Feature Refinement with Neighborhood Spatial Consistent Matching (NSCM)
3.4. Comparison among Feature Matching Algorithms
3.5. Pixel Alignment Based on Polynomial Fitting
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zitova, B.; Flusser, J. Image registration methods: A survey. Image Vis. Comput. 2003, 21, 977–1000. [Google Scholar] [CrossRef]
- Govindarajulu, S.; Reddy, K.N.K. Image Registration on satellite Images. IOSR-JECE 2012, 3, 10–17. [Google Scholar] [CrossRef]
- Xing, C.; Qiu, P. Intensity-based image registration by nonparametric local smoothing. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 2081–2092. [Google Scholar] [CrossRef] [PubMed]
- Jung, J.S.; Song, J.H.; Kwag, Y.K. High precision automatic geocoding method of SAR image using GSHHS. In Proceedings of the 2011 3rd International Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Seoul, Korea, 26–30 September 2011; pp. 1–4. [Google Scholar]
- Jianbin, X.; Wen, H.; Zhe, L.; Yirong, W.; Maosheng, X. The study of rough-location of remote sensing image with coastlines. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium (IGARSS’03), Toulouse, France, 21–25 July 2003; Volume 6, pp. 3964–3966. [Google Scholar]
- Liu, X.; Tian, Z.; Leng, C.; Duan, X. Remote sensing image registration based on KICA-SIFT descriptors. In Proceedings of the 2010 Seventh International Conference on Fuzzy Systems and Knowledge Discovery (FSKD), Singapore, 10–12 August 2010; Volume 1, pp. 278–282. [Google Scholar]
- Wang, G.-H.; Zhang, S.-B.; Wang, H.B.; Li, C.-H.; Tang, X.-M.; Tian, J.J.; Tian, J. An algorithm of parameters adaptive scale-invariant feature for high precision matching of multi-source remote sensing image. In Proceedings of the 2009 Joint Urban Remote Sensing Event, Shanghai, China, 20–22 May 2009; pp. 1–7. [Google Scholar]
- Fan, B.; Huo, C.; Pan, C.; Kong, Q. Registration of optical and SAR satellite images by exploring the spatial relationship of the improved SIFT. IEEE Geosci. Remote Sens. Lett. 2013, 10, 657–661. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y.; Wei, H.; Liu, F. An ASIFT-based local registration method for satellite imagery. Remote Sens. 2015, 7, 7044–7061. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Wang, Q.; Zhu, G.; Yuan, Y. Statistical quantization for similarity search. Comput. Vis. Image Underst. 2014, 124, 22–30. [Google Scholar] [CrossRef]
- Goncalves, H.; Corte-Real, L.; Goncalves, J.A. Automatic image registration through image segmentation and SIFT. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2589–2600. [Google Scholar] [CrossRef]
- Ma, J.; Chan, J.C.W.; Canters, F. Fully automatic subpixel image registration of multiangle CHRIS/Proba data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2829–2839. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Zhou, W.; Lu, Y.; Li, H.; Song, Y.; Tian, Q. Spatial coding for large scale partial-duplicate web image search. In Proceedings of the 18th ACM International Conference on Multimedia, Firenze, Italy, 25–29 October 2010; pp. 511–520. [Google Scholar]
- Zhou, W.; Li, H.; Lu, Y.; Tian, Q. Large scale image search with geometric coding. In Proceedings of the 19th ACM International Conference on Multimedia, Scottsdale, AZ, USA, 28 November–1 December 2011; pp. 1349–1352. [Google Scholar]
- Zheng, L.; Wang, S. Visual phraselet: Refining spatial constraints for large scale image search. IEEE Signal Proc. Lett. 2013, 20, 391–394. [Google Scholar] [CrossRef]
- Aguilar, W.; Frauel, Y.; Escolano, F.; Martinez-Perez, M.E.; Espinosa-Romero, A.; Lozano, M.A. A robust graph transformation matching for non-rigid registration. Image Vis. Comput. 2009, 27, 897–910. [Google Scholar] [CrossRef]
- Shi, Q.; Ma, G.; Zhang, F.; Chen, W.; Qin, Q.; Duo, H. Robust image registration using structure features. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2045–2049. [Google Scholar]
- Izadi, M.; Saeedi, P. Robust weighted graph transformation matching for rigid and nonrigid image registration. IEEE Trans. Image Proc. 2012, 21, 4369–4382. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; An, J.; Jing, Y. A simple and robust feature point matching algorithm based on restricted spatial order constraints for aerial image registration. IEEE Trans. Geosci. Remote Sens. 2012, 50, 514–527. [Google Scholar] [CrossRef]
- Zhang, K.; Li, X.Z.; Zhang, J.X. A robust point-matching algorithm for remote sensing image registration. IEEE Geosci. Remote Sens. Lett. 2014, 11, 469–473. [Google Scholar] [CrossRef]
- Jiang, J.; Shi, X. A Robust Point-Matching Algorithm Based on Integrated Spatial Structure Constraint for Remote Sensing Image Registration. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1716–1720. [Google Scholar] [CrossRef]
- Zhao, M.; An, B.; Wu, Y.; Van Luong, H.; Kaup, A. RFVTM: A Recovery and Filtering Vertex Trichotomy Matching for Remote Sensing Image Registration. IEEE Trans. Geosci. Remote Sens. 2017, 55, 375–391. [Google Scholar] [CrossRef]
- Battiato, S.; Bruna, A.R.; Puglisi, G. A robust block-based image/video registration approach for mobile imaging devices. IEEE Trans. Multimed. 2010, 12, 622–635. [Google Scholar] [CrossRef]
- Elibol, A. A Two-Step Global Alignment Method for Feature-Based Image Mosaicing. Math. Comput. Appl. 2016, 21, 30. [Google Scholar] [CrossRef]
- Adams, A.; Gelfand, N.; Pulli, K. Viewfinder Alignment. In Computer Graphics Forum; Blackwell Publishing Ltd.: Oxford, UK, 2008; Volume 27, pp. 597–606. [Google Scholar]
- Learned-Miller, E.G. Data driven image models through continuous joint alignment. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 236–250. [Google Scholar] [CrossRef] [PubMed]
- Cox, M.; Sridharan, S.; Lucey, S.; Cohn, J. Least squares congealing for unsupervised alignment of images. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2008), Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Vedaldi, A.; Guidi, G.; Soatto, S. Joint data alignment up to (lossy) transformations. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2008), Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Tang, F.; Zou, X.; Yang, H.; Weng, F. Estimation and correction of geolocation errors in FengYun-3C Microwave Radiation Imager Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 407–420. [Google Scholar] [CrossRef]
- Wang, Q.; Zou, C.; Yuan, Y.; Lu, H.; Yan, P. Image registration by normalized mapping. Neurocomputing 2013, 101, 181–189. [Google Scholar] [CrossRef]
- Wang, Q.; Yuan, Y.; Yan, P.; Li, X. Saliency detection by multiple-instance learning. IEEE Trans. Cybern. 2013, 43, 660–672. [Google Scholar] [CrossRef] [PubMed]
- Dollár, P.; Zitnick, C.L. Structured forests for fast edge detection. In Proceedings of the 2013 IEEE International Conference on Computer Vision (ICCV), Sydney, Australia, 1–8 December 2013; pp. 1841–1848. [Google Scholar]
- Gao, J.; Kim, S.J.; Brown, M.S. Constructing image panoramas using dual-homography warping. In Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011; pp. 49–56. [Google Scholar]
- Zaragoza, J.; Chin, T.J.; Brown, M.S.; Suter, D. As-projective-as-possible image stitching with moving DLT. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Portland, OR, USA, 23–28 June 2013; pp. 2339–2346. [Google Scholar]
- Chang, C.H.; Sato, Y.; Chuang, Y.Y. Shape-preserving half-projective warps for image stitching. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Toronto, ON, Canada, 23–28 June 2014; pp. 3254–3261. [Google Scholar]








| precision (%) | 96.2 | 95.2 | 95.3 | 96.0 | 94.2 | 95.7 | 95.6 | 95.2 |
| recall (%) | 50.8 | 61.9 | 49.5 | 67.4 | 61.8 | 42.8 | 47.4 | 63.7 |
| RMSE (pixel) | 1.14 | 1.18 | 1.15 | 1.16 | 1.40 | 1.34 | 1.38 | 1.44 |
| time (s) | 0.48 | 1.08 | 18.12 | 16.21 | 10.92 | 2.91 | 2.74 | 1.89 |
| precision (%) | 92.9 | 92.9 | 93.0 |
| recall (%) | 68.2 | 57.5 | 91.2 |
| RMSE (pixel) | 2.33 | 2.45 | 2.06 |
| precision (%) | 96.2 | 93.0 |
| recall (%) | 50.8 | 91.2 |
| RMSE (pixel) | 1.14 | 2.06 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, D.; Fang, R.; Ge, S.; Li, S.; Zhang, Z. Geometry-Based Global Alignment for GSMS Remote Sensing Images. Remote Sens. 2017, 9, 587. https://doi.org/10.3390/rs9060587
Zeng D, Fang R, Ge S, Li S, Zhang Z. Geometry-Based Global Alignment for GSMS Remote Sensing Images. Remote Sensing. 2017; 9(6):587. https://doi.org/10.3390/rs9060587
Chicago/Turabian StyleZeng, Dan, Rui Fang, Shiming Ge, Shuying Li, and Zhijiang Zhang. 2017. "Geometry-Based Global Alignment for GSMS Remote Sensing Images" Remote Sensing 9, no. 6: 587. https://doi.org/10.3390/rs9060587
APA StyleZeng, D., Fang, R., Ge, S., Li, S., & Zhang, Z. (2017). Geometry-Based Global Alignment for GSMS Remote Sensing Images. Remote Sensing, 9(6), 587. https://doi.org/10.3390/rs9060587





