Seasonal and Interannual Variability of Columbia Glacier, Alaska (2011–2016): Ice Velocity, Mass Flux, Surface Elevation and Front Position

Abstract

Alaskan glaciers are among the largest contributors to sea-level rise outside the polar ice sheets. The contributions include dynamic discharge from marine-terminating glaciers which depends on the seasonally variable ice velocity. Columbia Glacier is a large marine-terminating glacier located in Southcentral Alaska that has been exhibiting pronounced retreat since the early 1980s. Since 2010, the glacier has split into two branches, the main branch and the west branch. We derived a 5-year record of surface velocity, mass flux (ice discharge), surface elevation and changes in front position using a dense time series of TanDEM-X synthetic aperture radar data (2011–2016). We observed distinct seasonal velocity patterns at both branches. At the main branch, the surface velocity peaked during late winter to midsummer but reached a minimum between late summer and fall. Its near-front velocity reached up to 14 m day${}^{-1}$ in May 2015 and was at its lowest speed of ~1 m day${}^{-1}$ in October 2012. Mass flux via the main branch was strongly controlled by the seasonal and interannual fluctuations of its velocity. The west branch also exhibited seasonal velocity variations with comparably lower magnitudes. The role of subglacial hydrology on the ice velocities of Columbia Glacier is already known from the published field measurements during summers of 1987. Our observed variability in its ice velocities on a seasonal basis also suggest that they are primarily controlled by the seasonal transition of the subglacial drainage system from an inefficient to an efficient and channelized drainage networks. However, abrupt velocity increase events for short periods (2014–2015 and 2015–2016 at the main branch, and 2013–2014 at the west branch) appear to be associated with strong near-front thinning and frontal retreat. This needs further investigation on the role of other potential controlling mechanisms. On the technological side, this study demonstrates the potential of high-resolution X-band SAR missions with a short revisit interval to examine glaciological variables and controlling processes.

1. Introduction

Although Alaskan glaciers comprise ~12% of the world’s glaciated areas outside the large ice sheets [1], they contributed only 8% (0.07 mm SLE yr${}^{-1}$) to the globally observed sea-level rise during 1901–2009 [2]. Columbia Glacier is a large marine-terminating glacier in Alaska, which has rapidly retreated, accelerated and contributed significantly to sea level rise since the early 1980s [3,4]. Out of 27 marine-terminating Alaskan glaciers, Columbia Glacier accounted for about one-fourth (0.010 ± 0.002 mm SLE yr${}^{-1}$) of the mass loss due to frontal ablation during 1985–2013 [3]. Dynamic discharge from marine-terminating glaciers is also a significant source of sea-level rise [5]. The magnitude of frontal ablation including ice discharge depends on ice velocity, which itself is influenced by the subglacial drainage system, surface melt and runoff, and dynamic adjustment to thinning and retreat of the ice front [6,7].

It has been reported that marine-terminating glaciers can exhibit strong seasonal surface velocity variations due to above-mentioned physical processes (e.g., [7]). For Alaska, Burgess et al. (2013) [8] reported that wintertime velocity variations are regulated by summer melt. Sugiyama et al. (2011) [9] observed, at Perito Moreno Glacier in Patagonia, a close relation between basal water pressure and surface velocity. They attributed this process to the input of meltwater exceeding the capacity of the subglacial drainage system as the melt season advances. During late summer, the drainage system is completely developed and thus efficiently routes the meltwater, causing water pressure and velocity to drop [10]. The water pressure and velocity might even drop further when a high capacity drainage system evacuates water from the unchannelized regions [11]. Moon et al. (2014) [7] presented seasonal velocity variations of marine-terminating glaciers in Greenland using time series of TerraSAR-X satellite data. Their observed glaciers exhibited strong seasonal variations driven by meltwater availability. A group of glaciers, abbreviated as type 2, showed velocities which are relatively stable from late summer through spring, with a strong early summer speedup and midsummer slowdown [7]. In most cases, winter speed remained lower than the peak summer speed. The velocity of other set of glaciers, abbreviated as type 3, started to decrease during high runoff periods and achieved a pronounced minimum during late summer, when runoff is low [7]. In addition to basal hydrology, Howat et al. (2008) [6] inferred that the terminus retreat can also contribute to the surface flow by weakening the resistive stress. The authors also concluded that the terminus retreat might be triggered in case of significant near-front thinning. Van der Veen (1996) [12] empirically linked the terminus retreat with the terminal thickness in case of Columbia Glacier and concluded that the terminus retreat is likely to trigger when the terminal thickness becomes less than 50 m above the (local) flotation thickness.

Columbia Glacier accelerated by a factor of six between 1982 and 2000 [4]. Measurements based on optical imagery during 1985–2013 [3] and TerraSAR-X in 2011 [13] confirmed the near-front speedup even in recent years. However, the very high surface velocities of Columbia Glacier limited the utility of many satellite systems due to their insufficient temporal resolution. For instance, Burgess (2013) [14] could not retrieve the surface velocities for Columbia Glacier using ALOS PALSAR imagery with a repeat cycle of 46 days. Therefore, most of the available surface velocity measurements on Columbia Glacier have been based on single or very few image pairs falling within a narrow period of a given year. The observed values were generally considered representative for an annual scale and do not necessarily reflect any seasonal variability. In 2010, Columbia Glacier split into two branches, abbreviated as the main and the west branch (Figure 1). Little is known about the seasonal ice dynamics of the branches and their governing mechanisms. In this study, we use a dense time series of TerraSAR-X and TanDEM-X satellite data (2011–2016) to estimate surface velocities and changes in frontal position of Columbia Glacier. We also measure the relative elevation changes of the radar scattering phase center (PC) over time (with reference to 06/18/2011) applying bistatic SAR interferometry on the TanDEM-X data. Elevation of the PC depicts the surface elevation during the melt seasons as the radar signal is attenuated due to the water content on the glacier surface. Combining velocities, limited surface elevation data, elevation changes of the PC and changes in front position, we examine the ice dynamics of Columbia Glacier after its split and the potential controlling processes.

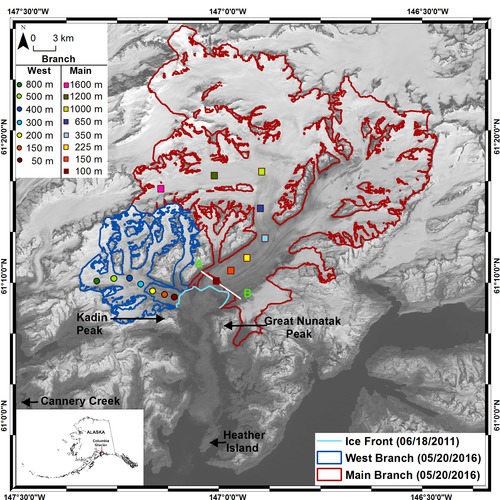
2. Study Area

Columbia Glacier (61.14${}^{\circ }$N, 147.10${}^{\circ }$W) is a large marine-terminating glacier located in Southcentral Alaska. The glacier extends from sea level to about 3050 m a.s.l. Due to its location in the Alaskan coastal range, the glacier experiences a maritime climate with mean annual precipitation of about 3080 mm yr${}^{-1}$ as measured at Cannery Creek Weather Station (61.01${}^{\circ }$N, 147.51${}^{\circ }$W, 26 m a.s.l.) during 1980–2015. Daily mean air temperatures at sea level rarely fall below −20 ${}^{\circ }$C in winter, but rise well above freezing point during spring and summer months.

In the following we outline some major facts about Columbia Glacier. The retreat and speedup of Columbia Glacier started in the 1980s and it is still ongoing. Although the glacier is grounded on its bed, part of its terminus might become afloat for brief periods. For instance, its terminus partially ungrounded in mid 2007 as it passed through an over-deepening region between Great Nunatak Peak and Kadin Peak (Figure 1) [15].

In 2010, the glacier split into two branches—the main and the west branch. As previous studies have revealed [13,16], the main branch comprises the main glacier flow and ice mass contribution. The catchment area of the main branch covers 752.9 km${}^2$ while the west branch covers only 109.4 km${}^2$ (May 2016). This reveals a loss in area of approximately 21.6% compared to ~1100 km${}^2$ in the early 1980s published by Krimmel et al. (2001) [4]. From 1957 to 2007, the mean thickness changed from 281 to 143 m with maximum thinning rates of 10 m yr${}^{-1}$ [13]. The modeled mean glacier-wide surface mass balance (SMB) was estimated to be −0.86 m w.e. yr${}^{-1}$ during 1995—2007 [17] and approximately −2.25 m w.e. yr${}^{-1}$ in 2010 [16]. These numbers show the large changes that occurred over the last 30 years at Columbia Glacier, but also indicate annual to multi-year differences of main glaciological observables (e.g., frontal change, mass balance, etc.).

3. Data

The TanDEM-X (TerraSAR-X add-on for Digital Elevation Measurement) is a German X-band radar mission operated by German Aerospace Center (DLR). This mission is a space-borne constellation of two X-band (3.1 cm wavelength) radar satellites [18,19]. The twin satellites, TerraSAR-X (TSX; launched on 06/15/2007) and TanDEM-X (TDX; launched on 06/21/2010), fly in a close helix orbit formation to acquire interferometric data [20]. Single images can be acquired in pursuit monostatic mode in which the satellite acts as both transmitter and receiver. In the bistatic mode of the satellite constellation, one of the satellites transmits the signal and both of them receive the backscattered signal, leading to two images being acquired simultaneously. The transmitting satellite is referred to as “active” and the other one as “passive”. The bistatic, single-pass configuration enables interferometric analysis specifically for elevation measurements without the limitations of changing surface conditions as in repeat-pass interferometric modes of previous missions (e.g., ERS-1/2).

Columbia Glacier had been defined as a super test site of the TanDEM-X mission, and hence data were acquired every 11 to 22 days during 2011−2014, but less frequently afterwards. The area was covered by ascending and descending orbit passes enabling the coverage of a majority of its catchment (~60% of the main branch and ~90% of the west branch). In addition, two monostatic TSX image pairs from September to October 2009 were also available. The active channel of monostatic and bistatic repeat acquisitions is utilized for the velocity measurements, while both channels are exploited for bistatic interferometric SAR processing (InSAR) to generate TanDEM-X DEMs. The bistatic scenes are composed of Coregistered Single Look Slant Range Complex (CoSSC) images. CoSSC images consist of already registered master (active channel) and slave (passive channel) Slant Look Complex (SLC) images. The multi-looked intensity images, generated from master SLCs, are used to manually delineate the glacier front position. A list of the data and its specifications is given in

Table 1. Specifications of TerraSAR-X and TanDEM-X stripmap mode datasets used for interferometric (InSAR) processing and intensity offset tracking (SV: Surface Velocity, EC: Elevation Change, AC: Area Change, MF: Mass Flux). The acquisition dates of the TerraSAR-X/TanDEM-X images used for deriving surface velocity, for generating TanDEM-X DEMs and for mapping glacier fronts are listed in Tables S1 and S2 in the supplementary material.

Acquisition Time	Orbital Pass	Depression Angle (${}^{\circ }$)	Az.(m) × Sl.Rg Resolution (m)	Product
2009	Ascending	58.98	2.06 × 0.90	SV
2009	Descending	54.55	1.89 × 1.36	SV
2011–2016	Ascending	49.63	2.0 × 0.90	SV, EC, AC, MF
2011–2016	Descending	46.82	1.84 × 0.90	SV, EC, AC, MF

.

The United States Geological Survey (USGS) digital elevation model (DEM) of 1957 is primarily used in the first iteration of geocoding the TanDEM-X DEMs. This DEM is the rasterized version of a topographic map at a scale of 1:63,360 provided by the USGS. Bed topography of Columbia Glacier, available from McNabb et al. (2012) [13], was derived by a mass conservation approach. The Cannery Creek weather station (ID- GHCND:USC00501240) is located about 27 km from Columbia Glacier. It continuously records daily minimum and maximum temperatures, snowfall (Figure 2a,b) and other meteorological variables.

4. Methods

4.1. Changes in Front Position

We multi-looked the master SLC images of TanDEM-X data by a factor of 5 in range and azimuth to generate speckle-reduced intensity images. The intensity images were geocoded using their corresponding TDX DEMs in an iterative approach (Section 4.3) and sampled with a spatial resolution of 10 m × 10 m. In case of unavailability of corresponding TDX DEMs, we geocoded the intensity images using the TDX DEM of 03/02/2012. The existing RGI 4.0 glacier inventory [21] was updated and the front position was regularly delineated using the time-series of intensity images. We used the terminus position of 06/18/2011 as a reference for measuring changes in front position during 2011–2016 (Figure 1). The errors are composed of a 5.4% error from RGI 4.0 glacier outline [22] and an uncertainty of ~2 pixels in the manual delineation of the glacier front. The approximate terminus width of the main branch and the west branch are ~8 km and ~3 km respectively. This leads to an estimated upper-bound error of about 5.5% for the area change measurements.

4.2. Surface Velocities

The TSX image pairs from 2009 and the TDX data during 2011–2016 were processed to obtain velocity fields using the SAR intensity offset tracking algorithm implemented in the GAMMA Remote Sensing software [23]. We precisely registered the master and slave data of the image pairs using a cross-correlation optimization technique [23,24,25] before implementing the tracking algorithm. The latter algorithm uses a normalized cross-correlation function based on a moving window and a predefined step size. Prominent structures or radar speckle in the moving window are identified in the amplitude image pairs to determine the displacement. A tracking window of 128 × 128 pixels (~116 m × ~237 m) in the range and azimuth directions and a step size of 30 × 30 pixels (~27 m × ~55 m) proved to be suitable for most of the image pairs. However, to track fast flowing features especially at the glacier terminus, we used a tracking window of 320 × 192 pixels (~290 m × ~355 m). A signal-to-noise ratio (SNR) threshold of 4.0 was taken as criterion to discard unreliable offset measurements. The velocity maps were subsequently geocoded using the TanDEM-X DEM acquired on 03/02/2012. A slant to ground range conversion was done by considering the local incidence angle computed from the DEM and orbital parameters of the respective master scene. In the last step, the displacement fields were scaled to daily velocities (m day${}^{-1}$).

Errors in the surface velocity measurements can be caused by inaccurate coregistration and errors in the tracking algorithm itself. The net error is the aggregated sum of these error contributions. We determined the coregistration error using 350 velocity measurements on stable ground (rocks and moraines). We estimated the root-mean-square error (RMSE) from these points resulting in an RMSE of <0.20 m day${}^{-1}$ in more than 90% of the image pairs. The error corresponding to the tracking algorithm ($e_t$) can be formulated as [13]

$$e_t=\frac{C▵x}{z▵t},$$

(1)

where (C) is the uncertainty of tracking algorithm (pixels), ($▵x$) is the pixel resolution in ground range geometry, (z) is the oversampling factor accounting for aliasing [24] and ($▵t$) is the time duration between master and slave image acquisitions. We assumed an uncertainty value (C) of 0.4 pixels and used an oversampling factor (z) of 2. The ground range resolution was computed for each image pair from the depression angle and range resolution of each data set (Table 1). The aggregate error amounts to <0.25 m day${}^{-1}$ for more than 90% of data pairs.

4.3. TanDEM-X DEM Generation

The DEM from TanDEM-X data is preferred when the data is acquired in a bistatic mode. Therefore, most of the TanDEM-X DEMs generated in this study belong to the period 2011–2014 as the TanDEM-X mission was operated in pursuit monostatic mode from October 2014 to February 2015. The TanDEM-X mission was set back to bistatic mode afterwards but with large spatial baselines (e.g., 700 m in some cases). With such large baselines radar interferometer loses its sensitivity to map elevation. Therefore, we could only process two bistatic scenes of 2015–2016 which had comparably short baselines (100–150 m).

We applied an interferometric processing approach in order to generate TanDEM-X DEMs [26]. The unwrapped phase ($\mathrm{\Phi }$) of the complex interferogram is related to the absolute height (h), while neglecting the phase related to motion, temporal decorrelation and atmospheric disturbances as can be assumed for bistatic interferometry [20], as

$$\mathrm{\Phi }=\frac{2\pi B_{per}h}{\lambda Rsin\theta },$$

(2)

where ($B_{per}$) is the perpendicular baseline, ($\lambda$) is the wavelength (3.1 cm for X-band), (R) is the slant range distance between sensor and the earth’s surface and ($\theta$) is the incidence angle. The simulation of two interferograms with 100 m height difference was chosen to precisely estimate the phase-to-height sensitivity and to account for its spatial variability depending on the sensor geometry. First we simulated the phase (${\mathrm{\Phi }}_{0.1}$) with $0.1$ m height in radar geometry and subtracted it from the complex interferometric phase to generate differential interferogram (${\mathrm{\Phi }}_d$) as

$${\mathrm{\Phi }}_d=\mathrm{\Phi }-\left({\mathrm{\Phi }}_{0.1}\right).$$

(3)

The phase noise associated with the differential interferogram was removed by a Goldstein filter with a filtering coefficient (${\alpha }_{filter}$) of 0.35 (${\alpha }_{filter}ϵ$ [0,1]). The areas of low coherence (<0.3), which mainly originate from layover, foreshortening, shadow [27] and water bodies, were masked out before unwrapping the differential phase with a Minimum Cost Flow (MCF) algorithm. The starting point of the phase unwrapping, referred to as the phase reference point, was taken on a stable and flat surface. The differential phase of this point was manually kept at 0.0 radians before phase unwrapping. We estimated the phase-to-height sensitivity ($\frac{\delta \mathrm{\Phi }}{\delta h}$ in radians m${}^{-1}$) by differencing the simulated phase for 100.1 m (${\mathrm{\Phi }}_{100.1}$) and 0.1 m (${\mathrm{\Phi }}_{0.1}$) in radar geometry, as calculated in Equation (4)

$$\frac{{\mathrm{\Phi }}_{100.1}}{100}-\frac{{\mathrm{\Phi }}_{0.1}}{100}=\frac{\delta \mathrm{\Phi }}{\delta h}(rad/m).$$

(4)

The unwrapped phase of the TDX differential interferogram was converted into elevation using the phase-to-height sensitivity. The phase to height conversion resulted in 0.0 m elevation of the phase reference point. This conversion also estimated the elevation of every pixel in the TanDEM-X scene relative to the phase reference point. The absolute elevation of this point ($h_{ref}$) was extracted from the reference DEM of 1957 and added to the relative DEMs. The resulting absolute elevation maps were geocoded from radar geometry using the DEM of 1957 and then in an iterative step with its own TDX elevations. The DEMs were generated with a spatial resolution of 10 m × 10 m.

4.4. Relative Elevation Changes of the Radar Scattering Phase Center

In this step, we measured relative elevation changes of the radar scattering phase center (PC) during 2011–2016. We used the TDX DEM of 06/18/2011 as reference and subtracted all subsequent DEMs from this reference TDX DEM of 2011. The location of the PC depends on the physical properties (e.g., roughness, structure and dielectric properties) of the surface and medium relative to the incident signal wavelength [28]. Hence, the seasonal change of the PC does not necessarily represent surface elevation changes, but the surface where the radar signal is reflected. Small amounts of liquid water on the glacier surface attenuate the radar signal substantially and therefore, the PC depicts the glacier surface, especially during the melt season [29]. However, fine-grained, cold snow is known as an almost transparent medium for X-band radar signals and radar penetration may reach up to several meters [30]. Also for frozen snow and firn radar penetration is known.

We measured the relative accuracy of the DEM differencing with 190 assessment points on rocky terrain of slope <10${}^{\circ }$. More than 80% of the DEM pairs show a root mean square error (RMSE) ranging from ±2.62 m to ±9.64 m. The error was mainly caused by the variable penetration depth of the X-band radar signal depending on the prevailing surface conditions (snow, no snow) as well as different heights of ambiguity (HoA) of the TDX pairs [31]. The summer comparisons reduced the error contributions (<±6.38 m) due to less penetration.

4.5. Mass Flux (Ice Discharge)

We estimated the mass flux through a flux gate near the terminus (08/02/2014) of the main branch of the glacier during 2011–2014 (see Figure 1). Ice thickness was calculated by subtracting the bed topography data [13] from the respective TanDEM-X DEMs. However, we restricted our mass flux estimations to the main branch since the bedrock reconstruction could be validated against field data for this branch only. In order to reduce the influence of seasonal variation of the X-band signal penetration, we approximated the ice thickness decrease with a linear trend based on an interpolation of the summer elevations between 07/21/2011 and 07/03/2014. The surface velocity was taken from the respective velocity fields year around. The gate was split into a number (n) of sections of constant length ($L_n$ = 20 m) and variable ice thickness ($H_n$) to compute the mass flux (F) as

$$F=\sum _{n}f*{\rho }_{ice}*L_n*H_n*{\vartheta }_n*sin\left({\alpha }_n\right),$$

(5)

where (f) is the ratio of surface-to-depth averaged velocity (f $ϵ$ [0.8,1]). For most tidewater glaciers the terminus velocity is driven by basal sliding [9] keeping the factor (f) closer to unity. We used a value of 0.93 ± 0.05 from the study by Andersen et al. (2015) [32] which covers fast flowing tidewater glaciers in Greenland. We assumed a mean ice density (${\rho }_{ice}$) of 917 kg m${}^{-3}$, (${\vartheta }_n$) is the magnitude of surface velocity and (${\alpha }_n$) is the angle of glacier flow direction with respect to the cross-sectional plane of the flux gate. Linear interpolation was applied where velocity data (${\vartheta }_n$) and the ice thickness ($H_n$) at a cell were missing for a given time step. Outliers of (${\alpha }_n$) were eliminated by setting a threshold of 90${}^{\circ }$ with reference to its deflection from the gate’s perpendicular direction. Applying error propagation, the error of the mass flux (F) is defined as

$${\epsilon }_F=\left|F\right|*\sqrt{[{\frac{{\delta }_f}{f}]}^2+[{\frac{{\delta }_H}{H}]}^2+[{\frac{{\delta }_{\vartheta }}{\vartheta }]}^2}$$

(6)

where ($\left|F\right|$) is the magnitude of mass flux and uncertainty in ice thickness (${\delta }_H$) is 26 m. The mean ice thickness (H) at the flux gate of the main branch is 105 m on the first sample date (07/21/2011) with values as high as 305 m at some points. The error in velocity (${\delta }_{\vartheta }$) <0.25 m day${}^{-1}$ in more than 90% of the data pairs, ($\vartheta$) is the mean velocity at the flux gate. No errors are included for the constant length ($L_n$) of 20 m and the assumed ice density (${\rho }_{ice}$). Therefore, the error amounts to ~25%.

5. Results

5.1. Surface Velocities

In Figure 2c,e and Figure 3a,b, we show the mean values of surface velocity and vertical change in PC during 2011−2016. The values are taken from the spatial subsets at different elevations (06/18/2011 TDX DEM) of 25 × 25 pixels, corresponding to ~255 m × 255 m on the ground, along the major flow lines of the main and the west branch. In Figure 2c, at the main branch a seasonal velocity pattern can be observed at elevations below 1000 m a.s.l. The highest velocities occurred from February to July (late winter–midsummer) and a pronounced minimum was noticed during September–October (late summer to fall). This seasonal pattern repeated every year during the observation period 2011–2016, but the magnitudes of the extreme values varied from year to year. The velocities near the terminus at M${}_{100}$ (Figure 2) were the lowest during October 2012 (~1 m day${}^{-1}$) while the highest flow was recorded in May 2015 (~14.38 m day${}^{-1}$). The velocities from September to October of 2009 (not shown in the plot) were comparable with the velocities during similar months of the time period 2011–2016.

The velocity of the west branch was comparably low during 2011–2013 with less seasonal variability (Figure 3a). During this period (2011–2013), the maximum velocity (6.47 m day${}^{-1}$ at W${}_{50}$) was observed in November 2011 (Figure 3a). However, from the beginning of 2014, the terminal velocity of the west branch became very high and reached up to 12.50 m day${}^{-1}$ during February–May 2015. These high velocities can also be observed at W${}_{200}$, located upglacier from its terminus position in May 2014, flowing with 10.5 m day${}^{-1}$. Similarly, the velocity at higher elevations, for instance W${}_{300}$, also rose significantly during 2014–2015. The terminus velocity reduced after the fall of 2015 and reached an annual maximum of ~9 m day${}^{-1}$ in February 2016.

5.2. Mass Flux

We observe that the seasonality of mass flux of the main branch varied synchronously with the surface velocities. Extrema vary by a factor of ten between 0.5 and 5 Mt day${}^{-1}$ (Figure 2d). We integrated the daily rates of mass flux (Mt day${}^{-1}$) to monthly rates, interpolated the data gaps and aggregated the values for the period between 2011 and 2014. The estimated averaged mass flux from the main branch amounted to ~1.18 ± 0.30 Gt yr${}^{-1}$ with a total of ~3.53 ± 0.90 Gt during 2011–2014.

5.3. Relative Elevation Changes of the Radar Scattering Phase Center

We mapped the elevation change of the radar scattering phase center (PC) with reference to its position on 06/18/2011. It was mapped with a high temporal resolution during 2011–2014 but limited afterwards due to data constraints. We noted two distinct patterns of elevation change of the PC during 2011–2014. The mean elevation change of the PC increases continuously in late winters while the peaks of elevation change can be observed between spring to midsummer (black line in Figure 2e and Figure 3b). At the main branch, this rise was most pronounced in June of 2012, but also observable in June of 2013 and March of 2014. The rise in the PC was also observed at the west branch in 2012, but the seasonal signal was accompanied by a strong drawdown in consecutive years. This change in the PC is influenced by the seasonally variable penetration depth of X-band radar signal into the glacier surface (snow, firn and ice) and thus does not depict the actual surface elevation change of the glacier throughout the year. However, we expect that the PC is located at the glacier surface when surface melt occurs. Hence, we used July for elevation change comparison. At the nearby glacier front of the main branch (M${}_{100}$), a positive elevation change (+7.6 m yr${}^{-1}$) was noticed during 2011–2012 followed by reductions in elevation in subsequent years (−16.3 m yr${}^{-1}$ in 2012–2013, −3.5 m yr${}^{-1}$ in 2013–2014).

The main branch went through a significant drawdown (~−32.5 m yr${}^{-1}$) during 2014–2016. The mean observations (black line in Figure 2e) followed the similar patterns of elevation change in these years. At the west branch, despite significant retreat of its terminus, its mean surface elevation was almost balanced in 2011–2012 (black line in Figure 3b). But it also went through significant elevation changes in consecutive years (~−44 m yr${}^{-1}$ in 2012–2013, ~−40 m yr${}^{-1}$ in 2013–2014, ~−41 m yr${}^{-1}$ in 2014–2016).

5.4. Changes in Front Position

Changes in the front positions of the main and the west branch are shown as changes in their area in Figure 2f and Figure 3c respectively. Although both the branches retreated during 2011–2016, their seasonal and interannual frontal changes differ considerably. In total, the west branch lost area much faster (9.30 km${}^2$) compared to the main branch (6.45 km${}^2$) in this period. The main branch repeatedly went through a retreat sequence during summer−fall, however, its terminus advanced during winter–spring. In terms of area changes, these repeated sequences of retreat and advance of the main branch were at the order of ~1 km${}^2$ during 2011–2013. However, it lost area about 2 km${}^2$ and 3 km${}^2$ in the summer-fall of 2014 and 2015, respectively, with relatively less area gain in the consecutive winter-spring. The west branch retreated significantly during summer–fall and maintained its front position (or minute advance) during winter-spring of 2011–2016 except 2014–2015. After the frontal retreat during summer–fall of 2013, the west branch continued to retreat throughout 2014 and lost 2.75 km${}^2$ of area until the spring of 2015 with a total area loss of ~6 km${}^2$.

6. Discussion

6.1. Terminus Change Rates, Velocity, Mass Flux and Elevation Change

Columbia Glacier has lost area at a rate of 0.64% yr${}^{-1}$ during 1980–2007 [4,16]. The west branch showed an even higher loss rate (1.56% yr${}^{-1}$) as compared to the main branch (0.17% yr${}^{-1}$) during 2011–2016. This corresponds to 2.81 km and 1.08 km mean length change of the terminus of the main branch and the west branch respectively. The glacier’s speed up since 1982 is quite evident and strongly linked with the fast glacier retreat [4]. The velocity of Krimmel (2001) [4]’s measurement point L${}_{50}$ (red circle in Figure 4) increased from <2 m day${}^{-1}$ in 1982 to ~8 m day${}^{-1}$ in 1998. Similarly, high velocities near its terminus was also noticed during 1980–2001 by O’Neel et al. (2005) [33]. Our results are in agreement with the observations of speedup and strong frontal retreat [4,16,33].

Nevertheless, the velocity observations by Krimmel (2001) and O’Neel et al. (2005) [4,33] are unevenly spaced in time and limited to few velocity estimates on an annual course. They, therefore, do not necessarily reflect any seasonal variability. Moreover, previous measurements during different time spans make direct comparison difficult. From 1985 to 2013, McNabb et al. (2015) [3] reported a mean ice flux of 2.6 Gt yr${}^{-1}$. They used the mean surface velocity (3.75 m day${}^{-1}$) through the flux gate and applied linear rates of surface change to fill temporal gaps of the DEMs during the study period. Their reported mass flux values are higher than those observed by us at the main branch (~1.18 ± 0.30 Gt yr${}^{-1}$). There may be various reasons for this: (i) our mass flux estimates correspond only to the main branch; (ii) different observation periods and most likely a different position of the flux gate used in McNabb et al. (2015) [3]; (iii) the seasonal variability of surface velocities were estimated using only few annual estimates; (iv) with the retreat on bedrock and split into two branches, surface lowering rates increased and flux was correspondingly reduced as well.

At the main branch, our mean elevation change of −3.09 m yr${}^{-1}$ (2011–2014) is slightly more negative compared to the long-term (1957–2007) change of −2.76 m yr${}^{-1}$ presented by McNabb et al. (2012) [13] for the entire glacier. Elevation change at the west branch is almost double (−5.65 m yr${}^{-1}$) during 2011–2014 than that observed by McNabb et al. (2012) [13]. O’Neel et al. (2005) [33] also reported an elevation change of ~12.5 m yr${}^{-1}$ during ~1977–2001, close to L${}_{50}$ (Figure 4). We observed a large interannual variability of elevation change with values ranging from +7 m yr${}^{-1}$ to −40 m yr${}^{-1}$ at the terminus. These strong interannual variations are most likely caused by the highly varying precipitation in Alaska’s coastal region as highlighted by O’Neel (2012) [16] during 1978–2010. Our differences with the published elevation change measurements in McNabb et al. (2012) and Krimmel (2001) [13,33] can be attributed primarily to different observation periods and measurement techniques. We showed short-term changes which these studies lack.

6.2. Variations in Ice Dynamics during 2011–2016

We observed distinct seasonal velocity patterns at the main and the west branch of Columbia Glacier during 2011–2016. The main branch flowed with high velocities during late winter to midsummer but the velocity declined towards autumn with a subsequent increase during winter again. The west branch has also seasonal velocity fluctuations with comparably lower magnitudes. We hypothesize that the development of the basal drainage system primarily controlled these seasonal velocity patterns. We expect that the subglacial drainage system was not yet sufficiently developed to fully route the meltwater in winter and the early melt season [10]. This increased the basal water pressure leading to an increase in basal motion and surface velocity of the glacier. During late summer the drainage system was fully formed to channelize the flow of the water. This caused a drop in basal water pressure at the bed outside the channels and correspondingly reduced velocity. As the season changed from autumn to winter, the drainage channels tended to close due to viscous deformation [34]. Consequently, the summer meltwater, retained in the firn and ice body could not be drained effectively through the channels and lubricated the ice-bed interface, leading to an increase in velocity. The loop closed when the drainage system started to develop again in the consecutive spring. Previous studies at Columbia Glacier [33,35,36] support our hypothesis by showing a link between velocity variations and subglacial hydrology. In order to show this link, O’Neel et al. (2005) and Kamb et al. (1994) [33,36] observed ice velocity, basal water pressure and rainfall data at Columbia Glacier on a diurnal scale between 07/05/1987 and 08/31/1987. Similarly, Sugiyama et al. (2011) [9] observed the coupling of ice dynamics to basal water pressure on Perito Moreno Glacier in Patagonia. The observed flow regime of the main branch is similar to the type 3 behavior of tidewater glaciers in Greenland [7]. These authors also attributed type 3 behavior to seasonal alteration between inefficient to efficient subglacial drainage system.

Although the seasonal behavior was consistent in every year of our observations, the magnitude of interannual surface velocity varied (e.g., the terminus velocity of ~6.5 m day${}^{-1}$ and ~1 m day${}^{-1}$ in autumn of 2011 and 2012, respectively). We could not observe a direct link or correlation to the meteorological variables. Also, no melt amount was available to test the hypothesis of Burgess et al. (2013) [8] of summer melt regulating winter glacier flow. One explanation might be that the variation in interannual velocity depended on the hydraulic capacity of the drainage system and its connectivity to the unchannelized drainage system [11].

After 2014, the rise in surface flow of the main branch coincided with its strong frontal retreat (Figure 2c,f). To explain the frontal retreat, we assume that the ice might be floating, and hence prone to retreat, if the near front surface elevation ($H_f$), above the sea surface, satisfies Equation (7), defined as

$$H_f<(\frac{{\rho }_{water}}{{\rho }_{ice}}-1)*H_s$$

(7)

where ($H_s$) is the depth of submerged ice, (${\rho }_{ice}$) and (${\rho }_{water}$) are the densities of ice (917 kg m${}^{-3}$) and water (1030 kg m${}^{-3}$) respectively. Krimmel (2001) [4] reported up to 400 m water depths of Columbia Glacier forebay based on boat-borne fathometer observations during 1995–1997 (his Figure 18). Recently, Boldt et al. (2016) [37] also showed an updated bathymetry of the fjord (2011) of maximum 420 m below sea level (their Figure 1). The terminus has retreated further behind their [4,37] water depth estimates and no other bathymetric measurements, especially nearby the terminus position during 2011–2016, are available in Columbia Bay. Therefore, we assumed a maximum water depth of 400 m which is equal to the depth of submerged ice ($H_s$) when the ice is grounded. Feeding the known variables in the Equation (7) indicates that the ice might be floating if $H_f$ is less than ~50 m. Hence, we analyzed those areas where less $H_f$ is less than 50 m during 2011–2016 (Figure 5) to check whether the retreat was triggered in those areas.

The terminus of the main branch was almost stable during 2011–2012 and positive elevation changes were observed in this period (Figure 2e). Only few areas showed $H_f$ less than 50 m (panel 06/15/2012 in Figure 5). However, more areas had thinned during 2014–2016 (panels 06/22/2014, 11/04/2015, 05/20/2016 in Figure 5). These thinned areas (zones C and D in Figure 4) have undergone significant retreat during 2014–2016. Zones A and D even retreated during 2011–2014 but the retreat was insignificant (Figure 4). In contrary to this, zone B had been almost stable during 2011–2016 which can be explained by its high surface elevation ($H_f$ > 50). We expect that extreme near-front thinning caused the main branch to retreat at times.

At the west branch, we also observed a close link between frontal retreat, thinning and ice velocity. The branch retreated almost twice as much in 2011 as compared to the retreat in 2012 (Figure 3c). This is most likely because the ice was thinner at more areas in 2011 compared to 2012 (panels 06/18/2011 and 06/15/2012 in Figure 6). In 2013 (panel 06/13/2013 in Figure 6), thinning increased, which might have triggered a very strong frontal retreat lasting almost 2 years (2013–2015). This major retreat sequence even broke the seasonality pattern of the terminus position (advance during winter–spring and retreat during summer–fall). The terminus of the west branch did not retreat much during summer–fall of 2015 and was almost balanced after the major retreat event. The velocities also reduced after the summers of 2015 and did not reach as high values as in 2014. This is also in line with the surface elevations in 2015–2016 (panels 04/11/2015, 05/20/2016 in Figure 6) when fewer areas had elevations below 50 m.

We give a hypothesis in order to explain such events at both the branches when very high surface velocities were associated with major retreating sequences and strong near-front thinning. We expect that the retreat was probably triggered by strong ice thinning which also caused reduction of resistive stress greater than the reduction of driving stress. Consequently friction at the bed decreased, inducing speedup. Similar conclusions were obtained by Howat et al. (2008) [6] in Greenland. At Columbia Glacier, O’Neel et al. (2005) [33] also found little correspondence between driving stress and ice velocity but the basal drag (a part of resistive stress) played a significant role for the same. The controlling processes for calving are an active area of research [38]. We stress that the role of driving and resistive stresses, bedrock topography, ice-ocean interaction, tidal influence and changes in water column temperature on the ice dynamics of Columbia Glacier need to be further investigated.

7. Conclusions

We presented the analysis of a new dataset (TanDEM-X) on changes in surface velocity, mass flux (only at the main branch during 2011–2014), surface elevation and front position of Columbia Glacier, Alaska during 2011–2016. Our results support the hypothesis that the transition from an inefficient to an efficient subglacial drainage system and associated changes in basal water pressure are primarily responsible for seasonal changes of the surface velocity of Columbia Glacier. This hypothesis is supported by the field investigations carried out at Columbia Glacier during summers of 1987. However, for short durations (2014–2015 and 2015–2016 at the main branch, and 2013–2014 at the west branch), an abrupt rise in surface velocity was coincident with strong frontal retreat and extreme near-front thinning. It appears that these retreat sequences were strong enough to break the seasonality of the front position of the west branch, in particular during 2013–2014 when it’s near front thinned incredibly (Figure 6). We expect that these strong retreat sequences initiated by near-front thinning which further reduced resistive stress and effective pressure, inducing the glacier flow. However, we stress that the influence of other physical variables (e.g., bedrock topography, tidal influence) on the ice dynamics of Columbia Glacier need further consideration and investigation. The mass flux from the main branch varied with the surface velocity. We stress that the seasonality and interannual velocity changes should be considered in order to precisely estimate frontal ablation including ice discharge.

We also conclude that short observation intervals are required in order to avoid decorrelation due to structural changes, especially for fast flowing glaciers like Columbia Glacier. The high temporal and spatial resolution of the German TanDEM-X mission is of additional benefit for tracking surface structures, especially for fast moving glaciers like Columbia Glacier, and delineating the front position. The time series of bistatic acquisitions proved to be highly suitable in deriving high-resolution DEMs (surface elevation) without the limitation of temporal decorrelation and estimating relative elevation changes during melt seasons. The X-band signal of TanDEM-X can be strongly influenced by the prevailing surface conditions (melt and freeze of firn and snow) and thus limits elevation change measurements.