On the Design of Radar Corner Reflectors for Deformation Monitoring in Multi-Frequency InSAR
Abstract
:1. Introduction
- what size of target is suitable for use with the commonly employed SAR frequencies,
- to what extent one size of target can be effectively used across all SAR frequencies, and
- what considerations should be made with respect to manufacturing and long-term or permanent installation of artificial targets.
2. Theoretical Considerations
2.1. Amplitude Measurements
2.2. Phase Measurements
2.3. Target RCS Requirements
2.4. Target Design
3. Manufacturing and Design Considerations
3.1. Losses Due to Manufacturing
3.2. Other Design Features
3.3. Target Characterisation
4. Field Experiments
4.1. Test Site
4.2. Target Alignment
4.3. SAR Imagery
4.4. Image Processing Methodology
- Read the SLC imagery and convert to Sigma Nought. For TSX and CSK this involves applying the annotated product calibration factor and then scaling the image by to get Sigma Nought. For RSAT-2 this involves applying the provided Sigma Nought look-up table.
- For each SAR sensor, coregister all SLC images to a single master image (chosen to be the earliest acquisition). Verify the co-registration of each image and determine the range (column) and azimuth (row) coordinates of each TCR in the co-registered images.
- Define a ‘target window’ that encompasses the impulse response of the target and four ‘clutter regions’ in the quadrants surrounding the side lobe response of the target (Figure 7b).
- Determine the mean signal clutter in the four ‘clutter regions’. By computing the clutter level as the mean of all pixel values falling within standard-sized windows, a representative view of the actual reflector RCS and SCR is obtained that removes any bias associated with the common practice of manually choosing the location of windows to sample only the lowest clutter in the general surrounds of the target.
- Calculate the integrated point target energy:where is the integrated (summed) energy in the ‘target window’, is the total integrated energy in the four ‘clutter regions’, is the number of samples contained within the four ‘clutter regions’ and is the number of samples in the ‘target window’.
- Compute the RCS of the point target by multiplying the integrated point target energy by the area of the ground range resolution cell:
- Compute the SCR; the ratio between the point target energy corrected for clutter and the average clutter level per pixel:
- Compute the phase error (Equation (4)) and convert to LOS displacement error (Equation (5)).
5. Results
5.1. Clutter Intensity
5.2. Radar Cross Section
5.3. Impact of Misalignment
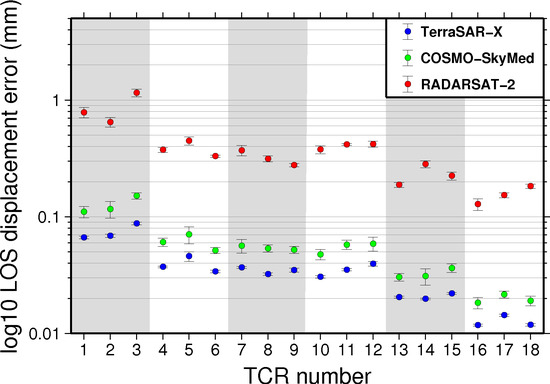
5.4. Displacement Error
6. Discussion
7. Conclusions
Acknowledgments
Conflicts of Interest
References
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Hooper, A.; Zebker, H.; Segall, P.; Kampes, B. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers. Geophys. Res. Lett. 2004, 31, L23611. [Google Scholar] [CrossRef]
- Kampes, B.M. Radar Interferometry—Persistent Scatterer Technique; Springer: Dordrecht, The Netherlands, 2006. [Google Scholar]
- Hooper, A.; Bekaert, D.; Spaans, K.; Arıkan, M. Recent advances in SAR interferometry time series analysis for measuring crustal deformation. Tectonophysics 2012, 514–517, 1–13. [Google Scholar] [CrossRef]
- Crosetto, M.; Monserrat, O.; Cuevas-González, M.; Devanthéry, N.; Crippa, B. Persistent scatterer interferometry: A review. ISPRS J. Photogramm. Remote Sens. 2016, 115, 78–89. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry—Data Interpretation and Error Analysis; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Ketelaar, V.B.H. Satellite Radar Interferometry—Subsidence Monitoring Techniques; Springer: Dordrecht, The Netherlands, 2009. [Google Scholar]
- Fu, W.; Guo, H.; Tian, Q.; Guo, X. Landslide monitoring by corner reflectors differential interferometry SAR. Int. J. Remote Sens. 2010, 31, 6387–6400. [Google Scholar] [CrossRef]
- Li, C.; Yin, J.; Zhao, J.; Zhang, G.; Shan, X. The selection of artificial corner reflectors based on RCS analysis. Acta Geophys. 2012, 60, 43–58. [Google Scholar] [CrossRef]
- Qin, Y.; Perissin, D.; Lei, L. The design and experiments on corner reflectors for urban ground deformation monitoring in Hong Kong. Int. J. Antennas Propag. 2013, 2013, 191685. [Google Scholar] [CrossRef]
- Strozzi, T.; Teatini, P.; Tosi, L.; Wegmüller, U.; Werner, C. Land subsidence of natural transitional environments by satellite radar interferometry on artificial reflectors. J. Geophys. Res. Earth Surf. 2013, 118, 1177–1191. [Google Scholar] [CrossRef]
- Caro-Cuenca, M.; Dheenathayalan, P.; Van-Rossum, W.; Hoogeboom, P. Deployment and design of bi-directional corner reflectors for optimal ground motion monitoring using InSAR. In Proceedings of the 10th European Conference on Synthetic Aperture Radar, Berlin, Germany, 3–5 June 2014; pp. 1–4. [Google Scholar]
- Mahapatra, P.S.; Samiei-Esfahany, S.; van der Marel, H.; Hanssen, R.F. On the use of transponders as coherent radar targets for SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1869–1878. [Google Scholar] [CrossRef]
- Singleton, A.; Li, Z.; Hoey, T.; Muller, J.P. Evaluating sub-pixel offset techniques as an alternative to D-InSAR for monitoring episodic landslide movements in vegetated terrain. Remote Sens. Environ. 2014, 147, 133–144. [Google Scholar] [CrossRef]
- Ferretti, A.; Savio, G.; Barzaghi, R.; Borghi, A.; Musazzi, S.; Novali, F.; Prati, C.; Rocca, F. Submillimeter accuracy of InSAR time series: Experimental validation. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1142–1153. [Google Scholar] [CrossRef]
- Marinkovic, P.; Ketelaar, G.; van Leijen, F.; Hanssen, R. InSAR quality control: Analysis of five years of corner reflector time series. In Proceedings of the Fringe 2007 Workshop (ESA SP-649), Frascati, Italy, 26-30 November 2007; pp. 26–30. [Google Scholar]
- Dheenathayalan, P.; Small, D.; Schubert, A.; Hanssen, R.F. High-precision positioning of radar scatterers. J. Geod. 2016, 90, 403–422. [Google Scholar] [CrossRef]
- Gisinger, C.; Willberg, M.; Balss, U.; Klügel, T.; Mähler, S.; Pail, R.; Eineder, M. Differential geodetic stereo SAR with TerraSAR-X by exploiting small multi-directional radar reflectors. J. Geod. 2017, 91, 53–67. [Google Scholar] [CrossRef]
- Freeman, A. SAR calibration: An overview. IEEE Trans. Geosci. Remote Sens. 1992, 30, 1107–1121. [Google Scholar] [CrossRef]
- Curlander, J.C.; McDonough, R.N. Synthetic Aperture Radar Systems and Signal Processing; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1991. [Google Scholar]
- Skolnik, M.I. Radar Handbook; McGraw-Hill: New York, NY, USA, 1970. [Google Scholar]
- Dong, Y. L-Band VV Clutter Analysis for Natural Land in Northern Territory; DSTO-RR-0254; Defence Science and Technology Organisation: Salisbury, Australia, 2003.
- Ketelaar, V.B.H.; Marinkovic, P.; Hanssen, R.F. Validation of point scatterer phase statistics in multi-pass InSAR. In Proceedings of the 2004 Envisat and ERS Symposium, Salzburg, Austria, 6–10 September 2004; European Space Agency: Salzburg, Austria, 2005. [Google Scholar]
- Adam, N.; Kampes, B.; Eineder, M. Development of a scientific permanent scatterer system: Modications for mixed ERS/Envisat time series. In Proceedings of the 2004 Envisat and ERS Symposium, Salzburg, Austria, 6–10 September 2004; European Space Agenc: Salzburg, Austria, 2005. [Google Scholar]
- Knott, E.F. Radar Cross Section Measurements; SciTech Publishing, Inc.: Raleigh, NC, USA, 2006. [Google Scholar]
- Doerry, A.W.; Brock, B.C. Radar Cross Section of Triangular Trihedral Reflector with Extended Bottom Plate; SAND2009-2993; Sandia National Laboratories: Albuquerque, NM, USA, 2009.
- Bird, P.J.; Keyte, G.E.; Kenward, D.R.D. An experiment for the radiometric calibration of the ERS-1 SAR. Can. J. Remote Sens. 1993, 19, 232–238. [Google Scholar] [CrossRef]
- Döring, B.J.; Schwerdt, M.; Bauer, R. TerraSAR-X calibration ground equipment. In Proceedings of the Wave Propagation in Communication, Microwave Systems and Navigation (WFMN07), Chemnitz, Germany, 4–5 July 2007; pp. 86–90. [Google Scholar]
- Shimada, M.; Isoguchi, O.; Tadono, T.; Isono, K. PALSAR radiometric and geometric calibration. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3915–3932. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, C.; Ma, L.; Yang, M.Y.; Liu, Q. Improved trihedral corner reflector for high-precision SAR calibration and validation. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 454–457. [Google Scholar]
- Sarabandi, K.; Tsen-Chieh, C. Optimum corner reflectors for calibration of imaging radars. IEEE Trans. Antennas Propag. 1996, 44, 1348–1361. [Google Scholar] [CrossRef]
- Ruck, G.T. Radar Cross Section Handbook; Plenum Publishing Corporation: New York, NY, USA, 1970; Volume 2. [Google Scholar]
- Döring, B.; Schmidt, K.; Jirousek, M.; Rudolf, D.; Reimann, J.; Raab, S.; Antony, J.; Schwerdt, M. Hierarchical bayesian data analysis in radiometric SAR system calibration: A case study on transponder calibration with RADARSAT-2 data. Remote Sens. 2013, 5, 6667–6690. [Google Scholar] [CrossRef]
- Robertson, S.D. Targets for microwave radar navigation. Bell Syst. Tech. J. 1947, 26, 852–869. [Google Scholar] [CrossRef]
- Zink, M.; Kietzmann, H. Next Generation SAR—External Calibration; German Aerospace Center (DLR): Köln, Germany, 1995; p. 45. [Google Scholar]
- Garthwaite, M.C.; Nancarrow, S.; Hislop, A.; Thankappan, M.; Dawson, J.H.; Lawrie, S. Design of Radar Corner Reflectors for the Australian Geophysical Observing System; Geoscience Australia: Canberra, Australia, 2015.
- Wegmüller, U.; Werner, C. Gamma SAR processor and interferometry software. In Proceedings of the 3rd ERS Scientific Symposium, Florence, Italy, 17–20 March 1997; European Space Agency: Florence, Italy, 1997. [Google Scholar]
- Gray, A.L.; Vachon, P.W.; Livingstone, C.E.; Lukowski, T.I. Synthetic aperture radar calibration using reference reflectors. IEEE Trans. Geosci. Remote Sens. 1990, 28, 374–383. [Google Scholar] [CrossRef]
- Pettinato, S.; Santi, E.; Paloscia, S.; Pampaloni, P.; Fontanelli, G. The intercomparison of X-band SAR images from COSMO‑SkyMed and TerraSAR-X satellites: Case studies. Remote Sens. 2013, 5, 2928–2942. [Google Scholar] [CrossRef]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.; Floury, N.; Brown, M.; et al. GMES Sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- Garthwaite, M.C.; Hazelwood, M.; Nancarrow, S.; Hislop, A.; Dawson, J.H. A regional geodetic network to monitor ground surface response to resource extraction in the northern Surat Basin, Queensland. Aust. J. Earth Sci. 2015, 62, 469–477. [Google Scholar] [CrossRef]














| Band | Sensor | Image Mode | Pixel Resolution (m) | Ground Range Resolution Area (m2) | Clutter (dB) | Pixel RCS (dBm2) | Required SCR (dB) | Required RCS (dBm2) | Equivalent Triangular Trihedral CR Size (m) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Azimuth | Slant Range | Ground Range | |||||||||
| X (9.65 GHz) | TerraSAR-X 1 | Staring Spotlight | 0.24 | 0.6 | 1.0 | 0.3 | −10 | −16.0 | 25 | 9.0 | 0.2 |
| High Res Spotlight | 1.1 | 1.2 | 2.1 | 2.3 | −10 | −6.4 | 25 | 18.6 | 0.4 | ||
| Stripmap | 3.3 | 1.2 | 2.1 | 6.9 | −10 | −1.6 | 25 | 23.4 | 0.5 | ||
| ScanSAR (4 beam) | 18.5 | 1.2 | 2.1 | 38.7 | −10 | 5.9 | 25 | 30.9 | 0.7 | ||
| COSMO-SkyMed 2 | Spotlight | 1.0 | 1.2 | 2.0 | 2.0 | −10 | −7.0 | 25 | 18.0 | 0.3 | |
| HIMAGE (Stripmap) | 3.0 | 3.5 | 6.0 | 18.1 | −10 | 2.6 | 25 | 27.6 | 0.6 | ||
| Wideregion (ScanSAR) | 16.0 | 8.1 | 14.1 | 225.5 | −10 | 13.5 | 25 | 38.5 | 1.1 | ||
| C (5.41 GHz) | Sentinel-1 3 | Stripmap | 5.0 | 5.0 | 8.7 | 43.6 | −12 | 4.4 | 30 | 34.4 | 1.2 |
| Interferometric Wide Swath | 20.0 | 5.0 | 8.7 | 174.3 | −12 | 10.4 | 30 | 40.4 | 1.7 | ||
| Extra Wide Swath | 40.0 | 20.0 | 34.9 | 1394.8 | −12 | 19.4 | 30 | 49.4 | 2.8 | ||
| RADARSAT-2 4 | Spotlight | 0.8 | 1.6 | 2.8 | 2.2 | −12 | −8.5 | 30 | 21.5 | 0.6 | |
| Ultra-Fine | 2.8 | 1.6 | 2.8 | 7.8 | −12 | −3.1 | 30 | 26.9 | 0.8 | ||
| Multi-Look Fine | 4.6 | 3.1 | 5.4 | 24.9 | −12 | 2.0 | 30 | 32.0 | 1.0 | ||
| Fine | 7.7 | 5.2 | 9.1 | 69.8 | −12 | 6.4 | 30 | 36.4 | 1.3 | ||
| Standard | 7.7 | 9.0 | 15.7 | 120.8 | −12 | 8.8 | 30 | 38.8 | 1.5 | ||
| Wide | 7.7 | 13.5 | 23.5 | 181.2 | −12 | 10.6 | 30 | 40.6 | 1.7 | ||
| L (1.27 GHz) | ALOS-2 5 | Spotlight | 1.0 | 3.0 | 5.2 | 5.2 | −15 | −7.8 | 43 | 35.2 | 2.6 |
| Stripmap Ultra-Fine | 3.0 | 3.0 | 5.2 | 15.7 | −15 | −3.0 | 43 | 40.0 | 3.4 | ||
| High-sensitive | 4.3 | 6.0 | 10.5 | 45.0 | −15 | 1.5 | 43 | 44.5 | 4.4 | ||
| Stripmap Fine | 5.3 | 9.1 | 15.9 | 84.1 | −15 | 4.2 | 43 | 47.2 | 5.2 | ||
| ScanSAR (28 MHz) | 77.7 | 47.5 | 82.8 | 6434.6 | −15 | 23.1 | 43 | 66.1 | 15.3 | ||
| TCR Type Group | TCR Size (m) | Plate Finish | Perforations | TCR Number | Misalignment (Degrees) | |
|---|---|---|---|---|---|---|
| Azimuth | Elevation | |||||
| A | 1.0 | Metallic | ☒ | 1 | 20 | 0 |
| 2 | 0 | 20 | ||||
| 3 | 0 | 0 | ||||
| B | 1.5 | Metallic | ☒ | 4 | 0 | −20 |
| 5 | 0 | 0 | ||||
| 6 | 0 | 20 | ||||
| C | 1.5 | Powder-coat | ☒ | 7 | 0 | −10 |
| 8 | 20 | 0 | ||||
| 9 | 20 | 20 | ||||
| D | 1.5 | Metallic | ☑ | 10 | 10 | 10 |
| 11 | 0 | 10 | ||||
| 12 | 10 | 0 | ||||
| E | 2.0 | Metallic | ☒ | 13 | 0 | 0 |
| 14 | 0 | 20 | ||||
| 15 | 20 | 0 | ||||
| F | 2.5 | Metallic | ☒ | 16 | 0 | 0 |
| 17 | 20 | 0 | ||||
| 18 | 0 | 20 | ||||
| Acquisition # | Date (UTC) | Time (UTC) | SAR Sensor | TCR Alignment Notes | Stable Clutter Period |
|---|---|---|---|---|---|
| 1 | 15 November 2013 | 19:27:59 | TSX | Before TCR deployment | ☒ |
| 2 | 7 December 2013 | 19:27:59 | TSX | Average; only 1.0 m and 1.5 m reflectors | ☒ |
| 3 | 11 December 2013 | 7:14:35 | CSK-1 | Average; only 1.0 m and 1.5 m reflectors | ☒ |
| 4 | 14 December 2013 | 19:18:48 | RSAT-2 | Average alignment | ☑ |
| 5 | 27 December 2013 | 7:14:31 | CSK-1 | Average alignment | ☑ |
| 6 | 29 December 2013 | 19:27:58 | TSX | Average alignment | ☑ |
| 7 | 7 January 2014 | 19:18:47 | RSAT-2 | Average alignment | ☑ |
| 8 | 9 January 2014 | 19:27:57 | TSX | Average alignment | ☑ |
| 9 | 12 January 2014 | 7:14:23 | CSK-1 | Average alignment | ☑ |
| 10 | 20 January 2014 | 19:27:58 | TSX | TSX | ☑ |
| 11 | 28 January 2014 | 7:14:18 | CSK-1 | CSK | ☑ |
| 12 | 31 January 2014 | 19:27:57 | TSX | RSAT-2 | ☑ |
| 13 | 31 January 2014 | 19:18:49 | RSAT-2 | RSAT-2 | ☑ |
| 15 | 11 February 2014 | 19:27:56 | TSX | TSX | ☑ |
| 16 | 13 February 2014 | 7:14:12 | CSK-1 | CSK | ☑ |
| 17 | 22 February 2014 | 19:27:56 | TSX | TSX but with misalignment | ☒ |
| 18 | 24 February 2014 | 19:18:44 | RSAT-2 | RSAT-2 but with misalignment | ☒ |
| 20 | 5 March 2014 | 19:27:57 | TSX | RISAT-1 * | ☒ |
| 21 | 25 March 2014 | 7:14:00 | CSK-2 | CSK but with misalignment | ☒ |
| 22 | 10 April 2014 | 7:13:59 | CSK-2 | CSK but with misalignment | ☒ |
| 23 | 14 April 2014 | 7:13:57 | CSK-4 | CSK but with misalignment | ☒ |
| 24 | 18 April 2014 | 7:13:57 | CSK-1 | CSK but with misalignment | ☒ |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garthwaite, M.C. On the Design of Radar Corner Reflectors for Deformation Monitoring in Multi-Frequency InSAR. Remote Sens. 2017, 9, 648. https://doi.org/10.3390/rs9070648
Garthwaite MC. On the Design of Radar Corner Reflectors for Deformation Monitoring in Multi-Frequency InSAR. Remote Sensing. 2017; 9(7):648. https://doi.org/10.3390/rs9070648
Chicago/Turabian StyleGarthwaite, Matthew C. 2017. "On the Design of Radar Corner Reflectors for Deformation Monitoring in Multi-Frequency InSAR" Remote Sensing 9, no. 7: 648. https://doi.org/10.3390/rs9070648
APA StyleGarthwaite, M. C. (2017). On the Design of Radar Corner Reflectors for Deformation Monitoring in Multi-Frequency InSAR. Remote Sensing, 9(7), 648. https://doi.org/10.3390/rs9070648