Geometric Potential Assessment for ZY3-02 Triple Linear Array Imagery

Abstract

ZiYuan3-02 (ZY3-02) is the first remote sensing satellite for the development of China’s civil space infrastructure (CCSI) and the second satellite in the ZiYuan3 series; it was launched successfully on 30 May 2016, aboard the CZ-4B rocket at the Taiyuan Satellite Launch Center (TSLC) in China. Core payloads of ZY3-02 include a triple linear array camera (TLC) and a multi-spectral camera, and this equipment will be used to acquire space geographic information with high-resolution and stereoscopic observations. Geometric quality is a key factor that affects the performance and potential of satellite imagery. For the purpose of evaluating comprehensively the geometric potential of ZY3-02, this paper introduces the method used for geometric calibration of the TLC onboard the satellite and a model for sensor corrected (SC) products that serve as basic products delivered to users. Evaluation work was conducted by making a full assessment of the geometric performance. Furthermore, images of six regions and corresponding reference data were collected to implement the geometric calibration technique and evaluate the resulting geometric accuracy. Experimental results showed that the direct location performance and internal accuracy of SC products increased remarkably after calibration, and the planimetric and vertical accuracies with relatively few ground control points (GCPs) were demonstrated to be better than 2.5 m and 2 m, respectively. Additionally, the derived digital surface model (DSM) accuracy was better than 3 m (RMSE) for flat terrain and 5 m (RMSE) for mountainous terrain. However, given that several variations such as changes in the thermal environment can alter the camera’s installation angle, geometric performance will vary with the geographical location and imaging time changes. Generally, ZY3-02 can be used for 1:50,000 stereo mapping and can produce (and update) larger-scale basic geographic information products.

1. Introduction

ZiYuan3-02 (ZY3-02) is the first remote sensing satellite for the development of China’s civil space infrastructure (CCSI) and the second satellite of the ZiYuan3 series. The ZY3-02 satellite was launched successfully on 30 May 2016, aboard the CZ-4B rocket at the Taiyuan Satellite Launch Center (TSLC) in China [1]. Phased 180° apart in the same orbit, the ZY3-02 and ZiYuan3-01 [2] (ZY3-01, China’s first domestic civil high-resolution stereo mapping satellite launched in January 2012) genuine constellation, beyond increasing the in-orbit data acquisition efficiency, will now enhance the acquisition of space geographic information as well as support mapping services and data collections for land resource surveys and monitoring. These satellites are of great significance in efforts to speed up the construction of China’s space geographic information data infrastructure and promote the development of geographical information industries.

The ZY3-02 satellite carries core payloads including a triple linear array camera (TLC) and multi-spectral camera. The TLC is comprised of a nadir (NAD) and forward (FWD) and backward (BWD) optical linear sensors, where the FWD and BWD sensors are arranged at an inclination of ±22° from NAD to realize a base-to-height (B/H) ratio of 0.88. Compared with the ZY3-01 satellite, the number of charge-coupled devices (CCDs) in the FWD/BWD focal plane of ZY3-02 was changed from four units to three units and the size was changed from 10 μm to 7 μm, which improved the ground sample distance (GSD) from 3.5 m to 2.7 m. Each sensor (NAD, BWD, and FWD) in the TLC of ZY3-02 adopts the optical butting system to realize multi-CCD splicing. As is shown in Figure 1, after the incident light is reflected by the half transparent and half reflecting prism, the incident light is imaged on the transmitting and reflection areas, respectively, thereby realizing CCD splicing. Each raw focal plane is composed of three units of a CCD with 8192 pixels; overlapping pixels between the adjacent CCDs amount to about 30 pixels. The design and specification information for ZY3-02 are listed in

Table 1. Design and specification information for the ZY3-02 satellite.

Sensor Parameters	Triple Line Array Camera	Multi-Spectral Camera
Orbit	Altitude: 506 km; Period: 94.7 min
	Type: SunSync. 10:30 a.m. descending node
Life	5 years
Field angle	6 degrees
Dynamic range	10-bits per pixel
Modular transfer function	>0.2
Focal length	1700 mm	1750 mm
Pixel size	7 μm	20 μm
Spectral range	0.5–0.8 μm	Blue: 0.45–0.52 μm
		Green: 0.52–0.59 μm
		Red: 0.63–0.69 μm
		Near infrared: 0.77–0.89 μm
Sensor resolution	nadir (NAD): 2.1 m	5.8 m
	forward (FWD): 2.7
	mbackward (BWD): 2.7 m
Swath width	NAD: >51 km	>50 km
	FWD/BWD: >52 km

.

Geometric quality is crucial for the performance and potential of satellite imagery and has a bearing on the mapping precision and subsequent applications. Therefore, many optical remote sensing satellites, both domestically and internationally, have been the subject of geometric calibrations and evaluations after being launched, with the goal of improving and assessing the geometric performance of the satellite imagery. The National Centre for Space Studies (CNES) Image Quality Team performed calibration operations with imagery from Pleiades-HR 1A&1B in the commissioning phase to assess and improve the geometric quality of the images [3,4]. Poli et al. [5] addressed the radiometric and geometric evaluations of the GeoEye-1, WorldView-2, and Pleiades-1A stereo images included in the Trento testfield and their potential for three-dimensional (3D) information extraction. Languille et al. [6] detailed calibration sites and methods to be used for geometrical parameter calibrations, and then, they presented a geolocation performance assessment for Sentinel-2A. Seo et al. [7] presented geometric calibration and validation work and checked the planimetric accuracy by bundle adjustment with ground control points (GCPs) for Kompsat-3A. Tadono et al. [8,9] described the results of calibration and validation, including the absolute accuracy, during stability evaluations over the course of one and half years for PRISM (Panchromatic Remote-sensing Instrument for Stereo Mapping) onboard ALOS (Advanced Land Observing Satellite). Wang et al. [10] described imaging error sources and introduced a calibration model for the GF4 satellite, and then, they performed a geometric quality assessment. Zhang et al. [11,12,13] introduced a geometric calibration model and validated the geometric calibration accuracy for ZY3-01. Thanks to these efforts, the geometric quality of imagery can be checked easily and the calibration procedures can be further refined by the corresponding accuracy results.

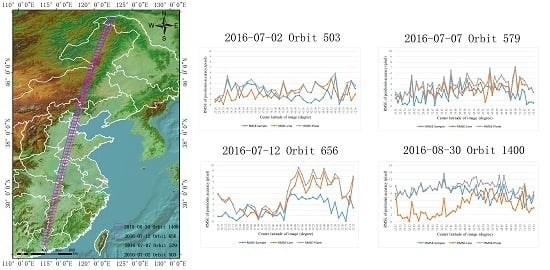
For the TLC camera of ZY3-02, similarly, it is essential to make a full assessment of its geometric potential. Therefore, a comprehensive evaluation of the geometric potential of ZY3-02 TLC imagery is performed in this paper. First, an on-orbit geometric calibration approach for ZY3-02 is presented to finely characterize the geometric model, and then, a model for sensor corrected products that can serve as basic products distributed to users is introduced. Furthermore, a thorough geometric quality evaluation, which includes the geometric calibration accuracy, absolute positioning accuracy, internal accuracy, stereoscopic measurements, and the derived digital surface model (DSM) accuracy, is made on a set of images covering reference sites. The experimental results demonstrate that the direct location performance is increased enormously and internal distortion is well-compensated after calibration. The geometric performance will however, vary with the geographical location and imaging time changes resulting from variations such as those due to thermal environment changes that alter the camera’s installation angle. In general, the TLC imagery of ZY3-02 can be used for 1:50,000 stereo mapping without GCPs and updates of larger-scale basic geographical information products are possible.

2. Methods

The rigorous geometric imaging model is a basic model used for satellite image geometric processing, and it also serves as the basis for the satellite sensor in-orbit geometric calibration [14,15,16,17]. According to observation data obtained by ZY3-02, the geometric model of the TLC was established as follows:

$${\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]}_{WGS84}={\left[\begin{array}{c}{X}_{GPS}(t)\\ Y_{GPS}(t)\\ Z_{GPS}(t)\end{array}\right]}_{WGS84}+\lambda ·Ma{t}_{Body}^{WGS84}(t)·\left\{{\left[\begin{array}{c}{B}_x\\ B_y\\ B_z\end{array}\right]}_{Body}+Ma{t}_{Cam}^{Body}·{\left[\begin{array}{c}x\\ y\\ f\end{array}\right]}_{I,n}\right\}$$

(1)

where $(x,y,f)$ are the coordinates of a pixel in the camera’s coordinate system, ${(X,Y,Z)}_{WGS84}$ are the coordinates in the World Geodetic System 1984 (WGS84) corresponding to the pixel, $I$ stands for the NAD/BWD/FWD sensor, $n$ is the number of CCDs, $t$ is the scanning time of an image line, $({\begin{array}{ccc}{X}_{GPS}(t),& Y_{GPS}(t),& Z_{GPS}(t))\end{array}}_{WGS84}$ are the coordinates of the Global Positioning System (GPS) antenna phase center, which are measured by a dual-frequency GPS receiver on the satellite in WGS84 at $t$, $\lambda$ is a scale factor, $Ma{t}_{Body}^{WGS84}$ and $Ma{t}_{Cam}^{Body}$ are the rotation matrix from the satellite’s body-fixed coordinate system in relation to WGS84 and the rotation matrix from the camera’s coordinate system in relation to the satellite’s body-fixed coordinate system, respectively, and ${(B_x,B_y,B_z)}_{Body}$ are the coordinates of the eccentric vector from the sensor’s projection center to the GPS antenna phase center in the satellite’s body-fixed coordinate system, which are prelaunch calibrated in the laboratory.

2.1. Geometric Calibration of the TLC Camera

According to Equation (1), the location performance for the geometric model of the ZY3-02 TLC is subject to bias from the camera installation angle $Ma{t}_{Cam}^{Body}$, bias from the GPS antenna phase, time measurement errors, attitude measurement errors, orbit measurement errors, and pixel errors induced by the camera’s internal distortion, including ones from the optical distortion of the camera lens, and other ones from CCD translation, scale, rotation, and changes of the principle distance. Owing to the fact that the ZY3-02 satellite adopts the use of 1 pps in the GPS to improve the precision of synchronization, the timing accuracy reaches 30 μs and the errors induced by time measurement errors are negligible.

The measurement errors of attitude and orbit are considered as constant errors within one standard scene, but a degree of random deviation occurs between several scenes imaged at different times [18]. Meanwhile, the external angle element and line element are strongly correlated in affecting the positioning accuracy, so the orbit measurement error can be treated as part of the attitude measurement error [19]. Additionally, the errors caused by biases of the camera installation angle and GPS antenna phase, as well as the camera distortion are systematic errors and vary little over time; they directly impact the location accuracy, which characterizes the deviation between the real position of any pixel on an image and its estimated positioning using the geometric model, so it is essential to build a corresponding calibration model to compensate for these errors.

In this paper, geometric parameters are divided into static interior parameters and dynamic exterior parameters. The dynamic exterior parameters $Ma{t}_{eI}$ are used for assessing the main bias of location, compensating for the biases of instruments, and determining the attitude of the camera coordinate system in space. The static interior parameters, by adopting the classic viewing angle model [20,21,22,23,24] as shown in Figure 2, are used to accurately describe the viewing directions of every pixel in the satellite’s body-fixed system and then improve the internal geometric accuracy of images by correcting the camera distortion.

According to the above analysis, the geometric calibration model can be constructed for the TLC of ZY3-02 as expressed in Equation (2):

$${\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]}_{WGS84}={\left[\begin{array}{c}{X}_{GPS}(t)\\ Y_{GPS}(t)\\ Z_{GPS}(t)\end{array}\right]}_{WGS84}+\lambda ·Ma{t}_{Body}^{WGS84}(t)·Ma{t}_{eI}·\left\{{\left[\begin{array}{c}{B}_x\\ B_y\\ B_z\end{array}\right]}_{Body}+Ma{t}_{Cam}^{Body}·{\left[\begin{array}{c}\tan {\psi }_x\\ \tan {\psi }_y\\ 1\end{array}\right]}_{I,n}\right\}$$

(2)

$Ma{t}_{eI}$ is defined as follows:

$$Ma{t}_{eI}=\left[\begin{array}{ccc}\cos \phi & 0& \sin \phi \\ 0& 1& 0\\ -\sin \phi & 0& \cos \phi \end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \omega & -\sin \omega \\ 0& \sin \omega & \cos \omega \end{array}\right]\left[\begin{array}{ccc}\cos \kappa & -\sin \kappa & 0\\ \sin \kappa & \cos \kappa & 0\\ 0& 0& 1\end{array}\right]$$

(3)

where $\phi ,\omega$, and $\kappa$ are rotation angles about the $X,Y$, and $Z$ axes, respectively.

$\tan {\psi }_x$ and $\tan {\psi }_y$ are defined by the following model:

$$\{\begin{array}{l}\tan {\psi }_x=a_0+a_{1}s+\cdots +a_i{s}^i\\ \tan {\psi }_y=b_0+b_{1}s+\cdots +b_j{s}^j\end{array},i,j\le 5$$

(4)

where $s$ denotes the number of the image row and $a_i,b_j$ are the parameters to be solved.

High-precision digital orthophoto map (DOM)/digital elevation model (DEM) reference data are used in the acquisition of GCPs by matching processes from which the $Ma{t}_{eI}$ and the coefficients $a_i,b_j$ of the viewing directions model correction can be deduced.

2.2. Geometric Model of Sensor Corrected (SC) Products

As shown in Figure 1, ZY3-02 adopts a multi-chip CCD design with an enlarged swath. However, this brings about much inconvenience to users when providing separated CCD images. Sensor corrected (SC) products successfully solve the problem of CCD mosaicking. Assume that a perfect sensor with only one CCD array is observing Earth in a nearly identical state of the ephemeris and attitude compared with the real, and its platform has no high attitude perturbations. Then, attitudes and ephemeris data transmitted by real sensors can be processed with polynomial fitting at ground level and then used as perfect in a camera orbit and attitude model. The focal plane of the perfect sensor is described in Figure 3, and its interior orientation can be modeled as shown in Equation (5), where $\tan {\psi }_x$ and $\tan {\psi }_y$ are determined by the calibrated parameters for the TLC:

$$\tan {\psi }_x=\mathrm{a}\tan {\psi }_y+\mathrm{b}$$

(5)

After establishing the geometric model of a perfect sensor, the SC product can be generated by the following steps:

(1)

Calculate the coordinates $(X,Y,Z)$ in the object space of any pixel $(x,y)$ in the SC image with the rigorous geometric model of the perfect sensor;

(2)

The image coordinates $(x^{\prime },y^{\prime })$ in the original image that corresponds to $(X,Y,Z)$ in step (1) are calculated by using the rigorous geometric model of the original multi-CCDs image;

(3)

The gray value of pixel $(x^{\prime },y^{\prime })$ in the original image is obtained by resampling using a raised cosine function, and it is assigned to pixel $(x,y)$ in the SC image;

(4)

The SC product is generated by repeating steps (1)–(3) for all pixels in the SC image;

(5)

The rational polynomial coefficients (RPCs) are then generated by adopting the terrain independent solution [25,26,27]. First, divide the image space into a regular space and generate the virtual control points (VCPs) by using the rigorous imaging model of the SC image at each grid point defined by $P(sample,line)$ to calculate the corresponding object space point $G(X,Y,Z)$ on different elevation datum from $H_{\min }$ to $H_{\max }$ by space intersection. In this case, the image point $P$ and the object space point $G$ constitute a set of VCPs, as shown in Figure 4. Second, calculate the coefficients of RPCs by the iterative algorithm principle of the spectrum correction [28]; the RPC is finally taken as the basic geometric model for ZY3-02 SC images and provided to users.

The flow chart for the generation of an SC product is presented in Figure 5:

As is shown in Figure 6, ${\theta }_0$ and ${\theta }_1$ denote the imaging angles of the conjugate points between the origin multi-chip CCDs and the perfect CCD defined in the orbit coordinate system, respectively; $\Delta h$ represents the height error, and $\Delta x$ is the parallax induced by $\Delta h$. Obviously, $\Delta x$ can be calculated by the following equation:

$$\Delta x=\Delta h(\tan {\theta }_0-\tan {\theta }_1)$$

(6)

Since the TLC of ZY3-02 adopts an optical butting system, the perfect sensor and origin sensors scan the same object with a small difference in the imaging angles, i.e., ${\theta }_0\approx {\theta }_1$. The loss of the SC product’s internal accuracy induced by height error can be neglected.

In this paper, SC products are mainly used in the full investigation of the geometric potential of ZY3-02 instead of raw data, which are composed of multi-CCD arrays and metadata.

3. Experiments and Discussion

3.1. Study Area and Data Collection

To assess sufficiently the geometric potential of ZY3-02 triple linear array imagery, a multitude of images covering some representative regions and four strips worth of data were collected as experimental data. Detailed information about the images in the representative regions is listed in

Table 2. Detailed information for experimental images in representative regions.

Area	Sensors	Scene ID	Orbit ID	Acquisition Data	Center Latitude and Longitude	Side Angle
Tianjin	NAD	07-02-TJ-N	503	2 July 2016	38.27°N, 117.02°E	0.00°
	BWD	07-02-TJ-B
	FWD	07-02-TJ-F
Shijiazhuang	NAD	07-26-SJZ-N	868	26 July 2016	38.60°N, 114.21°E	2.50°
	BWD	07-26-SJZ-B
	FWD	07-26-SJZ-F
Dengfeng	NAD	07-26-DF-N	868	26 July 2016	34.64°N, 113.13°E	2.49°
	BWD	07-26-DF-B
	FWD	07-26-DF-F
Yili	NAD	08-03-YL-N	991	3 August 2016	43.73°N, 82.94°E	0.00°
	BWD	08-03-YL-B
	FWD	08-03-YL-F
Tianjin	NAD	08-30-TJ-N	1400	30 August 2016	38.99°N, 117.29°E	3.02°
	BWD	08-30-TJ-B
	FWD	08-30-TJ-F
Zhangjiakou	NAD	09-28-ZJK-N	1841	28 September 2016	41.37°N, 115.51°E	4.28°
	BWD	09-28-ZJK-B
	FWD	09-28-ZJK-F
Songshan	NAD	10-03-SS-N	1917	3 October 2016	34.65°N, 113.53°E	0.00°
	BWD	10-03-SS-B
	FWD	10-03-SS-F

.

Among these data, images 07-02-TJ-N/07-02-TJ-B/07-02-TJ-F were collected for geometric calibration of the ZY3-02 TLC, and the 1:2000 scale DOM and DEM of Tianjin were used as the reference data to calculate calibration parameters. Moreover, other images were used to validate the geometric calibration accuracy, evaluate the stereoscopic capability, and conduct DSM product testing. Besides, the 1:5000 DOM/DEM of Songshan, 1:5000 DOM/DEM of Yili, and 1:2000 DOM/DEM of Dengfeng as well as GCPs measured primarily by using a static global positioning system and with an accuracy exceeding 0.1 m in the areas of Shijiazhuang and Zhangjiakou, were also applied as reference data to evaluate the geometric potential. Specific information about the reference data is given in

Table 3. Specific information about the reference data.

Area	GSD of DOM (m)	Plane Accuracy of DOM RMS (m)	Height Accuracy of DEM RMS (m)	Range (km2)
Songshan	0.5	1	1.5	50 $\times$ 41
Dengfeng	0.2	0.4	0.7	54 $\times$ 84
Tianjin	0.2	0.4	0.7	72 $\times$ 54
Yili	0.5	1	1.5	22 $\times$ 110

.

Four overlapping strips covering China, named Orbit 503, Orbit 579, Orbit 656, and Orbit 1400 were captured on 2 July 2016, 7 July 2016, 12 July 2016, and 30 August 2016, respectively, and data in these strips were used to evaluate the direct geolocation accuracy. There were at least two check points (CPs) distributed evenly on each standard scene of the four strips that were used to assess the geometric performance, and these data originated from the 1:5000 control points of photographs in aerial photography field work. Figure 7 presents the coverage of the four strips worth of data and a schematic diagram of the CPs.

3.2. Accuracy of the Geometric Calibration

As shown in Figure 8, a total of 2716, 2371, and 2465 evenly distributed GCPs in 07-02-TJ-N, 07-02-TJ-B, and 07-02-TJ-F, respectively, were obtained from the DOM and DEM of the Tianjin area by high-accuracy match methods [29].

The dynamic exterior orientation parameters $Ma{t}_{eI}$ and interior orientation parameters $a_i,b_j$ ($i,j\le 5$) in Equation (4) were solved successively by using the GCPs. The calibration accuracy is shown in

Table 4. Geometric positioning accuracy before and after exterior and interior calibration.

Scene ID	Accuracy	Line (Pixels)			Sample (Pixels)			Plane RMS (Pixels)
		MAX	MIN	RMSE	MAX	MIN	RMSE
07-02-TJ-N	(a)	285.7	267.9	276.3	47.81	36.07	42.49	279.6
	(b)	6.15	0.00	3.08	0.88	0.00	0.32	3.09
	(c)	0.49	0.00	0.19	0.42	0.00	0.18	0.26
07-02-TJ-B	(a)	21.02	18.43	19.84	36.42	0.00	21.13	28.97
	(b)	25.03	0.00	11.10	0.77	0.00	0.25	11.10
	(c)	0.48	0.00	0.20	0.49	0.00	0.18	0.27
07-02-TJ-F	(a)	10.76	8.55	9.55	41.21	0.00	23.60	25.46
	(b)	28.70	0.00	13.13	1.06	0.00	0.15	13.14
	(c)	0.47	0.00	0.21	0.52	0.00	0.19	0.28

(a) is the residual errors before solving matrix $Ma{t}_{eI}$; (b) is the residual errors after solving matrix $Ma{t}_{eI}$; (c) represents the residual errors after solving $Ma{t}_{eI}$ and $a_i,b_j$($i,j\le 5$) based on (a). Root-mean-square error (RMSE).

.

It can be seen from a) in Table 4 that the direct location accuracy yielded poor precision results, with the RMSE plane being 279.6 pixels (587.16 m) for NAD, 28.97 pixels (78.22 m) for BWD, and 25.46 pixels (68.74 m) for BWD. According to Figure 9a, the residual errors for NAD, BWD, and FWD mainly manifested as high systematic errors because they were based on the prelaunch calibration of parameters in a laboratory and such values can vary greatly after the launch. After solving the orientation parameters $Ma{t}_{eI}$, the residual errors of NAD reached about 3.09 pixels, that of BWD reached about 11.10 pixels, and that of FWD reached about 13.14 pixels according to (b) in Table 4. Moreover, residual errors in (b) should have mainly been caused by camera distortions since the effect of installation errors of instruments is manifested as translation errors. The residual errors mainly manifested as nonlinear along the track, as shown in Figure 9b. After further eliminating the installation angle errors and CCD distortions, the positioning accuracies were improved to be better than 0.3 pixels, and the residual errors manifested a random distribution as shown in Figure 9, which demonstrates that the systematic errors have been totally eliminated by the geometric calibration model.

3.3. Geometric Performance Assessment

To evaluate comprehensively the geometric performance of ZY3-02, parameters associated with different aspects of the geometrical accuracy, including the absolute positioning accuracy, internal accuracy, stereoscopic capability, and DSM quality, were evaluated as shown in

Table 5. Parameters associated with different aspects of the geometrical accuracy to be assessed.

Aspects of Geometrical Accuracy	Assessment Parameters
Absolute positioning accuracy	Root-mean-square error (RMSE) value of the check points (CPs)’ residuals; Circular error with a confidence level of 90% (CE90) for the CPs’ residuals
Internal accuracy	Planimetric standard deviation and planimetric RMSE in image space under four ground control points (GCPs); maximum error (MAX); minimum error (MIN)
Stereoscopic capability	Planimetric/height standard deviation and planimetric/height RMSE in object space under 0/4 GCPs
Digital surface model (DSM) product testing	RMSE, MAX and MIN error, and mean error of the test area

.

3.3.1. Absolute Positioning Accuracy

The absolute positioning accuracy is the image positioning accuracy without GCPs, which is an important item to assess during geometric capability evaluations. Considering the NAD, BWD, and FWD sensors onboard one platform, only the NAD sensor’s direct geometric performance needs to be assessed. Figure 10 presents the RMSE results for the four strips, and the statistical direct positioning accuracy was 5.87 pixels for the RMSE and 9.13 pixels for 90% of the measures as shown in Figure 11. According to the approximate map scale equivalencies based on the United States National Map Accuracy Standard [30] (see

Table 6. Approximate map scale equivalencies based on the United States National Map Accuracy Standard (UMAS).

Map Scale	RMSE (m)	CE90 (m)
1:2400	1	2
1:4800	2	4
1:12,000	5	10
1:24,000	6	12
1:50,000	15	25

), Table 6 the direct geometric positioning accuracy of ZY3-02 is satisfactory for 1:50,000 mapping.

However, with different positions of the satellite causing different solar illumination angles and with different distances from the satellite, the thermal averment around the satellite would vary, for which the installation angle would be altered as a consequence. Besides, the exterior calibration model simply models the errors of exterior elements (EO) within the imaging time of the current standard scene, but some actively operating instruments onboard the satellite platform and moving parts of the sensor itself need to be assessed, i.e., satellite micro-vibrations and variations of the platform velocity could bring about perturbations in the satellite position and attitude data at another imaging time [31]. It can be seen from the results in Figure 10 that there exists obvious variation in the direct geolocation accuracy with the imaging time along the latitude in the imaging data, and the positioning accuracy fluctuated slowly within one strip along the latitude and descended on average from RMSE-Plane 3 pixels on 2 July 2016, to RMSE-Plane 10 pixels on 30 August 2016. SPOT5 personnel established a latitudinal model to take into account this variation and guarantee the consistency of location performance based on approximately 20 calibration sites with a worldwide distribution [32]. Given the limited number of high quality testfields in China, it is necessary to conduct research on the local coherence under a few GCPs or even without to determine the sources of the effects and perturbations as well as their frequencies and magnitudes.

3.3.2. Internal Accuracy

To validate further the internal geometric data, DOMs and DEMs of Dengfeng, Yili, and Tianjin were taken as control data to evaluate the internal consistency performance of the SC products. An image space affine transformation model based on RPCs defined by Equation (7) was adopted as the exterior orientation model of SC products [33,34], and all the GCPs/CPs, which were used to calculate the parameters $a_0,a_1,a_2$ and $b_0,b_1,b_2$ of the exterior orientation model and check the accuracy, respectively, were all automatically extracted from the DOMs and DEMs.

$$\begin{array}{l}x+a_0+a_{1}x+a_{2}y=RP{C}_x(lat,lon,h)\\ y+b_0+b_{1}x+b_{2}y=RP{C}_y(lat,lon,h)\end{array}$$

(7)

Table 7. Internal accuracy of ZY3-02 SC products.

Area	Scene ID	No. GCPs/CPs	Line (Pixels)			Sample (Pixels)			Plane RMSE (Pixels)
			MAX	MIN	RMSE	MAX	MIN	RMSE
Dengfeng	07-26-DF-N	4/3230	0.42	0.00	0.17	0.62	0.00	0.20	0.26
	07-26-DF-B	4/3958	0.43	0.00	0.16	0.66	0.00	0.24	0.29
	07-26-DF-F	4/3486	0.60	0.00	0.18	0.69	0.00	0.26	0.31
Yili	08-03-YL-N	4/2948	0.61	0.00	0.20	0.63	0.00	0.20	0.28
	08-03-YL-B	4/2128	0.56	0.00	0.23	0.59	0.00	0.24	0.33
	08-03-YL-F	4/2057	0.49	0.00	0.25	0.87	0.00	0.18	0.30
Tianjin	08-30-TJ-N	4/1752	0.59	0.00	0.24	0.57	0.00	0.20	0.32
	08-30-TJ-B	4/1861	0.57	0.00	0.22	0.71	0.00	0.22	0.31
	08-30-TJ-F	4/1649	0.59	0.00	0.20	0.71	0.00	0.26	0.33

shows that the SC products’ internal accuracies were better than 0.35 pixels, which proves that the proposed calibration model can accurately recover the viewing directions of every pixel in the satellite body-fixed frame, thus ensuring the internal geometric accuracy and guaranteeing that the CCD distortion is well-compensated for. Compared with the absolute positioning accuracy, the variations in imaging time and area have less of an influence on the internal accuracy, with the maximum discrepancy being equal to 0.06 pixels.

3.3.3. Stereoscopic Capability Analysis

Bundle adjustment, based on image space affine transformation [35], was conducted to assess the stereoscopic capability, and it can be implemented via two methods, namely, either all the GCPs are used to check the forward intersection accuracy of the triplet images, or four GCPs distributed in four corners are used to correct errors of ephemeris and attitude and the remaining GCPs are used as CPs.

Table 8. Results for planimetric and height accuracy based on bundle adjustment in six representative regions.

Area	Orbit ID	No. of GCPs/CPs	RMSE of CPs (m)
			Line	Sample	Plane	Height
Shijianzhuang	868	0/27	6.48	3.14	7.21	5.04
		4/23	1.70	1.78	2.46	2.20
Dengfeng	868	0/45	6.16	1.02	6.24	5.14
		4/41	1.11	1.24	1.66	1.55
Yili	991	0/20	7.46	5.15	9.06	7.85
		4/16	1.42	2.11	2.54	2.03
Tianjin	1400	0/44	6.07	10.52	12.14	6.24
		4/40	1.62	1.96	2.55	1.26
Zhangjiakou	1841	0/26	9.58	7.59	12.23	8.77
		4/22	1.82	2.01	2.71	1.82
Songshan	1917	0/38	8.62	11.29	14.20	7.28
		4/34	0.87	0.87	1.27	1.61
Average					10.18	6.72
					2.20	1.75

shows the statistical results for the six regions and the calculated averages of the results, which presented a trend whereby the RMSE of both planimetric and height descended with time and changed with location similar to the case for the absolute positioning accuracy. For the six regions in the research area, the RMSE using the first adjustment method averaged 10.18 m for planimetric and 6.72 m for height, and the RMSE using the second method averaged 2.2 m for planimetric and 1.75 m for height.

According to previous references [36,37], the ratio between the height accuracy and planimetric accuracy is:

$$R=\frac{ho{r}_{error}}{ve{r}_{error}}=\frac{H}{S}$$

(8)

where $ho{r}_{error}$ and $ve{r}_{error}$ represent the horizontal error and vertical error, respectively. $S$ is the length of the baseline, and $H$ is the flight height. Thus, the vertical error can be calculated by the following equation:

$$ve{r}_{error}=\frac{S}{H}·ho{r}_{error}$$

(9)

The orbit height of ZY3-02 is 506 km, while the baseline between the BWD sensor and FWD sensor is about 405 km. According to Section 3.2, the calibration accuracy $e_c$ for the TLC is better than 0.3 pixels, and the corresponding point extraction accuracy $e_e$ is about 0.3 pixels too. The resolution $res$ of the BWD or FWD sensor is about 2.7 m. Thus, the horizontal and vertical errors for the TLC of ZY3-02 theoretically are as follows:

$$\begin{array}{l}ho{r}_{error}=(e_c+e_e)·res=2.16\mathrm{m}\\ ve{r}_{error}=\frac{S}{H}·(e_c+e_e)·ho{r}_{error}=1.9\mathrm{m}\end{array}$$

(10)

It can be seen that the results in Table 8 with four GCPs used in the bundle adjustment are coincident with the theoretical values, and the planimetric and height accuracy for ZY3-02 corresponded to 2.16 m and 1.9 m, respectively.

3.3.4. DSM Product Testing

Based on the work presented in Section 3.3.3, the triplet images of Dengfeng were used to generate the DSM, and the planimetric and height accuracies were 1.66 m and 1.55 m, respectively, after bundle adjustment with four GCPs. The Semi-Global Matching (SGM) method [38] was introduced to acquire corresponding points and the point cloud, and then, the DSM at a 5 m sampling distance was directly generated from the point cloud without filtering. With the use of one additional view in DSM generation, local blunders due to occlusions can be mitigated or solved by combining three views. However, the stereo configuration of the current triple is not mandatory, as two scenes are acquired with forward viewing and one scene with backward viewing [39,40]. The corresponding high accuracy DEM in the Dengfeng area was used as reference, and detailed information about Dengfeng is listed in Table 3. Figure 12a shows an example of part of a nadir-looking image for a SC product used in DSM generation over the Dengfeng area; Figure 12b shows the earlier DOM of the corresponding part of the target area; Figure 12c shows part of the generated 5 m-mesh DSM using triplet images of Figure 12a and visualized in color-shaded mode, and the white color shows mask areas in places with water bodies like rivers and lakes or cloudy locations; Figure 12d gives a schematic diagram of the reference DEM visualized in color-shaded mode.

To assess comprehensively the DSM quality, the generated DSM was tested for different terrain and land cover types such as mountainous, hilly, flat plain, and complex terrain areas, and profile analyses were compared with the reference DEM resampled as grid intervals of the generated DSM.

The height differences were computed between the DSM and DEM in the corresponding research area, and the resulting statistics are given in

Table 9. Statistics for the DSM height accuracy in Dengfeng over various terrain types.

Terrain	Size (km2)	Minimum (m)	Maximum (m)	Mean (m)	RMSE (m)
Mountainous	4.2 × 3.8	−77.98	67.52	0.69	4.36
Hilly	4.2 × 3.7	−37.26	30.53	0.87	3.07
Plain	4.3 × 3.9	−25.03	25.56	0.57	2.85
Complex	46 × 12	−95.90	127.5	0.30	5.45

. Given that vegetation and buildings contribute to differences in the statistical data for height, the height of the DSM will be higher than that of the reference DEM theoretically [41,42]. Consequently, there existed biases compared with the theoretical mean values, i.e., 0 in terms of the distribution of the height difference, and these amounted to 0.69 m in the mountainous, 0.87 m in the hilly, 0.57 m in the plain, and 0.3 m in the complex terrain. Besides, some matching failures were encountered that were caused by steeper slopes producing dark shadows and occlusions and the presence of temporary objects such as new construction sites as well as other changes in the environment between the acquisition dates of the reference DEM and images as shown in the red circle area of Figure 12; some blunders in test areas were thus inevitable. In general, an excellent accuracy was achieved for the plain terrain (2.85 m) followed by the hilly terrain (3.07 m) and mountainous terrain (4.36 m), and the results were even reasonable for the complex terrain type (5.45 m), which makes a difference in the quality of the orthorectified images.

Figure 13 shows the difference of elevation profiles along the red line between the generated DSM and reference DEM. It can be seen that the height of the DSM fits well with that of the DEM, with the RMSE of the height difference being 4.49 m, except for some small burrs due to generating the DSM without filtering.

4. Conclusions

Geometric quality plays an important role in the performance of satellite imagery and deeply influences the mapping precision and subsequent applications. In this paper, many images covering several regions and four strips worth of data including corresponding reference data were collected to perform a comprehensive assessment of the geometric potential for ZY3-02 triple linear array imagery. Several conclusions can be drawn from this work.

• The geometric calibration model as expressed in Equation (2) eliminates the external and internal errors well. After calibration, the direct location performance and internal accuracy of the TLC onboard ZY3-02 increased remarkably.
• Four strips were chosen as experimental data to evaluate the absolute positioning accuracy, and the results revealed that the accuracy is 5.87 pixels in terms of the RMSE and 9.13 pixels for 90% of the measurements, which meets the demands of 1:50,000 mapping.
• The SC products’ internal accuracies were better than 0.35 pixels. It should be noted that the internal accuracy was fairly stable compared with other geometric performances, as the maximum discrepancy was only 0.06 pixels within two months.
• For the stereoscopic capability, block adjustment based on a rational function model test showed planimetric and vertical accuracy values of 10 m and 6 m, respectively, without the use of ground control points (GCPs). The accuracy values were improved to 2.5 m and 2 m, respectively, with a few GCPs, and these values are coincident with the theoretical values. Moreover, the derived DSM accuracy was better than 3 m (RMSE) for flat terrain and 5 m (RMSE) for mountainous terrain compared with the reference DEM.
• The TLC of ZY3-02 generally can be used in 1:50,000 mapping applications and even produce (and update) larger-scale basic geographic information products. However, with the change of the camera’s installation angle resulting from thermal environment changes, some fluctuations will exist with differences in the imaging time and area. More in-depth studies should thus be carried out to guarantee the consistency of the absolute positioning accuracy under the use of a few GCPs or even without during different scenarios.