Study of PBLH and Its Correlation with Particulate Matter from One-Year Observation over Nanjing, Southeast China

The Planetary Boundary Layer Height (PBLH) plays an important role in the formation and development of air pollution events. Particulate Matter is one of major pollutants in China. Here, we present the characteristics of PBLH through three-methods of Lidar data inversion and show the correlation between the PBLH and the PM_2.5 (PM_2.5 with the diameter <2.5 μm) in the period of December 2015 through November 2016, over Nanjing, in southeast China. We applied gradient method (GRA), standard deviation method (STD) and wavelet covariance transform method (WCT) to calculate the PBLH. The results show that WCT is the most stable method which is less sensitive to the signal noise. 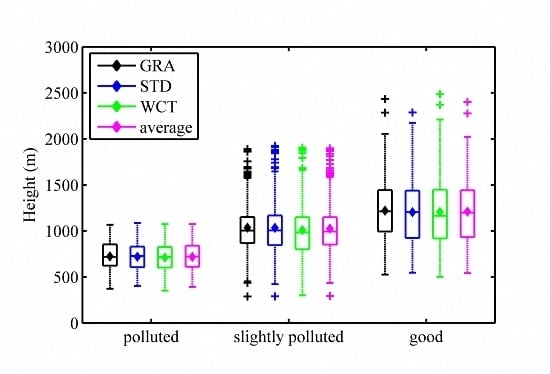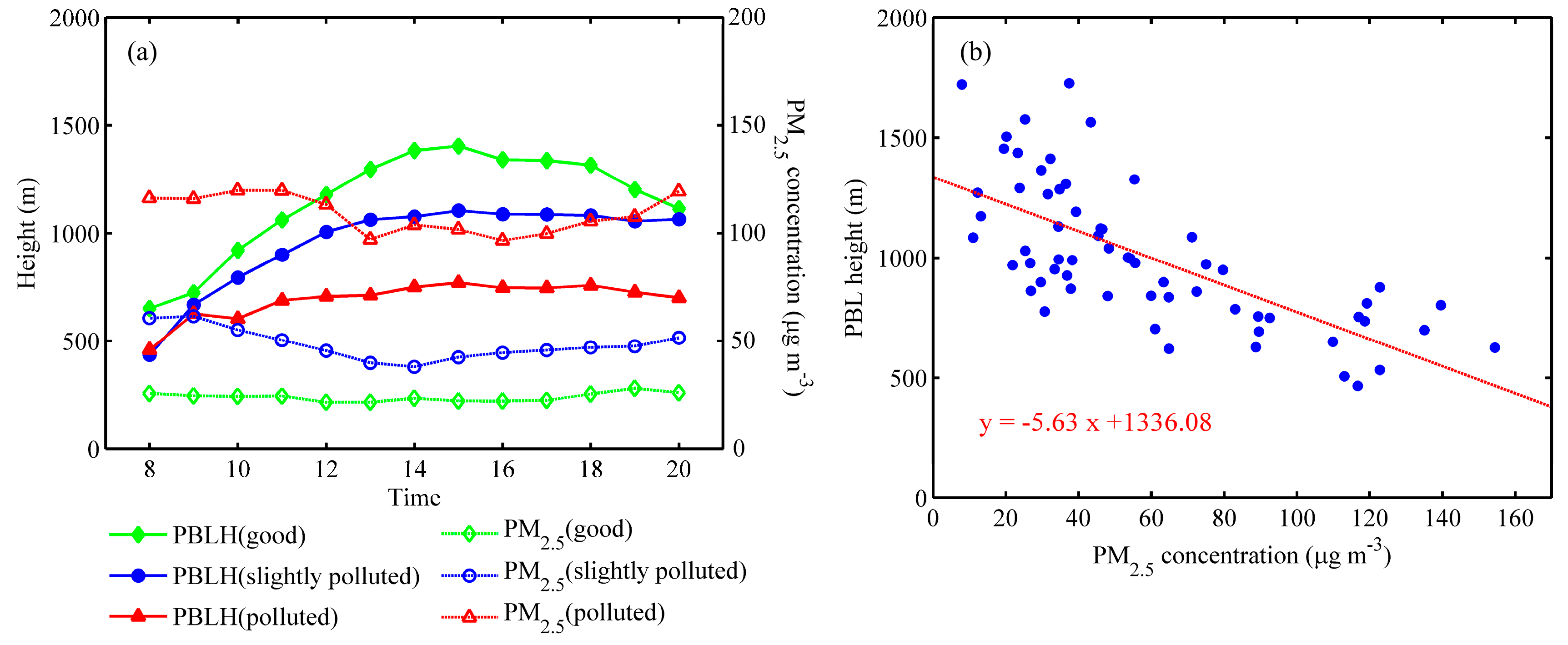We find that the PBLH shows typical seasonal variation trend with maximum in summer and minimum in winter, respectively. The yearly averaged PBLH in the diurnal cycle show the minimum of 570 m at 08:00 and the maximum of 1089 m at 15:00 Beijing time. Furthermore, we investigate the relationship of the PBLH and PM_2.5 concentration under different particulate pollution conditions. The correlation coefficient is about −0.70, which is negative correlation. The average PBLH are 718 m and 1210 m when the PM_2.5 > 75 μg/m³ and the PM_2.5 < 35 μg/m³ in daytime, respectively. The low PBLH often occurs with condition of the low wind speed and high relative humidity, which will lead to high PM_2.5 concentration and the low visibility. On the other hand, the stability of PBL is enhanced by high PM concentration and low visibility. View Full-Text