1. Introduction
Radar altimeters transmit modulated chirp pulses towards the sea at nadir, and then record the echoes reflected from the sea surface in an altimeter footprint [
1]. The time series of the power of the echoes received by altimeters is commonly referred to as a “waveform”. Waveforms are sampled with a specific time resolution, which is 3.125 ns for the Ocean Surface Topography Mission (OSTM)/Jason-2 satellite, and each cell within a waveform is called a “gate”. Geophysical parameters are retrieved by a process called “waveform retracking”, which consists of fitting a theoretical model to the measured waveforms. Over the open ocean, the so-called Brown mathematical model [
2,
3] is the standard model used for this process.
As shown in
Figure 1, a typical Brown waveform which is controlled by the altimeter antenna gain pattern, has a well-defined shape consisting of three parts, thermal noise, a fast-rising leading edge, and a decaying trailing edge. The fundamental parameters obtained through waveform retracking are the satellite height above the sea surface (range), the significant wave height (SWH), and the backscatter coefficient (sigma0,
), which is related to sea surface wind. Moreover, an antenna mispointing angle (
ξ) parameter, which is linked to the slope of the trailing edge, has a strong impact on sigma0 estimation because it reduces the apparent backscatter coefficient for the radar antenna (i.e., any deviation of the radar aiming point from nadir).
In contrast to the open ocean, waveforms collected when the altimeters operate in proximity to coastlines are often corrupted due to the heterogeneous surfaces.
Figure 2a shows the along-track waveforms (or azimuth-range radar-gram; hereafter referred to as an echogram) measured by the Jason-2 altimeter over the southern Tsushima Islands in Japan (pass 36, cycle 22). Each column of the echogram represents an individual waveform at a given latitude. Waveforms in the echogram have been realigned based on the tracker movements and rescaled by the automatic gain control (AGC) of the antenna [
4]. Waveforms measured over land areas are masked in the echogram because they cannot be properly realigned. As can be seen in
Figure 2a, land reflections are generally significantly weaker than reflections from the sea surface [
5]. This is why the trailing edge of a waveform will decay rapidly when an altimeter approaches land, thereby resulting in a power deficit area in the echogram [
6]. Moreover, several bright parabolic traces can be seen at the waveform trailing edge area, which indicate that bright targets exist within the altimeter footprint.
Figure 2b shows an example of a corrupted waveform measured at the location indicated by the red point in
Figure 2a (34.20°N). The black line represents the actual waveform and the red line represents the fitted waveform using the four-parameter Brown theoretical model. An unweighted least-squares estimator whose convergence is obtained through the Nelder-Mead algorithm is adopted in the present study. It is obvious that the estimated Brown waveform deviates seriously from an ideal undistorted waveform without redundant peaks around gates 60–80.
In the last couple of years, a significant amount of research has been aimed at overcoming the effect of waveform corruption on retracking over coastal zones. As a result, several dedicated parametric and non-parametric models have been proposed, a detailed review of which can be found in [
7]. In some previous studies, sub-waveform retrackers [
8,
9,
10,
11], which use only the waveform samples around the leading edge rather than the full waveforms, have been recommended for coastal waveform retracking. These retrackers successfully suppress trailing edge noise, and hence extend the capabilities of waveform retracking in coastal zones closer to the shorelines. However, loss of the trailing edge during the retracking process will also reduce the precision of estimated geophysical parameters, especially for sigma0 estimation [
10]. Moreover, although sub-waveform retrackers depend on the detection accuracy of the leading edge in a waveform, practically speaking, it is difficult to separate the leading edge from individual multi-peak waveforms when numerous speckles are present.
The previous concept regarding individual waveform noise detection was based on the on-board processing strategy of radar altimeters. However, more reliable detection is possible through post-processing using along-track waveforms because waveform noise at a given location can be expected to be geographically related to such noise in adjacent locations. Thus, trailing edge noise can be explicitly determined based on its spatial relationship in the echogram. Sub-waveform retrackers limit the analysis of waveform samples around the leading edge to avoid trailing edge noise. This is equivalent to limiting the altimeter footprint size near the nadir points where homogeneous sea surface conditions could be expected, even though the number of samples within the footprint is decreased. In contrast, in the present study, significant noise in the trailing edge caused by bright targets is removed or modified by using echograms. This approach will also assist in obtaining homogeneous sea surface conditions, which is necessary in order to adopt the Brown model, by keeping the number of samples within the footprints constant. A similar approach, in which bright peaks were removed by comparing them with waveforms in the adjacent open water, was examined in a recent study [
12]. In the present study, however, bright targets are more explicitly detected and removed by using spatial restriction conditions in the along-track waveforms.
The remainder of this paper is organized as follows. The dataset used in the present study is presented in
Section 2. Here, we selected Japan’s Tsushima Islands as our test site because it is an area where waveform corruption, such as that shown in
Figure 2, is often observed. The detection of noise caused by bright targets through their parabolic signatures within an echogram is introduced in
Section 3.1. In
Section 3.2, compensating for the waveform trailing edge power deficit due to weak land reflection is considered. The derived along-track sea surface height anomalies (SSHAs) are validated by tide gauge measurements and compared with sensor geophysical data record (SGDR) and adaptive leading-edge sub-waveform (ALES) products in
Section 4. Finally, a brief discussion and summary, focusing specifically on the geographical dependency of the results, is presented in
Section 5.
2. Dataset
The 20 Hz ALES coastal altimetry product of Jason-2 around the Tsushima Islands (pass 36, as shown in
Figure 3) are used in this study. This is an experimental product from the ALES processor that is included in SGDR-type files alongside the standard products and corrections. The specific description can be found at
http://www.coastalt.eu/community. The dataset covers the period from July 2008 to April 2015. The coastal features of the Tsushima Islands along the Jason-2 ground track are characterized by semi-closed bays within the altimeter footprints. Because semi-closed bays often appear as bright targets in radar echograms, waveforms measured in the complicated coastlines of the study area are seriously corrupted. For comparison purposes, another track (pass 164) crossing the relatively smooth coastlines of southern Taiwan is also processed, as described in
Section 5 (Figure 13).
The Global Self-Consistent, Hierarchical, High-Resolution Geography database (GSHHS) [
13] is used at full resolution to determine the coastline and estimate the ocean area located within altimeter annular footprints.
Hourly tide gauge data obtained from the Japan Oceanographic Data Center (JODC) are used to validate the quality of derived along-track sea surface heights (SSHs). A temporal interpolation was performed before validation to match the JODC data with the altimeter measurements. The shortest distance between tide gauge and Jason-2 ground track is about 6 km. Since tide gauge stations are located within port waters, the tidal amplitudes registered are not the same as those for the waters outside the harbors. Such discrepancies result in considerable height differences, although their spatial scale would be large.
4. Validation and Comparisons with Other Retrackers
In addition to the coastal zone, waveform corruption can also appear in open ocean areas where small-scale sigma0-bloom events and rain cells occur. A threshold of sigma0 is always adopted as the bloom detection criterion, e.g., the 15 dB and 18 dB criteria for the Environmental Satellite (Envisat) Radar Altimeter 2 (RA2) data discussed in [
14]. Considering the sigma0 differences between various altimeters, this study uses a relative large threshold of 18 dB for Jason-2 sigma0-bloom event detection. The sigma0-bloom events are found in 18 of 252 cycles at the study area. More specifically, about 7% of the Jason-2 measurements are corrupted by the sigma0-bloom events. This rate is consistent with the study on Jason-1 data (6%) as discussed in [
14]. Note that the sigma0-bloom effect on waveform retracking is out of the scope of the present study, and the 18 cycles of data have been directly removed from waveform retracking.
In order to validate the quality of the range estimation, the along-track SSHA is calculated as follows:
where
is the mean SSH from cycle 1 to cycle 252. In the present study, SSH values larger than 100 m or smaller than −130 m are treated as outliers (see the Jason-2 product handbook). In order to make a comparison with tide gauge measurements, the tidal components and the inverse barometric components are not removed from either the altimeter measurements or the tide gauge records.
Two statistics, the correlation coefficient (CC) and the RMSD between the time series of SSHA derived from altimeter and tide gauge measurements, are used to validate the data quality as discussed in [
16].
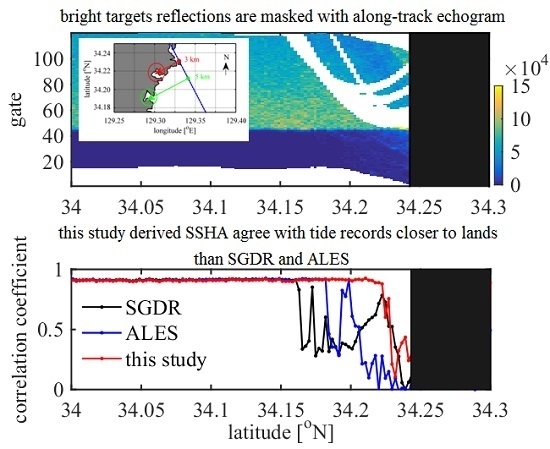
Figure 10a shows the CC variation along the track over the Tsushima Islands for the three different methods.
Figure 10b is the RMSD in centimeters. These results show that the conventional ocean retracker in the SGDR product cannot provide a correct estimation within 10 km from the coastline, which corresponds approximately to the radius of the Jason-2 altimeter footprint. Meanwhile, since the ALES retracker only uses the sub-waveform around the leading edge, the noise that first appears in the waveform trailing edge has no influence on the range estimation. As a result, the ALES range estimation can be extended to about 7 km from the coastline.
However, once the echoes used in the ALES estimation windows become corrupted, they will seriously influence the accuracy of range estimation due to reduced ALES retracker echo numbers, as shown in
Figure 11. Note that all echoes within the estimation windows whose widths are determined by the SWH are used in the ALES, regardless of reliability. In the present study, however, the range is estimated based on the modified waveforms from which the effects of the two primary sources of heterogeneous surface reflections, i.e., land and bright targets, are removed.
Figure 10a shows that the CC remains larger than 0.9 (99.9% confidence level) even at locations only about 3 km away from the coast. Overall, both the CC and RMSD comparison show that this method is more effective for examining areas very close to land than the ocean retracker and/or ALES retracker.
5. Discussion and Summary
Generally speaking, geophysical parameters can be correctly estimated over open ocean areas using the theoretical Brown model, which is based on the assumption of a homogeneous sea surface. However, altimeter waveforms are often corrupted at coastal zones due to heterogeneous surface reflections within the altimeter footprint. In particular, bright targets such as calm water in semi-closed bays and the vicinity of land have distinctly different scattering characteristics at nadir. Sub-waveform retrackers such as ALES use only waveform samples selected from around the leading edge in order to avoid trailing edge noise. This method is equivalent to reducing the altimeter footprint. Because homogeneous sea surface conditions are more easily anticipated for smaller footprints, such retrackers can extend their waveform retracking abilities closer to the coast. In contrast, this study considered a method of modifying waveforms in order to make them suitable for use in the Brown model.
Reflections from bright targets often appear as redundant peaks in coastal waveforms, which have sharp power variations similar to waveform leading edges (
Figure 2b). When multiple redundant peaks appear in a waveform trailing edge, it is difficult to identify this noise in an individual waveform. On the other hand, reflections from a fixed-point target trace a parabola in the sequential along-track waveforms (or, azimuth-range echogram). Therefore, by utilizing the parabolic signature in the radar echogram, noise caused by bright targets can be explicitly detected and masked, as discussed in
Section 3.1. When compared with an actual waveform, the masked waveform shows good agreement with the fitted Brown waveform (
Figure 6b), even though the unrealistic mispointing angle indicates an extra power deficit for waveform trailing edge due to weak land reflection. Thus, it is necessary to compensate for the power deficit by estimating the ratio of the sea surface area and each annular footprint, as discussed in
Section 3.2.
In
Section 4, waveforms measured south of the Tsushima Islands (pass 36) were retracked. Both significantly bright targets from calm water surfaces in semi-closed bays and power deficits due to land were modified in the echograms in order to obtain pseudo-homogeneous sea surface conditions. Our validations of altimeter-derived SSHA with tide gauge records showed that the results of the present method agree better than both the conventional ocean retracker used in the SGDR product and the ALES retracker. The CC and RMSD remain similar to the open ocean values (0.9 and 20 cm), even in the coastal sea about 3 km away from land. The above results reveal that the present method can retrieve SSHA as close as 3 km from the southeast coast of the Tsushima Islands.
However, the approach distance strongly depends on the area geography.
Figure 12 shows the results around the northwest coast of the Tsushima Islands. As can be seen in
Figure 12a, the northwest coastline is very complex due to the numerous small bays. In addition, a small cape (Karasaki) around 34.36°N separates Asou Bay from the open ocean. As shown in
Figure 12b echogram example, the section of pass 36 in Asou Bay (purple line in
Figure 12a) includes an excessive number of bright targets. Since the present method identifies and removes isolated bright targets in the trailing edge, it cannot be applied to that area of Asou Bay. For the north of Cape Karasaki (from 34.36 to 34.6°N), however, the method described in
Section 3 is successfully applied. At each latitude, the root mean squared (RMS) variation for the SSHA is calculated with three different retrackers (
Figure 12c). When approaching from the open ocean (34.6°N), the RMS gradually increases, but that of the SGDR SSHA suddenly increases about 13 km from the Cape Karasaki coastline. The other two products maintain a gradual growth rate until 7 km from the coastline, but the approach distances are larger than that in
Section 4.
For comparison purposes, retracking for another pass over a relatively smooth coastline is examined.
Figure 13a shows pass 164 over the southeast of Taiwan. An example of the along-track echogram (
Figure 13b) includes no obvious bright targets. As shown in
Figure 13c, the difference among the three retrackers is almost negligible, although the ALES retracker shows a relatively larger RMS within 5 km from the coast.
Overall, the present method enables proper SSHA retrieval even in areas within 10 km from land. Although the approach distance towards the land varies with the geography of the study area, a closer approach is expected using the present method than using the other retrackers. The present method works especially well for removing isolated bright targets, but other factors causing inhomogeneous sea surface reflection, such as internal waves, sigma0 bloom events, and rain cells [
17], are currently not considered. Hence, further studies in other coastal zones will be necessary to generalize the efficiency of the present method.