Performance Evaluation for China’s Planned CO2-IPDA
Abstract
:1. Introduction
2. Materials and Methods
2.1. Random Errors
2.2. Systematic Errors
2.3. Orbit Sampling
2.4. Environmental Parameters
2.5. CO2-IDPA Configuration
3. Results
3.1. Critical Orbit Parameters
3.2. Critical Hardware Parameters
3.3. Critical Environmental Parameters
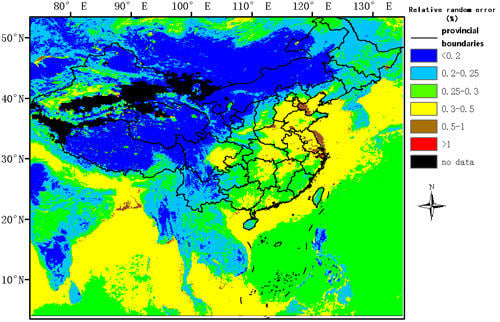
3.4. Performance Evaluation in China and Surrounding Regions
4. Discussion
4.1. Comparisons with Passive Sensors
4.2. Selection of an Appropriate Weighting Function
4.3. Usage of the Planned CO2-IPDA in China
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fan, S.; Gloor, M.; Mahlman, J.; Pacala, S.; Sarmiento, J.; Takahashi, T.; Tans, P. A large terrestrial carbon sink in North America implied by atmospheric and oceanic carbon dioxide data and models. Science 1998, 282, 442–446. [Google Scholar] [CrossRef] [PubMed]
- Tans, P.P.; Fung, I.Y.; Takahashi, T. Observational constraints on the global atmospheric CO2 budget. Science 1990, 247, 1431–1438. [Google Scholar] [PubMed]
- Rayner, P.J.; Enting, I.G.; Trudinger, C.M. Optimizing the CO2 observing network for constraining sources and sinks. Tellus Ser. B Chem. Phys. Meteorol. 1996, 48, 433–444. [Google Scholar] [CrossRef]
- Bousquet, P.; Peylin, P.; Ciais, P.; Ramonet, M.; Monfray, P. Inverse modeling of annual atmospheric CO2 sources and sinks: 2. Sensitivity study. J. Geophys. Res. Atmos. 1999, 104, 26179–26193. [Google Scholar] [CrossRef]
- Rayner, P.; O’Brien, D. The utility of remotely sensed CO2 concentration data in surface source inversions. Geophys. Res. Lett. 2001, 28, 175–178. [Google Scholar] [CrossRef]
- Breon, F.; Peylin, P. Study Final Report: The Potential of Spaceborne Remote Sensing to Contribute to the Quantification of Anthropogenic Emissions in the Frame of the Kyoto Protocol; ESA: Paris, France, 2003. [Google Scholar]
- Chédin, A.; Serrar, S.; Scott, N.; Crevoisier, C.; Armante, R. First global measurement of midtropospheric CO2 from NOAA polar satellites: Tropical zone. J. Geophys. Res. Atmos. 2003, 108, ACH 7-1. [Google Scholar] [CrossRef]
- Boesch, H.; Baker, D.; Connor, B.; Crisp, D.; Miller, C. Global characterization of CO2 column retrievals from shortwave-infrared satellite observations of the orbiting carbon observatory-2 mission. Remote Sens. 2011, 3, 270–304. [Google Scholar] [CrossRef]
- Liang, A.; Han, G.; Gong, W.; Yang, J.; Xiang, C. Comparison of global xCO2 concentrations from OCO-2 with TCCON data in terms of latitude zones. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2491–2498. [Google Scholar]
- Amediek, A.; Fix, A.; Wirth, M.; Ehret, G. Development of an opo system at 1.57 μm for integrated path dial measurement of atmospheric carbon dioxide. Appl. Phys. B 2008, 92, 295–302. [Google Scholar]
- Gibert, F.; Flamant, P.H.; Cuesta, J.; Bruneau, D. Vertical 2-μm heterodyne differential absorption lidar measurements of mean CO2 mixing ratio in the troposphere. J. Atmos. Ocean. Technol. 2008, 25, 1477–1497. [Google Scholar]
- Han, G.; Gong, W.; Ma, X.; Xiang, C.; Liang, A.; Zheng, Y. A ground-based differential absorption lidar for atmospheric vertical CO2 profiling. Acta Phys. Sin. 2015, 64, 244206. [Google Scholar]
- Kameyama, S.; Imaki, M.; Hirano, Y.; Ueno, S.; Kawakami, S.; Sakaizawa, D.; Nakajima, M. Development of 1.6 μm continuous-wave modulation hard-target differential absorption lidar system for CO2 sensing. Opt. Lett. 2009, 34, 1513–1515. [Google Scholar] [CrossRef] [PubMed]
- Sakaizawa, D.; Kawakami, S.; Nakajima, M.; Sawa, Y.; Matsueda, H. Ground-based demonstration of a CO2 remote sensor using a 1.57 μm differential laser absorption spectrometer with direct detection. J. Appl. Remote Sens. 2010, 4, 043548. [Google Scholar] [CrossRef]
- Abshire, J.B.; Ramanathan, A.; Riris, H.; Mao, J.P.; Allan, G.R.; Hasselbrack, W.E.; Weaver, C.J.; Browell, E.V. Airborne measurements of CO2 column concentration and range using a pulsed direct-detection ipda lidar. Remote Sens. 2014, 6, 443–469. [Google Scholar] [CrossRef]
- Lin, B.; Nehrir, A.R.; Harrison, F.W.; Browell, E.V.; Ismail, S.; Obland, M.D.; Campbell, J.; Dobler, J.; Meadows, B.; Fan, T.-F.; et al. Atmospheric CO2 column measurements in cloudy conditions using intensity-modulated continuous-wave lidar at 1.57 micron. Opt. Express 2015, 23, A582–A593. [Google Scholar] [CrossRef] [PubMed]
- Ramanathan, A.K.; Mao, J.P.; Abshire, J.B.; Allan, G.R. Remote sensing measurements of the CO2 mixing ratio in the planetary boundary layer using cloud slicing with airborne lidar. Geophys. Res. Lett. 2015, 42, 2055–2062. [Google Scholar] [CrossRef]
- Refaat, T.F.; Singh, U.N.; Yu, J.R.; Petros, M.; Ismail, S.; Kavaya, M.J.; Davis, K.J. Evaluation of an airborne triple-pulsed 2 μm ipda lidar for simultaneous and independent atmospheric water vapor and carbon dioxide measurements. Appl. Opt. 2015, 54, 1387–1398. [Google Scholar] [CrossRef] [PubMed]
- Spiers, G.D.; Menzies, R.T.; Jacob, J.; Christensen, L.E.; Phillips, M.W.; Choi, Y.; Browell, E.V. Atmospheric CO2 measurements with a 2 μm airborne laser absorption spectrometer employing coherent detection. Appl. Opt. 2011, 50, 2098–2111. [Google Scholar] [CrossRef] [PubMed]
- Menzies, R.T.; Spiers, G.D.; Jacob, J. Airborne laser absorption spectrometer measurements of atmospheric CO2 column mole fractions: Source and sink detection and environmental impacts on retrievals. J. Atmos. Ocean. Technol. 2014, 31, 404–421. [Google Scholar] [CrossRef]
- Yu, J.; Petros, M.; Singh, U.N.; Refaat, T.F.; Reithmaier, K.; Remus, R.G.; Johnson, W. An airborne 2 μm double-pulsed direct-detection lidar instrument for atmospheric CO2 column measurements. J. Atmos. Ocean. Technol. 2017, 34, 385–400. [Google Scholar] [CrossRef]
- Ingmann, P.; Bensi, P.; Durand, Y. A-Scope Advanced Space Carbon and Climate Observation of Planet Erath, Report for Assessment; ESA Communication Production: Noordwijk, The Netherlands, 2008. [Google Scholar]
- Ehret, G.; Kiemle, C.; Wirth, M.; Amediek, A.; Fix, A.; Houweling, S. Space-borne remote sensing of CO2, ch4, and n2o by integrated path differential absorption lidar: A sensitivity analysis. Appl. Phys. B 2008, 90, 593–608. [Google Scholar] [CrossRef] [Green Version]
- Kawa, S.; Mao, J.; Abshire, J.; Collatz, G.; Sun, X.; Weaver, C. Simulation studies for a space-based CO2 lidar mission. Tellus B 2010, 62, 759–769. [Google Scholar] [CrossRef]
- Kiemle, C.; Kawa, S.R.; Quatrevalet, M.; Browell, E.V. Performance simulations for a spaceborne methane lidar mission. J. Geophys. Res. Atmos. 2014, 119, 4365–4379. [Google Scholar] [CrossRef] [Green Version]
- Kiemle, C.; Quatrevalet, M.; Ehret, G.; Amediek, A.; Fix, A.; Wirth, M. Sensitivity studies for a space-based methane lidar mission. Atmos. Meas. Tech. 2011, 4, 2195–2211. [Google Scholar] [CrossRef] [Green Version]
- Stephens, G.L.; Vane, D.G.; Boain, R.J.; Mace, G.G.; Sassen, K.; Wang, Z.; Illingworth, A.J.; O’Connor, E.J.; Rossow, W.B.; Durden, S.L. The cloudsat mission and the a-train: A new dimension of space-based observations of clouds and precipitation. Bull. Am. Meteorol. Soc. 2002, 83, 1771–1790. [Google Scholar] [CrossRef]
- Dominici, F.; Greenstone, M.; Sunstein, C.R. Particulate matter matters. Science 2014, 344, 257–259. [Google Scholar] [CrossRef] [PubMed]
- Han, G.; Gong, W.; Lin, H.; Ma, X.; Xiang, Z. Study on influences of atmospheric factors on vertical CO2 profile retrieving from ground-based dial at 1.6 um. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3221–3234. [Google Scholar] [CrossRef]
- Han, G.; Cui, X.; Liang, A.; Ma, X.; Zhang, T.; Gong, W. A CO2 Profile Retrieving Method Based on Chebyshev Fitting for Ground-Based DIAL. IEEE Trans. Geosci. Remote Sens. 2017. [Google Scholar] [CrossRef]
- Demtröder, W. Laser Spectroscopy: Basic Concepts and Instrumentation; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Zhang, Y.-L.; Cao, F. Fine particulate matter (pm 2.5) in China at a city level. Sci. Rep. 2015. [Google Scholar] [CrossRef]
- Tie, X.; Huang, R.-J.; Dai, W.; Cao, J.; Long, X.; Su, X.; Zhao, S.; Wang, Q.; Li, G. Effect of heavy haze and aerosol pollution on rice and wheat productions in china. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed]
- Wunch, D.; Wennberg, P.O.; Osterman, G.; Fisher, B.; Naylor, B.; Roehl, C.M.; O’Dell, C.; Mandrake, L.; Viatte, C.; Griffith, D.W. Comparisons of the orbiting carbon observatory-2 (OCO-2) xCO2 measurements with TCCON. Atmos. Meas. Tech. 2017, 10, 2209–2238. [Google Scholar] [CrossRef]
- Mandrake, L.; O’Dell, C.W.; Wunch, D.; Wennberg, P.O.; Fisher, B.; Osterman, G.B.; Eldering, A. Orbiting Carbon Observatory-2(OCO-2) Warn Level, Bias Correction, and Lite File Product Description; Jet Propulsion Laboratory: Pasadena, CA, USA, 2015. [Google Scholar]
- U.S. Government Printing Office. NOAA-S/T76-1562. In U.S. Standard Atmosphere; U.S. Government Printing Office: Washington, DC, USA, 1976. [Google Scholar]
- Rothman, L.S.; Gordon, I.E.; Babikov, Y.; Barbe, A.; Chris Benner, D.; Bernath, P.F.; Birk, M.; Bizzocchi, L.; Boudon, V.; Brown, L.R.; et al. The HITRAN2012 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2013, 130, 4–50. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Wang, Y.G.; Houghton, R.; Tang, L.S. Hidden carbon sink beneath desert. Geophys. Res. Lett. 2015, 42, 5880–5887. [Google Scholar] [CrossRef]
- NBoSo. China Statistical Yearbook; NBoSo: Beijing, China, 2015. [Google Scholar]














| Category | Name | Uncertainty | Error a |
|---|---|---|---|
| atmospheric effect b | temperature | 0.5 K | 0.06 |
| pressure | 0.5 hPa | 0.11 | |
| humidity | 10% | 0.02 | |
| line parameter c | Line strength | 2% | 0.07 |
| Pressure shift | 1% | 0.08 | |
| Pressure broadening | 1% | 0.07 | |
| Temperature scaling exponent | 2% | 0.06 | |
| Laser d | Frequency drift | 0.6 MHz | 0.10 |
| spectral purity | 99.9% with a 0.45 nm filter | 0.24 | |
| fluctuation of ratio of on-line and off-line pulse energy e | 0.1% | - | |
| Satellite d | Doppler shift along track | 140 urad | 0.22 |
| Doppler shift across track | 1000 urad | 0.01 | |
| misalignment of footprint | 25 urad | 0.02 | |
| ranging accuracy | 2 m | 0.08 | |
| Total | 0.40 |
| Name | Description/Value | Unit |
|---|---|---|
| δ | The latitude | degree |
| α | The longitude | degree |
| n | The angular velocity of satellite | rad/s |
| t | Any given time | s |
| t0 | The time at which the satellite passes the ascending node | s |
| Δα | The differential longitude between the ascending node and the current nadir | degree |
| ω | The angular velocity of earth/7.29 × 10−5 | rad/s |
| i | The orbit inclination/98.2 | degree |
| μ | The geocentric gravitational constant/3.986 × 1014 | m3/s2 |
| a | The semi-major axis of satellite orbit | km |
| Hsatellite | The altitude of satellite/705 or 450 in this work | km |
| Tsatellite | The orbit period | s |
| Category | Parameter Name | Value | Unit |
|---|---|---|---|
| Laser Transmitter | Pulse length | 15 | ns |
| On-line wavelength | 6361.225 | cm−1 | |
| Off-line wavelength | 6360.981 | cm−1 | |
| Fluctuation of pulse energy | 1 | % | |
| Fluctuation of ratio of on-line and off-line pulse Energy | 0.1 | % | |
| Linewidth | 50 | MHz | |
| Stability of on-line wavelength | 0.6 | MHz | |
| Spectral purity | 99.9 | % | |
| Energy per pulse | 75 | mJ | |
| Repetition frequency(a pair of on-line and off-line) | 20 | Hz | |
| Divergence angle | 100 | urad | |
| Telescope | Time interval of contiguous pair | 0.2 | ms |
| Diameter | 1 | m | |
| Overall optical efficiency | 51.8 | % | |
| Optical filter bandwidth | 0.45 | nm | |
| Detector | Field of view | 0.2 | mrad |
| Electronic bandwidth | 3 | MHz | |
| Dark current(noise equivalent power) | 64 | fW/ | |
| Quantum efficiency | 73 | % | |
| Internal gain | 9 | mV/W | |
| Excess noise factor | 3.2 | - | |
| Other | Orbit altitude | 705 | km |
| Orbit type | 1 h/13 h sun-synchronous | - | |
| Viewing geometry | Nadir | - | |
| Reflectance over lands | 30 | % | |
| Reflectance over seas | 5 | % | |
| AOD | 0.3 | - | |
| RESOLUTION | 50 km (land)/100 km (ocean) | - |
| Unit: PPM | Liang et al. [9] | Wunch et al. [34] | |||||||
|---|---|---|---|---|---|---|---|---|---|
| V7 | V7r | FP | |||||||
| Latitude | Bias a | RMS | Bias | RMS | Bias | RMS | Bias | RMS | N |
| 75 N–85 N | 2.06 | 2.54 | 2.37 | 3.20 | 0.58 | 2.26 | 0.10 | 1.99 | 3 |
| 60 N–70 N | 2.30 | 1.58 | 2.02 | 1.48 | 2.80 | 0.79 | 3.15 | 3.21 | 2 |
| 45 N–55 N | 0.73 | 2.49 | 0.05 | 2.31 | 0.41 | 1.52 | 0.78 | 1.74 | 180 |
| 30 N–40 N | 0.51 | 1.95 | 0.58 | 1.98 | 0.73 | 1.78 | 0.31 | 1.39 | 331 |
| 20 S–0 | 0.57 | 1.49 | 0.13 | 1.56 | 0.19 | 1.00 | 0.34 | 0.88 | 299 |
| 60 S–30 S | 0.45 | 2.43 | 0.02 | 2.28 | 0.01 | 1.51 | 0.28 | 1.37 | 799 |
| Global | 1.10 | 2.15 | 0.86 | 2.03 | 0.79 | 1.74 | 0.36 | 1.33 | / |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, G.; Ma, X.; Liang, A.; Zhang, T.; Zhao, Y.; Zhang, M.; Gong, W. Performance Evaluation for China’s Planned CO2-IPDA. Remote Sens. 2017, 9, 768. https://doi.org/10.3390/rs9080768
Han G, Ma X, Liang A, Zhang T, Zhao Y, Zhang M, Gong W. Performance Evaluation for China’s Planned CO2-IPDA. Remote Sensing. 2017; 9(8):768. https://doi.org/10.3390/rs9080768
Chicago/Turabian StyleHan, Ge, Xin Ma, Ailin Liang, Tianhao Zhang, Yannan Zhao, Miao Zhang, and Wei Gong. 2017. "Performance Evaluation for China’s Planned CO2-IPDA" Remote Sensing 9, no. 8: 768. https://doi.org/10.3390/rs9080768
APA StyleHan, G., Ma, X., Liang, A., Zhang, T., Zhao, Y., Zhang, M., & Gong, W. (2017). Performance Evaluation for China’s Planned CO2-IPDA. Remote Sensing, 9(8), 768. https://doi.org/10.3390/rs9080768