Improving Super-Resolution Mapping by Combining Multiple Realizations Obtained Using the Indicator-Geostatistics Based Method

Abstract

Indicator-geostatistics based super-resolution mapping (IGSRM) is a popular super-resolution mapping (SRM) method. Unlike most existing SRM methods that produce only one SRM result each, IGSRM generates multiple equally plausible super-resolution realizations (i.e., SRM results). However, multiple super-resolution realizations are not desirable in many applications, where only one SRM result is usually required. These super-resolution realizations may have different strengths and weaknesses. This paper proposes a novel two-step combination method of generating a single SRM result from multiple super-resolution realizations obtained by IGSRM. In the first step of the method, a constrained majority rule is proposed to combine multiple super-resolution realizations generated by IGSRM into a single SRM result under the class proportion constraint. In the second step, partial pixel swapping is proposed to further improve the SRM result obtained in the previous step. The proposed combination method was evaluated for two study areas. The proposed method was quantitatively compared with IGSRM and Multiple SRM (M-SRM), an existing multiple SRM result combination method, in terms of thematic accuracy and geometric accuracy. Experimental results show that the proposed method produces SRM results that are better than those of IGSRM and M-SRM. For example, in the first example, the overall accuracy of the proposed method is 7.43–10.96% higher than that of the IGSRM method for different scale factors, and 1.09–3.44% higher than that of the M-SRM, while, in the second example, the improvement in overall accuracy is 2.42–4.92%, and 0.08–0.90%, respectively. The proposed method provides a general framework for combining multiple results from different SRM methods.

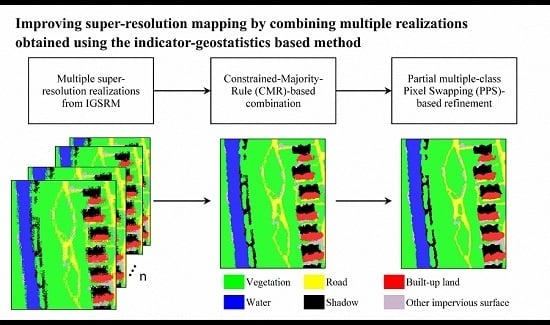
1. Introduction

Land cover classification is a major technique of mapping land cover types and monitoring their dynamics using remote sensing data. Many land cover classification methods have been developed in the past four decades [1,2,3,4]. Owing to the common occurrence of mixed pixels in remote sensing images, even in images with very high spatial resolution [5], spectral unmixing has been widely studied and is used in various applications [6,7,8]. However, spectral unmixing cannot provide location information of land cover classes at a sub-pixel scale [9,10,11,12,13]. Thus, super-resolution mapping (SRM), or sub-pixel mapping has recently been developed and is widely accepted for estimation of the spatial distribution of land cover classes at sub-pixel scale [14]. Specifically, SRM generates higher-resolution classification results from coarse-resolution class proportion images produced by spectral unmixing [15,16,17]. In other words, SRM provides a way to obtain land cover information at finer resolution from images with relatively coarse resolution. SRM has been successfully used in various applications to map different targets, such as waterlines [18,19], lakes [20], urban buildings [21], urban trees [22], forests [9,23,24] and regions of floodplain inundation [25,26,27]. It has also been used to monitor land cover change [28,29], to refine ground control points [30] and to calculate landscape pattern indices [31].

Since Atkinson [14] introduced the concept of SRM, many techniques have been proposed (e.g., [9,10,12,15,24,25,26,27,28,32,33,34,35,36,37,38,39,40,41,42]). Most existing SRM methods exploit the spatial dependence or spatial correlation between pixels (or coarse-resolution pixels, CR-pixels) or sub-pixels (or fine-resolution pixels, FR-pixels) [35,36], and some adopt the assumption of spatial correlation maximization at the target resolution for the prior model of the spatial structure [40,41,42,43,44]. Atkinson [40], for example, generated super-resolution land cover maps by maximizing spatial correlation among adjacent pixels using a pixel-swapping algorithm. The pixel-swapping algorithm is widely used in SRM because of its simplicity, and it works best for highly contiguous landscapes [45]. An improved pixel-swapping algorithm was then developed by Makido, Shortridge, and Messina [46] to handle multiple land cover classes. These SRM methods are iterative and thus time consuming and sensitive to the number of neighboring FR-pixels, especially when the scale factor (i.e., the ratio between coarse resolution and fine resolution) is large [47]. Because these methods only adopt the maximal spatial dependence principle for the prior spatial model, their results are often overly smooth [45,48].

In contrast to the aforementioned iterative methods, Boucher and Kyriakidis [33] proposed a different SRM method based on geostatistical methods of indicator Kriging [49] and indicator stochastic simulation [50]. For the sake of convenience, the method proposed in [33] is referred to as indicator-geostatistics based SRM (IGSRM) in this paper. In IGSRM, the prior model of the spatial structure is first explicitly parameterized in terms of a set of indicator variogram models, each characterizing the spatial variability of a land cover class at fine resolution, and the spatial structure is then applied to coarse resolution data for SRM. Moreover, IGSRM is non-iterative and has less computational burden. The method has been shown to perform well in SRM [16,33,51].

However, unlike most existing SRM methods that produce a single super-resolution land cover map, IGSRM generates multiple equally plausible super-resolution land cover maps [33]. Although multiple super resolution realizations from IGSRM can be used to assess classification accuracy and spatial uncertainty [15,52], many applications usually only require one SRM result. Methods have been proposed to deal with this problem [53,54]. Zhang [53], for example, produced a coastline map based on the class frequency of 1000 super-resolution realizations, and the FR-pixel whose number of the presence of seawater class equals 500 was considered as the coastline class. Li [54] proposed a multiple SRM (M-SRM) method that combines a set of SRM results obtained using single or multiple SRM methods. M-SRM uses plurality voting, where the class with the most votes is selected, to label each FR-pixel. Results show that the combination of multiple SRM outputs can use the different information of each output while addressing drawbacks of the individual method; M-SRM provided results more accurate than those obtained using an individual SRM [54]. However, the SRM results obtained using these methods [53,54] may change the class proportion of each CR-pixel, which is a general requirement in SRM (e.g., [33]). Methods that are more accurate and effective in combining multiple SRM realizations are thus required.

This paper proposes a novel method that combines multiple super-resolution realizations from IGSRM to produce a single SRM result with improved performance. The proposed method also considers the class proportion constraint throughout the SRM procedure.

2. IGSRM

The IGSRM algorithm [33] performs indicator cokriging (ICK) [49] and sequential indicator simulation (SIS) [50] in two steps to produce SRM results. In the first step, also called the sub-pixel sharpening step [55], ICK is used to estimate the probability that an FR-pixel belongs to a particular class, given the coarse-resolution class proportions obtained from spectral unmixing and the prior model of the spatial structure at fine resolution. An indicator variogram model is used to quantify the prior spatial structure of each land cover class at fine resolution [33].

The indicator variogram of the $k$th class pixels is defined as

$${\gamma }_k\left(\mathit{h}\right)=\frac{1}{2}\mathrm{E}{\left[I_k\left(\mathit{u}\right)-I_k\left(\mathit{u}+\mathit{h}\right)\right]}^2,$$

(1)

where $I_k\left(\mathit{u}\right)$ is a binary class indicator, defined as $I_k\left(\mathit{u}\right)=1$ if FR-pixel $\mathit{u}$ is identified as class $k$, and zero if not, and denotes the presence or absence of the $k$th class at FR-pixel $\mathit{u}$. The indicator variogram of the kth class ${\gamma }_k\left(\mathit{h}\right)$, calculated by half of the mathematical expectation (E) of the quadratic increments of all pixel pair values at a distance $\mathit{h}$, characterizes the joint probability of any two FR-pixels separated by $\mathit{h}$ to be different classes.

Using indicator variogram models, the probability for the $k$th class occurrence at FR-pixel $\mathit{u}$ is estimated through ICK as

$${\widehat{p}}_k\left(\mathit{u}\right)={\mathit{\eta }}_k{}^{\mathrm{T}}{a}_k+{\pi }_k\left[1-sum\left({\mathit{\eta }}_k{}^{\mathrm{T}}\right)\right],$$

(2)

where the ${\mathit{\eta }}_k$ is ICK weight for the $k$th class and ${\pi }_k$ is the mean of all elements in coarse resolution class proportions data $a_k$. The function $sum\left({\mathit{\eta }}_k{}^{\mathrm{T}}\right)$ takes the sums of all the elements in vector ${\mathit{\eta }}_k{}^{\mathrm{T}}$. As shown in Equation (2), such a probability is expressed as a weighted linear combination of class proportions data $a_k$.

$${\Gamma }_k^{\mathrm{VV}}{\mathit{\eta }}_k={\mathit{\gamma }}_k^{\mathrm{vV}}\left(\mathit{u}\right).$$

(3)

The ICK weight ${\mathit{\eta }}_k$ for the kth class are obtained by solving Equation (3), which consisted of several indicator variogram matrices that accounted for the correlation between all pairs of CR-pixels (${\Gamma }_k^{\mathrm{VV}}$), and ${\mathit{\gamma }}_k^{\mathrm{vV}}\left(\mathit{u}\right)$ denotes a vector of variogram values between the FR-pixel $\mathit{u}$ and the CR-pixels.

In the second step, called the class allocation step [55], SIS is adopted to generate classification results at fine resolution. A random path is first generated. Along this random path, each FR-pixel is assigned a class according to the ICK-derived conditional probability. A super-resolution realization is generated after repeating the above steps for all FR-pixels. A new super-resolution realization can be generated by repeating the above procedure with a different random path. Multiple equally plausible super-resolution realizations are thus generated. These super-resolution realizations reproduce: (i) the observed coarse class fractions; (ii) the prior structural information encapsulated in a set of indicator variogram models at fine resolution; and (iii) the fine-resolution class labels that might be available. The IGSRM algorithm is described in detail in the literature [33].

3. Method

A novel method was proposed in this study to address the problems with IGSRM, as mentioned previously. The proposed combination method uses multiple super-resolution realizations from the IGSRM algorithm [33] as inputs, extracts the frequency of the presence of each land cover class at each FR-pixel from all super-resolution realizations, and then uses these class frequencies to combine multiple super-resolution realizations into a refined SRM result. The method involves two steps: constrained-majority-rule (CMR)-based combination and partial multiple-class pixel swapping (PPS)-based refinement. Specifically, multiple super-resolution realizations from the IGSRM algorithm [33] are first combined to generate an SRM result through CMR-based combination. The PPS method is then presented to further refine the obtained SRM result from the previous step. The method takes the result of CMR-based combination as the input and uses a pixel-swapping strategy to produce a refined SRM result. A flowchart of the proposed multiple-realization combination method is shown in Figure 1.

3.1. Combination of Multiple Super-Resolution Realizations Using the CMR

As mentioned previously, IGSRM produces multiple equally plausible super-resolution realizations. One of the simplest methods of combining multiple realizations is to employ a majority rule, assigning each FR-pixel the label that has the maximal class frequency [54]. However, direct use of the majority rule may change the FR-pixel numbers of the classes in each CR-pixel, resulting in an SRM result that does not satisfy the class proportion constraint. Although the class proportion constraint is met in IGSRM using a progressive correction algorithm [33], this characteristic cannot be transmitted to the subsequent combination process. A correction step is needed to ensure that, after combination, the class proportions of the FR-pixels within the CR-pixels equal the corresponding class proportions derived from spectral unmixing. Therefore, to combine multiple SRM results from IGSRM into one SRM result while maintaining the class proportions, a CMR-based combination method is presented here. The method can be summarized as follows. Suppose there are n super-resolution realizations generated by IGSRM. The number of each class at each FR-pixel location is first counted using all n super-resolution realizations. A set of class frequency maps is then obtained by dividing the number of each class at each FR-pixel location by the total number of super-resolution realizations; i.e., one map per land cover class. Such class frequencies show the frequency of the presence of each land cover class for each FR-pixel.

For each CR-pixel, the obtained class frequencies of all its FR-pixels for all classes are first sorted in descending order. Each FR-pixel is then assigned to a specific class starting from the class having the highest class frequency until the total number of FR-pixels for each class is attained, so as to be consistent with the class proportions in the CR-pixel obtained from spectral unmixing. If the number of FR-pixels of a class in a CR-pixel reaches the class proportion, the remaining FR-pixels in the CR-pixel are not assigned to that class even though the frequency of the class is higher than the frequencies of other classes. If the frequencies of different land cover classes for an FR-pixel are the same, and the numbers of FR-pixels of these classes do not reach the class proportions, the FR-pixel is assigned to a class randomly. If the frequencies (of the same class or different classes) at different FR-pixels in a CR-pixel are the same, one of the FR-pixels is randomly selected.

The example shown in Figure 2 is given to further explain the CMR-based combination method. Suppose the scale factor is 3, i.e., each CR-pixel is divided into nine (i.e., 3 × 3) FR-pixels, indexed I to IX (Figure 2b). Suppose that a CR-pixel covers three land cover classes, where the red class accounts for five of the nine FR-pixels $\left(5/9\right)$, the green class accounts for three of the nine FR-pixels $\left(3/9\right)$ and the blue class accounts for one of the nine FR-pixels $\left(1/9\right)$ (Figure 2a). Suppose that 10 super-resolution realizations are generated by IGSRM (Figure 2c). The class frequency of each FR-pixel calculated from 10 super-resolution realizations is shown in Figure 2d. All these class frequencies are sorted in descending order (Figure 2e). Following this order and the rule described above, FR-pixels I, II, IV and III are sequentially assigned to the red class while FR-pixels IX and VI are sequentially assigned to the green class. For FR-pixel V, the frequencies of the FR-pixel are the same for the red class and green class (i.e., both are 0.5), so the FR-pixel V needs to be assigned to a class randomly. In this example, we suppose that FR-pixel V is assigned to the red class. Because the proportion of the red class in the CR-pixel has reached $5/9$ (i.e., it has reached the proportion of the red class), the remaining FR-pixels in the CR-pixel are not assigned to the red class. FR-pixel VIII is then assigned to the green class because the proportion of the green class has not been reached and the frequency of the green class (i.e., 0.4) is higher than the frequency of the blue class (i.e., 0.3). Finally, because only the proportion of the blue class has not been reached, FR-pixel VII is assigned to the blue class, even though the frequency of the red class at this FR-pixel location is higher than that of the blue class. The final result is shown in Figure 2f. In this way, 10 super-resolution realizations from IGSRM are combined into an SRM result, which also preserves the class proportions from the original spectral unmixing.

3.2. Refinement Using PPS

The CMR-based combination of multiple super-resolution realizations from the IGSRM algorithm presented in the previous section only considers the constraint of class proportions in a CR-pixel and the class frequency of FR-pixels, but does not explicitly take into consideration the spatial correlation between neighboring FR-pixels. PPS (partial multiple-class pixel swapping), which explicitly considers spatial correlation between neighboring FR-pixels, is thus proposed to further improve the SRM result obtained from the CMR-based combination.

As mentioned previously, pixel swapping [40] is a commonly used SRM method. The objective of pixel swapping is to change the spatial arrangement of FR-pixels in a CR-pixel in such a way that spatial correlation between neighboring FR-pixels is maximized, while the number of FR-pixels for each class within each CR-pixel (i.e., the class proportion) remains fixed throughout the process.

The present study modifies a multiple-class pixel swapping method, called simultaneous categorical swapping [46]. In the simultaneous categorical swapping algorithm, the attractiveness of each class at each FR-pixel location to its neighboring FR-pixels is quantified using the Nearest Neighbor (NN) function according to the current arrangement of FR-pixels. Suppose that $p_i$ is an FR-pixel within a CR-pixel $P_a$, and $p_j$ is one of the neighboring FR-pixels of $p_i$ (where $p_j$ may belong to $P_a$ or its neighboring CR-pixels). The neighborhood system is based on a square window that is composed of the FR-pixel $p_i$ and its neighboring FR-pixels. In the NN model, the attractiveness $A_{p_i}$ of an FR-pixel $p_i$ is simply the sum of class values at the neighboring locations:

$$A_{p_i}={{\displaystyle \sum }}_{j=1}^{N}I\left(p_j\right),$$

(4)

where N is the number of neighbors and $I\left(p_j\right)$ is a binary class indicator at the neighboring FR-pixel location $p_j$. If the class label of the neighbor $p_j$ is identical to that of $p_i$, $I\left(p_j\right)$ is assigned a value of 1; otherwise it is assigned a value of 0.

Once the attractiveness value of each FR-pixel within a CR-pixel for each class is computed, the attractiveness values are sorted in descending order for each class within the CR-pixels, and a pair of FR-pixels is selected to swap. We take a specific class $a$ as an example. Suppose that $A_1$ is the minimum attractiveness value for class $a$ at location $x$ occupied by class $a$, and $A_2$ is the maximum attractiveness value for class $a$ at location $y$ occupied by another class (e.g., class b). $A_3$ is the attractiveness value for class $b$ at location $y$, and $A_4$ is the attractiveness value for class $b$ at location $x$. The difference in attractiveness values $A_2-A_1$ indicates how much more class $a$ is attracted to location $y$ than the current location $x$, while $A_4-A_3$ indicates how much more class $b$ is attracted to location $x$ than current location $y$. Suppose that $A_5$ is the sum of $A_2-A_1$ and $A_4-A_3$, representing how much the attractiveness values for class $a$ and class $b$ would change if swapping the FR-pixels at locations $x$ and $y$. If $A_5$ is positive, swapping the two FR-pixels would increase the spatial correlation of the FR-pixels relative to the current arrangement. The larger the value of $A_5$, the greater the attractiveness value gain achieved by swapping this FR-pixel pair. The pair of FR-pixels with the maximum $A_5$ value among all classes is selected to swap. One pair of FR-pixels within a CR-pixel is swapped per iteration. The FR-pixel swapping stops when no further swaps are made or a specified number of iterations is reached.

In this study, instead of directly using simultaneous categorical swapping [46], we propose PPS. In PPS, only some FR-pixels in CRM-based combination results obtained in the first step are swapped. In the CRM-based combination SRM results, some FR-pixels have high class frequencies, which implies that more super resolution realizations from IGSRM have the same class label at this FR-pixel location, whereas other FR-pixels have low class frequencies, which means that fewer super resolution realizations from IGSRM have the same class label. Class frequency in a FR-pixel location can thus be considered a measure of reliability. In this study, not all FR-pixels in a CR-pixel in the combination results are to be swapped; only FR-pixels with low class frequencies obtained from multiple super resolution realizations will be swapped, whereas those FR-pixels with high class frequencies will not be swapped. A class frequency threshold (e.g., 0.9) should be determined. If the class frequency of the current class of an FR-pixel in the CRM-based combination result is lower than the class frequency threshold, the FR-pixel will be swapped. Otherwise, the FR-pixel will not be swapped and is called a fixed FR-pixel.

PPS includes three steps: selection of swappable FR-pixels, computation of attractiveness values and pixel swapping. In the first step, class frequency maps obtained from the CMR-based combination are used to select swappable FR-pixels. The second step of PPS is computation of attractiveness values. Instead of using the NN function (i.e., Equation (4)), we adopt a weighted NN function, which assigns different weights to swappable FR-pixels and FR-pixels not to be swapped (i.e., fixed FR-pixels). The attractiveness value $A_{p_i}$ of an FR-pixel $p_i$ is expressed as

$$A_{p_i}={{\displaystyle \sum }}_{j=1}^N{\lambda }_{j}I\left(p_j\right),$$

(5)

where N and $I\left(p_j\right)$ are the same as in Equation (4) and λ_j is the weight for $p_j$. The attractiveness value $A_{p_i}$ denotes the class attraction of its neighboring FR-pixels, and if the neighboring FR-pixel is a fixed FR-pixel, it should be given a larger weight as the fixed FR-pixels are more reliable. Therefore, the swappable FR-pixel is assigned a smaller weight while the fixed FR-pixel is assigned a larger weight in this study. Specific weight values can be given on a case by case basis.

Once the attractiveness value of each swappable FR-pixel for each class is computed, the simultaneous categorical swapping strategy [46] is modified to change the spatial arrangement of swappable FR-pixels in a CR-pixel iteratively. In the simultaneous categorical swapping algorithm [46], the pair of FR-pixels with the maximum $A_5$ value among all classes is selected to swap. In the proposed method, however, swapping is performed only if the maximum $A_5$ is larger than zero, as positive $A_5$ implies that swapping the two FR-pixels at locations $x$ and $y$ will increase the spatial correlation of the FR-pixels within a CR-pixel. However, the fixed FR-pixel will not be swapped.

3.3. Method Evaluation

Method evaluation is an indispensable step in SRM. In this study, method evaluation is conducted by comparing the SRM results with the reference map at the target resolution as in existing studies [33,35,56]. The reference map is produced by pixel-based or object-based classification of a higher-resolution image (target-resolution image) [35]. The SRM results are produced by using synthetic class proportion images at coarse-resolution (i.e., coarse-resolution land cover fraction images), which are generated by degrading the reference image using specific scale factors. A similar strategy has been used in many existing SRM studies [16,33,40,57].

The reason for using a synthetic image from a known reference map at the target resolution is to minimize the effect of other factors, such as errors associated with registration and spectral unmixing, on the quality of SRM results and to obtain reliable reference land cover maps at the target resolution for accuracy assessment [33,35]. The synthetic class proportion images are deemed as the outputs of a perfect spectral unmixing process. Although zero error in predicting class proportions is an unrealistic starting point for the super-resolution mapping algorithm, the test is directed at the super-resolution mapping algorithm itself and is thus appropriate at stage of method development; the perfect-proportion image represents greater control in the test [56].

Two accuracy assessment measures were adopted in this study to fully validate the proposed combination method: the thematic accuracy and geometric accuracy. For thematic accuracy assessment, overall accuracy was used, which was computed from confusion matrix [58,59]. Given that the kappa coefficient can be misleading [60], it was not used in this study. Instead, two additional error terms, quantity disagreement and allocation disagreement [60], were also adopted for thematic accuracy assessment. The quantity disagreement is defined as the difference between a classification map and the reference map in the proportions of land cover classes, and the allocation disagreement is defined as the difference between a classification map and the reference map in the spatial allocation of the classes. These two disagreements are components of the overall disagreement. The smaller the quantity disagreement and the allocation disagreement, the better the result. The two disagreement measures are described in detail in the literature [60].

Geometric accuracy indices are adopted to further verify the effectiveness of the proposed combination method, where the indices were originally proposed to evaluate the classification result of images having very high resolution [61]. Geometric accuracy is evaluated on object-based, i.e., connected areas are evaluation units. In this study, geometric accuracy indices used are the edge location error and shape index error [61]. The edge location error of a classification map describes the error in object edges recognized in the map with respect to those of the actual object. This error ranges from 0 to 1. A perfect match of the borders of two regions corresponds to an error value of zero, whereas a large mismatch among region edges corresponds to an error value close to 1. The shape index error is used to evaluate the shape difference between an object on the map derived and the corresponding region on the reference map. It is defined as the absolute difference of the two regions in terms of a specific shape factor. In this study, the shape factor ($sf$) of a region $O_i$ is defined by

$$sf\left(O_i\right)=4\pi S/P^2,$$

(6)

where $S$ is the area of $O_i$ and $P$ is the perimeter of $O_i$. The shape index error is normalized into the range [0, 1]. The smaller the shape index error, the more similar the shapes of the two regions [61].

To validate the proposed method, we quantitatively compare SRM results from the two steps of the proposed method with SRM results generated from IGSRM [33]. Furthermore, M-SRM [54], which is a method of combining multiple SRM results using plurality voting, is also used for comparison. M-SRM labels a FR-pixel based on the classes depicted in the multiple results for that FR-pixel and its neighboring FR-pixels [54]. The performance of the M-SRM was dependent on the neighborhood window size W and the range parameter r of the exponential model [54].

In addition, using the CMR-based combination as the input, PPS and simultaneous categorical swapping [46] in the second step are compared. Furthermore, we also analyze how the accuracy of SRM results changes with the scale factor.

4. Experimental Results

Two study areas were selected to evaluate the performance of the proposed method. One is an urban area, which mainly comprises artificial features, while the other is an agricultural area, mainly covered by natural features.

4.1. Example 1: Urban Area

In the first example, a land cover map of a portion of the Beijing urban area, China, was used as reference map. The reference land cover map was produced by the object-based classification of a pan-sharpened multispectral IKONOS image at 1-m resolution (Figure 3a). The reference map used consists of 945 × 945 pixels (Figure 3b). There are six land cover classes in the area, namely built-up land, road, vegetation, water, shadow, and other impervious surfaces.

As mentioned above, the reference land cover map was upscaled (or degraded) to simulate coarse-resolution class proportion images, using four scale factors of 3, 5, 7 and 9. The class proportion images obtained were used as inputs to IGSRM for SRM. The indicator variograms at fine resolution for six classes were calculated from the reference map and used as prior models of the spatial structure. In this example, 100 super-resolution realizations were produced by IGSRM for each scale factor and then used as the inputs of the proposed method and M-SRM [54]. In M-SRM, the window size W was set as 1, 3, 5, 7, and 9, and range value r was set as 1, 2, 3, and 10 as in [54]. The best result (i.e., with the highest accuracy) was selected for comparison. In the proposed method, the class frequency threshold used to select swappable FR-pixels was set from 0.9 to 1.0 to find an appropriate threshold value. It was found that a class frequency threshold of 1.0 produced the best performance; In order to set weight λ_j more simply, the weight for the swappable FR-pixel was set to 1 while weight for the fixed FR-pixel could be set to a larger integer value. The weight of the fixed FR-pixel was set from 2 to 5 to find an appropriate value. It was found that a weight of 2 produced almost the best performance, so it was set to 2. The neighboring window sizes in simultaneous categorical swapping [46] and the proposed PPS were set to 3 according to the results of experiments.

Accuracy assessment of different methods is presented in

Table 1. Thematic accuracies and geometric accuracies of different SRM methods for the Beijing area (All in percent).

Methods		Scale Factors	Thematic Accuracy (%)			Geometric Accuracy (%)
			OA	AD	QD	EE	SE
IGSRM 1		3	90.64	9.36	0.00	21.50	14.88
		5	85.19	14.81	0.00	35.50	17.74
		7	80.69	19.31	0.00	45.88	18.93
		9	76.86	23.14	0.00	53.75	20.27
M-SRM 2		3	96.98	2.71	0.31	14.05	8.67
		5	91.44	6.68	1.58	29.95	15.93
		7	89.49	8.93	1.57	32.23	18.13
		9	85.96	11.45	2.60	38.47	19.52
Proposed Method	Step 1 (IGSRM + CMR-based combination)	3	96.11	3.89	0.00	11.75	8.31
		5	92.56	7.44	0.00	20.63	11.24
		7	89.01	10.99	0.00	29.25	13.27
		9	85.52	14.48	0.00	36.17	14.76
	Step 2 (Step1 + PPS-based refinement)	3	98.07	1.93	0.00	7.04	4.62
		5	94.88	5.12	0.00	15.75	8.53
		7	91.38	8.62	0.00	23.94	11.11
		9	87.82	12.18	0.00	31.19	13.59

OA: Overall Accuracy; AD: Allocation Disagreement; QD: Quantity Disagreement; EE: Edge location Error; and SE: Shape index Error. ¹ The accuracies of IGSRM were the mean values of 100 assessments. ² The accuracies of M-SRM were the accuracies of the best results. The W of best results of M-SRM were 3, 5, 5 and 5; r were 2, 3, 3 and 2 for scale factors of 3, 5, 7 and 9, respectively.

. The table shows that overall accuracies of IGSRM were 90.64%, 85.19%, 80.69% and 76.86% for scale factors of 3, 5, 7 and 9, respectively. When the proposed method was applied, overall accuracies at all scale factors were considerably improved. Specifically, when the CMR-based combination, the first step of the proposed method, was adopted, overall accuracies of SRM results increased by 5.47%, 7.37%, 8.32% and 8.66% for scale factors of 3, 5, 7 and 9, respectively, relative to those of IGSRM. When PPS, the second step of the proposed method, was used, overall accuracies of SRM results improved by 7.43%, 9.69%, 10.69% and 10.96% for scale factors of 3, 5, 7 and 9, respectively, relative to overall accuracies of the IGSRM method. Furthermore, the proposed method also produced higher overall accuracies than the M-SRM method [54], with increases of 1.09%, 3.44%, 1.89% and 1.86% for scale factors of 3, 5, 7, and 9, respectively.

It is also seen in Table 1, in SRM results produced from IGSRM and the proposed method, the overall disagreements only include the allocation disagreements, whereas the quantity disagreements of the results are zero because these two methods preserve the proportions of land cover classes within each CR-pixel in the SRM process. However, the quantity disagreements of the results of M-SRM increase with scale factors. For the same scale factor, the allocation disagreement of the result of the proposed method was almost the lowest (Table 1). Specifically, the allocation disagreements of the results from the proposed method are lower than those from IGSRM for all four scale factors, and also lower than those from M-SRM for three scale factors of 3, 5, and 7.

Geometric errors were also reduced when the proposed method was used (Table 1). Compared with those of IGSRM, the edge location errors of the proposed method reduced by 14.46%, 19.75%, 21.94% and 22.56%, and the shape index errors reduced by 10.26%, 9.21%, 7.82% and 6.68% for the scale factors of 3, 5, 7 and 9, respectively. The proposed method also produced lower geometric errors, compared with those from M-SRM. In a word, less error in object edges was thus recognized in the results of the proposed method with respect to the edges of the actual object, and there was less difference in shape of object between the results of the proposed method and the reference map.

Table 1 also shows that, as the scale factor increased, the overall accuracies of all methods had similar decreasing trends, and corresponding allocation disagreements and geometric errors increased. However, the decrease in accuracy of the SRM result was less obvious when the proposed method was applied. For example, the overall accuracy of IGSRM decreased by 13.78% and that of M-SRM decreased by 11.02%, from a scale factor of 3 to a scale factor of 9, whereas the overall accuracy of the proposed method decreased by 10.25%.

The SRM results of the proposed method for a scale factor of 5 are shown in Figure 4a. Visual comparison suggests that the result of the proposed method (Figure 4a) is similar to the reference map (Figure 3b). Figure 4b–e shows a portion of the reference map and corresponding SRM results from IGSRM and two steps of the proposed method for more detailed comparison. Compared with reference map (Figure 4b), although the shapes of ground objects were partially recovered in the IGSRM-derived result, it is obvious that the SRM result from IGSRM contained substantial noise and fewer details, missed many small structures, and had discontinuous boundaries of classes (Figure 4c). After combining multiple IGSRM-derived results using CMR-based combination (the first step of the proposed method), noise in the SRM result was significantly reduced and class boundaries were more continuous. However, some linear features (e.g., trails and shadow) were still not smooth (Figure 4d). Furthermore, the SRM result obtained after use of PPS (the second step of the proposed method) was better (Figure 4e). Shapes of objects were more similar to those in the reference map, the boundaries of classes were smoother, and more importantly, the distributions of small structures were more similar to those in the reference map shown in Figure 4b. For example, the spatial pattern of trails at the center of the area was much better reconstructed than in the other results. However, although more linear features were properly recovered after the PPS was applied, some small linear features (e.g., small trails and shadow) were still discontinuous (Figure 4e).

Figure 5 shows the SRM results for a local area at several scale factors obtained using the proposed PPS (Figure 5a–d) and the simultaneous categorical swapping method [46] (Figure 5e–h), both of which use CMR-based combination results as inputs. Compared with the result of simultaneous categorical swapping, the result of the proposed method generally show better performance in terms of detail and connectivity of structures at the same scale factor. As shown by red rectangles in Figure 5, slender structures (e.g., trails) in SRM results obtained using PPS for refinement (Figure 5b–d) were more coherent and more similar to those in the reference map (Figure 4b), compared with the slender structures in the results of simultaneous categorical swapping (Figure 5f–h). We also quantitatively compared these SRM results in terms of thematic and geometric accuracies (detailed results not shown here). For all scale factors, overall accuracies of PPS were slightly higher than those of simultaneous categorical swapping, and allocation disagreements and geometric errors of PPS were lower than those of simultaneous categorical swapping. For example, at the scale factor of 7, the overall accuracy of PPS was 91.38%, which was 0.24% higher than that of simultaneous categorical swapping (91.14%), and the edge location error of PPS (23.94%) was 0.72% lower than that of simultaneous categorical swapping (24.66%).

Figure 5i–l shows the SRM results for the same portion at different scale factors obtained using M-SRM. From this figure, most objects and structures are recovered at scale of 3. However, slender structures (e.g. trails) were almost disappeared at larger scale factors (e.g., 5, 7 and 9). Compared with the M-SRM, our proposed method show better results (Figure 5a–d) in terms of detail, shape and connectivity of objects or structures, in particular at larger scale factors.

Furthermore, as shown in Figure 5, the SRM results from all methods have more details and continuous structures at a smaller scale factor (e.g., a scale factor of 3). It is hard to find an appreciable difference between the SRM results at smaller scale factors and the reference map (Figure 4b). However, as the scale factor increases, small structures gradually become discontinuous. For example, some small structures (e.g., trails and shadow) disappear at scale factor of 7 (Figure 5c,g,k). When the scale factor was 9, the SRM results are further smoothened, and many small structures are not well preserved (Figure 5d,h,l).

4.2. Example 2: Agricultural Area

To further evaluate the proposed method, an agricultural area in North Xinjiang, China, was selected as the second study area. The land use map of the area was obtained from visual interpretation of Landsat TM images of 30-m resolution by experts, and one of the Landsat TM images used is shown in Figure 6a. The size of the map used is 1575 × 1575 pixels (Figure 6b). There are five classes, namely built-up land, cropland, grassland, water and undeveloped land.

Following the same procedure as that used for the first example, scale factors of 3, 5, 7 and 9 were used for this example. The class proportion images generated from the reference map were used as inputs to IGSRM for SRM. One hundred super-resolution realizations were produced by IGSRM for each scale factor and used as the input to the proposed method and M-SRM [54]. Same as in the first example, after several trials, the parameters that produced the best performance were selected. In the proposed method, the class frequency threshold was set to 1.0, the weight parameter for the fixed FR-pixel was set to 2, and the neighboring window sizes in simultaneous categorical swapping and the proposed PPS were set to 3.

Accuracies of the results obtained from IGSRM, M-SRM [54] and the proposed method are given in

Table 2. Thematic accuracies and geometric accuracies of different SRM methods for the Xinjiang area (All in percent).

Methods		Scale Factors	Thematic Accuracy (%)			Geometric Accuracy (%)
			OA	AD	QD	EE	SE
IGSRM 1		3	96.94	3.06	0.00	9.60	19.14
		5	94.73	5.27	0.00	20.90	23.19
		7	92.59	7.42	0.00	34.27	25.51
		9	90.65	9.35	0.00	42.79	26.29
M-SRM 2		3	99.28	0.63	0.09	7.00	4.78
		5	97.81	1.85	0.34	19.82	9.71
		7	96.25	3.13	0.61	29.62	14.21
		9	94.70	4.41	0.89	37.35	18.27
Proposed Method	Step 1 (IGSRM + CMR-based combination)	3	99.26	0.74	0.00	4.48	4.93
		5	97.83	2.17	0.00	11.07	10.48
		7	96.23	3.77	0.00	18.78	14.87
		9	94.59	5.41	0.00	26.66	18.19
	Step 2 (Step1 + PPS-based refinement)	3	99.36	0.64	0.00	4.26	4.16
		5	98.44	1.57	0.00	8.89	6.52
		7	97.15	2.85	0.00	15.77	9.13
		9	95.57	4.43	0.00	23.12	11.84

OA: Overall Accuracy; AD: Allocation Disagreement; QD: Quantity Disagreement; EE: Edge location Error; and SE: Shape index Error. ¹ The accuracies of IGSRM were the mean values of 100 assessments. ² The accuracies of M-SRM were the accuracies of the best results. The W of best results of M-SRM were 3, 5, 5 and 5; r were 1, 3, 2 and 2 for scale factors of 3, 5, 7 and 9, respectively.

. Similar to the results for the first example, at the same scale factor, the proposed method produced the highest overall accuracy and the lowest allocation disagreement, edge location error and shape index error. The quantity disagreements of the results of M-SRM increased with scale factors, whereas the quantity disagreements in the results of IGSRM and the proposed method were zero. For example, at the scale factor of 5, the overall accuracy, allocation disagreement, edge location error and shape index error of the result of IGSRM were 94.73%, 5.27%, 20.90% and 23.19%, respectively, whereas when CMR-based combination (the first step of the proposed method) was adopted, the overall accuracy of result increased by 3.10% and the allocation disagreement, edge location error and shape index error of the result decreased by 3.10%, 9.83% and 12.71%, respectively. When PPS (the second step of the proposed method) was used, the overall accuracy of results improved by 3.71% and the allocation disagreement, edge location error and shape index error of the results decreased by 3.70%, 12.01% and 16.67%, respectively, relative to the results of IGSRM. Furthermore, the results of the proposed method also had higher thematic accuracies and lower geometric errors than those of M-SRM. For example, the edge location errors of the proposed method were 2.74%, 10.93%, 13.85% and 14.23% lower than those of M-SRM for scale factors of 3, 5, 7, and 9, respectively. Similar to the first example, as the scale factor increased, the accuracy of the results had a downward trend for all methods but the accuracy of the proposed method decreased least.

Figure 7a shows the SRM result produced using the proposed method at a scale factor of 5. By visual comparison, the result of the proposed method (Figure 7a) is similar to the reference map (Figure 6b). Shapes of ground objects were properly recovered, and the boundaries of classes were accurate and clear. Figure 7b–e shows a portion of the reference map and corresponding SRM results of IGSRM and the proposed method. Compared with the reference map (Figure 7b), the result of IGSRM was much more noisy. Most small structures were not recovered, and even boundaries of larger structures were discontinuous (Figure 7c). After combining multiple SRM results from IGSRM using CMR-based combination (the first step of the proposed method), noise was reduced and the class boundaries of large structures were smoother and more continuous. However, many details of the land cover still missed (Figure 7d). The SRM result obtained after PPS had more continuous and detailed structures. There was almost no noise in that result and the boundaries of classes were accurate and clear. For example, the spatial pattern of a river (e.g., the water at the center of the area) was much better reproduced than in the other results (Figure 7e).

Figure 8 shows the SRM results for a local area at several scale factors obtained using the proposed PPS (Figure 8a–d) and the simultaneous categorical swapping method [46] (Figure 8e–h). It was hard to find an appreciable difference between the SRM results of PPS and simultaneous categorical swapping method at smaller scale factors (e.g., the scale factor of 3 or 5). However, small and thin structures were better preserved in the result of the PPS method than the result of simultaneous categorical swapping at larger scale factors, as shown by black rectangles in Figure 8. Quantitative accuracy assessment showed that the results of PPS were more accurate than those of simultaneous categorical swapping (detailed results not shown here). At the same scale factor, overall accuracies of PPS were slightly higher than those of simultaneous categorical swapping, and allocation disagreements and geometric errors of PPS were lower than those of simultaneous categorical swapping. For example, at the scale factor of 7, the overall accuracy of PPS was 97.15%, which is 0.11% higher than that of simultaneous categorical swapping (97.04%), and the edge location error of PPS (15.77%) was 0.38% lower than that of simultaneous categorical swapping (16.15%).

Figure 8 also shows the SRM results for the same portion at different scale factor obtained using M-SRM [54] (Figure 8i–l). From the figure, most small structures were not recovered, and the spatial pattern of a river (e.g., the water at the center of the area) was almost disappeared at large scale factors (e.g., 7 and 9) (Figure 8k,l). In contrast, the proposed method produced significantly better results (Figure 8c,d) than the M-SRM at larger scale factors.

Furthermore, as shown in Figure 8, the SRM results for all methods preserved more detailed and more continuous structures at smaller scale factors (e.g., the scale factor of 3). However, the slender structures had more irregular boundaries and were more discontinuous at larger scale factors. For example, the shape of a river (e.g., the water at the center of the area) was accurately recovered at the scale factor of 3 and 5 (Figure 8a,b,e,f,i,j). However, at scale factors of 7 and 9, thin structures (river) were discontinuous and small objects were missed (Figure 8c,d,g,h,k,l).

5. Discussion

A new method of combining multiple realizations from the IGSRM algorithm [33] to improve SRM results was proposed. Qualitative and quantitative analyses in two study areas demonstrated that, compared with IGSRM and an existing combination method M-SRM [54], the proposed method not only improves thematic accuracy but also reduces geometric errors in SRM results.

The proposed method first combines multiple super-resolution realizations generated by IGSRM [33] into a single SRM result using CMR-based combination and then makes further improvement with the PPS method. In the first step of the proposed method, CMR-based combination is proposed to assign a specific class label to each FR-pixel by considering the class frequency at each FR-pixel calculated from multiple super-resolution realizations from IGSRM and the class proportion for each CR-pixel, which is a basic requirement of SRM methods. This is different from M-SRM [54], which only considers the class frequencies from multiple super-resolution results, but not the class proportions of CR-pixels from original coarse resolution class proportion images.

In the second step of the proposed method, PPS further improves the SRM result by considering spatial correlation between neighboring FR-pixels. Using the result of CMR-based combination as input, the PPS only partially changes the spatial arrangement of FR-pixels in a CR-pixel iteratively to maximize spatial correlation between neighboring FR-pixels.

There are three points of difference between the proposed PPS method and simultaneous categorical swapping method [46]. First, instead of swapping all FR-pixels as in simultaneous categorical swapping, only FR-pixels in CMR-based combination results whose class frequencies are lower than a specified class frequency threshold are swapped. Second, in calculating attractiveness values, instead of assigning the same weight to each FR-pixel, FR-pixels with a class frequency higher than a specified threshold are assigned higher weights than those FR-pixels with a class frequency lower than the specified threshold. Third, in the FR-pixel swapping process of the proposed method, instead of directly selecting the maximum attractiveness value sum ($A_5$) for swapping, swapping is performed only when maximum $A_5$ is larger than zero, which avoids a large number of invalid FR-pixel swaps. Experimental results showed that the proposed PPS method has two advantages over simultaneous categorical swapping. First, the proposed PPS method produced structures that were more continuous, as shown in Figure 5 and Figure 8. Second, there were far fewer FR-pixel swaps in the proposed PPS than in simultaneous categorical swapping because of the reduced number of swappable FR-pixels and reduced number of invalid FR-pixels swaps. Specifically, in the first example, for example, at the scale factor of 9, the total number of FR-pixel swaps in the PPS was 46,749 whereas the total number of FR-pixel swaps in simultaneous categorical swapping was 396,900. The total number of FR-pixel swaps in simultaneous categorical swapping was almost 8.5 times that in PPS. In the second example, at the scale factor of 9, the total numbers of FR-pixel swaps in PPS and simultaneous categorical swapping were 45,377 and 949,375, respectively. In summary, the proposed PPS method outperformed simultaneous categorical swapping for the second step.

In addition, as the scale factor increases, overall accuracies of the SRM results decrease, while the allocation disagreements and geometric errors increase. At a higher scale factor, classes are more likely to be located in wrong locations (i.e., higher allocation disagreement), fewer spatial details were preserved and structures were less continuous and even disappeared. This may be because larger scale factors increase the number of FR-pixels within a CR-pixel, and make the SRM problem (locating class labels) more complex [33,35].

It should be mentioned that, although the proposed method is defined for combining multiple SRM results from IGSRM method, it is also a general framework for combining multiple SRM results from different SRM methods. Although the proposed method produced very promising results, further work is still needed to improve the performance. For example, more effective methods of measuring spatial characteristics, such as shape and connectivity, should be adopted in the SRM.

6. Conclusions

This paper proposed a new method of combining multiple SRM realizations from IGSRM [33] to address the problems with IGSRM and to improve SRM results. Using multiple SRM results from IGSRM as input, two major steps were included to produce an improved SRM results. Several existing methods were used for both individual steps and the whole SRM process to fully evaluate the proposed method. The experimental results demonstrated that the proposed method achieved much improved SRM results, compared with SRM results from IGSRM and M-SRM methods, in terms of thematic accuracy and geometric accuracy. For example, in the first example, the overall accuracy of the proposed method is 7.43–10.96% and 1.09–3.44% higher than those of the IGSRM and M-SRM methods for different scale factors, while, in the second example, the improvements in overall accuracy are 2.42–4.92% and around 1% higher than those of the IGSRM and M-SRM. Compared with M-SRM [54], although the improvement in overall accuracy is marginal, the improvements in other accuracy measures and visual comparison are significant. Furthermore, the proposed method provides a general framework for combining multiple results from different SRM methods.

The proposed method code is developed in C++. The code and test data are available by contacting the authors.