Abstract
The TROpospheric WAter RAdiometer (TROWARA) is a ground-based microwave radiometer with an additional infrared channel observing atmospheric water parameters in Bern, Switzerland. TROWARA measures with nearly all-weather capability during day- and nighttime with a high temporal resolution (about 10 s). Using the almost complete data set from 2004 to 2016, we derive and discuss the diurnal cycles in cloud fraction (CF), integrated liquid water (ILW) and integrated water vapour (IWV) for different seasons and the annual mean. The amplitude of the mean diurnal cycle in IWV is 0.41 kg/m. The sub-daily minimum of IWV is at 10:00 LT while the maximum of IWV occurs at 19:00 LT. The relative amplitudes of the diurnal cycle in ILW are up to 25% in October, November and January, which is possibly related to a breaking up of the cloud layer at 10:00 LT. The minimum of ILW occurs at 12:00 LT, which is due to cloud solar absorption. In case of cloud fraction of liquid water clouds, maximal values of +10% are reached at 07:00 LT and then a decrease starts towards the minimum of −10%, which is reached at 16:00 LT in autumn. This breakup of cloud layers in the late morning and early afternoon hours seems to be typical for the weather in Bern in autumn. Finally, the diurnal cycle in rain fraction is analysed, which shows an increase of a few percent in the late afternoon hours during summer.
1. Introduction
Clouds and aerosols continue to contribute the largest uncertainty to estimates and interpretations of the Earth’s changing energy budget [1]. There is a consensus in the climate research community that man-made global warming is amplified by an increase of water vapour in a warmer world [2]. The Earth’s radiation budget between the incoming short-wave radiation of the Sun and the outgoing longwave radiation of the Earth is strongly influenced by the spatio-temporal distribution of clouds. Differing assumptions about how the Earth’s cloud distribution is maintained for doubling of the CO concentration in the atmosphere lead to estimated increases of global mean surface temperature in the range from 1.5 to 4.5 C [2].
The physical description of clouds involves microphysics and nonlinear radiative-dynamic processes over temporal scales from about 1 s to 1 decade and spatial scales from about 1 m to 1000 km. Observing and modelling of the Earth’s cloud distribution is still a challenge, even though large efforts have been undertaken in meteorology, atmospheric research, and climate sciences [3,4]. Diurnal variations in atmospheric water parameters are of high interest for measurement and atmospheric modelling since one day is the shortest regular period by which the Earth’s surface and atmosphere absorb energy from the Sun. Cloud formation and rainfall depend on orography and land-sea contrast [5]. The phase of the diurnal variation can change significantly within a small horizontal distance. Parameterisation of cloud formation and rainfall is difficult since these phenomena depend for example on the variable surface flux of moisture, orography, convective processes, turbulence, eddies and the growth of the planetary boundary layer during the daytime.
In the following, we focus on the diurnal cycle in integrated liquid water (or liquid water path). Two research communities are active in investigating the diurnal variation of cloud liquid water (ILW). The first group are scientists who generate world maps of cloud coverage, outgoing radiation, and rainfall data from polar-orbiting satellites imaging the Earth in the ultraviolet, visible, infrared, and microwave range [5,6,7,8,9]. Since the diurnal variations of cloud parameters and rainfall have strong amplitudes of about 10% or larger, construction of world maps and climatic trend analyses of cloud parameters from satellite observations have to correct for offsets caused by a varying local solar time at the observation places. The second group are atmospheric modellers who use the periodic signal of the diurnal cycle in atmospheric water to test the quality of weather and climate models. The models often provide incorrect phases and amplitudes of the diurnal variations of rainfall, cloud cover and ILW reflecting errors in the parameterization of clouds, convective processes, surface moisture flux, and microphysics [10,11].
There is no doubt that weather forecast and regional climate projections will not be correct if a fundamental process such as cloud formation and its diurnal variation is incorrectly simulated by the numerical model. Bergman, J.W. et al. [12] analysed that the cloud diurnal contribution to time-average surface energetics is as much as 20 W m in a regional climate (Amazon basin) after deforestation, which caused a shift from a high cloud distribution to a low cloud distribution. Cross-validation studies fostered the progress in remote sensing, data analysis, and modelling. Observed and simulated diurnal variations were compared [9,13]. Numerous cross-validations were organized within the Global Energy and Water Experiment (GEWEX) and the International Satellite Cloud Climatology project (ISCCP) [14].
There are only a few studies investigating the diurnal variation in ILW by means of ground-based microwave radiometers. This is rather surprising since ground-based microwave radiometers are well suited for the continuous measurement of ILW during the daytime and nighttime in all seasons. Thus, data sets of microwave radiometers are convenient for intercomparisons with results from polar-orbiting satellites, other ground-based instruments (e.g., lidar), and models. A review of meteorological applications of ground-based microwave and millimeter wavelength radiometry was given by [15]. Roebeling, R.A. et al. [16] compared the diurnal variation in liquid water path derived from the Spinning Enhanced Visible and Infrared Imager (SEVIRI) on board Meteosat-8 with those observed by two ground-based microwave radiometers of the CloudNET in northern Europe and found a good agreement. Snider, J.B. et al. [17] presented diurnal variations in IWV and ILW observed with ground-based microwave radiometers operating near 20, 23, 31, and 90 GHz. Cross-validation with coincident measurements of infrared brightness temperature of the sky confirmed the diurnal variations in ILW obtained by microwave radiometers. In addition, the observed diurnal variations in ILW are in a qualitative agreement with expectations from theory and satellite observations that a maximum of cloud liquid water occurs before sunrise in oceanic areas during summer [9]. Model simulations by [18] showed quite similar shapes of the diurnal cycles in CF and ILW for marine boundary layer clouds with a maximum at 06:00 LT and a minimum at 18:00 LT.
Ground-based microwave radiometers are well suited for measurement of the diurnal cycle in atmospheric water parameters. We suggest that modellers and observers should take more advantage of ground-based microwave radiometers for research and validation studies of the diurnal cycle in ILW. Here, we analyse the long-term time series of integrated liquid water, integrated water vapour, and cloud fraction observed by the TROWARA radiometer, which is located in Bern on the Swiss Plateau. Section 2 describes the instrument and the measurement technique as well as the data analysis. Section 3 shows the climatology of IWV, ILW and CF averaged over the time interval 2004–2016. Furthermore, we discuss the results from the spectral data analysis of the time series. Section 3 also presents the diurnal cycles in IWV, ILW and CF. Conclusions are given in Section 4.
2. Instrument, Data and Analysis
2.1. The Microwave Radiometer TROWARA
Observations of the TROpospheric WAter RAdiometer (TROWARA) are central to our study. Peter, R. et al. [19,20] described the design and the construction of the TROWARA instrument, which is a dual-channel microwave radiometer. Two ferrite circulator switches at each frequency switch between the antenna and noise diodes where the latter are taken as hot and cold reference loads. A radiometer model was developed based on measurements of the reflection and transmission coefficients of all radiometer components up to and including the ferrite switches [20]. Tipping calibrations are carried out with an external mirror in order to correct the sky brightness temperature calculated by the model. The instrument is sufficiently stable that a tipping calibration is only necessary once every few weeks.
TROWARA provides the vertically-integrated water vapour (IWV) and vertically-integrated cloud liquid water (ILW), also known as liquid water path (LWP). TROWARA is operated inside a temperature-controlled room on the roof of the EXWI building of the University of Bern (46.95N, 7.44E, 575 m a.s.l.). The indoor operation of TROWARA permits the measurement of IWV even during rainy periods. TROWARA’s antenna receives the atmospheric radiation through a microwave transparent window and is pointing the sky at a zenith angle of 50 towards the southeast.
The two microwave channels are at 21.4 GHz (bandwidth 100 MHz) and 31.5 GHz (bandwidth 200 MHz). The 21.4 GHz frequency is more sensitive to microwaves from water vapour, and the 31.5 GHz frequency is more sensitive to microwaves from atmospheric liquid water.
The radiative transfer equation of a non-scattering atmosphere can be expressed as
where is the observed brightness temperature of the i-th frequency channel (e.g., 21 GHz). is the opacity along the line of sight of the radiometer, and is the contribution of the cosmic microwave background. The effective mean temperature of the troposphere is given by [21,22].
Equation (1) leads to the opacities
where the radiances are observed by TROWARA.
For a plane-parallel atmosphere, the opacity is linearly related to IWV and ILW
where the coefficients and are not really constant since they can partly depend on air pressure. As shown by [22], the coefficients can be statistically derived by means of coincident measurements of radiosondes and fine-tuned at times of periods with a clear atmosphere. The coefficient is the mass absorption coefficient of cloud water. It depends on temperature (and frequency), but not on pressure. It is derived from the physical expression of Rayleigh absorption by clouds [22]. Once the coefficients are determined, combined opacity measurements at 21 and 31 GHz permit the retrieval of IWV and ILW from Equation (3). Thus, a dual channel microwave radiometer can monitor IWV and ILW with a time resolution of 6–11 s and nearly all-weather capability during daytime and nighttime.
The physical temperature at the cloud base is derived for optically thick clouds (ILW g/m) from measurements of an infrared radiometer channel at a wavelength of = 9.5–11.5 m. The narrowband infrared radiometer is a Heitronics KT15.85D pyrometer of type A, which was calibrated by the manufactor for the signal temperature range from −100 to +100 C [23]. Temperature resolution, filter curve, view of field, radiometer model at low temperatures and other characteristics of the Heitronics KT15.85D are described in [23]. The temperature resolution is less than 2 C for target temperatures from −100 to +100 C and a response time of 1 s.
The antenna coil of TROWARA has a full width at half power of 4 and is pointing the sky at a zenith angle of 50 towards the southeast. The view direction is constant, and the microwave and infrared channels of TROWARA observe the short-term temporal variations of the brightness temperature in the same volume of the atmosphere. This contributes to the high sensitivity of TROWARA for cloud detection. Cossu, F., Mätzler, C. and Morland, J. [22,24] give further details of the sensors and the retrieval technique.
TROWARA delivered an almost uninterrupted time series of ILW since 2004, with a time resolution of 11 s until end of 2009 and 6 s afterwards. Clouds are detected in the line of sight of TROWARA with the time resolution of the ILW series. Cossu, F. [24] determined the instrumental noise g/m of TROWARA from the noise of ILW during 245 days in which the sky was free of clouds. We emphasize that this is a remarkable sensitivity for a microwave radiometer. If an ILW value exceeds the level, then we are confident by 99.7% that the ILW value was generated by a cloud and not by instrumental noise. Thus, ILW g/m is the criterion for the existence of a cloud. In contrast to the ILW series, the time series of IWV have been used since 1994 for trend analyses [25,26].
CF (cloud fraction) is easily determined in the time domain—for example, CF is the quotient of the time intervals when ILW > 2.3 g/m and the total observation time. The high spatio-temporal variability of clouds floating through the fixed line-of-sight of TROWARA requires a high temporal resolution of about 10 s for the cloud flag. CF for different categories of liquid water clouds were derived by [27] using the TROWARA measurements. TROWARA’s coincident ILW and infrared brightness temperature measurements allow separation of the liquid water clouds into four categories:
- CF1: thin liquid water clouds (2.3 g/m< ILW < 30 g/m),
- CF2: thick supercooled liquid water clouds (ILW > 30 g/m and K),
- CF3: thick warm liquid water clouds (ILW > 30 g/m and K),
- CF4: all liquid water clouds (ILW g/m).
Quite similar criteria for the separation of supercooled liquid water clouds were described by [28]. The critical point is that the derived cloud distributions are possibly biased towards the low level clouds since the infrared channel mainly sees the cloud base of thick clouds. Mätzler, C. et al. [29] avoided this bias by using additional satellite data for the cloud-top temperature.
Hirsch, E. et al. [30] determined the microphysical and optical properties of thin liquid water clouds and emphasized that these clouds should be considered in climate studies since they are frequent and they change the radiative forcing of the climate system. Measurements indicated that the downwelling infrared radiance of a thin liquid water cloud is about 60% greater than that of clear sky. Thin liquid water cloud areas often occur at the edges of and in the inter-region between clouds (twilight zone of clouds).
Since TROWARA is not sensitive to ice clouds, CF of TROWARA is in general smaller than that of synoptic observations. Cossu, F. [24] found a CF difference of about 17% between TROWARA and synoptic observations in the same region over a period of six years. In addition, TROWARA may not see some of the very thin and tenuous clouds that are still visible by the naked eye.
The present study is not a cloud type study that would require the evaluation of coincident observations by ceilometer, lidar, radiosonde and hemispherical sky camera. In our study, the terms thin and thick refer to the magnitude of the optical depth at microwave frequencies that are proportional to the liquid water path. The terms should not be misunderstood by the geometrical thickness of the clouds, which is not measured by the microwave radiometer. A statistical cloud type study was performed by [31] for Payerne. Payerne is representative for Bern since Payerne is located just 40 km west of Bern in the Swiss plateau. About 38% of the clouds classified by a sky camera have the type Sc (stratocumulus), while 17% are cirrus-cirrostratus (Cr-Cs) and 12% are cirrocumulus-altocumulus (Cc-Ac). Bernet, L. et al. [31] also found that the relationship between the ILW value and the cloud type is ambiguous. Cumulus and cirriform clouds generally have a small ILW, but no tendency for stratiform clouds was found.
2.2. Data Analysis
Hourly means of IWV, ILW, CF1, CF2, CF3 and CF4 were obtained by averaging of the 10 s sampling data. An upper threshold of 400 g/m is used for ILW. This means that, in the presence of rain droplets, we take the value 400 g/m as an estimate of the ILW of the cloud droplets. During precipitation, TROWARA overestimates ILW of the cloud droplets because of the strong microwave emission from the rain droplets ( mm). This is the reason why we take an upper threshold of 400 g/m for vertically integrated cloud liquid water path during rainy periods. Generally, the results are not sensitive to the choice of the threshold as it was investigated by [32]. Furthermore, the rain periods are a small fraction of about 7% of the whole measurement time. Monthly means of IWV are well defined because of the continuous monitoring of IWV by TROWARA.
The arithmetic mean is removed from the time series of IWV, ILW or CF. Then, the Fast Fourier Transform (FFT) power spectra are obtained by folding these time series with a Hamming window and by applying zero padding at the beginning and end of the time series. The FFT power spectra are normalized by the power of the strongest spectral component, which is either the annual or the semi-annual oscillation.
Next, we derive amplitude spectra by means of bandpass filtering. The time series are filtered with a digital non-recursive, finite impulse response (FIR) bandpass filter performing zero-phase filtering by processing the time series in forward and reverse directions. The number of filter coefficients corresponds to a time window of three times the central period, and a Hamming window has been selected for the filter. Thus, the bandpass filter has a fast response time to temporal changes in the data series. The variable choice of the filter order permits the analysis of wave trains with a resolution that matches their scale. The bandpass cutoff frequencies are at , where is the central frequency. More details about the bandpass filtering are given by [33].
Climatologies of the time series are obtained by sorting the data for the month and taking the mean and the standard deviation. The mean diurnal cycles are obtained by sorting the data for the month and the hour of the day (in local time). Again, the arithmetic means of the sorted ensembles are taken. In order to intercompare the seasonal curves, we subtract the monthly mean values.
3. Results
3.1. Climatologies
We evaluated in total about 48 million samples of TROWARA measurements from 2004 to 2016 (sampling rates are between 6 and 11 s). The number of samples of IWV or ILW is about 48 million. The number of samples with cloud occurrence (group CF4) is about 24 million. The number of samples of the group CF1 is about 7 million. The number of samples of CF2 is 6 million, and the number of samples of CF3 is about 10 million. The number of samples of rain (ILW g/m) is about 4 million. The number of samples of IWV, rain, CF1, CF2, CF3 and CF4 are shown in Figure 1 as a function of month. Most critical might be the statistics of thick supercooled liquid water clouds (CF2) in summer.
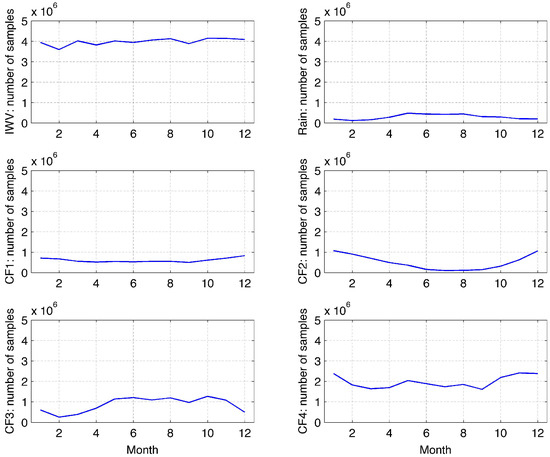
Figure 1.
Number of samples of integrated water vapour (IWV), rain (ILW g/m) and cloud fraction (CF) of four cloud categories (defined in the text) as a function of month observed by the TROWARA radiometer in Bern from 2004 to 2016.
The climatologies of IWV, ILW, CF1, CF2, CF3 and CF4 above Bern from 2004 to 2016 are shown in Figure 2. Generally, there are strong seasonal variations in Figure 2. The error bars indicate the standard deviation of the monthly mean from year to year. Next, we use the climatological curves for computation of the diurnal cycles with respect to the monthly means. IWV varies from 8 kg/m in winter to 24 kg/m in summer. This annual oscillation of IWV is due to the seasonal change in air temperature and the Clausius–Clapeyron equation. The seasonal cycle of ILW contains an annual and a semi-annual component where the latter is a bit stronger. Cloud fraction of thin liquid water clouds (CF1) is fairly constant during the year except during winter months when CF1 presents higher values. Thick supercooled liquid water clouds (CF2) almost disappear during the summer months when the air temperature is high. Thick warm liquid water clouds (CF3) are strongly reduced during the winter. Cloud fraction of all liquid water clouds (CF4) increases slightly during winter, and a semi-annual oscillation is present.
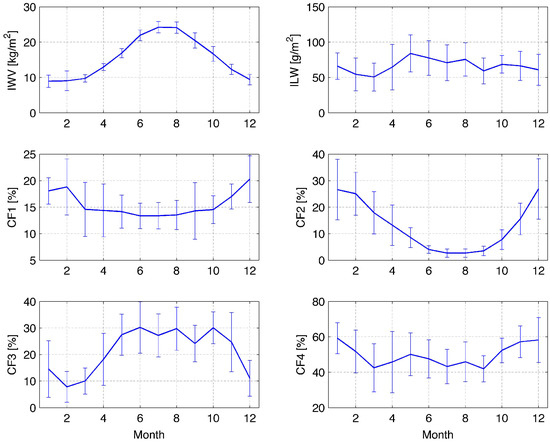
Figure 2.
Climatologies of integrated water vapour (IWV), integrated liquid water (ILW) and cloud fraction (CF) of four cloud categories (defined in the text) observed by the TROWARA radiometer in Bern from 2004 to 2016. The error bars indicate the standard deviation of the monthly mean from year to year.
3.2. Spectral Behaviour of the Time Series
The normalized FFT power spectra of the complete time series of fluctuations provide information on the occurrence and the strength of the diurnal and semi-diurnal cycles with respect to the annual oscillation. Only in the case of ILW, the semi-annual oscillation is stronger than the annual oscillation, and so we normalize ILW by the power of the semi-annual oscillation. The FFT power spectra mainly provide information on the phase-locked fluctuations, e.g., phase-locked to the daily or annual cycle of solar radiation. Thus, many intermittent short-term fluctuations may average out by taking the spectrum over the time interval 2004–2016. This is the reason why we show next the amplitude spectrum obtained by a wavelet-method.
Figure 3 shows the normalized FFT power spectra in a blue colour for the fluctuations of IWV, ILW, CF1, CF2, CF3 and CF4 above Bern from 2004 to 2016. The annual oscillation is the blue spike at 1/(365 day), which is near 0 cycles/day. Compared to the power of the annual oscillation in IWV, the diurnal cycle in IWV power is about 400 times smaller. This means that the amplitude of the diurnal cycle is about 0.4 kg/m, which is 20 times smaller than the annual cycle of IWV, which is about 8 kg/m in Figure 2. Furthermore, the amplitude of the diurnal cycle is about five times larger than the amplitude of the semi-diurnal cycle in IWV. The magnitudes of the annual and diurnal cycle in IWV are consistent with those of [25].
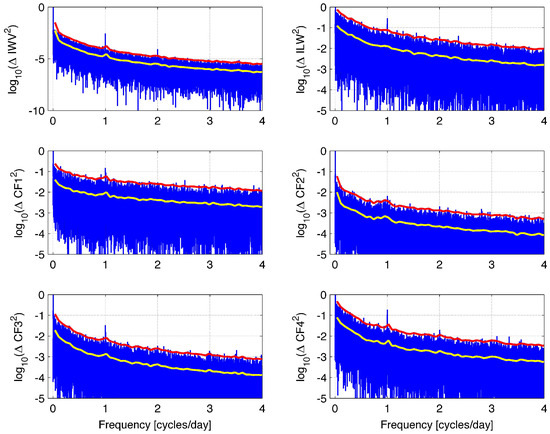
Figure 3.
Fast Fourier Transform (FFT) power spectra (blue line) of the temporal fluctuations of IWV, ILW and CF in Bern for the time interval from 2004 to 2016. The spectra are normalized by the power of the maximum (power of the annual or semi-annual oscillation). The yellow line is the mean of the spectrum averaged over 1000 frequency grid points. The red line is the five sigma level of confidence. A significant diurnal cycle shows up as a blue spike at 1 cycle/day in each parameter. A significant semidiurnal cycle (at 2 cycles/day) is present for IWV and CF4.
The amplitudes of the diurnal and semidiurnal oscillation in IWV are known to 5 -level confidence. This is indicated by the red line, which lies at a 5 distance above the yellow line, which is the mean power of the blue spectra sampled over 1000 frequency grid points. Here, we assumed that the mean power is equal to the noise .
In the case of ILW, we see a peak of the diurnal cycles that is rather close to those of the semi-annual oscillation, which is the dominant oscillation. There are several other significant oscillations with peaks closely above the red line, e.g., the semi-diurnal oscillation. In the cases of CF1, CF2, CF3 and CF4, we find significant diurnal cycles. The semi-diurnal cycle is well present for CF2 and CF4.
As a supplement to the FFT power spectra, we derive amplitude spectra by means of the fast response bandpass filter that takes care of phase-unlocked oscillations, which may persist only about time intervals of a few wave periods. Figure 4 shows the short-term variability of IWV, ILW, CF1, CF2, CF3 and CF4. An unresolved small peak is seen at the position of the diurnal cycle, which is marked by the red vertical line. The amplitude of the diurnal cycle in IWV is about 1 kg/m, which is larger than those obtained by the FFT power spectrum. This is reasonable since the phase of the diurnal cycle may change in time, and phase-unlocked intermittent oscillations with a one day period may occur as well. In case of the thin liquid water clouds (CF1), we can see that the maximal amplitudes are reached for periods smaller than one day. This is likely since small and thin clouds have a short life time and short horizontal scales. In the cases of IWV, ILW, CF3 and CF4, there are relatively strong oscillations with periods from two to ten days, which might be related to changes in synoptic weather patterns. The peak amplitude of IWV is around the seven-day period, whereas, for clouds, the peak is for shorter periods.
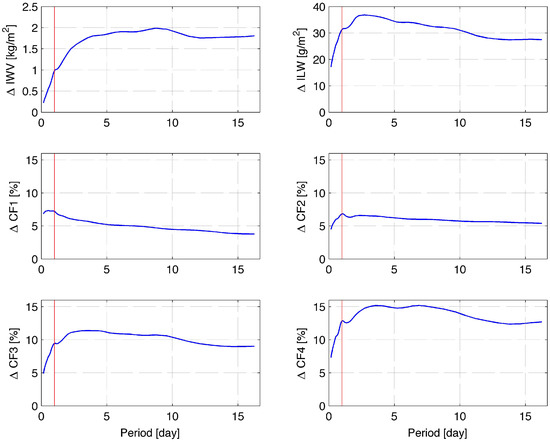
Figure 4.
Amplitude spectra of IWV, ILW and CF over Bern for the time interval 2004–2016 obtained by a fast response bandpass filter. The red line marks the position of the diurnal cycle. The short-term variability of fluctuations with periods <10 days is high for ILW and CF.
3.3. Seasonal Dependence and Annual Mean of the Diurnal Cycle in IWV
Figure 5 shows the absolute and the relative diurnal cycles in IWV with respect to the monthly mean . The subtraction of the monthly mean is necessary for the intercomparison of the seasonal curves since the monthly mean strongly varies from 8 kg/m in winter to 24 kg/m in summer. The absolute diurnal cycle is shown in the upper panel and is defined as . The relative diurnal cycle is shown in the lower panel and is defined as . The seasonal curves of the diurnal cycles are given in color while the black dots denote the annual mean of the diurnal cycle. The amplitude of the mean diurnal cycle is 0.41 kg/m. Morland, J. et al. [25] obtained a quite similar curve for the mean diurnal cycle in IWV using measurements of TROWARA from 2003 to 2007. They found a mean amplitude of 0.32 kg/m. The phase of the diurnal cycle with a maximum around 19:00 LT in Figure 5 was also found by [25]. In addition, they compared the TROWARA results with the mean diurnal cycle of a GPS station in Bern, and they found an excellent agreement for the amplitude and the phase of the diurnal cycle.
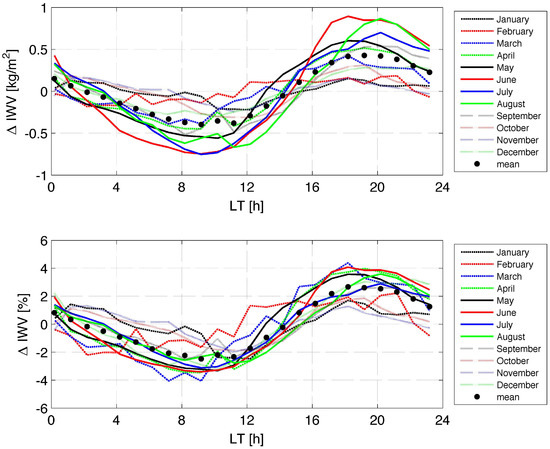
Figure 5.
Seasonal dependence of the diurnal cycle in IWV as a function of local time over Bern for the time interval 2004–2016. The upper panel shows the absolute diurnal cycle (IWV = IWV − monthly mean of IWV) while the lower panel shows the relative diurnal cycle with respect to the monthly mean and in percent. The black dots indicate the annual mean of the seasonal curves.
Morland, J. et al. [25] suggested that evaporation of soil moisture into the atmosphere may explain the shape of the diurnal cycle in IWV. Accumulation of the evaporated water in the atmosphere during the daytime leads to the maximum of IWV in the evening while accumulated condensation of water vapour during the nighttime induces the IWV minimum in the morning hours. The hydrological atlas of Switzerland shows that the daily evaporation rate ranges from about 0.1 kg/m per day in winter to about 3.8 kg/m per day in summer in the Swiss plateau, which is dominated by agriculture [34]. Since the surroundings of Bern also have forests and a river, we expect higher evaporation rates of about 0.5 kg/m per day in winter [34]. The annual mean of the rate of change of IWV in Figure 5 is about 0.82 kg/m from the morning to the evening, which lies within the range of values of the evaporation rate in Bern. Thus, we regard the diurnal cycle of insolation, evaporation and condensation as the main reason for the observed diurnal cycle in IWV. Other factors such as diurnal variations of the surface wind vector and the vertical mixing rate of moisture lead to additional modifications of the diurnal cycle in IWV.
Analyzing a GPS ground station network in Spain, Ortiz de Galisteo, J.P. et al. [35] found an amplitude of about 0.35 kg/m for the mean diurnal cycle in IWV of all stations. The time of the maximum is at 18:30 UTC (which is close to local time in Spain). These values agree well with TROWARA in Bern. However, we find a significant difference if we look at the time of the minimum of IWV. It is about 10:00 LT for TROWARA in Bern while the IWV minimum is about 05:00 LT for the GPS network in Spain.
Ortiz de Galisteo, J.P. et al. [35] found a semi-diurnal oscillation in IWV with an amplitude of 0.13 kg/m, which is consistent with our FFT power spectra in Figure 3. Although the mean diurnal cycle of the Spanish stations agrees quite well with TROWARA in Bern, the Spanish stations showed a remarkable variation amongst themselves. Ortiz de Galisteo, J.P. et al. [35] explained that the shape of the diurnal cycle depends on factors that cause condensation, evaporation and moisture transport. The diurnal cycle in solar radiation is possibly most important for the observed diurnal cycle in IWV since evaporation of water from the surface, increase of air temperature and the growth of the planetary boundary layer during the daytime are closely related to absorption of solar radiation. On the other hand, the decrease of air temperature during the night leads to enhanced condensation of water vapour and to the observed minimum of IWV in the early morning hours. The time lag of the IWV minimum and maximum with respect to those of the air temperature might be related to the slow accumulation processes of liquid water on the ground and water vapour in the air.
Dai, A. et al. [36] retrieved diurnal cycles in IWV from a GPS station network in North America and found amplitudes of 1.0–1.8 kg/m in the summer season and weaker in other seasons, which is greater than the 0.8 kg/m June and August amplitudes of TROWARA in Figure 5. There is a large variability in the diurnal IWV cycles of the North American stations, but there are several stations that show an increase in IWV during the afternoon hours and a maximum around 16:00–19:00 LT, which is similar to that of TROWARA in Bern. The time of the IWV minimum is often late in the morning hours from 07:00–10:00 LT. Generally, Dai, A. et al. [36] reported relative diurnal IWV cycles with amplitudes less than 5%, while Figure 5 shows maximal relative amplitudes of 4%. In the percentage scale, the seasonal curves come closer together and the strong absolute diurnal cycles of the summer months do not differ much from those of March, April and May. The smallest relative amplitudes (<2%) occur in winter from November to January in Bern.
3.4. Seasonal Dependence and Annual Mean of the Diurnal Cycle in ILW
Figure 6 shows the absolute and the relative diurnal cycles in ILW with respect to the monthly mean. We define ILW in the same manner as IWV as described in the subsection above. Compared to IWV, the diurnal cycle in ILW is more variable from month to month and relative amplitudes of 15 to 25% are reached especially during October, November and January. These strong diurnal cycles are connected with a break up of a cloud layer (stratus) at about 10:00 LT before noon and a relatively clear sky in the afternoon, which is consistent with our daily weather experience in Bern in late autumn and winter. The annual mean of the diurnal cycle (black dots) shows a minimum of about −10%, which occurs around noon. We suggest that this minimum is connected with the maximum evaporation or loss of cloud droplets at noon. During nighttime, a relative maximum of 9% is reached at around 03:00 LT.
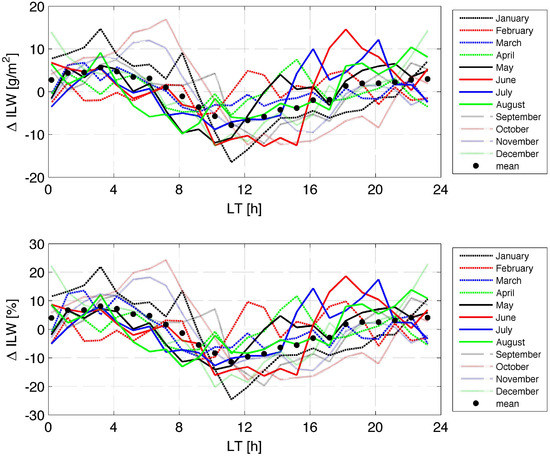
Figure 6.
Seasonal dependence of the diurnal cycle in ILW as a function of local time over Bern for the time interval 2004–2016. The upper panel shows the absolute diurnal cycle ( ILW = ILW − monthly mean of ILW) while the lower panel shows the relative diurnal cycle with respect to the monthly mean and in percent. The black dots indicate the annual mean of the seasonal curves.
Wood, R. et al. [37] reported diurnal ILW amplitudes of about 15–35% over the subtropical and tropical oceans observed by the Tropical Rainfall Measuring Mission Microwave Imager (TMI). The time of the ILW maximum is in the early morning (at 03:00 LT) and the time of the ILW minimum is at 15:00 LT, which is a bit later than for our measurements in Bern. They explain that the diurnal cycle in ILW is mainly driven by cloud solar absorption. Wood, R. [37] emphasize that the ILW measurements provide important constraints for models simulating the diurnal cycle of clouds. Snider, J.B. et al. [17] performed surface-based radiometric observations of water vapour and cloud liquid in the temperate zone and in the tropics. They found a sub-daily maximum of ILW at 05:00 LT and a minimum at 14:00 LT. The relative sub-daily variation of ILW was about 30%. In contrast with our study, Roebeling, R.A. et al. [16] reported diurnal variations in ILW values of the SEVIRI satellite experiment and ground-based microwave radiometers in France and England, which show increasing ILW values toward local solar noon.
The seasonal curves for June to August in Figure 6 show local maxima from 16:00–20:00 LT. We suggest that this effect could be due to diurnal water vapour convection during summer. This phenomenon was indicated by the increase of IWV during afternoon in Figure 5. Schlemmer, L. et al. [38] performed idealized cloud-resolving simulations for the study of mid-latitude diurnal convection over land. They found an increase of specific cloud water content from 15:00 to 21:00 LT at 2–3.5 km altitude. They explained that convection and evaporation determine the moisture content of the lower troposphere. Then, the moisture content regulates the timing and intensity of the diurnal convection.
3.5. Seasonal Dependence and Annual Mean of the Diurnal Cycle in CF
In the case of cloud fraction, we present and discuss only the diurnal variations . Figure 7 shows the diurnal cycle in CF1 (thin liquid water clouds) in the upper panel and those of CF2 (thick supercooled liquid water clouds) in the lower panel. The diurnal cycle in has a maximum of 2% at 10:00 LT. Generally, the sub-daily variation is less than 5%. The climatology of CF2 showed that the thick supercooled liquid water clouds mainly occur during winter. The lower panel of Figure 7 shows that the curves of December and January have a strong diurnal variation with a fast decrease of at 10:00 LT. This means that the occurrence of the thick supercooled liquid water clouds is favored during the nighttime and in the morning hours until 10:00 LT. Possibly, a part of the clouds are depleted by insolation during the daytime. The amplitude of the diurnal cycle in CF2 is about 4% in December and January.
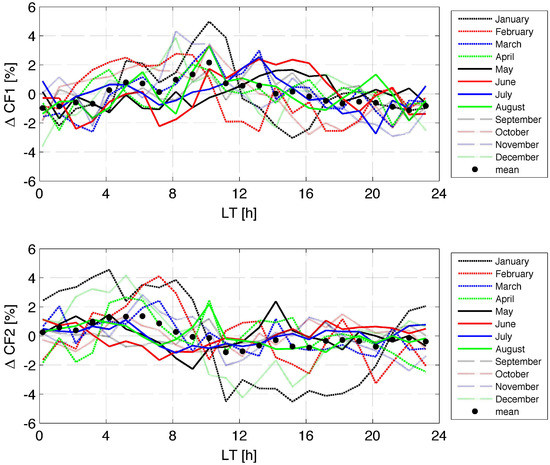
Figure 7.
Seasonal dependence of the diurnal cycle in cloud fraction CF1 (thin liquid water clouds) and CF2 (supercooled thick liquid water clouds) as a function of local time over Bern for the time interval 2004–2016. The panels show CF = (CF − monthly mean of CF). The black dots indicate the annual mean of the seasonal curves.
Figure 8 shows the diurnal cycle in CF3 (thick warm liquid water clouds) in the upper panel and those of CF4 (all liquid water clouds) in the lower panel. The strongest diurnal variation is found for CF3 and CF4 in October and November with deviations of about for CF4. Maximum values are reached at 07:00 LT and then a decrease starts towards the minimum, which is reached at 16:00 LT. Our daily experience with the cloud cover above Bern during autumn supports this objective measurement. Often, the clouds disappear around noon in autumn. A similar diurnal variation of cloud cover was derived by [13] from the ISCCP-C2 cloud climatology for the cloud category of maritime non-convective low-level clouds. “Maritime climate” may fit to Switzerland since it has a west coast climate and many lakes. The study of [13] showed that each cloud category has a different diurnal cycle. Min, M. and Zhang, Z. [39] presented a sinusoidal-like diurnal cycle in cloud fraction (five-year mean of SEVIRI observations over the southeast Atlantic). They found a slow 20% decrease of CF starting after sunrise and lasting until the evening.
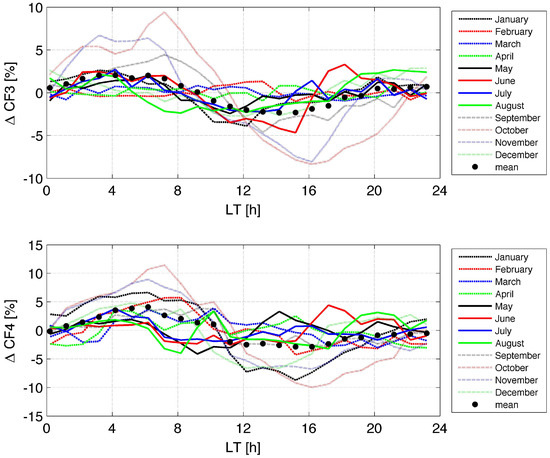
Figure 8.
Seasonal dependence of the diurnal cycle in cloud fraction CF3 (warm thick liquid water clouds) and CF4 (all liquid water clouds) as a function of local time over Bern for the time interval 2004–2016. The panels show CF = (CF − monthly mean of CF). The black dots indicate the annual mean of the seasonal curves.
In the case of CF3 in June, there seems to be an increase in the late afternoon, which might be connected to diurnal convection and cloud formation as described by [38].
3.6. Seasonal Variation and Diurnal Cycle in Rain Fraction
Analogously to cloud fraction, one can define rain fraction (RF), which is a measure of the occurrence of rain droplets in the measurements of TROWARA. Here, rain or rain droplets occur if the ILW measurements of TROWARA are greater than or equal to 400 g/m. At the edges of a time interval of rain, ILW increases or decreases within a short time from a small value to a high value or vice versa so that the choice of the threshold (e.g., 300, 400, or 500 g/m) plays a marginal role for the calculation of rain fraction [32].
Figure 9a shows the seasonal variation in rain fraction which varies from about 4% in winter to about 11% in summer. Figure 9b depicts the diurnal cycle in . Rain fraction is enhanced by a few percent in the late afternoon during the summer months of June and July. This diurnal cycle in rain fraction might be connected to diurnal convection and precipitation over land during summer as described by [38].
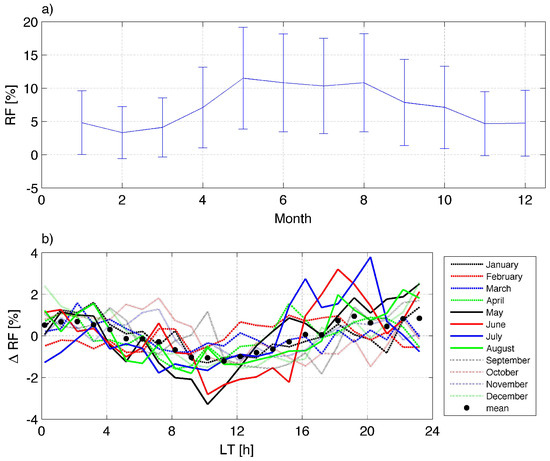
Figure 9.
(a) seasonal variation in rain fraction (defined in the text) observed by the TROWARA radiometer in Bern from 2004 to 2016. The error bars indicate the standard deviation of the monthly mean from year to year. (b) seasonal dependence of the diurnal cycle in rain fraction RF (for ILW as a function of local time over Bern for the time interval 2004–2016. The panel shows RF = (RF − monthly mean of RF). The black dots indicate the annual mean of the seasonal curves.
4. Conclusions
The TROpospheric WAter RAdiometer (TROWARA) continuously measured cloud fraction (CF), integrated liquid water (ILW) and integrated water vapour (IWV) in Bern in Switzerland from 2004 to 2016. For our study, we derived hourly means from the TROWARA data sampled every 10 s. We presented and discussed the diurnal cycles in cloud fraction (CF), integrated liquid water (ILW) and integrated water vapour (IWV) for different seasons and the annual mean. Furthermore, we divided CF into four categories: thin liquid water clouds (CF1), thick supercooled liquid water clouds (CF2), thick warm liquid water clouds (CF3) and all liquid water clouds (CF4).
The amplitude of the mean diurnal cycle in IWV is 0.41 kg/m. The sub-daily minimum of IWV is at 10:00 LT, while the maximum of IWV occurs at 19:00 LT. The relative amplitudes of the diurnal cycle in ILW are up to 25% in October, November and January, which is possibly related to a breakup of the cloud layer at 10:00 LT. The minimum of ILW occurs at 12:00 LT, possibly explained by the maximum loss of cloud droplets due to maximum insolation at noon. In the case of cloud fraction of liquid water clouds (CF4), maximum values of +10% are reached at 07:00 LT and then a decrease starts towards the minimum of −10%, which is reached at 16:00 LT in autumn. This breakup of cloud layers in the late morning and early afternoon hours during autumn seems to be typical for the weather in Bern. A similar behavior is observed for CF3 so that we conclude that mainly thick warm liquid water clouds are responsible for the described diurnal variation in autumn. Finally, the TROWARA observations show that rain fraction is enhanced in the late afternoon hours in June and July.
The study showed that long-term measurements of a microwave radiometer equipped with an additional infrared channel objectively provide information on the diurnal cycle in six atmospheric water parameters. This information is of great interest for cross-validations with satellite data, high-resolution reanalyses and model simulations.
Acknowledgments
The study was supported by Swiss National Science Foundation under Grant No. 200021-165516. We are grateful to all technicians and scientists of the Institute of Applied Physics for designing, building and operating the TROWARA instrument over the last two decades. We thank the reviewers for valuable comments and corrections.
Author Contributions
Klemens Hocke carried out the spectral analysis. Francisco Navas-Guzmán and Christian Mätzler took care of the radiometer. All authors contributed to the interpretation of the data set.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Boucher, O.; Randall, D.; Artaxo, P.; Bretherton, C.; Feingold, G.; Forster, P.; Kerminen, V.M.; Kondo, Y.; Liao, H.; Lohmann, U.; et al. Clouds and Aerosols, Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; Section 7; pp. 571–658. [Google Scholar]
- Held, I.; Soden, B.J. Water vapor feedback and global warming. Annu. Rev. Energy Environ. 2000, 25, 441–475. [Google Scholar] [CrossRef]
- Jiang, J.H.; Su, H.; Zhai, C.; Perun, V.S.; Del Genio, A.; Nazarenko, L.S.; Donner, L.J.; Horowitz, L.; Seman, C.; Cole, J.; et al. Evaluation of cloud and water vapor simulations in CMIP5 climate models using NASA A-Train satellite observations. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Gettelman, A.; Kay, J.E.; Shell, K.M. The Evolution of Climate Sensitivity and Climate Feedbacks in the Community Atmosphere Model. J. Clim. 2012, 25, 1453–1469. [Google Scholar] [CrossRef]
- Biasutti, M.; Yuter, S.E.; Burleyson, C.D.; Sobel, A.H. Very high resolution rainfall patterns measured by TRMM precipitation radar: Seasonal and diurnal cycles. Clim. Dyn. 2012, 39, 239–258. [Google Scholar] [CrossRef]
- Stubenrauch, C.J.; Chédin, A.; Rädel, G.; Scott, N.A.; Serrar, S. Cloud Properties and Their Seasonal and Diurnal Variability from TOVS Path-B. J. Clim. 2006, 19, 5531–5553. [Google Scholar] [CrossRef]
- Wylie, D. Diurnal Cycles of Clouds and How They Affect Polar-Orbiting Satellite Data. J. Clim. 2008, 21, 3989–3996. [Google Scholar] [CrossRef]
- Hong, G.; Heygster, G.; Notholt, J.; Buehler, S.A. Interannual to Diurnal Variations in Tropical and Subtropical Deep Convective Clouds and Convective Overshooting from Seven Years of AMSU-B Measurements. J. Clim. 2008, 21, 4168–4189. [Google Scholar] [CrossRef]
- Labow, G.J.; Herman, J.R.; Huang, L.K.; Lloyd, S.A.; DeLand, M.T.; Qin, W.; Mao, J.; Larko, D.E. Diurnal variation of 340 nm Lambertian equivalent reflectivity due to clouds and aerosols over land and oceans. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Dai, A.; Trenberth, K.E. The Diurnal Cycle and Its Depiction in the Community Climate System Model. J. Clim. 2004, 17, 930–951. [Google Scholar] [CrossRef]
- Dirmeyer, P.A.; Cash, B.A.; Kinter, J.L.; Jung, T.; Marx, L.; Satoh, M.; Stan, C.; Tomita, H.; Towers, P.; Wedi, N.; et al. Simulating the diurnal cycle of rainfall in global climate models: Resolution versus parameterization. Clim. Dyn. 2012, 39, 399–418. [Google Scholar] [CrossRef]
- Bergman, J.W.; Salby, M.L. The Role of Cloud Diurnal Variations in the Time-Mean Energy Budget. J. Clim. 1997, 10, 1114–1124. [Google Scholar] [CrossRef]
- Bergman, J.W.; Salby, M.L. Diurnal Variations of Cloud Cover and Their Relationship to Climatological Conditions. J. Clim. 1996, 9, 2802–2820. [Google Scholar] [CrossRef]
- Zhang, Y.; Long, C.N.; Rossow, W.B.; Dutton, E.G. Exploiting diurnal variations to evaluate the ISCCP-FD flux calculations and radiative-flux-analysis-processed surface observations from BSRN, ARM, and SURFRAD. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Westwater, E.R.; Crewell, S.; Matzler, C. Frontiers in surface-based microwave and millimeter wavelength radiometry. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Anchorage, AK, USA, 20–24 September 2004; Volume 2, pp. 1268–1272. [Google Scholar]
- Roebeling, R.A.; Deneke, H.M.; Feijt, A.J. Validation of Cloud Liquid Water Path Retrievals from SEVIRI Using One Year of CloudNET Observations. J. Appl. Meteorol. Climatol. 2008, 47, 206–222. [Google Scholar] [CrossRef]
- Snider, J.B.; Hazen, D.A. Surface-based radiometric observations of water vapor and cloud liquid in the temperate zone and in the tropics. Radio Sci. 1998, 33, 421–432. [Google Scholar] [CrossRef]
- Considine, G.; Curry, J.A.; Wielicki, B. Modeling cloud fraction and horizontal variability in marine boundary layer clouds. J. Geophys. Res. Atmos. 1997, 102, 13517–13525. [Google Scholar] [CrossRef]
- Peter, R.; Kämpfer, N. Radiometric Determination of Water-Vapor and Liquid Water and Its Validation with Other Techniques. J. Geophys. Res. Atmos. 1992, 97, 18173–18183. [Google Scholar] [CrossRef]
- Morland, J. TROWARA—Tropospheric Water Vapour Radiometer. Radiometer Review and New Calibration Model; IAP Research Report 2002-15; Institut für Angewandte Physik, Universität Bern: Bern, Switzerland, 2002. [Google Scholar]
- Ingold, T.; Peter, R.; Kämpfer, N. Weighted mean tropospheric temperature and transmittance determination at millimeter-wave frequencies for ground-based applications. Radio Sci. 1998, 33, 905–918. [Google Scholar] [CrossRef]
- Mätzler, C.; Morland, J. Refined Physical Retrieval of Integrated Water Vapor and Cloud Liquid for Microwave Radiometer Data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1585–1594. [Google Scholar] [CrossRef]
- Brocard, E. Ground-Based Remote Sensing of the Troposphere in the Thermal Infrared. Ph.D. Thesis, Philosophisch-Naturwissenschaftliche Fakultät, Universität Bern, Bern, Switzerland, 2008. [Google Scholar]
- Cossu, F.; Hocke, K.; Mätzler, C. A 10-Year Cloud Fraction Climatology of Liquid Water Clouds over Bern Observed by a Ground-Based Microwave Radiometer. Remote Sens. 2015, 7, 7768–7784. [Google Scholar] [CrossRef]
- Morland, J.; Collaud Coen, M.; Hocke, K.; Jeannet, P.; Mätzler, C. Tropospheric water vapour above Switzerland over the last 12 years. Atmos. Chem. Phys. 2009, 9, 5975–5988. [Google Scholar] [CrossRef]
- Hocke, K.; Kämpfer, N.; Gerber, C.; Mätzler, C. A complete long-term series of integrated water vapour from ground-based microwave radiometers. Int. J. Remote Sens. 2011, 32, 751–765. [Google Scholar] [CrossRef]
- Hocke, K.; Navas Guzmán, F.; Cossu, F.; Mätzler, C. Cloud Fraction of Liquid Water Clouds above Switzerland over the Last 12 Years. Climate 2016, 4. [Google Scholar] [CrossRef]
- Brocard, E.; Schneebeli, M.; Morland, J.; Mätzler, C. Detection of Supercooled Cloud Layers with Microwave and Infrared Radiometry and Additional Tools; IAP Research Report 2006-02-MW; Institut für Angewandte Physik, Universität Bern: Bern, Switzerland, 2006. [Google Scholar]
- Mätzler, C.; Rosenkranz, P.W.; Cermak, J. Microwave absorption of supercooled clouds and implications for the dielectric properties of water. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Hirsch, E.; Agassi, E.; Koren, I. Determination of optical and microphysical properties of thin warm clouds using ground based hyper-spectral analysis. Atmos. Meas. Tech. 2012, 5, 851–871. [Google Scholar] [CrossRef]
- Bernet, L.; Navas-Guzmàn, F.; Kämpfer, N. The effect of cloud liquid water on tropospheric temperature retrievals from microwave measurements. Atmos. Meas. Tech. Discuss. 2017, 2017, 1–35. [Google Scholar] [CrossRef]
- Cossu, F. Study of Atmospheric Water over Bern by Means of Ground-Based Observations and Numerical Simulations. Ph.D. Thesis, Philosophisch-Naturwissenschaftliche Fakultät, Universität Bern, Bern, Switzerland, 2015. [Google Scholar]
- Studer, S.; Hocke, K.; Kämpfer, N. Intraseasonal oscillations of stratospheric ozone above Switzerland. J. Atmos. Sol. Terr. Phys. 2012, 74, 189–198. [Google Scholar] [CrossRef]
- Menzel, L.; Lang, H.; Rohmann, M. Mean Annual Actual Evaporation 1973–1992. Plate 4.1 in Hydrological Atlas of Switzerland 1999. Available online: http://www.hydrologischeratlas.ch/en/products/printed-issue/evaporation/plate-4-1 (accessed on 31 August 2017).
- Ortiz de Galisteo, J.P.; Cachorro, V.; Toledano, C.; Torres, B.; Laulainen, N.; Bennouna, Y.; de Frutos, A. Diurnal cycle of precipitable water vapor over Spain. Q. J. R. Meteorol. Soc. 2011, 137, 948–958. [Google Scholar] [CrossRef]
- Dai, A.; Wang, J.; Ware, R.H.; Van Hove, T. Diurnal variation in water vapor over North America and its implications for sampling errors in radiosonde humidity. J. Geophys. Res. Atmos. 2002, 107. [Google Scholar] [CrossRef]
- Wood, R.; Bretherton, C.S.; Hartmann, D.L. Diurnal cycle of liquid water path over the subtropical and tropical oceans. Geophys. Res. Lett. 2002, 29. [Google Scholar] [CrossRef]
- Schlemmer, L.; Hohenegger, C.; Schmidli, J.; Bretherton, C.S.; Schär, C. An Idealized Cloud-Resolving Framework for the Study of Midlatitude Diurnal Convection over Land. J. Atmos. Sci. 2011, 68, 1041–1057. [Google Scholar] [CrossRef]
- Min, M.; Zhang, Z. On the influence of cloud fraction diurnal cycle and sub-grid cloud optical thickness variability on all-sky direct aerosol radiative forcing. J. Quant. Spectrosc. Radiat. Transf. 2014, 142, 25–36. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).