Estimating High Resolution Daily Air Temperature Based on Remote Sensing Products and Climate Reanalysis Datasets over Glacierized Basins: A Case Study in the Langtang Valley, Nepal
Abstract
:1. Introduction
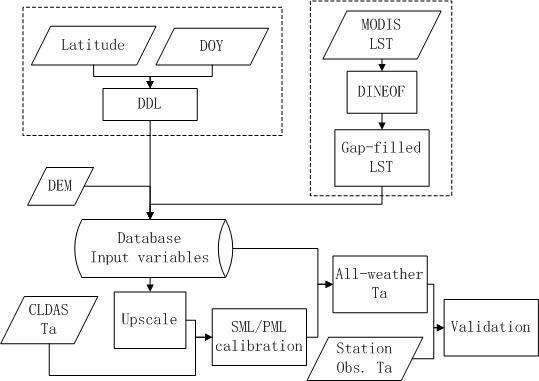
2. Materials and Methods
2.1. Study Area
2.2. Datasets
2.2.1. MODIS LST Product
2.2.2. The CLDAS Climate Reanalysis Dataset
2.2.3. Ground Observation at the Langtang Valley
2.3. Methods
2.3.1. The LST Gap-Filling Method
2.3.2. The Air Temperature Estimation Method
2.3.3. Statistical Metrics for Accuracy Assessment
3. Results and Analysis
3.1. The MODIS LST Reconstrution Result
3.2. Spatial Distribution Pattern of Estimated Ta
3.3. Accuracy Assessment of the Estimated Ta
4. Discussion
4.1. Impact of Weather Condition on the Ta Estimation Accuracy
4.2. Lapse Rate Derived from the Station Observed, CLDAS and Remote Sensing Based Ta
4.3. Relationship between Ta and Runoff at Glacierized Basins
5. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhao, W.; Li, A. A review on land surface processes modelling over complex terrain. Adv. Meteorol. 2015, 2015, 1–17. [Google Scholar] [CrossRef]
- Webb, B.W.; Clack, P.D.; Walling, D.E. Water-air temperature relationships in a Devon river system and the role of flow. Hydrol. Process. 2003, 17, 3069–3084. [Google Scholar] [CrossRef]
- Arnfield, A.J. Two decades of urban climate research: A review of turbulence, exchanges of energy and water, and the urban heat island. Int. J. Climatol. 2003, 23, 1–26. [Google Scholar] [CrossRef]
- Hansen, J.; Sato, M.; Ruedy, R. Radiative forcing and climate response. J. Geophys. Res. Atmos. 1997, 102, 6831–6864. [Google Scholar] [CrossRef]
- Fyffe, C.L.; Reid, T.D.; Brock, B.W.; Kirkbride, M.P.; Diolaiuti, G.; Smiraglia, C.; Diotri, F. A distributed energy-balance melt model of an alpine debris-covered glacier. J. Glaciol. 2014, 60, 587–602. [Google Scholar] [CrossRef]
- Hu, Q.; Willson, G.D. Effects of temperature anomalies on the Palmer Drought Severity Index in the central United States. Int. J. Climatol. 2000, 20, 1899–1911. [Google Scholar] [CrossRef]
- Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a global evapotranspiration algorithm based on MODIS and global meteorology data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar] [CrossRef]
- Mcmaster, G. Growing degree-days: One equation, two interpretations. Agric. For. Meteorol. 1997, 87, 291–300. [Google Scholar] [CrossRef]
- Hock, R. Temperature index melt modelling in mountain areas. J. Hydrol. 2003, 282, 104–115. [Google Scholar] [CrossRef]
- Oñate, J.J.; Pou, A. Temperature variations in spain since 1901: A preliminary analysis. Int. J. Climatol. 1996, 16, 805–815. [Google Scholar] [CrossRef]
- Berrisford, P.; Dee, D.; Poli, P.; Brugge, R.; Fielding, K.; Fuentes, M.; Kallberg, P.; Kobayashi, S.; Uppala, S.; Simmons, A. The ERA-Interim Archive Version 2.0. 2011. Available online: https://www.ecmwf.int/en/elibrary/8174-era-interim-archive-version-20 (accessed on 15 September 2017).
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.-K.; et al. MERRA: NASA’s Modern-Era Retrospective Analysis for Research and Applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Brown, M.E.; Racoviteanu, A.E.; Tarboton, D.G.; Gupta, A.S.; Nigro, J.; Policelli, F.; Habib, S.; Tokay, M.; Shrestha, M.S.; Bajracharya, S.; et al. An integrated modeling system for estimating glacier and snow melt driven streamflow from remote sensing and earth system data products in the Himalayas. J. Hydrol. 2014, 519, 1859–1869. [Google Scholar] [CrossRef]
- MODIS Atmosphere L2 Atmosphere Profile Product. Available online: https://ladsweb.modaps.eosdis.nasa.gov/api/v1/productGroupPage/name=atmospheric-profiles (accessed on 15 March 2017).
- Bisht, G.; Bras, R.L. Estimation of net radiation from the MODIS data under all sky conditions: Southern Great Plains case study. Remote Sens. Environ. 2010, 114, 1522–1534. [Google Scholar] [CrossRef]
- Zhu, W.; Lű, A.; Jia, S.; Yan, J.; Mahmood, R. Retrievals of all-weather daytime air temperature from MODIS products. Remote Sens. Environ. 2017, 189, 152–163. [Google Scholar] [CrossRef]
- Li, T.; Zheng, X.; Dai, Y.; Yang, C.; Chen, Z.; Zhang, S.; Wu, G.; Wang, Z.; Huang, C.; Shen, Y.; Liao, R. Mapping near-surface air temperature, pressure, relative humidity and wind speed over Mainland China with high spatiotemporal resolution. Adv. Atmos. Sci. 2014, 31, 1127–1135. [Google Scholar] [CrossRef]
- Pape, R.; Löffler, J. Modelling spatio-temporal near-surface temperature variation in high mountain landscapes. Ecol. Model. 2004, 178, 483–501. [Google Scholar] [CrossRef]
- Sun, Y.J.; Wang, J.F.; Zhang, R.H.; Gillies, R.R.; Xue, Y.; Bo, Y.C. Air temperature retrieval from remote sensing data based on thermodynamics. Theor. Appl. Climatol. 2005, 80, 37–48. [Google Scholar] [CrossRef]
- Zhou, W.; Peng, B.; Shi, J.C.; Dhital, Y.P.; Wang, T.X.; Ji, D.B.; Zhao, T.J.; Yao, P.P.; Cui, Y.R.; Shi, L.J.; et al. Estimating daytime surface air temperature using multi-source remote sensing and climate reanalysis data at glacierized basins: A case study at Langtang valley, Nepal. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Beijing, China, 10–15 July 2016; pp. 4143–4146. [Google Scholar]
- Zaksek, K.; Schroedter-Homscheidt, M. Parameterization of air temperature in high temporal and spatial resolution from a combination of the SEVIRI and MODIS instruments. ISPRS J. Photogramm. Remote Sens. 2009, 64, 414–421. [Google Scholar] [CrossRef]
- Zhu, W.; Lű, A.; Jia, S. Estimation of daily maximum and minimum air temperature using MODIS land surface temperature products. Remote Sens. Environ. 2013, 130, 62–73. [Google Scholar] [CrossRef]
- Goward, S.N.; Waring, R.H.; Dye, D.G.; Yang, J. Ecological remote sensing at OTTER: Satellite macroscale observations. Ecol. Appl. 1994, 4, 322–343. [Google Scholar] [CrossRef]
- Nemani, R.R.; Running, S.W. Estimation of regional surface resistance to evapotranspiration from NDVI and thermal-IR AVHRR data. J. Appl. Meteorol. 1989, 28, 276–284. [Google Scholar] [CrossRef]
- Ma, W.C.; Zhou, L.G.; Zhang, H.; Zhang, Y.; Dai, X.Y. Air temperature field distribution estimations over a Chinese mega-city using MODIS land surface temperature data: The case of Shanghai. Front. Earth Sci. 2016, 10, 38–48. [Google Scholar] [CrossRef]
- Meyer, H.; Katurji, M.; Appelhans, T.; Muller, M.U.; Nauss, T.; Roudier, P.; Zawar-Reza, P. Mapping daily air temperature for Antarctica based on MODIS LST. Remote Sens. 2016, 8, 732. [Google Scholar] [CrossRef]
- Noi, P.T.; Kappas, M.; Degener, J. Estimating daily maximum and minimum land air surface temperature using MODIS land surface temperature data and ground truth data in northern Vietnam. Remote Sens. 2016, 8, 1002. [Google Scholar] [CrossRef]
- Oyler, J.W.; Dobrowski, S.Z.; Holden, Z.A.; Running, S.W. Remotely sensed land skin temperature as a spatial predictor of air temperature across the conterminous United States. J. Appl. Meteorol. Climatol. 2016, 55, 1441–1457. [Google Scholar] [CrossRef]
- Pepin, N.C.; Maeda, E.E.; Williams, R. Use of remotely sensed land surface temperature as a proxy for air temperatures at high elevations: Findings from a 5000m elevational transect across Kilimanjaro. J. Geophys. Res. 2016, 121, 9998–10015. [Google Scholar] [CrossRef]
- Zhang, H.B.; Zhang, F.; Zhang, G.Q.; He, X.B.; Tian, L.D. Evaluation of cloud effects on air temperature estimation using MODIS LST based on ground measurements over the Tibetan Plateau. Atmos. Chem. Phys. 2016, 16, 13681–13696. [Google Scholar] [CrossRef]
- Bustos, E.; Meza, F.J. A method to estimate maximum and minimum air temperature using MODIS surface temperature and vegetation data: Application to the Maipo Basin, Chile. Theor. Appl. Climatol. 2015, 120, 211–226. [Google Scholar] [CrossRef]
- Chen, F.G.; Liu, Y.; Liu, Q.; Qin, F. A statistical method based on remote sensing for the estimation of air temperature in China. Int. J. Climatol. 2015, 35, 2131–2143. [Google Scholar] [CrossRef]
- Huang, R.; Zhang, C.; Huang, J.X.; Zhu, D.H.; Wang, L.M.; Liu, J. Mapping of daily mean air temperature in agricultural regions using daytime and nighttime land surface temperatures derived from terra and aqua MODIS data. Remote Sens. 2015, 7, 8728–8756. [Google Scholar] [CrossRef]
- Mutiibwa, D.; Strachan, S.; Albright, T. Land surface temperature and surface air temperature in complex terrain. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4762–4774. [Google Scholar] [CrossRef]
- Janatian, N.; Sadeghi, M.; Sanaeinejad, S.H.; Bakhshian, E.; Farid, A.; Hasheminia, S.M.; Ghazanfari, S. A statistical framework for estimating air temperature using MODIS land surface temperature data. Int. J. Climatol. 2017, 37, 1181–1194. [Google Scholar] [CrossRef]
- Zhang, H.B.; Zhang, F.; Ye, M.; Che, T.; Zhang, G.Q. Estimating daily air temperatures over the Tibetan Plateau by dynamically integrating MODIS LST data. J. Geophys. Res. 2016, 121, 11425–11441. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Pellicciotti, F.; Bierkens, M.F.P. Rising river flows throughout the twenty-first century in two Himalayan glacierized watersheds. Nat. Geosci. 2013, 6, 742–745. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; van Beek, L.P.H.; Bierkens, M.F.P. Climate Change Will Affect the Asian Water Towers. Science 2010, 328, 1382–1385. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Ding, Y.; Shangguan, D.; Zhang, Y.; Li, J.; Han, H.; Wang, J.; Xie, C. Glacier retreat as a result of climate warming and increased precipitation in the Tarim river basin, northwest China. Ann. Glaciol. 2006, 43, 91–96. [Google Scholar] [CrossRef]
- Yao, T.; Thompson, L.; Yang, W.; Yu, W.; Gao, Y.; Guo, X.; Yang, X.; Duan, K.; Zhao, H.; Xu, B.; et al. Different glacier status with atmospheric circulations in Tibetan Plateau and surroundings. Nat. Clim. Chang. 2012, 2, 663–667. [Google Scholar] [CrossRef]
- Kang, S.; Xu, Y.; You, Q.; Flügel, W.-A.; Pepin, N.; Yao, T. Review of climate and cryospheric change in the Tibetan Plateau. Environ. Res. Lett. 2010, 5, 15101. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Cheng, G.; Jin, H.; Kang, E.; Che, T.; Jin, R.; Wu, L.; Nan, Z.; Wang, J.; Shen, Y. Cryospheric change in China. Glob. Planet. Chang. 2008, 62, 210–218. [Google Scholar] [CrossRef]
- Cheng, G.; Wu, T. Responses of permafrost to climate change and their environmental significance, Qinghai-Tibet Plateau. J. Geophys. Res. 2007, 112, F02S03. [Google Scholar] [CrossRef]
- Wan, Z.; Li, Z. A physics-based algorithm for retrieving land-surface emissivity and temperature from EOS/MODIS data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 980–996. [Google Scholar] [CrossRef]
- Wan, Z.; Li, Z. Radiance-based validation of the V5 MODIS land-surface temperature product. Int. J. Remote Sens. 2008, 29, 5373–5395. [Google Scholar] [CrossRef]
- Collection-6 MODIS Land Surface Temperature Products Users’ Guide. Available online: https://icess.eri.ucsb.edu/modis/LstUsrGuide/MODIS_LST_products_Users_guide_C6.pdf (accessed on 10 January 2016).
- Wan, Z. New refinements and validation of the collection-6 MODIS land-surface temperature/emissivity product. Remote Sens. Environ. 2014, 140, 36–45. [Google Scholar] [CrossRef]
- Shi, C.; Xie, Z.; Qian, H.; Liang, M.; Yang, X. China land soil moisture EnKF data assimilation based on satellite remote sensing data. Sci. China Earth Sci. 2011, 54, 1430–1440. [Google Scholar] [CrossRef]
- Zhang, T. Multi-Source Data Fusion and Application Research Base on LAPS/STMAS. Master’s Thesis, Nanjing University of Information Science and Technology, Nanjing, China, 2013. [Google Scholar]
- Xie, Y.; Koch, S.; McGinley, J.; Albers, S.; Bieringer, P.E.; Wolfson, M.; Chan, M. A Space-Time Multiscale Analysis System: A Sequential Variational Analysis Approach. Mon. Weather Rev. 2011, 139, 1224–1240. [Google Scholar] [CrossRef]
- Jiang, H.; Albers, S.; Xie, Y.; Toth, Z.; Jankov, I.; Scotten, M.; Picca, J.; Stumpf, G.; Kingfield, D.; Birkenheuer, D.; et al. Real-Time Applications of the Variational Version of the Local Analysis and Prediction System (vLAPS). Bull. Am. Meteorol. Soc. 2015, 96, 2045–2057. [Google Scholar] [CrossRef]
- CMA Land Data Assimilation System Version2.0 (CLDAS-V2.0). Available online: http://data.cma.cn/data/detail/dataCode/NAFP_CLDAS2.0_NRT/keywords/CLDAS.html (accessed on 8 May 2017).
- Shea, J.M.; Wagnon, P.; Immerzeel, W.W.; Biron, R.; Brun, F.; Pellicciotti, F. A comparative high-altitude meteorological analysis from three catchments in the Nepalese Himalaya. Int. J. Water Resour. Dev. 2015, 31, 174–200. [Google Scholar] [CrossRef] [Green Version]
- Beckers, J.M.; Rixen, M. EOF calculations and data filling from incomplete oceanographic datasets. J. Atmos. Ocean. Technol. 2003, 20, 1839–1856. [Google Scholar] [CrossRef]
- Alvera-Azcárate, A.; Barth, A.; Rixen, M.; Beckers, J.M. Reconstruction of incomplete oceanographic data sets using empirical orthogonal functions: Application to the Adriatic Sea surface temperature. Ocean Model. 2005, 9, 325–346. [Google Scholar] [CrossRef] [Green Version]
- Beckers, J.M.; Barth, A.; Alvera-Azcárate, A. DINEOF reconstruction of clouded images including error maps—Application to the Sea-Surface Temperature around Corsican Island. Ocean Sci. 2006, 2, 183–199. [Google Scholar] [CrossRef]
- Alvera-Azcárate, A.; Barth, A.; Sirjacobs, D.; Beckers, J.M. Enhancing temporal correlations in EOF expansions for the reconstruction of missing data using DINEOF. Ocean Sci. 2009, 5, 475–485. [Google Scholar] [CrossRef]
- Zhou, W.; Peng, B.; Shi, J. Reconstructing spatial-temporal continuous MODIS land surface temperature using the DINEOF method. J. Appl. Remote Sens. 2017. under review. [Google Scholar]
- Chen, Y.; Quan, J.; Zhan, W.; Guo, Z. Enhanced statistical estimation of air temperature incorporating nighttime light data. Remote Sens. 2016, 8, 656. [Google Scholar] [CrossRef]
- User Guide for the Collection 6 Level-2 MOD06/MYD06 Product and Associated Level-3 Datasets. Available online: https://modis-atmosphere.gsfc.nasa.gov/sites/default/files/ModAtmo/C6MOD06OPUserGuide.pdf (accessed on 5 March 2017).
- Immerzeel, W.W.; Petersen, L.; Ragettli, S.; Pellicciotti, F. The importance of observed gradients of air temperature and precipitation for modeling runoff from a glacierized watershed in the Nepalese Himalayas. Water Resour. Res. 2014, 50, 2212–2226. [Google Scholar] [CrossRef]
- Kattel, D.B.; Yao, T.; Yang, W.; Gao, Y.; Tian, L. Comparison of temperature lapse rates from the northern to the southern slopes of the Himalayas. Int. J. Climatol. 2015, 35, 4431–4443. [Google Scholar] [CrossRef]
- Kattel, D.B.; Yao, T.; Yang, K.; Tian, L.; Yang, G.; Joswiak, D. Temperature lapse rate in complex mountain terrain on the southern slope of the central Himalayas. Theor. Appl. Climatol. 2013, 113, 671–682. [Google Scholar] [CrossRef]
- Grab, S.W. Fine-Scale Variations of Near-Surface-Temperature Lapse Rates in the High Drakensberg Escarpment, South Africa: Environmental Implications. Arctic Antarct. Alp. Res. 2013, 45, 500–514. [Google Scholar] [CrossRef]
- Wang, L.; Sun, L.; Shrestha, M.; Li, X.; Liu, W.; Zhou, J.; Yang, K.; Lu, H.; Chen, D. Improving snow process modeling with satellite-based estimation of near-surface-air-temperature lapse rate. J. Geophys. Res. Atmos. 2016, 121, 12005–12030. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, Y.; Zhang, Y.; Ding, Y. Estimation of glacier runoff and future trends in the Yangtze River source region, China. J. Glaciol. 2009, 55, 353–362. [Google Scholar] [CrossRef]
- Zhang, S.; Gao, X.; Ye, B.; Zhang, X.; Hagemann, S. A modified monthly degree-day model for evaluating glacier runoff changes in China. Part II: Application. Hydrol. Process. 2012, 26, 1697–1706. [Google Scholar] [CrossRef]
- Zhang, S.; Ye, B.; Liu, S.; Zhang, X.; Hagemann, S. A modified monthly degree-day model for evaluating glacier runoff changes in China. Part I: Model development. Hydrol. Process. 2012, 26, 1686–1696. [Google Scholar] [CrossRef]
- Zhang, Y.; Hirabayashi, Y.; Liu, S. Catchment-scale reconstruction of glacier mass balance using observations and global climate data: Case study of the Hailuogou catchment, south-eastern Tibetan Plateau. J. Hydrol. 2012, 444–445, 146–160. [Google Scholar] [CrossRef]
- Pradhananga, N.S.; Kayastha, R.B.; Bhattarai, B.C.; Adhikari, T.R.; Pradhan, S.C.; Devkota, L.P.; Shrestha, A.B.; Mool, P.K. Estimation of discharge from Langtang River basin, Rasuwa, Nepal, using a glacio-hydrological model. Ann. Glaciol. 2014, 55, 223–230. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, S.; Ding, Y. Observed degree-day factors and their spatial variation on glaciers in western China. Ann. Glaciol. 2006, 43, 301–306. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; van Beek, L.P.H.; Konz, M.; Shrestha, A.B.; Bierkens, M.F.P. Hydrological response to climate change in a glacierized catchment in the Himalayas. Clim. Chang. 2012, 110, 721–736. [Google Scholar] [CrossRef] [PubMed]
- Shea, J.M.; Immerzeel, W.W.; Wagnon, P.; Vincent, C.; Bajracharya, S. Modelling glacier change in the Everest region, Nepal Himalaya. Cryosphere 2015, 9, 1105–1128. [Google Scholar] [CrossRef] [Green Version]
- Chen, R.S.; Qing, W.W.; Liu, S.Y.; Han, H.D.; He, X.B.; Wang, J.; Liu, G.Y. The relationship between runoff and ground temperature in glacierized catchments in China. Environ. Earth Sci. 2012, 65, 681–687. [Google Scholar] [CrossRef]











| Maximum | Mean | Minimum | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE (K) | Bias (K) | RMSE (K) | Bias (K) | RMSE (K) | Bias (K) | |||
| Kyanging | Whole Year | CLDAS | 2.07 | −0.90 | 2.87 | −2.14 | 5.13 | −4.19 |
| SML | 2.21 | 0.17 | 2.55 | −1.22 | 4.77 | −3.83 | ||
| PML | 2.05 | 0.42 | 1.88 | −0.68 | 3.63 | −2.86 | ||
| summer | CLDAS | 1.27 | 0.46 | 0.94 | −0.74 | 2.23 | −2.09 | |
| SML | 2.23 | −0.75 | 3.20 | −2.46 | 5.72 | −5.09 | ||
| PML | 2.01 | 1.16 | 1.40 | −0.40 | 2.84 | −2.39 | ||
| winter | CLDAS | 2.40 | −1.66 | 3.51 | −2.92 | 6.18 | −5.36 | |
| SML | 2.19 | 0.70 | 2.09 | −0.51 | 4.13 | −3.11 | ||
| PML | 2.07 | −0.01 | 2.11 | −0.85 | 4.01 | −3.13 | ||
| Yala | Whole Year | CLDAS | 7.26 | 7.03 | 5.23 | 4.95 | 3.65 | 2.64 |
| SML | 4.81 | 4.30 | 2.93 | 2.12 | 2.84 | −0.37 | ||
| PML | 4.53 | 4.03 | 2.68 | 1.96 | 2.36 | −0.35 | ||
| summer | CLDAS | 7.28 | 7.15 | 5.29 | 5.24 | 3.71 | 3.59 | |
| SML | 5.07 | 4.84 | 2.83 | 2.45 | 1.85 | 0.28 | ||
| PML | 4.26 | 4.05 | 2.39 | 2.11 | 1.36 | 0.43 | ||
| winter | CLDAS | 6.09 | 4.67 | 4.82 | 2.60 | 5.00 | −0.08 | |
| SML | 4.61 | 3.90 | 3.01 | 1.87 | 3.39 | −0.85 | ||
| PML | 4.72 | 4.02 | 2.87 | 1.85 | 2.89 | −0.93 | ||
| Elevation (km) | Lapse Rate (K/km) |
|---|---|
| <2.5 | −3.35 |
| 2.5–3.5 | −4.50 |
| 3.5–4.5 | −5.12 |
| 4.5–5.5 | −5.25 |
| 5.5–6.5 | −5.27 |
| >6.5 | −5.67 |
| Aspect | Lapse Rate (K/km) |
|---|---|
| North | −4.7 |
| Northeast | −5.5 |
| East | −5.4 |
| Southeast | −5.3 |
| South | −5.1 |
| Southwest | −5.3 |
| West | −5.3 |
| Northwest | −5.0 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, W.; Peng, B.; Shi, J.; Wang, T.; Dhital, Y.P.; Yao, R.; Yu, Y.; Lei, Z.; Zhao, R. Estimating High Resolution Daily Air Temperature Based on Remote Sensing Products and Climate Reanalysis Datasets over Glacierized Basins: A Case Study in the Langtang Valley, Nepal. Remote Sens. 2017, 9, 959. https://doi.org/10.3390/rs9090959
Zhou W, Peng B, Shi J, Wang T, Dhital YP, Yao R, Yu Y, Lei Z, Zhao R. Estimating High Resolution Daily Air Temperature Based on Remote Sensing Products and Climate Reanalysis Datasets over Glacierized Basins: A Case Study in the Langtang Valley, Nepal. Remote Sensing. 2017; 9(9):959. https://doi.org/10.3390/rs9090959
Chicago/Turabian StyleZhou, Wang, Bin Peng, Jiancheng Shi, Tianxing Wang, Yam Prasad Dhital, Ruzhen Yao, Yuechi Yu, Zhongteng Lei, and Rui Zhao. 2017. "Estimating High Resolution Daily Air Temperature Based on Remote Sensing Products and Climate Reanalysis Datasets over Glacierized Basins: A Case Study in the Langtang Valley, Nepal" Remote Sensing 9, no. 9: 959. https://doi.org/10.3390/rs9090959
APA StyleZhou, W., Peng, B., Shi, J., Wang, T., Dhital, Y. P., Yao, R., Yu, Y., Lei, Z., & Zhao, R. (2017). Estimating High Resolution Daily Air Temperature Based on Remote Sensing Products and Climate Reanalysis Datasets over Glacierized Basins: A Case Study in the Langtang Valley, Nepal. Remote Sensing, 9(9), 959. https://doi.org/10.3390/rs9090959