Personalized Metabolic Avatar: A Data Driven Model of Metabolism for Weight Variation Forecasting and Diet Plan Evaluation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Population and Protocol
- Food diaries: users must register daily the foods eaten during breakfast, lunch, dinner and snacks.
- Physical activities (PA): users must wear a smart band all day and all night, especially during physical activities where they have to specify the type of activity performed. These include: jogging, walking, swimming, working out, general sports, etc. Whenever participants forget to track their own activities with the smart band, they must register them into the ArMOnIA app, where the calories burned from these activities are evaluated through the compendium [18]. This is also performed for other activities not monitored by the smart band, such as house cleaning, driving, etc.
- Weight monitoring: users have to weigh themselves barefoot every day after waking up using an impedentiometric balance.
2.2. Wearables and Devices
- MiBand 6, a smart band (Xiaomi Inc.®, Beijing, China), for tracking PA and estimating calories burned during exercises (walking, running, etc.).
- Mi Body Composition Scale, an impedance balance (Xiaomi Inc.®, Beijing, China), for tracking anthropometric data such as: weight, resting metabolism, fat rate, muscle rate, bone mass.
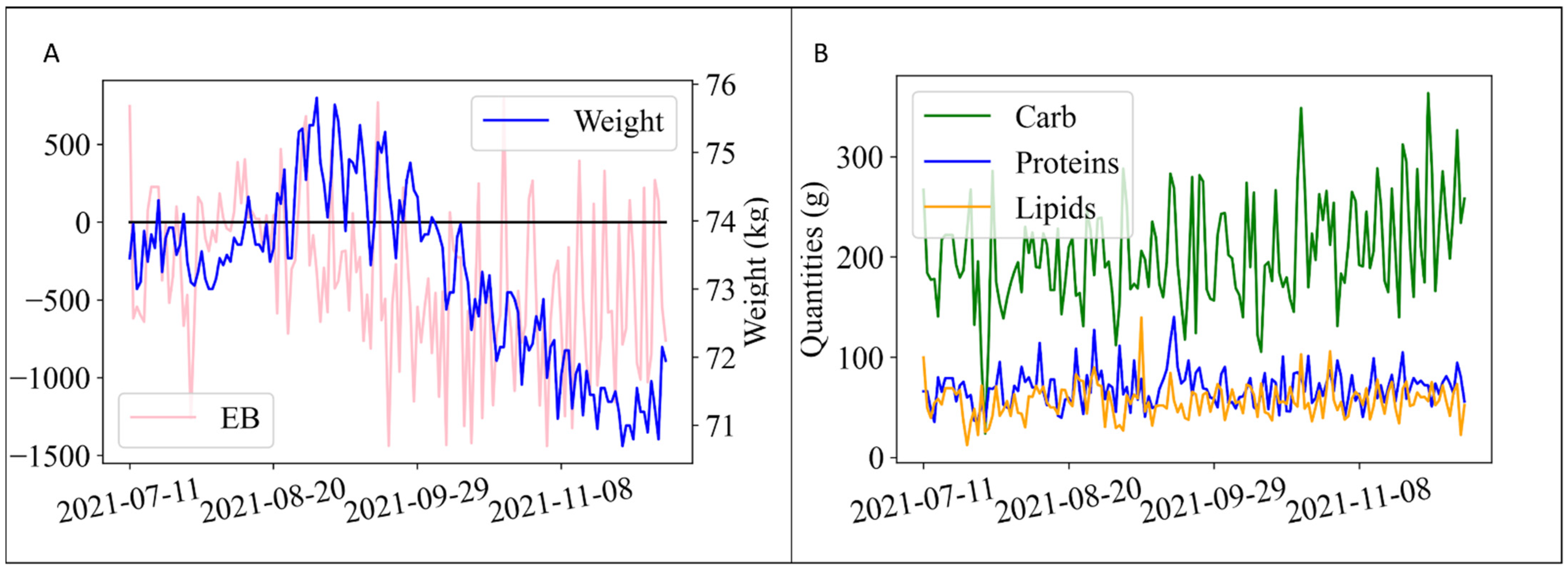
2.3. Data Collection, Storage and Retrieval through an Ad Hoc Developed Web App and Estimation of Personalized Energy Balance
2.3.1. Data Collection
2.3.2. Data Storage
2.3.3. Data Retrieval
- w is the weight acquired daily by the Mi Body Composition Scale.
- mC is the mass expressed in grams of total daily carbohydrate intake, mL is the mass expressed in grams of total daily lipid intake, and mP is the mass expressed in grams of total daily protein intake.
- daily energy balance, EB, calculated according to the formula
2.4. Data Preprocessing
- Weight: w(t) [kg]
- Energy balance: EB(t) [kcal]
- Daily carbohydrate intake: (t) [g]
- Daily protein intake: (t) [g]
- Daily lipid intake: (t) [g]
- Week cosine: cos()
- Week sine: sin()
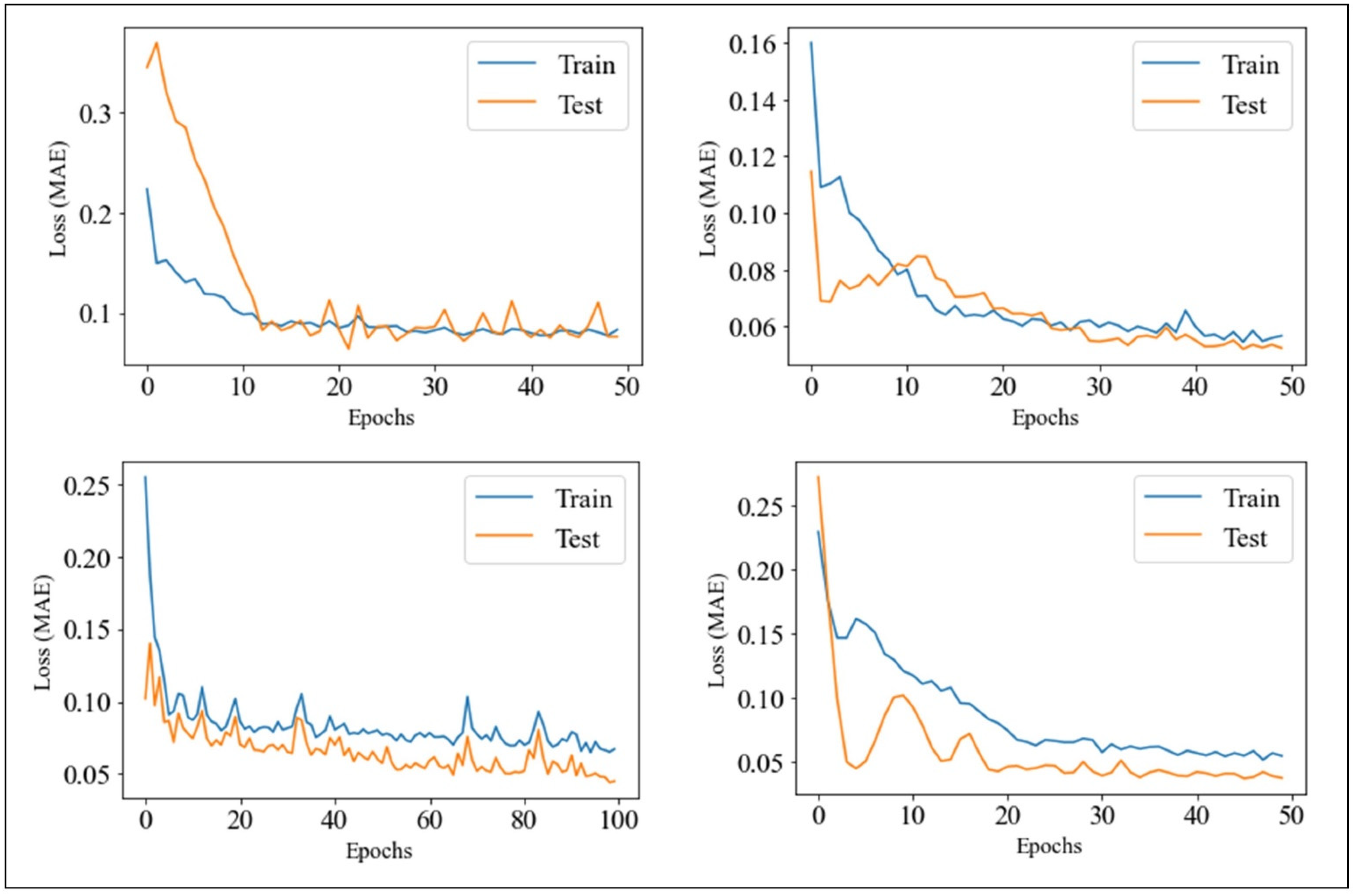
2.5. PMA Development with RNN Network
Data Preparation
2.6. Model Selection
- Input layer: weight and exogenous series such as EB and food composition (carbohydrate, protein and lipid content expressed in grams) at previous times with respect to the output (plus historical values from the time series target). This corresponds to the of Equation (S4), defined as follows: , , , , …, , , , with k the lagged observation (specific for each user, as explained below).
- Output layer: composed of one output, the weight w (t + 1) at time t + 1.
- for
- for
- has to be an increasing function of EB
2.7. Walk-Forward Validation and Simulation
2.8. Computer Performance
2.9. Python Libraries
3. Results
3.1. Selection of the Optimal Models through Grid Search of GRU Parameters and RMSE Overall Minimization on the Cohort of Users
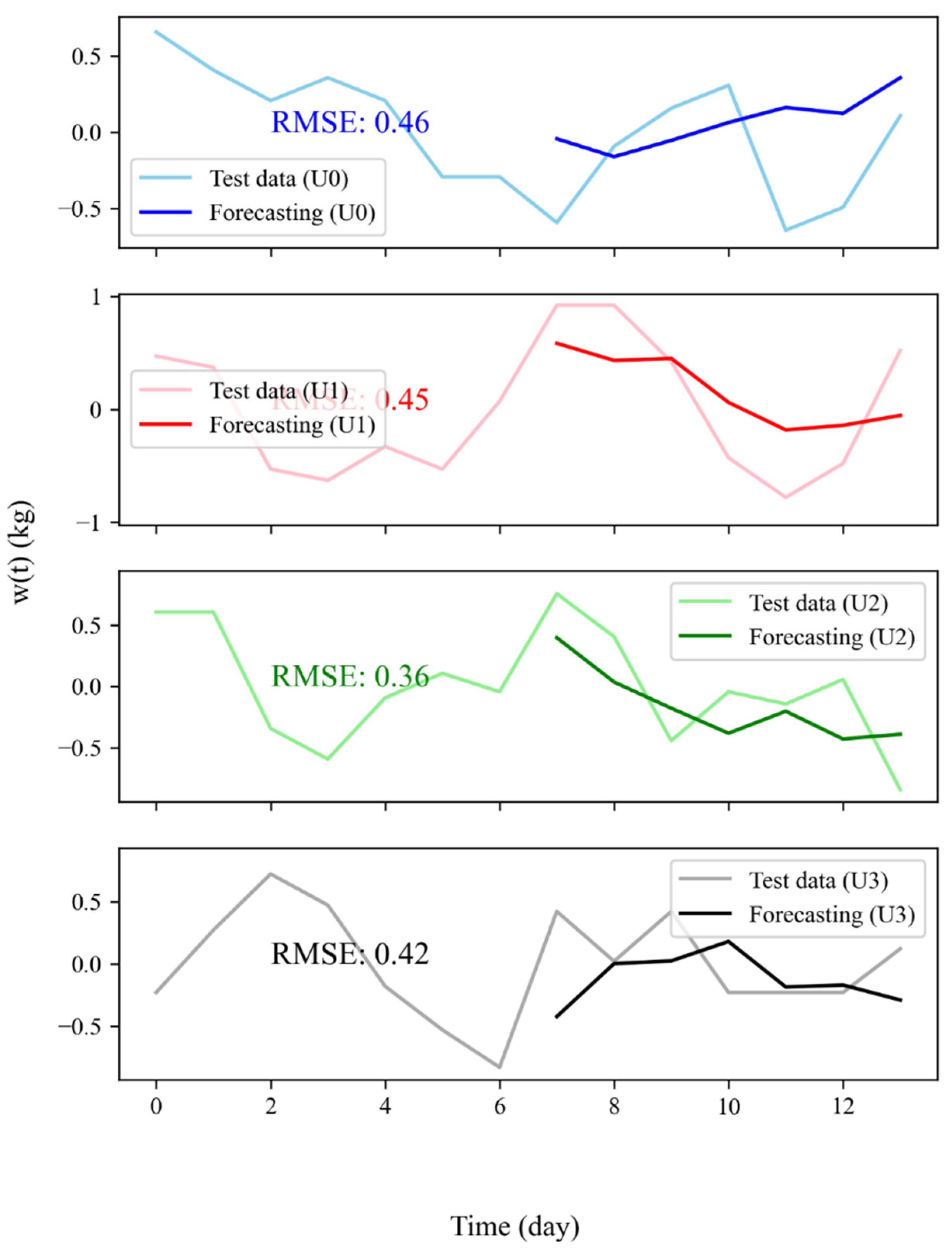
3.2. Weight Forecasting: Model Results, WFV and WFS
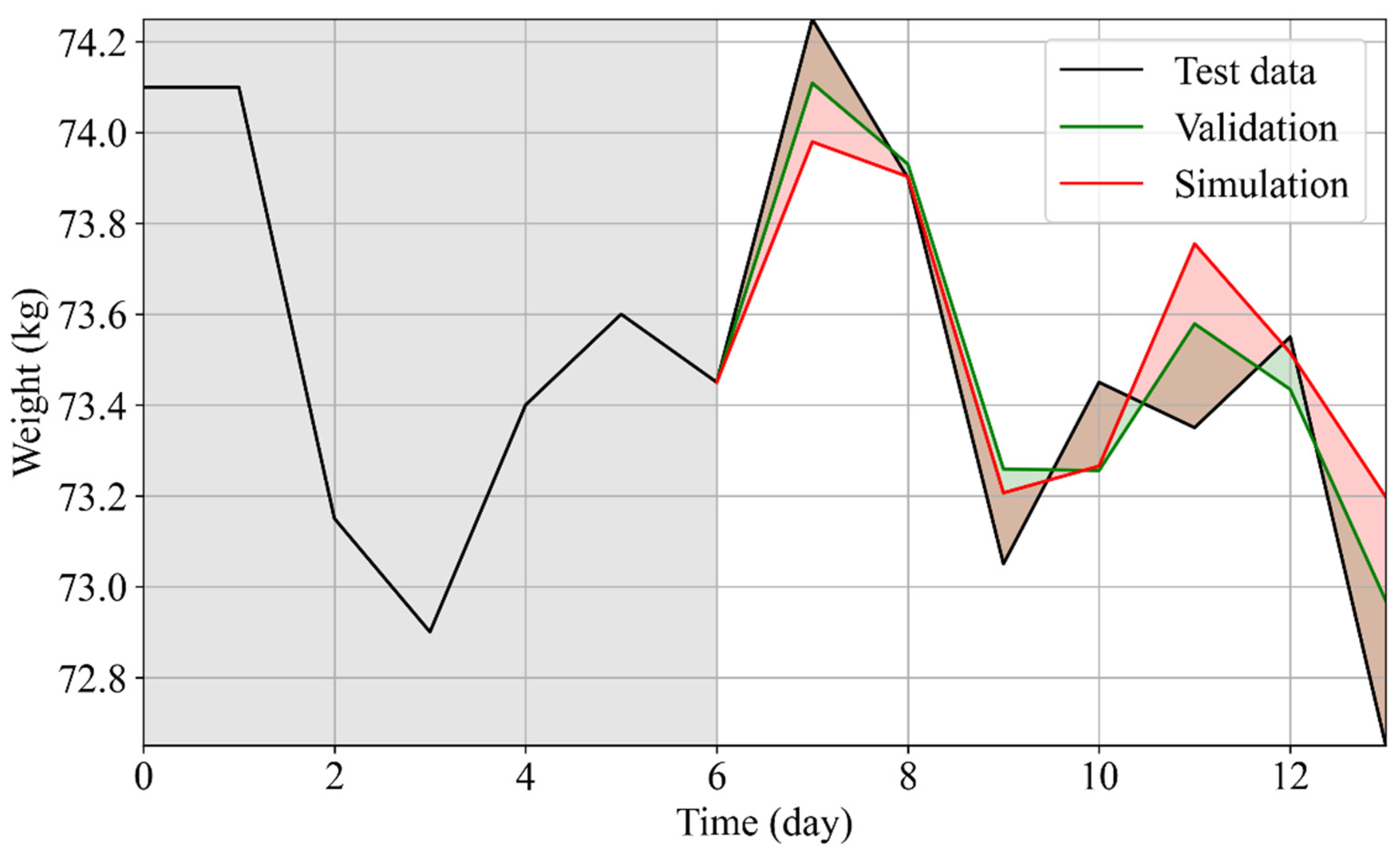
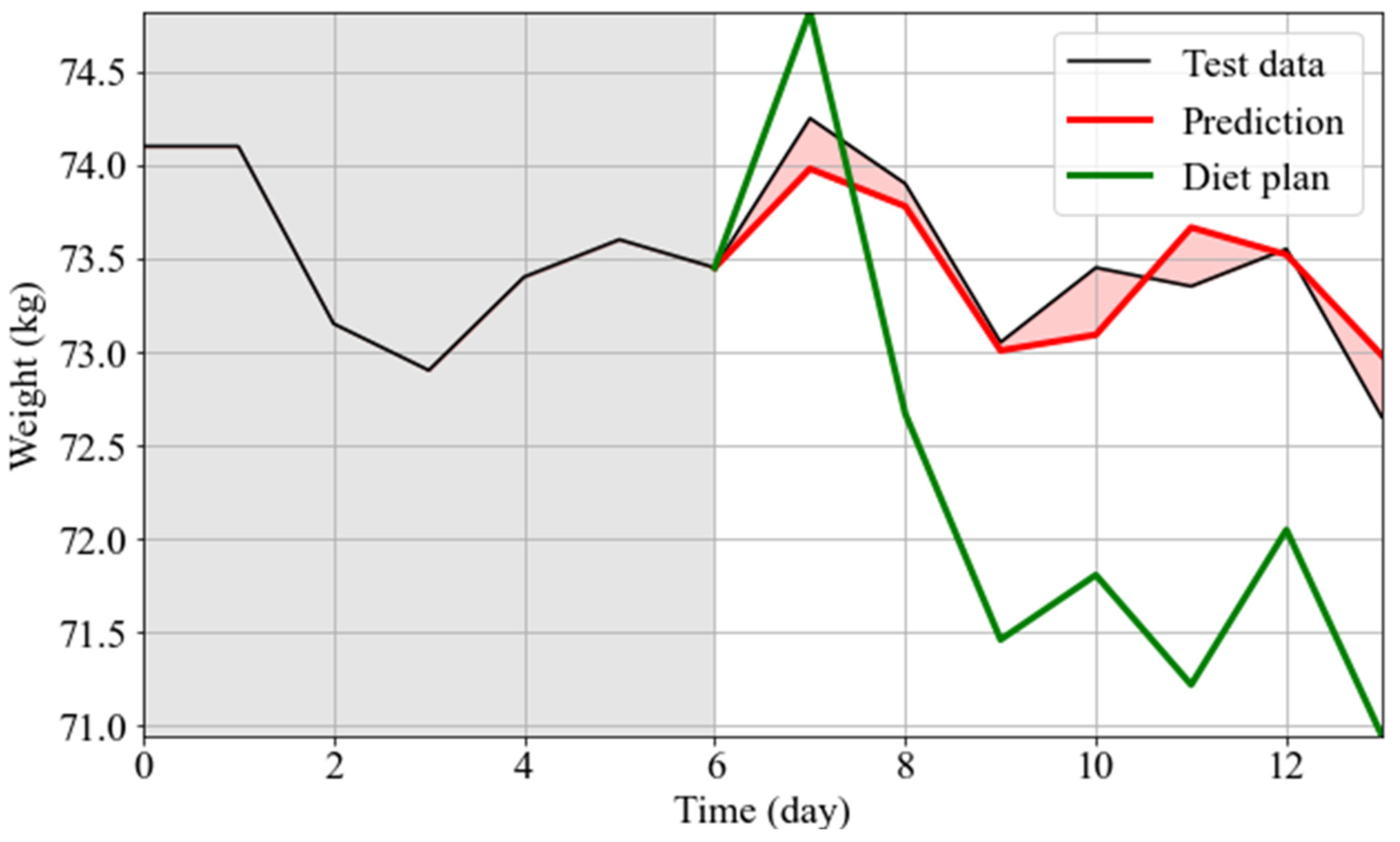
3.3. Simulation of the Personalized Effects of Diet Plans on Weight
3.4. Personalized Diet Plan: Use Case
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sharma, A.M. Obesity and Cardiovascular Risk. Growth Horm. IGF Res. 2003, 13, S10–S17. [Google Scholar] [CrossRef]
- Klop, B.; Elte, J.W.F.; Cabezas, M.C. Dyslipidemia in Obesity: Mechanisms and Potential Targets. Nutrients 2013, 5, 1218–1240. [Google Scholar] [CrossRef] [PubMed]
- Shahi, B.; Praglowski, B.; Deitel, M. Sleep-Related Disorders in the Obese. Obes. Surg. 1992, 2, 157–168. [Google Scholar] [CrossRef] [PubMed]
- Shields, M.; Tremblay, M.S.; Gorber, S.C.; Janssen, I. Abdominal Obesity and Cardiovascular Disease Risk Factors within Body Mass Index Categories. Health Rep. 2012, 23, 7–15. [Google Scholar] [PubMed]
- Kim, H.Y.; Kim, J.K.; Shin, G.G.; Han, J.A.; Kim, J.W. Association between Abdominal Obesity and Cardiovascular Risk Factors in Adults with Normal Body Mass Index: Based on the Sixth Korea National Health and Nutrition Examination Survey. J. Obes. Metab. Syndr. 2019, 28, 262–270. [Google Scholar] [CrossRef]
- Aggarwal, M.; Bozkurt, B.; Panjrath, G.; Aggarwal, B.; Ostfeld, R.J.; Barnard, N.D.; Gaggin, H.; Freeman, A.M.; Allen, K.; Madan, S.; et al. Lifestyle Modifications for Preventing and Treating Heart Failure. J. Am. Coll. Cardiol. 2018, 72, 2391–2405. [Google Scholar] [CrossRef]
- Chung, M.K.; Eckhardt, L.L.; Chen, L.Y.; Ahmed, H.M.; Gopinathannair, R.; Joglar, J.A.; Noseworthy, P.A.; Pack, Q.R.; Sanders, P.; Trulock, K.M. Lifestyle and Risk Factor Modification for Reduction of Atrial Fibrillation: A Scientific Statement from the American Heart Association. Circulation 2020, 141, e750–e772. [Google Scholar] [CrossRef]
- Maruthur, N.M.; Wang, N.Y.; Appel, L.J. Lifestyle Interventions Reduce Coronary Heart Disease Risk Results from the Premier Trial. Circulation 2009, 119, 2026–2031. [Google Scholar] [CrossRef]
- Wingerter, R.; Steiger, N.; Burrows, A.; Estes, N.A.M. Impact of Lifestyle Modification on Atrial Fibrillation. Am. J. Cardiol. 2020, 125, 289–297. [Google Scholar] [CrossRef]
- Hill, J.O.; Wyatt, H.R.; Peters, J.C. The Importance of Energy Balance. Eur. Endocrinol. 2013, 9, 111–115. [Google Scholar] [CrossRef]
- Thomas, D.M.; Martin, C.K.; Heymsfield, S.; Redman, L.M.; Schoeller, D.A.; Levine, J.A. A Simple Model Predicting Individual Weight Change in Humans. J. Biol. Dyn. 2011, 5, 579–599. [Google Scholar] [CrossRef] [PubMed]
- Brunk, E.; Sahoo, S.; Zielinski, D.C.; Altunkaya, A.; Dräger, A.; Mih, N.; Gatto, F.; Nilsson, A.; Preciat Gonzalez, G.A.; Aurich, M.K.; et al. Recon3D Enables a Three-Dimensional View of Gene Variation in Human Metabolism. Nat. Biotechnol. 2018, 36, 272–281. [Google Scholar] [CrossRef]
- Opdam, S.; Richelle, A.; Kellman, B.; Li, S.; Zielinski, D.C.; Lewis, N.E. A Systematic Evaluation of Methods for Tailoring Genome-Scale Metabolic Models. Cell Syst. 2017, 4, 318–329.e6. [Google Scholar] [CrossRef] [PubMed]
- van Zuuren, E.J.; Fedorowicz, Z.; Kuijpers, T.; Pijl, H. Effects of Low-Carbohydrate- Compared with Low-Fat-Diet Interventions on Metabolic Control in People with Type 2 Diabetes: A Systematic Review Including GRADE Assessments. Am. J. Clin. Nutr. 2018, 108, 300–331. [Google Scholar] [CrossRef] [PubMed]
- Johnston, B.C.; Kanters, S.; Bandayrel, K.; Wu, P.; Naji, F.; Siemieniuk, R.A.; Ball, G.D.C.; Busse, J.W.; Thorlund, K.; Guyatt, G.; et al. Comparison of Weight Loss among Named Diet Programs in Overweight and Obese Adults: A Meta-Analysis. JAMA 2014, 312, 923–933. [Google Scholar] [CrossRef] [PubMed]
- Wycherley, T.P.; Moran, L.J.; Clifton, P.M.; Noakes, M.; Brinkworth, G.D. Effects of Energy-Restricted High-Protein, Low-Fat Compared with Standard-Protein, Low-Fat Diets: A Meta-Analysis of Randomized Controlled Trials. Am. J. Clin. Nutr. 2012, 96, 1281–1298. [Google Scholar] [CrossRef]
- Bianchetti, G.; Abeltino, A.; Serantoni, C.; Ardito, F.; Malta, D.; de Spirito, M.; Maulucci, G. Personalized Self-Monitoring of Energy Balance through Integration in a Web-Application of Dietary, Anthropometric, and Physical Activity Data. J. Pers. Med. 2022, 12, 568. [Google Scholar] [CrossRef]
- Ainsworth, B.E.; Haskell, W.L.; Leon, A.S.; Jacobs, D.R., Jr.; Montoye, H.J.; Sallis, J.F.; Paffenbarger, R.S., Jr. Compendium of Physical Activities: Classification of Energy Costs of Human Physical Activities. Med. Sci. Sports Exerc. 1993, 25, 71–80. [Google Scholar] [CrossRef]
- Hao, Y.; Ma, X.K.; Zhu, Z.; Cao, Z.B. Validity of Wrist-Wearable Activity Devices for Estimating Physical Activity in Adolescents: Comparative Study. JMIR Mhealth Uhealth 2021, 9, e18320. [Google Scholar] [CrossRef]
- Lam, Y.Y.; Ravussin, E. Analysis of Energy Metabolism in Humans: A Review of Methodologies. Mol. Metab. 2016, 5, 1057–1071. [Google Scholar] [CrossRef]
- Calcagno, M.; Kahleova, H.; Alwarith, J.; Burgess, N.N.; Flores, R.A.; Busta, M.L.; Barnard, N.D. The Thermic Effect of Food: A Review. J. Am. Coll. Nutr. 2019, 38, 547–551. [Google Scholar] [CrossRef] [PubMed]
- Freire, R. Scientific Evidence of Diets for Weight Loss: Different Macronutrient Composition, Intermittent Fasting, and Popular Diets. Nutrition 2020, 69, 110549. [Google Scholar] [CrossRef] [PubMed]
- Fahey, M.C.; Klesges, R.C.; Kocak, M.; Talcott, G.W.; Krukowski, R.A. Seasonal Fluctuations in Weight and Self-Weighing Behavior among Adults in a Behavioral Weight Loss Intervention. Eat. Weight Disord. 2020, 25, 921–928. [Google Scholar] [CrossRef] [PubMed]
- Cheson, K.J.A. Methods in Nutrition the Measurement of Food and Energy Intake in Man-an Evaluation of Some Techniquess 3. Am. J. Clin. Nutr. 1980, 33, 1147–1154. [Google Scholar] [CrossRef] [PubMed]
- Ruineihart, D.E.; Hint, G.E.; Williams, R.J. Learning Internal Representations by error Propagation Two; MIT Press: Cambridge, MA, USA, 1985. [Google Scholar]
- Livieris, I.E.; Pintelas, P. A Novel Multi-Step Forecasting Strategy for Enhancing Deep Learning Models’ Performance. Neural Comput. Appl. 2022, 1–18. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Pachitariu, M.; Sahani, M. Regularization and Nonlinearities for Neural Language Models: When Are They Needed? arXiv 2013, arXiv:1301.5650. [Google Scholar]
- Egger, R.; Gretzel, U. Tourism on the Verge Series Editors; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Lai, S.-H.; Lepetit, V.; Nishino, K.; Sato, Y. (Eds.) Computer Vision—ACCV 2016; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2017; Volume 10112, ISBN 978-3-319-54183-9. [Google Scholar]
- Manore, M.M. Exercise and the Institute of Medicine Recommendations for Nutrition. Curr. Sports Med. Rep. 2005, 4, 193–198. [Google Scholar] [CrossRef]
- Park, H.; Kityo, A.; Kim, Y.; Lee, S.A. Macronutrient Intake in Adults Diagnosed with Metabolic Syndrome: Using the Health Examinee (HEXA) Cohort. Nutrients 2021, 13, 4457. [Google Scholar] [CrossRef]
- Marques, A.; Peralta, M.; Naia, A.; Loureiro, N.; de Matos, M.G. Prevalence of Adult Overweight and Obesity in 20 European Countries, 2014. Eur. J. Public Health 2018, 28, 295–300. [Google Scholar] [CrossRef]
- Gammone, M.A.; D’Orazio, N. COVID-19 and Obesity: Overlapping of Two Pandemics. Obes. Facts 2021, 14, 579–585. [Google Scholar] [CrossRef] [PubMed]
- Chadwick, R. Nutrigenomics, Individualism and Public Health. Proc. Nutr. Soc. 2004, 63, 161–166. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ordovas, J.M.; Ferguson, L.R.; Tai, E.S.; Mathers, J.C. Personalised Nutrition and Health. BMJ 2018, 361, bmj.k2173. [Google Scholar] [CrossRef]
- Flint, H.J. The Impact of Nutrition on the Human Microbiome. Nutr. Rev. 2012, 70, S10–S13. [Google Scholar] [CrossRef] [PubMed]
- Christensen, P.; Meinert Larsen, T.; Westerterp-Plantenga, M.; Macdonald, I.; Martinez, J.A.; Handjiev, S.; Poppitt, S.; Hansen, S.; Ritz, C.; Astrup, A.; et al. Men and Women Respond Differently to Rapid Weight Loss: Metabolic Outcomes of a Multi-Centre Intervention Study after a Low-Energy Diet in 2500 Overweight, Individuals with Pre-Diabetes (PREVIEW). Diabetes Obes. Metab. 2018, 20, 2840–2851. [Google Scholar] [CrossRef]
- Sazonov, E.S.; Fontana, J.M. A Sensor System for Automatic Detection of Food Intake through Non-Invasive Monitoring of Chewing. IEEE Sens. J. 2012, 12, 1340–1348. [Google Scholar] [CrossRef]
- Bianchetti, G.; Viti, L.; Scupola, A.; di Leo, M.; Tartaglione, L.; Flex, A.; de Spirito, M.; Pitocco, D.; Maulucci, G. Erythrocyte Membrane Fluidity as a Marker of Diabetic Retinopathy in Type 1 Diabetes Mellitus. Eur. J. Clin. Investig. 2021, 51, e13455. [Google Scholar] [CrossRef]
- Maulucci, G.; Cohen, O.; Daniel, B.; Ferreri, C.; Sasson, S. The Combination of Whole Cell Lipidomics Analysis and Single Cell Confocal Imaging of Fluidity and Micropolarity Provides Insight into Stress-Induced Lipid Turnover in Subcellular Organelles of Pancreatic Beta Cells. Molecules 2019, 24, 3742. [Google Scholar] [CrossRef]
- Maulucci, G.; Cohen, O.; Daniel, B.; Sansone, A.; Petropoulou, P.I.; Filou, S.; Spyridonidis, A.; Pani, G.; de Spirito, M.; Chatgilialoglu, C.; et al. Fatty Acid-Related Modulations of Membrane Fluidity in Cells: Detection and Implications. Free Radic. Res. 2016, 50, S40–S50. [Google Scholar] [CrossRef]
- Cordelli, E.; Maulucci, G.; de Spirito, M.; Rizzi, A.; Pitocco, D.; Soda, P. A Decision Support System for Type 1 Diabetes Mellitus Diagnostics Based on Dual Channel Analysis of Red Blood Cell Membrane Fluidity. Comput. Methods Programs Biomed. 2018, 162, 263–271. [Google Scholar] [CrossRef]
- Bianchetti, G.; Azoulay-Ginsburg, S.; Keshet-Levy, N.Y.; Malka, A.; Zilber, S.; Korshin, E.E.; Sasson, S.; de Spirito, M.; Gruzman, A.; Maulucci, G. Investigation of the Membrane Fluidity Regulation of Fatty Acid Intracellular Distribution by Fluorescence Lifetime Imaging of Novel Polarity Sensitive Fluorescent Derivatives. Int. J. Mol. Sci. 2021, 22, 3106. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Zhang, X. Is There Really a Proportional Relationship between VO2max and Body Weight? A Review Article. PLoS ONE 2021, 16, e0261519. [Google Scholar] [CrossRef]
- Serantoni, C.; Zimatore, G.; Bianchetti, G.; Abeltino, A.; de Spirito, M.; Maulucci, G. Unsupervised Clustering of Heartbeat Dynamics Allows for Real Time and Personalized Improvement in Cardiovascular Fitness. Sensors 2022, 22, 3974. [Google Scholar] [CrossRef] [PubMed]
- Zimatore, G.; Gallotta, M.C.; Innocenti, L.; Bonavolontà, V.; Ciasca, G.; de Spirito, M.; Guidetti, L.; Baldari, C. Recurrence Quantification Analysis of Heart Rate Variability during Continuous Incremental Exercise Test in Obese Subjects. Chaos 2020, 30, 033135. [Google Scholar] [CrossRef] [PubMed]

 |
| User | Number of Neurons | Activation Function | Dropout Rate | Epochs | Batch Size | Lookback | Seasonal Terms | RMSE |
|---|---|---|---|---|---|---|---|---|
| 0 | 100 | ReLU | 0.2 | 50 | 32 | 7 | No | 0.47 |
| 1 | 200 | ReLU | 0.2 | 200 | 128 | 4 | No | 0.49 |
| 2 | 150 | ReLU | 0.2 | 50 | 64 | 5 | No | 0.31 |
| 3 | 100 | ReLU | 0.2 | 50 | 128 | 5 | No | 0.4 |
| User | Quality Factor (q) [kg] | |
|---|---|---|
| 0 | 1.56·10−3 | 0.77 |
| 1 | 0.47·10−3 | −0.13 |
| 2 | 2.03·10−3 | 0.26 |
| 3 | 0.30·10−3 | −0.06 |
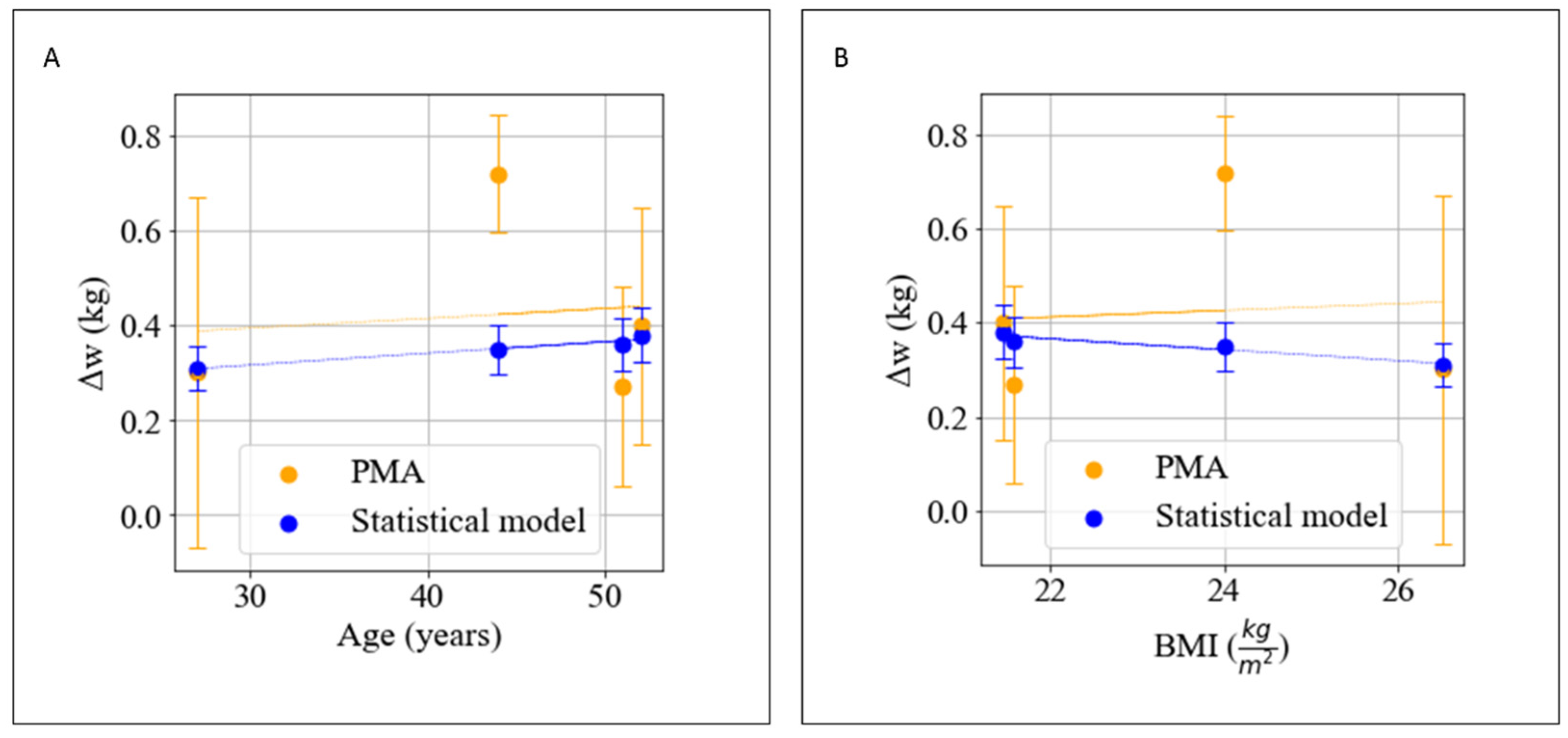
| User | Age | Sex | Height (cm) | wi [kg] | ∆w (PMA) [kg] | ∆w (Statistical Model) [kg] |
|---|---|---|---|---|---|---|
| 0 | 27 | M | 183 | 88.7 | 0.3 ± 0.37 | 0.31 ± 0.031 |
| 1 | 52 | M | 186 | 74.25 | 0.4 ± 0.25 | 0.38 ± 0.038 |
| 2 | 44 | M | 175 | 73.45 | 0.72 ± 0.12 | 0.35 ± 0.035 |
| 3 | 51 | F | 160 | 55.25 | 0.27 ± 0.21 | 0.4 ± 0.04 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abeltino, A.; Bianchetti, G.; Serantoni, C.; Ardito, C.F.; Malta, D.; De Spirito, M.; Maulucci, G. Personalized Metabolic Avatar: A Data Driven Model of Metabolism for Weight Variation Forecasting and Diet Plan Evaluation. Nutrients 2022, 14, 3520. https://doi.org/10.3390/nu14173520
Abeltino A, Bianchetti G, Serantoni C, Ardito CF, Malta D, De Spirito M, Maulucci G. Personalized Metabolic Avatar: A Data Driven Model of Metabolism for Weight Variation Forecasting and Diet Plan Evaluation. Nutrients. 2022; 14(17):3520. https://doi.org/10.3390/nu14173520
Chicago/Turabian StyleAbeltino, Alessio, Giada Bianchetti, Cassandra Serantoni, Cosimo Federico Ardito, Daniele Malta, Marco De Spirito, and Giuseppe Maulucci. 2022. "Personalized Metabolic Avatar: A Data Driven Model of Metabolism for Weight Variation Forecasting and Diet Plan Evaluation" Nutrients 14, no. 17: 3520. https://doi.org/10.3390/nu14173520
APA StyleAbeltino, A., Bianchetti, G., Serantoni, C., Ardito, C. F., Malta, D., De Spirito, M., & Maulucci, G. (2022). Personalized Metabolic Avatar: A Data Driven Model of Metabolism for Weight Variation Forecasting and Diet Plan Evaluation. Nutrients, 14(17), 3520. https://doi.org/10.3390/nu14173520










