Estimation of Left Ventricular Ejection Fraction Using Cardiovascular Hemodynamic Parameters and Pulse Morphological Characteristics with Machine Learning Algorithms
Abstract
1. Introduction
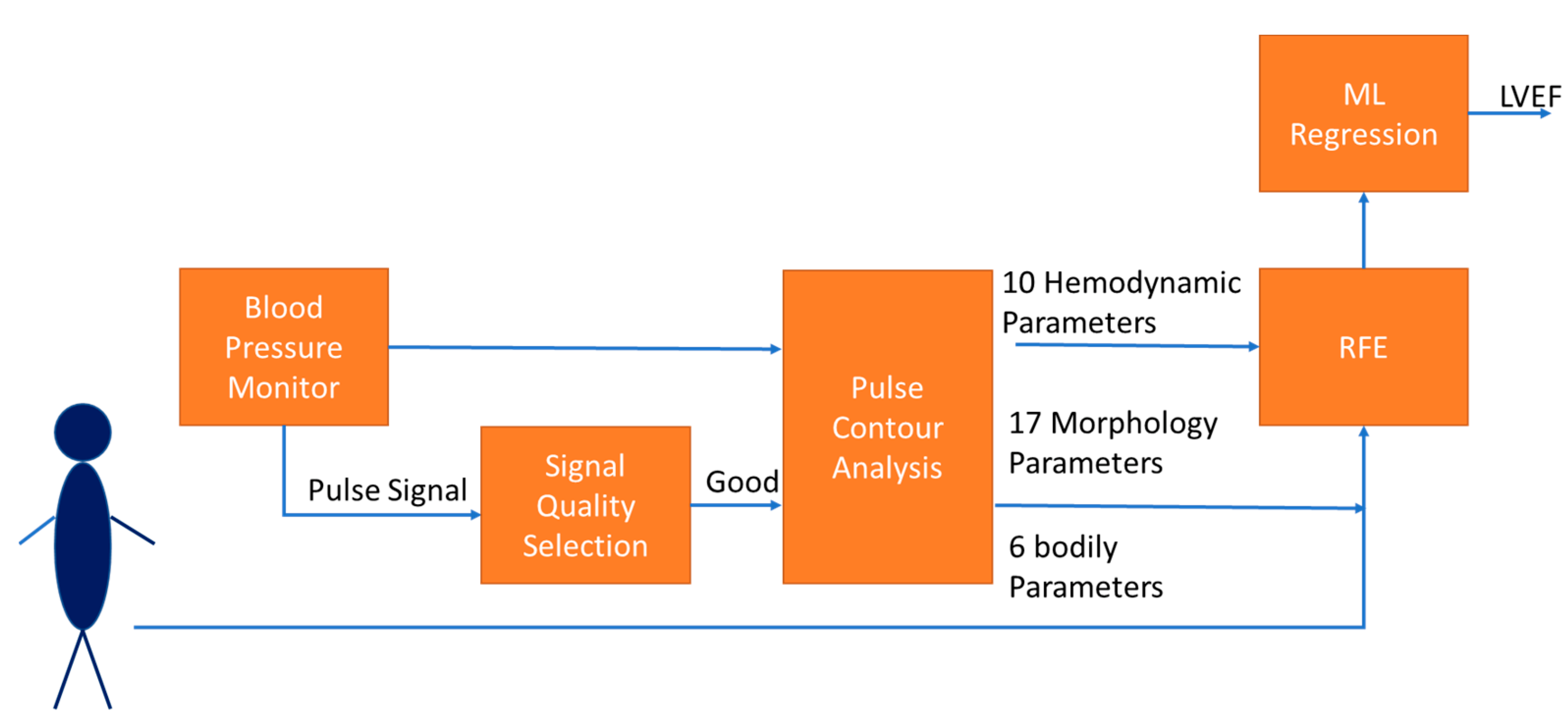
2. Materials and Methods
2.1. Cardiovascular Hemodynamic Parameters
2.2. Morphological Parameters of Pulse
2.2.1. Pulse Quality Analysis
2.2.2. Morphological Parameters
2.3. Bodily Information
2.4. Features Extraction and Regression
2.4.1. Features Extraction
2.4.2. XGBoost
2.4.3. Self-Constructing Neural Fuzzy Inference Network
2.5. Statistical Analysis
2.6. Data Collection
3. Results
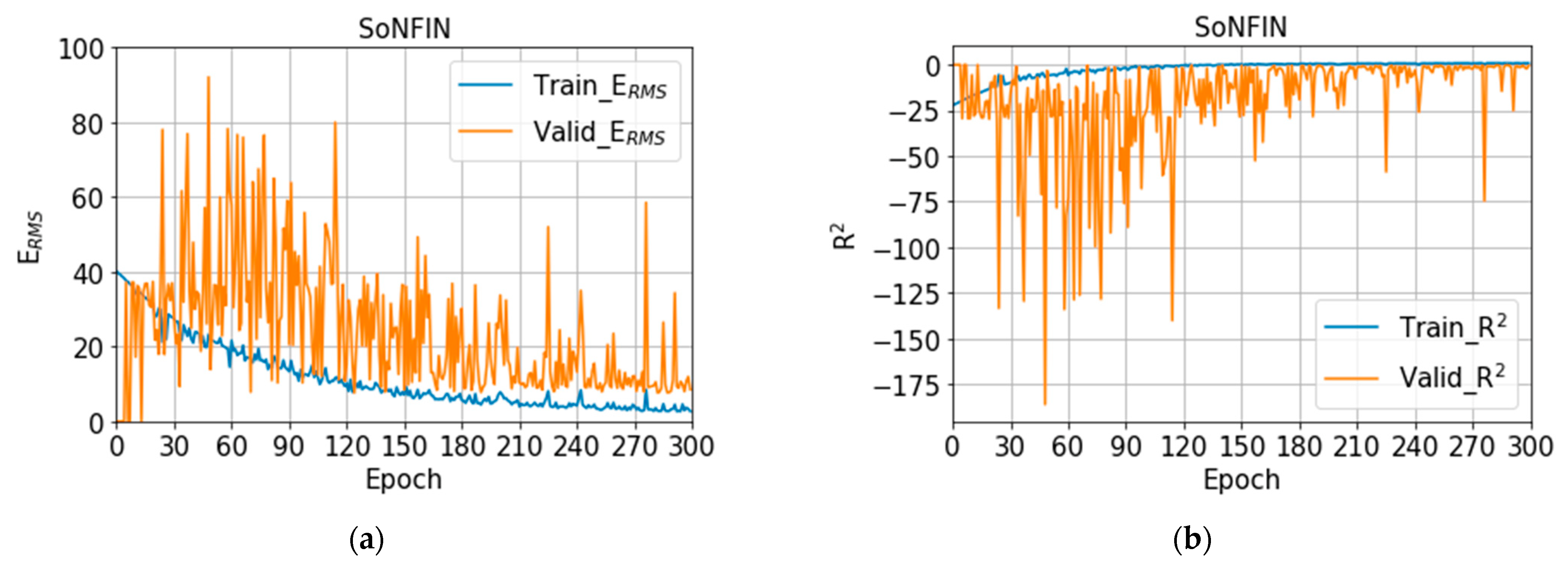
3.1. Training Models
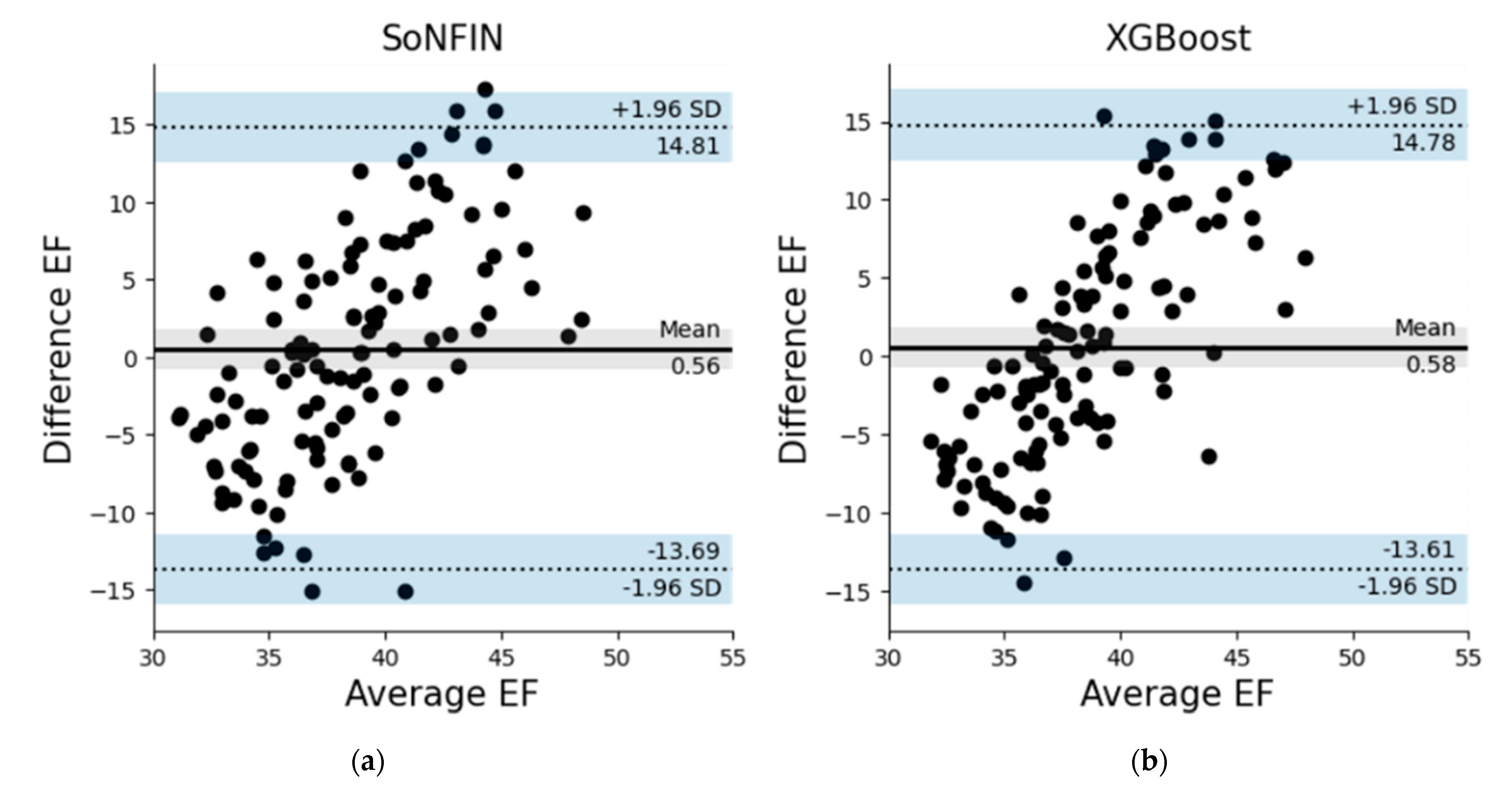
3.2. Testing Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- What is Heart Failure? 2017. Available online: https://www.heart.org/en/health-topics/heart-failure/what-is-heart-failure (accessed on 10 September 2022).
- King, M.; Kingery, J.; Casey, B. Diagnosis and evaluation of Heart Failure. Am. Fam. Physician 2012, 85, 1161–1168. [Google Scholar] [PubMed]
- Konstam, M.A.; Abboud, F.M. Ejection fraction: Misunderstood and overrated. Circulation 2017, 135, 717–719. [Google Scholar] [CrossRef] [PubMed]
- Wood, P.W. Left ventricular ejection fraction and volumes: It depends on the imaging method. Echocardiography 2014, 31, 87–100. [Google Scholar] [CrossRef] [PubMed]
- Wesseling, K.H.; Jansen, J.C.; Settels, J.J.; Schreuder, J.J. Computation of aortic flow from pressure in humans using a nonlinear three-element model. J. Appl. Physiol. 1993, 74, 2566–2573. [Google Scholar] [CrossRef]
- Langewouters, G.J.; Wesseling, K.H.; Goedhard, W.A. The static elastic properties of 45 human thoracic and 20 abdominal aortas in vitro and the parameters of a new model. J. Biomech. 1984, 17, 425–435. [Google Scholar] [CrossRef]
- Pollock, J.D.; Murray, I.; Bordes, S.; Makaryus, A.N. Physiology, Cardiovascular Hemodynamics; StatPearls: Treasure Island, CA, USA, 2022. [Google Scholar]
- Toorop, G.P.; Westerhof, N.; Elzinga, G. Beat-to-beat estimation of peripheral resistance and arterial compliance during pressure transients. Am. J. Physiol. 1987, 252, H1275–H1283. [Google Scholar] [CrossRef]
- Liu, S.-H.; Lin, T.-H.; Cheng, D.-C.; Wang, J.-J. Assessment of stroke volume from brachial Blood pressure using arterial characteristics. IEEE Trans. Biomed. Eng. 2015, 62, 2151–2157. [Google Scholar] [CrossRef]
- Su, C.-H.; Liu, S.-H.; Tan, T.-H.; Lo, C.-H. Using the pulse contour method to measure the changes in stroke volume during a passive leg raising test. Sensors 2018, 18, 3420. [Google Scholar] [CrossRef]
- Liu, S.-H.; Liu, L.-J.; Pan, K.-L.; Chen, W.; Tan, T.-H. Using the characteristics of pulse waveform to enhance the accuracy of blood pressure measurement by a multi-dimension regression model. Appl. Sci. 2019, 9, 2922. [Google Scholar] [CrossRef]
- Romano, S.M.; Pistolesi, M. Assessment of cardiac output from systemic arterial pressure in human. Crit. Care. Med. 2022, 30, 1834–1841. [Google Scholar] [CrossRef]
- Nosair, W.; Kadaru, T.; Amin, A.; Mammen, P.; Cox, J.; Araj, F. Pulse contour analysis: A useful tool for decision making during temporary mechanical circulatory support. J. Heart Lung Trans. 2022, 41, S238. [Google Scholar] [CrossRef]
- Teboul, J.L.; Saugel, B.; Cecconi, M.; De Backer, D.; Hofer, C.K.; Monnet, X.; Perel, A.; Pinsky, M.R.; Reuter, D.A.; Rhodes, A.; et al. Less invasive hemodynamic monitoring in critically ill patients. Intensive Care Med. 2016, 49, 1350–1359. [Google Scholar] [CrossRef]
- Roth, S.; Fox, H.; Fuchs, U. Noninvasive pulse contour analysis for determination of cardiac output in patients with chronic heart failure. Clin. Res. Cardiol. 2018, 107, 395–404. [Google Scholar] [CrossRef]
- Vaquer, S.; Chemla, D.; Teboul, J.-L. Influence of changes in ventricular systolic function and loading conditions on pulse contour analysis-derived femoral dP/dt max. Ann. Intensive Care 2019, 9, 61. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, J.; Chen, X.; Wang, Y.; Zhaoa, Z. Continuous blood pressure estimation based on multiple parameters from electrocardiogram and photoplethysmogram by Back-propagation neural network. Comput. Ind. 2017, 89, 50–59. [Google Scholar] [CrossRef]
- Cheng, K.-S.; Su, Y.-L.; Kuo, L.-C.; Yang, T.-H.; Lee, C.-L.; Chen, W.; Liu, S.-H. Muscle mass measurement using machine learning algorithms with electrical impedance myography. Sensors 2022, 22, 3087. [Google Scholar] [CrossRef]
- Pouladzadeh, P.; Kuhad, P.; Peddi, S.V.; Yassine, A.; Shirmohammadi, S. Food calorie measurement using deep learning neural network. In Proceedings of the 2016 IEEE International Instrumentation and Measurement Technology Conference Proceedings, Taipei, Taiwan, 23–26 May 2016. [Google Scholar]
- Ruede, R.; Heusser, V.; Frank, L.; Roitberg, A.; Haurilet, M.; Stiefelhagen, R. Multi-task learning for calorie prediction on a novel large-scale recipe dataset enriched with nutritional information. arXiv 2020, arXiv:2011.01082v1. [Google Scholar]
- Hrushikesh, N.; Mhaskar, S.V.P.; Maria, D.W. A deep learning approach to diabetic blood glucose prediction. Front. Appl. Math. Stat. 2017, 3, 14. [Google Scholar] [CrossRef]
- Kwon, H.-M.; Seo, W.-Y.; Kim, J.-M.; Shim, W.-H.; Kim, S.-H.; Hwang, G.-S. Estimation of stroke volume variance from arterial blood pressure: Using a 1-D convolutional neural network. Sensors 2021, 21, 5130. [Google Scholar] [CrossRef]
- Satija, U.; Ramkumar, B.; Manikandan, M.S. A review of signal processing techniques for electrocardiogram signal quality assessment. IEEE Rev. Biol. Eng. 2018, 11, 36–52. [Google Scholar] [CrossRef]
- Liu, S.-H.; Liu, H.-C.; Chen, W.; Tan, T.-H. Evaluating quality of photoplethymographic signal on wearable forehead pulse oximeter with supervised classification approaches. IEEE Access 2020, 8, 185121–185135. [Google Scholar] [CrossRef]
- Liu, S.-H.; Wang, J.-J.; Chen, W.; Pan, K.-L.; Su, C.-H. Classification of photoplethysmographic signal quality with fuzzy neural network for improvement of stroke volume measurement. Appl. Sci. 2020, 10, 1476. [Google Scholar] [CrossRef]
- Liu, S.-H.; Cheng, D.-C.; Lin, C.-M. Arrhythmia identification with two-lead electrocardiograms using artificial neural networks and support vector machines for a portable ECG monitor system. Sensors 2013, 13, 813–828. [Google Scholar] [CrossRef]
- Liu, S.-H.; Cheng, W.-C. Fall detection with the support vector machine during scripted and continuous unscripted activities. Sensors 2012, 12, 12301–12316. [Google Scholar] [CrossRef]
- Louridas, P.; Ebert, C. Machine learning. IEEE Softw. 2016, 33, 110–115. [Google Scholar] [CrossRef]
- Xin, Y.; Kong, L.; Liu, Z.; Chen, Y.; Li, Y.; Zhu, H.; Gao, M.; Hou, H.; Wang, C. Machine learning and deep learning methods for cybersecurity. IEEE Access 2018, 6, 35365–35381. [Google Scholar] [CrossRef]
- Beam, A.L.; Kohane, I.S. Big data and machine learning in health care. JAMA 2018, 319, 1317–1318. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.H.; Asch, S.M. Machine learning and prediction in medicine beyond the peak of inflated expectations. N. Eng. J. Med. 2017, 376, 2507–2509. [Google Scholar] [CrossRef]
- Packer, M.; McMurray, J.J.; Desai, A.S.; Gong, J.; Lefkowitz, M.P.; Rizkala, A.R.; Rouleau, J.L.; Shi, V.C.; Solomon, S.D.; Swedberg, K.; et al. Angiotensin receptor neprilysin inhibitio.n compared with enalapril on the risk of clinical progression in surviving patients with heart failure. Circulation 2015, 131, 54–61. [Google Scholar] [CrossRef]
- Heidenreich, P.A.; Bozkurt, B. 2022 AHA/ACC/HFSA guideline for the management of heart failure: A report of the american college of cardiology/american heart association joint committee on clinical practice guidelines. Circulation 2022, 145, e895–e1032. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Jung, C.-F.; Lin, C.-T. An on-line self-constructing neural fuzzy inference network and its application. IEEE Trans. Fuzzy Syst. 1998, 6, 12–32. [Google Scholar]
- Liu, S.-H.; Wang, J.-J.; Huang, K.-S. A new oscillometry-based method for estimating the dynamic brachial artery compliance under loaded conditions. IEEE Tran. Biol. Eng. 2008, 55, 2463–2470. [Google Scholar] [CrossRef] [PubMed]
- Drzewiecki, G.; Hood, R.; Apple, H. Theory of the oscillometric maximum and the systolic and diastolic detection ratios. Ann. Biomed. Eng. 1994, 22, 88–96. [Google Scholar] [CrossRef]
- Liu, S.-H.; Chen, W.; Su, C.-H.; Pa, K.-L. Convolutional neural network-based detection of deep vein thrombosis in a low limb with light reflection rheography. Measurement 2022, 189, 110457. [Google Scholar] [CrossRef]
- Liu, S.-H.; Li, R.-X.; Wang, J.-J.; Chen, W.; Su, C.-H. Classification of photoplethysmographic signal quality with deep convolution neural networks for accurate Measurement of cardiac stroke volume. Appl. Sci. 2020, 10, 4612. [Google Scholar] [CrossRef]
- Fischer, C.; Domer, B.; Wibmer, T.; Penzel, T. An algorithm for real-time pulse waveform segmentation and artifact detection in photoplethysmograms. IEEE J. Bio. Health Inf. 2017, 21, 372–381. [Google Scholar] [CrossRef]
- Hume, R.; Weyers, E. Relationship between total body water and surface area in normal and obese subjects. J. Clin. Pathol. 1971, 24, 234–238. [Google Scholar] [CrossRef]
- Meloni, A.; Aquaro, G.; Festa, P.; Gagliardotto, F.; Zuccarelli, A.; Gerardi, C.; Santodirocco, M.; Romeo, M.A.; Gamberini, M.R.; Smacchia, M.P.; et al. Left ventricular volumes, mass and function normalized to the body surface area, age and gender from CMR in a large cohort of well-treated thalassemia major patients without myocardial iron overload. J. Cardiol. Mag. Res. 2011, 13, P305. [Google Scholar] [CrossRef]
- Sharma, A.; Lavie, C.J.; Borer, J.S.; Vallakati, A.; Goel, S.; Lopez-Jimenez, F.; Arbab-Zadeh, A.; Mukherjee, D.; Lazar, J.M. Meta-analysis of the relation of body mass index to all-cause and cardiovascular mortality and hospitalization in patients with chronic heart failure. Am. J. Cardiol. 2015, 115, 1428–1434. [Google Scholar] [CrossRef]
- Ye, L.F.; Li, X.L.; Wang, S.M.; Wang, Y.F.; Zheng, Y.R.; Wang, L.H. Body mass index: An effective predictor of ejection fraction improvement in heart failure. Front. Cardiovasc. Med. 2021, 8, 586240. [Google Scholar] [CrossRef]
- You, W.; Yang, Z.; Ji, G. PLS-based recursive feature elimination for high-dimensional small sample. Know. Based Syst. 2014, 55, 15–28. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. Int. Conf. Knowl. Discov. Data Min. 2016, 785–794. [Google Scholar] [CrossRef]
- Lamia, B.; Chemla, D.; Richard, C.; Teboul, J.-L. Clinical review: Interpretation of arterial pressure wave in shock states. Critical Care. 2005, 9, 601–606. [Google Scholar] [CrossRef][Green Version]
- Oh, G.C.; Cho, H.-J. Blood pressure and heart failure. Clin. Hyper. 2020, 26, 1. [Google Scholar] [CrossRef]
- Curcio, F.; Testa, G.; Liguori, I.; Papillo, M.; Flocco, V.; Panicara, V.; Galizia, G.; Della-Morte, D.; Gargiulo, G.; Cacciatore, F.; et al. Sarcopenia and heart failure. Nutrients 2020, 12, 211. [Google Scholar] [CrossRef]
- Duscha, B.D.; Kraus, W.E.; Keteyian, S.J. Capillary density of skeletal muscle: A contributing mechanism for exercise intolerance in class II–III chronic heart failure independent of other peripheral alterations. J. Am. Coll. Cardiol. 1999, 33, 1956–1963. [Google Scholar] [CrossRef]
- Greenberg, J.A.; Boozer, C.N. Metabolic mass, metabolic rate, caloric restriction, and aging in male Fischer 344 rats. Mech. Ageing Dev. 2000, 113, 37–48. [Google Scholar] [CrossRef]
- Savarese, G.; Stolfo, D.; Sinagra, G.; Lund, L.H. Heart failure with mid-range or mildly reduced ejection fraction. Nat. Rev. Cardiol. 2022, 19, 100–116. [Google Scholar] [CrossRef]
- Ponikowski, P.; Voors, A.A.; Anker, S.D.; Bueno, H.; Cleland, J.G.F.; Coats, A.J.S.; Falk, V.; González-Juanatey, J.R.; Harjola, V.-P.; Jankowska, E.A.; et al. 2016 ESC guidelines for the diagnosis and treatment of acute and chronic heart failure: The task force for the diagnosis and treatment of acute and chronic heart failure of the European Society of Cardiology (ESC) developed with the special contribution of the Heart Failure Association of the ESC. Eur. Heart J. 2016, 37, 2129–2200. [Google Scholar]










| Ratio | Parameter | Ratio | Parameter |
|---|---|---|---|
| Time to Time | LVET/HD | Area to Area | A1/A |
| ER/HD | A2/A | ||
| Time to Area | LVET/A1 | Area to Time | A1/LVET |
| ER/A2 | A2/ER | ||
| HD/A | A/HD |
| Number | Parameter | ERMS (%) |
|---|---|---|
| 9 | SBP, CI, CO, C, A1/A, DBP, ER/HD, MAP, BSA | 5.80 |
| LVET, Pt, SBP, SV, C, HR, ER/HD, MAP, BSA | 6.53 | |
| SBP, SV, CI, CO, C, HR, ER/HD, MAP, BSA | 6.59 | |
| 8 | Pt, SBP, A2/A, HR, HD, ER/HD, MAP, BSA | 6.34 |
| Pt, SBP, SV, C, HR, ER/HD, MAP, BSA | 6.42 | |
| SBP, SV, C, HR, DBP, ER/HD, MAP, BSA | 6.45 | |
| 7 | SBP, SV, C, DBP, ER/HD, MAP, BSA | 6.43 |
| SBP, SV, CI, C, ER/HD, MAP, BSA | 6.54 | |
| Pt, SBP, SV, HR, ER/HD, MAP, BSA | 6.70 | |
| 6 | SBP, CI, C, R/HD, MAP, BSA | 6.42 |
| SBP, C, DBP, ER/HD, MAP, BSA | 6.48 | |
| SBP, C, HR, ER/HD, MAP, BSA | 6.51 | |
| 5 | SBP, SV, HR, HD, MAP | 6.51 |
| Pt, SBP, SV, HR, MAP | 6.51 | |
| SBP, C, ER/HD, MAP, BSA | 6.54 |
| Parameters | Range | Step | Final Value |
|---|---|---|---|
| Learning rate | (0.01, 0.2) | 0.01 | 0.07 |
| Maximum depth | (2, 5) | 1 | 3 |
| Minimum child weight | (1, 10) | 1 | 5 |
| gamma | (0.0, 1.0) | 0.1 | 0.2 |
| subsample | (0.0, 1.0) | 0.1 | 1 |
| subsample ratio | (0.0, 1.0] | 0.1 | 1 |
| reg_alpha | (0.0, 1.0) | 0.1 | 0 |
| reg_lambda | (0.0, 1.0) | 0.1 | 0 |
| Patient | Gender | Age (Years) | BH (cm) | BW (kg) | SBP (mmHg) | DBP (mmHg) |
|---|---|---|---|---|---|---|
| 1 | M | 39 | 174 | 72 | 79 | 38 |
| 2 | M | 77 | 164 | 54 | 109 | 61 |
| 3 | M | 62 | 166 | 66 | 116 | 67 |
| 4 | M | 68 | 165 | 98 | 109 | 82 |
| 5 | M | 64 | 160 | 77 | 106 | 83 |
| 6 | M | 78 | 168 | 67 | 135 | 76 |
| 7 | M | 79 | 168 | 59 | 99 | 61 |
| 8 | M | 48 | 175 | 73 | 99 | 67 |
| 9 | F | 84 | 156 | 53 | 121 | 63 |
| 10 | M | 67 | 166 | 61 | 93 | 64 |
| 11 | M | 79 | 167 | 59 | 133 | 72 |
| 12 | M | 82 | 158 | 56 | 115 | 73 |
| 13 | M | 80 | 162 | 59 | 127 | 64 |
| 14 | F | 54 | 155 | 41 | 116 | 73 |
| 15 | M | 79 | 159 | 63 | 115 | 72 |
| 16 | M | 69 | 168 | 66 | 107 | 69 |
| 17 | M | 67 | 161 | 63 | 107 | 70 |
| 18 | M | 66 | 154 | 54 | 103 | 62 |
| 19 | F | 49 | 162 | 51 | 111 | 79 |
| 20 | F | 44 | 160 | 57 | 117 | 82 |
| Patient | Interval I (N) | Interval II (N) | Interval III (N) | SoNFIN | XGBoost |
|---|---|---|---|---|---|
| ERMS (%) | |||||
| 1 | 2 | 1 | 6.60 | 2.05 | |
| 2 | 0 | 3 | 1 | 4.12 | 6.09 |
| 3 | 3 | 3 | 5.07 | 6.06 | |
| 4 | 7 | 1 | 2 | 4.24 | 3.93 |
| 5 | 1 | 0 | 2 | 3.15 | 2.5 |
| 6 | 3 | 1 | 2 | 6.63 | 6.88 |
| 7 | 1 | 1 | 2 | 9.21 | 10.58 |
| 8 | 3 | 0 | 2 | 8.36 | 6.71 |
| 9 | 1 | 3 | 10.10 | 7.07 | |
| 10 | 6 | 1 | 2 | 9.44 | 11.13 |
| 11 | 0 | 2 | 5 | 4.81 | 4.65 |
| 12 | 3 | 2 | 7.40 | 7.57 | |
| 13 | 3 | 1 | 2 | 8.85 | 8.2 |
| 14 | 5 | 2 | 2 | 7.04 | 6.95 |
| 15 | 3 | 1 | 2 | 9.38 | 8.94 |
| 16 | 2 | 0 | 2 | 10.08 | 6.33 |
| 17 | 4 | 1 | 2 | 6.41 | 7.13 |
| 18 | 2 | 5 | 2 | 8.88 | 9.67 |
| 19 | 4 | 3 | 3.74 | 4.9 | |
| 20 | 2 | 2 | 4.56 | 5.37 | |
| Sum mean ± sd | 55 | 33 | 30 | 6.9 ± 2.3 | 6.4 ± 2.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.-H.; Yang, Z.-K.; Pan, K.-L.; Zhu, X.; Chen, W. Estimation of Left Ventricular Ejection Fraction Using Cardiovascular Hemodynamic Parameters and Pulse Morphological Characteristics with Machine Learning Algorithms. Nutrients 2022, 14, 4051. https://doi.org/10.3390/nu14194051
Liu S-H, Yang Z-K, Pan K-L, Zhu X, Chen W. Estimation of Left Ventricular Ejection Fraction Using Cardiovascular Hemodynamic Parameters and Pulse Morphological Characteristics with Machine Learning Algorithms. Nutrients. 2022; 14(19):4051. https://doi.org/10.3390/nu14194051
Chicago/Turabian StyleLiu, Shing-Hong, Zhi-Kai Yang, Kuo-Li Pan, Xin Zhu, and Wenxi Chen. 2022. "Estimation of Left Ventricular Ejection Fraction Using Cardiovascular Hemodynamic Parameters and Pulse Morphological Characteristics with Machine Learning Algorithms" Nutrients 14, no. 19: 4051. https://doi.org/10.3390/nu14194051
APA StyleLiu, S.-H., Yang, Z.-K., Pan, K.-L., Zhu, X., & Chen, W. (2022). Estimation of Left Ventricular Ejection Fraction Using Cardiovascular Hemodynamic Parameters and Pulse Morphological Characteristics with Machine Learning Algorithms. Nutrients, 14(19), 4051. https://doi.org/10.3390/nu14194051








