Illustration of the Importance of Adjustment for within- and between-Person Variability in Dietary Intake Surveys for Assessment of Population Risk of Micronutrient Deficiency/Excess Using an Example Data Set
Abstract
1. Introduction
2. Materials and Methods
2.1. The Data Set
2.2. Dietary Intake Methodology
2.3. Application of the NCI Method in Estimation of Usual Intake of the Sample
2.3.1. Step 1: Input Day-1, Day-2 and Day-3 24-h Recall Intakes
2.3.2. Step 2: Calculate Balanced Repeated Replication Weights
2.3.3. Step 3: Fit the Model and Box-Cox Transform to Near Normality
2.3.4. Step 4: Simulate Usual Intakes Based on the Fitted Model
2.3.5. Step 5: Back-Transform to Original Scale
2.3.6. Step 6: Derive Percentiles and Proportions above/below Cut-Points
2.4. Statistics
3. Results
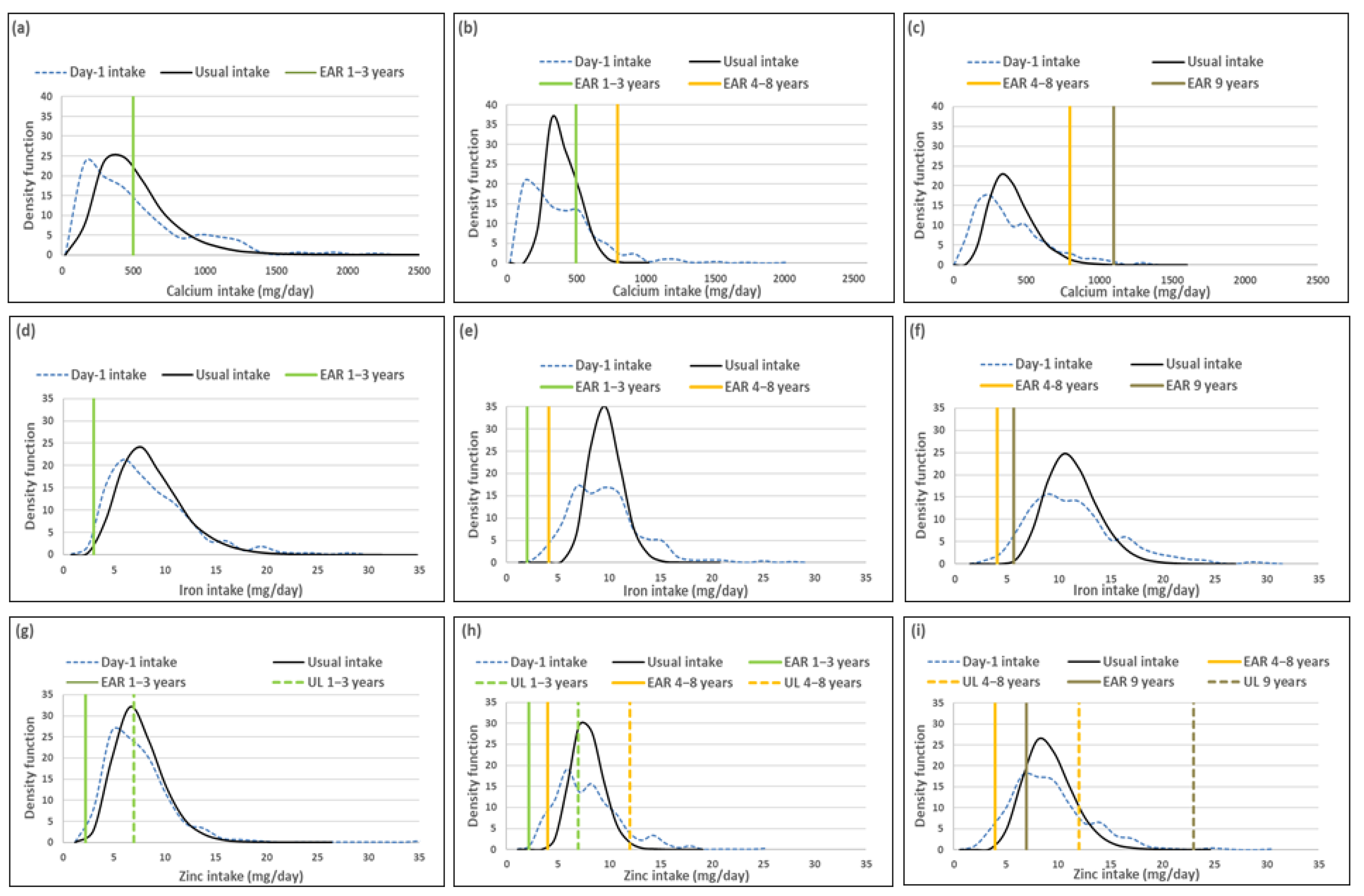
3.1. Minerals
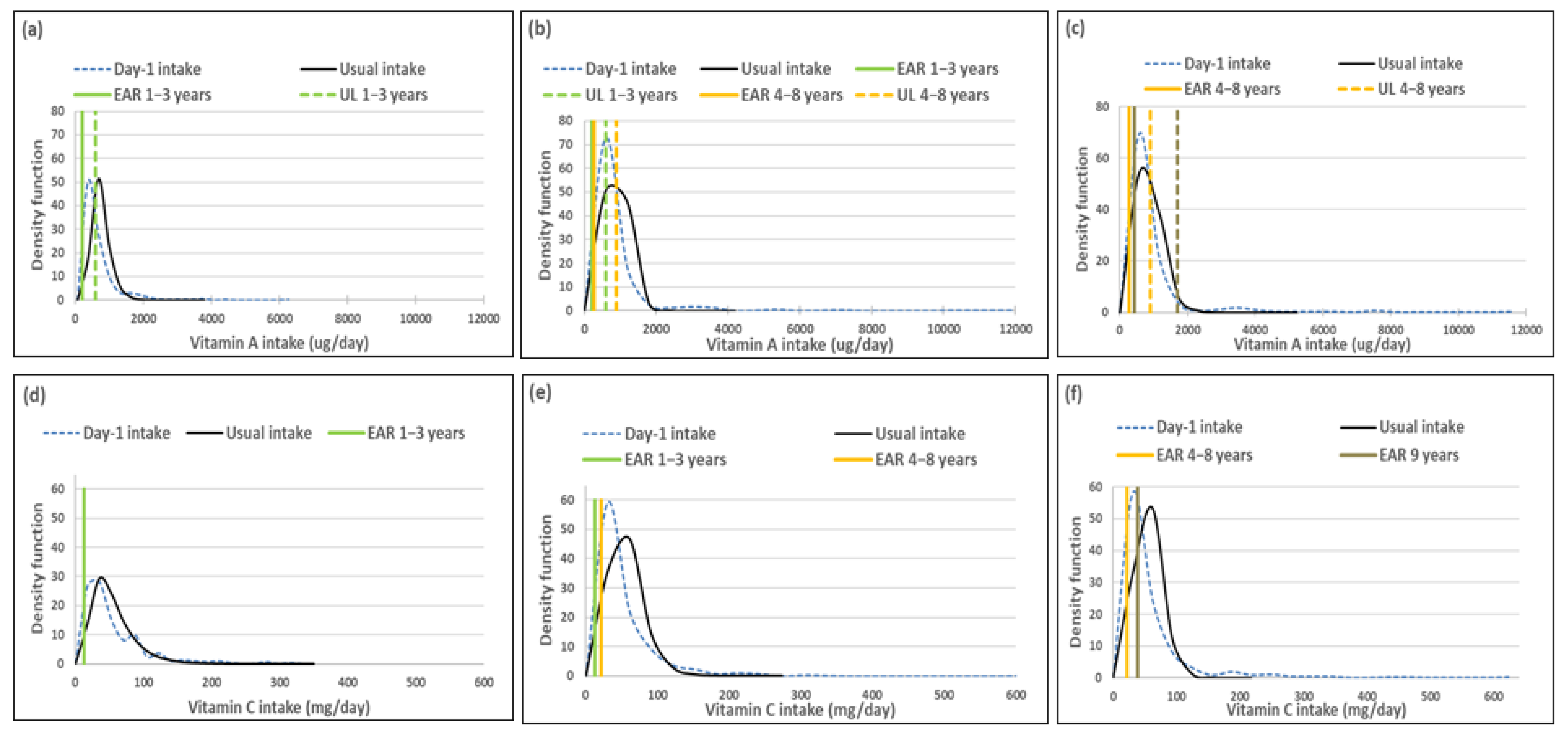
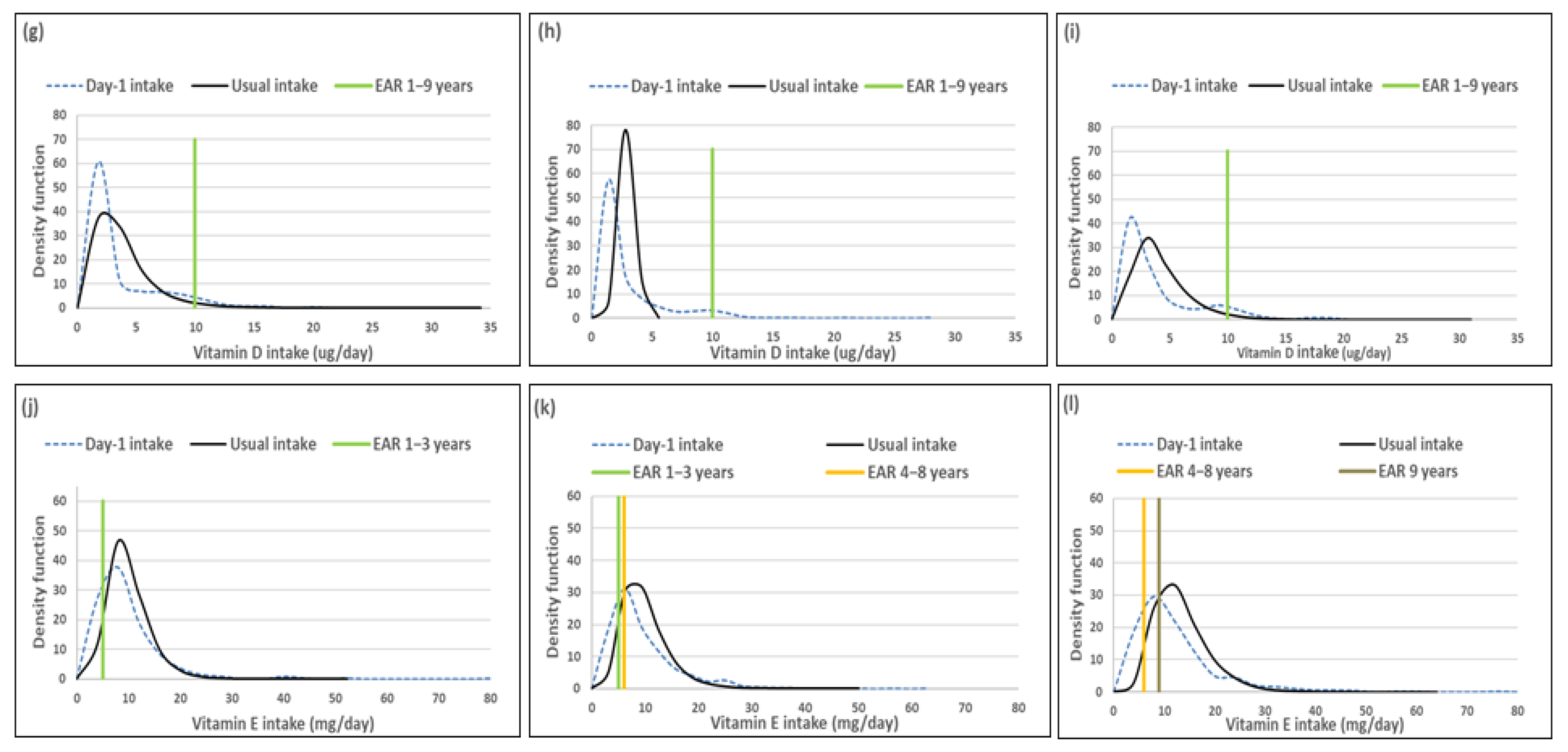
3.2. Vitamins (Excluding B Vitamins)
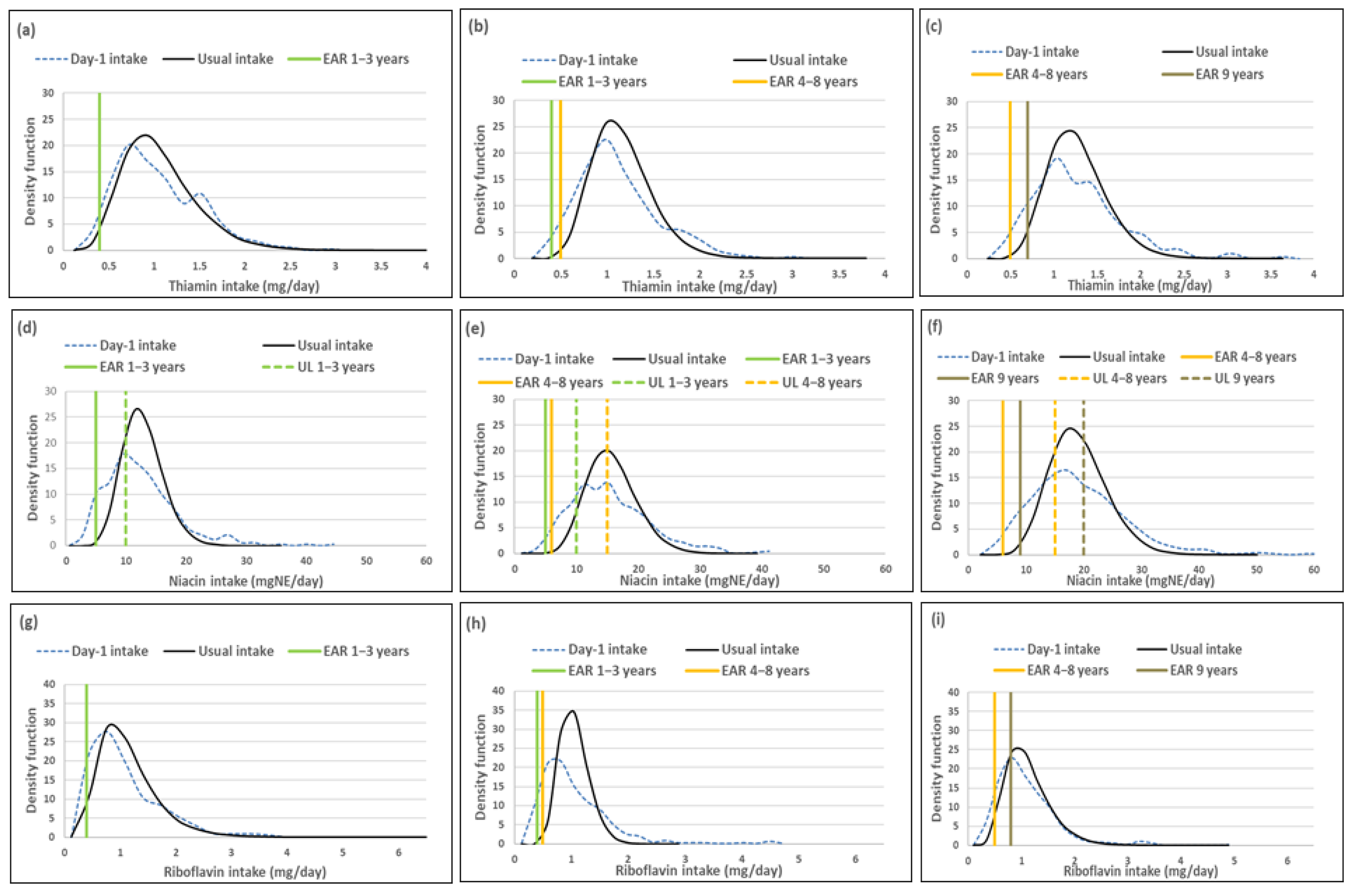
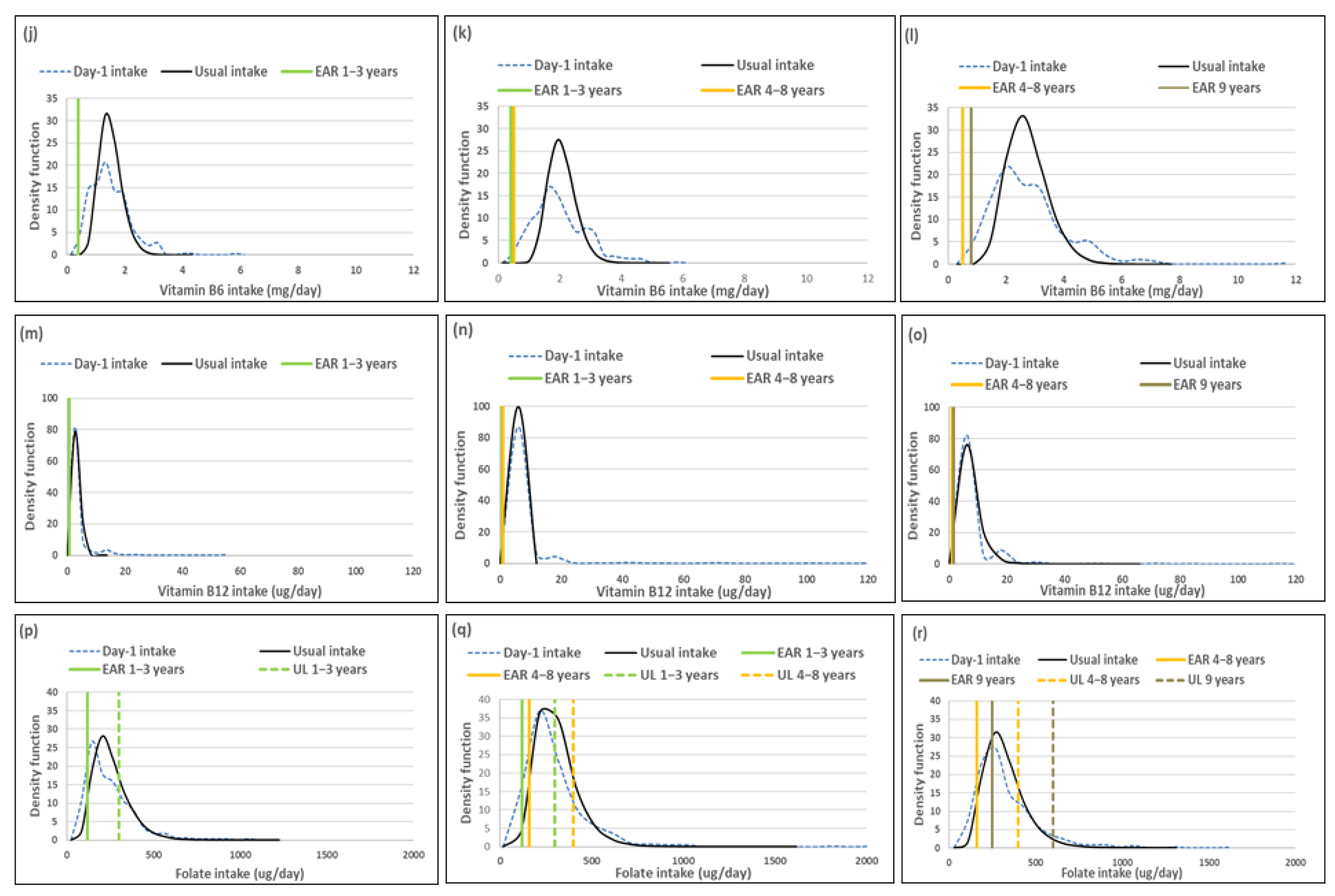
3.3. B-Vitamins
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Labadarios, D.; Steyn, N.P.; Maunder, E.; MacIntryre, U.; Gericke, G.; Swart, R.; Huskisson, J.; Dannhauser, A.; Vorster, H.H.; Nesmvuni, A.E.; et al. The National Food Consumption Survey (NFCS): South Africa, 1999. Public Health Nutr. 2005, 8, 533–543. [Google Scholar] [CrossRef] [PubMed]
- Senekal, M.; Nel, J.; Malczyk, S.; Drummond, L.; Steyn, N.P. Provincial Dietary Intake Study (PDIS): Micronutrient Intakes of Children in a Representative/Random Sample of 1- to <10-Year-Old Children in Two Economically Active and Urbanized Provinces in South Africa. Int. J. Environ. Res. Public Health 2020, 17, 5924. [Google Scholar] [CrossRef] [PubMed]
- Baye, K. Maximising benefits and minimising adverse effects of micronutrient interventions in low- and middle-income countries. Proc. Nutr. Soc. 2019, 78, 540–546. [Google Scholar] [CrossRef] [PubMed]
- Bhutta, Z.A.; Das, J.K.; Rizvi, A.; Gaffey, M.F.; Walker, N.; Horton, S.; Webb, P.; Lartey, A.; Black, R.E.; The Lancet Nutrition Interventions Review Group; et al. Evidence-based interventions for improvement of maternal and child nutrition: What can be done and at what cost? Lancet 2013, 382, 452–477. [Google Scholar] [CrossRef]
- Allen, L.; World Health Organization; Food and Agriculture Organization of the United Nations. Guidelines on Food Fortification with Micronutrients [Internet]; World Health Organization: Geneva, Switzerland; Food and Agriculture Organization of the United Nations: Rome, Italy, 2006; Available online: http://catalog.hathitrust.org/api/volumes/oclc/152582146.html (accessed on 26 November 2021).
- National Cancer Institute; Division of Cancer Control & Population Sciences. Usual Dietary Intakes. 2020. Available online: https://epi.grants.cancer.gov/diet/usualintakes/#overvi (accessed on 8 October 2021).
- Willet, W. Chapter 3. Nature of Variation in Diet. In Nutritional Epidemiology, 3rd ed.; Willet, W., Ed.; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Costa, M.d.M.; Takeyama, L.; Voci, S.M.; Slater, B.; Silva, M.V. Within- and between-person variations as determinant factors to calculate the number of observations to estimate usual dietary intake of adolescents. Rev. Bras. Epidemiol. 2008, 11, 541–548. [Google Scholar] [CrossRef]
- Piernas, C.; Wang, D.; Du, S.; Zhang, B.; Wang, Z.; Su, C.; Popkin, B.M. The double burden of under- and overnutrition and nutrient adequacy among Chinese preschool and school-aged children in 2009–2011. Eur. J. Clin. Nutr. 2015, 69, 1323–1329. [Google Scholar] [CrossRef]
- Dodd, K.W.; Guenther, P.M.; Freedman, L.S.; Subar, A.F.; Kipnis, V.; Midthune, D.; Tooze, J.A.; Krebs-Smith, S.M. Statistical methods for estimating usual intake of nutrients and foods: A review of the theory. J. Am. Diet. Assoc. 2006, 106, 1640–1650. [Google Scholar] [CrossRef]
- Tooze, J.A.; Kipnis, V.; Buckman, D.W.; Carroll, R.J.; Freedman, L.S.; Guenther, P.M.; Krebs-Smith, S.M.; Subar, A.F.; Dodd, K.W. A mixed-effects model approach for estimating the distribution of usual intake of nutrients: The NCI method. Stat Med. 2010, 29, 2857–2868. [Google Scholar] [CrossRef]
- Basiotis, P.P.; Welsh, S.O.; Cronin, F.J.; Kelsay, J.L.; Mertz, W. Number of days of food intake records required to estimate individual and group nutrient intakes with defined confidence. J. Nutr. 1987, 117, 1638–1641. [Google Scholar] [CrossRef]
- Laureano, G.H.C.; Torman, V.B.L.; Crispim, S.P.; Dekkers, A.L.M.; Camey, S.A. Comparison of the ISU, NCI, MSM, and SPADE Methods for Estimating Usual Intake: A Simulation Study of Nutrients Consumed Daily. Nutrients 2016, 8, 166. [Google Scholar] [CrossRef]
- Gibson, R.S. Principles of Nutritional Assessment; Oxford University Press: Oxford, UK, 2005; 930p. [Google Scholar]
- Baranowski, T. Chapter 4. 24 Hour Recall and Diet Methods. In Nutritional Epidemiology, 3rd ed.; Willet, W., Ed.; Oxford University Press: Oxford, UK, 2012; 547p. [Google Scholar]
- Herrick, K.A.; Rossen, L.M.; Parsons, R.; Dodd, K.W. Estimating Usual Dietary Intake from National Health and Nutrition Examination Survey Data Using the National Cancer Institute Method. Vital Health Stat. 2018, 2, 1–63. [Google Scholar]
- Knüppel, S.; Norman, K.; Boeing, H. Is a Single 24-hour Dietary Recall per Person Sufficient to Estimate the Population Distribution of Usual Dietary Intake? J. Nutr. 2019, 149, 1491–1492. [Google Scholar] [CrossRef] [PubMed]
- Nleya, N.; Thompson, L. Survey Methodology in Violence-prone Khayelitsha, Cape Town, South Africa. IDS Bull. 2009, 40, 50–57. [Google Scholar] [CrossRef][Green Version]
- Barbosa, F.d.S.; Sichieri, R.; Junger, W.L. Assessing usual dietary intake in complex sample design surveys: The National Dietary Survey. Rev. Saude Publica 2013, 47 (Suppl. 1), 171S–176S. [Google Scholar] [CrossRef] [PubMed]
- Nusser, S.M.; Carriquiry, A.L.; Dodd, K.W.; Fuller, W.A. A Semiparametric Transformation Approach to Estimating Usual Daily Intake Distributions. J. Am. Stat. Assoc. 1996, 91, 1440–1449. [Google Scholar] [CrossRef]
- Haubrock, J.; Nöthlings, U.; Volatier, J.-L.; Dekkers, A.; Ocké, M.; Harttig, U.; Illner, A.K.; Knüppel, S.; Andersen, L.F.; Boeing, H.; et al. Estimating usual food intake distributions by using the multiple source method in the EPIC-Potsdam Calibration Study. J. Nutr. 2011, 141, 914–920. [Google Scholar] [CrossRef]
- Dekkers, A.L.M.; Verkaik-Kloosterman, J.; van Rossum, C.T.M.; Ocké, M.C. SPADE, a new statistical program to estimate habitual dietary intake from multiple food sources and dietary supplements. J. Nutr. 2014, 144, 2083–2091. [Google Scholar] [CrossRef]
- Souverein, O.W.; Dekkers, A.L.; Geelen, A.; Haubrock, J.; de Vries, J.H.; Ocké, M.C.; Harttig, U.; Boeing, H.; Van’T Veer, P. Comparing four methods to estimate usual intake distributions. Eur. J. Clin. Nutr. 2011, 65 (Suppl. 1), S92–S101. [Google Scholar] [CrossRef]
- Pereira, J.L.; de Castro, M.A.; Crispim, S.P.; Fisberg, R.M.; Isasi, C.R.; Mossavar-Rahmani, Y.; Van Horn, L.; Carnethon, M.R.; Daviglus, M.L.; Perreira, K.M.; et al. Comparing Methods from the National Cancer Institute vs Multiple Source Method for Estimating Usual Intake of Nutrients in the Hispanic Community Health Study/Study of Latino Youth. J. Acad. Nutr. Diet. 2021, 121, 59–73.e16. [Google Scholar] [CrossRef]
- Steyn, N.P.; Nel, J.H.; Malczyk, S.; Drummond, L.; Senekal, M. Provincial Dietary Intake Study (PDIS): Energy and macronutrient intakes of children in a representative/random sample of 1–<10-year-old children in two economically active and urbanized provinces in South Africa. Int. J. Environ. Res. Public Health 2020, 17, 1717. [Google Scholar]
- StatsSA. Statistics South Africa, Mid-Year Population Estimates 2020; StatsSA: Pretoria, South Africa, 2021. [Google Scholar]
- ICF International. Demographic and Health Survey Sampling and Household Listing Manual: Measure DHS; Inner City Fund (ICF) International: Calverton, MD, USA, 2012. [Google Scholar]
- Moshfegh, A.J.; Rhodes, D.G.; Baer, D.J.; Murayi, T.; Clemens, J.C.; Rumpler, W.V.; Paul, D.R.; Sebastian, R.S.; Kuczynski, K.J.; Ingwersen, L.A.; et al. The US Department of Agriculture Automated Multiple-Pass Method reduces bias in the collection of energy intakes. Am. J. Clin. Nutr. 2008, 88, 324–332. [Google Scholar] [CrossRef] [PubMed]
- Subar, A.F.; Kipnis, V.; Troiano, R.P.; Midthune, R.D.; Schoeller, D.A.; Bingham, S.; Sharbaugh, C.O.; Trabulsi, J.; Runswick, S.; Ballard-Barbash, R.; et al. Using intake biomarkers to evaluate the extent of dietary misreporting in a large sample of adults: The OPEN Study. Am. J. Epidemiol. 2003, 158, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Van Graan, A.E.; Chetty, J.M.; Links, M.R. Food Composition Tables for South Africa, 5th ed.; South African Medical Research Council: Cape Town, South Africa, 2017. [Google Scholar]
- Davis, K.A.; Gonzalez, A.; Loukine, L.; Qiao, C.; Sadeghpour, A.; Vigneault, M.; Wang, K.C.; Ibañez, D. Early Experience Analyzing Dietary Intake Data from the Canadian Community Health Survey-Nutrition Using the National Cancer Institute (NCI) Method. Nutrients 2019, 11, 1908. [Google Scholar] [CrossRef] [PubMed]
- Australian Bureau of Statistics. Chapter—Data Quality [Internet]. c=AU; o=Commonwealth of Australia; ou=Australian Bureau of Statistics. 2015. Available online: https://www.abs.gov.au/AUSSTATS/abs@.nsf/Lookup/4363.0.55.001Chapter651042011-13 (accessed on 29 November 2021).
- Luo, H.; Dodd, K.W.; Arnold, C.D.; Engle-Stone, R. A new statistical method for estimating usual intakes of nearly-daily consumed foods and nutrients through use of only one 24-hour dietary recall. J. Nutr. 2019, 149, 1667–1673. [Google Scholar] [CrossRef] [PubMed]
- Korn, E.L.; Graubard, B.I. Analysis of Health Surveys; John Wiley & Sons: Hoboken, NJ, USA, 2011; 408p. [Google Scholar]
- Judkins, D. Fay’s method for variance estimation. J. Off. Stat. 1990, 6, 223–239. [Google Scholar]
- Box, G.E.P.; Cox, D.R. An analysis of transformations. J. R. Stat. Soc. Ser. B 1964, 26, 211–243. [Google Scholar] [CrossRef]
- Institute of Medicine. Dietary Reference Intakes: The Essential Guide to Nutrient Requirements. 2021. Available online: https://www.nap.edu/read/11537/chapter/1#iii (accessed on 30 November 2021).
- US Department of Health and Human Services. Software for Measurement Error in Nutrition Research. 2021. Available online: https://prevention.cancer.gov/research-groups/biometry/measurement-error-impact/software-measurement-error (accessed on 30 November 2021).
| Age 1–<3 Years n = 333 | Age 3–<6 Years n = 514 | Age 6–<10 Years n = 479 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Nutrient | Usual Intake | Day-1 Intake | % Diff | Usual Intake | Day-1 Intake | % Diff | Usual Intake | Day-1 Intake | % Diff | |
| Calcium (mg/day) | Mean (SE) | 423.3 (45.3) | 424.5 (19.1) | −0.3 | 350.9 (6.4) | 348.5 (19.2) | 0.7 | 351.8 (13.6) | 352.2 (13.5) | −0.1 |
| Median (SE) | 378.0 (39.2) | 339.0 (19.9) | 11.5 *** | 329.2 (4.4) | 288.3 (22.9) | 14.2 *** | 331.3 (15.0) | 299.9 (15.0) | 10.5 *** | |
| Iron (mg/day) | Mean (SE) | 7.8 (0.5) | 7.7 (0.3) | 1.3 | 8.9 (0.1) | 8.9 (0.3) | 0.0 | 10.6 (0.1) | 10.6 (0.2) | 0.0 |
| Median (SE) | 7.3 (0.4) | 7.2 (0.3) | 1.4 ** | 8.8 (0.1) | 8.6 (0.3) | 2.3 ** | 10.3 (0.1) | 9.7 (0.2) | 6.2 ** | |
| Zinc (mg/day) | Mean (SE) | 6.5 (0.4) | 6.4 (0.2) | 1.6 | 7.3 (0.1) | 7.3 (0.2) | 0.0 | 8.5 (0.2) | 8.5 (0.2) | 0.0 |
| Median (SE) | 6.2 (0.4) | 6.0 (0.2) | 3.3 * | 7.1 (0.1) | 6.8 (0.3) | 4.4 ** | 8.3 (0.1) | 7.9 (0.2) | 5.1 * | |
| Nutrient (Box-Cox TP) | Age: 1–<3 Years | Age: 3–<6 Years | Age: 6–<10 Years | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Var_e | Var_u | Ratio | CV (%) | Var_e | Var_u | Ratio | CV (%) | Var_e | Var_u | Ratio | CV (%) | |
| Calcium (λ = 0.24) | 7.12 | 4.48 | 1.58 | 10.7 | 7.30 | 1.13 | 6.46 | 1.8 | 4.67 | 2.51 | 1.86 | 3.9 |
| Iron (λ = 0.18) | 0.24 | 0.24 | 1.00 | 7.1 | 0.28 | 0.08 | 3.50 | 1.4 | 0.22 | 0.13 | 1.69 | 1.1 |
| Zinc (λ = 0.20) | 0.28 | 0.19 | 1.47 | 6.9 | 0.31 | 0.11 | 2.82 | 2.0 | 0.29 | 0.13 | 2.23 | 1.8 |
| Day-1 Intake | Usual Intake | Difference 1 for % < EAR and (% > UL) | ||||
|---|---|---|---|---|---|---|
| Age Group | % < EAR (95% CI) | % > UL (95% CI) | % < EAR (95% CI) | % > UL (95% CI) | ||
| Calcium (mg/day) EAR-UL: 1–3 years = 500–2500 mg; 4–8 years = 800–2500 mg; 9–<10 years = 1100–3000 mg | 1–<3 years (n = 333) | 66.2 (59.9–72.6) | 0.0 (-) | 70.2 (51.1–89.3) | 0.0 (-) | 4.0% (0.0%) |
| 3–<6 years (n = 514) | 87.3 (83.3–91.2) | 0.0 (-) | 94.8 (91.5–98.2) | 0.0 (-) | 7.5% (0.0%) | |
| 6–<10 years (n = 479) | 95.9 (93.5–98.2) | 0.0 (-) | 99.4 (98.3–100.0) | 0.0 (-) | 3.5% (0.0%) | |
| Iron (mg/day) EAR-UL: 1–3 years = 3–40 mg; 4–8 years = 4.1–40 mg; Male:9–<10 years = 5.9–40 mg; Female:9–<10 years = 5.7–40 mg | 1–<3 years (n = 333) | 3.4 (1.0–5.7) | 0.0 (-) | 1.0 (0.0–3.2) | 0.0 (-) | −2.4% (0.0%) |
| 3–<6 years (n = 514) | 2.7 (1.0–4.3) | 0.0 (-) | 0.01 (0.0–0.1) | 0.0 (-) | −2.7% (0.0%) | |
| 6–<10 years (n = 479) | 2.5 (0.9–4.2) | 0.0 (-) | 0.3 (0.0–0.8) | 0.0 (-) | −2.2% (0.0%) | |
| Zinc (mg/day) EAR-UL: 1–3 years = 2.2–7 mg; 4–8 years = 4–12 mg; 9–10 years = 7–23 mg | 1–<3 years (n = 333) | 1.6 (0.0–3.4) | 35.0 (28.8–41.2) | 0.1 (0.0–0.5) | 35.3 (13.5–57.1) | −1.5% (0.3%) |
| 3–<6 years (n = 514) | 8.9 (6.2–11.7) | 21.6 (16.9–26.3) | 0.5 (0.0–1.6) | 20.9 (17.2–24.6) | −8.4% (−0.7%) | |
| 6–<10 years (n = 479) | 12.4 (8.8–15.9) | 13.2 (9.7–16.8) | 4.9 (2.7–7.0) | 4.7 (0.0–9.5) | −7.5% (−8.5%) | |
| Mineral | Age Group (Years) | Foods Contributing to Nutrient Intake (% Eaters, % Contribution to Total Nutrient Intake) |
|---|---|---|
| Calcium | Age 1–<3 | Whole milk (44%, 24%), BMS (14%, 17%), Maize porridge (79%, 12%), Maas/sour milk (17%, 10%), Yoghurt (18%, 6%) |
| Age 3–<6 | Whole milk (49%, 24%), Maize porridge (74%, 15%), Maas/sour milk (11%, 8%), Yoghurt (14%, 7%), Pilchards/sardines (8%, 6%) | |
| Age 6–<10 | Whole milk (48%, 22%), Pilchards/sardines (13%, 11%), Maize porridge (72%, 10%), Cheese (11%, 6%), Dairy fruit mix (11%, 5%) | |
| Iron * | Age 1–<3 | Maize porridge (79%, 30%), BMS (14%, 10%), High fiber cereals (20%, 7%), White bread (25%, 5%), Brown bread (22%, 4%) |
| Age 3–<6 | Maize porridge (74%, 26%), White bread (38%, 10%), Brown bread (32%, 8%), High fiber cereals (22%, 7%), Organ meat (9%, 4%) | |
| Age 6–<10 | Maize porridge (72%, 21%), White bread (50%, 15%), Brown bread (32%, 10%), Low fiber cereals (14%, 5%), High fiber cereals (13%, 4%) | |
| Zinc * | Age 1–<3 | Maize porridge (79%, 32%), BMS (14%, 10%), Chicken (41%, 6%), Beef (11%, 6%), Whole milk (44%, 5%) |
| Age 3–<6 | Maize porridge (74%, 29%), Brown bread (32%, 11%), Beef (13%, 8%), Chicken (49%, 7%), White bread (38%, 7%) | |
| Age 6–<10 | Maize porridge (72%, 24%), Brown bread (32%, 13%), White bread (50%, 11%), Beef (16%, 9%), Chicken (45%, 6%) |
| Age 1–<3 Years n = 333 | Age 3–<6 Years n = 514 | Age 6–<10 Years n = 479 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Nutrient | Usual Intake | Day-1 Intake | % Diff | Usual intake | Day-1 intake | % Diff | Usual Intake | Day-1 Intake | % Diff | |
| Vitamin A (ug/day) | Mean (SE) | 574.2 (67.5) | 592.8 (41.5) | −3.1 | 607.0 (23.6) | 639.2 (50.2) | −5.0 | 623.8 (61.7) | 694.3 (58.8) | −10.2 |
| Median (SE) | 529.5 (54.3) | 367.6 (22.2) | 44.0 *** | 580.5 (47.8) | 400.7 (19.9) | 44.9 *** | 550.3 (31.7) | 433.2 (23.7) | 27.0 *** | |
| Vitamin C (mg/day) | Mean (SE) | 47.6 (2.9) | 46.6 (3.4) | 2.2 | 39.4 (1.5) | 40.8 (3.4) | −3.4 | 42.4 (2.9) | 43.6 (3.8) | −2.8 |
| Median (SE) | 40.2 (2.6) | 32.7 (4.0) | 22.9 *** | 36.6 (1.4) | 23.6 (2.0) | 55.1 *** | 37.2 (2.0) | 27.3 (1.7) | 36.3 *** | |
| Vitamin D (ug/day) | Mean (SE) | 2.8 (0.3) | 2.9 (0.3) | −3.4 | 2.4 (0.1) | 2.4 (0.2) | 0.0 | 3.3 (0.1) | 3.2 (0.2) | 3.1 |
| Median (SE) | 2.2 (0.3) | 1.1 (0.1) | 100.0 *** | 2.3 (0.1) | 1.2 (0.1) | 91.7 *** | 2.9 (0.2) | 2.0 (0.2) | 45.0 *** | |
| Vitamin E (mg/day) | Mean (SE) | 8.1 (0.3) | 7.9 (0.5) | 2.5 | 8.2 (0.2) | 8.2 (0.4) | 0.0 | 11.1 (0.4) | 11.0 (0.5) | 0.9 |
| Median (SE) | 7.3 (0.3) | 6.2 (0.3) | 17.7 *** | 7.5 (0.4) | 6.0 (0.3) | 25.0 *** | 10.1 (0.5) | 8.2 (0.4) | 23.2 *** | |
| Nutrient (Box-Cox TP) | Age: 1–<3 Years | Age: 3–<6 Years | Age: 6–<10 Years | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Var_e | Var_u | Ratio | CV(%) | Var_e | Var_u | Ratio | CV(%) | Var_e | Var_u | Ratio | CV(%) | |
| Vitamin A (λ = 0.00) | 0.48 | 0.15 | 3.20 | 11.8 | 0.67 | 0.07 | 9.57 | 3.9 | 0.45 | 0.24 | 1.88 | 9.9 |
| Vitamin C (λ = 0.29) | 5.93 | 4.31 | 1.38 | 6.0 | 7.3 | 0.98 | 7.45 | 3.8 | 5.59 | 2.68 | 2.09 | 6.7 |
| Vitamin D (λ = 0.26) | 1.82 | 1.11 | 1.64 | 11.5 | 2.71 | 0.01 | 271.00 | 5.1 | 2.14 | 0.67 | 3.19 | 4.2 |
| Vitamin E (λ = 0.14) | 0.93 | 0.32 | 2.91 | 3.5 | 0.78 | 0.36 | 2.17 | 2.9 | 0.77 | 0.44 | 1.75 | 3.4 |
| Day-1 Intake | Usual Intake | Difference 1 for % < EAR & (% < UL) | ||||
|---|---|---|---|---|---|---|
| % < EAR | % > UL | % < EAR | % > UL | |||
| Vitamin A (ug/day) EAR-UL: 1–3 years = 210–600 ug; 4–8 years = 275–900 ug; Male: 9–<10 years = 445–1700 ug; Female: 9–<10 years = 420–1700 ug | 1–<3 years (n = 333) | 16.1 (11.5–20.7) | 27.8 (22.3–33.3) | 1.2 (0.0–4.1) | 37.5 (10.3–64.7) | 14.9% (9.7%) |
| 3–<6 years (n = 514) | 24.5 (19.7–29.4) | 18.7 (13.6–23.9) | 0.4 (0.0–4.2) | 21.5 (16.1–27.0) | 24.1% (2.8%) | |
| 6–<10 years (n = 479) | 29.3 (24.9–33.8) | 12.1 (8.4–15.8) | 12.0 (6.9–17.0) | 13.7 (0.0–27.4) | 17.3% (1.6%) | |
| Vitamin C (mg/day) EAR-UL: 1–3 years = 13–400 mg; 4–8 years = 22–650 mg; 9–<10 years = 39–1200 mg | 1–<3 years (n = 333) | 21.3 (14.8–27.8) | 0.0 (-) | 7.4 (3.0–11.8) | 0.0 (-) | 13.9% (0.0%) |
| 3–<6 years (n = 514) | 39.1 (33.0–45.2) | 0.0 (-) | 9.0 (0.0–20.0) | 0.0 (-) | 30.1% (0.0%) | |
| 6–<10 years (n = 479) | 40.3 (34.4–46.2) | 0.0 (-) | 25.3 (11.8–38.8) | 0.0 (-) | 15.0% (0.0%) | |
| Vitamin D (ug/day) EAR-UL: 1–3 years = 10–63 ug; 4–8 years = 10–75 ug; 9–<10 years = 10–100 ug | 1–<3 years (n = 333) | 94.3 (90.8–97.8) | 0.0 (-) | 98.2 (96.9–99.4) | 0.0 (-) | 3.9% (0.0%) |
| 3–<6 years (n = 514) | 96.5 (94.3–98.7) | 0.0 (-) | 100.0 (-) | 0.0 (-) | 3.5% (0.0%) | |
| 6–<10 years (n = 479) | 93.8 (91.0–96.5) | 0.0 (-) | 99.3 (98.3–100.0) | 0.0 (-) | 5.5% (0.0%) | |
| Vitamin E (mg/day) EAR-UL: 1–3 years = 5–90 mg; 4–8 years = 6–135 mg; 9–<10 years = 9–270 mg | 1–<3 years (n = 333) | 36.2 (29.5–43.0) | 0.0 (-) | 18.2 (7.9–28.4) | 0.0 (-) | −18.0% (0.0%) |
| 3–<6 years (n = 514) | 46.6 (41.7–51.5) | 0.0 (-) | 26.9 (10.2–43.5) | 0.0 (-) | −19.7% (0.0%) | |
| 6–<10 years (n = 479) | 35.2 (29.9–40.5) | 0.0 (-) | 18.8 (8.5–29.2) | 0.0 (-) | 16.4% (0.0%) | |
| Vitamin | Age Group (Years) | Foods Contributing to Nutrient Intake (% Eaters, % Contribution to Total Nutrient Intake) |
|---|---|---|
| Vitamin A * | Age 1–<3 | Maize porridge (79%, 27%), Vegetables-carotene (other) (9%, 14%), Organ meat (5%, 11%), BMS (14%, 10%), Whole milk (44%, 7%) |
| Age 3–<6 | Organ meat (9%, 32%), Maize porridge (74%, 22%), Vegetables-carotene (other) (10%, 12%), Whole milk (49%, 5%), PUM fat (28%, 4%) | |
| Age6–<10 | Organ meat (9%, 27%), Maize porridge (72%, 22%), Vegetables-carotene (other) (9%, 10%), White bread (50%, 7%), PUM fat (35%, 7%) | |
| Vitamin C | Age 1–<3 | Fruit fresh vitamin C rich (12%, 15%), BMS (14%, 15%), Potato/sweet potato (33%, 14%), Fruit juice (6%, 14%), Vegetables- vitamin C rich (24%, 8%) |
| Age 3–<6 | Fruit juice (7%, 18%), Potato/sweet potato (31%, 16%), Fruit fresh vitamin C (8%, 16%), Vegetables-vitamin C rich (28%, 12%), Maize porridge (74%, 9%) | |
| Age 6–<10 | Fruit juice (7%, 23%), Fruit fresh-vitamin C rich (9%, 17%), Potato/sweet potato (33%, 15%), Vegetables-vitamin C rich (31%, 13%), Maize porridge (72%, 5%) | |
| Vitamin D | Age 1–<3 | BMS (14%, 30%), eggs (14%, 25%), Pilchards/sardines (6%, 16%), PUM fat (21%, 5%), Whole milk (44%, 3%) |
| Age 3–<6 | Eggs (11%, 26%), Pilchards/sardines (8%, 25%), PUM fat (28%, 12%), Dairy fruit mix (13%, 5%), Chicken (49%, 4%) | |
| Age 6–<10 | Pilchards/sardines (13%, 32%), Eggs (12%, 23%), PUM fat (35%, 13%), Fat cakes (7%, 4%), Cereal low fiber (14%, 4%) | |
| Vitamin E | Age 1–<3 | PU fat/oil (12%, 15%), Maize porridge (79%, 11%), BMS (14%, 11%), Salty snacks (44%, 8%), PUM fat (21%, 7%) |
| Age 3–<6 | PU fat/oil (14%, 17%), PUM fat (28%, 13%), Maize porridge (74%, 11%), Salty snacks (48%, 9%), Vegetables- vitamin C (28%, 6%) | |
| Age 6–<10 | PU fat/oil (18%, 18%), PUM fat (35%, 17%), Salty snacks (54%, 9%), Maize porridge (72%, 7%), Fat cakes (7%, 7%) |
| Age 1–<3 Years n = 333 | Age 3–<6 Years n = 514 | Age 6–<10 Years n = 479 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Nutrient | Usual Intake | Day-1 Intake | % Diff | Usual Intake | Day-1 Intake | % Diff | Usual Intake | Day-1 Intake | % Diff | |
| Thiamine (mg/day) | Mean (SE) | 1.0 (0.03) | 1.0 (0.04) | 0.0 | 1.0 (0.01) | 1.0 (0.03) | 0.0 | 1.2 (0.03) | 1.2 (0.02) | 0.0 |
| Median (SE) | 0.9 (0.01) | 0.9 (0.04) | 0.0 | 1.0 (0.02) | 0.9 (0.03) | 11.1 *** | 1.1 (0.03) | 1.1 (0.04) | 0.0 * | |
| Niacin (mgNE/day) | Mean (SE) | 11.5 (0.4) | 11.5 (0.4) | 0.0 | 14.2 (0.2) | 14.2 (0.4) | 0.0 | 17.2 (0.4) | 17.3 (0.4) | −0.6 |
| Median (SE) | 11.3 (0.3) | 10.6 (0.4) | 6.6 ** | 13.8 (0.2) | 13.2 (0.4) | 4.6 ** | 16.8 (0.4) | 16.7 (0.5) | 0.6 * | |
| Riboflavin (mg/day) | Mean (SE) | 0.9 (0.1) | 0.9 (0.04) | 0.0 | 0.9 (0.02) | 0.9 (0.03) | 0.0 | 1.0 (0.03) | 1.0 (0.04) | 0.0 |
| Median (SE) | 0.8 (0.1) | 0.8 (0.04) | 0.0 ** | 0.9 (0.02) | 0.8 (0.05) | 12.5 *** | 0.9 (0.02) | 0.9 (0.04) | 0.0 *** | |
| Vitamin B6 (mg/day) | Mean (SE) | 1.4 (0.05) | 1.4 (0.05) | 0.0 | 1.8 (0.01) | 1.8 (0.04) | 0.0 | 2.5 (0.04) | 2.5 (0.1) | 0.0 |
| Median (SE) | 1.3 (0.04) | 1.2 (0.1) | 8.3 * | 1.8 (0.02) | 1.7 (0.05) | 5.9 *** | 2.4 (0.04) | 2.2 (0.1) | 9.1 ** | |
| Vitamin B12 (ug/day) | Mean (SE) | 2.2 (0.1) | 2.3 (0.3) | −4.4 | 2.9 (0.1) | 3.3 (0.4) | −12.1 | 4.3 (0.4) | 4.7 (0.6) | −8.5 |
| Median (SE) | 1.7 (0.5) | 1.1 (0.1) | 54.6 *** | 2.9 (0.2) | 1.3 (0.1) | 123.1 *** | 3.5 (0.3) | 1.7 (0.1) | 105.8 *** | |
| Folate (ug/day) | Mean (SE) | 225.4 (12.7) | 225.0 (12.1) | 0.2 | 253.2 (4.0) | 253.2 (11.6) | 0.0 | 282.1 (7.5) | 284.6 (7.9) | −0.9 |
| Median (SE) | 210.1 (10.5) | 200.0 (9.8) | 5.1 ** | 238.7 (9.9) | 202.3 (11.8) | 18.0 *** | 266.0 (5.5) | 242.9 (5.5) | 9.5 ** | |
| Nutrient (Box-Cox TP) | Age: 1–<3 Years | Age: 3–<6 Years | Age: 6–<10 Years | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Var_e | Var_u | Ratio | CV (%) | Var_e | Var_u | Ratio | CV (%) | Var_e | Var_u | Ratio | CV (%) | |
| Thiamine (λ = 0.26) | 0.11 | 0.11 | 1.00 | 2.9 | 0.12 | 0.07 | 1.71 | 1.3 | 0.10 | 0.08 | 1.25 | 2.9 |
| Niacin (λ = 0.34) | 1.06 | 0.19 | 5.58 | 3.2 | 0.76 | 0.44 | 1.73 | 1.7 | 0.85 | 0.54 | 1.57 | 2.2 |
| Riboflavin (λ = 0.18) | 0.22 | 0.16 | 1.38 | 9.8 | 0.24 | 0.06 | 4.00 | 2.7 | 0.17 | 0.15 | 1.13 | 2.7 |
| Vitamin B6 (λ = 0.20) | 0.21 | 0.06 | 3.50 | 3.4 | 0.25 | 0.06 | 4.17 | 0.8 | 0.23 | 0.13 | 1.77 | 1.5 |
| Vitamin B12 (λ = 0.13) | 1.27 | 0.62 | 2.05 | 5.9 | 2.48 | 0.03 | 2.67 | 4.2 | 2.01 | 0.71 | 2.83 | 9.0 |
| Folate (λ = 0.07) | 0.44 | 0.28 | 1.57 | 5.7 | 0.52 | 0.23 | 2.26 | 1.6 | 0.38 | 0.23 | 1.65 | 2.7 |
| Day-1 Intake | Usual Intake | Difference 1 in % < EAR & % > UL | ||||
|---|---|---|---|---|---|---|
| % < EAR | % > UL | % < EAR | % > UL | |||
| Thiamine (mg/day)EAR: 1–3 years = 0.4 mg; 4–8 years = 0.5 mg; 9–<10 years = 0.7 mg; No UL | 1–<3 years (n = 333) | 4.8 (1.5–8.0) | - | 1.6 (0.0–4.8) | - | 3.2% |
| 3–<6 years (n = 514) | 6.9 (4.0–9.7) | 0.7 (0.0–2.7) | 6.2% | |||
| 6–<10 years (n = 479) | 4.8 (2.0–7.6) | 1.3 (0.0–3.1) | 3.5% | |||
| Niacin (mgNE/day) EAR-UL: 1–3 years = 5–10 mgNE; 4–8 years = 6–15 mgNE; 9–<10 years = 9–20 mgNE | 1–<3 years (n = 333) | 10.7 (6.6–14.9) | 56.0 (49.5–62.4) | 0.1 (0.0–0.9) | 0.0 (-) | 10.6% (−56.0%) |
| 3–<6 years (n = 514) | 5.9 (3.3–8.5) | 51.2 (46.5–55.9) | 0.3 (0.0–1.0) | 0.0 (-) | 5.6% (−51.2%) | |
| 6–<10 years (n = 479) | 5.4 (3.1–7.7) | 56.8 (51.7–61.8) | 0.5 (0.2–0.8) | 0.0 (-) | 4.9% (−56.8%) | |
| Riboflavin (mg/day) EAR: 1–3 years = 0.4 mg; 4–8 years = 0.5 mg; 9–<10 years = 0.8 mg; No UL | 1–<3 years (n = 333) | 17.4 (11.2–23.7) | 5.6 (0.0–12.6) | 11.8% | ||
| 3–<6 years (n = 514) | 19.5 (14.3–24.7) | 2.3 (0.0–8.1) | 17.2% | |||
| 6–<10 years (n = 479) | 23.4 (18.5–28.2) | 11.4 (4.9–18.0) | 12.0% | |||
| Vitamin B6 (mg/day) EAR-UL: 1–3 years = 0.4–30 mg; 4–8 years = 0.5–40 mg; 9–<10 years = 0.8–60 mg | 1–<3 years (n = 333) | 2.5 (0.7–4.3) | 0.0 (-) | 0.0 (-) | 0.0 (-) | 2.5% (0.0%) |
| 3–<6 years (n = 514) | 2.6 (0.9–4.3) | 0.0 (-) | 0.0 (-) | 0.0 (-) | 2.6% (0.0%) | |
| 6–<10 years (n = 479) | 0.8 (0.0–1.6) | 0.0 (-) | 0.0 (-) | 0.0 (-) | 0.8% (0.0%) | |
| Vitamin B12 (ug/day) EAR: 1–3 years = 0.7 ug; 4–8 years = 1.0 ug; 9–<10 years = 1.5 ug; No UL | 1–<3 years (n = 333) | 34.4 (27.0–41.8) | 14.3 (0.0–56.4) | 20.1% | ||
| 3–<6 years (n = 514) | 36.7 (30.9–42.4) | 0.0 (-) | 36.7% | |||
| 6–<10 years (n = 479) | 35.0 (29.6–40.3) | 5.4 (0.0–13.2) | 29.6% | |||
| Folate (ug/day) EAR-UL: 1–3 years = 120–300 ug; 4–8 years = 160–400 ug; 9–<10 years = 250–600 ug | 1–<3 years (n = 333) | 22.9 (16.6–29.3) | 20.8 (15.5–26.0) | 9.6 (0.0–22.1) | 18.6 (6.1–31.2) | 13.3% (−2.4%) |
| 3–<6 years (n = 514) | 26.5 (21.1–31.9) | 21.6 (16.1–27.1) | 10.3 (0.0–22.2) | 14.6 (9.2–19.9) | 16.2% (−7.0%) | |
| 6–<10 years (n = 479) | 27.8 (23.4–32.2) | 16.2 (11.5–20.9) | 15.5 (12.4–18.6) | 11.1 (6.4–15.9) | 12.3% (−4.4%) | |
| Vitamin | Age Group (Years) | Foods Contributing to Nutrient Intake (% Eaters, % Contribution to Total Nutrient Intake) |
|---|---|---|
| Thiamine * | Age 1–<3 | Maize porridge (79%, 42%), BMS (14%, 9%), High fiber cereal (20%, 6%), Potato/sweet potato (33%, 4%), Brown bread (22%, 4%) |
| Age 3–<6 | Maize porridge (74%, 39%), Brown bread (32%, 8%), High fiber cereal (22%, 7%), White bread (38%, 7%), Potato/sweet potato (31%, 4%) | |
| Age 6–<10 | Maize porridge (72%, 35%), White bread (50%, 11%), Brown bread (32%, 10%), Low fiber cereal (14%, 5%), Processed meat (32%, 4%) | |
| Niacin * | Age 1–<3 | Maize porridge (79%, 26%), Chicken (41%, 20%), High fiber cereal (20%, 7%), Brown bread (22%, 6%), White bread (25%, 5%) |
| Age 3–<6 | Chicken (49%, 20%), Maize porridge (74%, 20%), Brown bread (32%, 10%), White bread (38%, 10%), High fiber cereal (22%, 7%) | |
| Age 6–<10 | Maize porridge (72%, 17%), Chicken (45%, 17%), White bread (50%, 15%), Brown bread (32%, 12%), Pilchards/sardines (13%, 6%) | |
| Riboflavin * | Age 1–<3 | Maize porridge (79%, 17%), BMS (14%, 14%), Whole milk (44%, 14%), High fiber cereal (20%, 9%), Maas/sour milk (17%, 4%) |
| Age 3–<6 | Maize porridge (74%, 17%), Whole milk (49%, 12%), High fiber cereal (22%, 10%), Organ meat (9%, 10%), Chicken (49%, 5%) | |
| Age 6–<10 | Maize porridge (72%, 15%), Whole milk (48%, 10%), Organ meat (9%, 8%), Low fiber cereal (14%, 8%), High fiber cereal (13%, 6%) | |
| Vitamin B6 * | Age 1–<2 | Maize porridge (79%, 33%), White bread (25%, 12%), Brown bread (22%, 12%), Potato/sweet potato (33%, 6%), BMS (14%, 5%) |
| Age 3–<6 | Maize porridge (74%, 24%), White bread (38%, 22%), Brown bread (32%, 20%), Potato/sweet potato (31%, 6%), Chicken (49%, 3%) | |
| Age 6–<10 | White bread (50%, 31%), Brown bread (32%, 21%), Maize porridge (72%, 18%), Potato/sweet potato (33%, 5%), Low fiber cereal (14%, 3%) | |
| Vitamin B12 | Age 1–<2 | Pilchards/sardines (6%, 32%), Whole milk (44%, 15%), Organ meat (5%, 11%), Eggs (14%, 6%), Beef (11%, 6%) |
| Age 3–<6 | Organ meat (9%, 42%), Pilchards/sardines (8%, 24%), Whole milk (49%, 8%), Beef (13%, 6%), Eggs (11%, 3%) | |
| Age 6–<10 | Pilchards/sardines (13%, 36%), Organ meat (9%, 30%), Beef (16%, 8%), Whole milk (48%, 6%), Eggs (12%, 3%) | |
| Folate * | Age 1–<2 | Maize porridge (79%, 56%), BMS (14%, 5%), Brown bread (22%, 5%), Organ meat (5%, 5%), White bread (25%, 4%) |
| Age 3–<6 | Maize porridge (74%, 48%), Organ meat (9%, 9%), Brown bread (32%, 9%), White bread (38%, 7%), Low fiber cereal (10%, 3%) | |
| Age 6–<10 | Maize porridge (72%, 43%), White bread (50%, 12%), Brown bread (32%, 11%), Organ meat (9%, 7%), Low fiber cereal (14%, 4%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nel, J.H.; Steyn, N.P.; Senekal, M. Illustration of the Importance of Adjustment for within- and between-Person Variability in Dietary Intake Surveys for Assessment of Population Risk of Micronutrient Deficiency/Excess Using an Example Data Set. Nutrients 2022, 14, 285. https://doi.org/10.3390/nu14020285
Nel JH, Steyn NP, Senekal M. Illustration of the Importance of Adjustment for within- and between-Person Variability in Dietary Intake Surveys for Assessment of Population Risk of Micronutrient Deficiency/Excess Using an Example Data Set. Nutrients. 2022; 14(2):285. https://doi.org/10.3390/nu14020285
Chicago/Turabian StyleNel, Johanna H., Nelia P. Steyn, and Marjanne Senekal. 2022. "Illustration of the Importance of Adjustment for within- and between-Person Variability in Dietary Intake Surveys for Assessment of Population Risk of Micronutrient Deficiency/Excess Using an Example Data Set" Nutrients 14, no. 2: 285. https://doi.org/10.3390/nu14020285
APA StyleNel, J. H., Steyn, N. P., & Senekal, M. (2022). Illustration of the Importance of Adjustment for within- and between-Person Variability in Dietary Intake Surveys for Assessment of Population Risk of Micronutrient Deficiency/Excess Using an Example Data Set. Nutrients, 14(2), 285. https://doi.org/10.3390/nu14020285






