How Does Energy Intake Change in China? A Life Cycle Perspective
Abstract
:1. Introduction
2. Materials and Methods
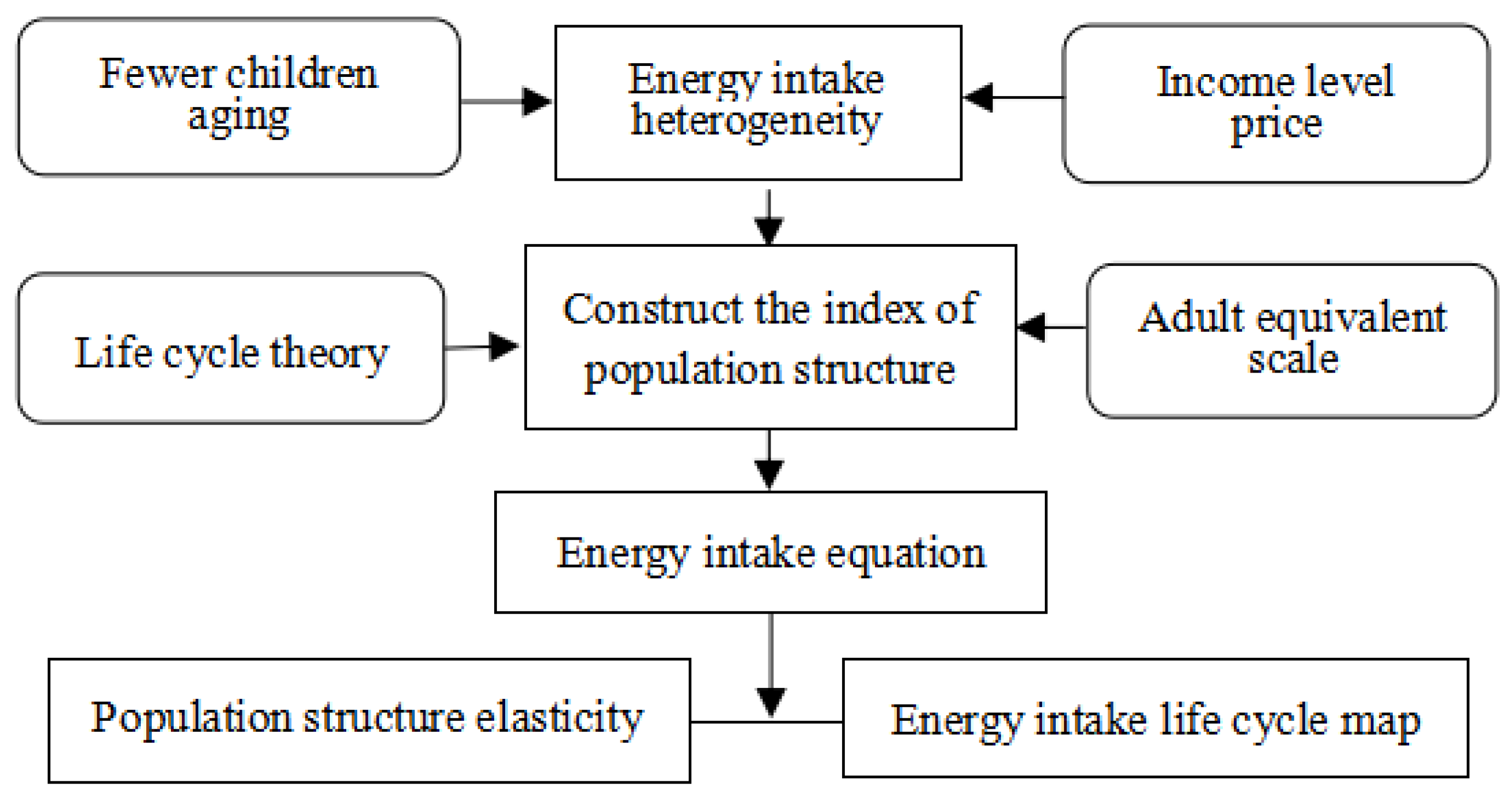
2.1. Analysis Framework
2.2. Model Setting
2.2.1. Construction of Variables Representing Population Structure
2.2.2. Construction of Variables Representing Population Structure
2.3. Data Description
2.4. Statistical Description of Variables
3. Results
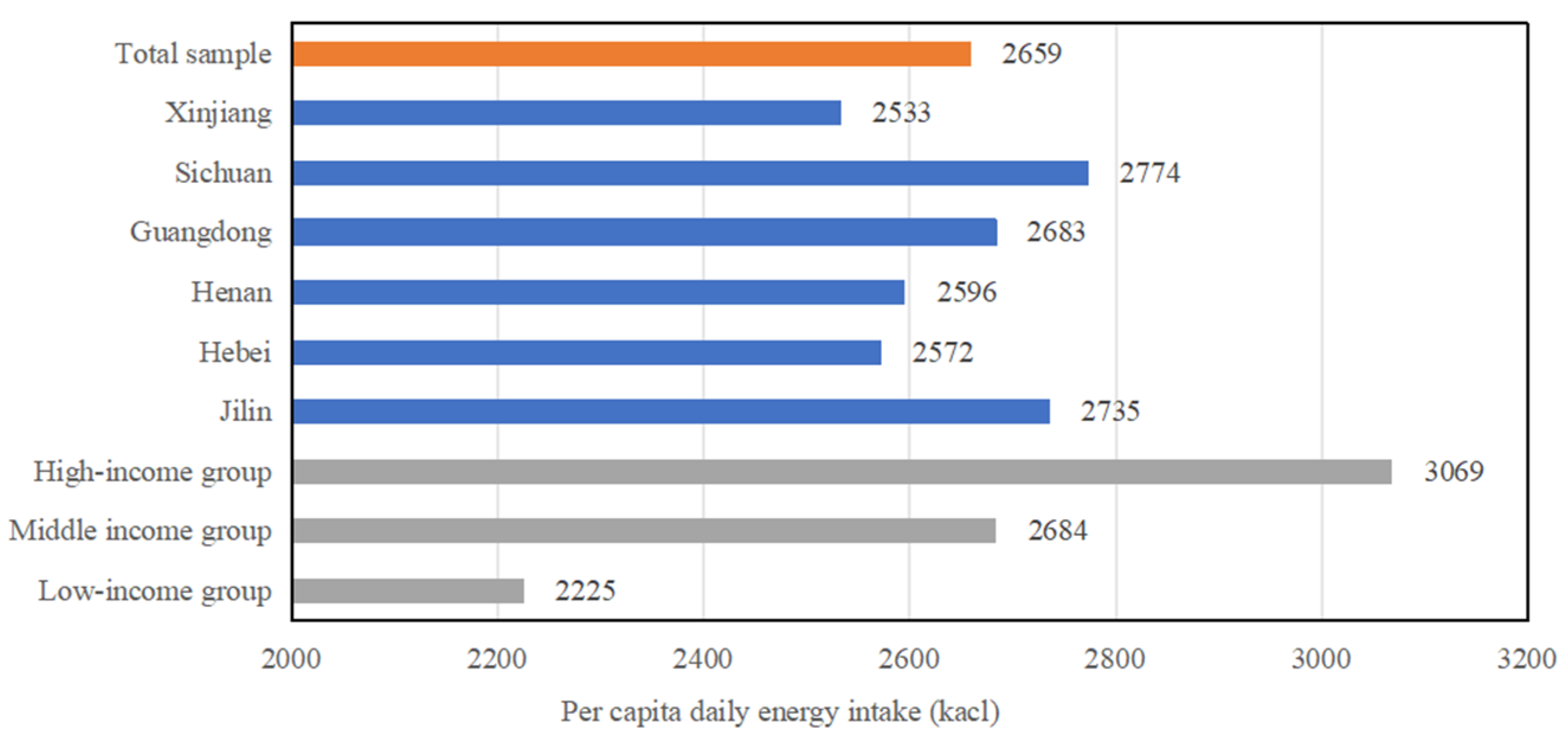
3.1. Classification and Comparative Analysis of Resident Energy Intake
3.2. Population Structure Factors That Significantly Affect the Energy Intake of Urban Residents
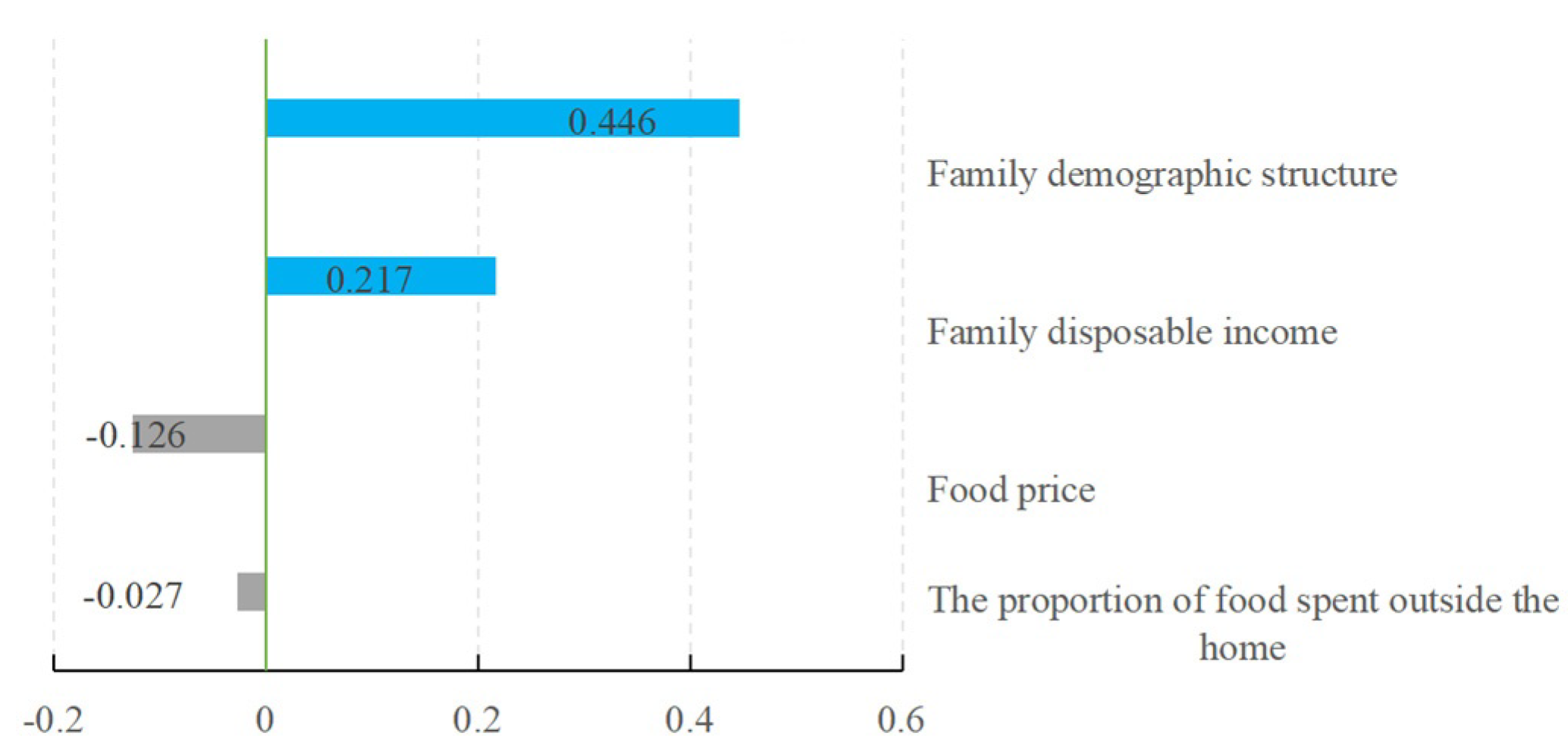
3.3. Household Energy Intake Is More Responsive to Changes in Population Structure
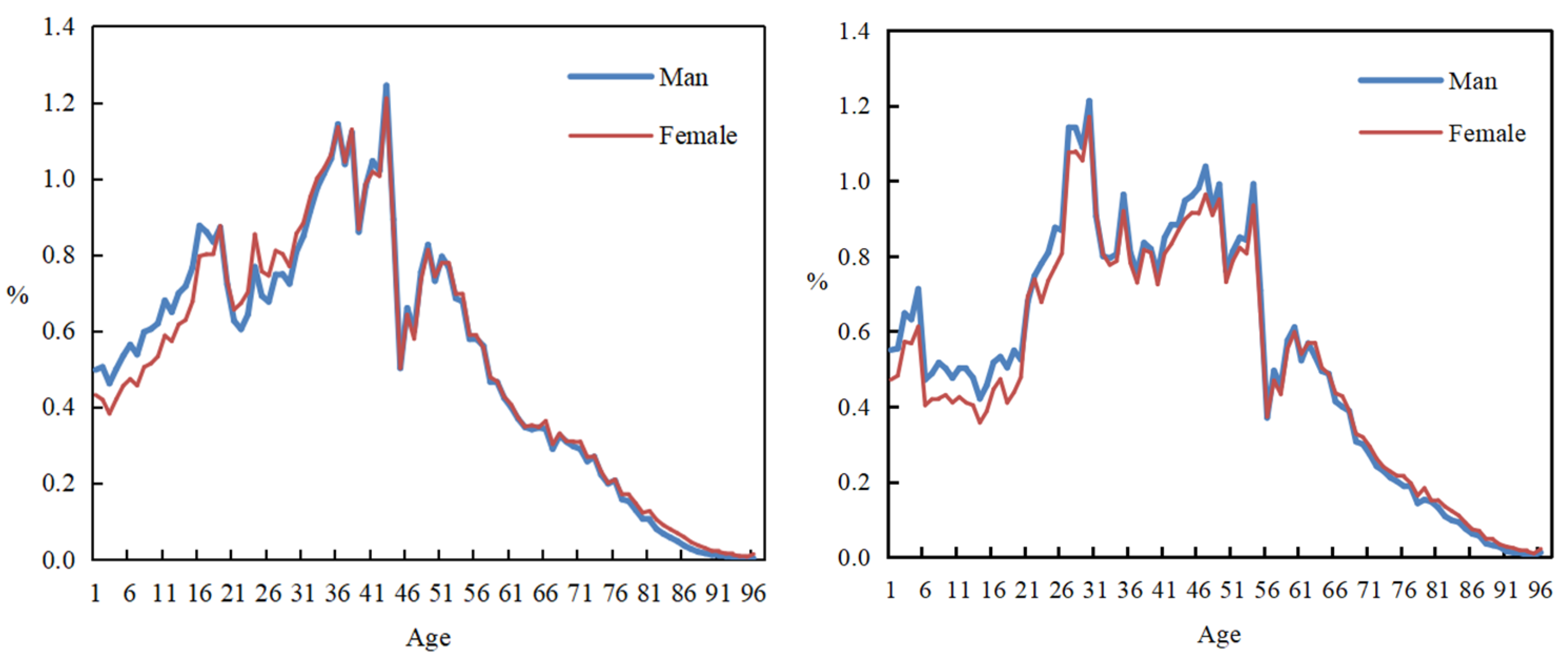
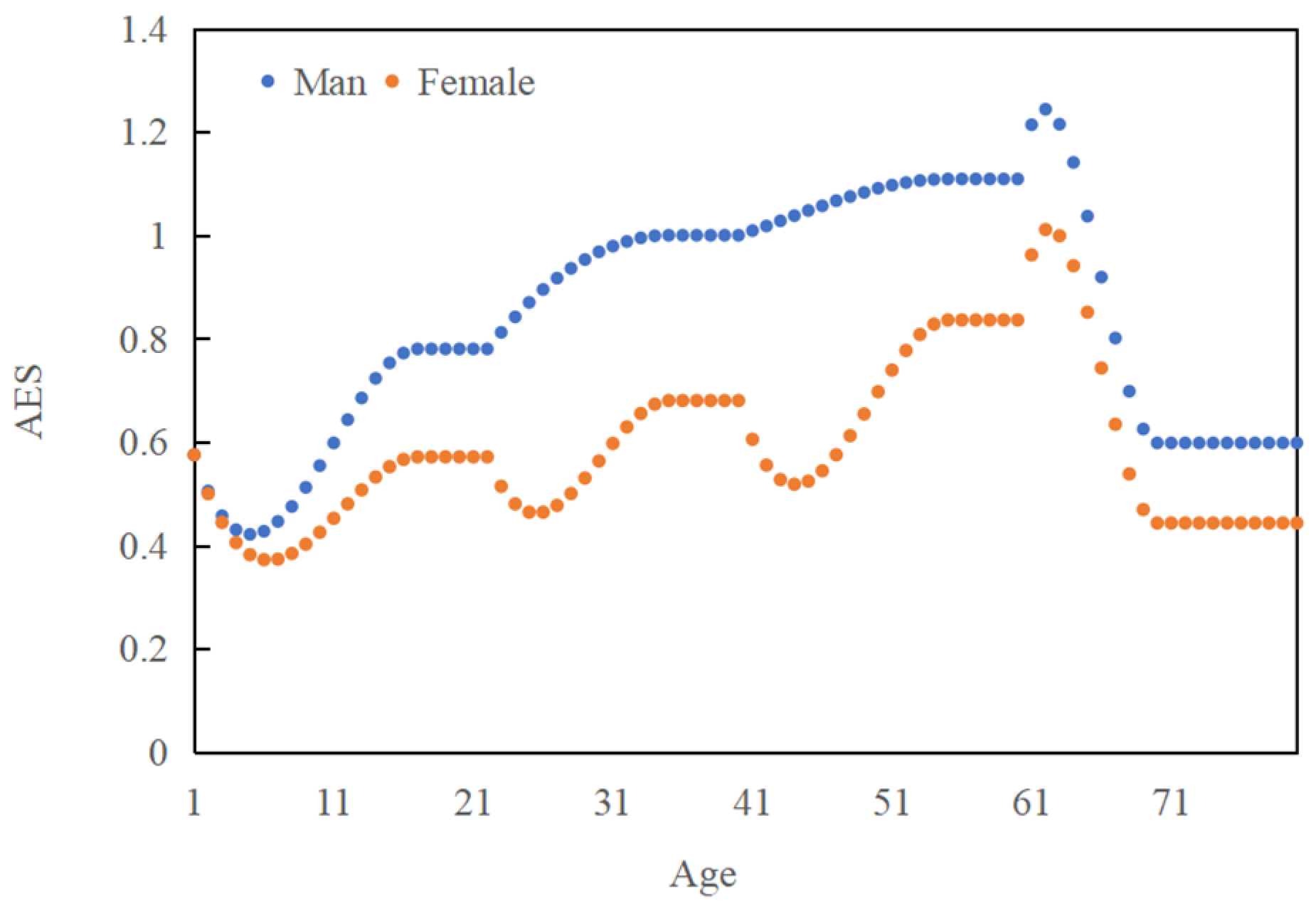
3.4. Residents’ Energy Intake Varies Significantly over the Life Cycle
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Food and Agriculture Organization of the United Nations. The State of Food Security and Nutrition in the World 2021: Transforming Food Systems for Food Security, Improved Nutrition and Affordable Healthy Diets for All; Food and Agriculture Organization of the United Nations: Rome, Italy, 2022. [Google Scholar]
- Food and Agriculture Organization of the United Nations, World Health Organization. Sustainable Healthy Diets—Guiding Principles; Food and Agriculture Organization of the United Nations: Rome, Italy, 2019. [Google Scholar]
- Development Initiatives Poverty Research Ltd. Global Nutrition Report 2022: Stronger Commitments for Greater Action; Development Initiatives Poverty Research Ltd.: Bristol, UK, 2022. [Google Scholar]
- Neufingerl, N.; Eilander, A. Nutrient Intake and Status in Adults Consuming Plant-based Diets Compared to Meat-eaters: A systematic Review. Nutrients 2021, 14, 29. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Zheng, Z.H.; Henneberry, S.R. Is nutritional status associated with income growth? Evidence from Chinese adults. China Agric. Econ. Rev. 2020, 12, 507–525. [Google Scholar] [CrossRef]
- Ma, L.; Shen, H.; Shang, X.; Zhou, S.; Lyu, B.; Zhao, X.; Li, J.; Zhao, Y.; Wu, Y. Dietary Intake of Multiple Nutrient Elements and Associated Health Effects in the Chinese General Population from a Total Diet Study. Nutrients 2023, 15, 2613. [Google Scholar] [CrossRef] [PubMed]
- Gouel, C.; Guimbard, H. Nutrition transition and the structure of global food demand. Am. J. Agric. Econ. 2019, 101, 383–403. [Google Scholar] [CrossRef]
- Liu, X.; Ho, M.S.; Hewings, G.J.; Dou, Y.; Wang, S.; Wang, G.; Guan, D.; Li, S. Aging Population, Balanced Diet and China’s Grain Demand. Nutrients 2023, 15, 2877. [Google Scholar] [CrossRef] [PubMed]
- Komarek, A.; Dunston, S.; Enahoro, D.; Godfray, H.C.J.; Herrero, M.; Mason-D’Croz, D.; Rich, K.M.; Scarborough, P.; Springmann, M.; Sulser, T.B.; et al. Income, consumer preferences, and the future of livestock- derived food demand. Glob. Environ. Chang. 2021, 70, 102343. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Tian, X. Food accessibility, diversity of agricultural production and dietary pattern in rural China. Food Policy 2019, 84, 92–102. [Google Scholar] [CrossRef]
- Zhang, P. The Change of the Fertility Level and the Development of China’s Population Structure Under the Two-Child Policy. J. Dalian Univ. Technol. (Soc. Sci.) 2021, 42, 113–122. (In Chinese) [Google Scholar] [CrossRef]
- Wang, G. 70 Years of China: The Changes of Population Age Structure and the Trend of Population Aging. Chin. J. Popul. Sci. 2019, 3, 2–15. (In Chinese) [Google Scholar]
- Zheng, Z.H.; Henneberry, S.R.; Zhao, Y.Y.; Gao, Y. Predicting the changes in the structure of food demand in China. Agribusiness 2019, 35, 301–328. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, W.; Tian, T.; Zhang, J.; Zhu, Q.; Pan, D.; Xu, D.; Lu, Y.; Sun, G.; Dai, Y. The relationship between dietary patterns and high blood glucose among adults based on structural equation modelling. Nutrients 2022, 14, 4111. [Google Scholar] [CrossRef] [PubMed]
- Food and Agriculture Organization of the United Nations; International Fund for Agricultural Development; United Nations International Children’s Emergency Fund. The State of Food Security and Nutrition in the World 2020: Transforming Food Systems for Affordable Healthy Diets; Food and Agriculture Organization of the United Nations: Rome, Italy, 2020. [Google Scholar]
- Qi, Y.; Qiang, W.; Ma, X. Spatiotemporal Pattern Evolution of Food and Nutrient Production in China. Foods 2023, 12, 3791. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Li, Y.; Yang, X.; Hemler, E.C.; Fang, Y.; Zhao, L.; Zhang, J.; Yang, Z.; Wang, Z.; He, L.; et al. The dietary transition and its association with cardiometabolic mortality among Chinese adults, 1982–2012: A cross-sectional population-based study. Lancet Diabetes Endo 2019, 7, 540–548. [Google Scholar] [CrossRef] [PubMed]
- National Health Commission of the People’s Republic of China. Report on Nutrition and Chronic Disease Status of Chinese Residents (2020). Acta Nutr. Sin. 2020, 42, 521. (In Chinese) [Google Scholar]
- Zhou, M.; Wang, H.; Zeng, X.; Yin, P.; Zhu, J.; Chen, W.; Li, X.; Wang, L.; Wang, L.; Liu, Y. Mortality, morbidity, and risk factors in China and its provinces, 1990–2017: A systematic analysis for the Global Burden of Disease Study 2017. Lancet 2019, 394, 1145–1158. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Qiang, W.; Niu, S.; Growe, A.; Yan, S.; Tian, N. Multi-Scenario simulation analysis of grain production and demand in China during the peak population period. Foods 2022, 11, 1566. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Wahl, T.I.; Seale Jr, J.L.; Bai, J. Household composition, income, and food-away-from-home expenditure in urban China. Food Policy 2015, 51, 97–103. [Google Scholar] [CrossRef]
- Yang, T.; Wang, Q. The nonlinear effect of population aging on carbon emission-Empirical analysis of ten selected provinces in China. Sci. Total Environ. 2020, 740, 140057. [Google Scholar] [CrossRef] [PubMed]
- Tian, X.; Yu, X. The demand for nutrients in China. Front. Econ. China 2013, 8, 186–206. [Google Scholar]
- You, J.; Imai, K.S.; Gaiha, R. Declining nutrient intake in a growing China: Does household heterogeneity matter? World Dev. 2016, 77, 171–191. [Google Scholar] [CrossRef]
- Xin, L.; Li, P.; Fan, Y. Change of food consumption with population age structure in China. Trans. Chin. Soc. Agric. Eng. 2018, 34, 296–302. (In Chinese) [Google Scholar]
- Jiang, S.F.; Qin, X.Z. The inequality of nutrition intake among adults in China. J. Chin. Econ. Bus. Stud. 2018, 17, 65–89. [Google Scholar] [CrossRef]
- Deaton, A.S.; Muellbauer, J. On measuring child costs: With applications to poor countries. J. Political Econ. 1986, 94, 720–744. [Google Scholar] [CrossRef]
- Zhong, F.; Xiang, J.; Zhu, J. Impact of demographic dynamics on food consumption—A case study of energy intake in China. China Econ. Rev. 2012, 23, 1011–1019. [Google Scholar] [CrossRef]
- Wang, J.; Fu, X. Econometric Analysis of China’s Consumption Function Considering Changes in Population Age Structure -- Also on the Impact of China’s Aging Population on Consumption. Popul. Res. 2006, 30, 29–36. (In Chinese) [Google Scholar]
- Gould, B.W. Household composition and food expenditures in China. Agribusiness 2002, 18, 387–407. [Google Scholar] [CrossRef]
- Claro, R.M.; Levy, R.B.; Bandoni, D.H.; Mondini, L. Per capita versus adult-equivalent estimates of calorie availability in household budget surveys. Cad. Saude Publica 2010, 26, 2188–2195. [Google Scholar] [CrossRef] [PubMed]
- De Ree, J.; Alessie, R.; Pradhan, M. The price and utility dependence of equivalence scales: Evidence from Indonesia. J. Public Econ. 2013, 97, 272–281. [Google Scholar] [CrossRef]
- Li, G.; Chen, Y. Ageing with Fewer Children, Household Composition and Food Expenditure in Urban China: Based on the Empirical Study of Adult Equivalent Scale. Nankai Econ. Study 2018, 3, 83–99. (In Chinese) [Google Scholar]
- Liu, N.; Li, X.; Yang, L. The Child Costs in Chinese Family: A Welfare Estimate Using Equivalence Scale. Popul. Res. 2021, 1, 50–67. [Google Scholar]
- Liu, Z.; Lan, Y.; Deng, M.; Zhang, Y. Accurate identification of energy poverty in China: An Analysis based on an equivalent Scale. J. Quant. Technol. Econ. 2023, 40, 136–157. (In Chinese) [Google Scholar]
- Thomas, D. Like father, like son; like mother, like daughter: Parental resources and child height. J. Hum. Resour. 1994, 29, 950–988. [Google Scholar] [CrossRef]
- Nie, P.; Sousa-Poza, A. A fresh look at calorie-income elasticities in China. China Agric. Econ. Rev. 2016, 8, 55–80. [Google Scholar] [CrossRef]
- Bai, J.F.; Seale, J.L.; Wahl, T.I. Meat demand in China: To include or not to include meat away from home? Aust. J. Agric. Resour. Econ. 2020, 64, 150–170. [Google Scholar] [CrossRef]
- Yang, Y.; Xing, G.; Pan, X. Chinese Food Composition Table; Peking University Medical Press: Beijing, China, 2009; Volume 2. [Google Scholar]
- Zheng, Z.H.; Henneberry, S.R. Estimating the impacts of rising food prices on nutrient intake in urban China. China Econ. Rev. 2012, 23, 1090–1103. [Google Scholar] [CrossRef]
- Chinese Nutrition Society. Scientific Research Report on Dietary Guidelines for Chinese Residents (2021); People’s Health Publishing House: Beijing, China, 2021. [Google Scholar]
- Chinese Nutrition Society. Chinese Dietary Reference Intakes (2013); China Science Publishing & Media Ltd.: Beijing, China, 2014. [Google Scholar]
- Bernheim, B.D.; Skinner, J.; Weinberg, S. What accounts for the variation in retirement wealth among US households? Am. Econ. Rev. 2001, 91, 832–857. [Google Scholar] [CrossRef]
- Chen, Q.; Deng, T.; Bai, J.; He, X. Understanding the retirement-consumption puzzle through the lens of food consumption-fuzzy regression-discontinuity evidence from urban China. Food Policy 2017, 73, 45–61. [Google Scholar] [CrossRef]
- Huang, L.; Wang, Z.; Wang, H.; Zhao, L.; Jiang, H.; Zhang, B.; Ding, G. Nutrition transition and related health challenges over decades in China. J. Integr. Agric. 2021, 75, 247–252. [Google Scholar] [CrossRef]
| Weight Variable | Age | Equal Standard Consumption Weight Formula S(aij, gij) | Population Quantity |
|---|---|---|---|
| Newborn baby | |||
| S0 | aij = 0 | c1 | n0 |
| Male | |||
| S1 | 0 < aij ≤ 17 | c1 + e11aij − [0.1176e11 + 0.0104(c1 − c2)] aij2 + [0.0035e11 + 0.0004(c1 − c2)] aij3 | n1 |
| S2 | 17 < aij ≤ 22 | c2 | n2 |
| S3 | 22 < aij ≤ 35 | c2 + e21(aij − 22) − [0.1538e21 + 0.0176(c2 − c3)](aij − 22)2 + [0.0059e21 + 0.0009(c2 − c3)](aij − 22)3 | n3 |
| S4 | 35 < aij ≤ 40 | c3 = 1 | n4 |
| S5 | 40 < aij ≤ 55 | c3 + e31(aij − 40) − [0.1333e31 + 0.0133(c3 − c4)](aij − 40)2 + [0.0044e31 + 0.0006(c3 − c4)](aij − 40)3 | n5 |
| S6 | 55 < aij ≤ 60 | c4 | n6 |
| S7 | 60 < aij ≤ 70 | c4 + e41(aij − 60) − [0.2e41 + 0.03(c4 − c5)](aij − 60)2 + [0.01e41 + 0.002(c4 − c5)](aij − 60)3 | n7 |
| S8 | aij > 70 | c5 | n8 |
| Female | |||
| S9 | 0 < aij ≤ 17 | c1 + e12aij − [0.1176e12 + 0.0104(c1 − c6)] aij2 + [0.0035e12 + 0.0004(c1 − c6)] aij3 | n9 |
| S10 | 17 < aij ≤ 22 | c6 | n10 |
| S11 | 22 < aij ≤ 35 | c6 + e22(aij − 22) − [0.1538e22 + 0.0176(c6 − c7)](aij − 22)2 + [0.0059e22 + 0.0009(c6 − c7)](aij − 22)3 | n11 |
| S12 | 35 < aij ≤ 40 | c7 | n12 |
| S13 | 40 < aij ≤ 55 | c7 + e32(aij − 40) − [0.1333e32 + 0.0133(c7 − c8)](aij − 40)2 + [0.0044e32 + 0.0006(c7 − c8)]aij − 40)3 | n13 |
| S14 | 55 < aij ≤ 60 | c8 | n14 |
| S15 | 60 < aij ≤ 70 | c8 + e42(aij − 60) − [0.2e42 + 0.03(c8 − c9)](aij − 60)2 + [0.01e42 + 0.002(c8 − c9)](aij − 60)3 | n15 |
| S16 | aij > 70 | c9 | n16 |
| Variable | Total Sample | Standard Deviation | Minimum | Maximum |
|---|---|---|---|---|
| Daily household energy intake (kcal) | 6949 | 2757.857 | 719 | 22,587 |
| Household disposable income (CNY) | 44,435.27 | 26,063.39 | 1820 | 238,163 |
| Education level of head of household (1 = college and upper level, 0 = other) | 0.418 | 0.493 | 0 | 1 |
| Account status (1 = local account, 0 = other) | 0.966 | 0.182 | 0 | 1 |
| City size (1 = small city, 0 = other) | 0.183 | 0.386 | 0 | 1 |
| Proportion of spending on eating out (%) | 0.16 | 0.145 | 0 | 0.933 |
| Food price (CNY/kg) | 9.476 | 2.958 | 3.162 | 28.349 |
| Henan (1 = yes, 0 = other) | 0.153 | 0.360 | 0 | 1 |
| Hebei (1 = yes, 0 = other) | 0.185 | 0.388 | 0 | 1 |
| Jilin (1 = yes, 0 = other) | 0.117 | 0.321 | 0 | 1 |
| Guangdong (1 = yes, 0 = other) | 0.227 | 0.419 | 0 | 1 |
| Sichuan (1 = yes, 0 = other) | 0.215 | 0.411 | 0 | 1 |
| Xinjiang (1 = yes, 0 = other, reference group) | 0.104 | 0.305 | 0 | 1 |
| Instrumental variable (as follows) | ||||
| Durable goods expenditure (CNY) | 9730.95 | 14,119.14 | 0 | 274,162.6 |
| Percentage of people working in households | 0.608 | 0.308 | 0 | 1 |
| Number of other properties (units) | 0.118 | 0.366 | 0 | 6 |
| Sample size | 10,462 |
| Variable and Parameters | OLS Model | IV Model | ||
|---|---|---|---|---|
| Coefficient | Standard Error | Coefficient | Standard Error | |
| Logarithm of household disposable income | 0.325 *** | 0.008 | 0.217 *** | 0.033 |
| Head of household education level | −0.049 *** | 0.008 | −0.017 | 0.012 |
| Household registration status | 0.070 *** | 0.019 | 0.054 *** | 0.020 |
| City size | −0.077 *** | 0.009 | −0.067 *** | 0.010 |
| Proportion of spending on eating out | −0.280 *** | 0.026 | −0.166 *** | 0.043 |
| Logarithm of food price | −0.172 *** | 0.020 | −0.126 *** | 0.024 |
| Henan | −0.108 *** | 0.014 | −0.082 *** | 0.017 |
| Hebei | −0.125 *** | 0.014 | −0.096 *** | 0.017 |
| JiLin | −0.023 | 0.015 | −0.009 | 0.016 |
| Guodong | 0.019 | 0.017 | 0.043 ** | 0.018 |
| Sichuan | 0.071 *** | 0.014 | 0.073 *** | 0.014 |
| α4 × c1 | 0.125 *** | 0.025 | 0.128 *** | 0.025 |
| α4 × c2 | 0.146 *** | 0.010 | 0.149 *** | 0.010 |
| α4 × c3 (c3 = 1) | 0.155 *** | 0.014 | 0.191 *** | 0.018 |
| α4 × c4 | 0.175 *** | 0.016 | 0.212 *** | 0.019 |
| α4 × c5 | 0.081 *** | 0.016 | 0.114 *** | 0.019 |
| α4 × c6 | 0.105 *** | 0.010 | 0.109 *** | 0.010 |
| α4 × c7 | 0.113 *** | 0.015 | 0.130 *** | 0.016 |
| α4 × c8 | 0.136 *** | 0.016 | 0.159 *** | 0.018 |
| α4 × c9 | 0.067 *** | 0.015 | 0.084 *** | 0.016 |
| α4 × e11 | −0.020 ** | 0.009 | −0.021 ** | 0.009 |
| α4 × e21 | 0.001 | 0.008 | 0.006 | 0.008 |
| α4 × e31 | −0.001 | 0.006 | 0.002 | 0.006 |
| α4 × e41 | 0.029 ** | 0.012 | 0.028 ** | 0.012 |
| α4 × e12 | −0.019 ** | 0.009 | −0.021 ** | 0.009 |
| α4 × e22 | −0.019 ** | 0.007 | −0.013 * | 0.008 |
| α4 × e32 | −0.015 ** | 0.006 | −0.017 *** | 0.006 |
| α4 × e42 | 0.033 ** | 0.013 | 0.032 ** | 0.013 |
| Constant term | 5.371 *** | 0.081 | 6.310 *** | 0.294 |
| Endogeneity test: DWH test | 11.319 *** | |||
| Weak instrumental variable test: F test | 287.778 *** | |||
| Sargan test | 1.533 | |||
| Observed value | 10,462 | 10,462 | ||
| Goodness of fit | 0.296 | 0.282 | ||
| Null Hypothesis | F-Value |
|---|---|
| Whether the age structure variable parameters are jointly significant: c1 = c2 = c2 = c3 = c4 = c5 = c6 = c7 = c8 = c9 = e11 = e21 = e31 = e41 = e12 = e22 = e32 = e42 | 38.60 *** |
| Whether the variable parameters of male age structure were jointly significant: c2 = c3 = c4 = c5 = e11 = e21 = e31 = e41 | 52.50 *** |
| Whether the variable parameters of female age structure were jointly significant: c6 = c7 = c8 = c9 = e12 = e22 = e32 = e42 | 30.95 *** |
| Is there a difference in the adult equivalence scale between males and females aged 17–22: c2 = c6 | 132.03 *** |
| Is there a difference in the adult equivalence scale between males and females aged 35–40: c3 = c7 | 101.96 *** |
| Is there a difference in the adult equivalence scale between males and females aged 55–60 years: c4 = c8 | 124.58 *** |
| Is there a difference in the adult equivalence scale between men and women older than 70 years: c5 = c9 | 39.47 *** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Li, Y.; Luo, Q.; Lu, H.; Lun, R.; Chen, Y. How Does Energy Intake Change in China? A Life Cycle Perspective. Nutrients 2024, 16, 43. https://doi.org/10.3390/nu16010043
Li G, Li Y, Luo Q, Lu H, Lun R, Chen Y. How Does Energy Intake Change in China? A Life Cycle Perspective. Nutrients. 2024; 16(1):43. https://doi.org/10.3390/nu16010043
Chicago/Turabian StyleLi, Guojing, Yulin Li, Qiyou Luo, Hongwei Lu, Runqi Lun, and Yongfu Chen. 2024. "How Does Energy Intake Change in China? A Life Cycle Perspective" Nutrients 16, no. 1: 43. https://doi.org/10.3390/nu16010043
APA StyleLi, G., Li, Y., Luo, Q., Lu, H., Lun, R., & Chen, Y. (2024). How Does Energy Intake Change in China? A Life Cycle Perspective. Nutrients, 16(1), 43. https://doi.org/10.3390/nu16010043







