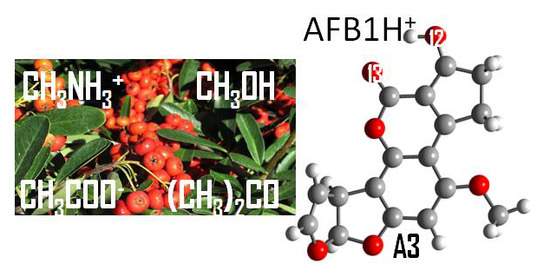
A Theoretical Study of the Adsorption Process of B-aflatoxins Using Pyracantha koidzumii (Hayata) Rehder Biomasses
Abstract
1. Introduction
2. Results and Discussion
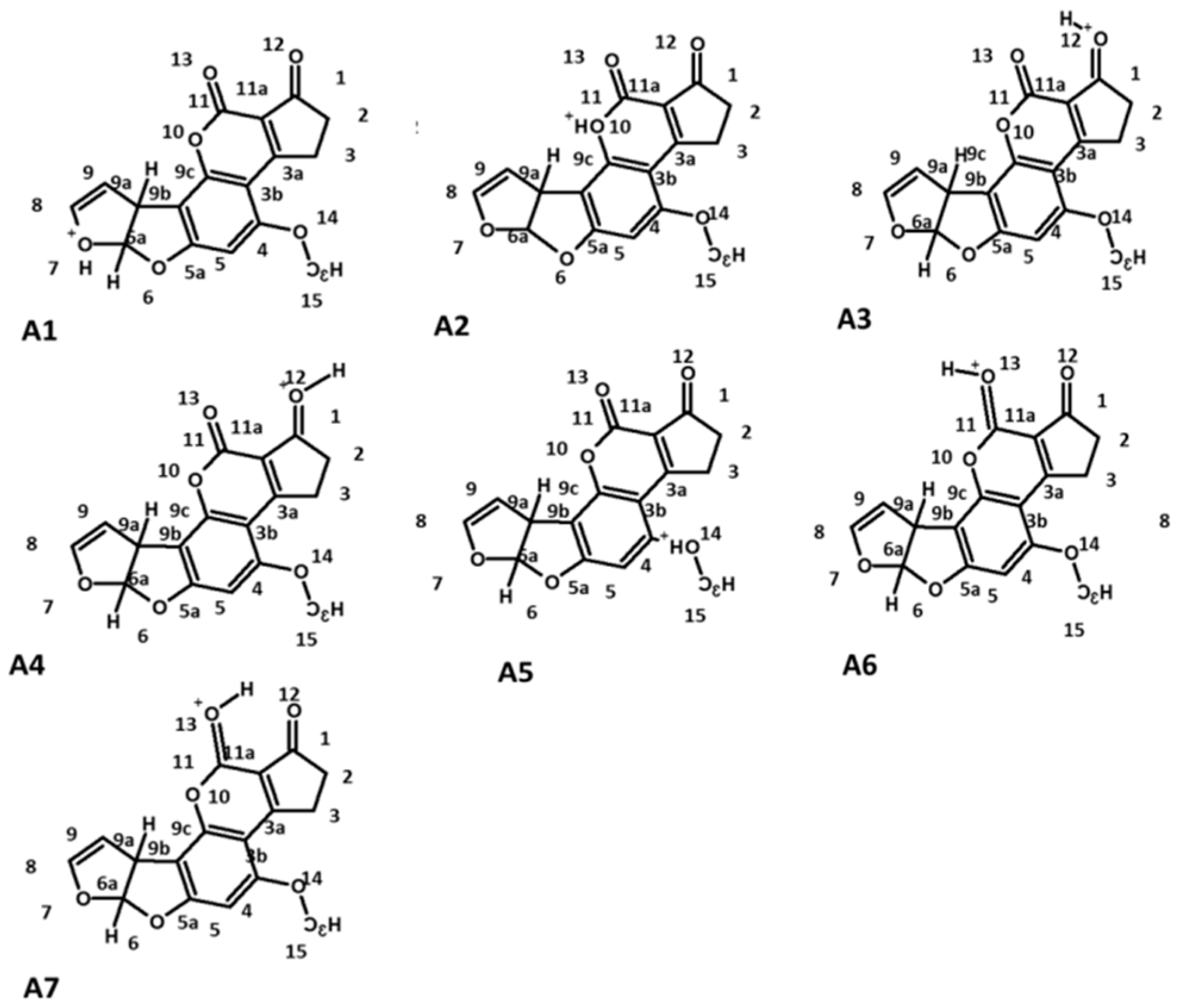
2.1. Study of the Protonation of Aflatoxin B1 (AFB1)
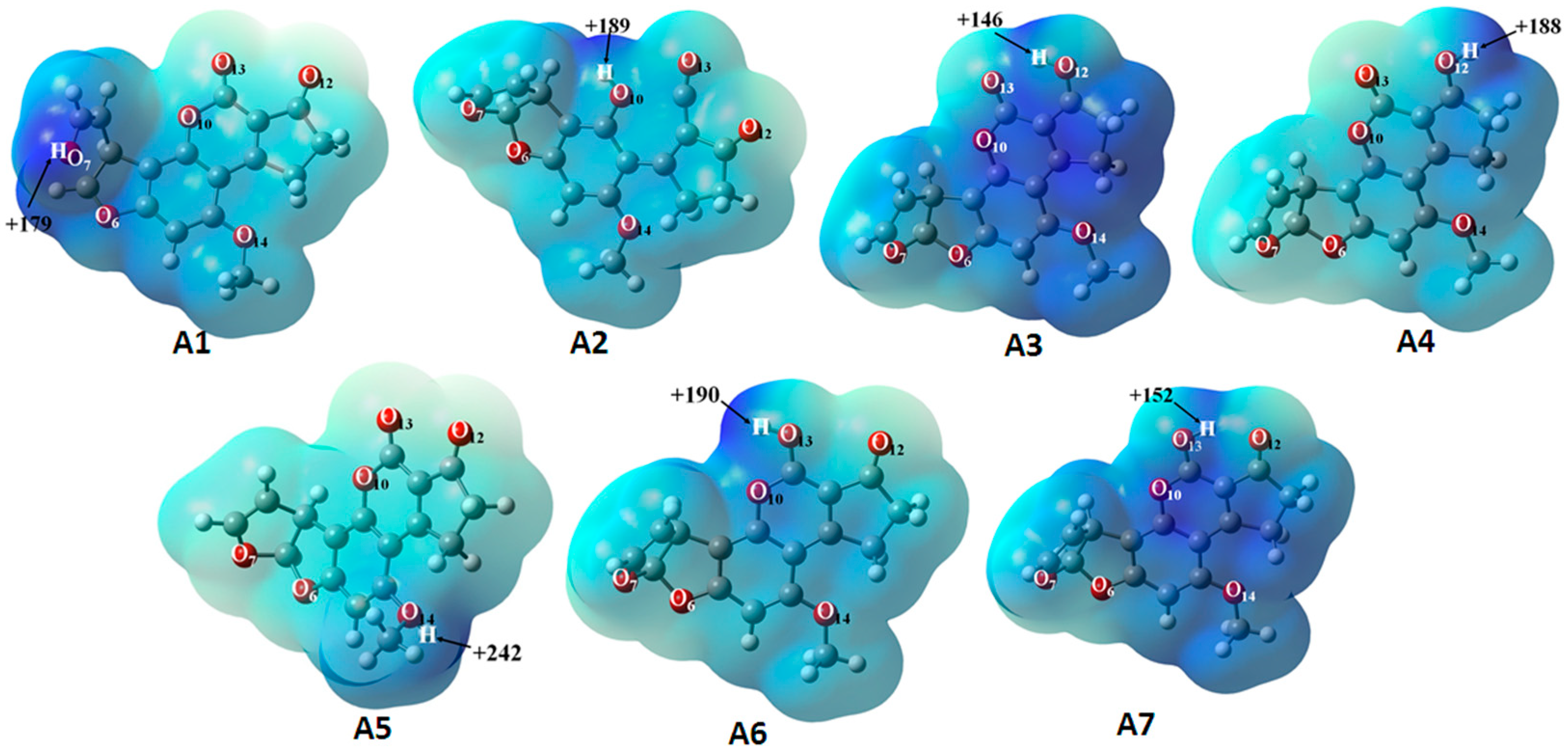
2.2. Molecular Electrostatic Potential Surface
2.3. Studies of Protonated Aflatoxin B1 (AFB1H+) Interaction with Molecular Models
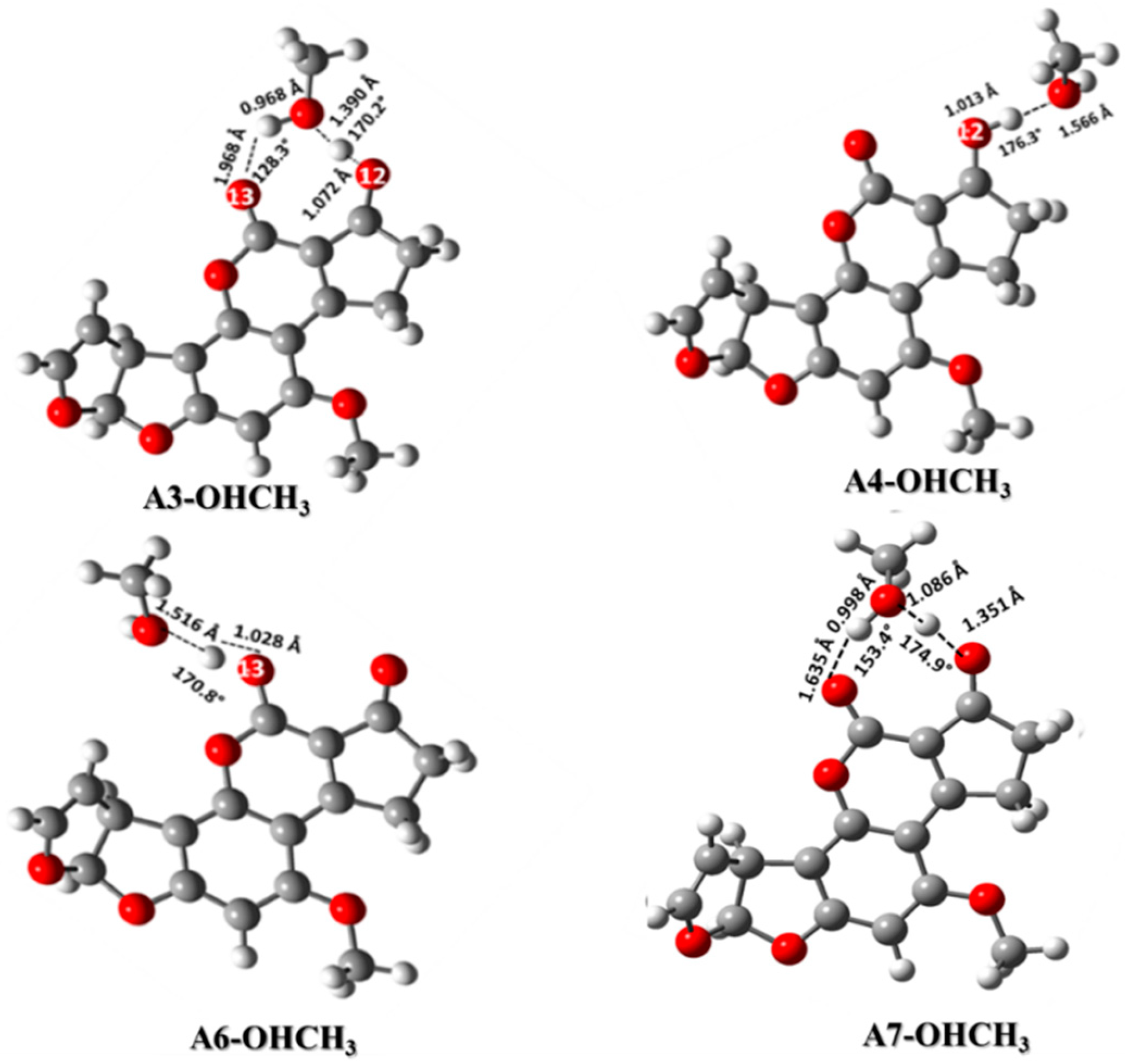
2.3.1. Hydroxyl Groups: CH3OH
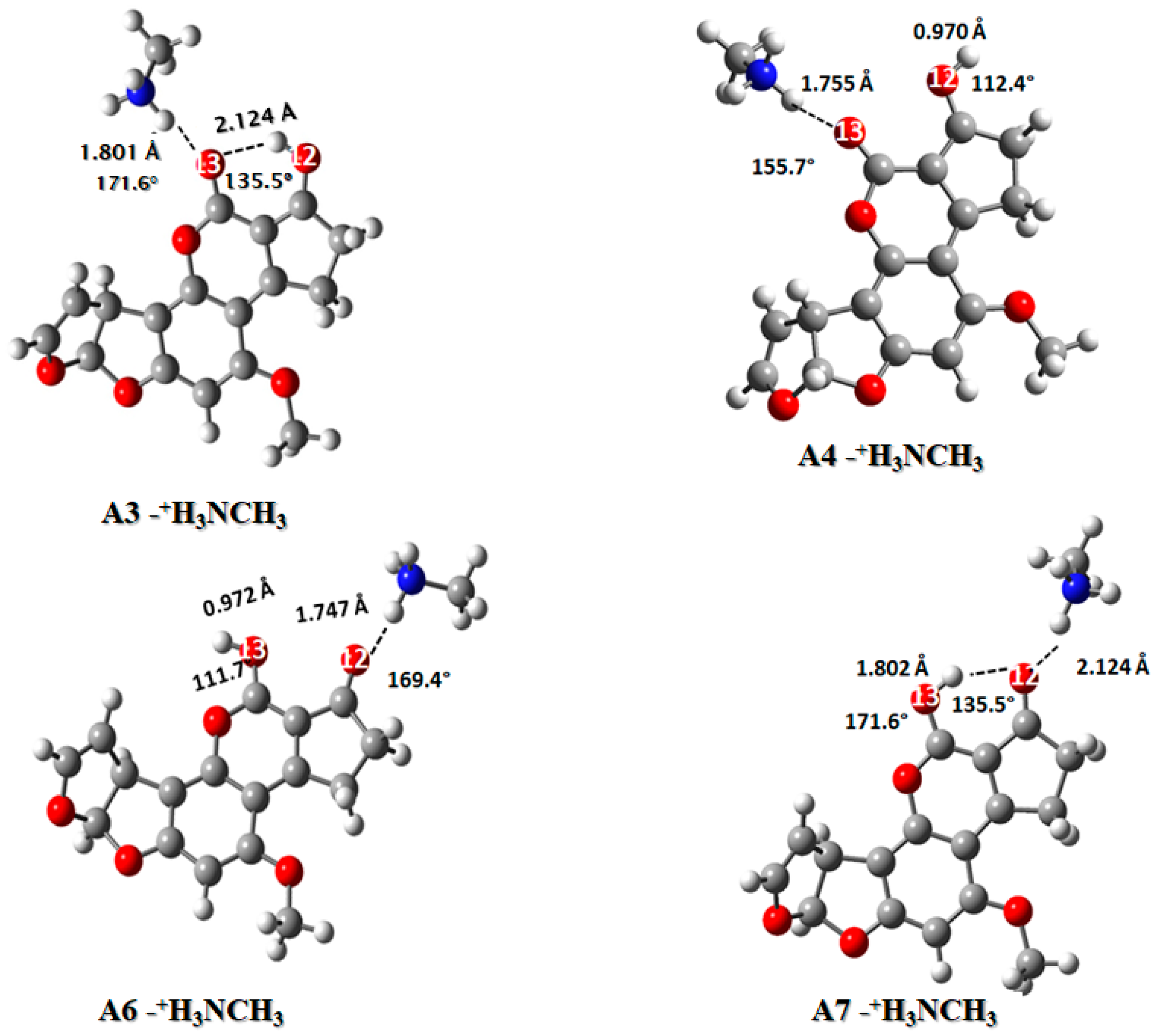
2.3.2. Ammonium Ion: CH3NH3+
2.3.3. Carboxylate Ion: CH3COO−
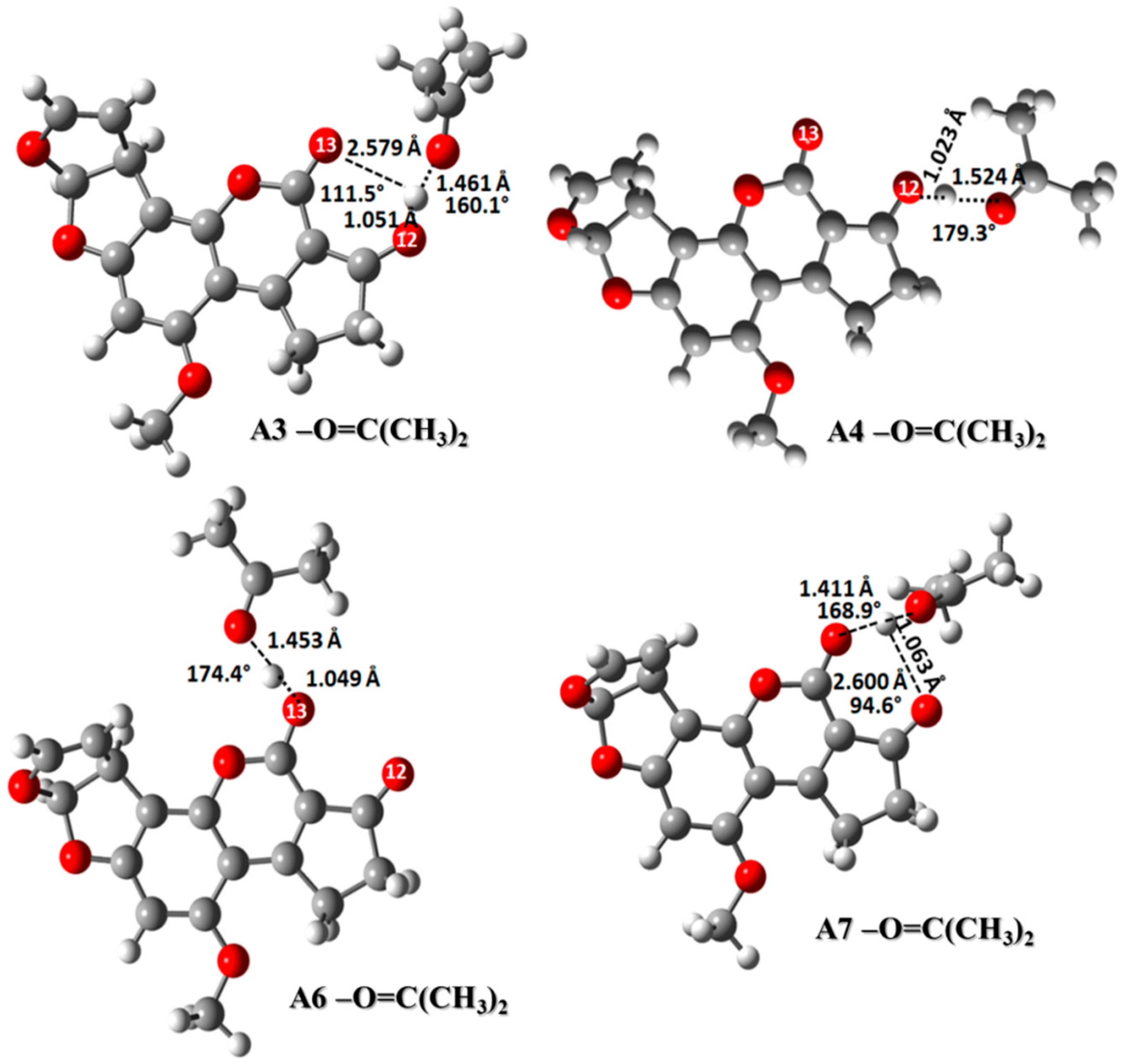
2.3.4. Carbonyl Group: (CH3)2C=O
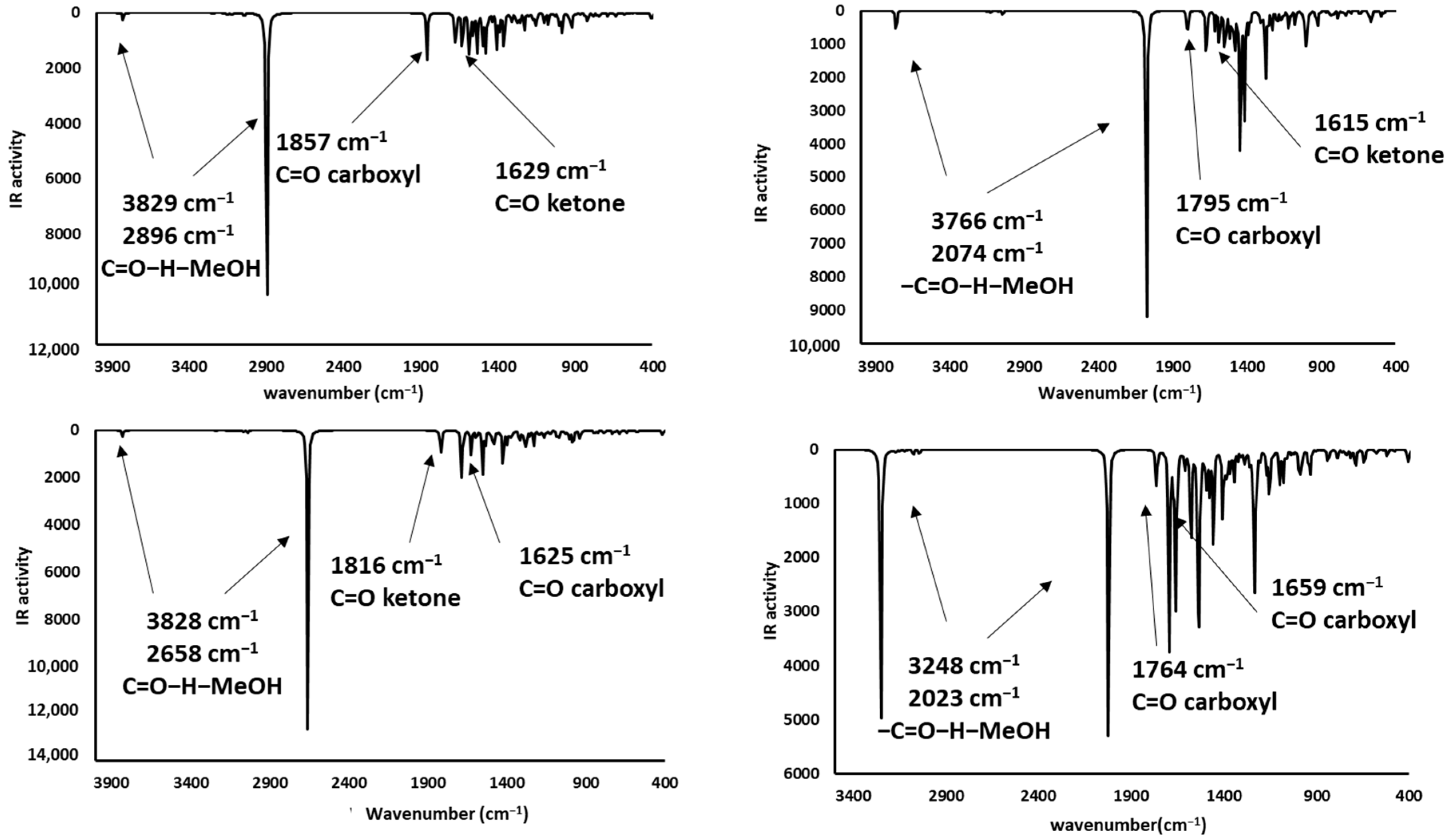
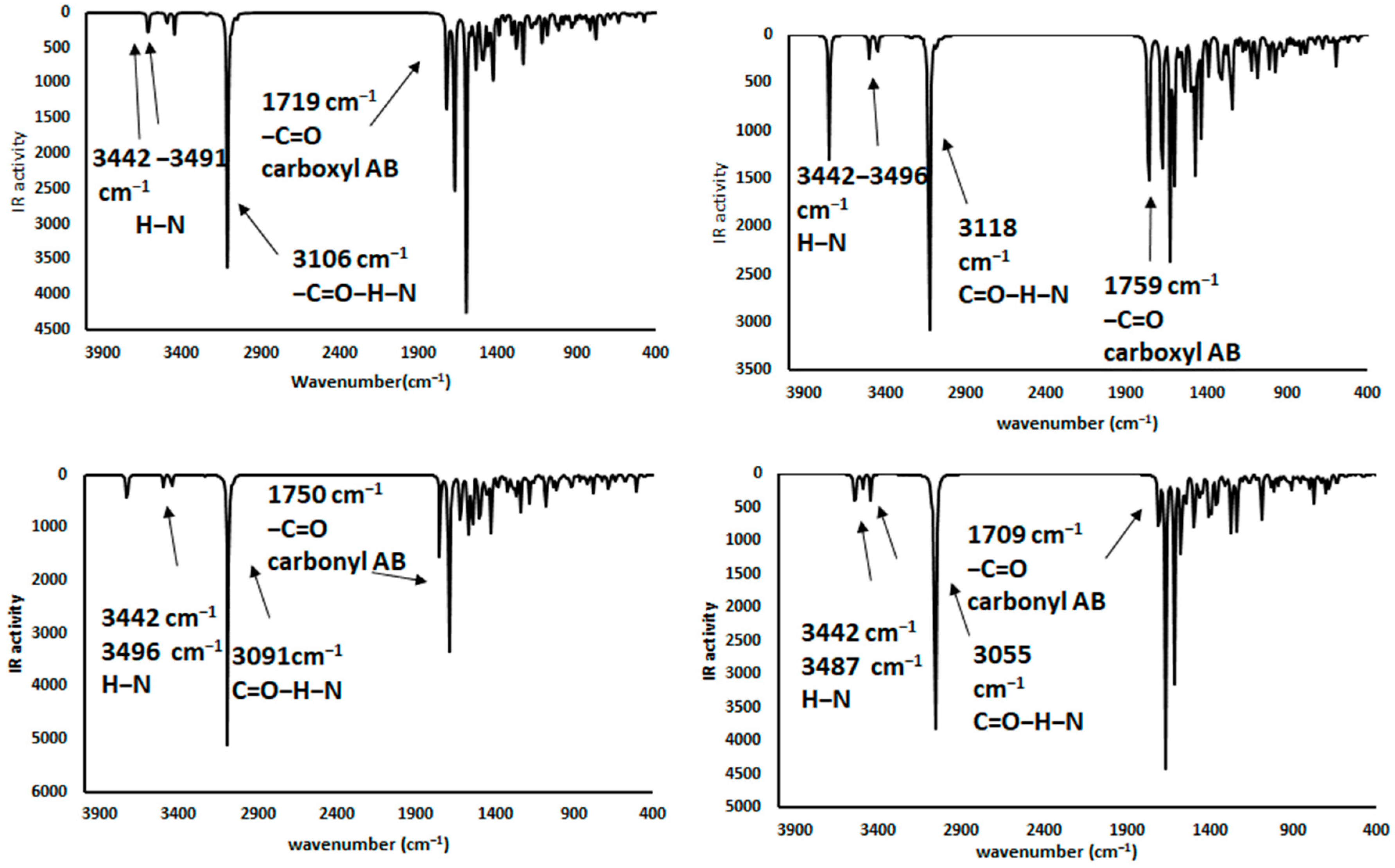
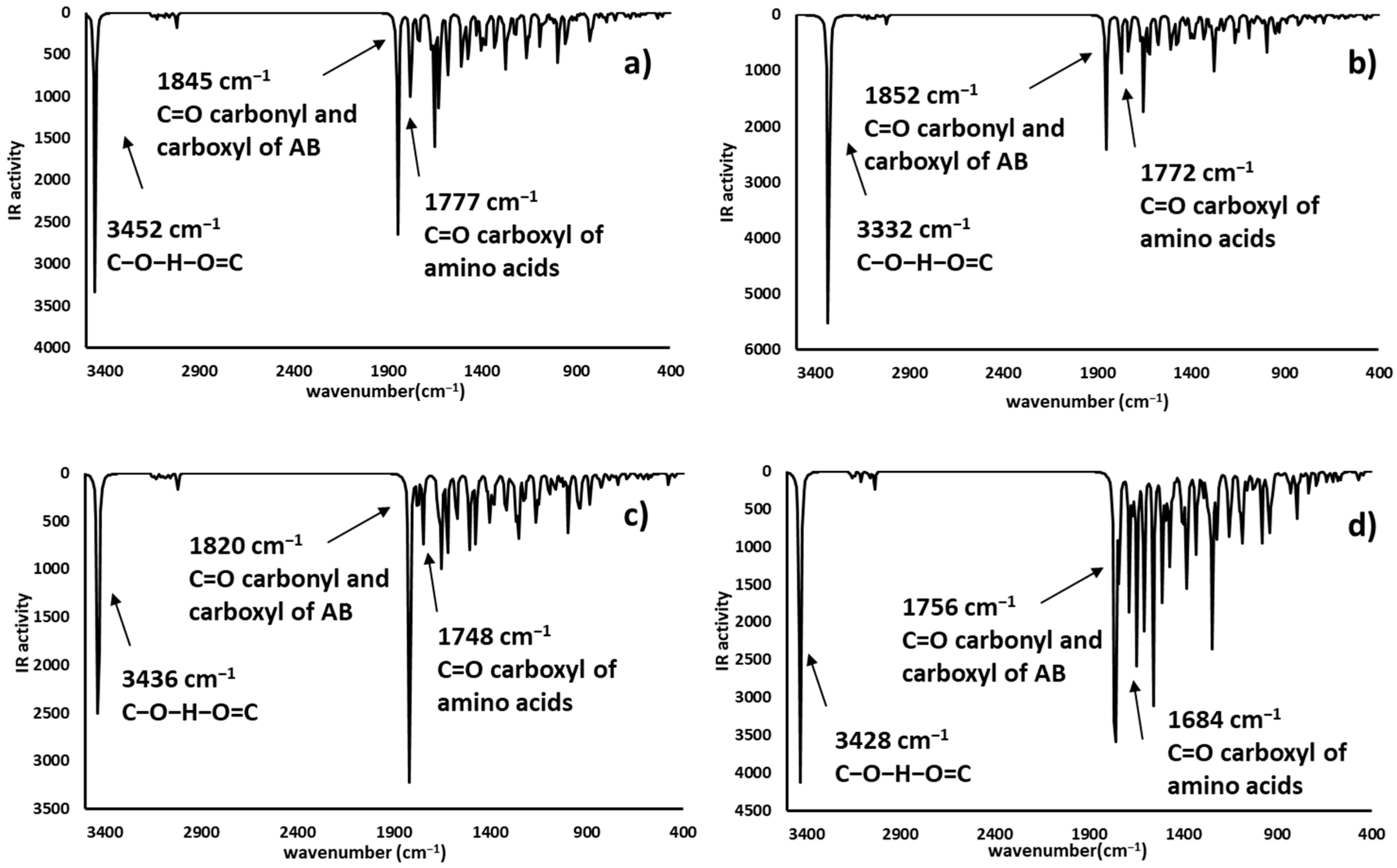
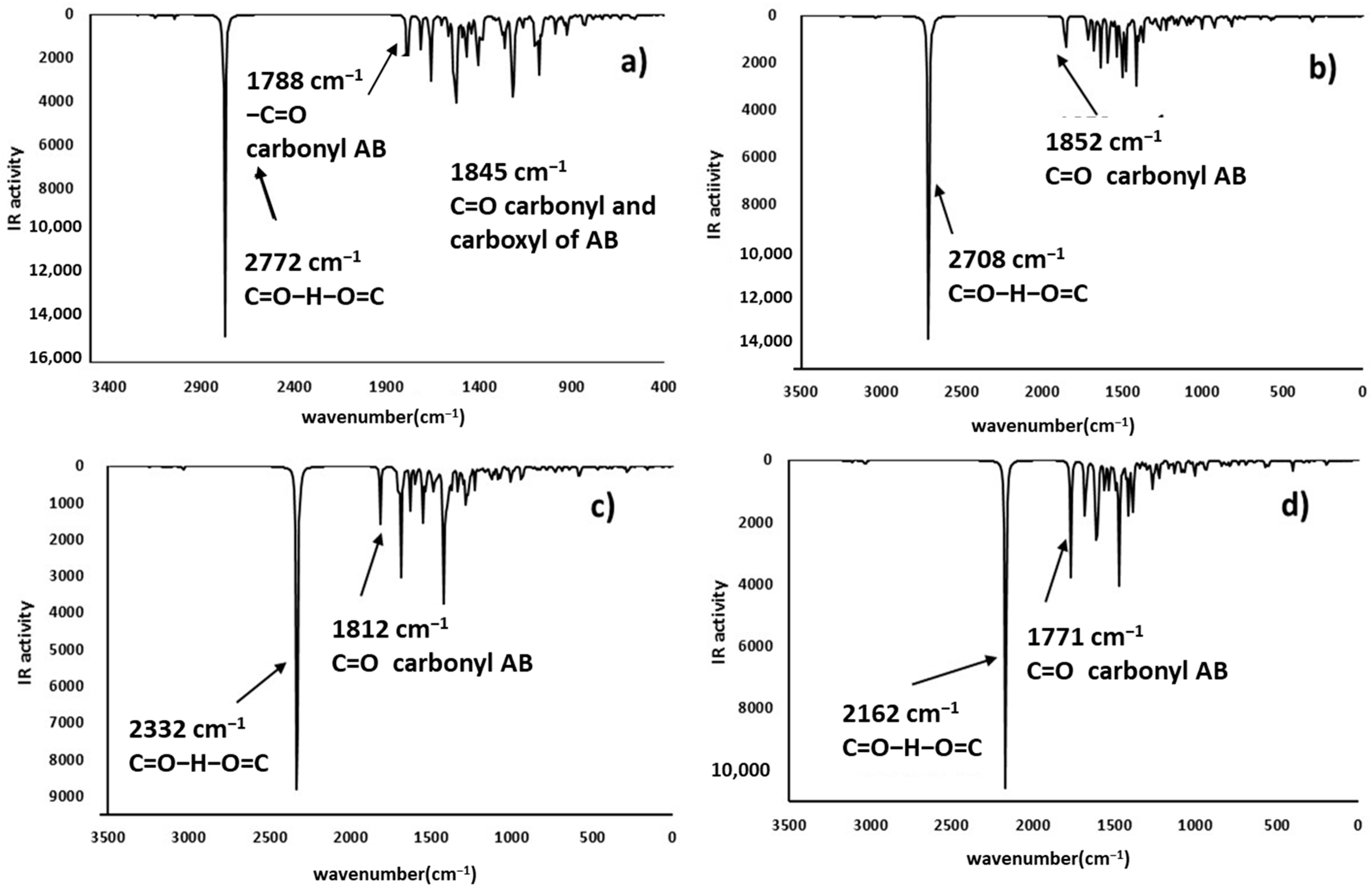
2.4. Infrared Spectrophotometric Studies of the Interactions
3. Conclusions
4. Materials and Methods
4.1. Optimization of the Structures
4.2. Thermochemical Parameters and Acidity of the Structure and Models
4.3. Molecular Electrostatic Surface
4.4. Vibrational Analysis
4.5. Interaction Energy Calculations
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Feibelman, T.P.; Cotty, P.J.; Doster, M.; Michailides, T. A morphologically distinct strain of Aspergillus nomius. Mycologia 1998, 90, 618–623. [Google Scholar] [CrossRef]
- Nesci, A.; Gsponer, N.; Etcheverry, M. Natural maize phenolic acids for control of aflatoxigenic fungi on maize. J. Food Sci. 2007, 72, M180–M185. [Google Scholar] [CrossRef] [PubMed]
- Phillips, T.D. Dietary clay in the chemoprevention of aflatoxin-induced disease. Toxicol. Sci. Off. J. Soc. Toxicol. 1999, 52, 118–126. [Google Scholar] [CrossRef] [PubMed]
- Ramales-Valderrama, R.; Vázquez-Durán, A.; Méndez-Albores, A. Biosorption of B-aflatoxins Using Biomasses Obtained from Formosa Firethorn [Pyracantha koidzumii (Hayata) Rehder]. Toxins 2016, 8, 218. [Google Scholar] [CrossRef]
- Smela, M.E.; Currier, S.S.; Bailey, E.A.; Essigmann, J.M. The chemistry and biology of aflatoxin B1: From mutational spectrometry to carcinogenesis. Carcinogenesis 2001, 22, 535–545. [Google Scholar] [CrossRef]
- Essigmann, J.M.; Croy, R.G.; Nadzan, A.M.; Busby, W.F.; Reinhold, V.N.; Büchi, G.; Wogan, G.N. Structural identification of the major DNA adduct formed by aflatoxin B1 in vitro. Proc. Natl. Acad. Sci. USA 1977, 74, 1870–1874. [Google Scholar] [CrossRef]
- Hernández-Meléndez, D.; Salas-Téllez, E.; Zavala-Franco, A.; Téllez, G.; Méndez-Albores, A.; Vázquez-Durán, A. Inhibitory effect of flower-shaped zinc oxide nanostructures on the growth and aflatoxin production of a highly toxigenic strain of aspergillus flavus link. Materials 2018, 11, 1265. [Google Scholar]
- Doyle, M.P.; Applebaum, R.S.; Brackett, R.E.; Marth, E.H. Physical, chemical and biological degradation of mycotoxins in foods and agricultural commodities. J. Food Prot. 1982, 45, 964–971. [Google Scholar] [CrossRef] [PubMed]
- Goldblatt, L. Aflatoxin: Scientific Background, Control, and Implications; Academic Press: London, UK, 1969; ISBN 0323148492. [Google Scholar]
- Nicolás-Vázquez, I.; Méndez-Albores, A.; Moreno-Martínez, E.; Miranda, R.; Castro, M. Role of Lactone Ring in Structural, Electronic, and Reactivity Properties of Aflatoxin B1: A Theoretical Study. Arch. Environ. Contam. Toxicol. 2010, 59, 393–406. [Google Scholar] [CrossRef]
- Sabbioni, G.; Skipper, P.L.; Büchi, G.; Tannenbaum, S.R. Isolation and characterization of the major serum albumin adduct formed by aflatoxin B 1 in vivo in rats. Carcinogenesis 1987, 8, 819–824. [Google Scholar] [CrossRef]
- Ivanova, B.; Spiteller, M. Raman Spectroscopic and Mass Spectrometric Determination of Aflatoxins. Food Anal. Methods 2014, 7, 242–256. [Google Scholar] [CrossRef]
- Martin, C.N.; Garner, R.C. Aflatoxin B-oxide generated by chemical or enzymic oxidation of aflatoxin B1 causes guanine substitution in nucleic acids. Nature 1977, 267, 863–865. [Google Scholar] [CrossRef] [PubMed]
- Nicolás-Vázquez, I.; Torres, J.H.; Borbolla, J.C.; Ruvalcaba, R.M.; Aceves-Hernández, J.M. Orlistat interaction with sibutramine and carnitine. A physicochemical and theoretical study. J. Mol. Struct. 2014, 1062, 1–12. [Google Scholar] [CrossRef]
- Moyers-Montoya, E.; García-Casillas, P.; Vargas-Requena, C.; Escobedo-González, R.; Martel-Estrada, S.-A.; Martínez-Pérez, C.A. Polycaprolactone/amino-β-cyclodextrin inclusion complex prepared by an electrospinning technique. Polymers 2016, 8, 395. [Google Scholar] [CrossRef] [PubMed]
- Vazquez-Flores, A.A.; Martinez-Gonzalez, A.I.; Alvarez-Parrilla, E.; Díaz-Sánchez, Á.G.; de la Rosa, L.A.; González-Aguilar, G.A.; Aguilar, C.N. Proanthocyanidins with a low degree of polymerization are good inhibitors of digestive enzymes because of their ability to form specific interactions: A hypothesis. J. Food Sci. 2018, 83, 2895–2902. [Google Scholar] [CrossRef]
- Martínez, J.; Rodríguez, M.H.; Escobedo-González, R.; Nicolás-Vázquez, M.I.; Saavedra-Leos, Z.; Ruvalcaba, R.M. Computational Characterization of Perezone, Isoperezone and their Sulfur-Derivatives: Anti-inflammatory Activity. ChemistrySelect 2019, 4, 13333–13346. [Google Scholar] [CrossRef]
- Tóth, K.; Nagy, L.; Mándi, A.; Kuki, Á.; Mézes, M.; Zsuga, M.; Kéki, S. Collision-induced dissociation of aflatoxins. Rapid Commun. Mass Spectrom. 2013, 27, 553–559. [Google Scholar] [CrossRef]
- Kumar, A.; Mohan, C.G.; Mishra, P.C. Molecular electrostatic potential and field as descriptors of hydrogen bonding and molecular activity. Effects of hybridization displacement charge. J. Mol. Struct. THEOCHEM 1996, 361, 135–144. [Google Scholar] [CrossRef]
- Escobedo-González, R.; Vargas-Requena, C.L.; Moyers-Montoya, E.; Aceves-Hernández, J.M.; Nicolás-Vázquez, M.I.; Miranda-Ruvalcaba, R. In silico study of the pharmacologic properties and cytotoxicity pathways in cancer cells of various indolylquinone analogues of perezone. Molecules 2017, 22, 1060. [Google Scholar] [CrossRef]
- Politzer, P.; Laurence, P.R.; Jayasuriya, K. Molecular electrostatic potentials: An effective tool for the elucidation of biochemical phenomena. Environ. Health Perspect. 1985, 61, 191. [Google Scholar] [CrossRef]
- Desiraju, G.R.; Steiner, T. The Weak Hydrogen Bond: In Structural Chemistry and Biology; Oxford university, Ed.; International Union of Crystal: New York, NY, USA, 2001; Volume 9. [Google Scholar]
- Smith, G.T.; Howard, J.A.K.; Wallis, J.D. Characterisation of weak intramolecular interactions in the topology of the experimental charge density of 2, 2′-ethynylenedibenzoic acid. Phys. Chem. Chem. Phys. 2001, 3, 4501–4507. [Google Scholar] [CrossRef]
- Steiner, T.; Desiraju, G.R. Distinction between the weak hydrogen bond and the van der Waals interaction. Chem. Commun. 1998, 891–892. [Google Scholar] [CrossRef]
- Oliveira, B.G.; Pereira, F.S.; de Araújo, R.; Ramos, M.N. The hydrogen bond strength: New proposals to evaluate the intermolecular interaction using DFT calculations and the AIM theory. Chem. Phys. Lett. 2006, 427, 181–184. [Google Scholar] [CrossRef]
- Wojtulewski, S.; Grabowski, S.J. Different donors and acceptors for intramolecular hydrogen bonds. Chem. Phys. Lett. 2003, 378, 388–394. [Google Scholar] [CrossRef]
- Cyrański, M.; Jezierska, A.; Klimentowska, P.; Panek, J.J.; Sporzyński, A. Impact of intermolecular hydrogen bond on structural properties of phenylboronic acid: Quantum chemical and X-ray study. J. Phys. Org. Chem. 2008, 21, 472–482. [Google Scholar] [CrossRef]
- Perrin, C.L.; Nielson, J.B. “Strong” hydrogen bonds in chemistry and biology. Annu. Rev. Phys. Chem. 1997, 48, 511–544. [Google Scholar] [CrossRef]
- Chen, J.; McAllister, M.A.; Lee, J.K.; Houk, K.N. Short, Strong Hydrogen Bonds in the Gas Phase and in Solution: Theoretical Exploration of pKa Matching and Environmental Effects on the Strengths of Hydrogen Bonds and Their Potential Roles in Enzymatic Catalysis. J. Org. Chem. 1998, 63, 4611–4619. [Google Scholar] [CrossRef]
- Shan, S.-O.; Herschlag, D. The change in hydrogen bond strength accompanying charge rearrangement: Implications for enzymatic catalysis. Biochemistry 1996, 93, 14474–14479. [Google Scholar] [CrossRef]
- Stewart, R.; Yates, K. The Protonation of the Carbonyl Group. I. The Basicity of Substituted Acetophenones. J. Am. Chem. Soc. 1958, 80, 6355–6359. [Google Scholar] [CrossRef]
- Berthelot, M.; Besseau, F.; Laurence, C. The Hydrogen-Bond Basicity pKHB Scale of Peroxides and Ethers. European J. Org. Chem. 1998, 1998, 925–931. [Google Scholar] [CrossRef]
- Shokri, A.; Abedin, A.; Fattahi, A.; Kass, S.R. Effect of Hydrogen Bonds on pKa Values: Importance of Networking. J. Am. Chem. Soc. 2012, 134, 10646–10650. [Google Scholar] [CrossRef] [PubMed]
- Nelson, D.L.; Lehninger, A.L.; Cox, M.M. Lehninger Principles of Biochemistry, 4th ed.; Freeman: New York, NY, USA, 2008. [Google Scholar]
- Včeláková, K.; Zusková, I.; Kenndler, E.; Gaš, B. Determination of cationic mobilities and pKa values of 22 amino acids by capillary zone electrophoresis. Electrophoresis 2004, 25, 309–317. [Google Scholar] [CrossRef] [PubMed]
- Brown, R.J.C. Hydrogen bonding of the ammonium ion. J. Mol. Struct. 1995, 345, 77–81. [Google Scholar] [CrossRef]
- Hillenbrand, E.A.; Scheiner, S. Analysis of the Principles Governing Proton-Transfer Reactions. Carboxyl Group. J. Am. Chem. Soc. 1986, 108, 7178–7186. [Google Scholar] [CrossRef]
- Mills, B.E.; Martin, R.L.; Shirley, D.A. Further Studies of the Core Binding Energy-Proton Affinity Correlation in Molecules. J. Am. Chem. Soc. 1976, 98, 2380–2385. [Google Scholar] [CrossRef][Green Version]
- Smith, S.R.; Thomas, T.D. Acidities and Basicities of Carboxylic Acids. Correlations between Core-Ionization Energies, Proton Affinities, and Gas-Phase Acidity. J. Am. Chem. Soc. 1978, 5460–5464. [Google Scholar]
- Stewart, R.; Yates, K. The Position of Protonation of the Carboxyl Group. J. Am. Chem. Soc. 1960, 82, 4059–4061. [Google Scholar] [CrossRef]
- Lommerse, J.P.M.; Price, S.L.; Taylor, R. Hydrogen bonding of carbonyl, ether, and ester oxygen atoms with alkanol hydroxyl groups. J. Comput. Chem. 1997, 18, 757–774. [Google Scholar] [CrossRef]
- Liang, C.Y.; Marchessault, R.H. Infrared spectra of crystalline polysaccharides. I. Hydrogen bonds in native celluloses. J. Polym. Sci. 1959, 37, 385–395. [Google Scholar] [CrossRef]
- Gellman, S.H.; Dado, G.P.; Liang, G.B.; Adams, B.R. Conformation-directing effects of a single intramolecular amide-amide hydrogen bond: Variable-temperature NMR and IR studies on a homologous diamide series. J. Am. Chem. Soc. 1991, 113, 1164–1173. [Google Scholar] [CrossRef]
- Zavala-Franco, A.; Hernández-Patlán, D.; Solís-Cruz, B.; López-Arellano, R.; Tellez-Isaias, G.; Vázquez-Durán, A.; Méndez-Albores, A. Assessing the Aflatoxin B1 Adsorption Capacity between Biosorbents Using an In Vitro Multicompartmental Model Simulating the Dynamic Conditions in the Gastrointestinal Tract of Poultry. Toxins 2018, 10, 484. [Google Scholar] [CrossRef] [PubMed]
- Billes, F.; Móricz, Á.M.; Tyihák, E.; Mikosch, H. Simulated vibrational spectra of aflatoxins and their demethylated products and the estimation of the energies of the demethylation reactions. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2006, 64, 600–622. [Google Scholar] [CrossRef] [PubMed]
- Asao, T.; Büchi, G.; Abdel-Kader, M.M.; Chang, S.B.; Wick, E.L.; Wogan, G.N. The Structures of Aflatoxins B and G1. J. Am. Chem. Soc. 1965, 87, 882–886. [Google Scholar] [CrossRef] [PubMed]
- Escobedo-González, R.; Méndez-Albores, A.; Villarreal-Barajas, T.; Aceves-Hernández, J.M.; Miranda-Ruvalcaba, R.; Nicolás-Vázquez, I. A Theoretical Study of 8-Chloro-9-Hydroxy-Aflatoxin B 1, the Conversion Product of Aflatoxin B 1 by Neutral Electrolyzed Water. Toxins 2016, 8, 225. [Google Scholar] [CrossRef]
- Deppmeier, B.J.; Driessen, A.J.; Hehre, T.S.; Hehre, W.J.; Johnson, J.A.; Klunzinger, P.E.; Leonard, J.M.; Pham, I.N.; Pietro, W.J.; Jianguo, Y.; et al. Spartan 06; Wavefunction Inc.: Irvine, CA, USA, 2006. [Google Scholar]
- Frisch, M.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D. 01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Beke, A.D. Density-functional exchanges-energy approximation with correct asymptotic behavior. Phys. Chem. Chem. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. [Google Scholar] [CrossRef]
- Gill, P.M.W.; Johnson, B.G.; Pople, J.A.; Frisch, M.J. The performance of the Becke-Lee-Yang-Parr (B-LYP) density functional theory with various basis sets. Chem. Phys. Lett. 1992, 197, 499–505. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. IV. A new dynamical correlation functional and implications for exact-exchange mixing. J. Chem. Phys. 1998, 104, 1040–1046. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Clark, T.; Chandrasekhar, J.; Spitznagel, G.W.; Schleyer, P.V.R. Efficient diffuse function-augmented basis sets for anion calculations. III. The 3-21+ G basis set for first-row elements, Li--F. J. Comput. Chem. 1983, 4, 294–301. [Google Scholar] [CrossRef]
- Hariharan, P.C.; Pople, J.A. The influence of polarization functions on molecular orbital hydrogenation energies. Theoretica Chim. Acta 1973, 28, 213–222. [Google Scholar] [CrossRef]
- Escobedo-González, R.G.; Pérez Martínez, H.; Nicolás-Vázquez, M.I.; Martínez, J.; Gómez, G.; Serrano, J.N.; Carranza Téllez, V.; Vargas-Requena, C.L.; Miranda Ruvalcaba, R. Green production of indolylquinones, derivatives of perezone, and related molecules, promising antineoplastic compounds. J. Chem. 2016, 2016, 1–10. [Google Scholar] [CrossRef]
- Foresman, J.B.; Frisch, A. Exploring Chemistry with Electronic Structure Methods: A Guide to using Gaussian; Gaussian, Inc.: Pittsburgh, PA, USA, 1996. [Google Scholar]
- Cossi, M.; Barone, V.; Cammi, R.; Tomasi, J. Ab initio study of solvated molecules: A new implementation of the polarizable continuum model. Chem. Phys. Lett. 1996, 255, 327–335. [Google Scholar] [CrossRef]
- Cances, E.; Mennucci, B.; Tomasi, J. A new integral equation formalism for the polarizable continuum model: Theoretical background and applications to isotropic and anisotropic dielectrics. J. Chem. Phys. 1997, 107, 3032–3041. [Google Scholar] [CrossRef]
- Silva, C.O.; da Silva, E.C.; Nascimento, M.A.C. Ab Initio Calculations of Absolute pKa Values in Aqueous Solution II. Aliphatic Alcohols, Thiols, and Halogenated Carboxylic Acids. J. Phys. Chem. A 2000, 104, 2402–2409. [Google Scholar] [CrossRef]
- Huczyński, A.; Janczak, J.; Łowicki, D.; Brzezinski, B. Monensin A acid complexes as a model of electrogenic transport of sodium cation. Biochim. Biophys. Acta BBA Biomembr. 2012, 1818, 2108–2119. [Google Scholar] [CrossRef]
- Alam, M.J.; Ahmad, S. Anharmonic vibrational studies of L-aspartic acid using HF and DFT calculations. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2012, 96, 992–1004. [Google Scholar] [CrossRef]
- Ramalingam, S.; Babu, P.D.S.; Periandy, S.; Fereyduni, E. Vibrational investigation, molecular orbital studies and molecular electrostatic potential map analysis on 3-chlorobenzoic acid using hybrid computational calculations. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2011, 84, 210–220. [Google Scholar] [CrossRef]
- Escobedo-González, R.G.; Bahena, L.; Arias Tellez, J.L.; Hinojosa Torres, J.; Ruvalcaba, R.M.; Aceves-Hernández, J.M. Characterization and comparison of perezone with some analogues. Experimental and theoretical study. J. Mol. Struct. 2015, 1097, 98–105. [Google Scholar] [CrossRef]
- Fragoso-Medina, A.J.; Escobedo-González, R.G.; Nicolás-Vázquez, M.I.; Arroyo-Razo, G.A.; Noguez-Córdova, M.O.; Miranda-Ruvalcaba, R. A DFT study of the geometrical, spectroscopical and reactivity properties of diindolylmethane-phenylboronic acid hybrids. Molecules 2017, 22, 1744. [Google Scholar] [CrossRef] [PubMed]
- Handy, N.C.; Murray, C.W.; Amos, R.D. Study of methane, acetylene, ethene, and benzene using Kohn-Sham theory. J. Phys. Chem. 1993, 97, 4392–4396. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab initio Calculation of Vibrational Absorption and Circular Dichroism Spectra using Density Functional force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Devlin, F.J.; Finley, J.W.; Stephens, P.J.; Frisch, M.J. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields: A comparison of local, nonlocal, and hybrid density functionals. J. Phys. Chem. 1995, 99, 16883–16902. [Google Scholar] [CrossRef]
- Lee, S.Y.; Boo, B.H. Density functional theory study of vibrational spectra of anthracene neutral and radical cation. Bull. Korean Chem. Soc. 1996, 17, 754–759. [Google Scholar]
- Rui-Zhou, Z.; Xiao-Hong, L.; Xian-Zhou, Z. Molecular structure, vibrational spectra and NBO analysis on 1N-acetyl-3-(2, 4dichloro-5-fluoro-phenyl)-5-(p-methyl-phenyl)-2-pyrazoline using DFT method. Indian J. Pure Appl. Phys. 2011, 49, 731–739. [Google Scholar]




| Protonated Structures AFB1 | Water Solution | Gas Phase | ||
|---|---|---|---|---|
| Energy Kcal/mol | ΔE Kcal/mol | Energy Kcal/mol | ΔE Kcal/mol | |
| A1 | −694,634.98 | 25.91 | −694,577.79 | 38.45 |
| A2 | −694,633.57 | 27.32 | −694,585.85 | 30.38 |
| A3 | −694,660.89 | 0 | −694,616.24 | 0 |
| A4 | −694,657.58 | 3.31 | −694,608.31 | 7.96 |
| A5 | −694,629.32 | 31.57 | −694,560.57 | 55.66 |
| A6 | −694,651.91 | 8.98 | −694,602.81 | 13.43 |
| A7 | −694,655.76 | 5.14 | −694,611.20 | 5.03 |
| AFB1H+ ⇆ AFB1 + H+ | ||||
|---|---|---|---|---|
| Structure | ΔG Formation kcal/mol | ΔG Dissociation Reaction kcal/mol | Ka | pKa |
| A1 | −694,440.146 | −30.914 | 4.575 × 1022 | −22.661 |
| A2 | −694,447.074 | −37.843 | 5.483 × 1027 | −27.739 |
| A3 | −694,473.686 | −64.454 | 1.759 × 1047 | −47.245 |
| A4 | −694,466.299 | −57.067 | 6.767 × 1041 | −41.830 |
| A5 | −694,420.522 | −11.291 | 1.888 × 108 | −8.276 |
| A6 | −694,461.097 | −51.865 | 1.041 × 1038 | −38.018 |
| A7 | −694,468.856 | −59.625 | 5.071 × 1043 | −43.705 |
| AFB1H+ ⇆ AFB1 + H+ | ||||
|---|---|---|---|---|
| Structure | ΔG Formation kcal/mol | ΔG Dissociation Reaction kcal/mol | Ka | pKa |
| A1 | −694,497.342 | −0.230 | 0.68 | 0.17 |
| A2 | −694,494.788 | −2.324 | 50.53 | −1.70 |
| A3 | −694,518.340 | 21.228 | 2.76 × 1016 | 15.56 |
| A4 | −694,515.571 | 18.459 | 2.95 × 1014 | 13.53 |
| A5 | −694,489.274 | −7.838 | 556,713.56 | −5.76 |
| A6 | −694,510.194 | 13.082 | 2.58 × 1010 | 9.59 |
| A7 | −694,513.410 | 16.298 | 1.13 × 1012 | 11.95 |
| Phase | Structure/Stability | A3-OHCH3 | A4-OHCH3 | A6-OHCH3 | A7-OHCH3 |
|---|---|---|---|---|---|
| Gas | Structure energy (kcal/mol) | −767,270.3 | −767,265.1 | −767,259.8 | −767,269.4 |
| Interaction energy (kcal/mol) | −15.8 | −10.7 | −18.8 | −19.9 | |
| Water | Structure energy (kcal/mol) | −767,310.6 | −767,310.8 | −767,305.8 | −767,310.6 |
| Interaction energy (kcal/mol) | −7.7 | −7.9 | −12.0 | −12.8 |
| Phase | Structure/Stability | A3-+H3NCH3 | A4-+H3NCH3 | A6-+H3NCH3 | A6-+H3NCH3 |
|---|---|---|---|---|---|
| Gas | Structure energy (kcal/mol) | −754,981.1 | −754,979.8 | −754,976.5 | −754,977.8 |
| Interaction energy (kcal/mol) | 27.8 | 29.1 | 27.4 | 26.1 | |
| Water | Structure energy (kcal/mol) | −755,123.2 | −755,120.4 | −755,115.5 | −755,118.8 |
| Interaction energy (kcal/mol) | 0.3 | −1.2 | −5.3 | -8.6 |
| Phase | Structure/Stability | A3-−OOCCH3 | A4-−OOCCH3 | A6-−OOCCH3 | A7-−OOCCH3 |
|---|---|---|---|---|---|
| Gas | Structure energy (kcal/mol) | −838,180.2 | −838,181.1 | −838,180.1 | −838,177.7 |
| Interaction energy (kcal/mol) | −124.5 | −125.3 | −137.8 | −126.9 | |
| Water | Structure energy (kcal/mol) | −838,197.7 | −838,198.0 | −838,197.2 | −838,196.9 |
| Interaction energy (kcal/mol) | −31.7 | −32.0 | −40.2 | −36.0 |
| Phase | Structure/Stability | A3-O=C(CH3)2 | A4-O=C(CH3)2 | A6-O=C(CH3)2 | A7-O=C(CH3)2 |
|---|---|---|---|---|---|
| Gas | Structure energy (kcal/mol) | −815,867.5 | −815,867.3 | −815,862.2 | −815,865.0 |
| Interaction energy (kcal/mol) | −14.0 | −18.9 | −22.1 | −16.6 | |
| Water | Structure energy (kcal/mol) | −815,908.0 | −815,910.0 | −815,905.2 | −815,903.0 |
| Interaction energy (kcal/mol) | −5.2 | −7.3 | −11.4 | −5.4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Méndez-Albores, A.; Escobedo-González, R.; Aceves-Hernández, J.M.; García-Casillas, P.; Nicolás-Vázquez, M.I.; Miranda-Ruvalcaba, R. A Theoretical Study of the Adsorption Process of B-aflatoxins Using Pyracantha koidzumii (Hayata) Rehder Biomasses. Toxins 2020, 12, 283. https://doi.org/10.3390/toxins12050283
Méndez-Albores A, Escobedo-González R, Aceves-Hernández JM, García-Casillas P, Nicolás-Vázquez MI, Miranda-Ruvalcaba R. A Theoretical Study of the Adsorption Process of B-aflatoxins Using Pyracantha koidzumii (Hayata) Rehder Biomasses. Toxins. 2020; 12(5):283. https://doi.org/10.3390/toxins12050283
Chicago/Turabian StyleMéndez-Albores, Abraham, René Escobedo-González, Juan Manuel Aceves-Hernández, Perla García-Casillas, María Inés Nicolás-Vázquez, and René Miranda-Ruvalcaba. 2020. "A Theoretical Study of the Adsorption Process of B-aflatoxins Using Pyracantha koidzumii (Hayata) Rehder Biomasses" Toxins 12, no. 5: 283. https://doi.org/10.3390/toxins12050283
APA StyleMéndez-Albores, A., Escobedo-González, R., Aceves-Hernández, J. M., García-Casillas, P., Nicolás-Vázquez, M. I., & Miranda-Ruvalcaba, R. (2020). A Theoretical Study of the Adsorption Process of B-aflatoxins Using Pyracantha koidzumii (Hayata) Rehder Biomasses. Toxins, 12(5), 283. https://doi.org/10.3390/toxins12050283