The Influence of Piezoelectric Transducer Stimulating Sites on the Performance of Implantable Middle Ear Hearing Devices: A Numerical Analysis
Abstract
:1. Introduction
2. Materials and Methods
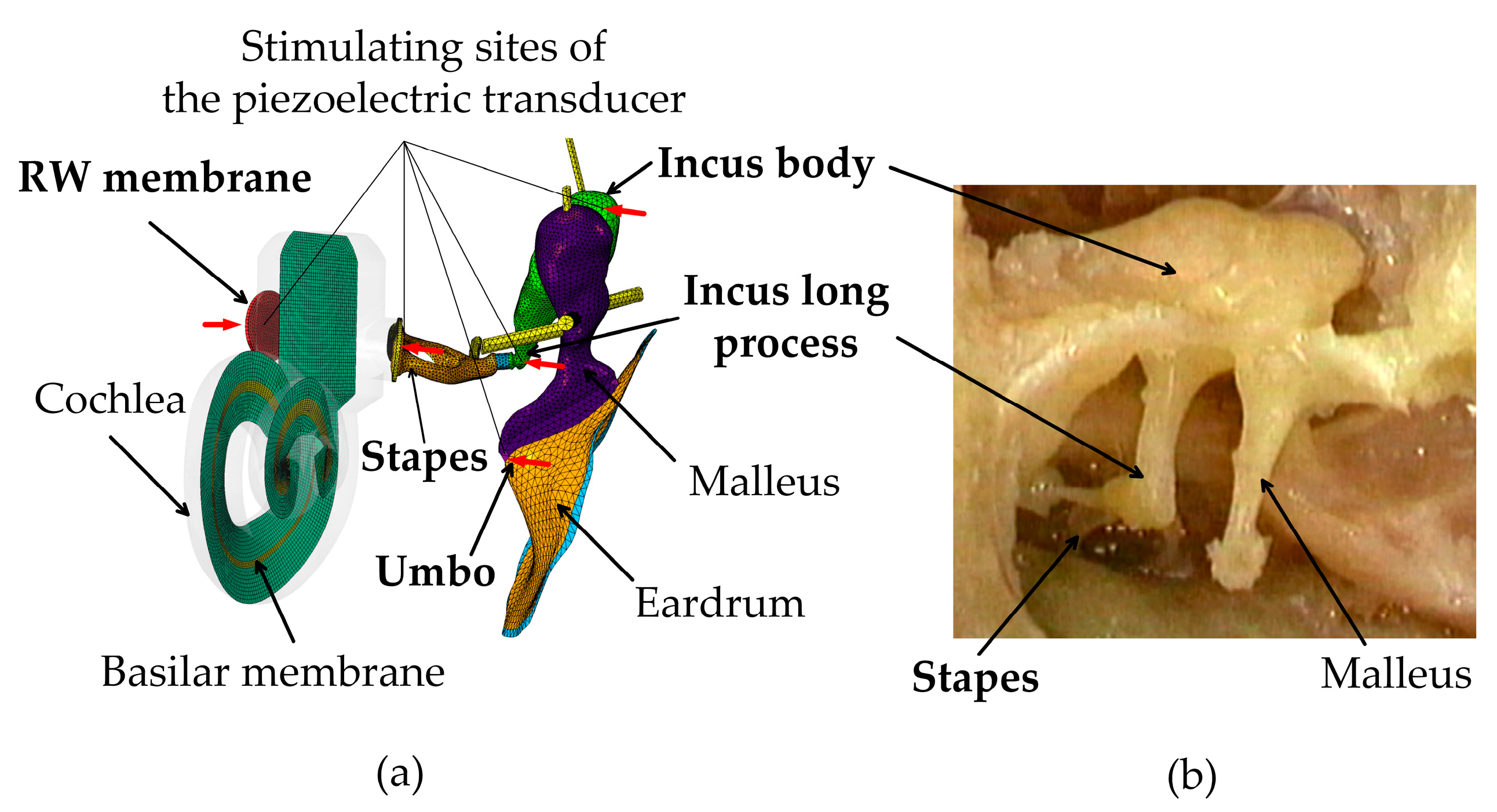
2.1. Constructions of the Human Ear FE Model
2.2. Material Properties
2.3. Piezoelectric Transducer Simulation
2.4. Equivalent Sound Pressure Level
3. Results
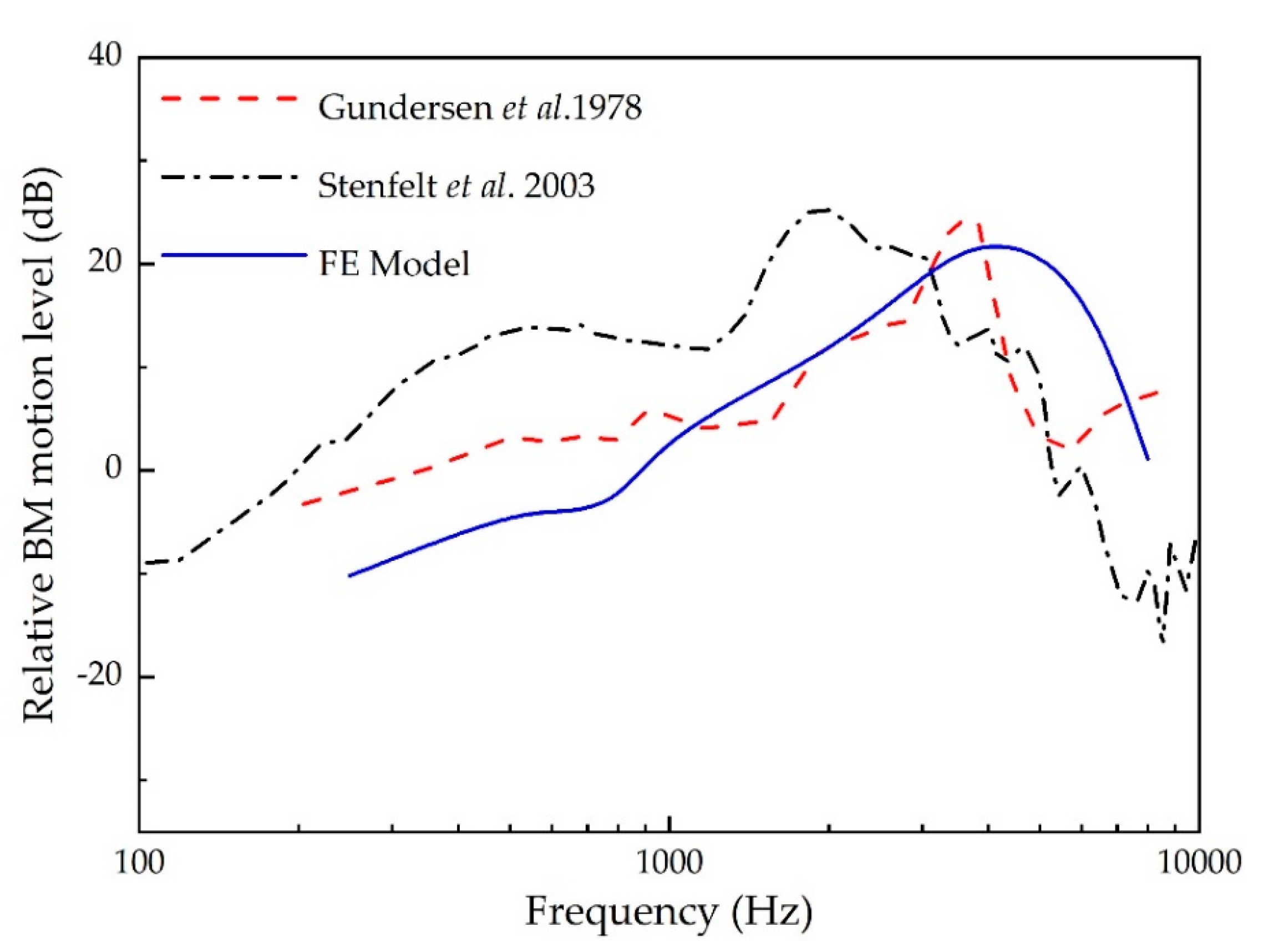
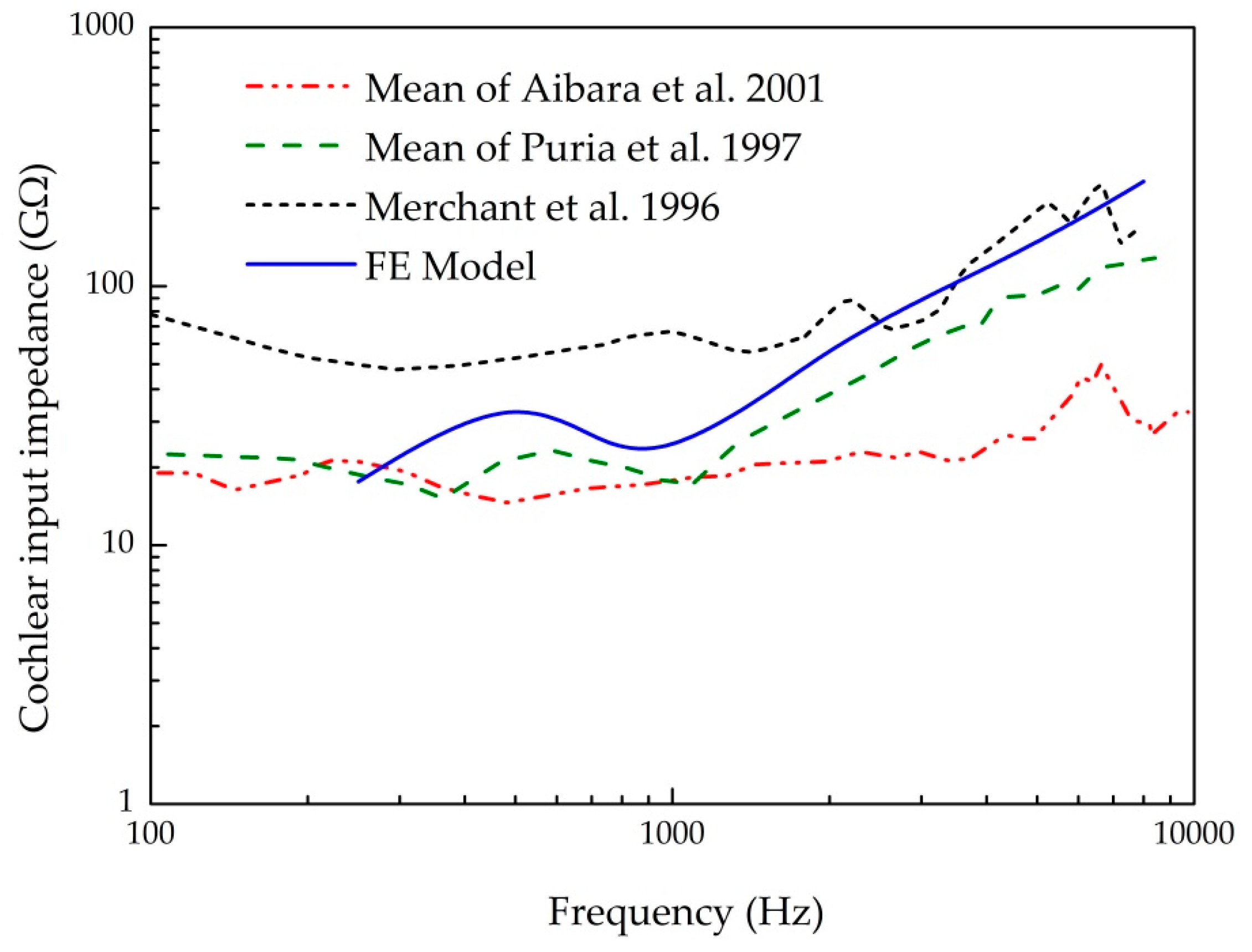
3.1. Validation of the Human Ear Finite Element Model
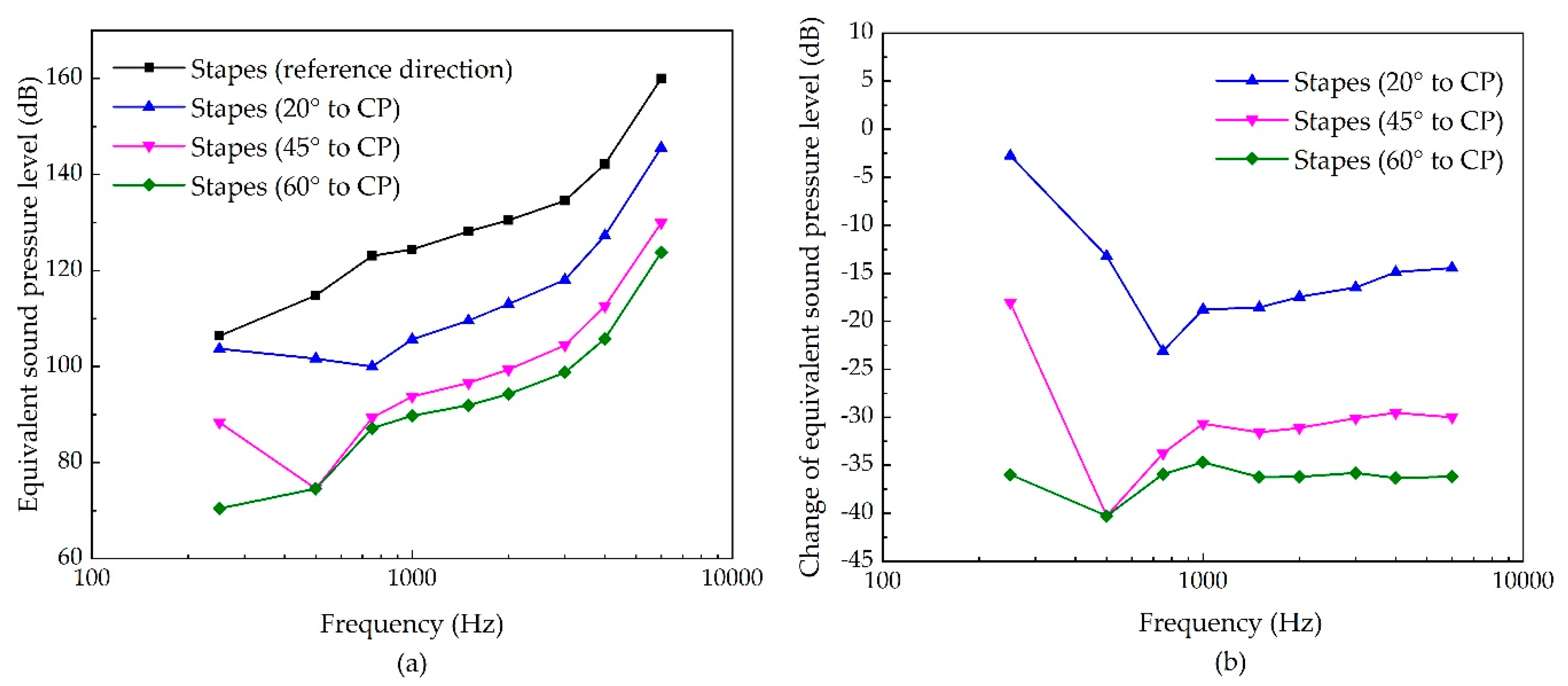
3.2. The Stimulating Site’s Influence on the Piezoelectric Transducer’s Performance
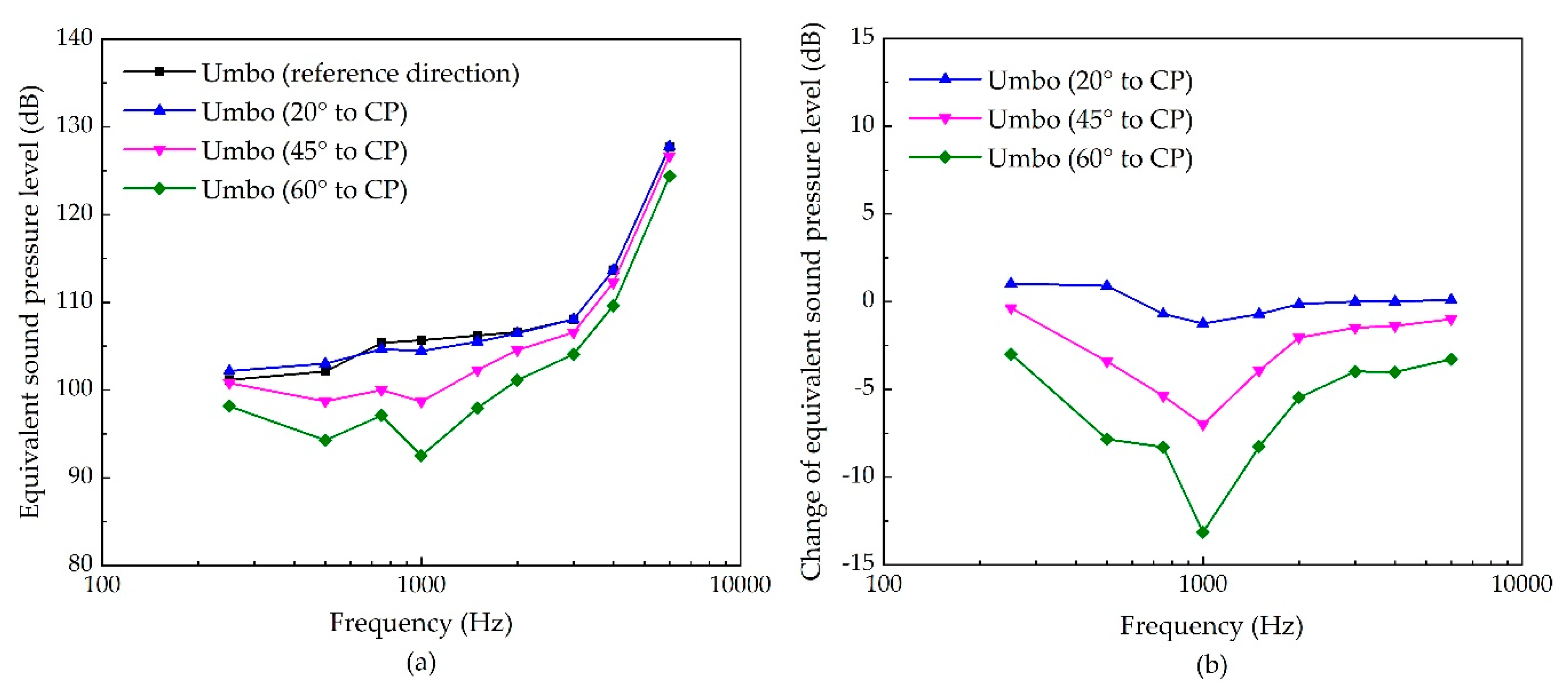
3.3. The Sensitivities of Each Stimulating Site to the Changes of Excitation’s Direction
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- World Health Organization. Deafness and Hearing Loss. Key Facts. Available online: https://www.who.int/en/news-room/fact-sheets/detail/deafness-and-hearing-loss (accessed on 30 September 2019).
- Angeli, S.I.; Yan, D.; Telischi, F.; Balkany, T.J.; Ouyang, X.M.; Du, L.L.; Eshraghi, A.; Goodwin, L.; Liu, X.Z. Etiologic diagnosis of sensorineural hearing loss in adults. Otolaryngol. Head Neck Surg. 2005, 132, 890–895. [Google Scholar] [CrossRef] [PubMed]
- Moore, B.C.J. Cochlear Hearing Loss: Physiological, Psychological and Technical Issues, 2nd ed.; Wiley Chichester: John Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Hong, E.-P.; Kim, M.-K.; Park, I.-Y.; Lee, S.-H.; Roh, Y.; Cho, J.-H. Vibration Modeling and Design of Piezoelectric Floating Mass Transducer for Implantable Middle Ear Hearing Devices. IEICE Trans. Fundam. 2007, E90-A, 1620–1627. [Google Scholar] [CrossRef]
- Haynes, D.S.; Young, J.A.; Wanna, G.B.; Glasscock, M.E. Middle ear implantable hearing devices: An overview. Trends Amplif. 2009, 13, 206–214. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Cheng, J.; Yang, J.; Rao, Z.; Cheng, G.; Yang, S.; Huang, X.; Wang, M. Concept and Evaluation of a New Piezoelectric Transducer for an Implantable Middle Ear Hearing Device. Sensors 2017, 17, 2515. [Google Scholar] [CrossRef]
- Maurer, J.; Savvas, E. The Esteem System: A totally implantable hearing device. Adv. Otorhinolaryngol. 2010, 69, 59–71. [Google Scholar] [CrossRef] [PubMed]
- Perkins, R.; Fay, J.P.; Rucker, P.; Rosen, M.; Olson, L.; Puria, S. The EarLens system: New sound transduction methods. Hear. Res. 2010, 263, 104–113. [Google Scholar] [CrossRef]
- Song, Y.-L.; Jian, J.-T.; Chen, W.-Z.; Shih, C.-H.; Chou, Y.-F.; Liu, T.-C.; Lee, C.-F. The development of a non-surgical direct drive hearing device with a wireless actuator coupled to the tympanic membrane. Appl. Acoust. 2013, 74, 1511–1518. [Google Scholar] [CrossRef]
- Hong, E.-P.; Park, I.-Y.; Seong, K.-W.; Cho, J.-H. Evaluation of an implantable piezoelectric floating mass transducer for sensorineural hearing loss. Mechatronics 2009, 19, 965–971. [Google Scholar] [CrossRef]
- Wang, Z.; Mills, R.; Luo, H.; Zheng, X.; Hou, W.; Wang, L.; Brown, S.I.; Cuschieri, A. A micropower miniature piezoelectric actuator for implantable middle ear hearing device. IEEE Trans. Biomed. Eng. 2011, 58, 452–458. [Google Scholar] [CrossRef]
- Komori, M.; Yanagihara, N.; Hinohira, Y.; Hato, N.; Gyo, K. Long-term results with the Rion E-type semi-implantable hearing aid. Otolaryngol. Head Neck Surg. 2010, 143, 422–428. [Google Scholar] [CrossRef]
- Shin, D.H.; Cho, J.H. Piezoelectric Actuator with Frequency Characteristics for a Middle-Ear Implant. Sensors 2018, 18, 1694. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Wang, H.; Rao, Z.; Yang, J.; Yang, S. Numerical Study and Optimization of a Novel Piezoelectric Transducer for a Round-Window Stimulating Type Middle-Ear Implant. Micromachines 2019, 10, 40. [Google Scholar] [CrossRef] [PubMed]
- Brkic, F.F.; Riss, D.; Auinger, A.; Zoerner, B.; Arnoldner, C.; Baumgartner, W.D.; Gstoettner, W.; Vyskocil, E. Long-Term Outcome of Hearing Rehabilitation With An Active Middle Ear Implant. Laryngoscope 2019, 129, 477–481. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Gan, R.Z. A comprehensive model of human ear for analysis of implantable hearing devices. IEEE Trans. Biomed. Eng. 2011, 58, 3024–3027. [Google Scholar] [CrossRef] [PubMed]
- Deveze, A.; Koka, K.; Tringali, S.; Jenkins, H.A.; Tollin, D.J. Techniques to improve the efficiency of a middle ear implant: Effect of different methods of coupling to the ossicular chain. Otol. Neurotol. 2013, 34, 158–166. [Google Scholar] [CrossRef] [PubMed]
- Bornitz, M.; Hardtke, H.J.; Zahnert, T. Evaluation of implantable actuators by means of a middle ear simulation model. Hear. Res. 2010, 263, 145–151. [Google Scholar] [CrossRef]
- Lee, J.; Seong, K.; Lee, S.-H.; Lee, K.-Y.; Cho, J.-H. Comparison of auditory responses determined by acoustic stimulation and by mechanical round window stimulation at equivalent stapes velocities. Hear. Res. 2014, 314, 65–71. [Google Scholar] [CrossRef]
- Gentil, F.; Parente, M.; Martins, P.; Garbe, C.; Jorge, R.N.; Ferreira, A. The influence of the mechanical behaviour of the middle ear ligaments: A finite element analysis. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2011, 225, 68–76. [Google Scholar] [CrossRef]
- Francesca, A.; Maurizio, B.; Helge, R.A. Is the human round window really round? An anatomic study with surgical implications. Otol. Neurotol. 2014, 35, 1354–1360. [Google Scholar]
- Zhang, J.; Zou, D.; Tian, J.; Ta, N.; Rao, Z. A comparative finite-element analysis of acoustic transmission in human cochlea during forward and reverse stimulations. Appl. Acoust. 2019, 145, 278–289. [Google Scholar] [CrossRef]
- Sun, Q.; Gan, R.Z.; Chang, K.H.; Dormer, K.J. Computer-integrated finite element modeling of human middle ear. Biomech. Modeling Mechanobiol. 2002, 1, 109–122. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Gan, R.Z. Finite element modeling of energy absorbance in normal and disordered human ears. Hear. Res. 2013, 301, 146–155. [Google Scholar] [CrossRef] [PubMed]
- Zhou, K.; Liu, H.; Yang, J.; Zhao, Y.; Rao, Z.; Yang, S. Influence of middle ear disorder in round-window stimulation using a finite element human ear model. Acta Bioeng. Biomech. 2019, 21. [Google Scholar] [CrossRef]
- Gundersen, T.; Skarstein, O.; Sikkeland, T. A study of the vibration of the basilar membrane in human temporal bone preparations by the use of the Mossbauer effect. Acta Oto-Laryngologica 1978, 86, 225–232. [Google Scholar] [CrossRef]
- Gan, R.Z.; Cheng, T.; Dai, C.; Yang, F.; Wood, M.W. Finite element modeling of sound transmission with perforations of tympanic membrane. J. Acoust. Soc. Am. 2009, 126, 243–253. [Google Scholar]
- Stenfelt, S.; Puria, S.; Hato, N.; Goode, R.L. Basilar membrane and osseous spiral lamina motion in human cadavers with air and bone conduction stimuli. Hear. Res. 2003, 181, 131–143. [Google Scholar] [CrossRef]
- Aibara, R.; Welsh, J.T.; Puria, S.; Goode, R.L. Human middle-ear sound transfer function and cochlear input impedance. Hear. Res. 2001, 152, 100–109. [Google Scholar] [CrossRef]
- Puria, S.; Peake, W.T.; Rosowski, J.J. Sound-pressure measurements in the cochlear vestibule of human-cadaver ears. J. Acoust. Soc. Am. 1997, 101, 2754–2770. [Google Scholar] [CrossRef]
- Merchant, S.N.; Ravicz, M.E.; Rosowski, J.J. Acoustic input impedance of the stapes and cochlea in human temporal bones. Hear. Res. 1996, 97, 30–45. [Google Scholar] [CrossRef]
- Lee, C.F.; Chen, P.R.; Lee, W.J.; Chen, J.H.; Liu, T.C. Three-dimensional reconstruction and modeling of middle ear biomechanics by high-resolution computed tomography and finite element analysis. Laryngoscope 2006, 116, 711–716. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, H.; Yang, J.; Huang, X.; Liu, W.; Xue, L. Influence of ossicular chain malformation on the performance of round-window stimulation: A finite element approach. Proc. Inst. Mech. Eng. H 2019, 233, 584–594. [Google Scholar] [CrossRef] [PubMed]
- Yao, W.; Tang, D.; Chen, Y.; Li, B. Study on vibration characteristics and transmission performance of round window membrane under inverse excitation. J. Mech. Med. Biol. 2018, 18, 1850033. [Google Scholar] [CrossRef]
- Liu, H.; Xu, D.; Yang, J.; Yang, S.; Cheng, G.; Huang, X. Analysis of the influence of the transducer and its coupling layer on round window stimulation. Acta Bioeng. Biomech. 2017, 19, 103–111. [Google Scholar] [PubMed]
- Koch, M.; Essinger, T.M.; Bornitz, M.; Zahnert, T. Examination of a mechanical amplifier in the incudostapedial joint gap: FEM simulation and physical model. Sensors 2014, 14, 14356–14374. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, X.; Hu, Y.; Wang, Z.; Shi, H. Finite element analysis of the coupling between ossicular chain and mass loading for evaluation of implantable hearing device. Hear. Res. 2011, 280, 48–57. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Guan, X.; Zhang, T.; Gan, R.Z. Measurement of basilar membrane motion during round window stimulation in guinea pigs. J. Assoc. Res. Otolaryngol. 2014, 15, 933–943. [Google Scholar] [CrossRef] [Green Version]
- Edom, E.; Obrist, D.; Henniger, R.; Kleiser, L.; Sim, J.H.; Huber, A.M. The effect of rocking stapes motions on the cochlear fluid flow and on the basilar membrane motion. J. Acoust. Soc. Am. 2013, 134, 3749–3758. [Google Scholar] [CrossRef] [Green Version]
- Koike, T.; Wada, H.; Kobayashi, T. Modeling of the human middle ear using the finite-element method. J. Acoust. Soc. Am. 2002, 111, 1306–1317. [Google Scholar] [CrossRef]
- Wang, Z.G.; Abel, E.W.; Mills, R.P.; Liu, Y. Assessment of multi-layer piezoelectric actuator technology for middle-ear implants. Mechatronics 2002, 12, 3–17. [Google Scholar] [CrossRef]
- Park, I.Y.; Shimizu, Y.; O’Connor, K.N.; Puria, S.; Cho, J.H. Comparisons of electromagnetic and piezoelectric floating-mass transducers in human cadaveric temporal bones. Hear. Res. 2011, 272, 187–192. [Google Scholar] [CrossRef] [Green Version]
- Arnold, A.; Kompis, M.; Candreia, C.; Pfiffner, F.; Häusler, R.; Stieger, C. The floating mass transducer at the round window: Direct transmission or bone conduction? Hear. Res. 2010, 263, 120–127. [Google Scholar] [CrossRef] [PubMed]
- Sprinzl, G.M.; Wolf-Magele, A.; Schnabl, J.; Koci, V. The active middle ear implant for the rehabilitation of sensorineural, mixed and conductive hearing losses. Laryngorhinootologie 2011, 90, 560–572. [Google Scholar] [CrossRef] [PubMed]
- Ko, W.H.; Zhu, W.L.; Kane, M.; Maniglia, A.J. Engineering principles applied to implantable otologic devices. Otolaryngol. Clin. N. Am. 2001, 34, 299–314. [Google Scholar] [CrossRef]
- De Greef, D.; Pires, F.; Dirckx, J.J. Effects of model definitions and parameter values in finite element modeling of human middle ear mechanics. Hear. Res. 2017, 344, 195–206. [Google Scholar] [CrossRef] [PubMed]








| Components | Layer | Young’s Modulus (N/m2) | Density (kg/m3) |
|---|---|---|---|
| Eardrum annulus ligament | 2.00 × 105 | 1.20 × 103 | |
| Eardrum pars tensa | Outer layer | 1.00 × 107 | 1.20 × 103 |
| Middle layer | Eθ = 2.00 × 107, Er = 3.20 × 107 | ||
| Inner layer | 1.00 × 107 | ||
| Eardrum pars flaccida | 1.00 × 107 | 1.20 × 103 | |
| Malleus handle | 1.41 × 1010 | 3.70 × 103 | |
| Malleus neck | 1.41 × 1010 | 4.53 × 103 | |
| Malleus head | 1.41 × 1010 | 2.55 × 103 | |
| Incus body | 1.41 × 1010 | 2.36 × 103 | |
| Incus short process | 1.41 × 1010 | 2.26 × 103 | |
| Incus long process | 1.41 × 1010 | 5.08 × 103 | |
| Stapes | 1.41 × 1010 | 2.20 × 103 | |
| Incudomallear joint | 6.00 × 107 | 3.20 × 103 | |
| Incudostapedial joint | 2.00 × 106 | 1.20 × 103 | |
| Lateral malleolar ligament | 6.70 × 106 | 2.50 × 103 | |
| Superior malleolar ligament | 4.90 × 106 | 2.50 × 103 | |
| Anterior malleolar ligament | 8.00 × 106 | 2.50 × 103 | |
| Posterior incudal ligament | 6.50 × 106 | 2.50 × 103 | |
| Superior incudal ligament | 4.90 × 106 | 1.00 × 103 | |
| Tensor tympani tendon | 8.00 × 106 | 2.50 × 103 | |
| Stapedial tendon | 5.20 × 107 | 1.00 × 103 | |
| Stapedial annulus ligament | 1.00 × 104 | 1.20 × 103 |
| Components | e1 | τ1 (μs) |
|---|---|---|
| Eardrum annulus ligament | 3.2 | 28 |
| Eardrum pars flaccida | 2.29 | 25 |
| Eardrum pars tensa | 2.8 | 25 |
| Incudomallear joint | 3.0 | 20 |
| Incudostapedial joint | 50 | 20 |
| Stapedial annulus ligament | 2.4 | 25 |
| RW membrane | 3.0 | 30 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Zhao, Y.; Yang, J.; Rao, Z. The Influence of Piezoelectric Transducer Stimulating Sites on the Performance of Implantable Middle Ear Hearing Devices: A Numerical Analysis. Micromachines 2019, 10, 782. https://doi.org/10.3390/mi10110782
Liu H, Zhao Y, Yang J, Rao Z. The Influence of Piezoelectric Transducer Stimulating Sites on the Performance of Implantable Middle Ear Hearing Devices: A Numerical Analysis. Micromachines. 2019; 10(11):782. https://doi.org/10.3390/mi10110782
Chicago/Turabian StyleLiu, Houguang, Yu Zhao, Jianhua Yang, and Zhushi Rao. 2019. "The Influence of Piezoelectric Transducer Stimulating Sites on the Performance of Implantable Middle Ear Hearing Devices: A Numerical Analysis" Micromachines 10, no. 11: 782. https://doi.org/10.3390/mi10110782
APA StyleLiu, H., Zhao, Y., Yang, J., & Rao, Z. (2019). The Influence of Piezoelectric Transducer Stimulating Sites on the Performance of Implantable Middle Ear Hearing Devices: A Numerical Analysis. Micromachines, 10(11), 782. https://doi.org/10.3390/mi10110782





