MEMS Gyroscope Bias Drift Self-Calibration Based on Noise-Suppressed Mode Reversal
Abstract
:1. Introduction
2. The Self-Calibration Method Based on Noise-Suppressed Mode Reversal
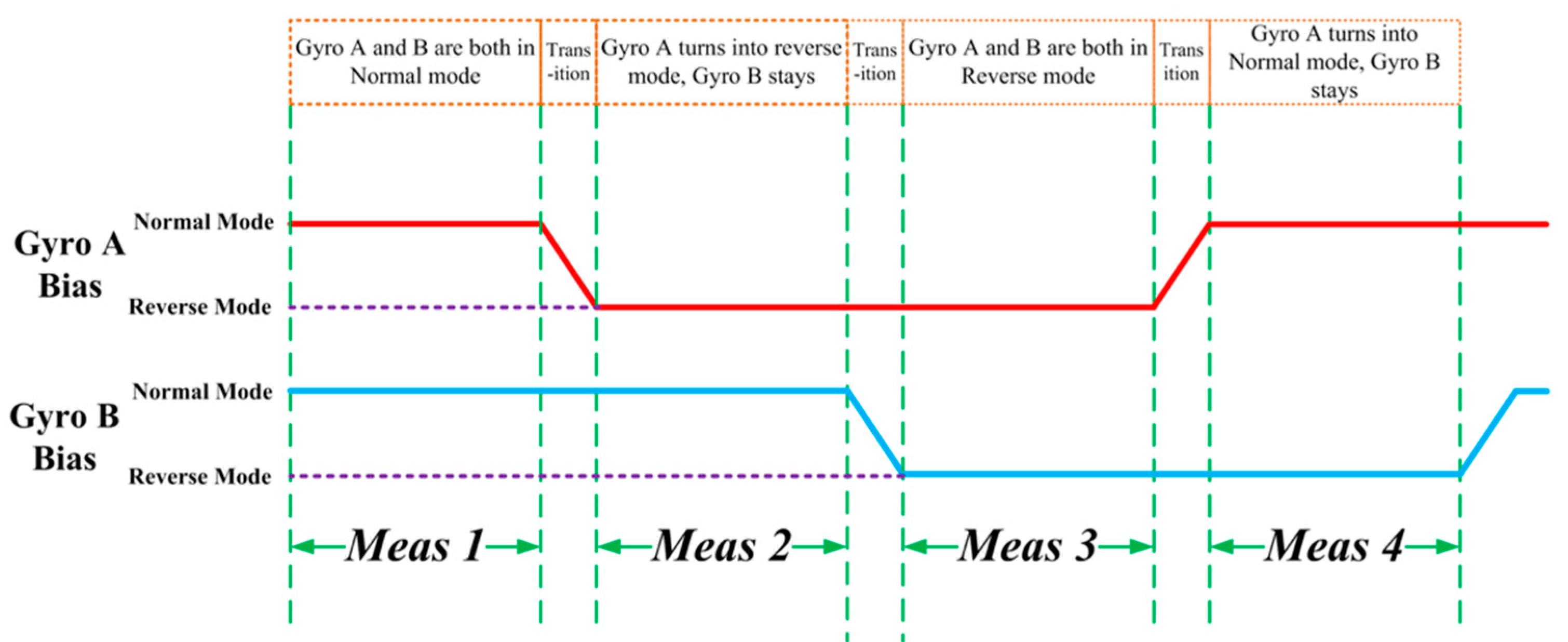
2.1. The Principle and Theoretical Analysis of Mode Reversal
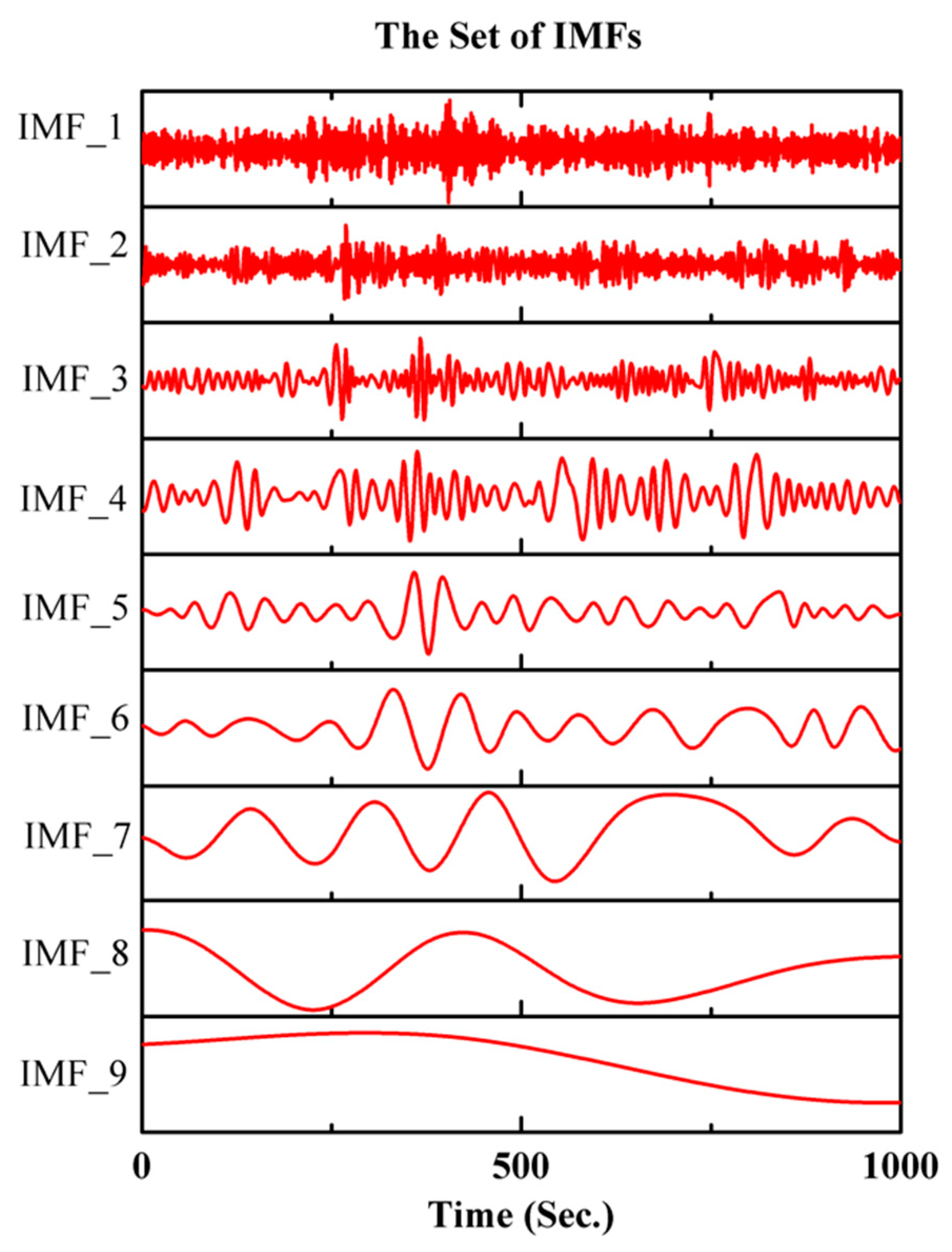
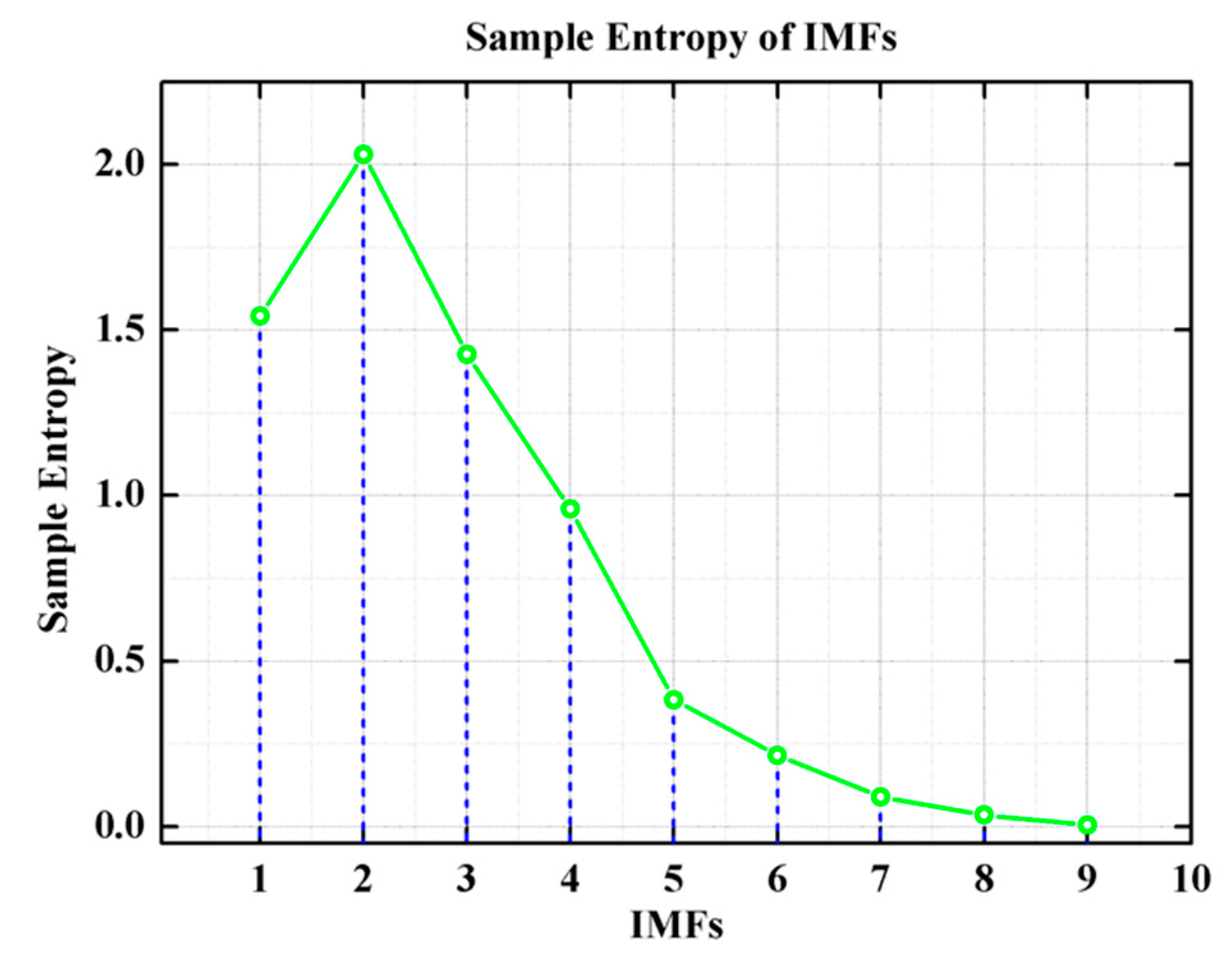
2.2. The Threshold Denoising Algorithm Based on Improved CEEMDAN
2.3. The Self-Calibration System Based on Noise-Suppressed Mode Reversal
3. Experimental Results and Discussion
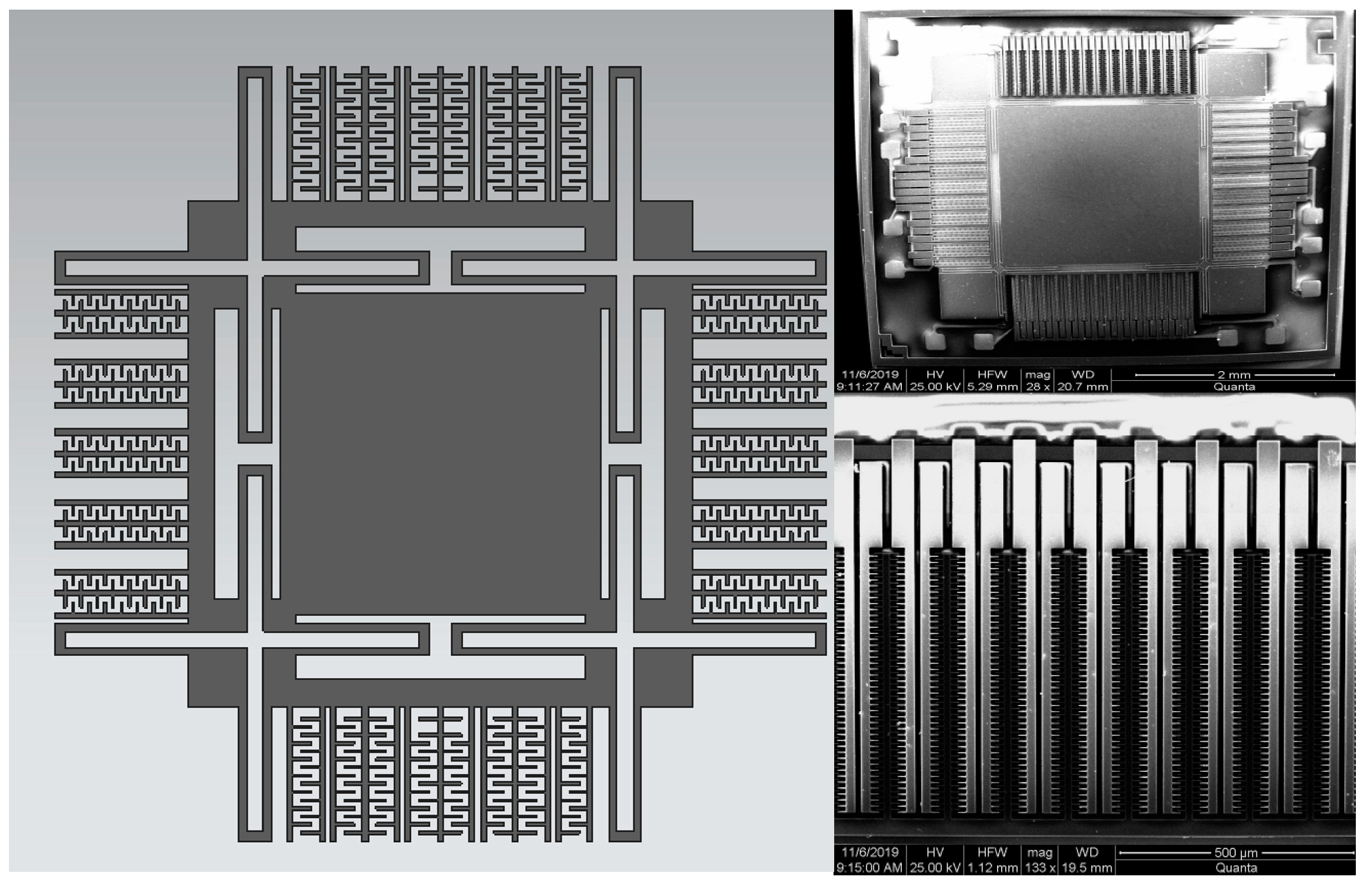
3.1. The Implemention of the Proposed Self-Calibration System
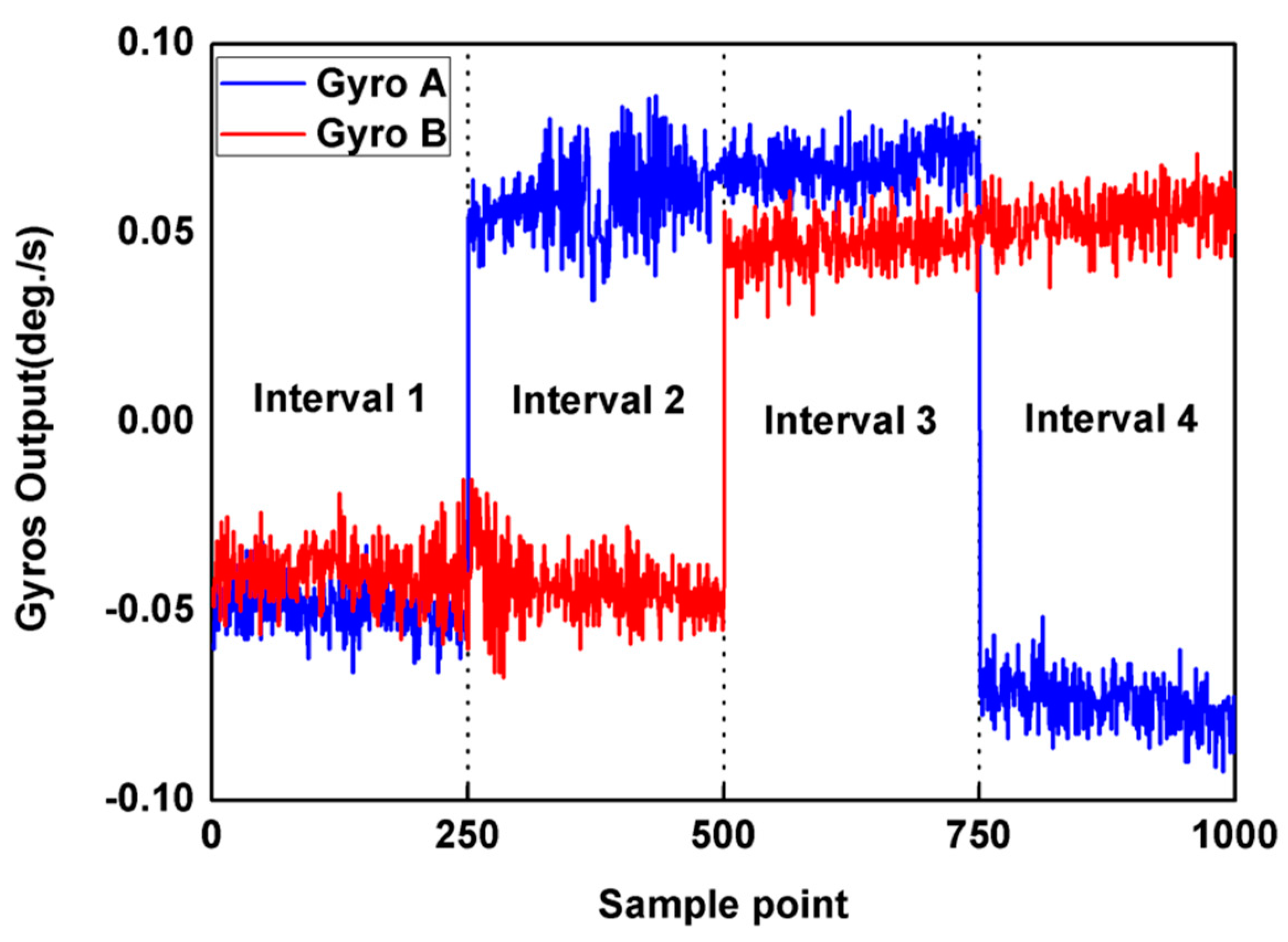
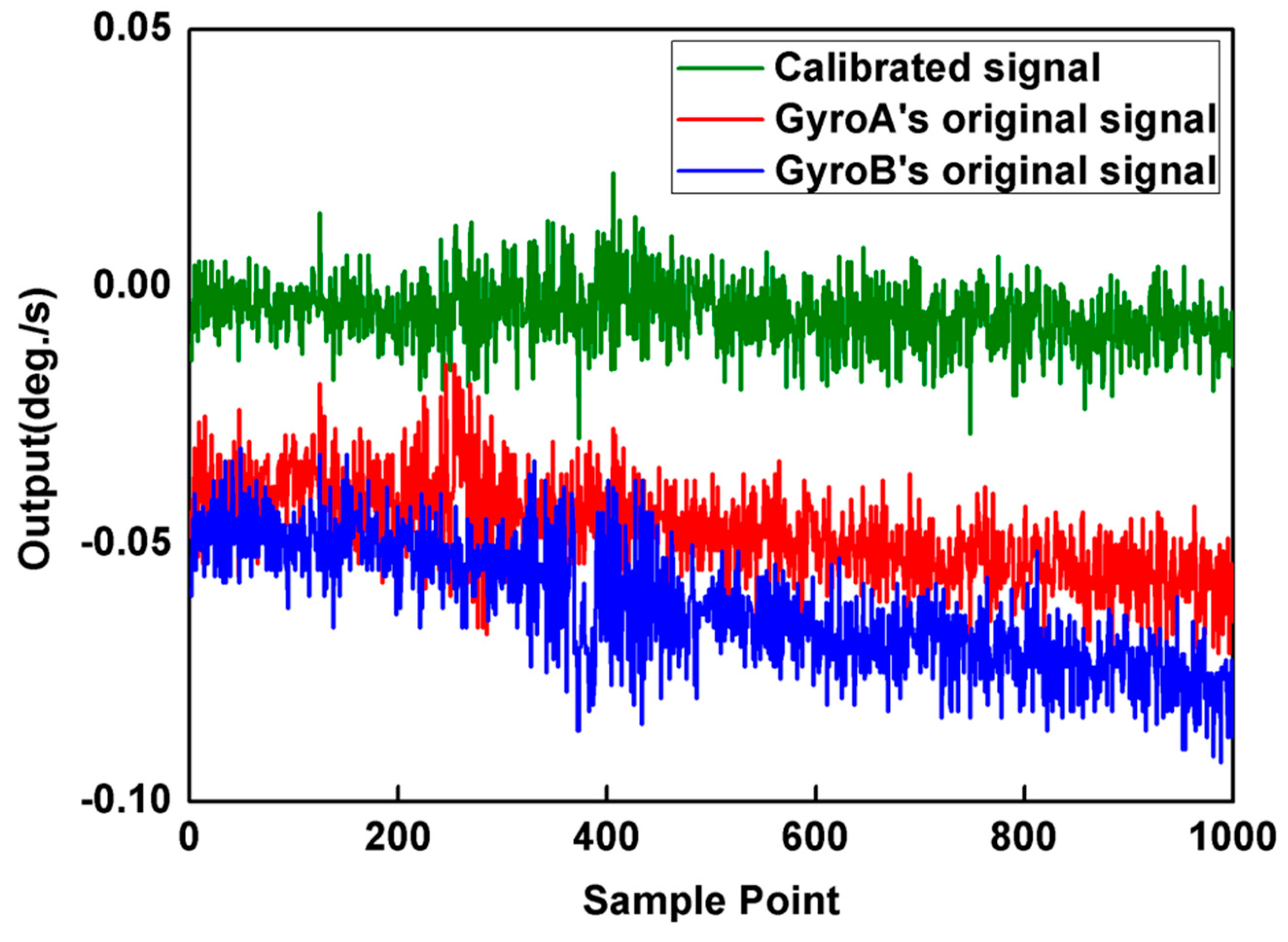
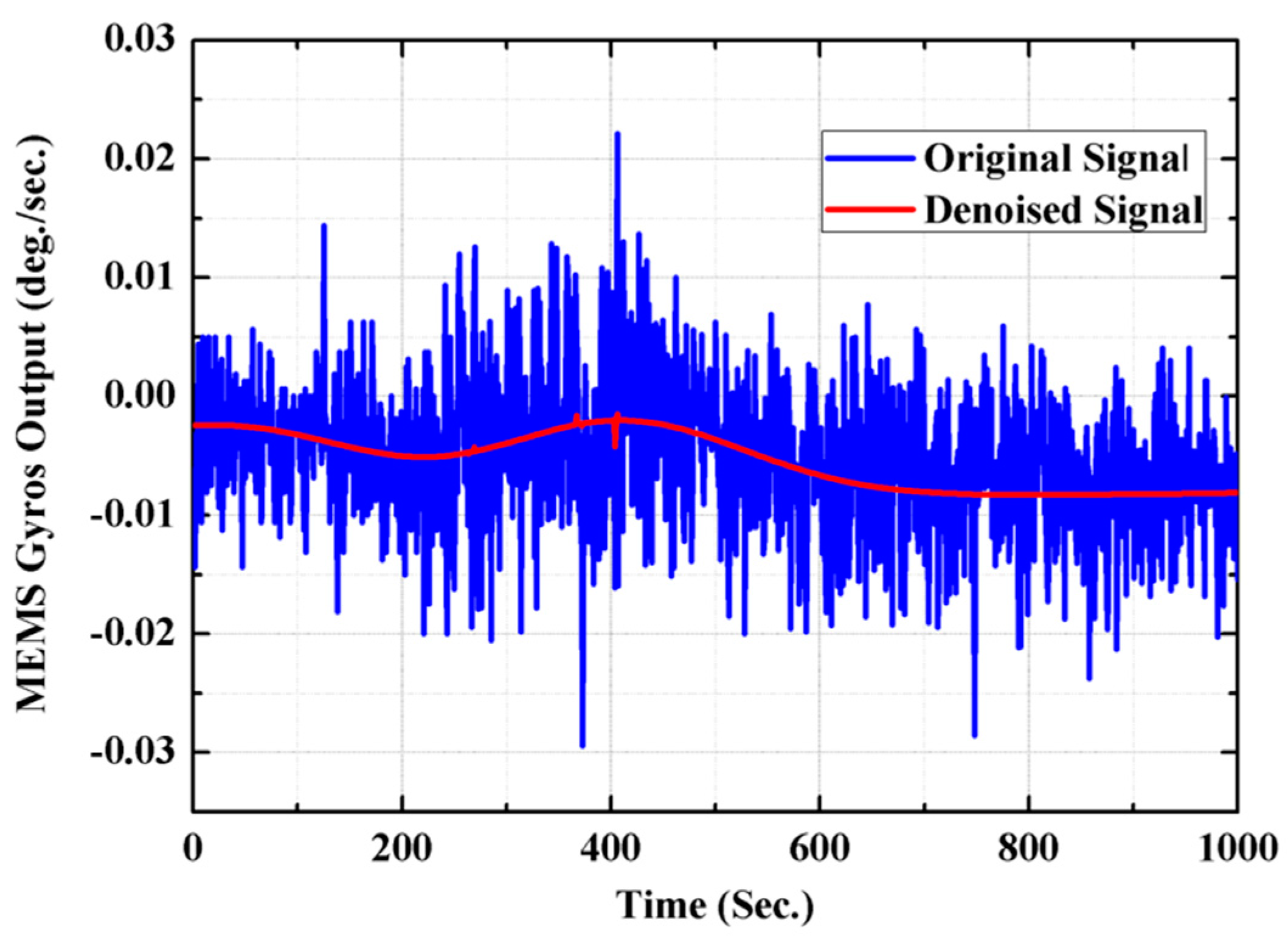
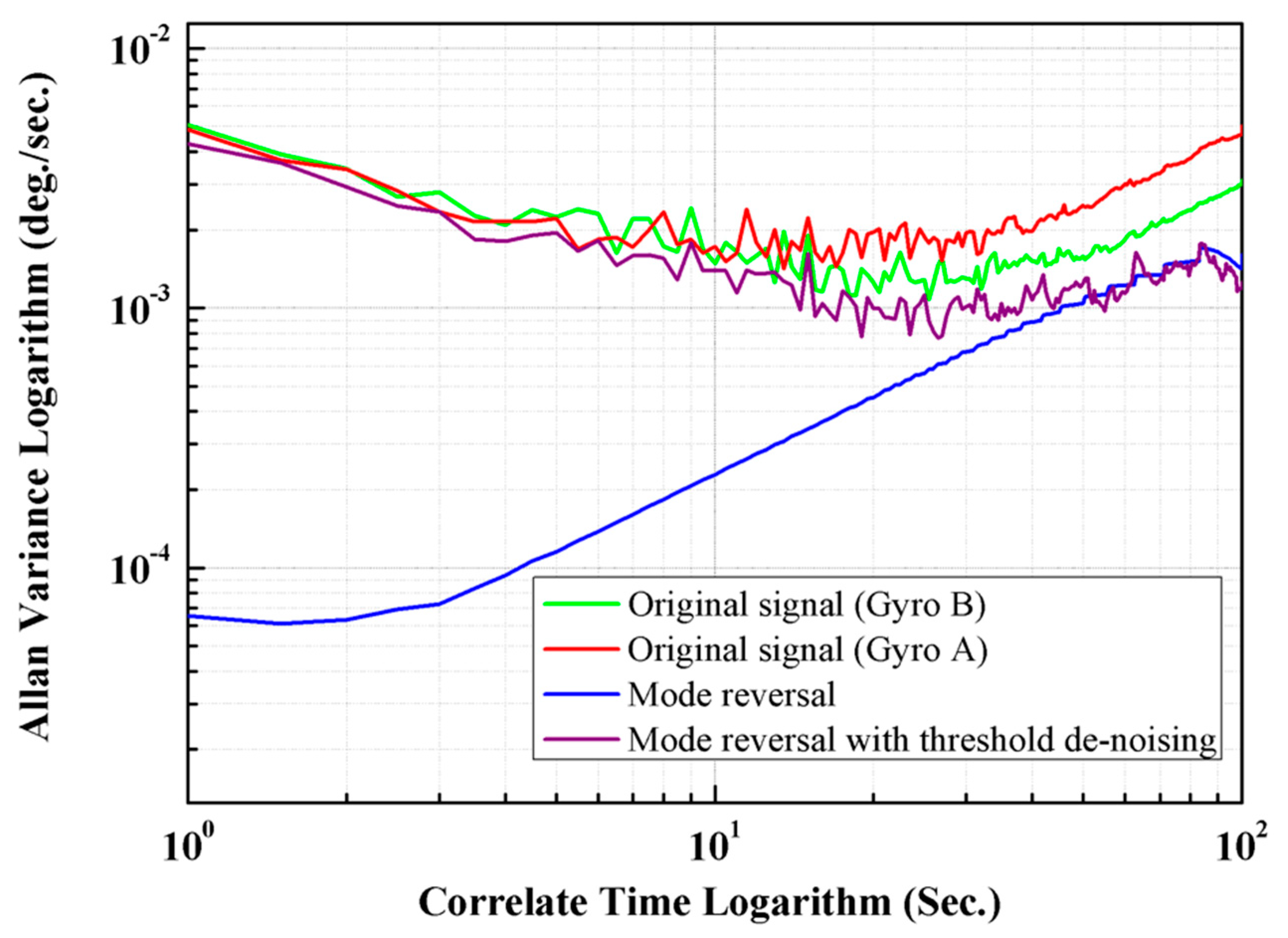
3.2. Experimental Testing
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sheng, H.L.; Zhang, T.H. MEMS-based low-cost strap-down AHRS research. Measurement 2015, 59, 63–72. [Google Scholar] [CrossRef]
- Chang, H.L.; Zhang, Y.F.; Xie, J.B.; Zhou, Z.G.; Yuan, W.Z. Integrated behavior simulation and verification for a MEMS vibratory gyroscope using parametric model order reduction. J. Microelectromech. Syst. 2010, 19, 282–293. [Google Scholar] [CrossRef]
- Chang, H.L.; Xie, J.B.; Fu, Q.Y.; Shen, Q.; Yuan, W.Z. Micromachined inertial measurement unit fabricated by a SOI process with selective roughening under structures. Micro Nano Lett. 2011, 6, 486–489. [Google Scholar] [CrossRef]
- Ayazi, F. A high Aspect-Ratio High-Performance Poly-Silicon Vibrating Ring Gyroscope. Ph.D. Dissertation, University of Michigan, Ann Arbor, MI, USA, 2000. [Google Scholar]
- Xie, J.B.; Hao, Y.C.; Shen, Q.; Chang, H.L.; Yuan, W.Z. A dicing-free SOI process for MEMS devices based on the lag effect. J. Micromech. Microeng. 2013, 23, 1235033. [Google Scholar] [CrossRef]
- Acar, C.; Shkel, A.M. Structurally decoupled micromachined gyroscopes with post-release capacitance enhancement. J. Micromech. Microeng. 2015, 15, 1092–1101. [Google Scholar] [CrossRef]
- Putty, M.W. A Micromachined Vibrating Ring Gyroscope. Ph.D. Dissertation, University of Michigan, Ann Arbor, MI, USA, 1995. [Google Scholar]
- Sharma, A.; Zaman, M.; Ayazi, F. A Sub-0.2°/hr Bias Drift Micromechanical Gyroscope with Automatic CMOS Mode-Matching. IEEE J. Solid-State Circuits 2009, 44, 1593–1608. [Google Scholar] [CrossRef]
- Prikhodko, I.; Gregory, J.; Merrit, G.; Geen, J.; Chang, J.; Bergeron, J.; Clark, W.; Judy, M. In-Run Bias Self Calibration for Low-Cost MEMS Vibratory Gyroscopes. In Proceedings of the IEEE Symposium on Position Location and Navigation (PLANS), Monterey, CA, USA, 5–8 May 2014; pp. 515–518. [Google Scholar]
- Prikhodko, I.; Gregory, J.; Merrit, G.; Geen, J.; Chang, J.; Bergeron, J.; Clark, W.; Judy, M. Continuous Self-Calibration Canceling Drive-Induced Errors In MEMS Vibratory Gyroscopes. Transducers 2015, 2015, 35–38. [Google Scholar]
- Eminoglu, B.; Kline, M.H.; Izyumin, I.; Yeh, Y.C.; Boser, B.E. Background calibrated MEMS gyroscope. In Proceedings of the Sensors IEEE, Valencia, Spain, 2–5 November 2014. [Google Scholar]
- Rozelle, D. Self-Calibrating Gyroscope System. U.S. Patent 7,912,664, 11 September 2011. [Google Scholar]
- Kline, M.H.; Yeh, Y.; Eminoglu, B.; Izyumin, I.; Daneman, M.; Horsley, D.A.; Boser, B.E. MEMS gyroscope bias drift cancellation using continuous-time mode reversal. In Proceedings of the International Conference on Solid State Sensors and Actuators (TRANSDUCERS), Barcelona, Spain, 16–20 June 2013; pp. 1855–1858. [Google Scholar]
- Li, C.; Wen, H.R.; Wisher, S.; Norouzpour-Shirazi, A. An FPGA-Based Interface System for High Frequency Bulk-Acoustic-Wave (BAW) Micro-Gyroscopes with In-Run Automatic Mode-Matching. IEEE Trans. Instrum. Meas. 2019, 1. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for non-linear and non-stationary time series analysis. Proc. R. Soc. Lond. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Yeh, J.R.; Shieh, J.S.; Huang, N.E. Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method. Adv. Adapt. Data Anal. 2010, 2, 135–156. [Google Scholar] [CrossRef]
- Colominas, M.A.; Schlotthauer, G.; Torres, M.E. Improved complete ensemble EMD: A suitable tool for biomedical signal processing. Biomed. Signal Process. Control. 2014, 14, 19–29. [Google Scholar] [CrossRef]
- Kopsinis, Y.; Mclaughlin, S. Development of EMD-based denoising methods inspired by wavelet thresholding. IEEE Trans. Signal Process. 2009, 57, 1351–1362. [Google Scholar] [CrossRef]
- Gan, Y.; Sui, L.F.; Wu, J.F.; Wang, B.; Zhang, Q.H.; Xiao, G.R. An EMD threshold de-noising method for inertial sensors. Measurement 2014, 49, 34–41. [Google Scholar] [CrossRef]
- Zhou, H.; Zhao, B.L.; Liu, X.X.; Tang, B.; Yang, B. Simulation analysis of air damping of MEMS gyroscope in non-vacuum encapsulation. In Proceedings of the CSIT’s 7th Conference on Inertial Technology, Wuhan, China, 11–14 October 2015; pp. 232–238. [Google Scholar]
- IEEE Standards Borad. IEEE Standard Specification Format Guide and Test Procedure for Single-Axis Interferometric Fiber Optic Gyros; IEEE Standard 952-1997(R2003); IEEE: New York, NY, USA, 2003. [Google Scholar]






| Parameter | Values |
|---|---|
| Drive mode resonant frequency | 8195 Hz |
| Sense mode resonant frequency | 8142 Hz |
| Quality factor of drive mode | 184 |
| Quality factor of sense mode | 195 |
| Drive effective mass | 5.49 |
| Sense effective mass | 5.3 |
| Capacitance of drive mode | 4.5 pF |
| Capacitance of sense mode | 4 pF |
| Original (Gyro A) | Original (Gyro B) | Mode Reversal | Mode Reversal with Threshold Denoising | |
|---|---|---|---|---|
| 0.0026 | 0.0021 | 0.0020 | 8.26 | |
| 1.18 | 2.04 | 5.67 | 2.19 | |
| 0.0066 | 0.0055 | 0.0022 | 0.0011 | |
| 0.0456 | 0.0494 | 0.0513 | 0.0045 | |
| 0.2094 | 0.1709 | 0.302 | 0.0195 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, H.; Zhao, B.; Zhou, H.; Liu, X.; Su, W. MEMS Gyroscope Bias Drift Self-Calibration Based on Noise-Suppressed Mode Reversal. Micromachines 2019, 10, 823. https://doi.org/10.3390/mi10120823
Gu H, Zhao B, Zhou H, Liu X, Su W. MEMS Gyroscope Bias Drift Self-Calibration Based on Noise-Suppressed Mode Reversal. Micromachines. 2019; 10(12):823. https://doi.org/10.3390/mi10120823
Chicago/Turabian StyleGu, Haoyu, Baolin Zhao, Hao Zhou, Xianxue Liu, and Wei Su. 2019. "MEMS Gyroscope Bias Drift Self-Calibration Based on Noise-Suppressed Mode Reversal" Micromachines 10, no. 12: 823. https://doi.org/10.3390/mi10120823




