Effect of Enhanced Squeezing Needle Structure on the Jetting Performance of a Piezostack-Driven Dispenser
Abstract
:1. Introduction
2. Principles of Dispensing
3. Theory and Simulation of the Dispensing Process
3.1. Theoretical Analysis
3.2. Molding and Simulation
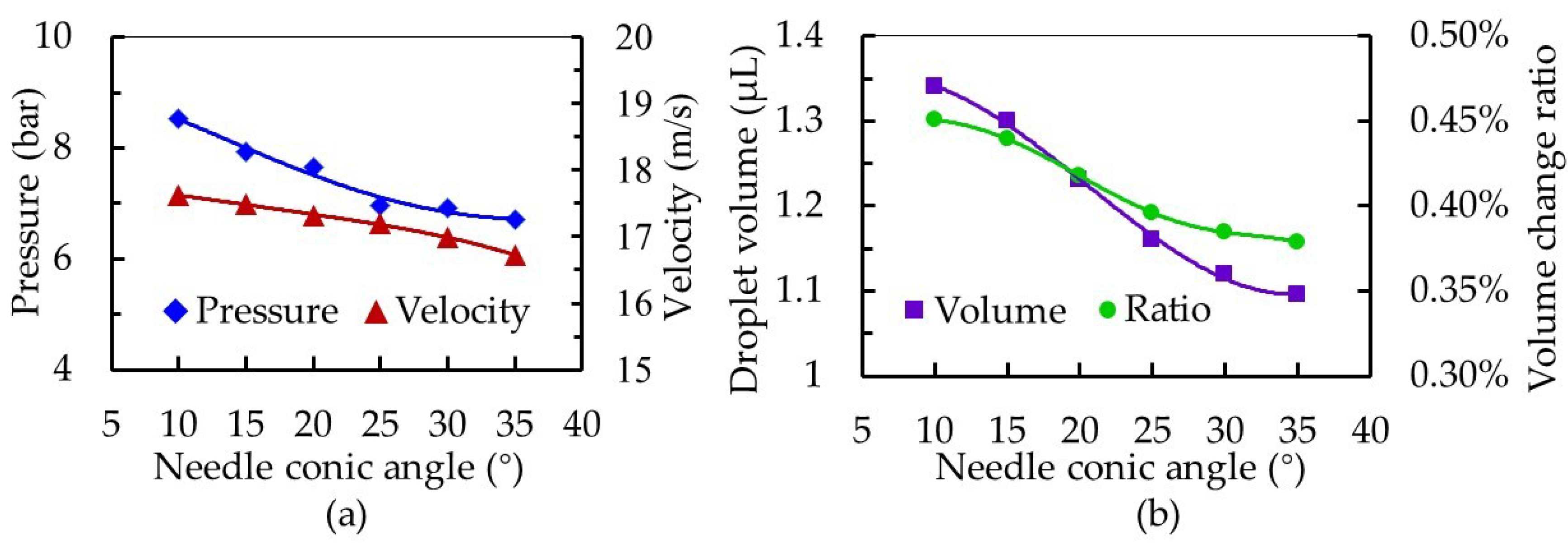
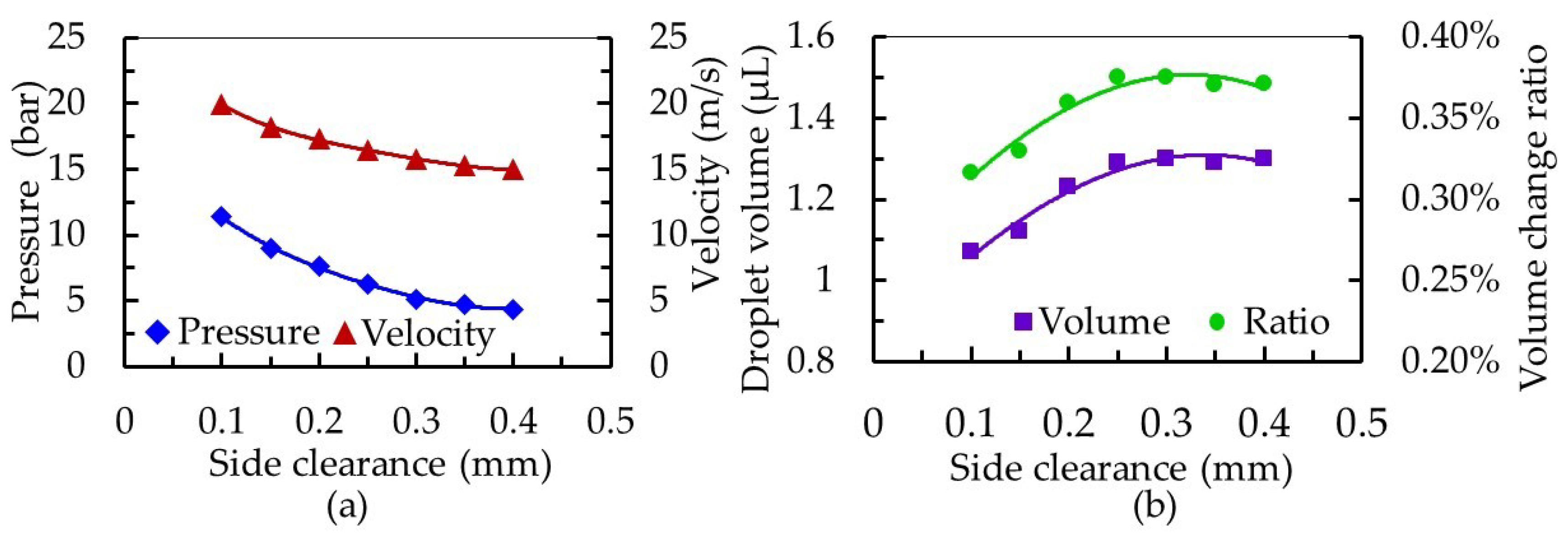
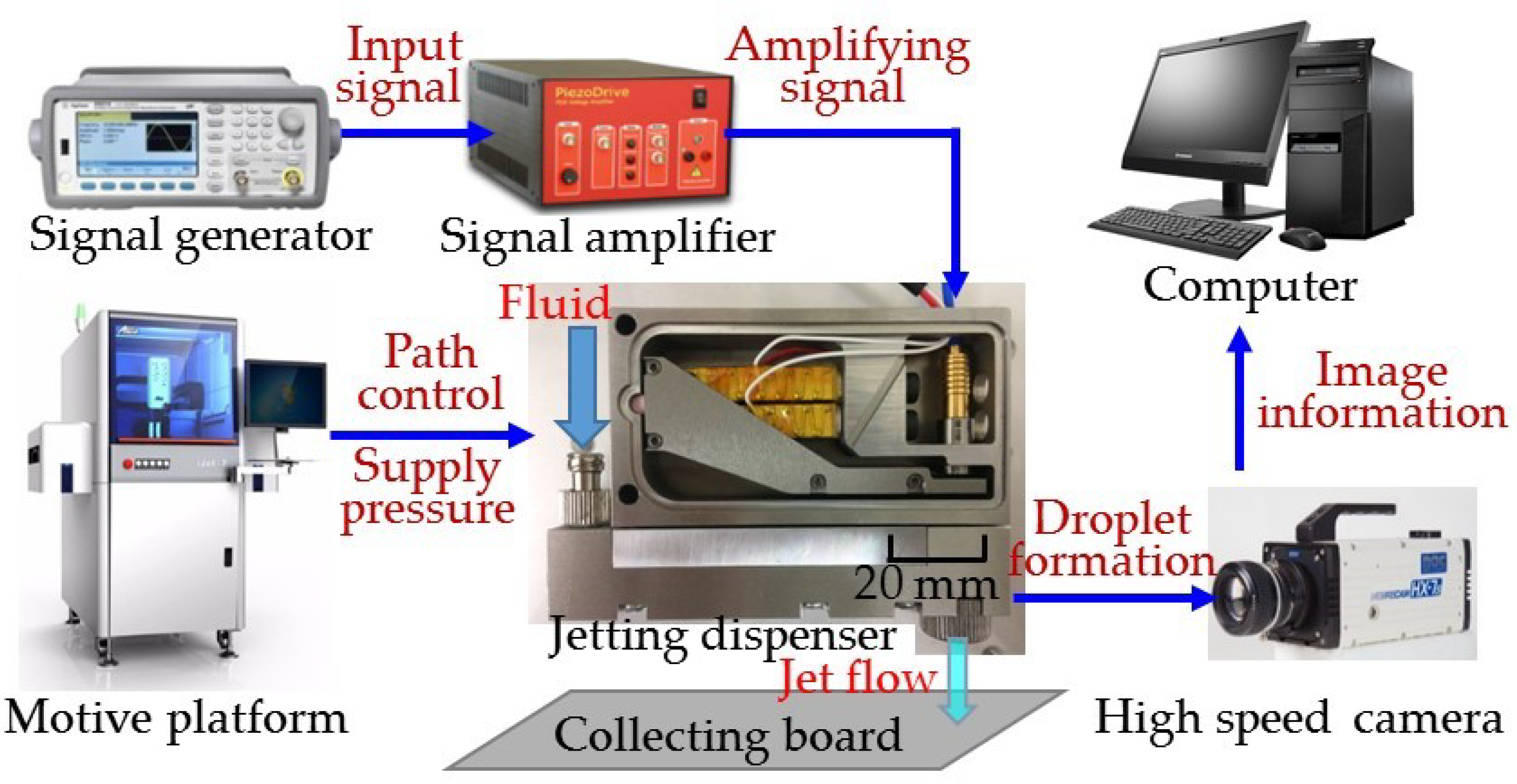
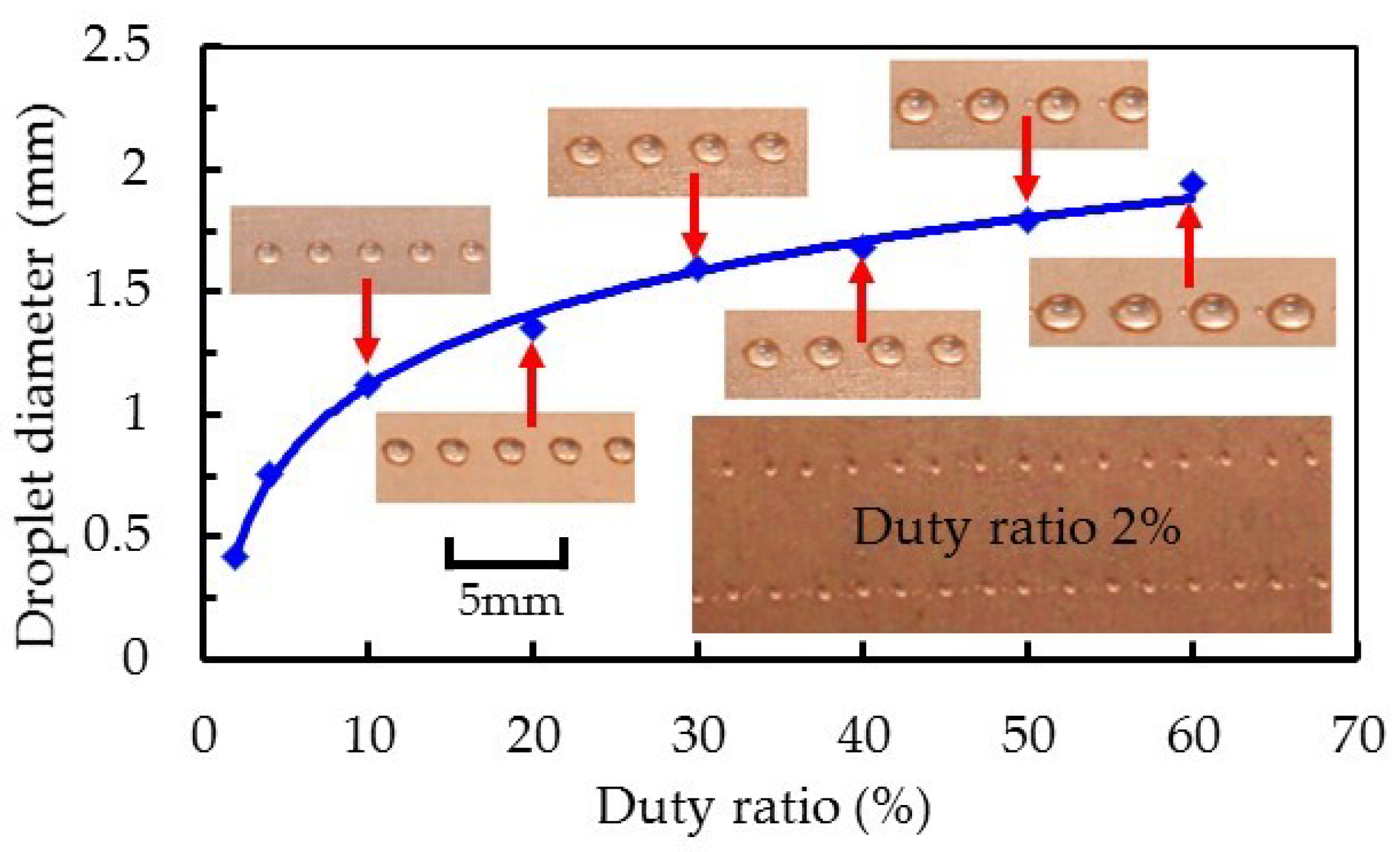
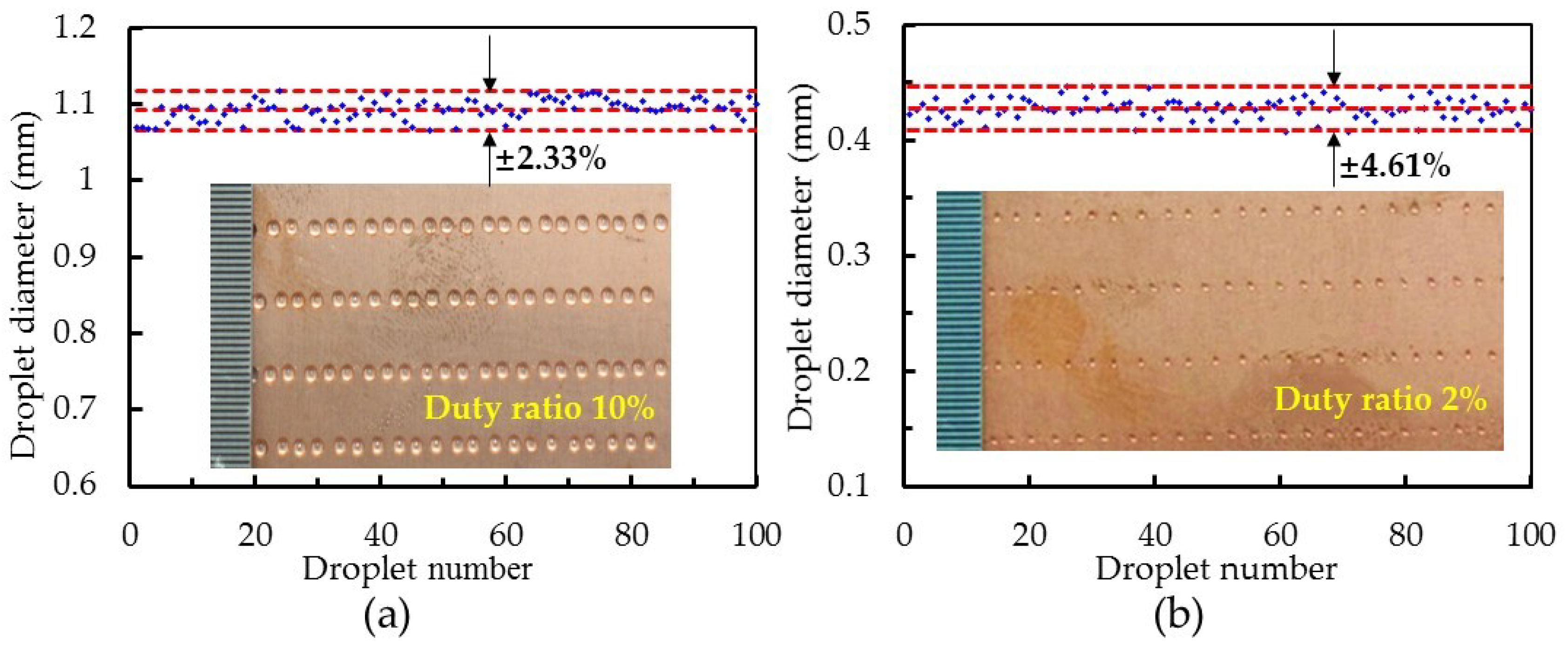
4. Experiments of Droplet Dispensing
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nguyen, Q.H.; Choi, S.B. Performance evaluation of a high-speed jetting dispenser actuated by a ring-type piezostack. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2009, 223, 1401–1413. [Google Scholar] [CrossRef]
- Shan, X.; Li, H.X.; Si, H.; Yun, C. Integrated sensing-/model-based online estimation of jet dispensing. IEEE Trans. Compon. Packag. Manuf. Technol. 2018, 8, 300–309. [Google Scholar] [CrossRef]
- Zhou, C.; Duan, J.A.; Deng, G.; Li, J. A novel high speed jet dispenser driven by double piezoelectric stacks. IEEE Trans. Ind. Electron. 2016, 64, 412–419. [Google Scholar] [CrossRef]
- Kim, K.Y.; Lee, Y.C.; Chang, H.; Lee, R.F.; Wu, H.W. Jetting dispenser height effect on the accuracy of test strip for blood glucose. J. Med. Biol. Eng. 2018, 39, 109–116. [Google Scholar] [CrossRef]
- Zhou, C.; Peng, D.; Feng, Z.; Cui, W.; Deng, G. Influence of bi-piezoelectric micro-valve’s parameters on jet performance. Optik 2018, 167, 129–135. [Google Scholar] [CrossRef]
- Nguyen, Q.H.; Choi, M.K.; Choi, S.B. A new type of piezostack-driven jetting dispenser for semiconductor electronic packaging:Modeling and control. Smart Mater. Struct. 2008, 17, 015033. [Google Scholar] [CrossRef]
- Nguyen, Q.H.; Han, Y.M.; Choi, S.B.; Hong, S.M. Design of a new mechanism for jetting dispenser featuring piezoactuator. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2008, 222, 711–722. [Google Scholar] [CrossRef]
- Liu, S.Z.; Zhang, Y.B.; Chen, X.B. Experiment and dynamic model of motor for rotary-screw-driven dispensing system. Appl. Mech. Mater. 2012, 220, 1071–1076. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, Y.; Hui, C.; He, N. Research on micro-liquid dispensing anomaly monitoring system based on pressure sensor. Nanosci. Nanotechnol. Lett. 2017, 9, 859–866. [Google Scholar] [CrossRef]
- Wang, L.; Du, J.; Luo, Z.; Du, X.; Li, Y.; Liu, J.; Sun, D. Design and experiment of a jetting dispenser driven by piezostack actuator. IEEE Trans. Compon. Packag. Manuf. Technol. 2013, 3, 147–156. [Google Scholar] [CrossRef]
- Jeon, J.; Hong, S.M.; Choi, M.; Choi, S.B. jetting dispenser system using two piezostack actuators. Smart Mater. Struct. 2015, 24, 015020. [Google Scholar] [CrossRef]
- Lu, S.; Liu, Y.; Yao, Y.; Bo, H.; Sun, L. Design and analysis of a piezostack driven jetting dispenser for high viscosity adhesives. In Proceedings of the 2014 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Besançon, France, 8–11 July 2014. [Google Scholar]
- Lu, S.; Cao, G.; Hai, Z.; Li, D.; Qi, J. Simulation and Experiment on Droplet Formation and Separation for Needle-Type Micro-Liquid Jetting Dispenser. Micromachines 2018, 9, 330. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bu, Z.; Lin, S.; Xiang, H.; Li, A.; Wu, D.; Yang, Z.; Luo, Z.; Wang, L. A novel piezostack-driven jetting dispenser with corner-filleted flexure hinge and high-frequency performance. J. Micromech. Microeng. 2018, 28, 075001. [Google Scholar] [CrossRef]
- Sohn, J.W.; Jeon, J.; Choi, M.; Choi, S.B. Critical operating factors of a jetting dispenser driven by piezostack actuators: Statistical analysis of experimental results. J. Adhes. Sci. Technol. 2017, 32, 359–374. [Google Scholar] [CrossRef]
- Wang, L.; Huang, X.; Lin, S.; Lin, X.; Lin, Z. Design and Experiment of High Frequency Jetting Dispenser Driven by Double Piezoelectric Stacks. Editor. Office Opt. Precis. Eng. 2019, 27, 1128–1137. [Google Scholar] [CrossRef]
- Deng, G.; Na, W.; Zhou, C.; Li, J. A simplified analysis method for the piezo jet dispenser with a diamond amplifier. Sensors 2018, 18, 2115. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nguyen, Q.H.; Choi, S.B.; Kim, J.D. The design and control of a jetting dispenser for semiconductor electronic packaging driven by a piezostack and a flexible beam. Smart Mater. Struct. 2008, 17, 065028. [Google Scholar] [CrossRef]
- Peng, D.; Deng, G.; Zhou, C.; Tao, W. In Simulation and experiment study on the jetting dispensing process driven by mechanical collision. In Proceedings of the 16th International Conference on Electronic Packaging Technology, Shanghai, China, 11–14 August 2015. [Google Scholar]
- Zhou, C.; Deng, G.; Li, J.; Duan, J. Flow channel influence of a collision-based piezoelectric jetting dispenser on jet performance. Sensors 2018, 18, 1270. [Google Scholar] [CrossRef] [Green Version]
- Song, L.; Hai, J.; Li, M.; Liu, J.; Gu, S.; Jiao, X.; Liu, X. Nozzle and needle during high viscosity adhesive jetting based on piezoelectric jet dispensing. Smart Mater. Struct. 2015, 24, 105023. [Google Scholar]
- Wang, L.; Du, X.; Li, Y.; Luo, Z.; Zheng, G.; Sun, D. Simulation and experiment study on adhesive ejection behavior in jetting dispenser. J. Adhes. Sci. Technol. 2014, 28, 53–64. [Google Scholar] [CrossRef]
- Zhang, J.; Jia, H.; Zhang, J. In A fluid dynamic analysis in the chamber and nozzle for a jetting dispenser design. In Proceedings of the 11th International Conference on Electronic Packaging Technology & High Density Packaging, Xi’an, China, 16–19 August 2010. [Google Scholar]
- Nguyen, Q.H.; Choi, S.B. Modeling of unsteady laminar flow based on steady solution in jetting dispensing process. IEEE Trans. Electron. Packag. Manuf. 2008, 31, 134–142. [Google Scholar] [CrossRef]
- Huang, D.; Yuan, S.; Chu, X.; Cui, H.; Zhang, S. Design and experiment of a piezoelectric driven non-contact dispenser. Piezoelectr. Acoustooptics 2016, 38, 11–15. [Google Scholar]
- Zhou, C.; Junhui, L.; Ji-An, D.; Guiling, D. Direct-Acting Piezoelectric Jet Dispenser with Rhombic Mechanical Amplifier. IEEE Trans. Compon. Packag. Manuf. Technol. 2018, 8, 910–913. [Google Scholar] [CrossRef]
- Zhou, C.; Duan, J.A.; Deng, G. Giant magnetostrictive material based jetting dispenser. Optik 2015, 126, 5859–5860. [Google Scholar] [CrossRef]
- Nguyen, Q.; Yun, B.; Choi, S. Performance characteristics of a high frequency jetting dispenser featuring piezoelectric actuator. Act. Passive Smart Struct. Integr. Syst. Int. Soc. Opt. Photonics 2008, 6928, 69281U. [Google Scholar]


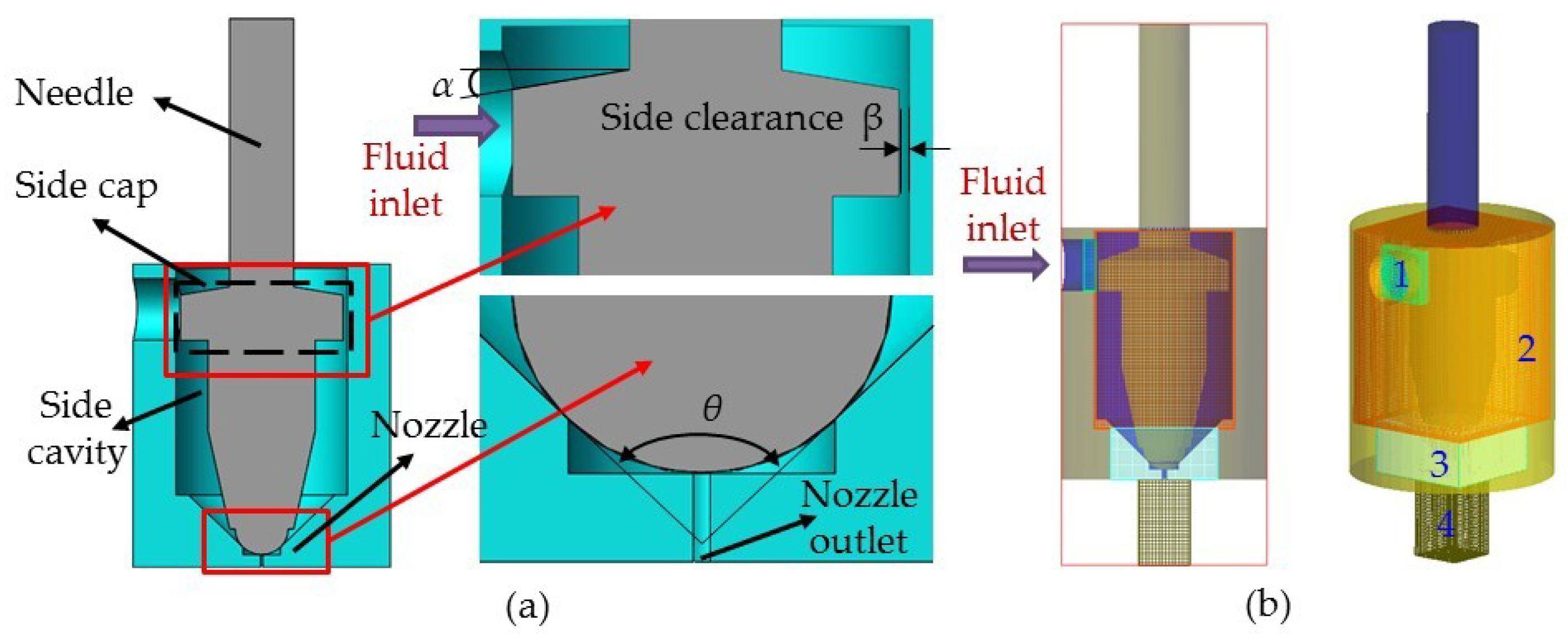
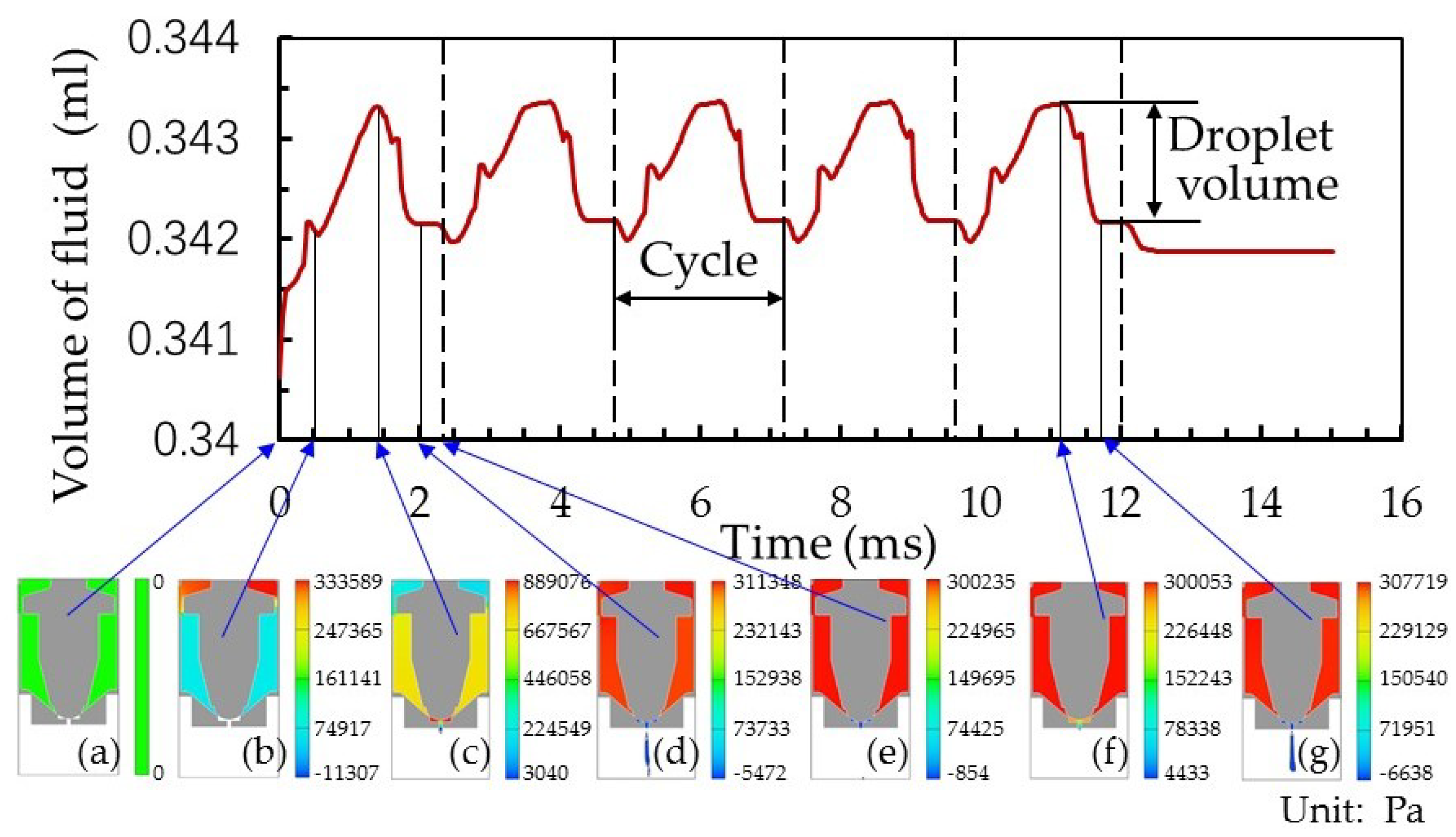
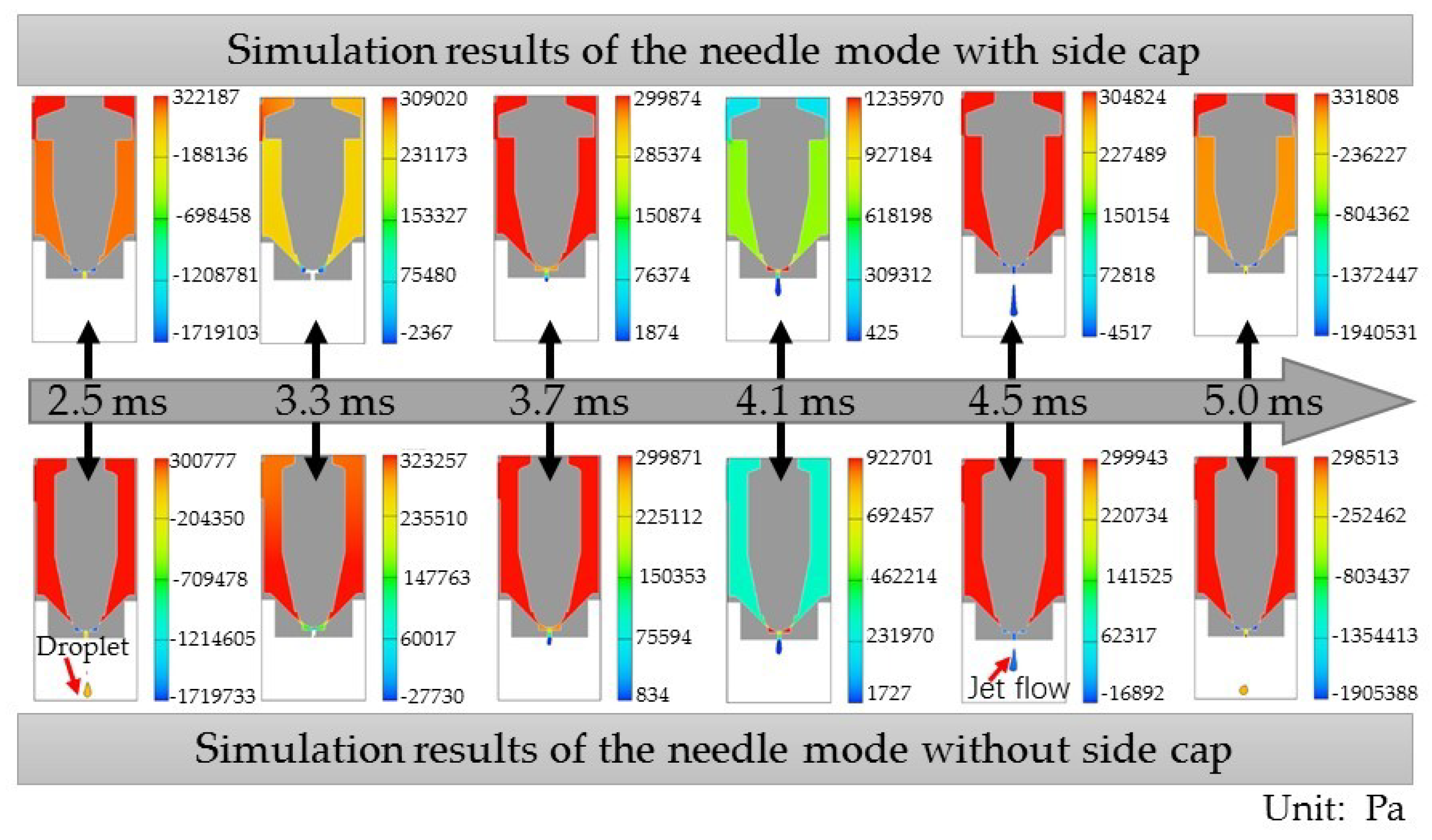

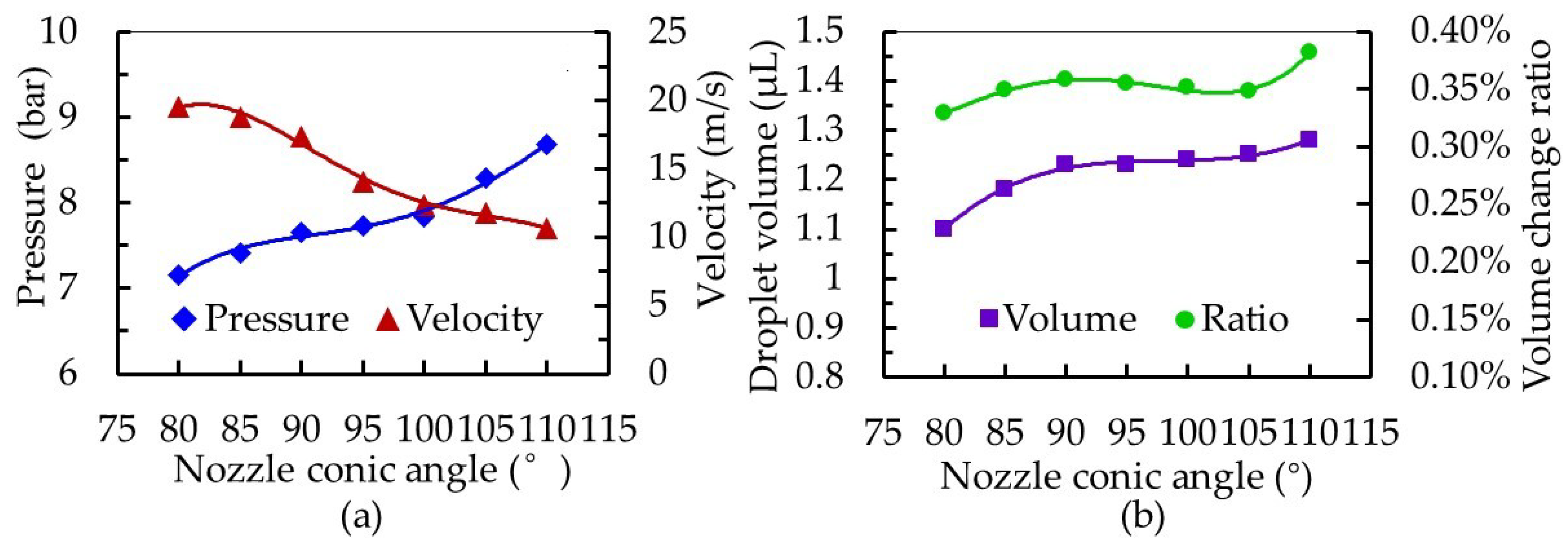

| Parameter | Density of Adhesive | Dynamic Viscosity | Surface Tension Coefficient | Temperature of Adhesive |
| Initial value | 1263.31 kg/m3 | 500 mPa∙s | 0.4 N/m | 20 °C |
| Parameter | Feed Pressure | Acceleration of Gravity | Needle Stroke | Velocity of Needle |
| Initial value | 0.3 MPa | 9.8 m/s2 | 0.20 mm | Rising 0.3 m/s Falling 0.5 m/s |
| Needle Structure | Droplet Volume (μL) | |||||
|---|---|---|---|---|---|---|
| First Cycle | Second Cycle | Third Cycle | Fourth Cycle | Fifth Cycle | Average | |
| Needle with side cap | 1.15 | 1.15 | 1.17 | 1.18 | 1.18 | 1.166 |
| Needle without side cap | 1.24 | 1.22 | 1.24 | 1.23 | 1.24 | 1.234 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Lin, X.; Jin, H.; Lin, S.; Bu, Z.; He, G.; Sun, D.; Wang, L. Effect of Enhanced Squeezing Needle Structure on the Jetting Performance of a Piezostack-Driven Dispenser. Micromachines 2019, 10, 850. https://doi.org/10.3390/mi10120850
Huang X, Lin X, Jin H, Lin S, Bu Z, He G, Sun D, Wang L. Effect of Enhanced Squeezing Needle Structure on the Jetting Performance of a Piezostack-Driven Dispenser. Micromachines. 2019; 10(12):850. https://doi.org/10.3390/mi10120850
Chicago/Turabian StyleHuang, Xiang, Xiaolong Lin, Hang Jin, Siying Lin, Zhenxiang Bu, Gonghan He, Daoheng Sun, and Lingyun Wang. 2019. "Effect of Enhanced Squeezing Needle Structure on the Jetting Performance of a Piezostack-Driven Dispenser" Micromachines 10, no. 12: 850. https://doi.org/10.3390/mi10120850
APA StyleHuang, X., Lin, X., Jin, H., Lin, S., Bu, Z., He, G., Sun, D., & Wang, L. (2019). Effect of Enhanced Squeezing Needle Structure on the Jetting Performance of a Piezostack-Driven Dispenser. Micromachines, 10(12), 850. https://doi.org/10.3390/mi10120850




