Active On-Chip Dispersion Control Using a Tunable Silicon Bragg Grating
Abstract
:1. Introduction
2. Results
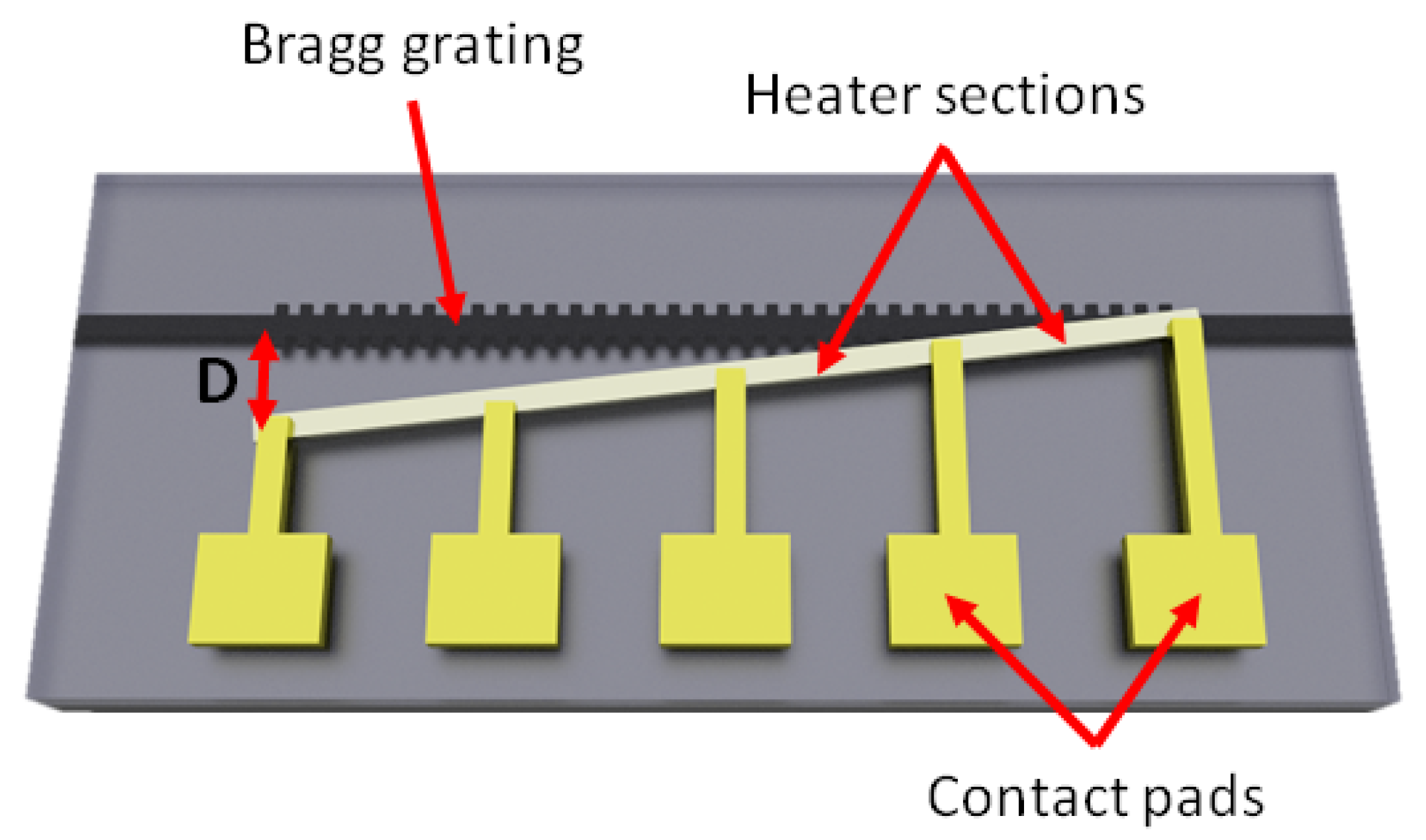
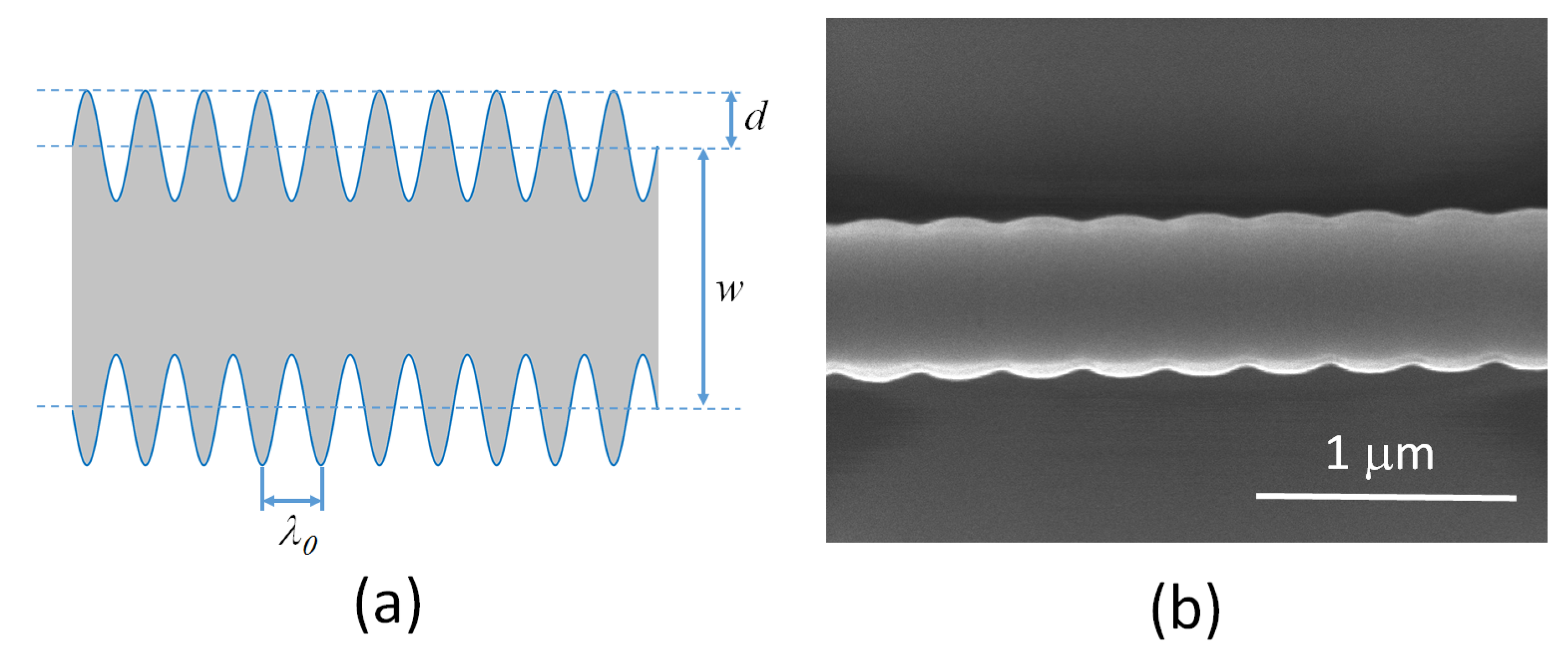
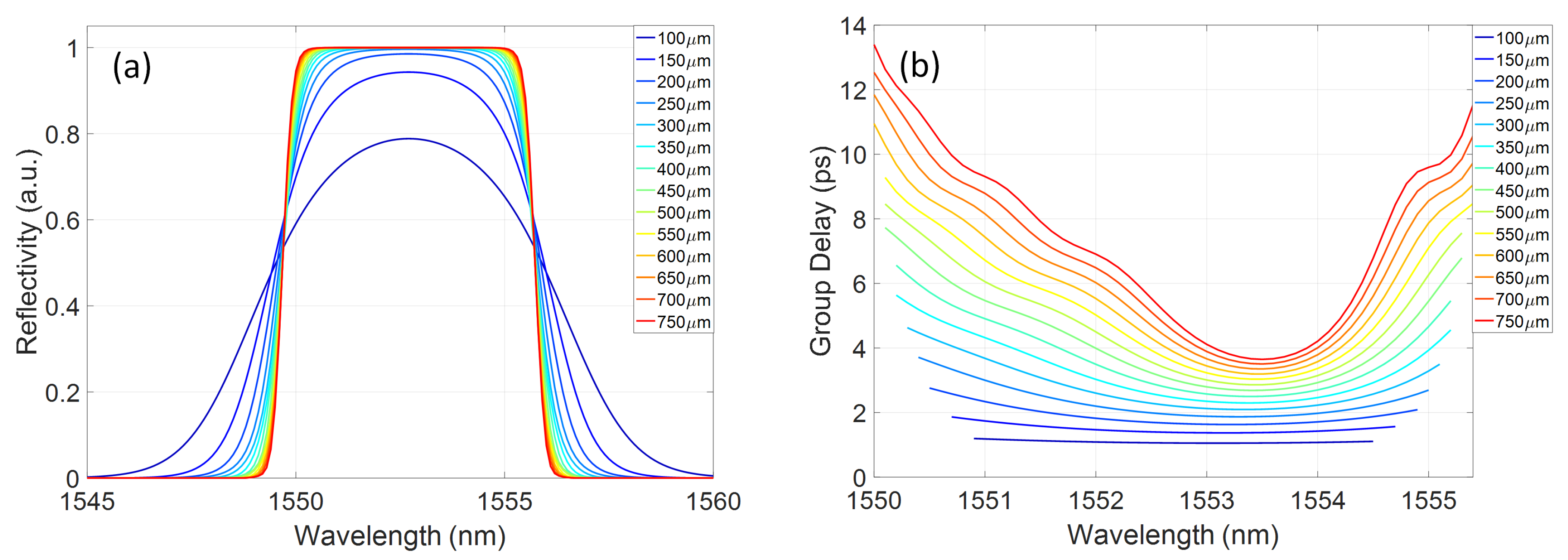
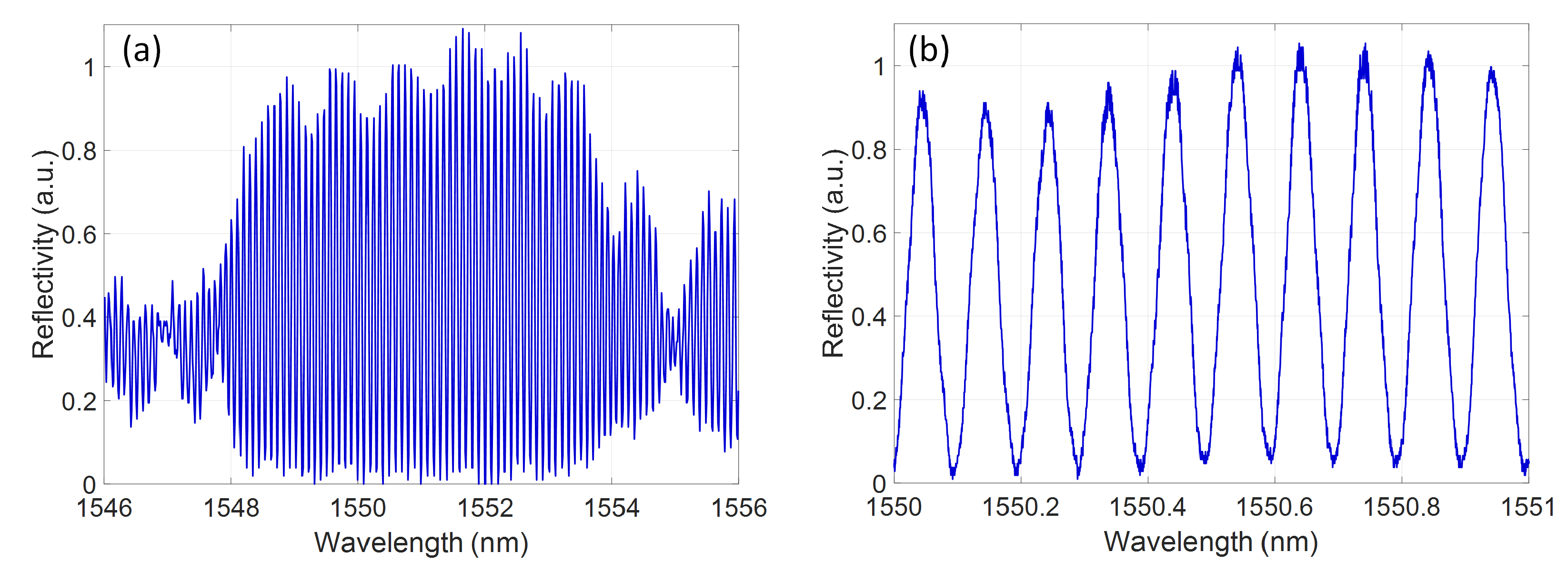
2.1. Actively Tunable Bragg Grating Design
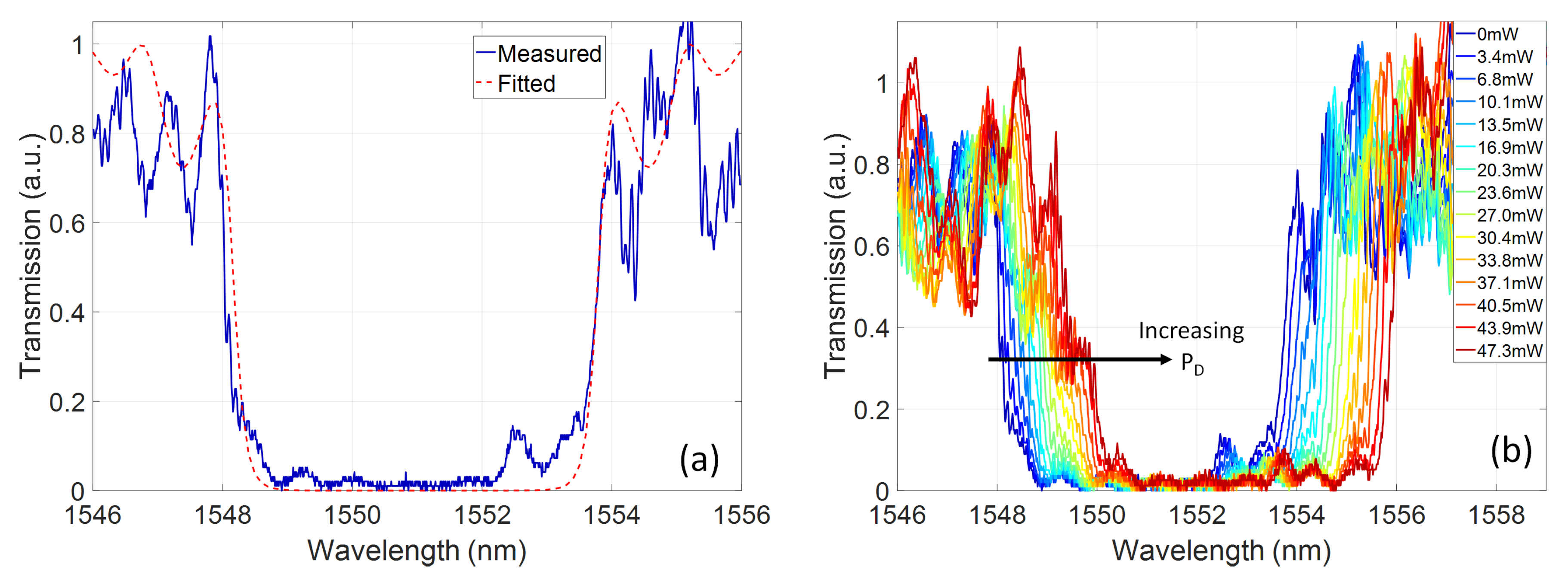
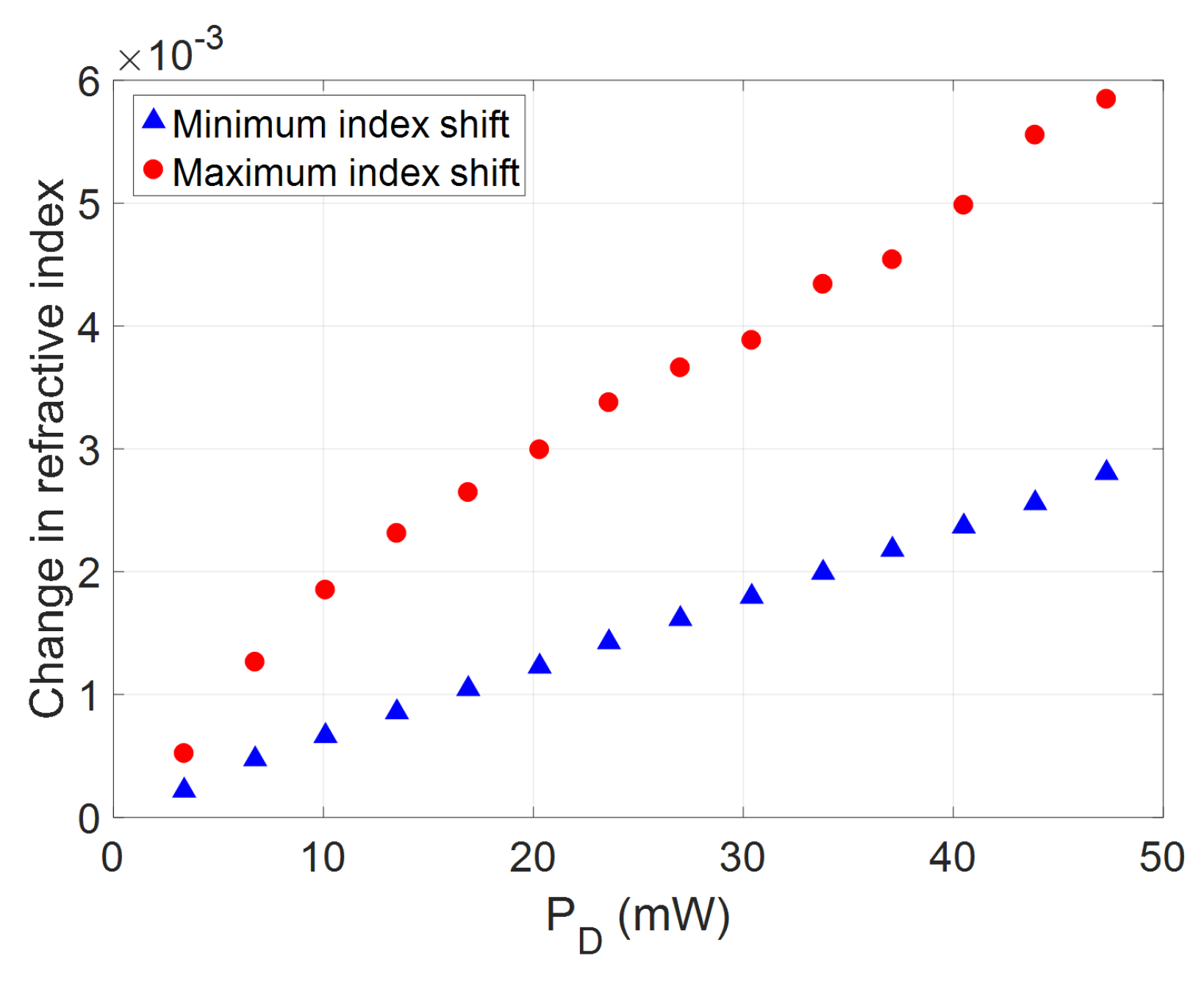
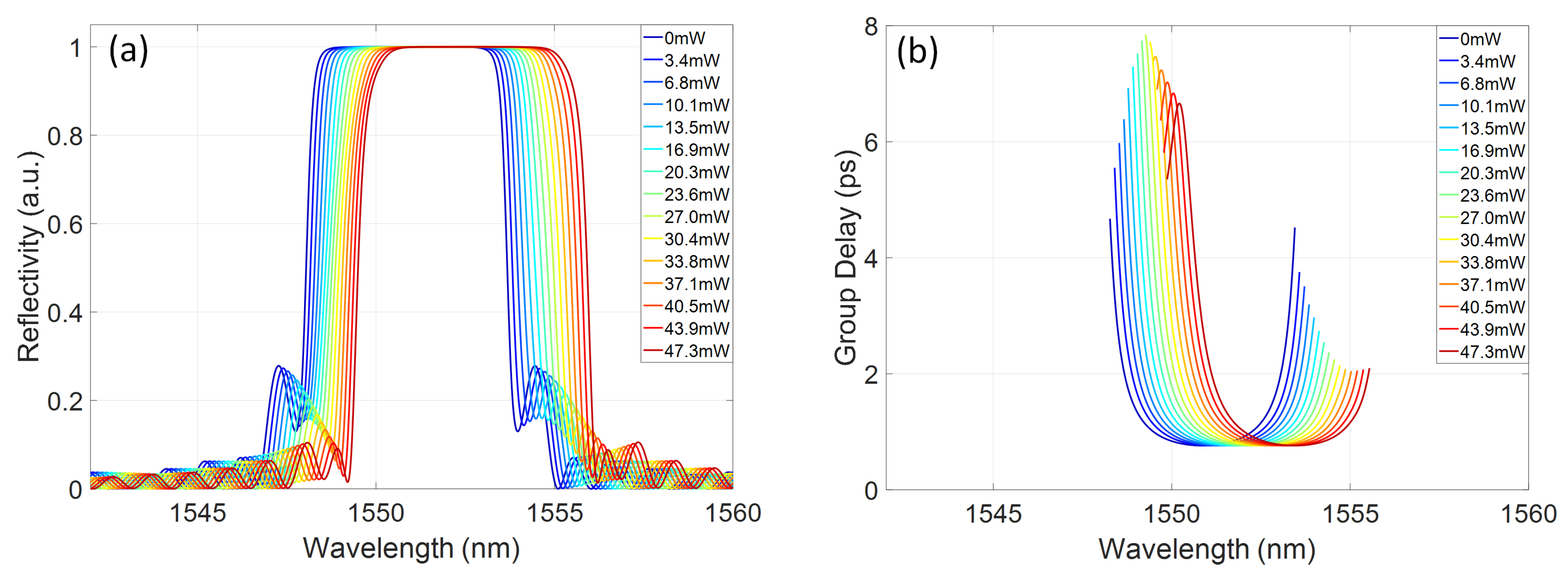
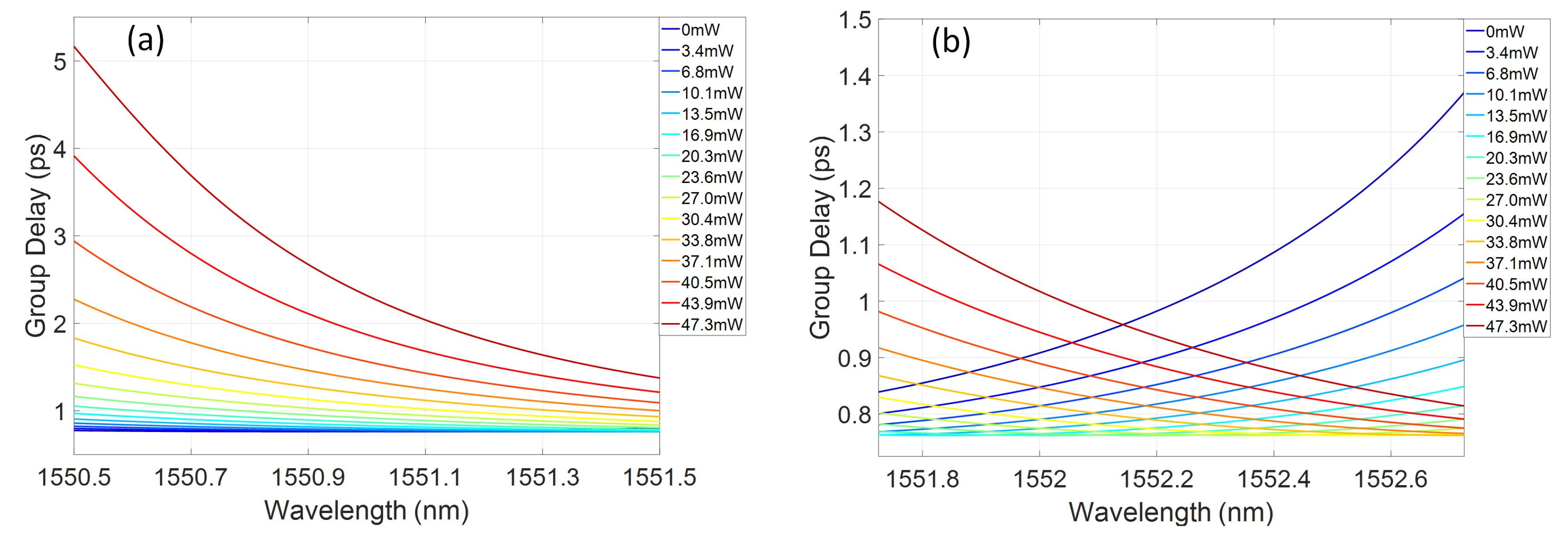
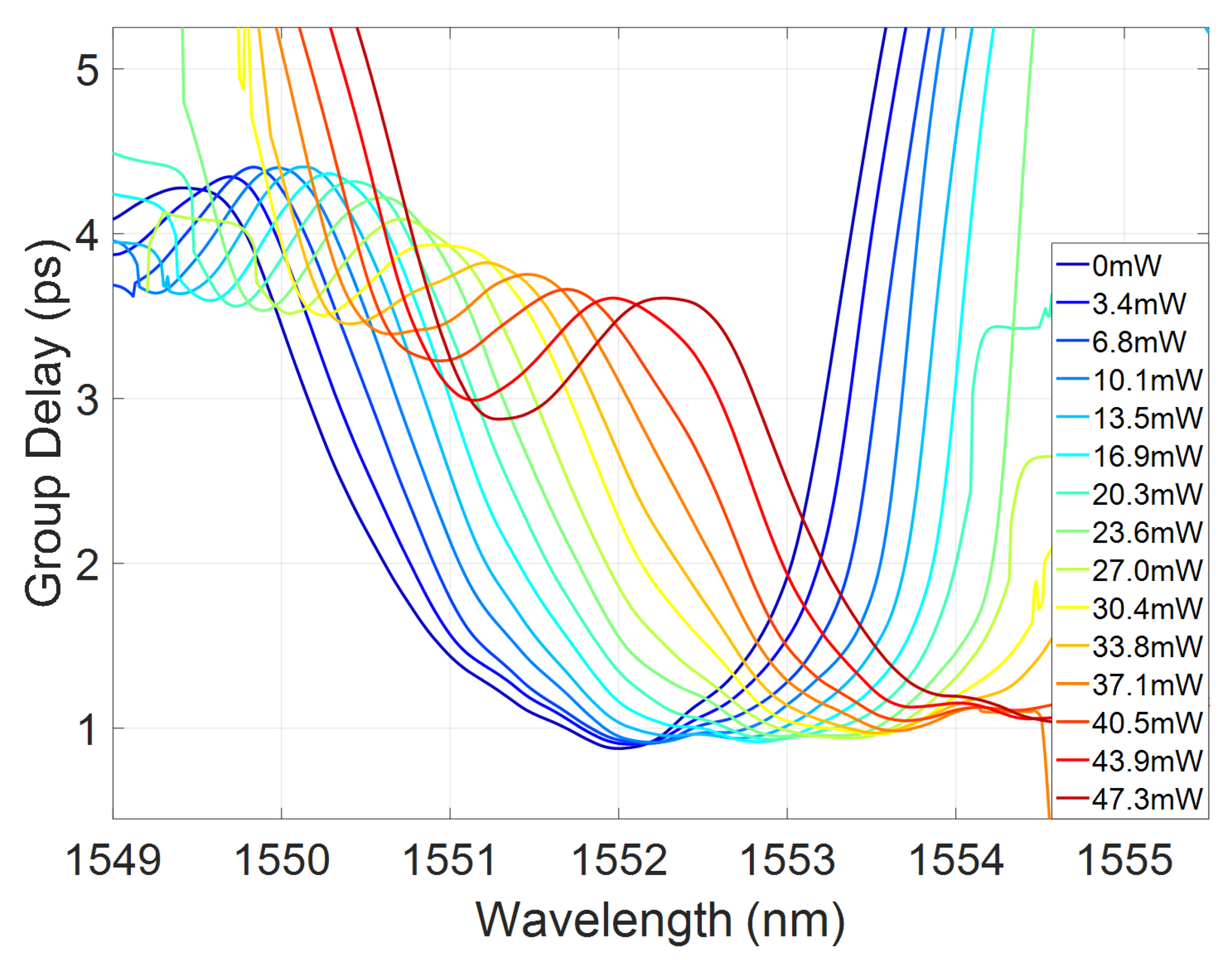
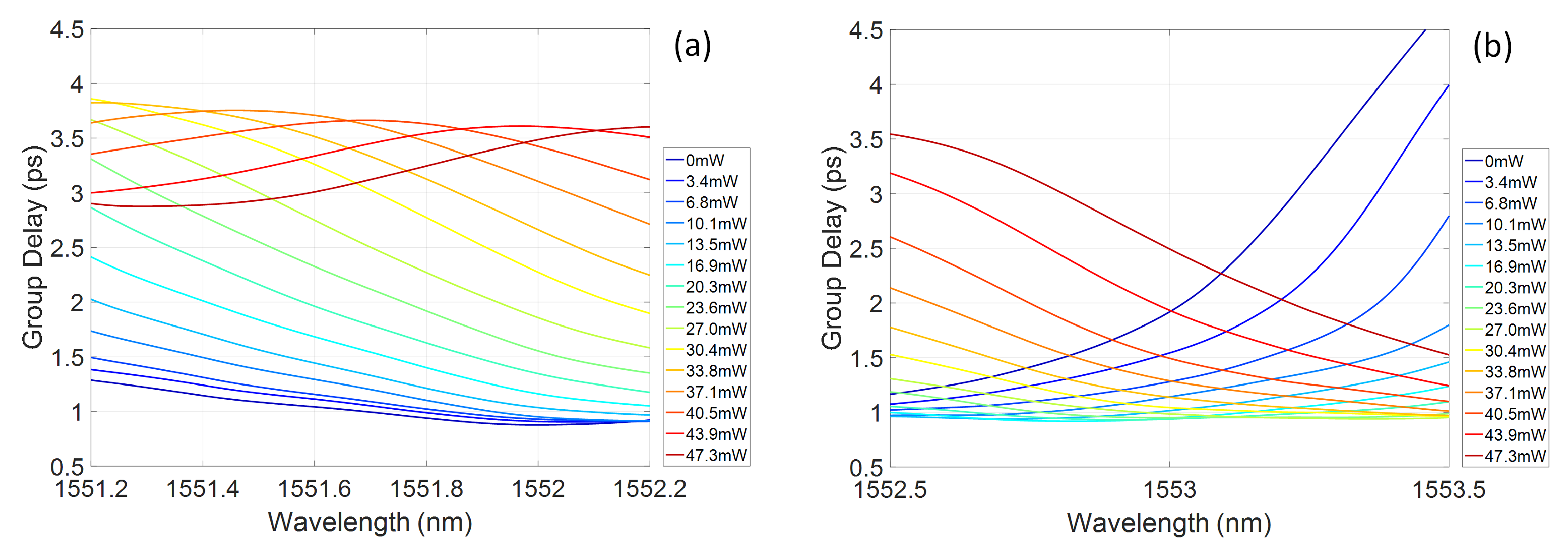
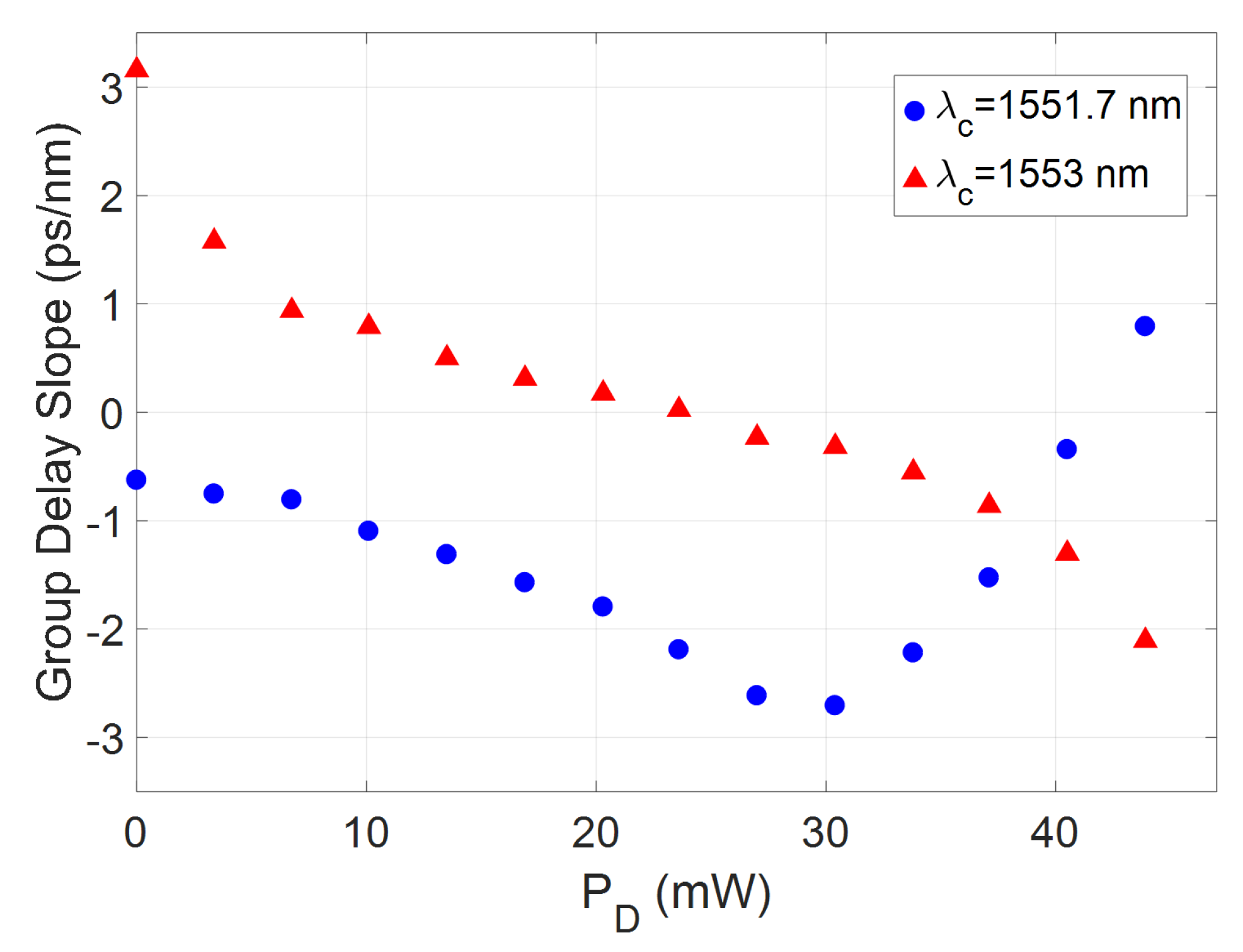
2.2. Group Delay Chirp Control
3. Discussion
4. Conclusions
5. Materials and Methods
5.1. Device Fabrication
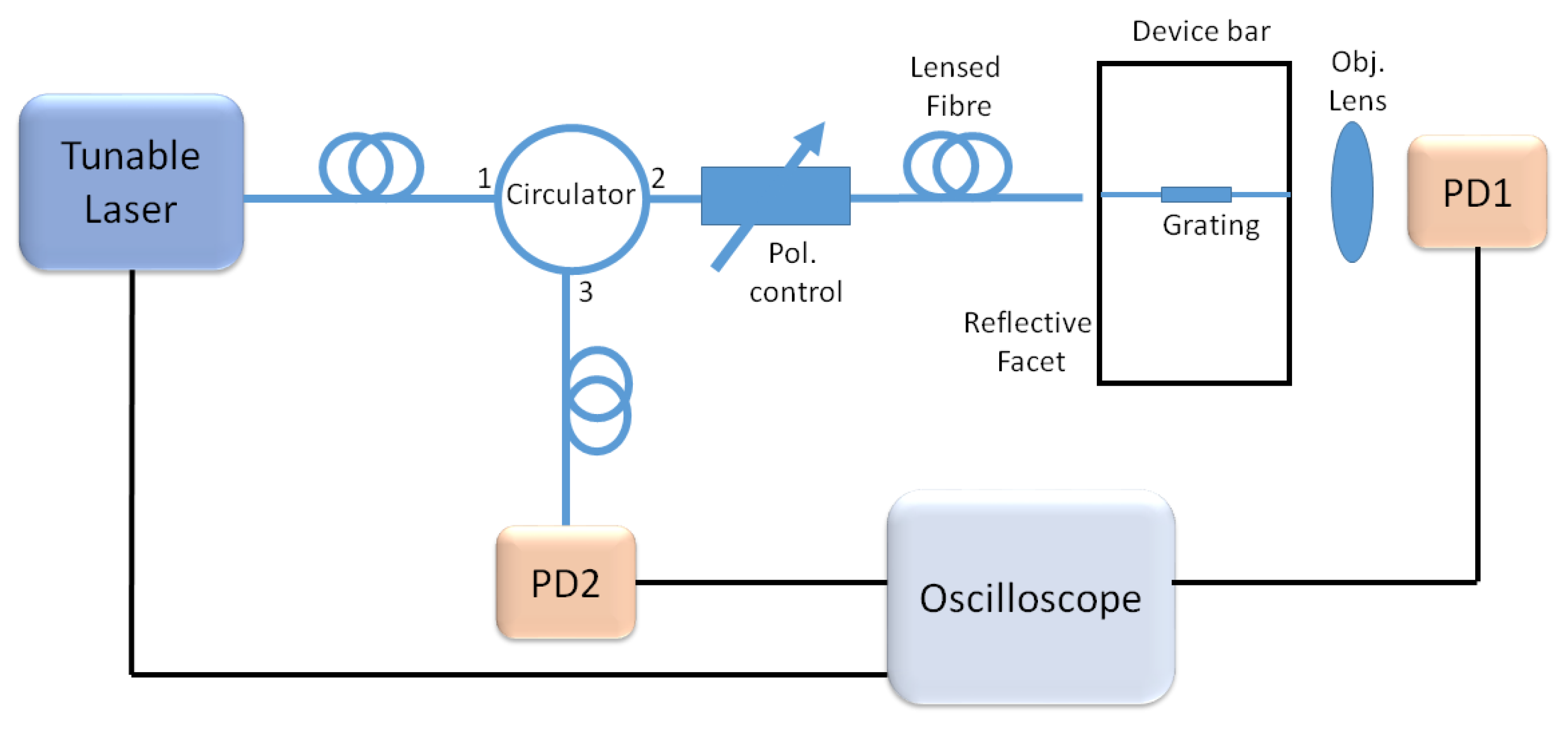
5.2. Transmission and Group Delay Measurements
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Harris, N.C.; Grassani, D.; Simbula, A.; Pant, M.; Galli, M.; Baehr-jones, T.; Hochberg, M.; Englund, D.; Bajoni, D.; Galland, C. Integrated Source of Spectrally Filtered Correlated Photons for Large-Scale Quantum Photonic Systems. Phys. Rev. X 2014, 4, 041047. [Google Scholar] [CrossRef]
- Oser, D.; Mazeas, F.; Le Roux, X.; Pérez-Galacho, D.; Alibart, O.; Tanzilli, S.; Labonté, L.; Marris-Morini, D.; Vivien, L.; Cassan, É.; et al. Coherency-Broken Bragg Filters: Overcoming On-Chip Rejection Limitations. Laser Photonics Rev. 2019, 13, 1800226. [Google Scholar] [CrossRef]
- Prabhathan, P.; Murukeshan, V.M.; Jing, Z.; Ramana, P.V. Compact SOI nanowire refractive index sensor using phase shifted Bragg grating. Opt. Express 2009, 17, 15330–15341. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Srinivasan, S.; Tang, Y.; Heck, M.J.R.; Davenport, M.L.; Bowers, J.E. Low threshold and high speed short cavity distributed feedback hybrid silicon lasers. Opt. Express 2014, 22, 10202–10209. [Google Scholar] [CrossRef] [PubMed]
- Burla, M.; Cortés, L.R.; Li, M.; Wang, X.; Chrostowski, L.; Azaña, J. Integrated waveguide Bragg gratings for microwave photonics signal processing. Opt. Express 2013, 21, 25120–25147. [Google Scholar] [CrossRef] [PubMed]
- Rutkowska, K.A.; Duchesne, D.; Strain, M.J.; Morandotti, R.; Sorel, M.; Azaña, J. Ultrafast all-optical temporal differentiators based on CMOS-compatible integrated-waveguide Bragg gratings. Opt. Express 2011, 19, 19514–19522. [Google Scholar] [CrossRef]
- Wang, X.; Shi, W.; Yun, H.; Grist, S.; Jaeger, N.A.; Chrostowski, L. Narrow-band waveguide Bragg gratings on SOI wafers with CMOS-compatible fabrication process. Opt. Express 2012, 20, 15547–15558. [Google Scholar] [CrossRef]
- Veerasubramanian, V.; Beaudin, G.; Giguere, A.; Le Drogoff, B.; Aimez, V.; Kirk, A.G. Design and Demonstration of Apodized Comb Filters on SOI. IEEE Photonics J. 2012, 4, 1133–1139. [Google Scholar] [CrossRef]
- Chen, G.F.R.; Wang, T.; Donnelly, C.; Tan, D.T.H. Second and third order dispersion generation using nonlinearly chirped silicon waveguide gratings. Opt. Express 2013, 21, 29223–29230. [Google Scholar] [CrossRef]
- Cheng, R.; Han, Y.; Chrostowski, L. Characterization and compensation of apodization phase noise in silicon integrated Bragg gratings. Opt. Express 2019, 27, 9516–9535. [Google Scholar] [CrossRef]
- Strain, M.J.; Sorel, M. Design and fabrication of integrated chirped Bragg gratings for on-chip dispersion control. Quantum Electron. IEEE J. 2010, 46, 774–782. [Google Scholar] [CrossRef]
- Zhang, W.; Yao, J. A fully reconfigurable waveguide Bragg grating for programmable photonic signal processing. Nat. Commun. 2018, 9, 1396. [Google Scholar] [CrossRef] [PubMed]
- Rivas, L.M.; Strain, M.J.; Duchesne, D.; Carballar, A.; Sorel, M.; Morandotti, R.; Azaña, J. Picosecond linear optical pulse shapers based on integrated waveguide Bragg gratings. Opt. Lett. 2008, 33, 2425–2427. [Google Scholar] [CrossRef] [PubMed]
- Tan, D.T.H.; Ikeda, K.; Saperstein, R.E.; Slutsky, B.; Fainman, Y. Chip-scale dispersion engineering using chirped vertical gratings. Opt. Lett. 2008, 33, 3013–3015. [Google Scholar] [CrossRef] [PubMed]
- Strain, M.J.; Thoms, S.; MacIntyre, D.S.; Sorel, M. Multi-wavelength filters in silicon using superposition sidewall Bragg grating devices. Opt. Lett. 2014, 39, 413–416. [Google Scholar] [CrossRef] [PubMed]
- Cheng, R.; Chrostowski, L. Apodization of Silicon Integrated Bragg Gratings through Periodic Phase Modulation. IEEE J. Sel. Top. Quantum Electron. 2019, 26. [Google Scholar] [CrossRef]
- Kim, M.s.; Ju, J.J.; Park, S.K.; Lee, M.H.; Kim, S.H.; Lee, K.D. Tailoring Chirp Characteristics of Waveguide Bragg Gratings Using Tapered Core Profiles. IEEE Photonics Technol. Lett. 2006, 18, 2413–2415. [Google Scholar] [CrossRef]
- Giuntoni, I.; Stolarek, D.; Kroushkov, D.I.; Bruns, J.; Zimmermann, L.; Tillack, B.; Petermann, K. Continuously tunable delay line based on SOI tapered Bragg gratings. Opt. Express 2012, 20, 11241–11246. [Google Scholar] [CrossRef]
- Khan, S.; Baghban, M.A.; Fathpour, S. Electronically tunable silicon photonic delay lines. Opt. Express 2011, 19, 11780–11785. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.; Huang, Z.R. Integrated Cascaded Bragg Gratings for On-Chip Optical Delay Lines. IEEE Photonics Technol. Lett. 2018, 30, 499–502. [Google Scholar] [CrossRef]
- Chung, C.J.; Xu, X.; Wang, G.; Pan, Z.; Chen, R.T. On-chip optical true time delay lines featuring one-dimensional fishbone photonic crystal waveguide. Appl. Phys. Lett. 2018, 112, 071104. [Google Scholar] [CrossRef]
- Zheng, X.; Patil, D.; Lexau, J.; Liu, F.; Li, G.; Thacker, H.; Luo, Y.; Shubin, I.; Li, J.; Yao, J.; et al. Ultra-efficient 10 Gb/s hybrid integrated silicon photonic transmitter and receiver. Opt. Express 2011, 19, 5172–5186. [Google Scholar] [CrossRef] [PubMed]
- Orlandi, P.; Morichetti, F.; Strain, M.J.; Sorel, M.; Bassi, P.; Melloni, A. Photonic Integrated Filter with Widely Tunable Bandwidth. J. Light. Technol. 2014, 32, 897–907. [Google Scholar] [CrossRef]
- Pérez, D.; Gasulla, I.; Crudgington, L.; Thomson, D.J.; Khokhar, A.Z.; Li, K.; Cao, W.; Mashanovich, G.Z.; Capmany, J. Multipurpose silicon photonics signal processor core. Nat. Commun. 2017, 8, 636. [Google Scholar] [CrossRef] [PubMed]
- Reed, G.T.; Mashanovich, G.; Gardes, F.Y.; Thomson, D.J. Silicon optical modulators. Nat. Photonics 2010, 4, 518–526. [Google Scholar] [CrossRef] [Green Version]
- Atabaki, A.H.; Eftekhar, A.A.; Yegnanarayanan, S.; Adibi, A. Sub-100-nanosecond thermal reconfiguration of silicon photonic devices. Opt. Express 2013, 21, 18312–18323. [Google Scholar] [CrossRef] [PubMed]
- Densmore, A.; Janz, S.; Ma, R.; Schmid, J.H.; Xu, D.X.; Delâge, A.; Lapointe, J.; Vachon, M.; Cheben, P. Compact and low power thermo-optic switch using folded silicon waveguides. Opt. Express 2009, 17, 10457–10465. [Google Scholar] [CrossRef] [PubMed]
- Dong, P.; Qian, W.; Liang, H.; Shafiiha, R.; Feng, D.; Li, G.; Cunningham, J.E.; Krishnamoorthy, A.V.; Asghari, M. Thermally tunable silicon racetrack resonators with ultralow tuning power. Opt. Express 2010, 18, 20298–20304. [Google Scholar] [CrossRef] [PubMed]
- Orlandi, P.; Morichetti, F.; Strain, M.J.; Sorel, M.; Melloni, A.; Bassi, P. Tunable silicon photonics directional coupler driven by a transverse temperature gradient. Opt. Lett. 2013, 38, 863–865. [Google Scholar] [CrossRef] [PubMed]
- Yamada, M.; Sakuda, K. Analysis of almost-periodic distributed feedback slab waveguides via a fundamental matrix approach. Appl. Opt. 1987, 26, 3474–3478. [Google Scholar] [CrossRef]
- Turner, A.C.; Manolatou, C.; Schmidt, B.S.; Lipson, M.; Foster, M.a.; Sharping, J.E.; Gaeta, A.L. Tailored anomalous group-velocity dispersion in silicon channel waveguides. Opt. Express 2006, 14, 4357–4362. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sahin, E.; Ooi, K.J.; Png, C.E.; Tan, D.T. Large, scalable dispersion engineering using cladding-modulated Bragg gratings on a silicon chip. Appl. Phys. Lett. 2017, 110, 161113. [Google Scholar] [CrossRef]
- Samarelli, A.; Macintyre, D.S.; Strain, M.J.; De La Rue, R.M.; Sorel, M.; Thoms, S. Optical characterization of a hydrogen silsesquioxane lithography process. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. 2008, 26, 2290–2294. [Google Scholar] [CrossRef]
- Roelkens, G.; Dumon, P.; Bogaerts, W.; Van Thourhout, D.; Baets, R. Efficient silicon-on-insulator fiber coupler fabricated using 248-nm-deep UV lithography. IEEE Photonics Technol. Lett. 2005, 17, 2613–2615. [Google Scholar] [CrossRef]
- Skaar, J. Measuring the group delay of fiber Bragg gratings by use of end-reflection interference. Opt. Lett. 1999, 24, 1020–1022. [Google Scholar] [CrossRef] [PubMed]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klitis, C.; Sorel, M.; Strain, M.J. Active On-Chip Dispersion Control Using a Tunable Silicon Bragg Grating. Micromachines 2019, 10, 569. https://doi.org/10.3390/mi10090569
Klitis C, Sorel M, Strain MJ. Active On-Chip Dispersion Control Using a Tunable Silicon Bragg Grating. Micromachines. 2019; 10(9):569. https://doi.org/10.3390/mi10090569
Chicago/Turabian StyleKlitis, Charalambos, Marc Sorel, and Michael J. Strain. 2019. "Active On-Chip Dispersion Control Using a Tunable Silicon Bragg Grating" Micromachines 10, no. 9: 569. https://doi.org/10.3390/mi10090569
APA StyleKlitis, C., Sorel, M., & Strain, M. J. (2019). Active On-Chip Dispersion Control Using a Tunable Silicon Bragg Grating. Micromachines, 10(9), 569. https://doi.org/10.3390/mi10090569





