Simulation and Experimental Study on the Surface Generation Mechanism of Cu Alloys in Ultra-Precision Diamond Turning
Abstract
:1. Introduction
2. Modeling of the Surface Topography
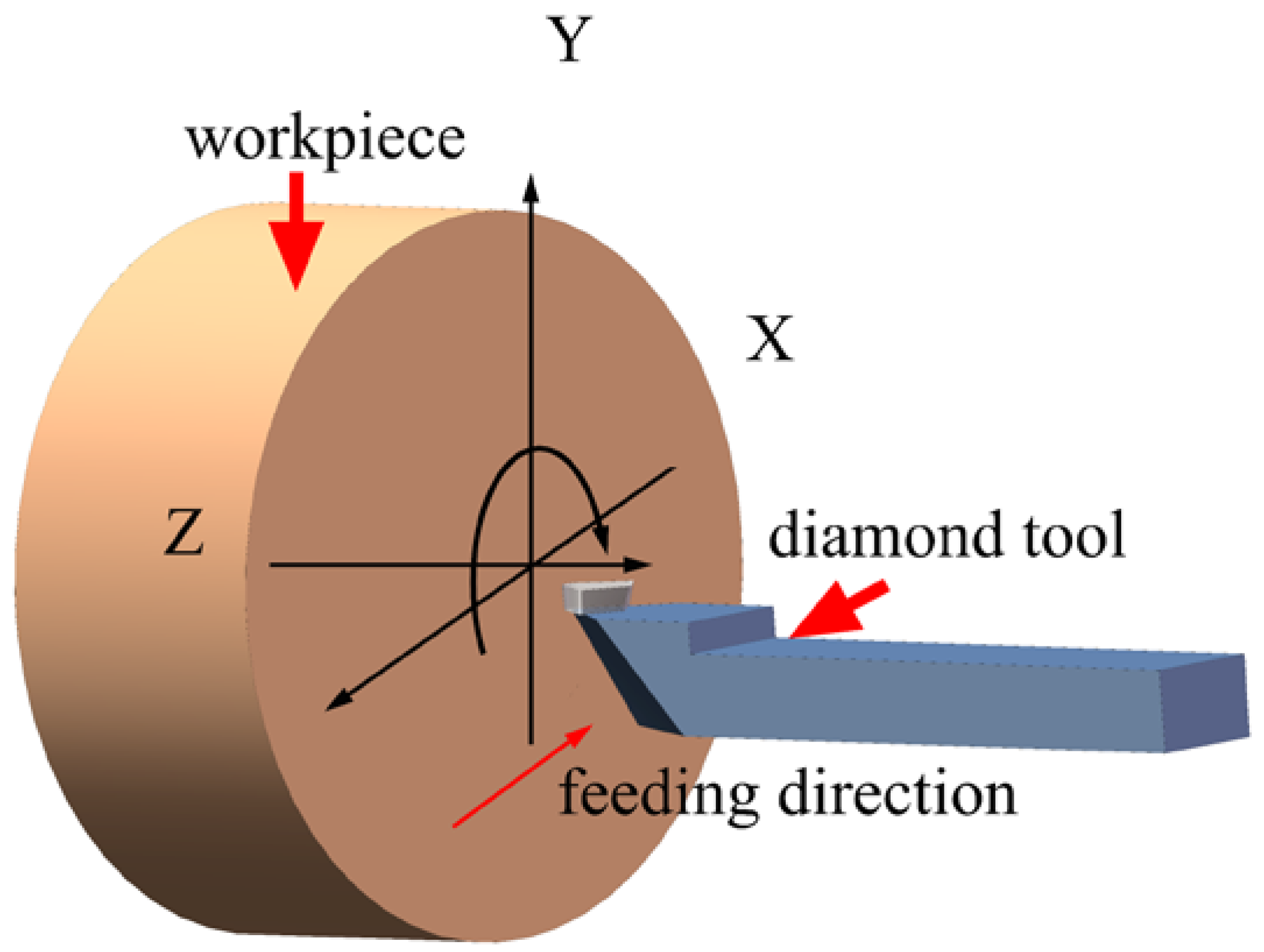
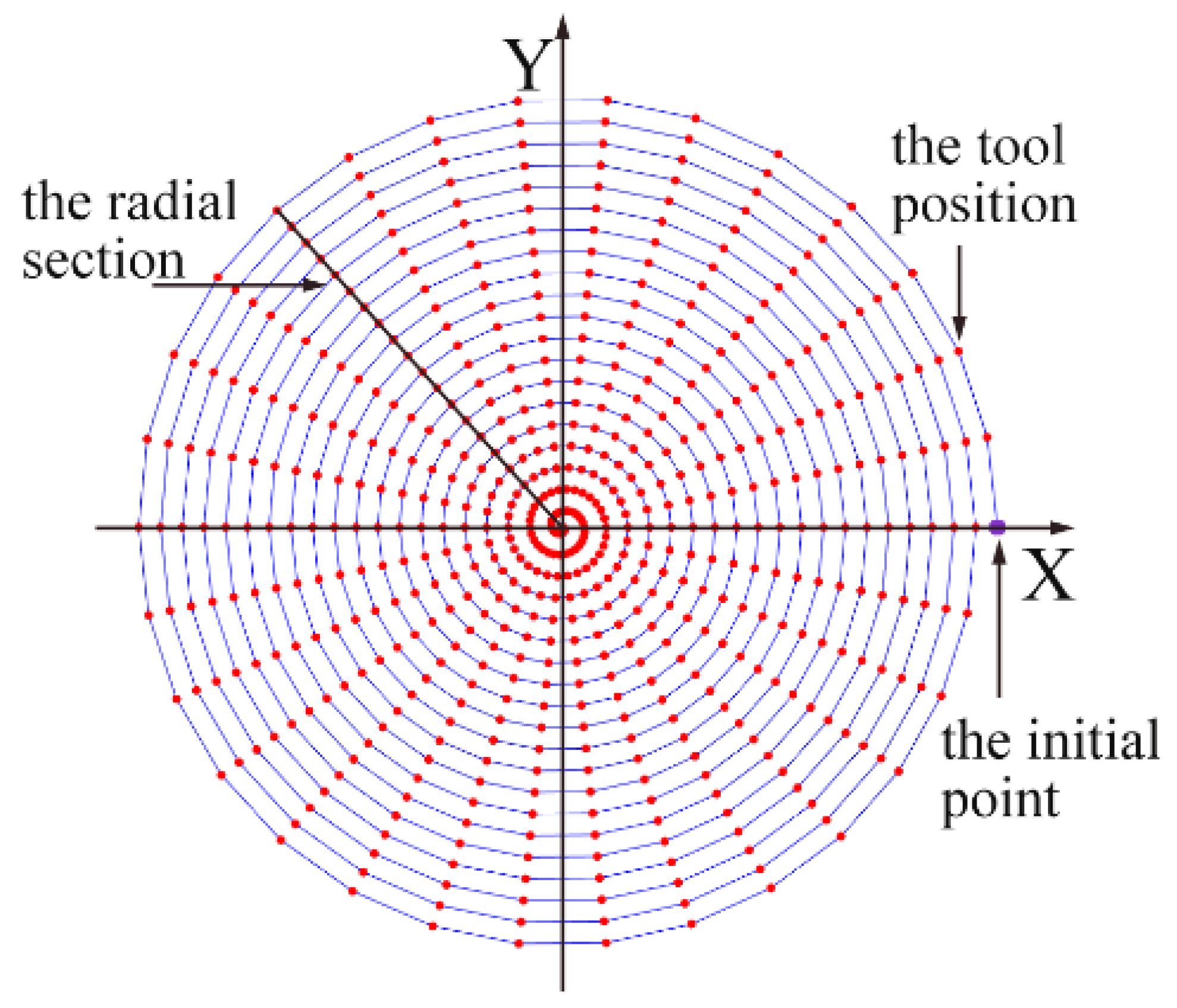
2.1. Principles of the 3D Surface Topography Simulation in Ultra-Precision Diamond Turning
- Firstly, the length and width of the workpiece are input as initial parameters, and the resolution is defined with the height data set at every point at the initial value.
- Secondly, the tool is moved along the calculated spiral trajectory. When the tool arrives at the fixed point in the trajectory, the height of the workpiece within a small area under the cutting tool is compared with the lower surface of the tool. If the area is higher than the lower surface of the tool, the area will be removed and the geometry of the tool is copied to the machined surface.
- Finally, when the cutting tool reaches the center of the workpiece, the simulation is completed, and the surface heights of the points we set in the first step can be obtained.
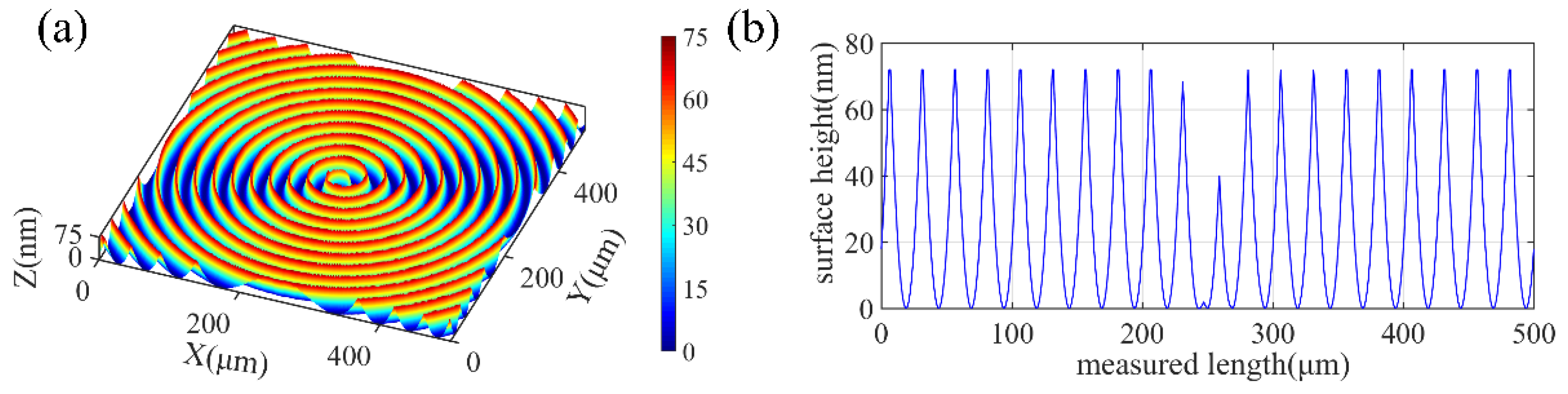
2.2. Simulation of the 3D Surface Topography at Different Machining Parameters
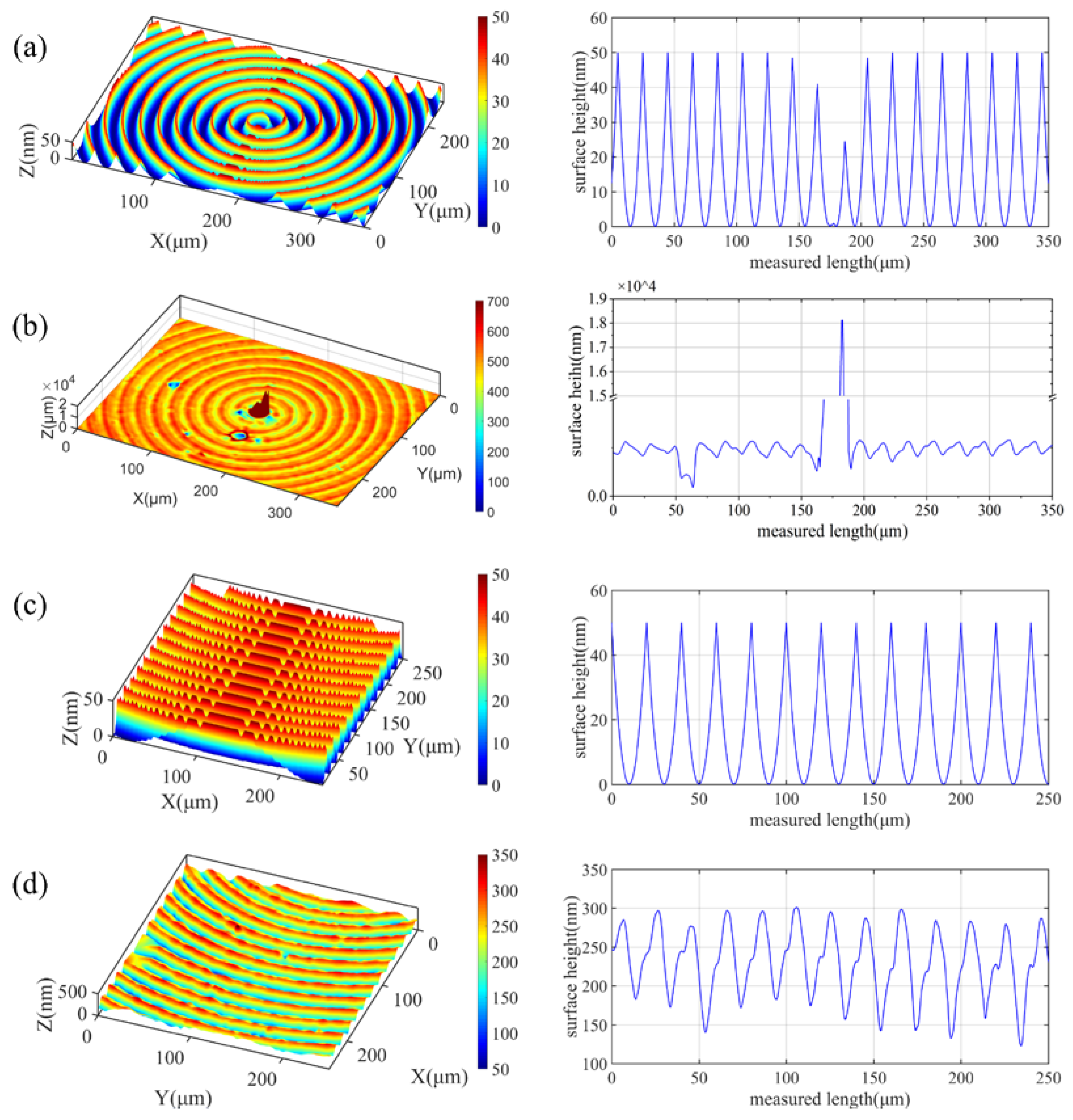
3. Experiments Verification
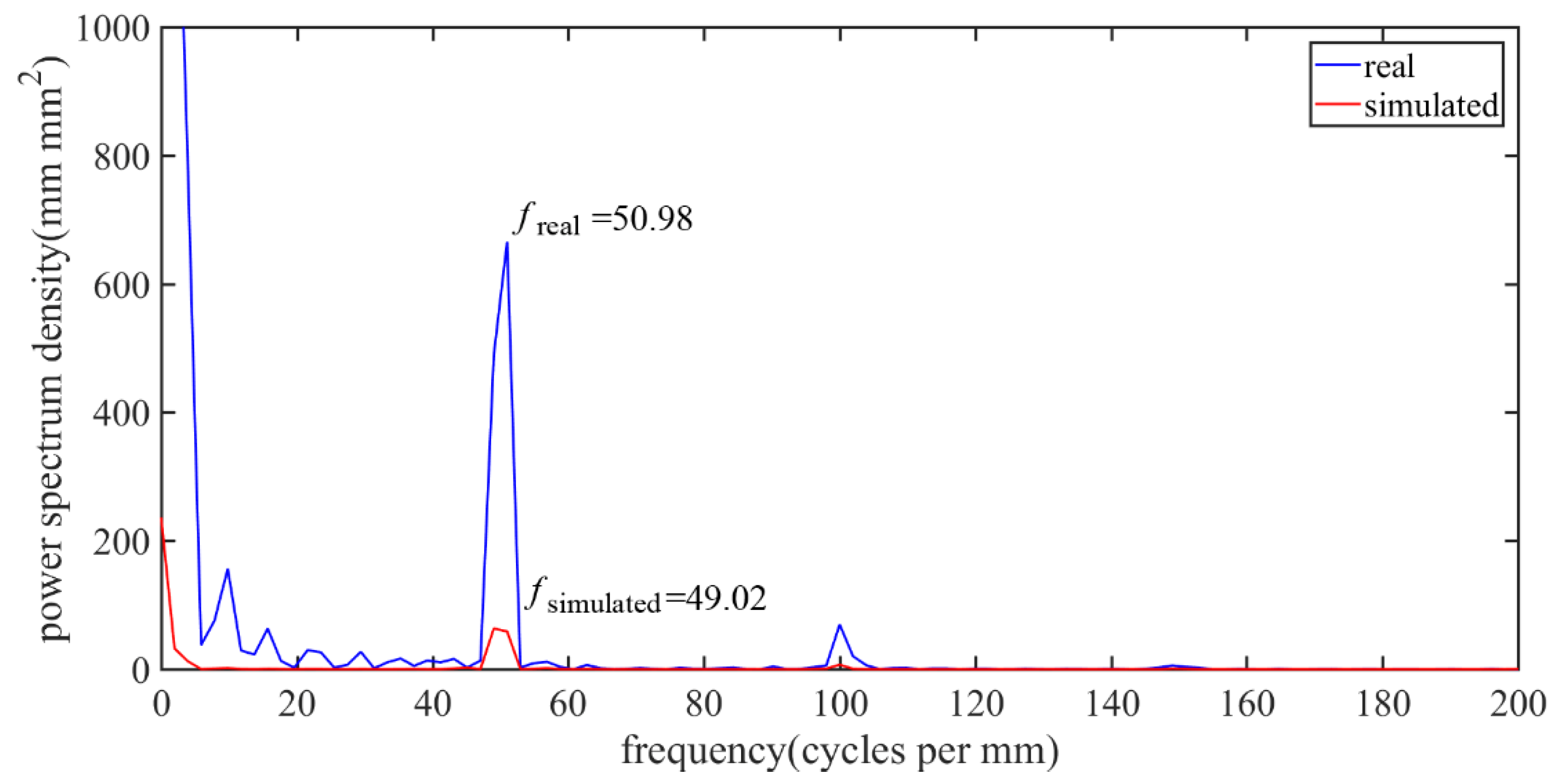
4. Results and Discussion
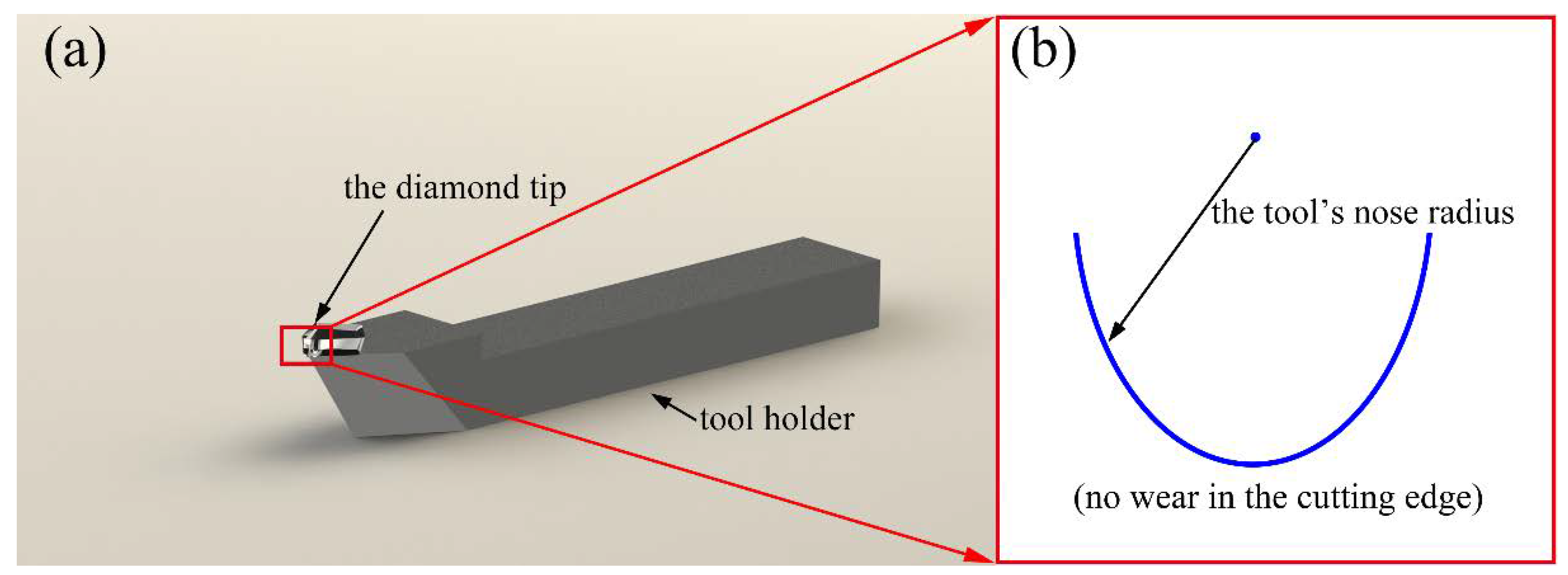
4.1. Effects of the Tool Wear
4.2. Effects of the Materials Microstructure
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Notation
| freal | Specific spatial frequency of the real machined surface |
| fs | Feed rate (mm/min) |
| fsimulated | Specific spatial frequency of the simulated machined surface |
| i | Index for the tool tip position along the trajectory |
| j | Index for the point of the surface height profile |
| PV | Maximum peak-to-valley value (nm) |
| R | Distance from the tool tip position to the center of the workpiece |
| R0 | Radius of the workpiece |
| Ra | Arithmetic roughness (nm) |
| radt | Tool nose radius (mm) |
| Sa | Arithmetic surface roughness (nm) |
| ss | Feed rate per revolution of the workpiece (mm/rev) |
| t | Machining time (s) |
| Xi | x coordinate of the tool tip position |
| Yi | y coordinate of the tool tip position |
| zj | Height of jth point of the profile |
| zmean | Mean height of the surface profile |
| θi | ith tool tip position of the tool in the trajectory |
| ω | Rotational speed (rad/s) |
References
- Ikawa, N.; Donaldson, R.R. Ultraprecision metal cutting-the past, the present and the future. CIRP Ann. 1991, 40, 587–594. [Google Scholar] [CrossRef]
- Zhang, S.J.; To, S. A review of surface roughness generation in ultra-precision machining. Int. J. Mach. Tools Manuf. 2015, 91, 76–95. [Google Scholar] [CrossRef]
- Tauhiduzzaman, M.; Yip, A.; Veldhuis, S.C. Form error in diamond turning. Precis. Eng. 2015, 42, 22–36. [Google Scholar] [CrossRef]
- Li, D.; Wang, B.; Qiao, Z.; Jiang, X.Q. Ultraprecision machining of microlens arrays with integrated on-machine surface metrology. Opt. Express 2019, 27, 212–224. [Google Scholar] [CrossRef] [PubMed]
- Lee, W.B.; Cheung, C.F.; To, S. Materials induced vibration in ultra-precision machining. J. Mater. Process. Technol. 1999, 89, 318–325. [Google Scholar] [CrossRef]
- He, C.L.; Zong, W.J.; Xue, C.X.; Sun, T. An accurate 3D surface topography model for single-point diamond turning. Int. J. Mach. Tools Manuf. 2018, 134, 42–68. [Google Scholar] [CrossRef]
- Huang, C.; Liang, R. Modeling of surface topography in single-point diamond turning machine. Appl. Opt. 2015, 54, 6979. [Google Scholar] [CrossRef] [PubMed]
- Kong, L.B.; Cheung, C.F.; Kwok, T.C. Theoretical and experimental analysis of the effect of error motions on surface generation in fast tool servo machining. Precis. Eng. 2014, 38, 428–438. [Google Scholar] [CrossRef]
- Li, D.; Qiao, Z.; Walton, K.; Liu, Y.; Xue, J.; Wang, B.; Jiang, X.Q. Theoretical and experimental investigation of surface topography generation in slow tool servo ultra-precision machining of freeform surfaces. Materials 2018, 11, 2566. [Google Scholar] [CrossRef]
- Brookes, E.J.; Greenwood, P.; Xing, G. Friction and wear of synthetic diamond. Int. J. Refract. Met. Hard Mater. 1999, 17, 69–77. [Google Scholar] [CrossRef]
- De Oliveira, L.J.; Bobrovnitchii, G.S.; Filgueira, M. Processing and characterization of impregnated diamond cutting tools using a ferrous metal matrix. Int. J. Refract. Met. Hard Mater. 2007, 25, 328–335. [Google Scholar] [CrossRef]
- Sawangsri, W.; Cheng, K. An innovative approach to cutting force modelling in diamond turning and its correlation analysis with tool wear. Proc. IMechE Part B J. Eng. Manuf. 2016, 230, 405–415. [Google Scholar] [CrossRef]
- Zhang, G.Q.; To, S. Diamond tool wear detection method using cutting force and its power spectrum analysis in ultra-precision fly cutting. In Proceedings of the 7th International Symposium on Advanced Optical Manufacturing and Testing Technologies, Harbin, China, 26–29 April 2014. [Google Scholar]
- Zhang, G.Q.; To, S. Relation between tool wear and workpiece modal vibration in ultra-precision raster fly cutting. Int. J. Adv. Manuf. Technol. 2017, 93, 3505–3515. [Google Scholar] [CrossRef]
- Deng, J.X.; Zhang, H.; Wu, Z.; Liu, A. Friction and wear behavior of polycrystalline diamond at temperatures up to 700 °C. Int. J. Refract. Met. Hard Mater. 2011, 29, 631–638. [Google Scholar]
- Cheung, C.F.; Lee, W.B. A multi-spectrum analysis of surface roughness formation in ultra-precision machining. Precis. Eng. 2000, 24, 77–87. [Google Scholar] [CrossRef]
- Zhang, G.Q.; Dai, Y.Q.; To, S.; Wu, X.Y.; Lou, Y. Tool interference at workpiece centre in single-point diamond turning. Int. J. Mech. Sci. 2019, 151, 1–12. [Google Scholar] [CrossRef]
- Zhang, G.Q.; To, S.; Wu, X.Y.; Lou, Y. Steady tool wear and its influence on tool geometry in ultra-precision fly cutting of CuZn30. Int. J. Adv. Manuf. Technol. 2019, 101, 2653–2662. [Google Scholar] [CrossRef]
- Brinksmeier, E.; Preuss, W.; Riemer, O.; Rentsch, R. Cutting forces, tool wear and surface finish in high speed diamond machining. Precis. Eng. 2017, 49, 293–304. [Google Scholar] [CrossRef]
- Li, G.X.; Yi, S.; Sun, S.J.; Ding, S.L. Wear mechanisms and performance of abrasively ground polycrystalline diamond tools of different diamond grains in machining titanium alloy. J. Manuf. Process. 2017, 29, 320–331. [Google Scholar] [CrossRef]
- Wang, J.C.; Xin, M.M.; Cao, S.Y.; Zhao, T. Graphitization wear of diamond tool in nanometric cutting of single crystal silicon. Key Eng. Mater. 2014, 609, 751–757. [Google Scholar] [CrossRef]
- Goel, S.; Luo, X.; Reuben, R.L. Molecular dynamics simulation model for the quantitative assessment of tool wear during single point diamond turning of cubic silicon carbide. Comp. Mater. Sci. 2012, 51, 402–408. [Google Scholar] [CrossRef]
- Xie, F.; Jin, Z.J.; Guo, X.G.; Shi, S.J. Wear mechanism of diamond tool against mold steel in single point diamond by molecular dynamics. Appl. Mech. Mater. 2016, 851, 186–190. [Google Scholar] [CrossRef]
- Li, G.X.; Rahim, M.Z.; Ding, S.L.; Sun, S.J. Performance and wear analysis of polycrystalline diamond (PCD) tools manufactured with different methods in turning titanium alloy Ti-6Al-4V. Int. J. Adv. Manuf. Technol. 2016, 85, 825–841. [Google Scholar] [CrossRef]
- Takasu, S.; Masuda, M.; Nishiguchi, T.; Kobayashi, A. Influence of study vibration with small amplitude upon surface roughness in diamond machining. CIRP Ann. 1985, 34, 463–467. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, J.; Xu, Z.; Zhang, J.; Hassan, H.; Li, G.; Zhang, H.; Hartmaier, A.; Fang, F.; Yan, Y.; et al. Crystal plasticity finite element modeling and simulation of diamond cutting of polycrystalline copper. J. Manuf. Process. 2019, 38, 187–195. [Google Scholar] [CrossRef]
- Cheung, C.F.; Lee, W.B. Study of factors affecting the surface quality in ultra-precision diamond turning. Mater. Manuf. Process. 2000, 15, 481–502. [Google Scholar] [CrossRef]
- Sharma, A.; Datta, D.; Balasubramaniam, R. An investigation of tool and hard particle interaction in nanoscale cutting of copper beryllium. Comp. Mater. Sci. 2018, 145, 208–223. [Google Scholar] [CrossRef]

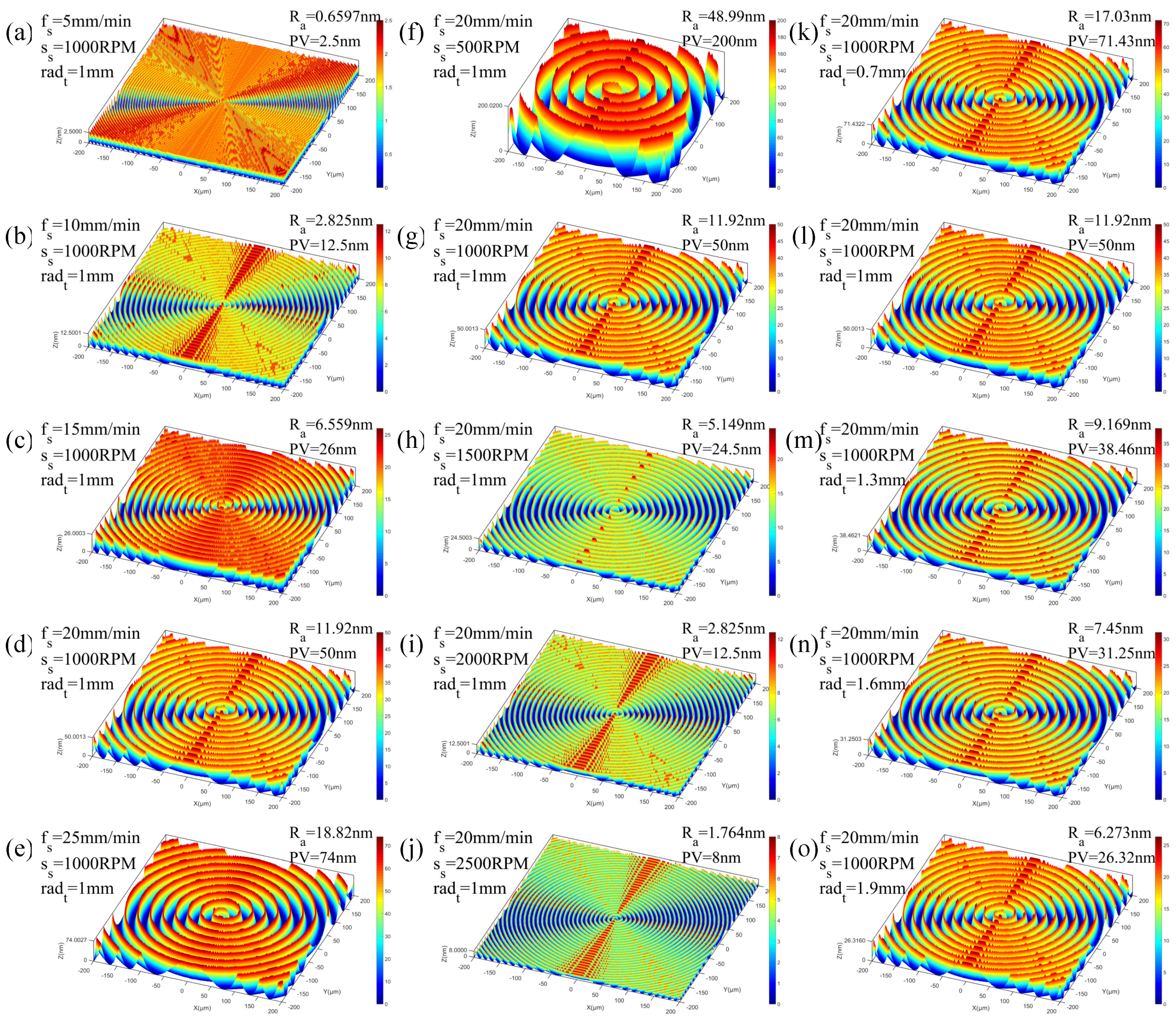
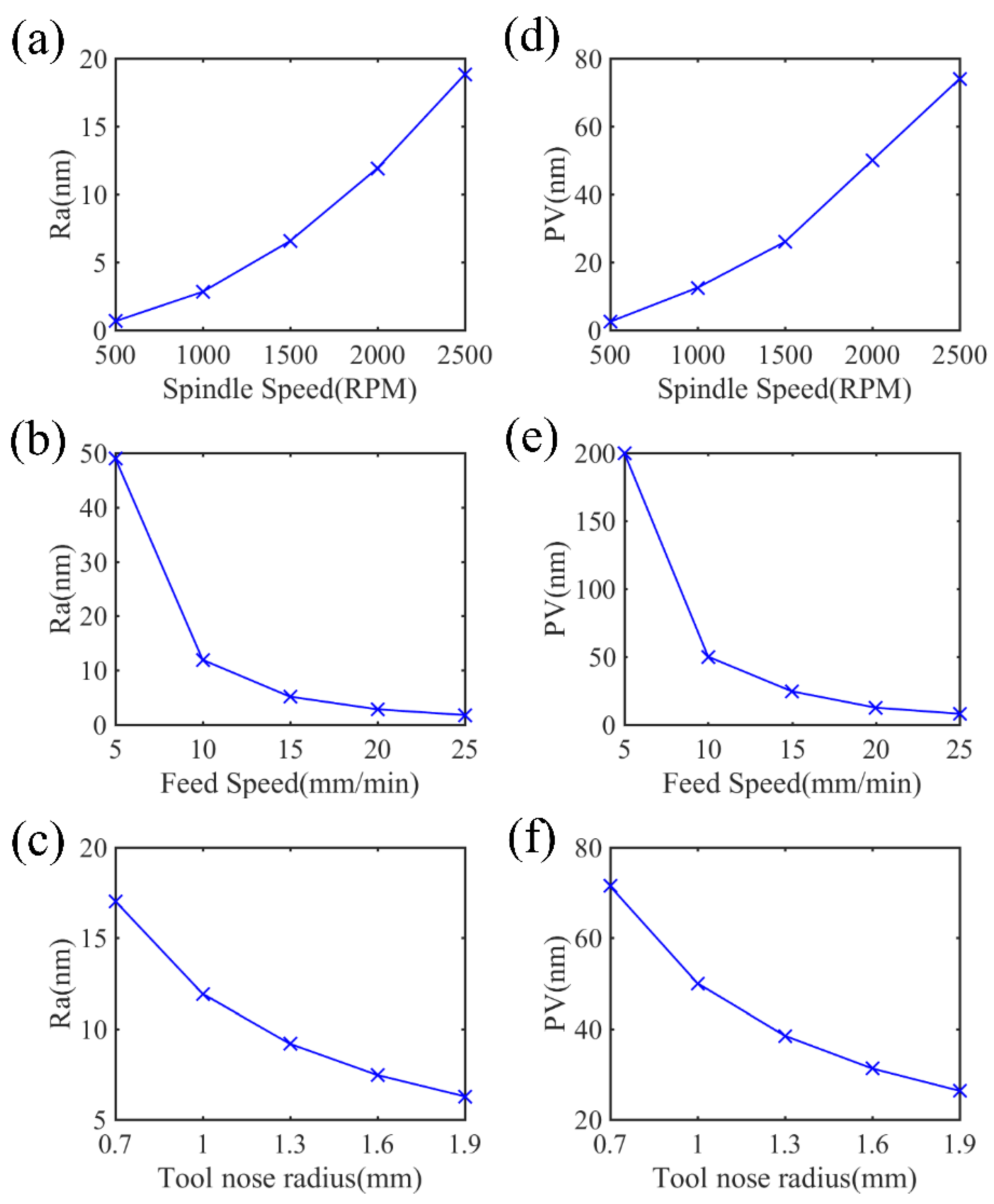




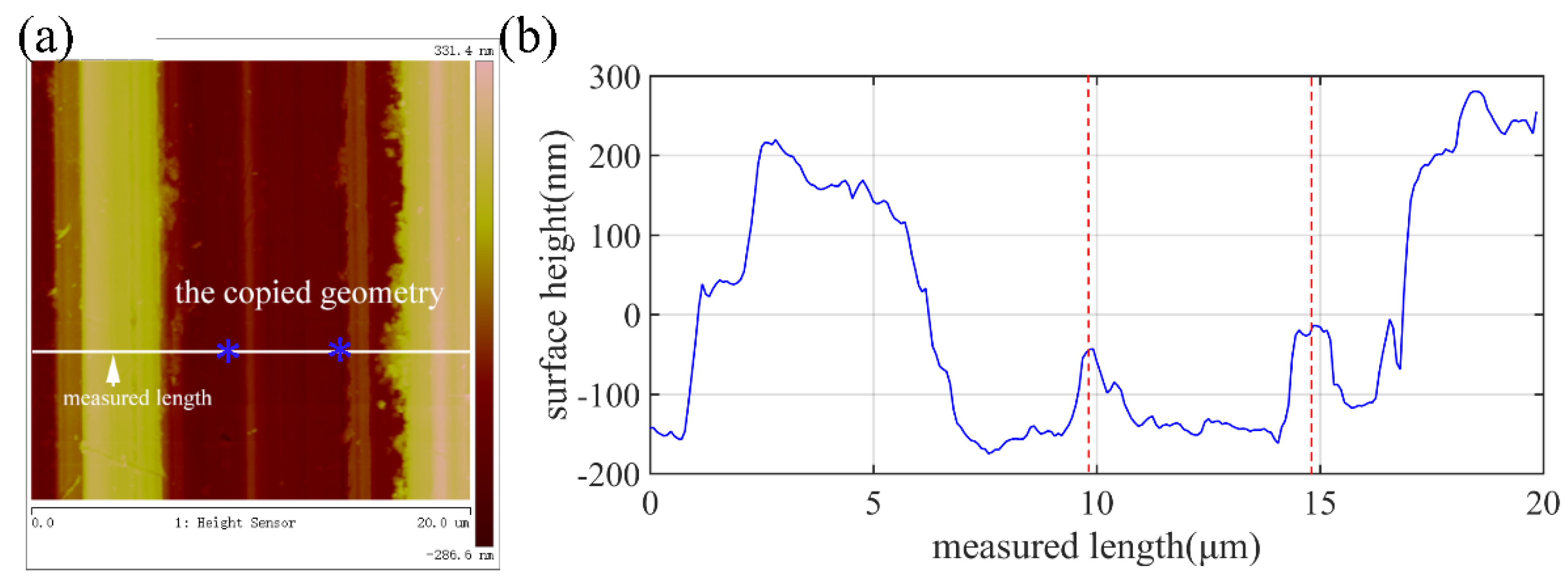


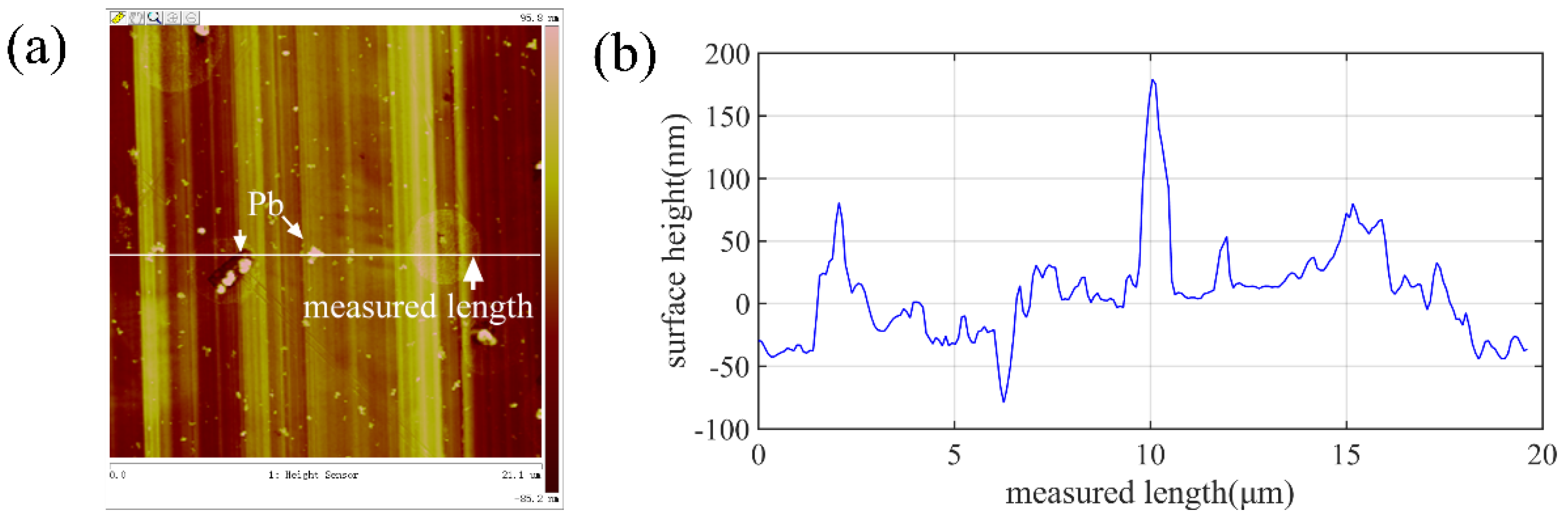
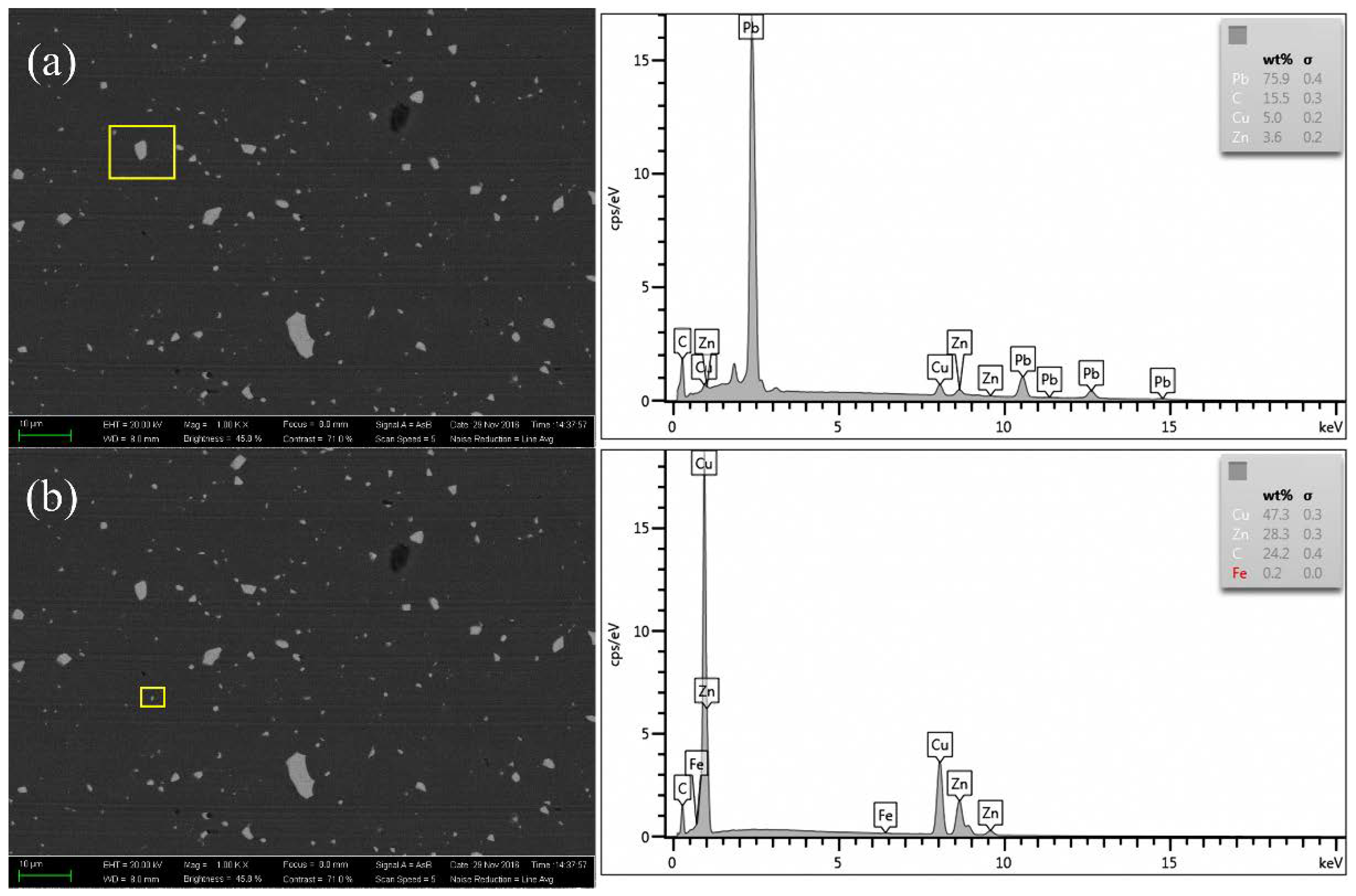
| Set No. | Condition No. | Spindle Rotation Speed | Feed Rate | Tool Nose Radius |
|---|---|---|---|---|
| S1 | C1 | 500 RPM | 20 mm/min | 1 mm |
| C2 | 1000 RPM | 20 mm/min | 1 mm | |
| C3 | 1500 RPM | 20 mm/min | 1 mm | |
| C4 | 2000 RPM | 20 mm/min | 1 mm | |
| C5 | 2500 RPM | 20 mm/min | 1 mm | |
| S2 | C1 | 1000 RPM | 5 mm/min | 1 mm |
| C2 | 1000 RPM | 10 mm/min | 1 mm | |
| C3 | 1000 RPM | 15 mm/min | 1 mm | |
| C4 | 1000 RPM | 20 mm/min | 1 mm | |
| C5 | 1000 RPM | 25 mm/min | 1 mm | |
| S3 | C1 | 1000 RPM | 20 mm/min | 0.7 mm |
| C2 | 1000 RPM | 20 mm/min | 1 mm | |
| C3 | 1000 RPM | 20 mm/min | 1.3 mm | |
| C4 | 1000 RPM | 20 mm/min | 1.6 mm | |
| C5 | 1000 RPM | 20 mm/min | 1.9 mm |
| Element | Composition (%) |
|---|---|
| Copper | 57.5–59.5 |
| Iron | 0.5 |
| Nickel | 0.5 |
| Plumbum | 2.0–3.0 |
| Zinc | balance |
| Spindle speed (RPM) | 1000 |
| Feed rate (mm/min) | 20 |
| Depth of cut (μm) | 20 |
| Tool nose radius (mm) | 1.028 |
| Tool rake angle (°) | 0 |
| Parameters | Real (Center) | Real (0.3 mm Away) | Simulated |
|---|---|---|---|
| Sa (nm) | 49.45 | 39.06 | 12.90 |
| PV (nm) | 18127.53 | 194.23 | 50.00 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Guo, N.; Chen, Y.; Fu, Y.; Zhao, Q. Simulation and Experimental Study on the Surface Generation Mechanism of Cu Alloys in Ultra-Precision Diamond Turning. Micromachines 2019, 10, 573. https://doi.org/10.3390/mi10090573
Zhang Q, Guo N, Chen Y, Fu Y, Zhao Q. Simulation and Experimental Study on the Surface Generation Mechanism of Cu Alloys in Ultra-Precision Diamond Turning. Micromachines. 2019; 10(9):573. https://doi.org/10.3390/mi10090573
Chicago/Turabian StyleZhang, Quanli, Nan Guo, Yan Chen, Yucan Fu, and Qingliang Zhao. 2019. "Simulation and Experimental Study on the Surface Generation Mechanism of Cu Alloys in Ultra-Precision Diamond Turning" Micromachines 10, no. 9: 573. https://doi.org/10.3390/mi10090573
APA StyleZhang, Q., Guo, N., Chen, Y., Fu, Y., & Zhao, Q. (2019). Simulation and Experimental Study on the Surface Generation Mechanism of Cu Alloys in Ultra-Precision Diamond Turning. Micromachines, 10(9), 573. https://doi.org/10.3390/mi10090573





