Automatic Sorting System for Rigid Piezoelectric Transducer Wafers Used in Displacement Adjustment
Abstract
:1. Introduction
2. Structural Systematic Design
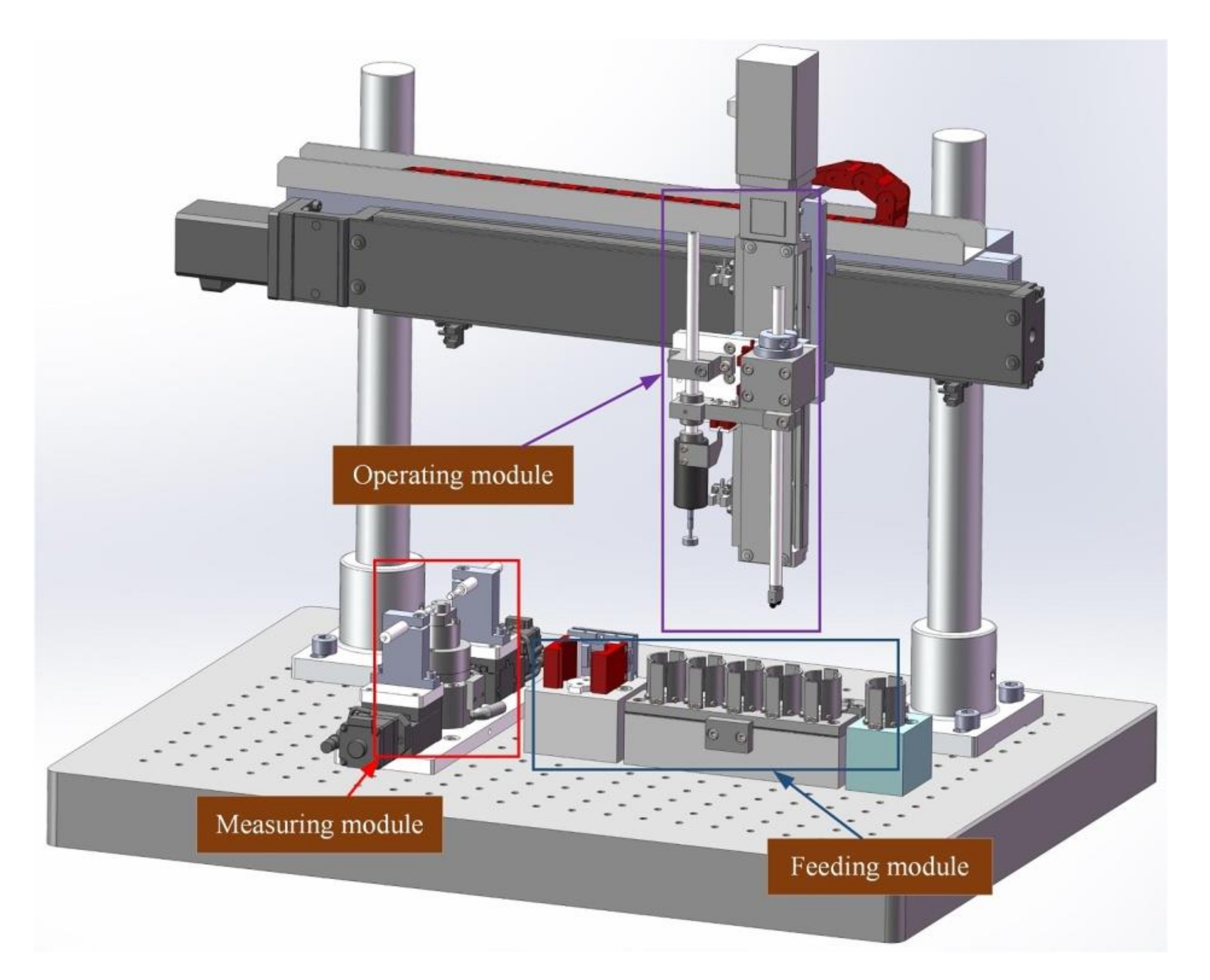
2.1. Overall Design
- Pick up the wafer to be tested from a feeding platform.
- Transfer the wafer and place it on a measurement platform.
- Apply the excitation voltage and then measure the corresponding deformation.
- Unload the excitation voltage and remove the wafer to a certain recovering platform, according to the measurement results.
2.2. Functional Modules
2.2.1. Feeding Module
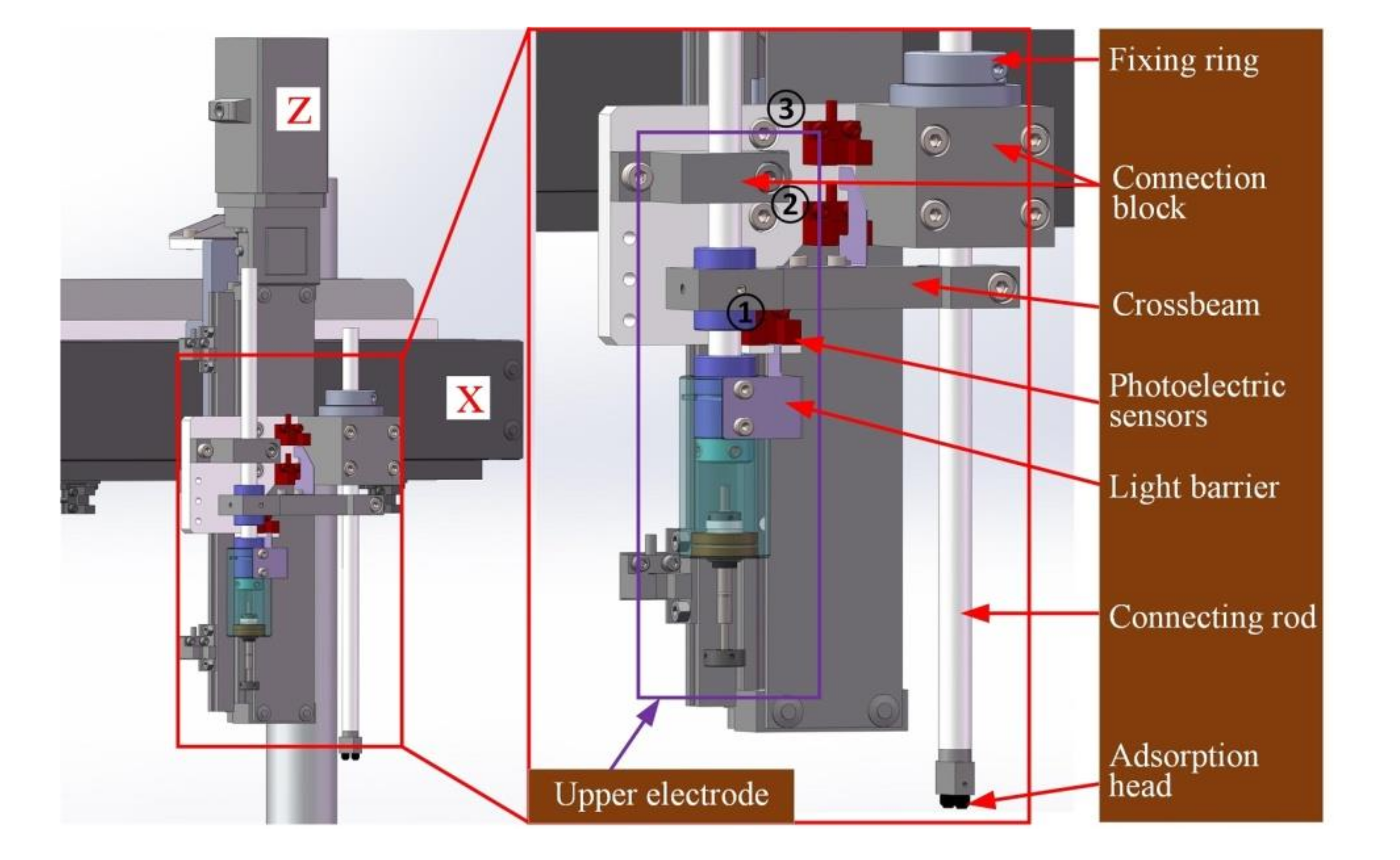
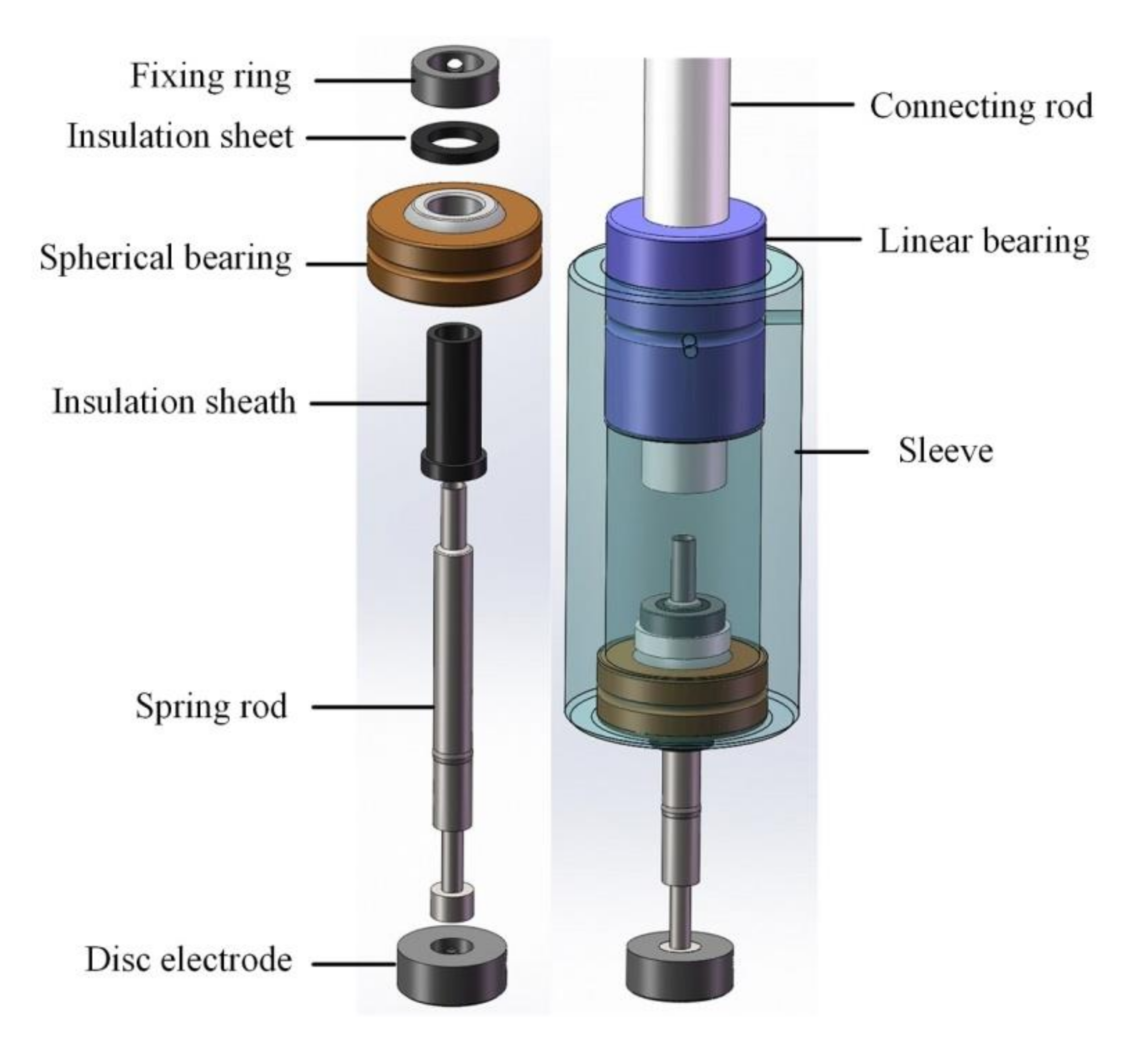
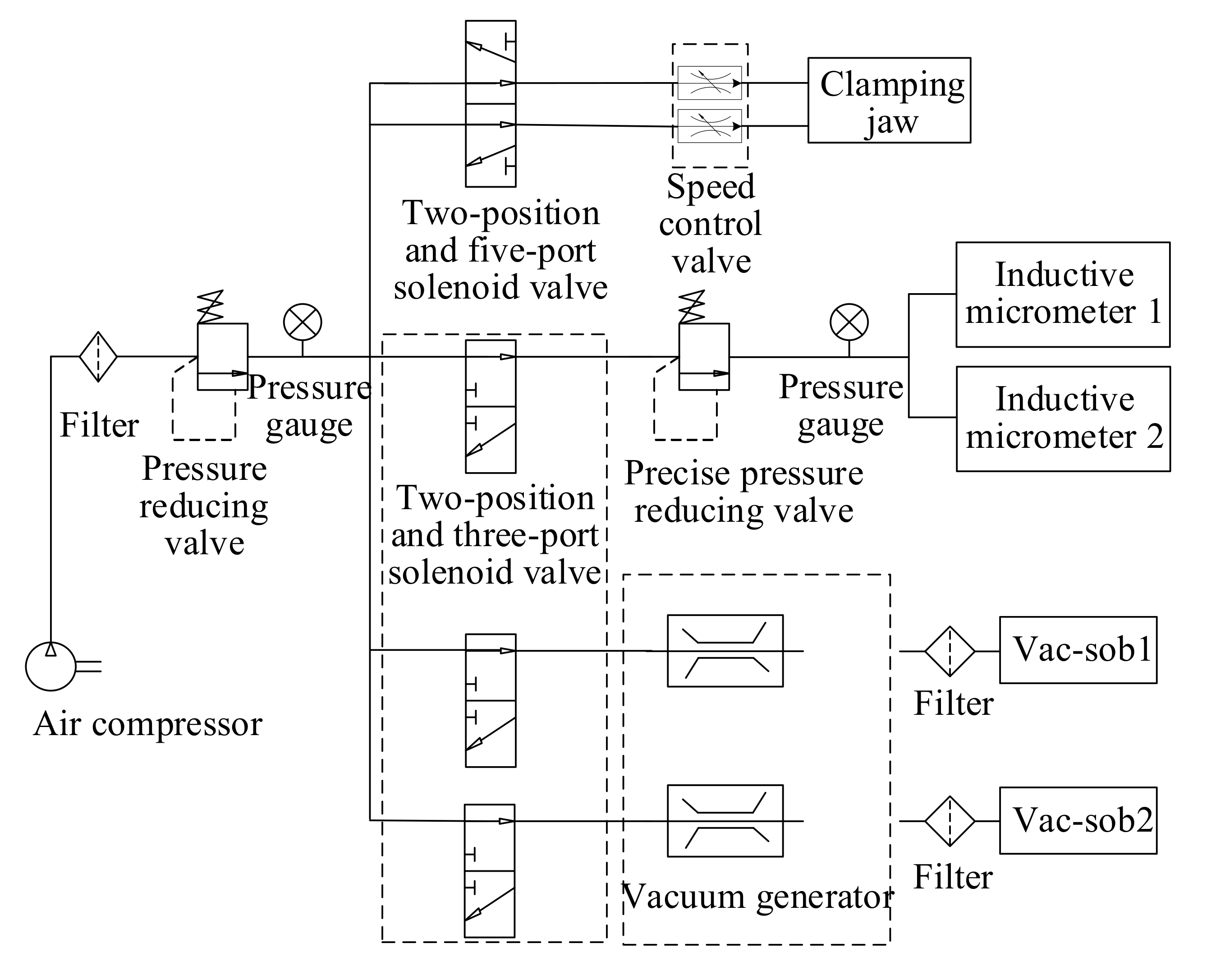
2.2.2. Operating Module
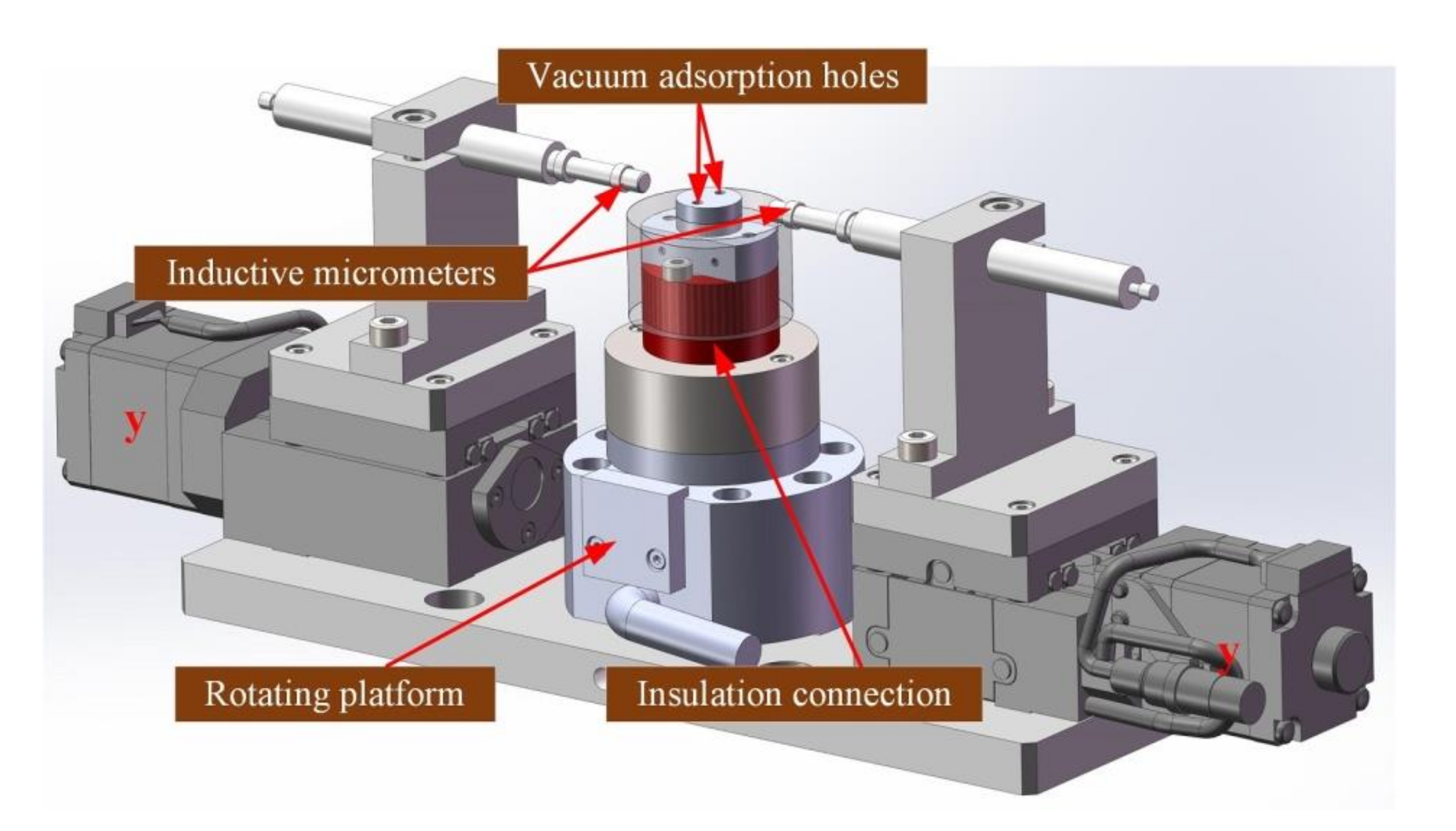
2.2.3. Measuring Module
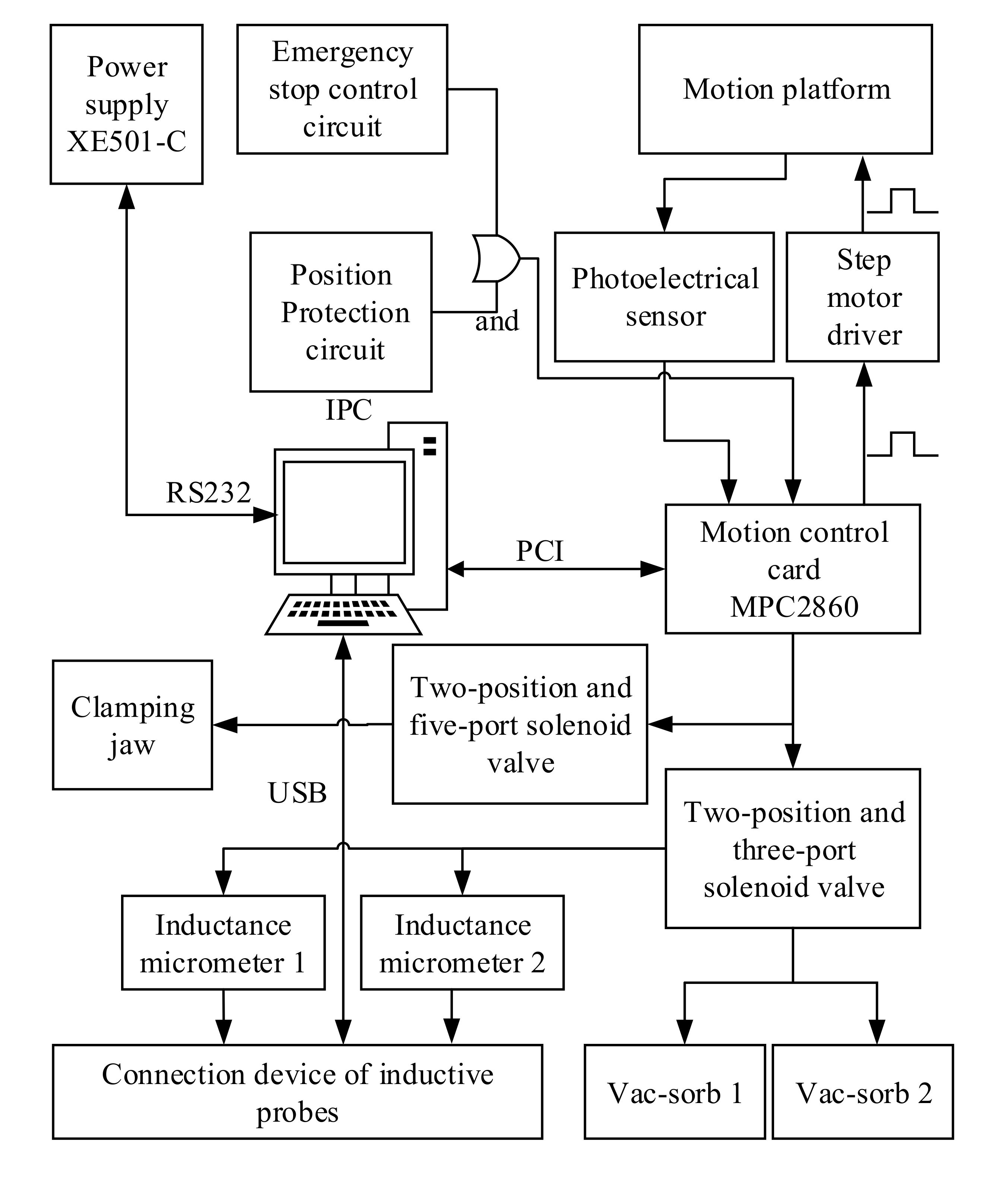
2.2.4. Control System
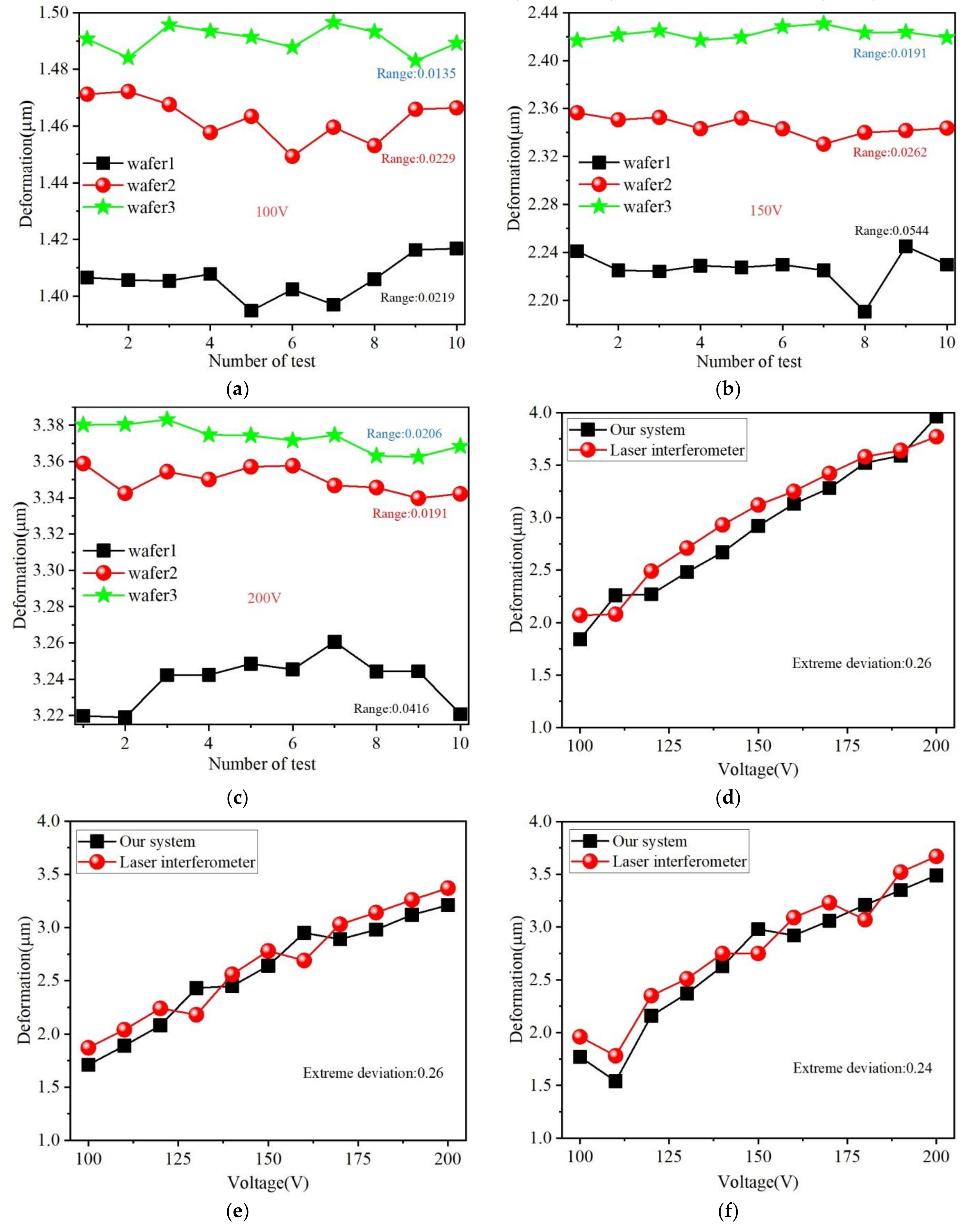
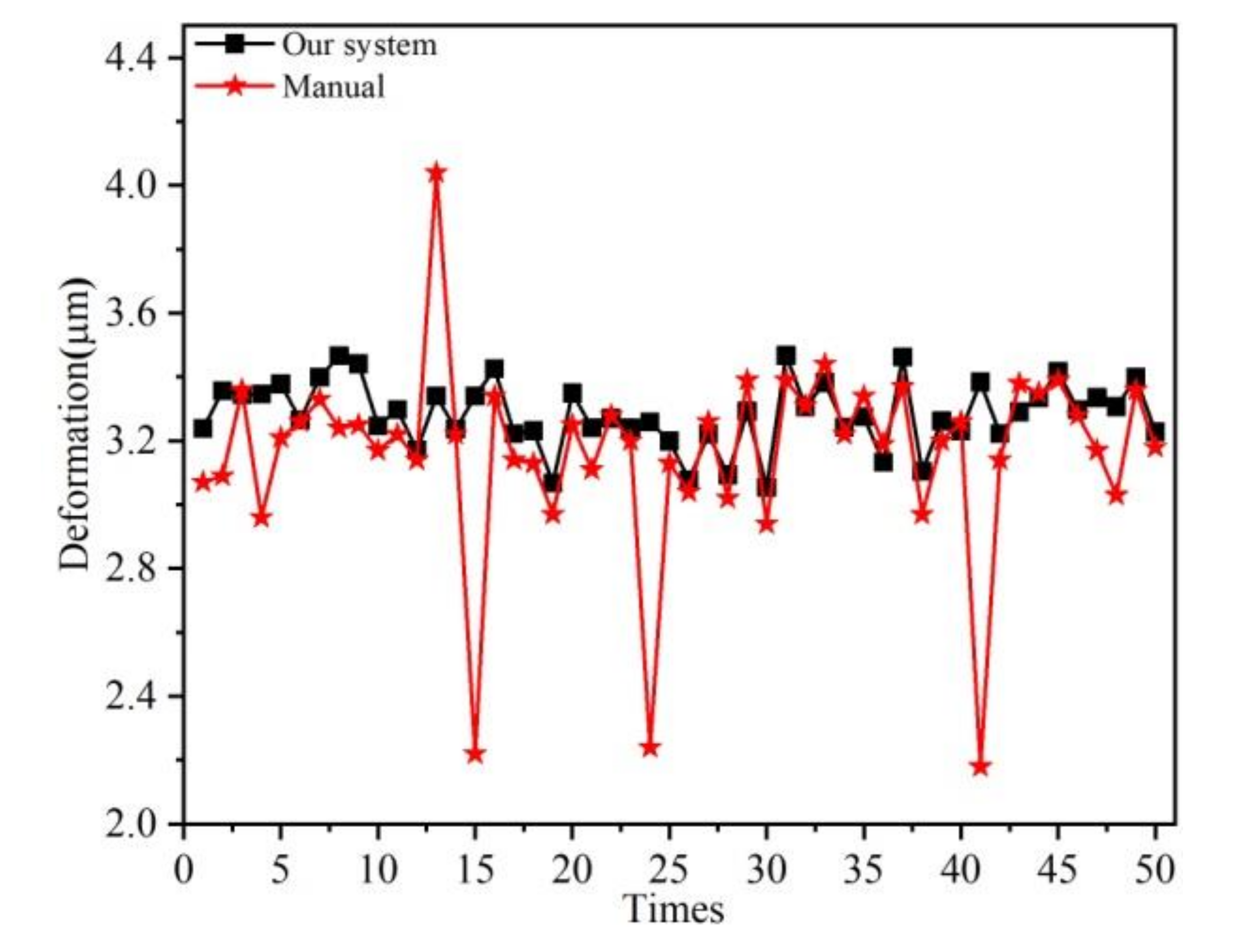
3. Experiments and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Passaro Vittorio, M.N.; Cuccovillo, A.; Vaiani, L.; De Carlo, M.; Campanella, C.E. Gyroscope technology and applications: A review in the industrial perspective. Sensors 2017, 17, 2284. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schwartz, S.; Gutty, F.; Feugnet, G.; Pocholle, J.P.; Desilles, G. Solid-state ring laser gyro for aerospace applications. In Proceedings of the SPIE-International Society for Optical Engineering, Ajaccio, Corsica, France, 9–12 October 2017. [Google Scholar]
- Hinüber Edgar, L.V.; Reimer, C.; Schneider, T.; Stock, M. INS/GNSS integration for aerobatic flight applications and aircraft motion surveying. Sensors 2017, 17, 941. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kuznetsov, A.G.; Molchanov, A.V.; Chirkin, M.V.; Izmailov, E.A. Precise laser gyroscope for autonomous inertial navigation. Quantum. Electron. 2015, 45, 78–88. [Google Scholar] [CrossRef]
- Ding, J.C.; Zhang, J.; Huang, W.Q.; Chen, S. Laser gyro temperature compensation using modified RBFNN. Sensors 2014, 14, 18711–18727. [Google Scholar] [CrossRef] [PubMed]
- Wei, G.; Li, G.; Wu, Y.; Long, X.W. Application of least squares-support vector machine in system-level temperature compensation of ring laser gyroscope. Measurement 2011, 44, 1898–1903. [Google Scholar] [CrossRef]
- Wang, L.; Wu, W.; Pan, X. Dynamic error compensation and parameter optimization for RLG SINS in vibration environments. In Proceedings of the 2017 24th Saint Petersburg International Conference on Integrated Navigation Systems, Saint Petersburg, Russia, 29–31 May 2017. [Google Scholar]
- Yin, S.H.; Liu, W.Y.; Pan, Z.W.; Tao, Y.; Zhu, J.B.; Tang, J.; Liu, J. Laser frequency combination tuning and locking technology in resonant optical gyro. Appl. Phys. B 2020, 126, 1–7. [Google Scholar] [CrossRef]
- Zapotyl’ko, N.R.; Katkov, A.A.; Nedzvetskaya, A.A. Piezo adjuster for compensating the thermal variations of the optical path length of the cavity of a laser gyroscope. J. Opt. Technol. 2011, 78, 644–645. [Google Scholar] [CrossRef]
- Belfi, J.; Di Virgilio, A.; Beverini, N.; Carelli, G.; Maccioni, E.; Simonelli, A.; Santagata, R. Geometrical scale-factor stabilization of square cavity ring laser gyroscopes. In Proceedings of the 2015 Joint Conference of the IEEE International Frequency Control Symposium and the European Frequency and Time Forum, Denver, CO, USA, 12–16 April 2015. [Google Scholar]
- Su, S.Q.; Li, J.M. Steady frequency control technology of mechanically dithered ring laser gyroscope. Nanotechnol. Precis. Eng. 2013, 11, 551–556. [Google Scholar]
- Zhang, C.F.; Liu, W.Y.; Zheng, Y.Q.; An, P.L.; Tang, J.; Liu, J. Resolution improvement for digital closed loop resonator micro-optic gyro based on tunable resonator. Opt. Eng. 2018, 57, 097102. [Google Scholar] [CrossRef]
- Wu, F.; Zhang, M.H.; Fu, X.; Guo, X.; Wang, J.L.; Wang, J.X. Design of AC laser frequency stabilization system for space three-axis mechanical dithering laser gyro. J. Chin. Inert. Technol. 2017, 25, 265–268. (In Chinese) [Google Scholar]
- Sivaramakrishnan, S.; Mardilovich, P.; Schmitz-Kempen, T.; Tiedke, S. Concurrent wafer-level measurement of longitudinal and transverse effective piezoelectric coefficients (d33,f and e31,f) by double beam laser interferometry. J. Appl. Phys. 2018, 123, 014103. [Google Scholar] [CrossRef]
- Wu, H.; He, L.B.; Zhou, J.L.; Yang, P. The displacement characteristics of piezoelectric ceramic micro actuators evaluated by laser interferometer. Key Eng. Mat. 2015, 645–646, 920–925. [Google Scholar] [CrossRef]
- Wang, Z.H.; Zhu, W.G.; Miao, J.M.; Chao, C.; Tan, O.K. Measurement of longitudinal piezoelectric coefficient of film with scanning-modulated interferometer. Sens. Actuator A Phys. 2006, 128, 327–332. [Google Scholar] [CrossRef]
- Gu, G.Q.; Xu, G.Z.; Xu, B. Synchronous measurement of out-of-plane displacement and slopes by triple-optical-path digital speckle pattern interferometry. Metrol. Meas. Sys. 2018, 1, 3–14. [Google Scholar]
- Sapuppo, F.; Llobera, A.; Schembri, F.; Intaglietta, M.; Cadarso, V.J.; Bucolo, M. A polymeric micro-optical interface for flow monitoring in biomicrofluidics. Biomicrofluidics 2010, 2, 014002BMF. [Google Scholar]
- Gagliano, S.; Stella, G.; Bucolo, M. Real-time detection of slug velocity inmicrochannels. Micromachines 2020, 3, 241. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Malakooti Mohammad, H.; Sodano Henry, A. Noncontact and simultaneous measurement of the d33 and d31 piezoelectric strain coefficients. Appl. Phys. Lett. 2013, 102, 061901. [Google Scholar] [CrossRef]
- Steinhausen, R.; Kerna, S.; Pientschke, C.; Beige, H.; Clemens, F.; Heiber, J. A new measurement method of piezoelectric properties of single ceramic fibres. J. Eur. Ceram. Soc. 2010, 30, 206–209. [Google Scholar] [CrossRef]
- Pientschke, C.; Steinhausen, R.; Kern, S.; Beige, H. Modelling of the measured longitudinal piezoelectric coefficient of single ceramic fibres with annular electrodes. Smart Mater. Struct. 2011, 20, 055015. [Google Scholar] [CrossRef]
- Al Ahmad, M.; Plana, R. Piezoelectric coefficients of thin film aluminum nitride characterizations using capacitance measurements. IEEE Microwave Compon. Lett. 2009, 19, 140–142. [Google Scholar] [CrossRef]
- Ballas, R.G.; Schoen, D. A non-contact inductive sensor for high-Accuracy tip deflection measurements of piezoceramic bending actuators. In Proceedings of the 2017 International Conference on Research and Education in Mechatronics, Wolfenbuettel, Germany, 14–15 September 2017. [Google Scholar]
- Smitha, W.F.; Axelrod, B.W. Measurements of the double piezoelectric effect. Rev. Sci. Instrum. 2000, 71, 1772–1775. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Y.H.; Fu, Y.X.; Tang, D.M.; Zhu, Y.Q. Standard measuring device for thickness of silicon wafer based on laser compensation system. In Proceedings of the 2017 4th International Conference on Systems and Informatics, Hangzhou, China, 11–13 November 2017. [Google Scholar]
- Ren, T.Q.; Liu, Z.R.; Wang, X.D.; Liu, Y. Clearance measurement equipment for gas lubricated dynamic pressure bearing of gyro motor. Int. J. Precis. Eng. Manuf. 2019, 20, 2051–2060. [Google Scholar] [CrossRef]
- An, D.; Li, H.D.; Xu, Y.; Zhang, L.X. Compensation of hysteresis on piezoelectric actuators based on tripartite PI model. Micromachines 2018, 2, 44. [Google Scholar] [CrossRef] [Green Version]
- Fan, W. Research on the Drive System and Control Method for Nano-Table with Six Degrees of Freedom. Ph.D. Thesis, Hefei University of Technology, Hefei, China, 2009. [Google Scholar]
- Zhang, L.S.; Huang, J.C.; Tang, Y.; Li, R.J.; Huang, Q.X.; Cheng, R.J.; Wang, C.Q. Independent driving method for significant hysteresis reduction of piezoelectric stack actuators. Rev. Sci. Instrum. 2019, 11, 115006. [Google Scholar] [CrossRef] [PubMed]





| Measurement Range | Maximum Permissible Errors | Hysteresis Error | Repeatability | Measuring Force (Typical Value) |
|---|---|---|---|---|
| ±1.5 mm | 0.2 + 2.4 L2 μm | 0.25 μm | 0.015 μm | 0.2 N |
| Basic Output Characteristics | Style |
|---|---|
| Output voltage V (0~Uo) | 300 |
| Average power W/channel | 35 ± 20% |
| Peak power W/channel | 100 ± 20% |
| Average current W/channel | 110 ± 20% |
| Peak current W/channel | 330 ± 20% |
| No-load full bandwidth KHz | 10 ± 20% |
| Voltage stability | <0.1%F.S./8 h |
| Output ripple mV | 5 ± 20% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, T.; Li, X.; Wang, X.; Xu, Z.; Liu, Y.; Yang, J.; Guo, J. Automatic Sorting System for Rigid Piezoelectric Transducer Wafers Used in Displacement Adjustment. Micromachines 2020, 11, 915. https://doi.org/10.3390/mi11100915
Ren T, Li X, Wang X, Xu Z, Liu Y, Yang J, Guo J. Automatic Sorting System for Rigid Piezoelectric Transducer Wafers Used in Displacement Adjustment. Micromachines. 2020; 11(10):915. https://doi.org/10.3390/mi11100915
Chicago/Turabian StyleRen, Tongqun, Xin Li, Xiaodong Wang, Zheng Xu, Yugang Liu, Jin Yang, and Jiang Guo. 2020. "Automatic Sorting System for Rigid Piezoelectric Transducer Wafers Used in Displacement Adjustment" Micromachines 11, no. 10: 915. https://doi.org/10.3390/mi11100915
APA StyleRen, T., Li, X., Wang, X., Xu, Z., Liu, Y., Yang, J., & Guo, J. (2020). Automatic Sorting System for Rigid Piezoelectric Transducer Wafers Used in Displacement Adjustment. Micromachines, 11(10), 915. https://doi.org/10.3390/mi11100915






