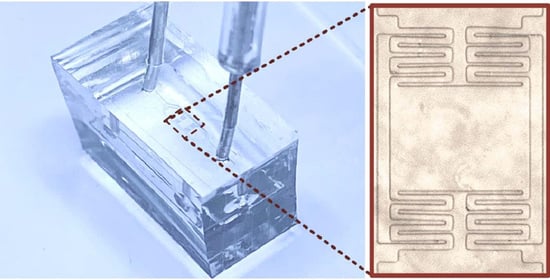
Microfluidic Viscometer Using a Suspending Micromembrane for Measurement of Biosamples
Abstract
:1. Introduction
2. Materials and Methods
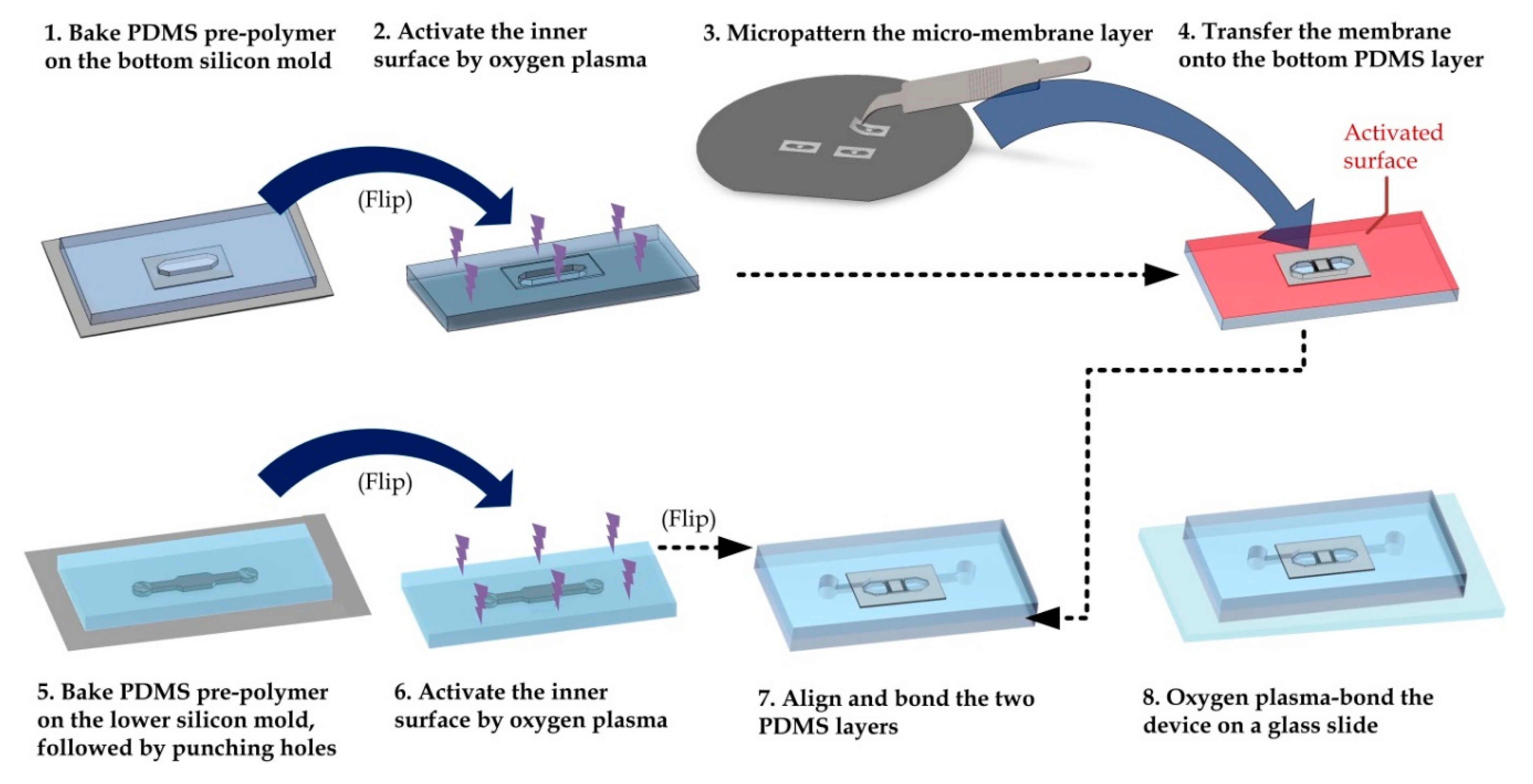
2.1. Device Fabrication and Preparation
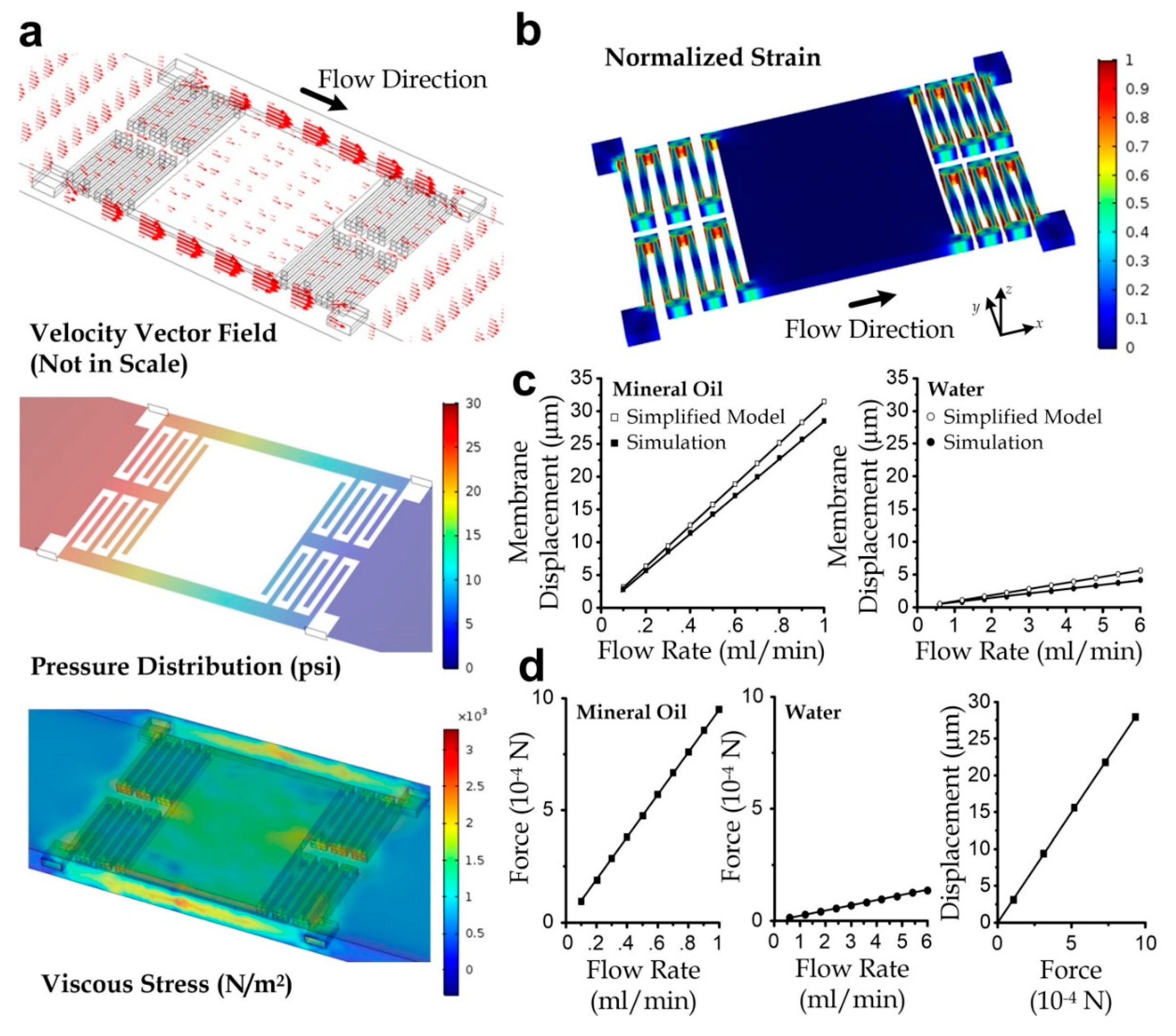
2.2. Simulation
2.3. Image Capture and Processing
2.4. Blood Sample Preparation
2.5. Statistics
3. Results and Discussion
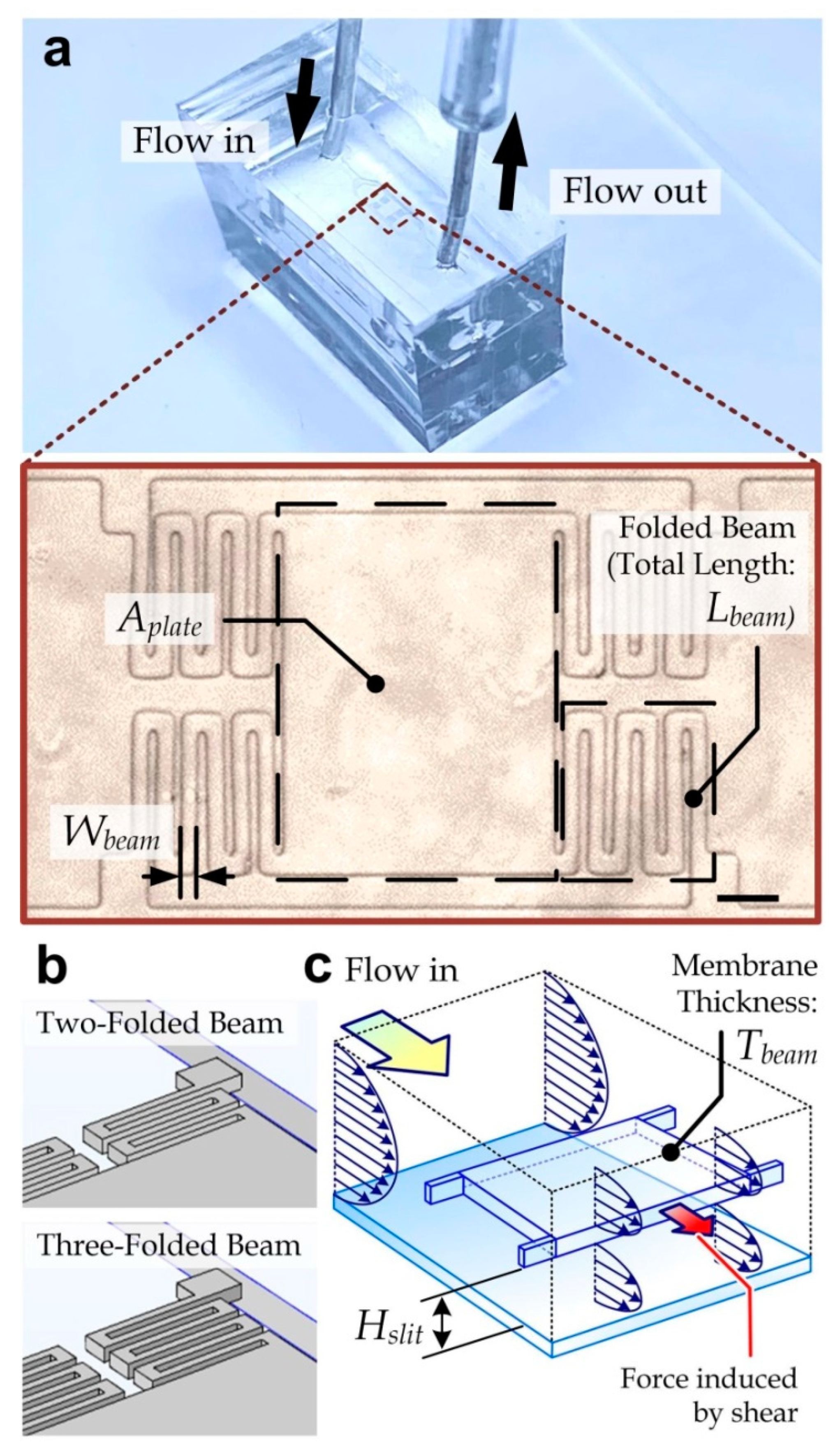
3.1. Device Design
3.2. Simulation Analysis
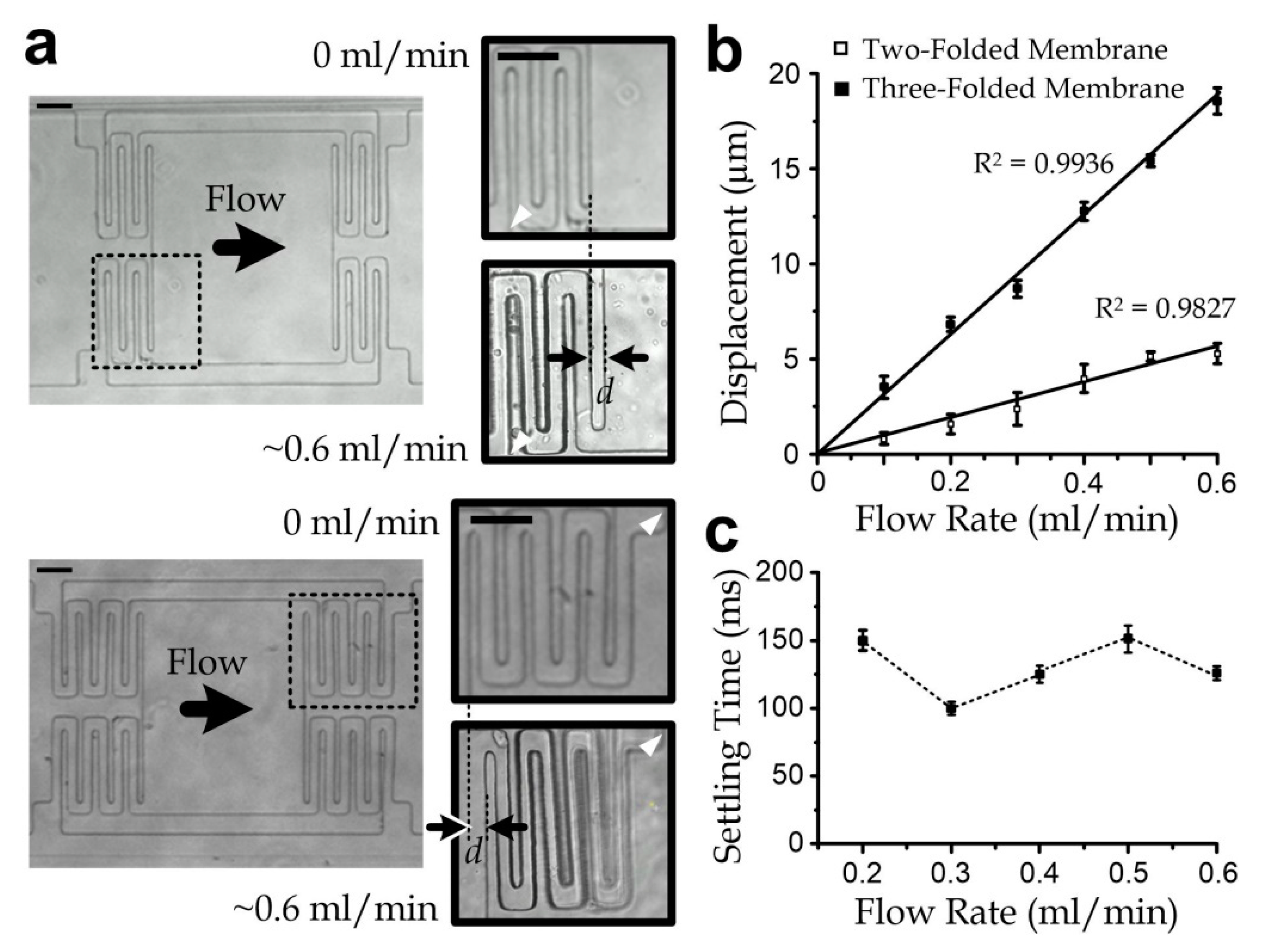
3.3. Sensor Characterization
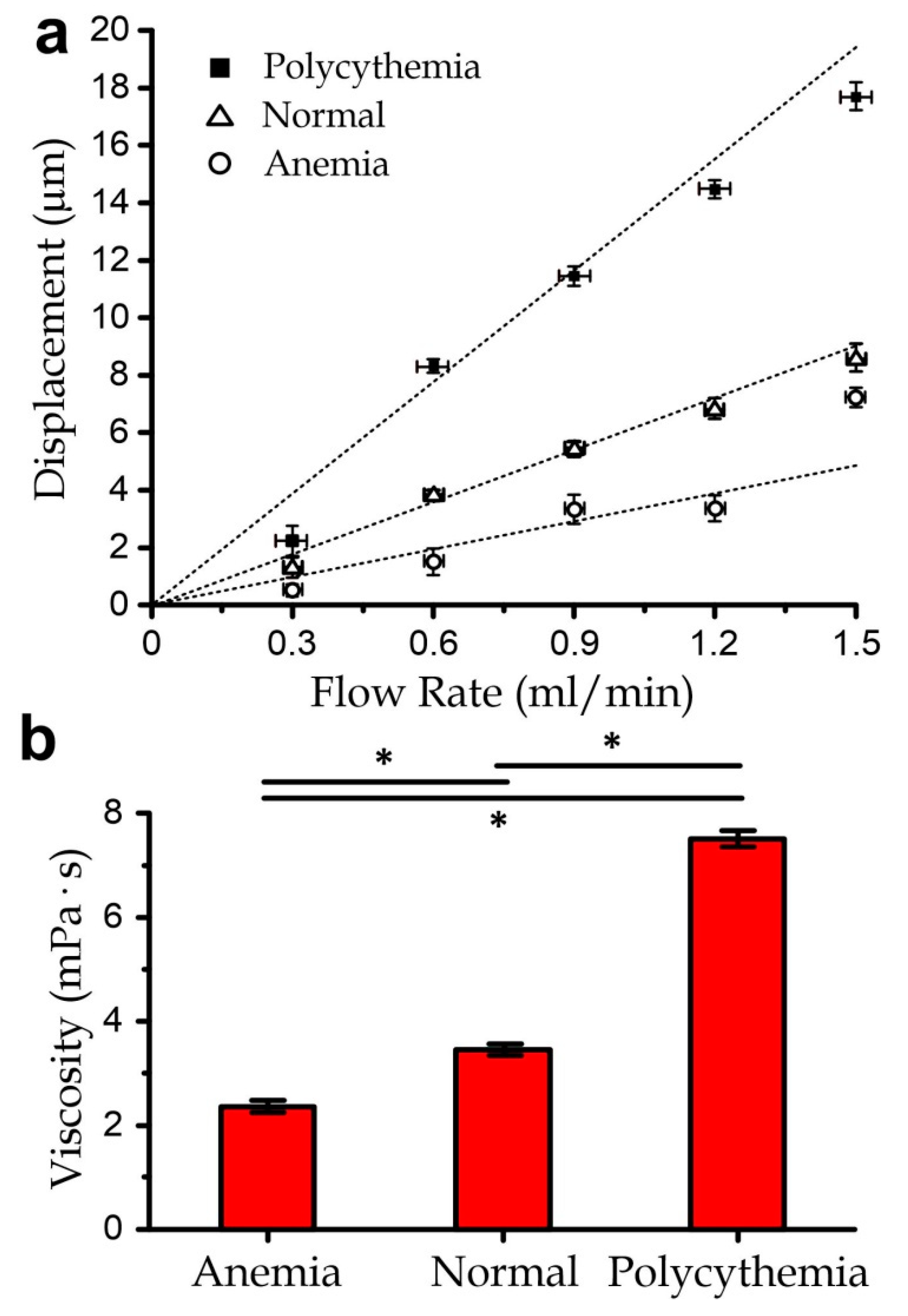
3.4. Measurement of Blood Samples with Varied Viscosity
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A

References
- Wand, A.J.; Ehrhardt, M.R.; Flynn, P.F. High-resolution NMR of encapsulated proteins dissolved in low-viscosity fluids. Proc. Natl. Acad. Sci. USA 1998, 95, 15299–15302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gyawali, P.; Richards, R.S.; Nwose, E.U.; Bwititi, P.T. Whole-blood viscosity and metabolic syndrome. Clin. Lipidol. 2012, 7, 709–719. [Google Scholar] [CrossRef]
- Pries, A.R.; Neuhaus, D.; Gaehtgens, P. Blood viscosity in tube flow: Dependence on diameter and hematocrit. Am. J. Physiol. Heart Circ. Physiol. 1992, 263, H1770–H1778. [Google Scholar] [CrossRef] [PubMed]
- Gong, D.; Turner, B.; Bhaskar, K.; Lamont, J. Lipid binding to gastric mucin: Protective effect against oxygen radicals. Am. J. Physiol. Gastrointest. Liver Physiol. 1990, 259, G681–G686. [Google Scholar] [CrossRef] [PubMed]
- Stokes, J.R.; Davies, G.A. Viscoelasticity of human whole saliva collected after acid and mechanical stimulation. Biorheology 2007, 44, 141–160. [Google Scholar]
- Yabuno, H.; Higashino, K.; Kuroda, M.; Yamamoto, Y. Self-excited vibrational viscometer for high-viscosity sensing. J. Appl. Phys. 2014, 116, 124305. [Google Scholar] [CrossRef] [Green Version]
- Qi, Q.; Li, Y.; You, Y.; Liao, F. The criteria for evaluating shear stress measuring range and the lowest measurable shear stress of rotational viscometer. Clin. Hemorheol. Microcirc. 2009, 42, 71–73. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grupi, A.; Minton, A.P. Capillary viscometer for fully automated measurement of the concentration and shear dependence of the viscosity of macromolecular solutions. Anal. Chem. 2012, 84, 10732–10736. [Google Scholar] [CrossRef] [Green Version]
- Tzeng, B.B.; Sun, Y.S. Design and fabrication of a microfluidic viscometer based on electrofluidic circuits. Micromachines 2018, 9, 375. [Google Scholar] [CrossRef] [Green Version]
- Dietrich, T.; Freitag, A.; Schlecht, U. New micro viscosity sensor—A novel analytical tool for online monitoring of polymerization reactions in a micro reaction plant. Chem. Eng. J. 2010, 160, 823–826. [Google Scholar] [CrossRef]
- Wu, S.; Lin, Q.; Yuen, Y.; Tai, Y.-C. MEMS flow sensors for nano-fluidic applications. Sens. Actuators A Phys. 2001, 89, 152–158. [Google Scholar] [CrossRef] [Green Version]
- Yusop, R.M.; Unciti-Broceta, A.; Bradley, M. A highly sensitive fluorescent viscosity sensor. Bioorganic Med. Chem. Lett. 2012, 22, 5780–5783. [Google Scholar] [CrossRef]
- Yu, H.; Lou, L.; Gu, Y.A. Capacitive micromachined ultrasonic transducer (CMUT) based micro viscosity sensor. Sens. Actuators B Chem. 2016, 227, 346–351. [Google Scholar] [CrossRef]
- Fedorchenko, A.I.; Stachiv, I.; Wang, W.-C. Method of the viscosity measurement by means of the vibrating micro-/nano-mechanical resonators. Flow Meas. Instrum. 2013, 32, 84. [Google Scholar] [CrossRef]
- Andreas, K. Polyimide membrane with ZnO piezoelectric thin film pressure transducers as a differential pressure liquid flow sensor. J. Micromech. Microeng. 2003, 13, S103–S107. [Google Scholar] [CrossRef]
- Czaplewski, D.A.; Ilic, B.R.; Zalalutdinov, M.; Olbricht, W.L.; Zehnder, A.T.; Craighead, H.G.; Michalske, T.A. A micromechanical flow sensor for microfluidic applications. J. Microelectromech. Syst. 2004, 13, 576–585. [Google Scholar] [CrossRef]
- Xia, Y.; Whitesides, G.M. Soft lithography. Annu. Rev. Mater. Sci. 1998, 28, 153–184. [Google Scholar] [CrossRef]
- Chen, W.; Lam, R.H.W.; Fu, J. Photolithographic surface micromachining of polydimethylsiloxane (PDMS). Lab Chip 2011, 12, 391–395. [Google Scholar] [CrossRef] [Green Version]
- Unger, M.A.; Chou, H.P.; Thorsen, T.; Scherer, A.; Quake, S.R. Monolithic microfabricated valves and pumps by multilayer soft lithography. Science 2000, 288, 113. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.E.Y.; Seshia, A.A. Parasitic feedthrough cancellation techniques for enhanced electrical characterization of electrostatic microresonators. Sens. Actuators A Phys. 2009, 156, 36–42. [Google Scholar] [CrossRef]
- Lee, J.E.Y.; Zhu, Y.; Seshia, A.A. A bulk acoustic mode single-crystal silicon microresonator with a high-quality factor. J. Micromech. Microeng. 2008, 18, 064001. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.; Chou, T.-C.; Kang, D.; Kang, H.; Chen, J.; Baek, K.I.; Wang, W.; Ding, Y.; Carlo, D.D.; Tai, Y.-C.; et al. A rapid capillary-pressure driven micro-channel to demonstrate Newtonian fluid behavior of zebrafish blood at high shear rates. Sci. Rep. 2017, 7, 1980. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fedosov, D.A.; Pan, W.; Caswell, B.; Gompper, G.; Karniadakis, G.E. Predicting human blood viscosity in silico. Proc. Natl. Acad. Sci. USA 2011, 108, 11772–11777. [Google Scholar] [CrossRef] [Green Version]
- Litwin, M.S.; Chapman, K. Physical factors affecting human blood viscosity. J. Surg. Res. 1970, 10, 433–436. [Google Scholar] [CrossRef]
- Cui, X.; Liu, Y.; Hu, D.; Qian, W.; Tin, C.; Sun, D.; Chen, W.; Lam, R.H.W. A fluorescent microbead-based microfluidic immunoassay chip for immune cell cytokine secretion quantification. Lab Chip 2018, 18, 522–531. [Google Scholar] [CrossRef] [PubMed]
- Huang, N.T.; Chen, W.; Oh, B.R.; Cornell, T.T.; Shanley, T.P.; Fu, J.; Kurabayashi, K. An integrated microfluidic platform for in situ cellular cytokine secretion immunophenotyping. Lab Chip 2012, 12, 4093–4101. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Liu, Y.; Ren, J.; Tay, B.Z.; Luo, T.; Fan, L.; Sun, D.; Luo, G.; Lau, D.; Lam, R.H. Antibody-coated microstructures for selective isolation of immune cells in blood. Lab Chip 2020, 20, 1072–1082. [Google Scholar] [CrossRef]
- Li, X.; Chen, W.; Liu, G.; Lu, W.; Fu, J. Continuous-flow microfluidic blood cell sorting for unprocessed whole blood using surface-micromachined microfiltration membranes. Lab Chip 2014, 14, 2565–2575. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Su, J.; Li, J.; Peng, F.; Wu, H.; Ye, D.; Chen, H. A microfluidic platform for osmotic fragility test of red blood cells. Rsc Adv. 2012, 2, 7161–7165. [Google Scholar] [CrossRef]
- Cluitmans, J.C.; Chokkalingam, V.; Janssen, A.M.; Brock, R.; Huck, W.T.; Bosman, G.J. Alterations in red blood cell deformability during storage: A microfluidic approach. BioMed Res. Int. 2014, 2014, 764268. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Hu, D.; Lam, R.H.W. Microfluidic Viscometer Using a Suspending Micromembrane for Measurement of Biosamples. Micromachines 2020, 11, 934. https://doi.org/10.3390/mi11100934
Liu L, Hu D, Lam RHW. Microfluidic Viscometer Using a Suspending Micromembrane for Measurement of Biosamples. Micromachines. 2020; 11(10):934. https://doi.org/10.3390/mi11100934
Chicago/Turabian StyleLiu, Lelin, Dinglong Hu, and Raymond H. W. Lam. 2020. "Microfluidic Viscometer Using a Suspending Micromembrane for Measurement of Biosamples" Micromachines 11, no. 10: 934. https://doi.org/10.3390/mi11100934
APA StyleLiu, L., Hu, D., & Lam, R. H. W. (2020). Microfluidic Viscometer Using a Suspending Micromembrane for Measurement of Biosamples. Micromachines, 11(10), 934. https://doi.org/10.3390/mi11100934